Pulse-like and crack-like ruptures in experiments mimicking crustal earthquakes

Abstract

Theoretical studies have shown that the issue of rupture modes has important implications for fault constitutive laws, stress conditions on faults, energy partition and heat generation during earthquakes, scaling laws, and spatiotemporal complexity of fault slip. Early theoretical models treated earthquakes as crack-like ruptures, but seismic inversions indicate that earthquake ruptures may propagate in a self-healing pulse-like mode. A number of explanations for the existence of slip pulses have been proposed and continue to be vigorously debated. This study presents experimental observations of spontaneous pulse-like ruptures in a homogeneous linear-elastic setting that mimics crustal earthquakes; reveals how different rupture modes are selected based on the level of fault prestress; demonstrates that both rupture modes can transition to supershear speeds; and advocates, based on comparison with theoretical studies, the importance of velocity-weakening friction for earthquake dynamics.

Destructive large earthquakes occur as dynamic frictional ruptures along preexisting interfaces (or faults) in the Earth's crust. Inversions of seismic and other field observations have significantly advanced our understanding of earthquake ruptures. At the same time, detailed inversions often are impossible due to limited data availability or limited knowledge of the structure and properties of the crust. Numerical modeling of earthquakes helps pinpoint potential rupture scenarios but, in turn, requires a number of still poorly known inputs that are being actively researched. Such inputs include fault friction laws and initial stress conditions.

This reality highlights the need for highly instrumented laboratory experiments that reproduce some of the basic physics governing rupture dynamics of crustal earthquakes while preserving enough simplicity so that clear conclusions can be obtained by direct observation. One example of such experiments is the work of Xia et al. (1, 2), which has demonstrated the ability of spontaneous dynamic ruptures to transition from sub-Rayleigh to supershear speeds. In the present study, we use their experimental configuration to investigate conditions leading to the selection of pulse-like vs. crack-like rupture modes in a setting that mimics crustal earthquakes. The geometry, loading, and nucleation mechanism are essentially 2D. This configuration is relevant for understanding the dynamics of large strike–slip earthquakes, which are dominated by in-plane sliding, and constitutes an experimental equivalent of 2D in-plane or Mode II numerical models of dynamic rupture, which are common in earthquake studies (3–12).

Numerical simulations in models that involve homogeneous elastic and interface properties and velocity-independent fault strength result in the crack-like mode of earthquake propagation, in which the duration of slip at each point on the fault is comparable to the overall rupture duration (3, 13–16). However, seismic inversions indicate (17) that ruptures on real faults may propagate in the pulse-like mode, in which slip duration at a point is much shorter than the overall rupture duration. Theoretical and numerical studies have shown that the issue of rupture modes may have important implications for fault constitutive laws, stress conditions on faults, energy partition and heat generation during earthquakes, scaling laws, and the spatiotemporal complexity of slip (5, 8, 12, 17–24). Pulse-like ruptures have been obtained in a number of numerical simulations that include significant weakening of interface friction with sliding velocity (5, 12, 18–22, 24). The simulations imply that fault friction may be characterized by significant velocity weakening, a conclusion further supported by a number of recent rock experiments and theoretical studies that have uncovered strongly velocity-weakening friction at seismic slip velocities (25–28). Other explanations for the occurrence of pulse-like ruptures include interaction of rupture with fault geometry or local heterogeneities (29–33) and normal stress variation due to differences in material properties across the interface (bimaterial effect) (6–8). Which mechanism dominates in real earthquakes remains an open research question.

In our experiments, there are no heterogeneities in interface properties or prestress and no bimaterial effect. Our goal is to determine whether pulse-like ruptures can occur in such a homogeneous configuration and, if so, what controls the selection of rupture modes. The only prior experimental study of different rupture modes under similarly homogeneous conditions was done with strong impact loading and interfaces with no shear prestress (34). However, those loading conditions are quite different from the ones on tectonically loaded faults in the Earth's crust. In the present study, we use an experimental configuration with an interface prestressed both in compression and in shear (1), simulating a tectonically loaded fault, and combine it with experimental diagnostics that let us conclusively determine the mode and speed of rupture propagation (34, 35). By systematically varying loading parameters, we observe pulse-like and crack-like ruptures, and systematic transition between them. Our results are consistent with the theoretical study of Zheng and Rice (21) who considered velocity-weakening interfaces and showed that selection of rupture modes depends on fault prestress and velocity-weakening properties of faults. We also present experimental observations of pulse-like ruptures transitioning to supershear speeds.

Experimental Design

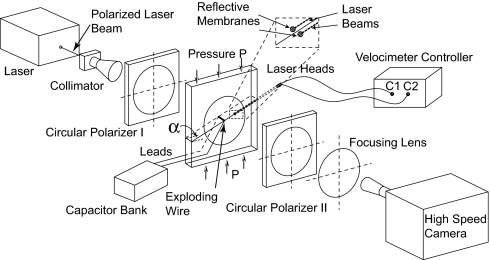
The Earth's crust was simulated by a square (150 × 150 mm) photoelastic plate with a thickness of 9.5 mm. The plate was cut into two identical quadrilaterals, introducing an interface inclined at an angle α to the horizontal (Fig. 1). Care was taken to polish and then roughen the surfaces of the cut for each sample so that all samples had the same, highly controlled, roughness and, hence, the same friction properties. Uniform pressure, denoted by P, was applied at the top and bottom ends of the plate, inducing shear traction τ₀ = Psinαcosα and normal traction σ₀ = Pcos²α on the interface. Hence, the interface simulates a tectonically loaded fault locked due to friction. Both the inclination angle α and far-field pressure P are system variables. The nondimensional parameter f₀ = τ₀/σ₀ = tanα characterizes shear prestress on the experimental fault. The inclination angle α was chosen so that the shear prestress remained below the static frictional resistance (static strength) of the fault and slip did not occur during the static preloading stage. Initiation of spontaneous dynamic rupture was achieved by means of local wire explosion acting in the middle of the plate interface across the entire plate thickness. Details of the initiation procedure are described in supporting information (SI) Experimental Design and Methods.

Fig. 1.

Specimen configuration and experimental setup. Far-field pressure P and the inclination angle α are system variables. Dynamic photoelasticity and high-speed photography were used along the optical axis. Two velocimeters measured fault-parallel particle velocity histories above and below the simulated fault. The capacitor bank and exploding wire configuration provided the rupture initiation mechanism and the synchronizing trigger.

As a laboratory earthquake grows bilaterally away from the hypocenter, high-speed photography in conjunction with dynamic photoelasticity (1, 34, 35) is used to obtain full field images of the distribution of maximum shear stress in the sample. Rupture behavior is studied only until the arrival of waves reflected from the boundaries; the useful time window of observation is typically of the order of 70 μs. A digital high-speed camera capable of producing 16 frames at a framing rate up to 10 million frames per second was used to record time series of photoelastic images. The interframe time in the experiments was 2–4 μs. A birefringent (photoelastic) polymer, Homalite-100, was chosen as the model material because its mechanical properties are well documented and it is known to behave purely elastically at strain rates higher than 10³ s⁻¹.

In addition to the full-field photographs, two high-speed laser, interferometry-based velocimeters (34, 36) were used to measure the time history of particle velocities at two points just above and below the interface and, hence, to infer sliding velocity at a location along the interface. Two separate laser beams were directed at the same inclination angle α as that of the interface (Fig. 1) to measure two in-plane velocity histories along that direction. The laser beams were focused at two 66-μm spots, each located at a distance of ≈250 μm from the interface. The velocimeters used feature a maximum recording frequency of 1.5 MHz and allow for particle speeds of up to 10 m/s to be accurately measured. The difference between the two particle velocity histories represents the sliding (or slip) velocity of the interface plus a small addition due to elastodynamic deformation between the two measurement points. In interpreting the measurements, we took into account the elastodynamic deformation, as discussed in Three Representative Rupture Modes and SI Experimental Design and Methods.

The geometrical simplicity of the configuration together with the simultaneous use of two types of diagnostic techniques capable of providing independent but synchronized measurements of high temporal and spatial resolution allow for the conclusive identification of various types of sliding modes and their rupture speeds.

Three Representative Rupture Modes

We report results corresponding to a number of angles α ranging from 20° to 30°. Larger values of α result in higher prestress f₀ = τ₀/σ₀ = tanα and, hence, facilitate rupture growth. In this section, we discuss three representative cases, α = 20°, 25°, and 30°, each with the uniaxial compressive load P = 10 MPa. In the following sections, cases with P = 14 MPa are also presented.

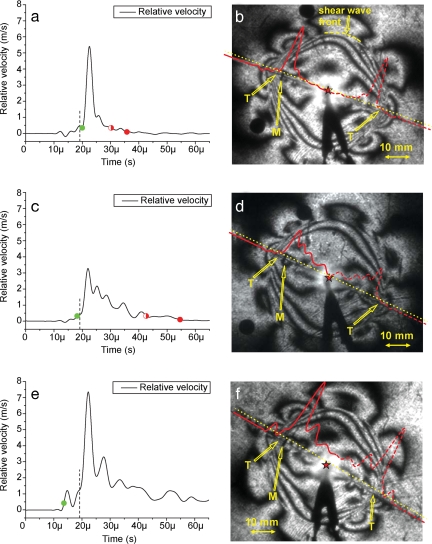
The first representative case is α = 20°. The isochromatic pattern shown in Fig. 2b provides a snapshot of the rupture process and the associated maximum shear stress field at t = 22 μs after nucleation. The simulated hypocenter (or the rupture initiation site) is marked by a star. The circular trace of the shear wave front (c_s = 1,249 m/s) emitted at the early stages of the nucleation process is visible in Fig. 2b; part of the front is marked with a dashed line. Two concentrations of fringes, located just behind two intersections of the shear wave front with the interface, correspond to two propagating rupture tips. These features are indicated by arrows and letters T in Fig. 2b and propagate with speeds close to the Rayleigh wave speed of Homalite-100 (c_R = 1,155 m/s).

Fig. 2.

Three representative rupture modes corresponding to different inclination angles. (a and b) A narrow sub-Rayleigh pulse for α = 20°. (c and d) A wider (e and f) A sub-Rayleigh pulse for α = 25°.(e and f) A sub-Rayleigh crack-like rupture for α = 30°. Compression load P is 10 MPa for all three cases. (Left) Relative velocity histories recorded at 20 mm distance from the hypocenter. The dashed lines indicate the time of the shear wave arrival. The green fully filled dots indicate the estimated initiation time of interface sliding. The red half-filled and fully filled dots indicate two estimates of interface locking time. Note that there are no estimates of locking time marked in panel e because the interface in that case experiences no locking at the measurement location within the window of observation. (Right) Contours of maximum shear stress captured at 22 μs after rupture initiation. Letters T indicate rupture tips. Letters M indicates the measurement location for the two velocimeters. The relative velocity record is superimposed on the photoelastic pattern to facilitate the analysis of rupture behavior. The yellow dotted lines indicate the value of the elastic cut-off velocity for each case.

The arrow originating at the letter M denotes the location of the two measurement sites of particle velocity histories, the subtraction of which is shown in Fig. 2a. These sites are located at a distance of 20 mm from the simulated hypocenter. The record of relative velocity shown in Fig. 2a reflects the sliding velocity of the interface plus the (relatively small) rate of elastodynamic deformation that exists between the two measurement sites. Given that the shear wave arrives at this location at 19.2 μs (the time is marked in Fig. 2a by a dashed line) and that the rupture seems to be sub-Rayleigh at that time, as indicated by photoelastic images, the interface rupture should arrive at the measurement location shortly after 19.2 μs. Hence, the slow buildup of relative velocity before that time is due to elastic deformation in response to shear stress increase ahead of the rupture front and not yet due to the onset of interfacial sliding.

We determine the rupture initiation time as the time at which the accumulated relative displacement between the measurement points becomes equal to the displacement δ_c needed to bring shear prestress τ₀ to static friction strength f_sσ₀:

where f_s = 0.6 is the static friction coefficient of the interface, μ = 1.4 GPa is the shear modulus of Homalite-100, and D = 500 μm is the approximate distance between the two measurement locations. We call the relative velocity at the time of rupture initiation “elastic cut-off velocity.” More details are given in SI Experimental Design and Methods. Note that normal stress on the interface is not altered by sliding in this experimental configuration in the time window of observation, before the reflected waves arrive from the plate boundaries, and the only changes in normal stress at the location of the measurement would come from the wave-mediated stress changes due to the rupture initiation procedure. Those normal stress variations at the location of particle velocity measurements at the time of rupture arrival should be small; Xia et al. (37) estimated them to be <0.35 MPa, whereas initial normal stresses range from 7.50 MPa to 12.36 MPa for experimental parameters used in this study. Hence, we can assume that normal stress σ is approximately equal to the initial normal stress σ₀.

The application of Eq. 1 to the case of Fig. 2a gives 20 μs as the time of sliding onset. This time coincides with a drastic increase of relative velocity, and it is corroborated by the synchronization of high-speed photography and velocimetry records discussed later. After the drastic increase of relative velocity, a peak of 5.4 m/s is reached. The peak is followed by rapid decrease in relative velocity and eventual locking of the interface. The resulting shape is clearly a well formed sliding pulse. Two different criteria for interface locking, described in SI Experimental Design and Methods, estimate the time of interface locking as either 30.2 or 35.8 μs. Hence, the duration of this pulse is determined to be between 10.2 and 15.8 μs.

To further analyze the rupture mode, the relative velocity record was superimposed on the photoelastic fringe map (Fig. 2b). This superposition, done for visualization purposes, clarifies the nature of various fringe structures in the vicinity of the interface and provides a clear view of the pulse width relative to the total length traveled by each rupture front since the time of nucleation. Converting the time history of the sliding speed into spatial variation along the fault is based on the assumption of a constant rupture speed. The full high-speed photography record clearly shows that, in this case, the two rupture fronts propagate with a constant speed that is very close to the Rayleigh wave speed of Homalite. Because rupture is equibilateral, a mirrored profile (with respect to the nucleation site) was added for visualization purposes. The length of the pulse in this case is 11.78–18.25 mm, whereas the length traveled by each rupture front is 22.31 mm.

In the second representative case, the inclination angle α is increased from 20° to 25°. The relative velocity record (Fig. 2c) exhibits a wider pulse compared with the previous case. Eq. 1 gives 18.2 μs as the time of sliding initiation, a time that is consistent with the arrival of the photoelastic fringe concentration. The two criteria of interface locking result in locking times of 42.6 and 54.6 μs, respectively. These times correspond to a rupture duration between 24.4 and 36.4 μs. Fig. 2d shows the superposition of the relative velocity record and photoelastic image for this case and demonstrates that the pulse is closer to a crack-like mode in the sense that locking occurs near the nucleation site.

For α = 30°, the prestress f₀ = 0.577 is close to the static coefficient of friction, f_s = 0.6, for the interface. In this case, the interface is close to the state of uniform sliding along the entire fault. Measurements presented in Fig. 2 e and f reveal that the sliding mode is now fully crack-like in the sense that sliding at the measurement location does not stop during the observation time. The average relative velocity is ≈2 m/s (the maximum relative velocity is 7.35 m/s). A small “precursor” pulse precedes the arrival of both the shear wave front and the crack-like rupture that follows it and shows that the rupture begins to transition to supershear speeds close to the location of the relative velocity measurement. The details of such transitions are discussed in Transition of Pulse-Like and Crack-Like Modes to Supershear Speeds.

Collective Analysis of Rupture Modes

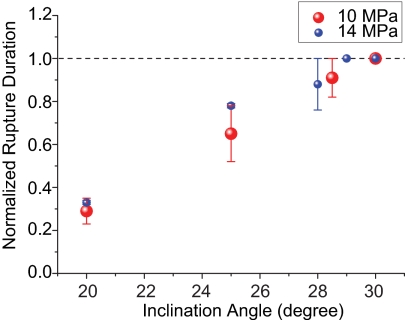
The three cases described in the preceding section were selected to demonstrate the existence of both pulse-like and crack-like ruptures in the experiments and to showcase the systematic transition of subRayleigh rupture modes from pulse-like to crack-like under increasing shear prestress. In addition to these three cases, a number of other experiments were conducted to examine the phenomenon in a more complete angle and prestress spectrum and to test the reliability of the results. Fig. 3 displays rupture durations for a collection of these experimental observations. In Fig. 3, rupture duration for each experiment is normalized by the maximum potential sliding time, which is equal to the time window of observation minus the arrival time of the rupture front. This normalized rupture duration ranges from 0 (no sliding at the measurement location) to 1 (continued sliding from the rupture arrival to the end of the observation). Crack-like ruptures correspond to the normalized rupture duration of 1, with smaller values indicating pulse-like ruptures of progressively shorter duration. For each experiment, the ends of the interval correspond to two estimates of the rupture duration, with a filled dot giving the average value.

Fig. 3.

Rupture duration, normalized by the maximum potential sliding time, plotted as a function of inclination angle α for two values of far-field pressure P. Normalized rupture duration of 1 corresponds to crack-like ruptures, whereas smaller values correspond to progressively narrower pulse-like ruptures.

Fig. 3 clearly shows that the inclination angle α and, hence, the prestress f₀ are the dominant factors in determining the rupture mode, with smaller angles and, hence, lower prestress favoring pulse-like ruptures of shorter duration. For angles α = 20° and α = 25°, the rupture is clearly pulse-like. Above α = 28°, the more conservative estimate of rupture duration gives the normalized rupture duration of 1, indicating that those ruptures may be fully crack-like. For angles α = 29° and α = 30°, the ruptures are clearly crack-like. Fig. 3 presents results for inclination angles between 20° and 30°. Angles below 20° were not studied, but those experiments would have likely produced dying pulses or no sliding at the measurement location. For angles larger than 31°, prestress f₀ = τ₀/σ₀ = tanα would exceed the static friction coefficient of 0.6, which would cause the sliding to occur over the entire interface at once.

The systematic transition of rupture modes from pulse-like to crack-like presented in this work is qualitatively consistent with the theoretical study of velocity-weakening interfaces by Zheng and Rice (21). Their analysis emphasized the determining role of velocity-weakening friction τ_ss (V) in promoting either pulse-like or crack-like behavior depending on the level of prestress τ₀. If τ_pulse is the maximum value of τ₀ that satisfies τ_el = τ₀ − μV/(2c_s) ≤ τ_ss(V) for all V ≥ 0, then no crack-like solutions exist for τ₀ < τ_pulse. (Note that τ_el gives the elastodynamic stress for the case of uniform sliding along the entire interface.) For larger values of τ₀, parameter T is defined as follows. The values of slip velocity V are found that solve τ_el(V) = τ_ss(V). Let us denote the larger of the two possible solutions by V_dyna. Then

That is, parameter T is the ratio of the slopes of the steady-state friction curve τ_ss and elastodynamic stress τ_el evaluated at their intersection V = V_dyna. When T exists, it is a nondimensional scalar between zero and one. If T is close to zero, the rupture mode is crack-like. If T is close to one, the rupture mode is pulse-like. If T does not exist, the rupture mode is either pulse-like or there is no rupture propagation.

To apply the analysis of Zheng and Rice (21) to our experiments, we describe the frictional properties of the interface by Dieterich–Ruina rate-and-state friction law (38–43) enhanced with additional velocity weakening at high slip velocities, as appropriate for flash heating (28). For steady-state sliding, the friction law reduces to

where f_* and V_* are, respectively, the reference friction coefficient and slip velocity, a and b are rate-and-state friction coefficients, V_w is the characteristic slip velocity for flash heating, and f_w is the residual friction coefficient at high sliding rates. Based on previous studies of frictional phenomena on Homalite interfaces (1, 44), we use the following values: f_* = 0.6, V_* = 1 × 10⁻⁶ m/s, a = 0.014, b = 0.019, f_w = 0.3, and V_w = 1.0 m/s. In addition, we continue to assume that normal stress σ is approximately equal to the initial normal stress σ₀ at the location where we interpret the rupture mode. By following the Zheng and Rice analysis summarized above, we can explain the major effect of the prestress level on rupture mode and predict the rupture mode type for different inclination angles.

This application of Zheng and Rice analysis additionally indicates that, for a given angle α, there should be a dependence of the rupture mode on the compressive load P, with higher values of P promoting more crack-like behavior. The analysis predicts that, for the ranges of α and P studied in the presented experiments, such dependence is much more subtle than the dependence on the inclination angle. Fig. 3 contains some hints of such subtle dependence, with P = 14 MPa corresponding to slightly longer durations than P = 10 MPa for most angles. However, the difference between results for P = 10 MPa and 14 MPa is rather small and, hence, cannot be claimed conclusively. The theoretical analysis indicates that one should compare results for P = 10 MPa with those for at least 20 MPa to expect significant differences in terms of rupture modes.

The agreement of our experiments with the theory of Zheng and Rice (21) over a wide range of conditions provides indirect evidence of the presence of velocity weakening on the Homalite-100 interfaces and supports the importance of velocity-weakening friction for rupture dynamics.

Transition of Pulse-Like and Crack-Like Modes to Supershear Speed

In addition to rupture mode transitioning from pulse-like to crack-like for different experimental parameters, another type of transition may occur in a given experiment. This is the transition from a sub-Rayleigh to a supershear rupture speed. Such transitions have been inferred for a number of large strike–slip earthquakes (32, 45–49). Early theoretical and numerical results (3, 4, 50, 51) have predicted the possibility of supershear Mode II ruptures and proposed a transition mechanism that is often referred to as the Burridge–Andrews mechanism or the daughter-crack mechanism (35). In that scenario, a supershear daughter crack nucleates ahead of the initially sub-Rayleigh main (or mother) crack, and the two cracks eventually merge. The mechanism was visualized by recent atomistic calculations of dynamic shear rupture (52, 53) at an entirely different length scale. More recent numerical studies showed that supershear transition also can occur by an abrupt change of the speed of the main crack (11, 54). However, the above-mentioned analyses have all dealt with speed transition in crack-like ruptures. This fact is perhaps not surprising because fault-strength models used in these studies are all of the slip-weakening type, which is known to promote, in the absence of geometric effects or heterogeneities, the formation of crack-like rupture modes (3, 13–16). Recently, there have been some numerical simulations of supershear pulses (9, 10, 12). From the experimental point of view, Xia et al. (1) have reported the phenomenon of sub-Rayleigh to supershear speed transition and have explored the parameter space for its occurrence. Those experiments, however, were unable to conclude whether the transitioning ruptures were crack-like or pulse-like.

We provide experimental evidence of supershear transition for both pulse-like and crack-like ruptures. To obtain the data, additional experiments were done with particle velocity measurements at a larger distance, 40 mm, from the hypocenter. This new measurement location was chosen to ensure that the transition is well underway and thus can be visualized easily. For the same reason, P = 14 MPa is used, because higher far-field pressure has been shown (1) to promote supershear transition.

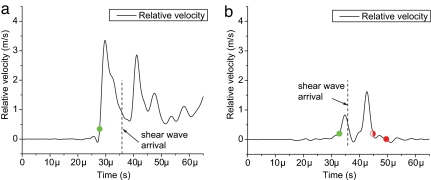
Fig. 4a displays the relative velocity record for the case of α = 30°, an angle that results in a crack-like rupture as judged by measurements at the location 20 mm away from the hypocenter (Fig. 3). At 40 mm away from the hypocenter, the rupture is still crack-like in the sense that sliding does not arrest in the time window of observation. It is also clear that the rupture is supershear, as it arrives at the measurement location before the shear wave whose arrival is marked in Fig. 4a by a vertical dashed line. From photoelastic images (data not shown), we find that this supershear crack-like rupture propagates with the speed of 1,960 m/s, which is between $\sqrt{2c_s}=\mathrm{1,766}$ m/s and the P-wave speed c_p = 2,187 m/s of Homalite-100. Photoelastic data suggest that the transition occurs by the Burridge–Andrews mechanism mentioned earlier. The first and second peaks in relative velocity in Fig. 4a correspond to the supershear front of the daughter crack and the remnants of the sub-Rayleigh front of the mother crack, respectively; at this stage, the two cracks have joined.

Fig. 4.

Relative velocity records, at 40 mm away from the hypocenter, that capture the sub-Rayleigh to supershear transition. (a) A sub-Rayleigh crack transitioning to a supershear crack (α = 30°, P = 14 MPa). (b) A sub-Rayleigh pulse transitioning to a supershear pulse (α = 27.5°, P = 14 MPa).

It would be even more interesting to confirm the possibility of pulse-like ruptures to transition to supershear speeds. Indeed, such transition is observed for α = 27.5° as shown in Fig. 4b. The sub-Rayleigh mother rupture is pulse-like and trails behind the shear wave trace in Fig. 4b. In contrast to the case of α = 30° (Fig. 4a), the daughter pulse is less developed and has not yet joined with the trailing mother pulse. Furthermore, photoelastic images show that this newly created supershear pulse propagates with a speed of 1,792 m/s, which also is between $\sqrt{2c_s}=\mathrm{1,766}$ = 1,766 m/s and c_p = 2,187 m/s but closer to $\sqrt{2c_s}$ than the higher rupture speed of the supershear crack-like rupture in the previous case.

It should be noted that, in both cases, the supershear daughter ruptures grow at speeds within the open interval $\sqrt{2c_s}$ to c_p. This interval, according to the asymptotic analysis of velocity-weakening interfaces by Samudrala et al. (55), corresponds to stable supershear rupture growth. The analysis of Samudrala et al. (55) also predicts larger stable supershear speeds for ruptures with larger prestress, and that is exactly what we observe.

Conclusion

By varying the inclination angle, we have experimentally observed pulse-like and crack-like rupture modes, and a systematic transition between them, in an experimental configuration that contains an interface prestressed both in compression and in shear, similarly to faults in the Earth's crust. Our results indicate that pulse-like ruptures can exist on such interfaces in the absence of a bimaterial effect or local heterogeneities. The systematic transition of rupture modes from pulse-like to crack-like presented in this work is qualitatively consistent with the theoretical study of velocity-weakening interfaces by Zheng and Rice (21). We also establish experimentally that both pulse-like and crack-like rupture modes can transition to supershear speeds. The resulting supershear rupture speeds are consistent with the analytical predictions of the velocity-weakening model of Samudrala et al. (55). The agreement between our experimental observations and models of velocity-weakening faults suggests that velocity-weakening friction plays an important role in dynamic behavior of ruptures and implies that expressing dynamic weakening of friction solely in terms of slip may not be a sufficiently general description.

Some recent numerical studies have pointed out the importance of the rupture initiation process for subsequent rupture dynamics, especially for supershear transition but also for the establishment of the mode of rupture (9–12, 44). Our current work is focused on modeling the experimental setup numerically to gain further insight into implications of the presented experimental observations, including the role of the nucleation procedure used in experiments. To make a meaningful comparison between simulations and experiments, it is necessary to quantify independently a number of input parameters, including parameters of the rupture nucleation mechanism and friction properties of Homalite interfaces.