In search of an optimal ring to couple microtubule depolymerization to processive chromosome motions

Abstract

Mitotic chromosome motions are driven by microtubules (MTs) and associated proteins that couple kinetochores to MT ends. A good coupler should ensure a high stability of attachment, even when the chromosome changes direction or experiences a large opposing force. The optimal coupler is also expected to be efficient in converting the energy of MT depolymerization into chromosome motility. As was shown years ago, a “sleeve”-based, chromosome-associated structure could, in principle, couple MT dynamics to chromosome motion. A recently identified kinetochore complex from yeast, the “Dam1” or “DASH” complex, may function as an encircling coupler in vivo. Some features of the Dam1 ring differ from those of the “sleeve,” but whether these differences are significant has not been examined. Here, we analyze theoretically the biomechanical properties of encircling couplers that have properties of the Dam1/DASH complex, such as its large diameter and inward-directed extensions. We demonstrate that, if the coupler is modeled as a wide ring with links that bind the MT wall, its optimal performance is achieved when the linkers are flexible and their binding to tubulin dimers is strong. The diffusive movement of such a coupler is limited, but MT depolymerization can drive its motion via a “forced walk,” whose features differ significantly from those of the mechanisms based on biased diffusion. Our analysis identifies key experimental parameters whose values should determine whether the Dam1/DASH ring moves via diffusion or a forced walk.

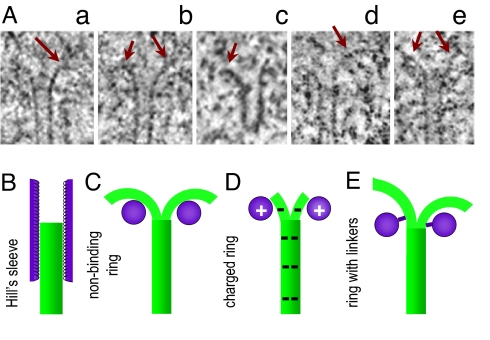
Chromosome segregation during cell division depends on the activities of microtubules (MTs), which are cylindrical arrangements of 13 linear polymers of αβ-tubulin dimers called protofilaments (PFs) (1). Tubulin complexed with GTP elongates PF ends, but this GTP is hydrolyzed soon after dimers have added (2). The preferred conformation of the GDP dimers is more bent, so the PFs tend to curve (3, 4). In a growing MT, this tendency is counteracted by a relatively straight “GTP cap,” but if the terminal layers are lost, the PFs are no longer restrained (1, 2). As they splay out, the dimers dissociate from their longitudinal neighbors, and the MT shortens (5, 6). Consequently, the ends of depolymerizing MTs in vitro and in vivo display curved PFs (3, 5–9). Representative images of kinetochore MTs are shown in Fig. 1A; the length of PF flares in anaphase mammalian cells is 53 ± 7 nm, n = 368 PFs (J.R.M., E.L.G., A.E., K. Zhudenkov, M. Morphew, et al., unpublished work).

Fig. 1.

Structure of kinetochore MT ends and models for force-bearing ring-like coupling. (A) Axial slices from electron tomograms of kinetochore MTs from PtK1 (a and b), Schizosaccharomyces pombe (c), S. cerevisiae (d and e). PFs have extensive flare (arrows) but different lengths. (B) In Hill's model, a sleeve has 65 low-affinity-binding sites along each PF (20). This mechanism does not use the PF's power stroke, because a MT tip is buried in a narrow sleeve. (C) A PF power stroke pushes with maximal force on a ring, which is ≈10-nm wider than the MT. This mechanism has no restrictions on PF length. (D) In the electrostatic model, the ring moves at the ends of the curved PFs, which therefore extend only ≈1 dimer beyond the ring (based on ring diameter and PF curvature). (E) A model that combines the power stroke, as in C, and attributes ring–MT interaction to site-specific protein–protein bonds, as in B, but the bonds are now formed by the linkers. The resulting motions are significantly different from those in other models.

It is well documented that MTs can move chromosomes or microbeads that associate with their shortening ends (9–15). Several hypotheses have explained these force-transducing attachments with the help of a coupler that encircles the MT (16–18). Movement in these models is driven ultimately by the energy released during hydrolysis of tubulin-associated GTP (≈12 k_BT; k_B, Boltzmann constant). However, the design of a coupler, e.g., its geometry and size and the nature of its interaction with MTs, determines the fraction of this energy that can be converted into useful work. Below we analyze several biomechanical designs, focusing on their efficiency and the stability of their attachment to the MT end.

Biased Diffusion of a Cylindrical Coupler.

The 40-nm-long “sleeve,” proposed by Hill, had numerous binding sites for enclosed tubulin dimers (Fig. 1B) (19, 20). Because protein–protein interactions act over very short distances, the sleeve could be only 0.1–0.2 nm wider than the MT, whose outside diameter is 25 nm. The interaction between a dimer and a binding site in the sleeve was postulated to decrease the total MT-sleeve energy by 2.5 k_BT, but the activation energy for the transitions between the binding sites was 0.1–0.2 k_BT. These assumptions are key for MT-dependent motility in this model. As the sleeve diffuses on the MT surface, it adopts a MT-sleeve overlap that minimizes the system's energy; with no opposing load, the steady state is achieved when 90–95% of binding sites are occupied (20, 21). As the MT shortens by loss of tubulin dimers through the narrow channel of a sleeve, sleeve diffusion relocates the bonds to preserve the overlap, thereby causing the sleeve to move with the MT end. With increased opposing force, the amount of overlap decreases; a ≈15-pN tension leads to complete loss of attachment. This coupler has relatively low efficiency (≈20%), because 100% efficiency, when all of the energy of GTP hydrolysis is converted into useful work, would produce ≈80 pN (20–22).

Although a coupler with Hill's design has not yet been found, this physically solid model has had a significant impact on thinking in the mitosis field. Since the model was proposed, however, it has been learned that the ends of shortening MTs, including those at kinetochores, display flared PFs, a feature that is not compatible with the above mechanism. A long narrow sleeve (or a shorter ring) can reside only over the cylindrical part of the wall, away from the tip where the PFs flare. When the sleeve is over the wall, all of its binding sites are occupied, so its diffusion is not biased. However, a sleeve (or a ring) with structure similar to Hill's proposal might be biased to move with a shortening MT by some other mechanism, as has been proposed for directed motions of various microobjects (23–26).

Power Stroke Mechanism.

Bending PFs have been proposed to move a circular coupler by pushing on it directly (Fig. 1C) (12, 27). Indeed, the existence of a PF power stroke has been experimentally confirmed with nonencircling couplers (13). Analysis of force transduction by a ring coupler with a model that takes into account current knowledge of the PF bending pathway suggests that the efficiency of a ring coupler can be very high, but it depends strongly on ring diameter (22, 28). A narrow ring, similar to Hill's sleeve, constricts PF bending, and the resulting force is <10 pN (22). Maximal efficiency (≈90%) is achieved by a ring with diameter 35–40 nm, which is similar to the inner diameter of a Dam1 ring (29, 30). Such a wide ring could bind directly to the MT wall only when positioned asymmetrically, but Dam1 rings appear to be coaxial with MTs. Furthermore, Dam1 rings assemble spontaneously around MTs, strongly suggesting there is an interaction between the ring's inner surface and the MT wall (29, 30). We have hypothesized that such binding might be accomplished by “linkage” between Dam1 heterodecamers and tubulin dimers (22), an idea that is supported by recent structural studies of Dam1–MT complexes (29, 31, 32). There are indications that the linking structure is flexible, but its exact properties are unknown (30–32).

An electrostatic mechanism has been also proposed for coupling a 32-nm ring to MTs (33) in which PFs bend, as in ref. 22. This ring is proposed to interact weakly with the MT wall (12 k_BT per ring) over a 3.5-nm gap between these structures. Ring and tubulin are also supposed to have opposite charges, so the ring is attracted strongly to the splayed PFs. In this model, ring movement is promoted by the instantaneous removal of terminal dimers; the ring is always at the PF ends, where it transduces <12-pN force (Fig. 1D). MTs are described as nonhelical (although MTs in vivo are helices), so the terminal dimers on all PFs must dissociate synchronously. These restrictions appeared to us ill-justified, so we sought a different approach.

A Combined Approach to Examine MT-Dependent Movements of Various Ring Couplers.

Tools are now available to build a versatile model that addresses the mechanisms of Dam1 motility. For example, thermal motions of the coupler (essential in a biased-diffusion mechanism) can be analyzed with a Hill-like coupler, which assumes an explicitly defined energy relationship with tubulin. It is reasonable, though, to change the dimensions of the coupler, as well as its number of tubulin-binding sites, to match those of the Dam1 ring. The impact of a PF power stroke can best be analyzed as in refs. 22 and 28, because this approach takes into account the energetics of tubulin–tubulin interactions during PF bending in a 13_3 MT (13 PFs arranged in a three-start helix). Because the molecular details of Dam1–tubulin interactions are not known, the model should explore the unknown parameters, e.g., the number of subunits per ring, the number of bonds to the MT wall, and the flexibility of linkers. Below, we define the design of such a coupler.

Mathematical Model

Model Assumptions.

The coupler is a ring with a fixed inner diameter of 33 nm. As in the above models, the coupler is solid and does not deform.

1. Because Dam1 complexes bind MT walls, we assume the ring has extensions that bridge the gap between the ring subunits and tubulin dimers in the wall of a straight MT. Each subunit has ≈4-nm-long linkers; for simplicity, we model them as rods (Fig. 1E).

2. We assume a direct and specific interaction between tubulin and the linker, characterized by negative potential energy d:

where k_DAM and r_DAM are parameters for the depth and width of the potential well, respectively; ρ is the distance between the MT-proximal end of the linker and the closest binding site on the MT wall; for simplicity, the sites on the MT wall are positioned in the middle of tubulin's outer surface. The interaction sites used for model calculations should not be confused with real contacts between Dam1 heterodecamers and tubulin dimers. The interacting proteins usually form various bonds (electrostatic, hydrophobic, and others) between multiple amino acid residues. Specific binding is characterized by strong forces that act over a short range (34) and are described appropriately by the above equation. The exact parameters of the Dam1–tubulin interaction, k_DAM and r_DAM, however, are not known. Cosedimentation of Dam1 complexes with taxol-stabilized MTs estimated a dissociation constant at 0.2 μM (29), which suggests an interaction free energy of −15 k_BT for each Dam1 subunit with the MT wall. This value may overestimate Dam1-tubulin binding, e.g., because of the unknown strength of interactions between the ring subunits. We will therefore analyze model solutions for a range of Dam1-tubulin binding energies (parameter k_DAM).

4. We assume that each tubulin dimer binds a single linker, based on analogy with other MT-binding proteins, such as kinesins (35). We did explore models based on two Dam1-binding sites per tubulin dimer, but the results gave a poor description of the Dam1 ring's properties (below).

Mathematical Modeling and Data Analysis.

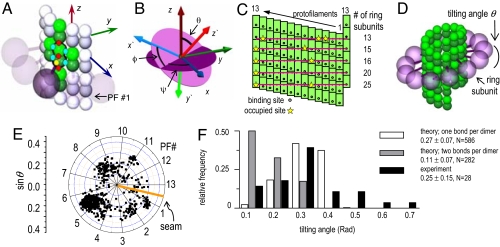
A 13_3 MT was modeled as an ensemble of subunits connected by fixed “interaction points” with explicitly defined energy relationships, based on our original model (28) [Fig. 2A; see supporting information (SI) Text and SI Table 1]. Here, however, a tubulin monomer is the unit structure, which allows intradimer bending (4). We also take thermal fluctuations into account (SI Text). The position of the ring coupler is defined by the three coordinates of its center (x_cy_cz_c) and its Euler's angles (θ, ϕ, and χ) (Fig. 2B and SI Table 2). Linkers, which are rigid, lie in the plane of the ring. A detailed description of the ring and its interaction with the MT is provided in SI Text. The model contains no additional assumptions that would bias the ring's diffusion. Numerical calculations were carried out with the Metropolis method for Monte-Carlo simulation (36). Errors are standard deviations.

Fig. 2.

Ring with linkers on a 13_3 MT. (A) Interaction points between dimers (light, β tubulins; dark, α tubulins). Each dimer interacts at seven points; four are lateral bonds (blue dots) with adjacent PFs (green), and three are longitudinal junctions, one within the dimer and two with dimers in the same PF (red dots). The Dam1 linker binds to a tubulin monomer (yellow dot). Axis z coincides with the MT axis and points to its plus end; x and y axes lie in a perpendicular plane, and x points to PF no. 13. (B) Angular variables of ring orientation. (C) MT wall-ring configurations as calculated in the model. Purple lines show ring backbones. (D) Shown is a 13-fold ring, but similar models can be drawn for a range of ring symmetries, because the number of bonds is defined by the MT surface, which has a lower radial symmetry than the ring. (E) Preferred ring orientations. A ring that is perfectly perpendicular to the MT axis would correspond to a central dot, where θ = 0. The ring is sensitive to the MT seam, as seen from the nonsymmetric distribution of data points relative to the orange line. (F) Experimental tilting angles were estimated from electron micrographs of Dam1 rings decorating taxol-stabilized MTs (29, 30). The resulting distribution is statistically identical (95% confidence, Mann–Whitney t test) to that calculated from our model, assuming a single binding site per dimer. Highly tilted rings in some EM images could have resulted from specimen distortions that frequently accompany the negative staining procedure.

Results

Rigid Linkers Decrease the Number of Dam1–MT Connections, Thereby Reducing the Affinity of This Coupler for the MT Wall.

First, we considered geometrical aspects of how a rigid 33-nm ring with linkers would form connections with the wall of a 13_3 MT. There is a mismatch between the symmetry of such a MT and the Dam1 ring, which is thought to have ≥16 subunits (31, 37). We have examined the minimum energy configurations for rings with 13–25 subunits. When linkers are modeled as stiff 4-nm rods, three or fewer linkers can bind dimers in the MT wall (Fig. 2C). Additional bonds are sterically prohibited by the incompatibilities of a helical MT and a rigid planar ring. A small number of connections is disadvantageous, because it impairs the stability of ring–MT attachment. If the energy of a single Dam1-tubulin bond is −2 k_BT, similar to the sleeve–MT bond (20), the paraxial force that would detach the 13 subunit ring from the MT end is only 4 pN. Stronger binding increases the stability of attachment, but it is still far from the maximum possible, because of the limited number of ring–MT bonds. In rings with more subunits, the number of possible ring–MT connections is even smaller, so this conclusion is independent of the number of ring subunits.

Rigid Dam1–Tubulin Linkers also Limit the Efficiency of Energy Transduction.

As a MT begins to depolymerize, bending PFs push on the coupler. The total paraxial force on the ring can be estimated, as in the model with noninteracting ring (22), but here the force is applied to the linkers. As the PFs bend, all linkers are affected, regardless of whether they have formed a bond with the MT wall. The geometrical differences between the noninteracting ring (22) and the coupler considered here are not important. Indeed, a 33-nm ring with any number of nondeformable 4-nm-long linkers is mechanically equivalent to a narrow ring. Therefore, the force experienced by a ring with rigid linkers is virtually identical to that calculated for a rigid ring with a diameter <26 nm. For example, when the free energy of a dimer–linker bond is −2 k_BT, the maximal force generated is only 12 pN; for stronger binding, it is even smaller.

Based on these considerations, we conclude that couplers with stiff linkers are far from optimal. To examine the effect of flexible linkers, we modeled them as linear rods that could stretch and compress along their length (parameter k_spring) and bend away from the ring's plane (parameter k_flex) (SI Text). Model calculations show that 10-fold variations in a linker's longitudinal stiffness have little effect on model solutions (not shown), so this parameter was fixed at k_spring = 0.13 N/m for all our calculations. For a linker 4 × 1 × 1 nm, the corresponding Young modulus is 5 × 10⁸ N/m², close to that of globular proteins and MTs (38). The flexural rigidity k_flex was varied from 5–2,000 k_BT/Rad. As described above, very rigid linkers (>2,000 k_BT/Rad) are equivalent to a narrow rigid ring, which is a poor transducer (22). When linkers are very soft (< 5 k_BT/Rad), their impact on the mechanics of the system is negligible; the ring behaves like the 33-nm ring that does not interact with the MT wall (22). Thus, this parameter was examined over a range of 20–200 k_BT/ Rad. A 10-fold change in linker-bending stiffness in this range does not appreciably affect the ring's properties, e.g., its diffusion, so all calculations were carried out for k_flex = 20 k_BT/Rad.

The Preferred Configuration of the Dam1 Ring Is Tilted Relative to the MT Axis.

When linkers are flexible, they can reach more binding sites on the MT surface, so a 13-subunit ring can establish connections with 13 dimers in the MT wall. However, rings with more subunits can still bind only 13 sites, because the number of bonds is limited by the number of PFs in the MT. To establish more bonds, the linkers in a 33-nm Dam1 ring with 15–25 subunits would have to stretch >1.5-fold, an implausible scenario. Because the free energy of the ring–MT system is determined by the number of protein–protein bonds established, not the number of available linkers, rings with more subunits should behave much like a “minimal” ring with only 13 subunits per linkers. We have therefore carried out all calculations with rings of 13 subunits, each of which has a flexible linker.

When such a ring encircles a MT, it orients to maximize the number of Dam1–tubulin bonds, while minimizing their total bending deformations, thus minimizing the total system's energy. Calculations show there are several configurations with similarly low energies, but in all of them, the ring is tilted relative to the MT axis (Fig. 2D). Fig. 2E shows projections of the unit vector normal to the ring (red arrow on Fig. 2B) onto the plane perpendicular to the MT axis (dark circle on Fig. 2B), as viewed from the MT-plus end. Each dot corresponds to a configuration characterized by the ring's tilting angle θ (radii of the diagram's circles show sinθ with 0.05 increments; scale on the left) relative to positions of the different PFs (the numbered radial spokes). The dots are distributed nonuniformly because of the MT's helicity and asymmetry, which results from its seam. Most frequently, the ring is oriented so its axis forms a 15–16° angle with PF no. 5.

We have compared the predicted distribution of θs with the orientations of Dam1 rings, as visualized by electron microscopy (Fig. 2F). If there is only one Dam1-binding site per dimer (assumption 4), the degrees of tilting of the theoretical ring correspond well with those obtained by experiment. If the linkers have one bond per monomer, the predicted average tilting angle is ≈2.4-fold smaller than that observed. In general, more binding sites per tubulin dimer should lead to a less pronounced tilting, whereas rings that do not have specific binding sites on MT surfaces should have no tilt.

A Weakly Bound Ring Will Follow a Shortening MT End via Biased Diffusion.

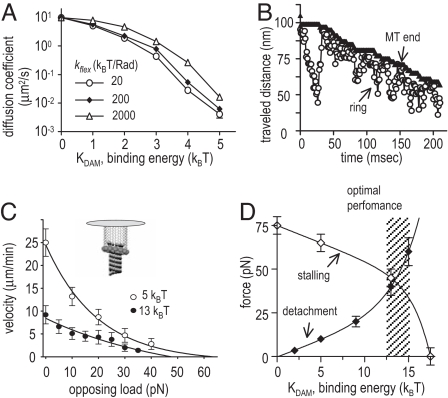
After eliminating unimportant parameters and unfavorable designs, we analyzed the diffusion of the resulting coupler on a MT. When ring–MT interaction is very weak (k_DAM < 2 k_BT), ring diffusion is fast and depends little on bond strength (Fig. 3A). For stronger binding (2–5 k_BT), the dependence is exponential, and a 1-k_BT change reduces diffusion 10-fold. This result is almost insensitive to the exact value of linker flexibility within the above-determined range. Experiments suggest that Dam1 complexes diffuse on an MT surface ≈250-fold slower than in solution (30, 37). If these complexes are the MT-encircling rings, this implies relatively weak Dam1-tubulin binding, which matches the model coupler with k_DAM ≈4 k_BT.

Fig. 3.

Role of the ring-MT-binding energy. (A) Ring diffusion on the MT surface is fast only for k_DAM < 6 k_BT. (B) Thermal motions of a weakly bound ring (k_DAM 3 k_BT) are biased by the shortening MT end (shown is the z coordinate of the uppermost lateral bond between two adjacent PFs). (C) Force-velocity curves for weak and strong binding. (D) Detachment force grows for stronger linker-tubulin binding, but the stalling force gets smaller.

As a MT shortens, the random walk of such a ring becomes biased (Fig. 3B; SI Movie 1). When the ring approaches the MT end, its motion in this direction is interrupted, because the flared PFs present a significant barrier; the energy required to straighten them, so the ring could slide over that area, is ≥12 k_BT per tubulin dimer. This energy is so high the ring's thermal energy is not sufficient to pass this barrier. Although technically the PFs push on the weakly bound ring when it comes in contact, this aspect of their interactions is mechanically insignificant, because of the low resistance to ring sliding.

Weakly Bound Rings Are Energy-Efficient, but Have a Low Stability of Attachment.

We examined the force-transduction by a weakly bound ring (k_DAM = 1–6 k_BT) by analyzing its motions under a load that was distributed evenly among its subunits. In vivo, a Dam1 ring is probably attached to a chromosome via other proteins that transmit the load in roughly this fashion (Fig. 3C Inset). Unlike Hill's sleeve, this coupler slows with increasing resistance (Fig. 3C). Even a small load retards the weakly bonded ring significantly, but this ring stalls only when the opposing force is 60–70 pN. Because the maximal force that is energetically possible from a disassembling MT is ≈80 pN (22), the weakly bound ring achieves up to 90% efficiency in energy transduction.

What happens when this ring stops moving toward the MT minus end? The ring blocks separation of lateral tubulin–tubulin bonds downstream from the ring, and ring motion in the opposite direction is blocked by flared PFs. Such a ring is stalled on the MT, but it will not detach so long as there are some splayed PFs upstream from the ring. However, as the longitudinal bonds between tubulin dimers in the flared PFs dissociate, the PFs upstream from the ring will shorten and no longer protect the ring from detachment. If the opposing force exceeds what is required to break all ring–MT bonds, the ring will disconnect from the MT end. Strikingly, the detachment force for a weakly bound ring is <15 pN, significantly less than its stalling force in the presence of flared PFs (Fig. 3D). This feature of a weakly bound ring seems highly disadvantageous for use as a coupler in mitosis.

Strongly Bound Ring Couplers Move via a Forced Walk Mechanism.

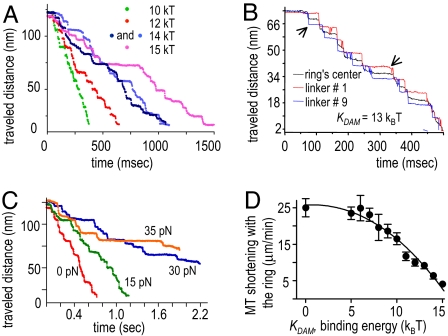
If the energy of the linker–tubulin binding is large (k_DAM = 9–15 k_BT), the dynamic and coupling properties of the ring change dramatically. Such rings would show negligible diffusion (<10⁻² · μm² per sec), but bending PFs can exert enough force to displace them in a robust and deterministic manner. This contrasts with the saltatory motions of a weakly bound coupler (Fig. 4A), so we call such motility a “forced walk.” Ring movements will be unidirectional, although they occur by various paths, even when calculations are repeated for rings with the same binding energy and initial conditions (Fig. 4A). The paths differ because of the variable pauses, which frequently interrupt the ring's motion and PFs splitting. The pausing is caused by the stochastic behavior of individual PFs and the random transitions of the ring between successive preferred positions on the MT lattice (SI Movie 2). As a PF bends and pushes on the associated linker, the linker remains at its binding site but bends away from ring's plane, accumulating energy in linker strain. The linker's transition to the next-closest binding site occurs abruptly with an 8-nm step (SI Movie 3). The center of the ring moves less regularly, because the ring can form up to 13 linker-mediated bonds with the MT (Fig. 4B). Interestingly, when the same ring is placed on a nonhelical MT (13_0), the ring does not move under the depolymerization force. MT helicity is significant, because it allows linkers to step asynchronously, thereby minimizing the energy barriers for ring transitions.

Fig. 4.

Forced walk of the ring. (A) With increasing ring-tubulin affinity, the ring steps slower. The irregular features of ring forward motion are caused by the stochasticity and asynchrony in PF splitting and walking of different linkers. (B) The linkers step asynchronously (shown are the z coordinates of their MT-associated ends) and in 8-nm steps (arrows point to some), whereas the steps of the ring's center are more variable in size. (C) With increasing load, the duration of ring pauses increases, and the ring walks more slowly (k_DAM 13 k_BT). (D) The rate of coupler's movement with the depolymerizing MT end is a blueprint for the strength of its affinity to the MT wall and thus for the mechanism of its motion.

The number of bonds that can form between the MT and the ring is independent of linker-binding strength. The detachment force, however, increases with growing linker affinity (Fig. 3D). Tension applied to the coupler provides a load that slows ring movement (Figs. 3C and 4C). The dwell periods become longer, and when ring–MT binding is very strong, the ring stalls even under a small load (Fig. 3D). When k_DAM >13 k_BT, the ring will maintain attachment, even when stalled at a blunt MT end, thereby increasing the fidelity of its MT-dependent motion. Thus, strong ring–MT binding improves the coupler's stability of attachment but reduces the load it can carry.

Discussion

Specifying the Ring's Design.

We have developed a versatile molecular-mechanical model of ring–MT coupling by combining highlights from previous theoretical approaches; assumptions about binding energetics, and mechanical forces that act between bending PFs and the ring. Different aspects of these interactions were analyzed to narrow the range of important model parameters. This approach has identified two possible mechanisms for movement for a Dam1-like ring, both of which differ significantly from the mechanism proposed by Hill and Kirschner (19, 20). The two modes of movement and other ring characteristics have been explained in terms of specific features of the coupler's design. For example, that Dam1 rings are significantly wider than MTs (29, 30) is important for maximizing force transduction (22). The exact number of subunits in the ring is virtually inconsequential (when it is >13, the number of PFs in a MT), but the number of bonds that can be formed between the ring and the MT wall is critical. The latter is greatly influenced by the flexibility of the binding structures. We have chosen linkers whose flexibility is just enough to maximize the number of bonds yet not limit the force transduction processes. The main model conclusions, however, are unchanged with a 10-fold change of this parameter. Recent structural studies indicate that the core of the ring, not just the linkers, may be flexible (31, 32). The mechanical properties of a rigid ring with flexible linkers should be highly similar to those of a flexible ring with rigid linkers, but this issue will require further work.

Strength of Ring–MT Binding.

The parameter that is most crucial for MT-dependent ring movement is the strength of linker binding to the MT wall. We have analyzed couplers with a 1- to 15-k_BT range of this energy, which encompasses the strengths of typical protein–protein interactions as well as the various estimates of Dam1–tubulin-binding energy. Some data support the idea that Dam1–MT interactions are weak. The measured diffusion of the Dam1 complexes that were interpreted as rings (37) suggests that Dam1–tubulin-binding energy is ≈4 k_BT (Fig. 3A). The forces that detach Dam1-coated microbeads from shortening MTs in vitro are <3 pN (14), implying even weaker binding (<2 k_BT, Fig. 3D). Without knowledge of the pathway for Dam1 oligomerization and MT binding, the Dam1–MT dissociation constant determined biochemically (29) does not define binding energy unambiguously and can be used only as an upper estimate (15 k_BT). However, the MT affinity of a mutant Dam1 complex with reduced ability to form rings is the same as that of wild-type Dam1 (29, 32), suggesting that a large fraction of the observed interaction corresponds to Dam1–MT binding. We therefore think this energy is toward the upper end of the range considered.

Biased-Diffusion Mode.

When the binding is relatively weak (< 6 k_BT), the ring diffuses fast (1–10⁻³/μm² per sec), and its diffusion will be biased by MT shortening. The latter motion, however, is produced by a mechanism that is different from Hill's model, in which the sleeve moves directionally only when MT is not fully inserted. Ring motions are affected simply by the presence of the flared PFs at the shortening MT end. Such a coupler, in principle, can move under a large opposing load, but for loads >12 pN, its retention by the MT end depends entirely on the presence of flared PFs. If the PFs should happen to shorten, the ring would swiftly be removed from the MT end, even by a small load. If the Dam1-tubulin binding is 1–3 k_BT, thermal motions would detach such rings from a “blunt” MT end almost every time they approach it, even without a load. Most of the plus ends of MT growing in vitro are blunt, although some have long PF extensions (5, 6). These, however, are curved only gently compared with the PFs on depolymerizing MTs (39) and are unlikely to prevent detachment of 33-nm rings from growing MT tips, as suggested in ref. 14. Thus, the MT attachment of the weakly bound ring should be highly vulnerable to variations in the rate and direction of MT length change. In vivo, moving chromosomes frequently pause and even reverse their direction. Therefore, for this coupling to be biologically successful, there must be some additional mechanism that ensures its attachment. For example, the stability of Dam1 ring attachment might be augmented by other kinetochore proteins and/or proteins that bind MT plus ends (40). Such interactions are possible, but their effects on ring motility are speculative.

Forced Walk.

A similar coupler with stronger MT binding provides an attractive solution to the above problem. Such rings will diffuse by undetectable amounts under normal experimental conditions. They can, however, be forced to walk by the action of PF power strokes. The persistent association of such a ring with the MT wall just below the PF flare is a natural consequence of its design and does not require additional assumptions. Rings that bind very strongly (>15 k_BT) would maintain their association with MT ends of any geometry, even under a large opposing force (Fig. 3D). Such rings, however, move very slowly with the shrinking MT end, and they will stall frequently (Fig. 4D), so very strong binding may not be optimal. Microbeads coated by Dam1 heterodecamers maintain attachment to MT tips, even as the MT elongates (14), a behavior more consistent with weak Dam1–MT binding that permits ring diffusion. However, these movements were seen in the absence of soluble bead-free Dam1, and it remains to be determined whether such coupling is ring-based.

Our model defines an inverse relationship between the efficiency of force transduction and the stability of coupler attachment, leaving a relatively narrow window of “successful” ring–MT bond energies, i.e., those in which coupler performance is optimal by the postulated standards (Fig. 3D, shaded area). A compromise between reduced efficiency of force transduction and increased strength of attachment appears important for the coupler in an organism like Saccharomyces cerevisiae, where a kinetochore is stably attached to only one MT (41, 42). We therefore favor a tight-binding mechanism with k_DAM = 10–14 k_BT and consider it better suites for budding yeast than the one based on biased diffusion. However, a choice between different coupler designs is impossible on strictly theoretical grounds. For example, although the forces that oppose kinetochore motions may be large in some organisms (43), in budding yeast, their size has not been measured.

Experimental Approaches to Study the Mechanism of Dam1 Motility.

If the Dam1 ring is similar to our theoretical ring, our results suggest that its mechanism of motility in vitro can be determined by characterizing ring motion at a depolymerizing MT end. If the ring moves by biased diffusion, the MT end serves only to ratchet the ring's random walk. Thus, the coupler's speed will be determined simply by the rate of MT depolymerization (Fig. 4D). The same result is expected in an electrostatic model (33), as well as in any other model in which the ring slides freely on the MT surface (37). If the ring binds strongly, however, it will reduce the rate of MT disassembly. A reduced rate of PF splitting has been verified experimentally for the force-transducing couplers under opposing tension (13, 44). Examination of the Dam1 ring's motility in the absence of a load, however, is lacking. Additional information will be available from an analysis of mutant Dam1 complexes with reduced MT binding (29). If strong ring–MT binding is facilitated by linkers, complexes with reduced binding linker should slow MT depolymerization less than wild type. If, however, these linkers serve other purposes, e.g., if they facilitate the sliding (32, 37), the above mutant should retard MT disassembly more than wild type. Experimental testing of these predictions should help clarify the mechanism of Dam1 ring motility.