The early stage of folding of villin headpiece subdomain observed in a 200-nanosecond fully solvated molecular dynamics simulation

Abstract

A new approach in implementing classical molecular dynamics simulation for parallel computers has enabled a simulation to be carried out on a protein with explicit representation of water an order of magnitude longer than previously reported and will soon enable such simulations to be carried into the microsecond time range. We have used this approach to study the folding of the villin headpiece subdomain, a 36-residue small protein consisting of three helices, from an unfolded structure to a molten globule state, which has a number of features of the native structure. The time development of the solvation free energy, the radius of gyration, and the mainchain rms difference from the native NMR structure showed that the process can be seen as a 60-nsec “burst” phase followed by a slow “conformational readjustment” phase. We found that the burial of the hydrophobic surface dominated the early phase of the folding process and appeared to be the primary driving force of the reduction in the radius of gyration in that phase.

Understanding the mechanism of protein folding has been a grand challenge in protein chemistry for a few decades. Important advances in this area can have a profound impact in many biologically relevant fields. A direct benefit from the understanding of the mechanism should be the ability to predict protein structures more accurately, which in turn should enable the pharmaceutical industry to improve drug discovery. The recent hypothesis of folding-related diseases is another example of the significance of folding (1, 2). Despite great progress made by a variety of experimental and theoretical approaches, it has been difficult to establish detailed descriptions of the folding process and mechanism at an atomic level.

Computer simulation has been a powerful tool that can provide rich information at various levels of resolution. Simulation has been instrumental in understanding protein folding mechanisms. One such approach is lattice model simulations (3–5). These types of models use reduced representations by treating the residues as (one or two) linked beads. A more detailed approach is the atomic level model, either united-atom or all-atom, which represents all or most of the atoms of the protein explicitly, with an implicit representation of the solvent (6, 7). Molecular dynamics (MD) simulations with full atomic representation of both protein and solvent possess a unique advantage to study protein folding because of their atomic level resolution and accuracy. This method with associated simulation parameters (i.e., the force field) derived from experiments and from gas-phase quantum mechanical calculations has been tested by using smaller molecular systems in many comparisons with experimental results.

Because of the complexity of this approach, the large number of atoms, and the need to take time steps of 1 to 2 fsec, such simulations have to date been limited to a few nanoseconds; the longest single MD trajectories of proteins with explicit water have been <10 nsec (8). This has precluded the simulation of even the early stages of protein folding. Nevertheless, insights have been gained from unfolding simulations (9–12) of the denaturation process, in which the proteins were forced to unfold by altering the free energy landscape either through high temperature to accelerate the process to the nanosecond scale or by adding denaturant. Attempts also have been made to reconstruct the free energy landscape of folding through unfolding simulations at high temperature (12, 13). In these simulations, both proteins and solvent are represented explicitly and at the atomic level. Direct folding simulations using this approach, however, have been limited to small peptide fragments and have been carried out for as long as 50 nsec (14, 15).

High performance massively parallel computers provide opportunities to study complex molecular systems and are capable of generating microsecond trajectories of small proteins with full representation of solvent. This is ≈100 times longer than has been reported for simulations on such systems to date. We have carried out optimization and parallelization on the MD software that makes it possible to simulate a small protein to the microsecond time scale on a massively parallel platform, such as the CRAY T3E, within a reasonable amount of real time (e.g., 2 months). Recent experimental studies on apomyoglobin suggested that the upper limit of the time scale for (small) proteins to form marginally stable structures [often called molten globules (17)] with partially formed secondary structures is on the order of 10 μsec (18), a time scale the simulations are now approaching. This implies that direct comparisons will soon be possible between simulation results and experimental findings in the early stages of protein folding. Proteins can have marginally stable nonnative states (17). Understanding these states has been an important challenge. However, because of their inherent instability, it is difficult to find their structures by using NMR or x-ray experimental approaches. Computer simulation can play an important role in identifying these structures because of its extremely high time resolution and detailed atomic level representation.

Because of the advances in software and a generous allocation of time on a CRAY T3D at the Pittsburgh Supercomputing Center (PSC), we have conducted a 200-nsec simulation on the villin headpiece subdomain, a 36-residue peptide (HP-36) (19, 20). HP-36 is one of the smallest proteins that can fold “autonomously” (19). It contains only naturally occurring amino acids and does not require disulfide bonds, oligomerization, or ligand binding for stabilization; its melting temperature is >70°C in aqueous solution (19). The NMR studies revealed three short helices with a closely packed hydrophobic core (20). These physical properties make it an ideal target for our simulation studies.

METHODS

Parallelization and Optimization Methods.

MD simulation at atomic level representation with explicit inclusion of water molecules (often typically 10,000 particles) can be an accurate method to simulate the structures and dynamics of molecular systems within the framework of classical mechanics. This high accuracy is associated with complex interactions that often result in a low computational efficiency compared with many other lower resolution representations (e.g., lattice models). Another difficulty is the inherent long range nature of the interactions. These interactions may require relatively extensive communications among processors. The highest level of parallelization, after a few years of concerted effort, has reached typically 32 to 64 central processing units (CPUs) on the CRAY T3D and T3E and has remained stagnant (21). Consequentially, MD simulations of biologically important systems, such as proteins in aqueous solvent, have typically only reached 10 nsec. Recent progress has been made in the effort to achieve high level parallelization by spatial decomposition (22), in which the system is decomposed into subdomains according to spatial location, and each subdomain is allocated a single CPU. We recently have made considerable progress in the parallelization of a Message Passing Interface code designed for the CRAY T3D and T3E platforms, both in single CPU performance and scaling, by using a simple but effective approach that is fully compatible with the original version of the program, the module sander from amber 5.0 (23). Here, we briefly summarize the approaches applied in the parallelization and optimization of the MD program.

The advantage of spatial decomposition is its reduced communication overhead. In the same spirit, we reimplemented the force collection and coordinate distribution parts to be done on an “as needed” basis. To further reduce the communication overhead, we group the water molecules into adjacent blocks and renumber and redistribute the water molecules when the neighbor list is updated. To maintain the compatibility with the existing program, the solute part (i.e., the protein) always resides in fixed CPUs. This implementation has several advantages. First, it is relatively easy to implement, and there is, in general, no need to rewrite any other part of the program. Second, it is easy to achieve good load balance because calculations are not restricted to specific CPUs. Load balance is inherently difficult in the spatial decomposition method, particularly for high level parallelization when the average number of atoms on each CPU becomes too small (<100). In theory, the fractional load imbalance of the spatial decomposition method is proportional to the square root of the number of CPUs. The method we use can reach much better load balance. Third, it improves cache performance because spatially adjacent water molecules are now sequentially adjacent and are likely to share the same neighbors. This is one of the key features that has enhanced single CPU performance by ≈70% over the sander code despite the fact that the original code has been optimized very well for single CPU performance. In summary, our current code achieves a speedup of ≈170 over a single processor by using 256 processors with a small system (≈12,000 atoms), ≈6 times faster than the existing code, and an overall throughput of better than 5 nsec a day on a 256 CPU of CRAY T3D.

SUMMARY OF SIMULATION METHODS

Force Field and Simulation Conditions.

The force field (24) of Cornell et al was used with full representation of solvent by using the TIP3P water model (25). Periodic boundary conditions were imposed via a nearest image convention in a truncated octahedron box. Long range nonbonded interactions (both electrostatic and van der Waals) were truncated by using an 8-Å residue-based cutoff. When applicable, temperature and pressure controls were imposed via Berendsen’s algorithms (26). The simulation was conducted on a CRAY T3D with 256 processing elements that was provided generously by PSC. The trajectories were produced by numerical integration by using the Verlet–leapfrog algorithm (27, 28) by using a 2-fsec time step. Bond constraints were imposed on all bonds involving hydrogen atoms via shake (29) and settle (30).

Preparation.

The starting coordinates were the NMR structure of villin headpiece subdomain by McKnight et al. (20) [Protein Data Bank (31) accession code 1vii]. The protein was denatured by carrying out a 1.0-nsec simulation in water at 1,000 K by using constant volume. The denatured molecule then was immersed in a truncated octahedron water box constructed from a cubic box of 76.5 Å. A total of 6,510 water molecules were retained. The large number of water molecules was needed to accommodate possible expansion and rotation of the protein. The excess water molecules were removed after ≈20 nsec, when a semistable compact structure was formed, to reduce the computational cost. Water molecules (≈3,000 molecules) were retained for the remainder of the simulation.

Production.

The simulation was started from an equilibration phase of 1.0 nsec at 200 K and 1 atm pressure (1 atm = 101.3 kPa). The long equilibration phase was intended to mimic an equilibrated, fully denatured state and for adequate solvation of the molecule. The density of the system was initially 0.90 g/cc, reached 1.05 g/cc within 10 psec, and remained so for the remaining of the trajectory. The simulation then was conducted for 200 nsec (100 million integration steps), with the temperature and pressure controlled at physiological conditions (i.e., 300 K and 1 atm) via the methods described above. The trajectory was saved at 20-psec intervals for the analysis.

RESULTS AND DISCUSSIONS

In the following, we number the residues from 1 to 36, where our residue 1 corresponds to residue 41 in the NMR structure (20). We refer to the three helices as helices 1, 2, and 3 for residues 4–8, 15–18, and 23–30, respectively. They are held together by a loop (residues 9 through 14), a turn (residues 19 to 22), and the hydrophobic core.

A simulation was conducted for 20 nsec, starting from the native NMR structure of the same fragment (20). The simulation methods were identical to those described in the Methods section. The N-terminal helix 1 rotated ≈30° while maintaining its helical structure. The C-terminal residue Phe³⁶, which was found disordered in the NMR structure, also exhibited large scale movement. Phe³⁶ was initially in the solvent, as given by the NMR structure. It (together with Leu³⁵) soon moved toward the C terminus of helix 1, was loosely packed against the middle of Lys⁸, and formed a small hydrophobic cluster comprising Lys⁸, Leu³⁵, and Phe³⁶. Judging from the reduction of the hydrophobic surface, the formation appears energetically reasonable. The middle portion (helices 2 and 3) and the hydrophobic core remained stable in the simulation. The average rms difference (rmsd) from the NMR structure was 2.2 Å for the mainchain atoms of residues 9–32 whereas this rmsd varied from 3.2 Å to 8.8 Å during the last 160 nsec of our 200-nsec folding trajectory.

Overall Collapse Occurred Within 100 nsec.

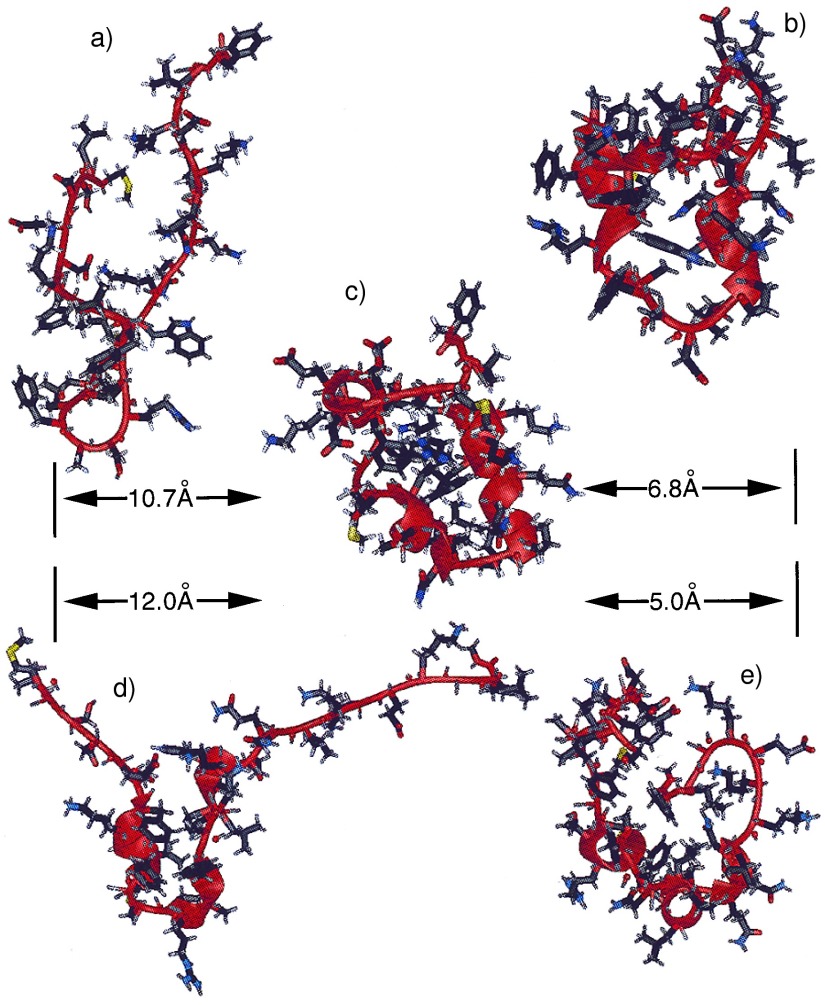
To illustrate some of the structures during the trajectory, Fig. 1 shows a ribbon representation of the native NMR structure (Fig. 1c), the partially folded structures (Fig. 1 b, d, and e), and the fully unfolded starting structure (Fig. 1a). The unfolded starting structure, which was generated from the NMR native structure by a 1.0-nsec MD simulation at 1,000 K, was in an extended state with very few native contacts (<3%) and no helical content. Most of the structural features of the native structure were absent in the unfolded structure. However, the turn feature (Asn²⁰-Leu²¹-Pro²²-Leu²³) was retained partially, even at such an extreme temperature. This observation suggests that the turn may be present even in the fully unfolded forms under typical experimental unfolding conditions. We speculate that the turn structure could be removed with even higher temperature and longer simulation. However, in our opinion, this is not necessary because first, any structure that can be retained at such high temperature should have a high probability to be present in the experimentally unfolded structure, and secondly, such a strong motif should have a high probability to form at the very early stage of the folding process.

Figure 1.

Ribbon representations of the unfolded (a) and the native (c) structures, and the snapshots at 85 nsec (b), at 104 nsec (d), and at 182 nsec (e), generated by using University of California at San Francisco’s midasplus. rmsds from the native state are given in the figure.

The protein was able to find a partially folded structure to a mainchain rms deviation below 6Å within 20 nsec, suggesting that the initiation of folding can occur on the 10–100 nsec time scale for this small protein. The partially folded structure at 85 nsec (Fig. 1b) shows striking similarities to the native structure. It consists of three short helices that are held together by hydrophobic clusters. These three helices correspond approximately to the helical sequences of the native structure. Most of the hydrophobic sidechains became buried, forming hydrophobic clusters. It is also clear that the hydrophobic clusters are different from those in the native structure, resulting in a loosely packed core. The structure bears similarities to molten globules, i.e., extensive secondary structures, partial or incomplete tertiary structures, and a loosely packed hydrophobic core (17).

It should be noted that the definition of a molten globule state of a protein is under discussion. A protein may go through a series of partially folded states before reaching its final folded native state. These partially folded states may feature partially correctly folded secondary and tertiary structures. It is probably semantic (32) to classify the partially folded structures either as molten globule or as premolten globule. However, the partially folded structures from the simulation, as exhibited in Fig. 1, do have the features typical of molten globules. In these compact states, the sidechain mobility, as indicated by the rms fluctuation of the dihedral angle χ, reached a level comparable to that of the folded state and about half of the level of fluctuation exhibited in the unfolded states.

The protein spent ≈13% of the 200 nsec in compact states whose radius of gyration (R_γ) ≤ 9.87 Å (105% of the native structure R_γ, 9.40 Å). Among these compact structures, almost half had water molecules within 5 ņ from the center of the protein. Comparatively, there is no water molecule in the corresponding sphere of the native structure. This suggests that the compact states can be in both “wet” and “dry” forms, (33) water may not be a necessary ingredient of the molten globule states, and full “dehydration” can occur in early stage of folding.

Overall Expansion–Contraction Process Dominated the Trajectory.

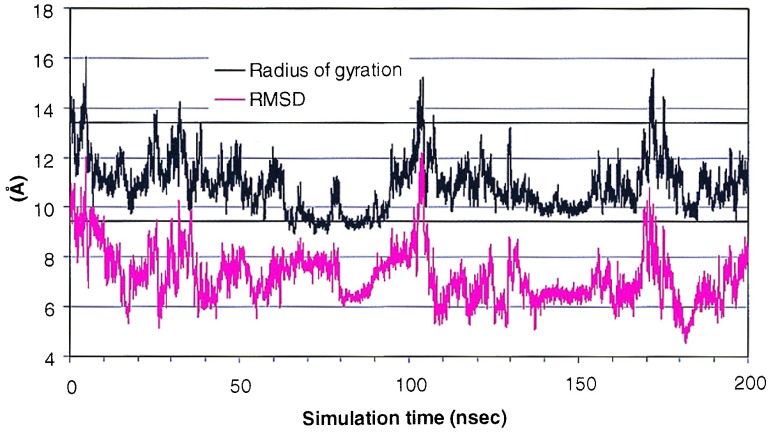
As a simple measure of this complicated process, the R_γ gauges the overall shape of the protein in the folding process. Fig. 2 shows the time development of the R_γ during the course of the simulation. The R_γ of the native structure is 9.4 Å and that of the starting structure was 13.4 Å. The structure underwent further expansion and the R_γ reached 15.9 Å at 4.7 nsec. It quickly collapsed, with an R_γ below that of the native structure, to 9.2 Å at 64.7 nsec. It remained collapsed until ≈100 nsec and then underwent dramatic expansion, and the R_γ reached 14.8 Å at 103.2 nsec. The collapsing–expansion process occurred two more times in the remaining 100 nsec, with slightly smaller magnitude and a shorter “cycle”.

Figure 2.

R_γ and the mainchain rmsd from the native structure as a function of time. The straight lines represent the R_γ of the starting structure (upper line) and the native structure (lower line).

The rmsd is a simple measure of the difference between the simulated and the native structures. Illustrated in Fig. 2 is the time development of the mainchain rmsd along the trajectory. The protein started from initial rmsd of 10.0 Å. It quickly approached the native structure to an rmsd of 5.5 Å at 17.2 nsec. In the subsequent ≈180 nsec, the rmsd fluctuated between ≈6 Å and 10 Å, reaching a low rmsd of 4.8 Å at 182 nsec. This process was accompanied by the collapse of the overall structure. The rmsd and the R_γ showed a significant correlation. The correlation coefficient between the rmsd and the R_γ was 0.52 for 0–100 nsec, 0.70 for 100–200 nsec, and 0.56 overall.

There were also interesting examples of a lack of correlation between rmsd and R_γ. For example, at ≈80 nsec, the structure underwent a sudden expansion from a R_γ of 9 Å to >11 Å for a short period of time while the rmsd changed from ≈8 Å to ≈6 Å. This type of event took place a few times in the trajectory (e.g., at ≈18 nsec, ≈105 nsec, etc.). This suggests that large scale structural changes can occur that can lead to overall expansion of the protein in a short period of time. This expansion may be one of the mechanisms for the protein to overcome energy barriers to find energetically more favorable states. Taken together, both local adjustment and large scale structural changes are possible routes for conformational search. The latter can be effective for “jumping” out of the deep free energy minima, enabling further search of the conformations.

It is noteworthy that previous studies have indicated that proteins may unfold when trapped in misfolded structures. An example is the involvement of the molecular chaperonins in protein folding (34). One of the possible mechanisms for the molecular chaperonins to rescue a misfolded protein is by unfolding the misfolded intermediates (35). The chaperonins are thought to bind favorably to the hydrophobic patches exposed on the protein surface and to unfold the protein, allowing the folding process to start over. Our trajectory suggests that unfolding is one of the intrinsic mechanisms for the protein to jump out of the local minima when trapped in a misfolded state. On the other hand, the quick turnover from a partially folded state to the unfolded state within 10 nsec also suggests that the free energy barrier between the early-stage partially folded and unfolded states may be small. However, an accurate calculation of the free energy profile requires complete sampling in the respective conformational regions, which is beyond the scope of present study. Nevertheless, the simulation suggests that early stage folding has the characteristics of shallow free energy “traps” that allow the protein to unfold within 10 nsec. After carrying out high temperature unfolding of ubiquitin, Alonso and Daggett (36) also observed a collapse and reexpansion of the molecule when the unfolded structure was simulated at 300 K for 2.0 nsec. It is thus reasonable to expect that such collapse and expansion cycles are general, with the time scale governed by the stability of the collapsed states. It remains to be seen whether the shallow free energy traps are features unique to small proteins whereas larger proteins (≈100 residues) might have deeper traps in the early stage.

Formation of Secondary Structure Elements.

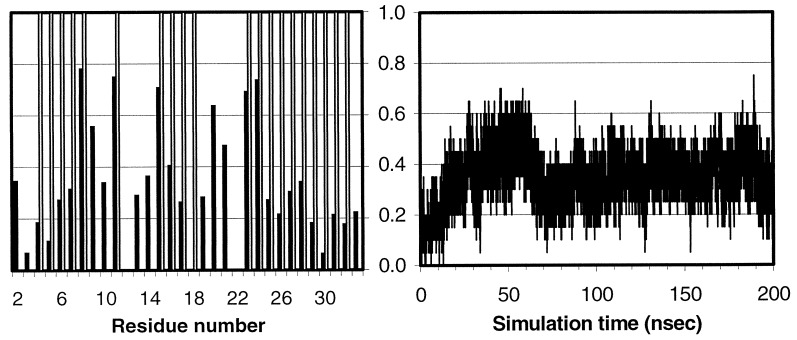
Experimental evidence has shown that nascent secondary structure elements can form in an early stage of folding (37). Fig. 3 shows the fractional native helical content over the course of the simulation and the fractional average helical content (see caption). The helices started to form almost immediately (<1.0 nsec) and reached a 40% level within 20 nsec. At ≈50 nsec, the native helical content reached >50%, sometimes even to the 70% level. This time scale is in good qualitative agreement with experimentally observed values (38). However, the native helical content started to drop at ≈60 nsec and reached a level <20%. It then fluctuated at ≈36 ± 7% in the remaining time. Overall, the helical content (averaged over the molecule) was 36%, close to the overall helical percentage of all proteins as observed in currently available crystal structures (39). Of the residues in the HP-36, 11 spent >36% and 8 spent >50% of time in helical region. This is in line with the expectation that early stage helix formation is nonspecific in nature.

Figure 3.

Helical content measured by the mainchain φ-ψ angle (−60 ± 30, −40 ± 30) from 10,000 snapshots (20 psec intervals). (Left) The average over the trajectory. The shaded bars represent the residues that are helical in the NMR structure. (Right) The fractional native helical content (i.e., those presented in both the native and the simulated structures divided by the total in the native structure) as a function of time.

The formation started from isolated residues whose mainchain φ-ψ angles fell into the helical region (−60, −40). These isolated helical “domains” then grew to form short helices, and neighboring “domains” also merged together to form longer helices. This process was accompanied by the melting-down of the helices that has been typical in the unfolding process, indicating that these helices were not stable. Through these formation-breaking cycles, the protein was also able to sample local conformations. The instability of the helices also was indicated by their nascent nature. Therefore, it is natural to conclude that the helices were stabilized at least partially by the interactions with other parts of the protein in addition to the intrinsic stability of the helices. This is consistent with experimental studies of secondary structures; namely, the completion of the secondary structures is correlated with the formation of the tertiary structure, and the intrinsic stability of the secondary structures is low when exposed in the aqueous solvent (40).

Native Contacts.

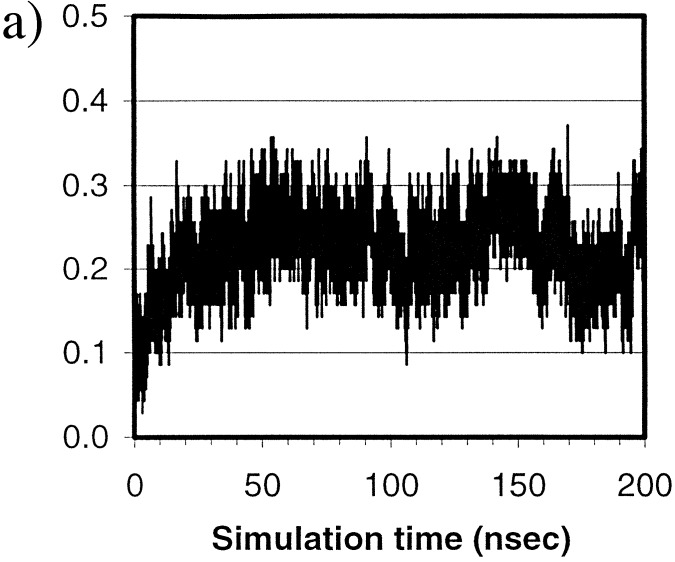
Fig. 4a shows the overall fractional native contacts, Q, (see legend) in the simulation. There are a total of 70 native contacts in the native structure. Overall, the Q started from below 3% and reached 30% within ≈20 nsec and fluctuated at ≈25% for the remaining simulation time.

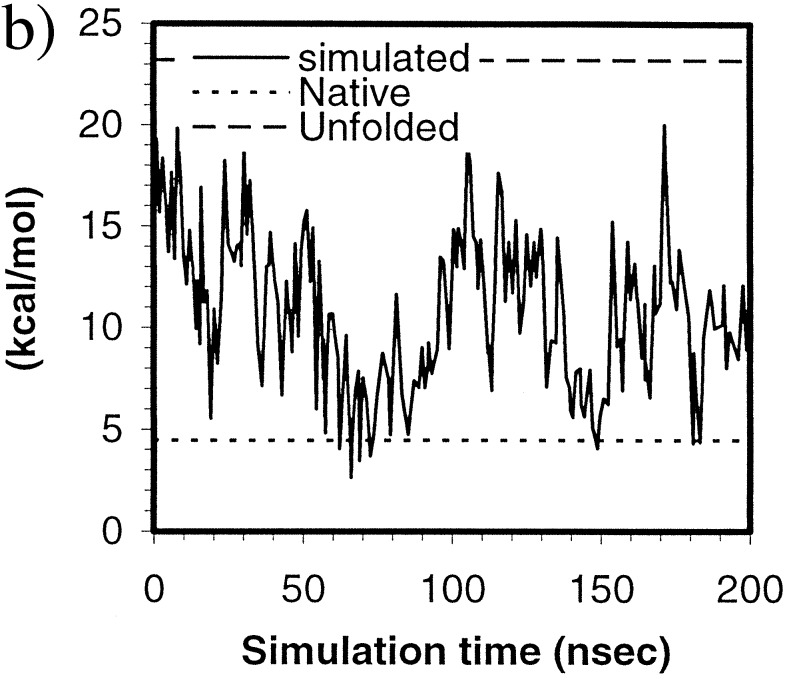
Figure 4.

(a) Fractional native contacts, Q, as a function of time. The native contacts were measured as the number of neighboring residues presented in the native structure. Residues are taken to be in contact if any of the atom pairs (including both sidechain and mainchain atoms) are closer than 2.8 Å, excluding residues i and i+1, which always have the contacts through mainchain atoms. Fractional native contact is the number of total native contacts presented in the simulated structure divided by the number of native contacts in the native structure. (b) SFE of the protein as a function of time. The upper dashed line represents the SFE of the starting structure, and the lower dotted line represents that of the native structure. The parameters are those by Eisenberg and McLachlan (43), (i.e., 0.0163, −0.00637, 0.02114, −0.02376, −0.05041, in kcal/mole/Ų, for the surface areas of nonpolar, polar, sulfur, charged oxygen, and charged nitrogen, respectively).

At ≈100 nsec, the structure started to unfold and became fully unfolded at 103.2 nsec; the R_γ reached 14.8 Å, higher than the starting value of 13.4 Å; the rmsd reached 11.9 Å, also higher than the starting value of 10.0 Å. However, Q was maintained at or above 10%, higher than the starting value of 3%. In fact, Q was always above the starting value throughout the simulation despite the fact that the protein continued to expand and collapse. Evidently, some of the native contacts and native features were maintained in those unfolded states in contrast to the starting structure. Therefore, the search from these “unfolded” states after the beginning was not a true “start-over”. Rather, the refolding started from a somewhat different state than the starting one. These states can be comparable in radius of gyration but nevertheless have more native contacts than the starting structure.

The 30% level of the native contacts is typical for early stage folding, as indicated by unfolding simulations (41). Simulation studies on the chymotrypsin inhibitor 2 also have suggested that a free energy barrier (7, 42), characterized by entropic contributions (7), occurs in the early stage of folding at the vicinity of 25–30% native contacts. It is interesting to observe the similar qualitative behavior in this simulation. As demonstrated vividly by the folding simulation, the protein quickly approached the level of 30% native contacts within ≈20 nsec but remained essentially at a similar level for the remaining of the simulation, suggesting two distinct phases involved in the early stage of protein folding. The first phase is a burst phase. The protein quickly reached a 30% native contact level within 20 nsec. Meanwhile, both the R_γ and the rmsd also approached native levels quickly. The second phase is a slow adjustment phase. The level of native contacts remained between 20% and 30% throughout the remaining of the trajectory whereas adjustments of the R_γ and the rmsd took place.

Among the native contacts, seven maintained contacts for better than 60% of the simulation time. They are all helical contacts (i.e., I, I+3 and I, I+4). In contrast, most of the helix–helix contacts remained in contact for <10% of the time, suggesting that formation of secondary structures dominated early stages of folding and that tertiary contacts are still nonspecific.

The Solvation Free Energy (SFE).

SFEs were calculated by using the formalism of Eisenberg and McLachlan (43) and are shown in Fig. 4b. As one can see, the structure reached a near-native SFE at ≈60 nsec and fluctuated near that value for ≈30 nsec. There was generally a correlation between the SFE and the R_γ, (Table 1) as expected; the correlation coefficient was 0.72.

Table 1.

Correlation coefficients between the energy and surface terms (column) and the R_γ and the rmsd from the NMR strucutre (20), obtained from 200 structures (≈1.0 nsec interval)

	rγ	Mainchain rmsd
SFE	0.72	0.36
Nonpolar surface area	0.85	0.47
Polar surface area	0.51	0.18
Sulfur surface area	0.57	0.29
Charged oxygen surface area	0.14	0.01
Charged nitrogen surface area	0.39	0.22
Mainchain oxygen and nitrogen	0.56	0.33
Number of hydrogen bonds	−0.54	−0.35
Total potential energy	0.45	0.06
Protein internal energy	0.70	0.43
Protein–water interaction energy	−0.64	−0.42
Water–water interaction energy	0.51	0.16
Water–water + water–protein energy	−0.06	−0.15

Also given in Table 1 are the correlation coefficients between various energy and surface terms and the R_γ and rmsd. The strongest correlations were between the R_γ and the nonpolar surface area (0.85), the protein internal energy (0.70), the protein–water interaction energy (−0.64), the number of intramolecular hydrogen bonds (−0.54), and the total water–water energy (0.51). The data suggest that the primary driving force was the burial of hydrophobic surface; the secondary driving force appeared to be the loss of water–protein hydrogen bonds. These observations are in good agreement with other theoretical studies, including those low resolution simulations (5). Taking together, both the water–water interaction and the intramolecular interactions of the protein were among the driving forces of the initial collapse and the early stage (submicrosecond) folding process of HP-36. These favorable interactions, however, were compensated partially by the protein–water interactions. Overall, the water energy (including water–water and water–protein) had a very weak (almost negligible) correlation with the R_γ, only −0.06. Because the release of water is certainly entropically favorable, the simulation suggests that the contributions of water are primarily entropic in nature. The surface area and energy terms had much weaker correlation with the rmsd, also listed in Table 1, and the strongest was the nonpolar surface area, 0.47.

The Initiation Site.

As shown in Fig. 3, the residues Lys⁸, Phe¹¹, Arg¹⁵, Leu²³, and Trp²⁴ spent >70% of the 200 nsec in the helical region. These residues are either at the beginning of a helix or at the end of a helix. Leu²³ and Trp²⁴ are at the beginning of helix 3. Residues Lys⁸, Phe¹¹, and Arg¹⁵ are part of helix 1 and 2. The correct formation of these helical residues is important for the overall topology of the structure. The early formation of these motifs (within 100 nsec) suggests that the folding of this small protein may be initiated in these regions.

CONCLUSIONS AND PERSPECTIVE

In this paper, we present a detailed molecular simulation of the early stage folding events of a real protein by using a reasonably realistic all-atom and explicit water representation of the system for 200 nsec. We observed a “burst” phase within 60 nsec, characterized by the quick increase of both native contacts and native helical content and quick decreases of both R_γ and rmsd. A “slow” adjustment phase also was observed, characterized by somewhat stagnant native contacts and adjustments of R_γ and rmsd. These adjustments can sometimes be dramatic and of large scale.

We also found secondary structure elements forming on the 10-nsec time scale and the primary mechanism for secondary structure formation is by “growing and merging”. Burial of the hydrophobic surface dominated the early-stage folding process and appeared to be the primary driving force, the hydrogen bonding formation played a secondary role in the collapse, and the energy was one of the driving forces. Among the energy components, both the protein internal energy and the water–water interaction energy contributed to the collapsing process; the protein–water interactions, however, had a negative correlation with R_γ. The overall contribution from water, including both water–water and water–protein, are entropic in nature.

Our simulation suggests that small proteins can “find” structures within ≈5 Å rmsd from the native structures within 20–100 nsec. These partially folded structures share the characteristics of molten globules, namely, partially formed secondary structures with a loosely packed hydrophobic core. These structures are only marginally stable and can unfold before becoming more stable structures.

Being able to visualize the folding process of even a small protein in a realistic environment has been a goal of many researchers. We believe our work marks the beginning of a new era of the active participation of full scale simulations in helping to understand the mechanism of protein folding in addition to the active role such simulations have played in the past, such as unfolding simulations. Microsecond scale simulations of small proteins in a fully solvated environment are now feasible and are underway in our lab. We note that, because a T3E is ≈4 times the speed of a T3D and our code scales the same on both machines, had our simulation been run on the T3E for the same amount of real time (40 days), a trajectory of 800 nsec would have been generated. Equally exciting, the experimental methods soon should allow experimentalists to study protein folding on a time scale below 20 μsec. Thus, we are within an order of magnitude or so of direct and realistic comparisons between experimental and simulation studies of protein folding on the same time scale. These comparisons also should provide a useful and critical assessment of the accuracy of the simulation models, such as force fields. From that, further refinement of such model parameters can be made. This is particularly exciting given the fact that a fast folding small protein has been produced that is capable folding completely to its native structure within 20 μsec (44). It is expected, with the promises of even faster CPU and higher level parallelism, that the simulation of a complete folding process of a fast folding small protein is on the horizon.

We have presented only a single trajectory of protein folding and, to be complete, a number of trajectories should be run starting with different structures. The chaotic nature of MD trajectories has been discussed recently (45, 46). It is clear that the trajectories are only representative in a statistical sense. Nonetheless, our preliminary simulations on protein G B1 domain suggests that the initial stage of formation of some secondary structures and a hydrophobic core is similar.

Finally, the use of nonbonded cutoffs used here is an inherent source of “noise” in the simulation trajectory. Such noise is not as deleterious in small proteins with limited formal charges as it is in, for example, RNA and DNA. (47) But accurate inclusion of long range electrostatic effects (16) does provide an additional challenge for achieving high parallelism in the MD code. Work is in progress in our group to include long range electrostatics while achieving a level of parallelism and speed comparable to that presented here.

ABBREVIATIONS

MD

molecular dynamics

PSC

Pittsburgh Supercomputing Center

CPU

central processing unit

SFE

solvation free energy

rmsd

rms difference