Abstract
Cyclin-dependent kinase 2 (CDK2) is the most thoroughly studied of the cyclin-dependent kinases that regulate essential cellular processes, including the cell cycle, and it has become a model for studies of regulatory mechanisms at the molecular level. This contribution identifies flexible and rigid regions of CDK2 based on temperature B-factors acquired from both X-ray data and molecular dynamics simulations. In addition, the biological relevance of the identified flexible regions and their motions is explored using information from the essential dynamics analysis related to conformational changes of CDK2 and knowledge of its biological function(s). The conserved regions of CMGC protein kinases’ primary sequences are located in the most rigid regions identified in our analyses, with the sole exception of the absolutely conserved G13 in the tip of the glycine-rich loop. The conserved rigid regions are important for nucleotide binding, catalysis, and substrate recognition. In contrast, the most flexible regions correlate with those where large conformational changes occur during CDK2 regulation processes. The rigid regions flank and form a rigid skeleton for the flexible regions, which appear to provide the plasticity required for CDK2 regulation. Unlike the rigid regions (which as mentioned are highly conserved) no evidence of evolutionary conservation was found for the flexible regions.
Keywords: protein, dynamics, evolutionary conservation, cell cycle, protein kinase
The dynamic motions of proteins are being intensively studied by structural biologists. These motions are known to play essential roles (inter alia) in protein folding, enzyme catalysis, recognition processes, and signaling (Iakoucheva et al. 2002; Daidone et al. 2003; Daniel et al. 2003; Teague 2003; Yuan et al. 2003; Chen et al. 2005; Eisenmesser et al. 2005; Hung et al. 2005; Schlessinger and Rost 2005; Olsson et al. 2006). This implies that proteins must have appropriate dynamics, and sufficient flexibility, to fulfill their biological functions. If so, proteins’ flexibility is presumably subject to selective pressures. Similar pressures are generally accepted to have led to the evolutionary conservation of the structure and sequence of homologous proteins, allowing us to assign proteins to homologous families, construct homology models, etc. (Lesk and Chothia 1980; Chothia and Lesk 1986; Russell et al. 1997; Wood and Pearson 1999). Thus, we can further hypothesize that certain aspects of protein dynamics that are related to key functions may be conserved in homologous proteins. This hypothesis is explored in the study presented here.
To test the hypothesis we have identified flexible and rigid regions in human cyclin-dependent kinase-2 (CDK2), assigned biological roles to these regions, and analyzed the primary sequences of CMGC protein kinases (see next paragraph) to identify putatively correlated regions of conserved primary sequences. CDK2 (Fig. 1A) was chosen for the study because (i) its regulation and functions have been intensively investigated (see next paragraph), (ii) major structural changes appear to be essential for the successful execution of its biological functions (Tobi and Bahar 2005), (iii) structural changes involved in its regulation correlate with its intrinsic dynamics (Tobi and Bahar 2005), and (iv) the evolutionary conservation of primary sequences and structures in the PK family of proteins have been thoroughly examined (Kannan and Neuwald 2004).
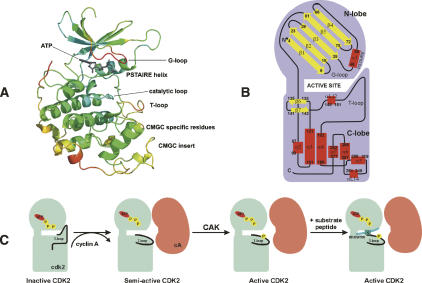
Figure 1.
Cartoon representation of the CDK2/ATP complex with ATP in licorice housed by the active site. (A) Secondary-structure elements are colored according to their B-factors, from highly flexible red regions, through moderately flexible yellow and green regions, to rigid blue regions. The G-loop covers the ATP phosphate moiety-binding site. The PSTAIRE helix is the CDK contact site for regulatory subunits. The activation segment, known as the T-loop, is labeled. CDKs (and MAPK, GSK, and Cdc-like kinases) contain the CMGC insert. CMGC-specific residues form the contact site between the CMGC insert and the T-loop. (B) Schematic representation of secondary structure elements of cyclin-dependent protein kinase-2; α-helixes in red and β-strands in yellow. This scheme illustrates the structure of human CDK2 in complex with ATP in various activity states. The monomer CDK2, where the T-loop blocks the active site cleft, is inactive, and its activation requires cyclin binding. When cyclin A (cA) binds, the PSTAIRE helix rotates to the active conformation and the ATP phosphates obtain a proper orientation for catalytic reaction (Morgan 1996). (C) CDK2 requires for its complete activation phosphorylation by CAK at Thr160 in the T-loop. The substrate peptide (HHASPRK) binds between T- and G-loops.
CDK2 is a cyclin-dependent kinase (CDK), and hence a member of the CMGC subfamily of protein kinases (PKs), which includes CDKs, MAPK, GSK, and Cdc-like (CLK) kinases (classification according to Hanks and Quinn) (Hanks and Quinn 1991; Manning et al. 2002). The best-characterized members of CDKs are involved in controlling progression through the cell cycle (Morgan 1997; Malumbres and Barbacid 2005). The kinase activity of cell cycle-controlling CDKs is tightly regulated during the course of the cell cycle at several levels, including interactions with activation subunits (cyclins) (Morgan 1995; Otyepka et al. 2006; Zhang et al. 2006), binding to negative protein regulators (CDK inhibitors or CKIs) (Sielecki et al. 2000; Knockaert et al. 2002; Fischer et al. 2003; Meijer and Raymond 2003), (de)phosphorylation (Russo et al. 1996b; Brown et al. 1999; Johnson and Lewis 2001; Bártová et al. 2004; Bártová et al. 2005), and subcellular localization (Dhavan and Tsai 2001; Mapelli and Musacchio 2003). The mechanism of CDK2 regulation has been investigated in many structural (De Bondt et al. 1993; Morgan 1996; Russo et al. 1996a; Russo et al. 1996b; Johnson et al. 1998; Johnson and Lewis 2001), mutational (Grant et al. 1996; Hemmer et al. 1997; Sharma et al. 1999), and theoretical studies (Bártová et al. 2004; Barrett and Noble 2005; Bártová et al. 2005; De Vivo et al. 2006) and is now widely used as a model of CDK activation. Full activation of CDK2 requires both binding of cyclin A or cyclin E and phosphorylation of residue T160 in the activation segment (also known as the T-loop) by the CDK-activating kinase (CAK) (Fig. 1C; Russo et al. 1996b). In the absence of these features, it has negligible activity because the residues that form the catalytic and substrate-recognition sites are disordered (De Bondt et al. 1993). The structure of cyclin A (Brown et al. 1995) does not change significantly during CDK2 activation, but many of the CDK2 residues are realigned toward their active configuration (Jeffrey et al. 1995).
Results
Dynamics from X-ray data
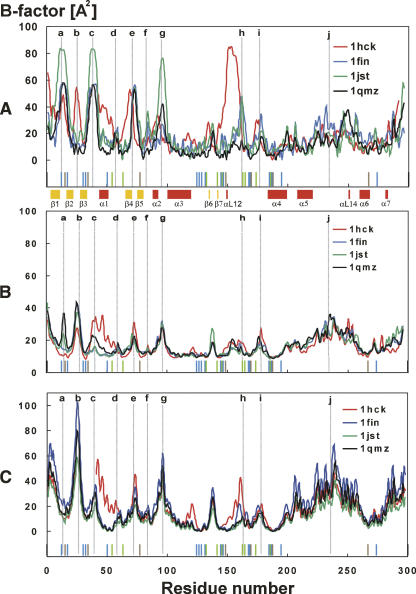
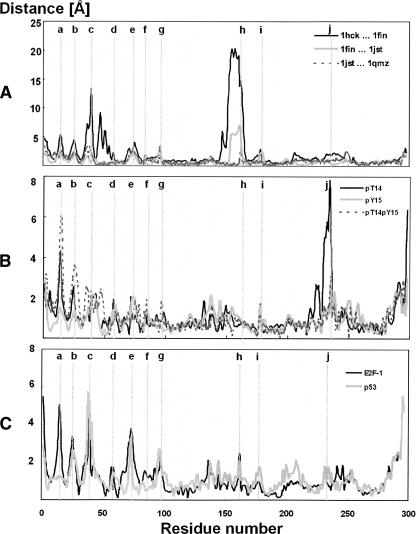
Some information about the flexibility of the studied systems can be acquired from temperature B-factors obtained from the X-ray data and their differences among the studied systems (Fig. 2A). The highly flexible residues 13–15 (Fig. 2A, peak a) belong to the glycine-rich loop (G-loop), which has been identified as an inhibitory segment of CDK2 roofing the ATP-binding site (Bossemeyer 1994). The flexibility and motion of this loop are dependent on phosphorylation of this region, and this has been discussed elsewhere (Bártová et al. 2004, 2005). The peak at residue 25 (Fig. 2A, peak b) corresponds to the loop between the β2 and β3 strands (Fig. 1B) in the N-terminal lobe and creates a hinge between these secondary structure elements. The B-factor value of this residue corresponds to the flexibility of the G-loop. Residues 36–42 (Fig. 2A, peak c) in the loop preceding the α1-helix (C-helix or PSTAIRE helix in CDK2) provide the flexibility of the α1-helix required to allow its shift during activation, i.e., after binding of the regulatory subunit (Russo et al. 1996b; Kannan and Neuwald 2004). The high flexibility of this loop is observed in the X-ray structures of the active CDK2, and its flexibility in the noncomplexed CDK2 is underlined by the fact that it is disordered in several X-ray crystal structures (for example, 1AQ1, 1CKP, 1HCK, 1HCL). Residues 71–76 (Fig. 2A, peak e) form another flexible loop between strands β4 and β5 of the N-terminal lobe. This region contacts the regulatory subunit and presumably also CDK2 substrates. Residues 95–98 (Fig. 2A, peak g) correspond to the loop between the α2 and α3 helices. The flexibility of this loop increases when CDK2 is in complex with cyclin A, while α3-helix flexibility is decreased after cyclin A binding (Bártová et al. 2004). Residues 150–158, corresponding to the activation segment (T-loop), are extremely flexible in CDK2 that is not bound to cyclin but not in any of the CDK2–cyclin complexes. In cases where cyclin A is present, this peak vanishes because of the intensive interaction between the T-loop and cyclin A (Jeffrey et al. 1995). In contrast, the regions spanning residues 177–180 (Fig. 2A, peak i) and 220–260 (Fig. 2A, peak j) are highly flexible, according to the X-ray structures, in all of the inactive, semi-active, and active forms of CDK2 examined. The highly flexible 220–260 region includes nearly all of the highly mobile CMGC insert (also called the “CDK insert” region: residues 219–251), the flexibility of which has been recently discussed (Barrett and Noble 2005).
Figure 2.
(A) Comparison of temperature B-factors from the X-ray crystal structures; 1hck (free CDK2) is shown in red, 1fin (CDK2/cyclin A/ATP) in blue, 1jst (pT160-CDK2/cyclin A/ATP) in green, and 1qmz (pT160-CDK2/cyclin A/ATP/HHASPRK) in black. (B) Comparison of temperature B-factors calculated from the MD simulations; 1hck (free CDK2) is shown in red, 1fin (CDK2/cyclin A/ATP) in blue, 1jst (pT160-CDK2/cyclin A/ATP) in green, and 1qmz (pT160-CDK2/cyclin A/ATP/HHASPRK) in black. (C) Theoretical B-factors calculated using oGNM; 1hck (free CDK2) is shown in red, 1fin (CDK2/cyclin A/ATP) in blue, 1jst (pT160-CDK2/cyclin A/ATP) in green, and 1qmz (pT160-CDK2/cyclin A/ATP/HHASPRK) in black. Regions discussed in the text are labeled by small letters: “a” identifies residue 15, “b” residues 25 and 26, “c” residues 38 and 39, “d” residue 57, “e” residue 73, “f” residue 84, “g” residues 95 and 96, “h” residue 162, “i” residue 178, and “j” residue 234. The evolutionarily conserved residues in primary sequences of the CMGC group of kinases are marked above the residue number scale: The residues marked in blue sticks represent the identical entities in the CMGC group, residues in red sticks are semi-conserved residues in the CMGC group, and residues in green sticks represent the conserved residues in the CMGC group.
Dynamics from molecular dynamics simulations
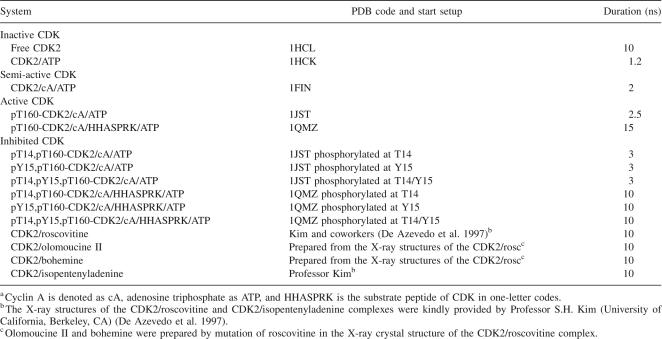
Molecular dynamics (MD) simulations provide detailed information about the motions and dynamics of the system studied (Table 1). Analyses of trajectories from MD simulations allow us to calculate temperature B-factors from time-averaged atomic fluctuations. Although these B-factors are not directly comparable with the X-ray B-factors, as they are averaged over space, they provide information about flexibility. In addition, MD provides valuable data about long-range motions and correlated motions, and it allows thermal fluctuations and long-period motions to be distinguished (Garcia 1992; Cui and Bahar 2006).
Table 1.
Summary of simulations performed and the CDK2 forms investigateda
The B-factors calculated from MD generally correlate well with the B-factors determined from X-ray data. The Spearman correlation coefficients are equal to 0.60, 0.49, 0.46, and 0.73 for 1HCK, 1FIN, 1JST, and 1QMZ, respectively, and all coefficients are statistically significant at the α = 0.05 level of significance. They identify the same flexible regions: the G-loop (Fig. 2B, peak a), the β2/β3-loop (Fig. 2B, peak b), the loop preceding the α1-helix (Fig. 2B, c), the β4/β5-loop (Fig. 2B, e), the α2/α3-loop (Fig. 2B, g), the β6/β7-loop (residues 135–141), the T-loop (Fig. 2B, h), the αL12/α4-loop (residues 173–183) (Fig. 2B, i), and a large region (residues 169–260) including part of the CMGC insert (residues 220–235) (Fig. 2B, j). The B-factors obtained from the MD simulations indicate that the flexibility of the α1-helix and its preceding loop is reduced, while that of the G-loop and the β2/β3-loop is increased, by cyclin A binding (Fig. 2B, peak c). A corresponding reduction can be seen in the X-ray–based B-factors for the α1-helix but not for the preceding loop, which is disordered in the X-ray structures of the free CDK2. Furthermore, no high B-factors were detected for the T-loop region in free CDK2 corresponding to those obtained from the X-ray data. This apparent discrepancy may be explained by the existence of two or more conformations of the T-loop preventing a clear electron density in X-ray analysis. On the other hand, the MD simulations fluctuate around one local conformation at the available nanosecond timescale, and large conformational changes may occur beyond this timescale.
The B-factors calculated from the MD simulations were also used to define the rigid regions of CDK2. The N-terminal β-sheet formed by five strands (β1–β5) is highly rigid. The N-terminal domain forms the ATP-binding site (β3), the nucleotide-binding site (β4), and the hinge region (residues 80–83). Ile10 (located in the C terminus of the β1 strand) and Val18 (located in the β2 N terminus) are both highly rigid. These residues interact with the ATP adenine moiety and flank the highly flexible G-loop. The Lys33 in the middle of the β3 strand is also highly rigid. This residue interacts with ATP and plays an important role in proper alignment of the ATP phosphate moiety for the γ-phosphate transfer reaction. A high degree of rigidity is also observed at the catalytic loop (residues 125–132) and β7–αL12 region, where residues involved in the ATP γ-phosphate transfer to the peptide substrate are localized. Helices forming the C-terminal helical bundle (namely, the large α3 and α4 helices) and the other regions with α-helical secondary structure are also very rigid. Residues forming the proline pocket (e.g., V164) also belong to elements with high degrees of rigidity. The highly rigid region (residues 80–83) forms a rigid hinge that is important for mutual motions of the N- and C-terminal lobes of CDK2 (Otyepka et al. 2002) and makes a wall for the ATP active site.
Normal modes calculated by the Gaussian network model (GNM)
The B-factors calculated by the GNM method identify the same flexible regions as MD (Fig. 2C) with an only exception in the G-loop (Fig. 2C, peak a). The flexibility of the G-loop depends on the r c cutoff parameter used. In general, the flexibility of the G-loop increases with decreasing cutoff distance. The cutoff distance considerably influences the GNM results as shown recently in Sen and Jernigan (2006). The authors conclude that it would be useful to introduce a special amino acid type based spring. In general, the GNM results correlate more tightly with MD than with X-ray results as documented by the Spearman correlation coefficients between B-factors calculated from GNM and MD being equal to 0.55, 0.88, 0.87, and 0.84 for 1HCK, 1FIN, 1JST, and 1QMZ, respectively. The same correlation coefficients calculated from GNM and X-ray data are 0.36, 0.50, 0.49, and 0.68 for 1HCK, 1FIN, 1JST, and 1QMZ, respectively. It is obvious that the GNM rapidly evaluates system flexibility. On the other hand, the MD simulations reflect precisely a unique environment for each residue, and in general these should provide more detailed information about system flexibility. But the price is high because of computer time demands required by MD runs at timescales suitably long to acquire converged results.
Essential motions of inactive CDK2
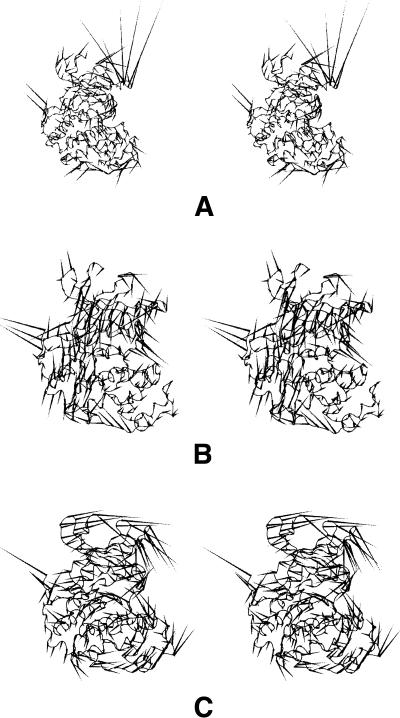
Essential dynamics analysis finds the long-period motions of biological significance. Porcupine plots illustrate the motions exhibited by the first several eigenvectors from the MD simulations of free CDK2 and the CDK2/ATP complex (Fig. 3). In both cases, the first motion is localized to the β3/α1- and β4/β5-loops in the N-terminal lobe (Fig. 3A), which form the binding site for the CDK2 regulatory subunit. These loops were found to be flexible in both the X-ray and MD analyses. The first concerted motions are further spread over the T-loop and some parts of the C-terminal lobe CMGC insert and αL14 helix with adjacent loops (residues 238–242 and 244–249). The T-loop motion is directed toward the entrance to the active site. The next (Fig. 3B) motion is localized to loops forming the ATP-binding site and the T-loop and leads to the ATP-binding site opening. The first three motions of the CDK2/ATP complex (Fig. 3C) are situated near the site where cyclin binding occurs. These motions lead to the opening/closure of CDK2’s lobes, like the opening or closure of a seashell's aperture.
Figure 3.
(A) “Porcupine” plots illustrating the motions represented by the first eigenvector and the second eigenvector (B) from the free CDK2 and the first three motions of CDK2/ATP (C) simulations. In both cases, the first motion is localized in the N-terminal lobe, where the binding site for the CDK2 regulatory subunit (cyclin) is formed (A, C). (B) The next motions lead to the ATP-binding site opening.
Essential motions of semi-active CDK2
The motions of the semi-active CDK2 (i.e., the CDK2/cyclin A/ATP complex) are mainly localized to the β4/β5-loop, T-loop, and CMGC insert, where cyclin-activating kinase (CAK) binds. These motions seem to facilitate access of CAK to the T-loop phosphorylation site (T160 in CDK2) (Fig. 4A,B). The first essential motion is spread over the same parts of the CDK2/ATP and CDK2/cyclin A/ATP complexes but has opposite directions in the two cases.
Figure 4.
(A, B) “Porcupine” plots illustrating the motions represented by the first two eigenvectors from the semi-active CDK2 (i.e., CDK2/ATP/cyclin A complex) simulations. (A) The most significant motions are localized at sites where cyclin-activating kinase (CAK) binds.
Essential motions of active CDK2
The first essential motion of the active CDK2 (pT160-CDK2/cyclin A/ATP) is localized to the β2/β3- and β3/α1-loops in the N-terminal lobe, the α2/α3-loop, and the CMGC insert in the C-terminal lobe (Fig. 5A). The first and third motions also affect the part of the active site where a peptide substrate binds (Fig. 5A,B). This motion provides a “rocking” of the N- and C-terminal domains that coordinate mutual movements of both lobes causing active site opening/closing. A hinge of the motion goes from α1-helix N terminus to α2-helix C terminus and crosses the active site in the proximity of catalytic loop. A similar motion has been identified in previous simulations of CDK2 (Otyepka et al. 2002; Barrett and Noble 2005) and also in PKA (Lu et al. 2005). This motion may assist access or binding of the substrate to the active site. The third motion is spread over residues forming the substrate-binding site.
Figure 5.
“Porcupine” plots illustrating the motions represented by the first eigenvector (A) and the third eigenvector (B) from the active CDK2 (i.e., pT160-CDK2/ATP/cyclin A complex). These motions are localized at loops in the N-terminal lobe and the CMGC insert in the C-terminal lobe. These parts of CDK2 are important for formation and stabilization of the substrate-binding site. (C) The most significant essential motions are localized on segments that also form the peptide substrate-binding site in the CDK2/peptide substrate complex (i.e., pT160-CDK2/cyclin A/ATP/HHASPRK complex).
The most significant essential motions are localized in CDK2 segments that form the peptide substrate-binding site in the pT160-CDK2/cyclin A/ATP/HHASPRK complex (Fig. 5C). The probable effect of these motions is to press the peptide substrate toward the ATP phosphate moiety, which may facilitate the transfer of the ATP γ-phosphate group to the serine of the peptide substrate HHASPRK. The second significant motion involves the G-loop, which also interacts with the peptide substrate. When a substrate peptide is present, this loop has increased flexibility and moves toward it.
Essential motions of CDK2 inhibited by phosphorylation in the G-loop
The most significant essential motions of the pT14,pT160-CDK2/cyclin A/ATP complex are spread over the active site, the regions adjacent to it, and the CMGC insert. Additional essential motions accompany movement of the G-loop away from the ATP-binding site. Such motions open the active site and broaden the substrate-binding site. Similarly, the most significant motions of the pY15,pT160-CDK2/cyclin A/ATP complex cause the active site to open, accompanied by opening of the substrate-binding box (Fig. 6A). The other essential motions are located to flexible loops of the N-terminal lobe, namely, the CMGC insert (Fig. 6A). The significant essential motions of the triply phosphorylated system (pT14,pY15,pT160-CDK2/cyclin A/ATP) are similar to those observed for the systems inhibited by phosphorylation in the G-loop. Similar essential motions were also identified for systems where the substrate peptide HHASPRK is present (Fig. 6B,C).
Figure 6.
(A) “Porcupine” plots illustrating the motions represented by the first several eigenvectors from the simulations of the CDK2 inhibited by phosphorylation of the Y15 residue in the G-loop (i.e., pY15,pT160-CDK2/cyclin A/ATP complex). Similar essential motions were identified after phosphorylation at T14 (i.e., pT14,pT160-CDK2/cyclin A/ATP/HHASPRK complex) (B) and after phosphorylation at Y15 residues (i.e., pY15,pT160-CDK2/cyclin A/ATP/HHASPRK complex) (C) in the system where the substrate peptide is bound to CDK2. The most significant motions in these systems lead to the substrate-binding site opening.
Essential motions of CDK2 complexes with small-molecule inhibitors
The first essential motion of the CDK2/roscovitine complex is localized to the T-loop. The direction of this motion is away from the ATP-binding site, leading to the opening of the substrate-binding site (Fig. 7A). The other essential motions are spread over segments near the ATP-binding site, but the directions of these motions resemble those of explosive or somewhat chaotic motions (see, for instance, Fig. 7B). The first essential motion of the CDK2/olomoucine II complex is localized to flexible loops of the C- and N-terminal lobes and the T-loop (Fig. 7C). The second one affects the T- and G-loops with directions away from the ATP-binding site. The other essential motions are difficult to describe because they resemble chaotic motions, and the essential motions of the CDK2/bohemine complex are even more difficult to characterize since they all appear to be chaotic (Fig. 7D). Only the second essential motion of the CDK2/isopenthenyladenine complex can be easily described and interpreted since it is localized to the flexible N-terminal loop, namely the G-loop, and causes the ATP-binding site to open (Fig. 7E). The other essential motions of the complex can be characterized as chaotic. The connection between binding of CDK2 inhibitors and motions in G- and T-loops has been also reported by Park et al. (2004).
Figure 7.
“Porcupine” plots illustrating the motions represented by the first two eigenvectors from the simulations of the CDK2 in complex with roscovitine (A, B) and by the first eigenvectors from the simulations of the CDK2 in complexes with: olomoucine II (C), bohemine (D), and isopentenyladenine (E). The most significant motions in the complexes of CDK2 with these inhibitors are located at the G- and T-loop, and lead to the ATP-binding site opening. The other motions of these complexes can be characterized as chaotic.
Positional changes during activation processes
We can now identify regions where the most significant conformational changes during the course of CDK2 regulation processes occur, using both the X-ray and MD simulations data. A positional shift of a residue can be easily measured as the mean distance between Cα atom coordinates of the same residue in two superimposed structures. The plot (Fig. 8A) of the positional changes between inactive (1HCK, CDK2/ATP) and semi-active CDK2 (1FIN, complex CDK2/cyclin A/ATP) indicates that the largest positional shifts between these forms are in the T-loop, the α1-helix, and its preceding loop. These changes occur during the course of cyclin A binding, in which the T-loop moves toward the cyclin and the α1-helix rotates, thereby maximizing its contacts with the cyclin. Activating phosphorylation of Thr160 (from 1FIN to 1JST, pT160-CDK2/cyclin A/ATP complex) causes rearrangements in the T-loop conformation accompanied by minor changes in other CDK2 regions. The short peptide substrate binding (from 1JST to 1QMZ, pT160-CDK2/cyclin A/ATP/HHASPRK complex) does not significantly change the CDK2 structure in comparison with previous changes. Nonetheless, binding of peptide substrates (short peptides from E2F and p53 proteins) may induce positional changes in the G-loop, the β2/β3-loop, the loop preceding the α1-helix and the β4/β5-loop i.e., regions where the substrate touches the CDK2 surface (Fig. 8C). Some pronounced structural changes also occur following inhibitory phosphorylations of T14 and/or Y15 (Fig. 8B), not only in the phosphorylated G-loop, but surprisingly also in the CMGC insert.
Figure 8.
(A) Comparison of the changes in CDK2 Cα positions between: cdk2/atp (1hck) and cdk2/cyclin A/ATP (1fin), cdk2/cyclin A/ATP (1fin) and pT160-cdk2/cyclin A/ATP (1jst), and pT160-cdk2/cyclin A/ATP (1jst) and pT160-cdk2/cyclin A/ATP/HHASPRK (1qmz). Comparison of the changes in CDK2 Cα positions between the fully active CDK2 (i.e., pT160-CDK2/cyclin A/ATP complex) and CDK2 inhibited by phosphorylation at T14 (denoted pT14), Y15 (denoted pY15), and T14/Y15 (denoted pT14pY15) residues altogether (B) and between fully active CDK2 and CDK2 in complex with CKI (cyclin kinase inhibitors: E2F-1 and p53) (C). The most significant changes in the CDK2 Cα positions are labeled in the plot, in which label “a” identifies residue 15, “b” residues 25 and 26, “c” residues 38 and 39, “d” residue 57, “e” residue 73, “f” residue 84, “g” residues 95 and 96, “h” residue 162, “i” residue 178, and “j” residue 234.
Discussion
The flexibility of the studied CDK2 systems was explored using thermal B-factors, obtained from both MD simulations, GNM model and X-ray data, and essential dynamics analyses. The B-factors calculated by all approaches correlate well and identify the same flexible regions, except that the T-loop is highly flexible according to the X-ray data but not according to the MD simulations. However, the reason for this apparent discrepancy may be that the T-loop flexibility only appears in timescales that are beyond the range of the nanosecond simulations currently available in classical MD. This well-known limitation of classical MD is called the local conformational trap; it is being intensively investigated, and many techniques with more robust phase-space sampling are being developed to overcome it (Elber and Karplus 1990). The GNM method provides a useful alternative to describe protein flexibility with a relatively low cost.
The essential dynamics analyses have identified the movable regions and revealed correlations between their movements. We have described the essential motions of several CDK2 forms related to its regulation. The most significant motions in the inactive CDK2 are localized in the N-terminal lobe, which forms the binding site for the CDK regulatory subunit. The motions in the free CDK2 are also spread over the T-loop and loops forming the ATP-binding site. These motions correlate with CDK2’s requirement to bind to the regulatory subunit (cyclin) and phosphorylation in the T-loop in order to become active. In the semi-active CDK2 (CDK2/cyclin A complex) the motions were localized to the T-loop phosphorylation site, and these motions may facilitate access of the CAK to the CDK2 phosphorylation site. The most significant motions in the fully active CDK2 seem to facilitate access of the substrate peptide to its binding site on CDK2. Inhibitory phosphorylation on the CDK2 G-loop initiates motions that lead to the opening of the active site and the substrate-binding site. The essential dynamics of CDK2 in complex with purine-like inhibitors is characterized by chaotic essential motions spread over all the flexible loops.
The analyses of positional changes identified regions with the largest shifts in the course of CDK2 regulation processes. Summarized results of all analyses have identified movable regions of CDK2 and changes in their motions during the regulation processes. The N-terminal loops (G-loop, β3/α1-loop, and β4/β5-loop), T-loop, and CMGC insert in the C-terminal lobe are the most flexible regions of CDK2. The largest structural changes also occur in the same regions, which were identified as being highly flexible. Recently, Tobi and Bahar (2005) identified similar correlations between structural changes and intrinsic motions. It can be concluded here that the identified flexible regions allow structural changes that occur during the regulation processes of CDK2.
Since the structural changes in CDK2’s regulatory machinery are crucial for the successful execution of its biological functions, we can further deduce that the flexibility of CDK2 is essential for its biological function. CDK2 regulation involves both interactions with proteins and post-translational modification. So, it is not surprising that the most flexible regions we identified are exposed and involved in many recognition processes that influence CDK2’s biological activities, e.g., interaction with regulatory subunits, kinases, phosphatases, inhibitory proteins, etc.
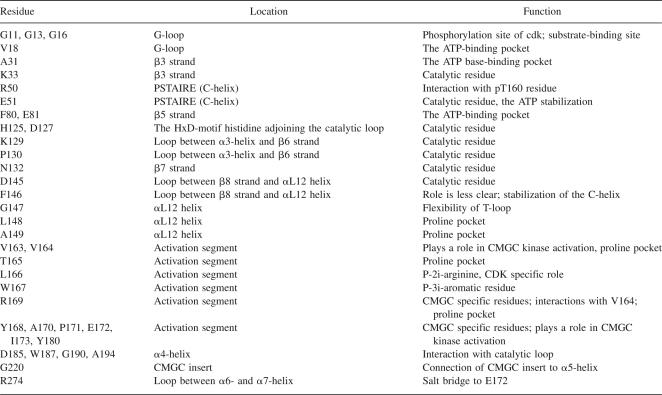
On the other hand, the identified rigid regions are located deep in the CDK2 structure. They create both the ATP-binding site and the substrate-binding box, they are involved in the catalysis of ATP γ-phosphate transfer to its peptide substrates, and they mediate contacts to the activation segment and the CMGC insert (Table 2). Recently, several excellent papers concerned with evolutionary conservation in the CMGC group and larger PK families have been published (Manning et al. 2002; Kannan and Neuwald 2004, 2005). These studies have considered evolutionary conservation in the context of a catalytic cycle i.e., ATP binding, substrate positioning, and ATP γ-phosphate-group transfer, and they have identified highly conserved regions responsible for ATP binding and for alignment of the ATP γ-phosphate-group for catalytic transfer. Comparison of the primary sequence conservation patterns clearly shows that highly evolutionarily conserved regions of CMGC kinases are spread over the rigid regions, with the sole exception of Gly13, which is highly conserved although it is located at the tip of the highly flexible G-loop. This exception can be explained by the presence of three glycines in the G-loop. The biological role of these conserved glycines has been discussed in the literature many times (for examples, see Hanks and Quinn 1991; Bártová et al. 2004).
Table 2.
Summary of conserved residues (using CDK2 numbering) of protein kinases with assigned functions
The regulation of CDK2 is highly dependent on conformational changes that occur in its flexible, exposed regions. The flexible regions, which appear to provide the plasticity required for CDK2 to fulfill its functions, are flanked by other regions that form a rigid skeleton. The rigidity of these regions is attributable to intense intramolecular contacts within the CDK2 molecule and intermolecular contacts with ATP-Mg2+ in the active site. The analysis of the evolutionary conservation of the CMGC kinases’ primary sequences in terms of CDK2 flexibility indicated that the conserved residues are involved in processes that evolved long ago connected with ATP binding and catalysis, i.e., functions common for the whole PK family. These evolutionarily conserved residues are imprinted in the identified highly rigid regions. To our surprise, the flexible regions important for CDK2 function (and probably also for the function of other CMGC kinases) do not correlate with primary sequence conservation patterns, with the sole exception of the glycine-rich loop. We may also hypothesize that the flexibility is conserved in an indirect way, i.e., the evolutionarily conserved residues are important for proper fold with corresponding flexibility. On the other hand, we may also ask whether the available bioinformatics tools are capable to identify evolutionary conservation of flexibility. So, we may conclude that the catalytic function of PK is highly evolutionarily conserved while the regulation strategy has evolved specifically for the biological purpose of each PK and is not shared by other PKs. Nonetheless, the question about flexibility and its evolutionary conservation remains still open and should be investigated at large in future.
Materials and Methods
Molecular dynamics simulations of all CDK2 systems listed in Table 1 were carried out using AMBER 6.0 (http://amber.scripps.edu) with the parm99 force field (Wang et al. 2000). The starting structures were taken from the PDB database (PDB codes 1HCK, 1FIN, 1JST, and 1QMZ), two CDK2/inhibitor complexes were kindly provided by Prof. S.H Kim, and several systems were prepared by (de)phosphorylation and modification of the analogous structures (see Table 1). The MD simulation protocol used was as follows (Bártová et al. 2004, 2005; Otyepka et al. 2006). First, the protonation states of all histidines were checked by WHAT IF (http://swift.cmbi.kun.nl/whatif) to create an optimal H-bond network. Then, all hydrogens were added using the xLeap program from the AMBER 6.0 package (http://amber.scripps.edu). The structures were neutralized by adding Cl– counter-ions for all systems. Each system was inserted in a rectangular water box in which the depth of the layer of water molecules was 10 Å. Then, each system was minimized prior to the production part of the molecular dynamics run in the following way. The protein was frozen and the solvent molecules, and counter-ions, were allowed to move during a 1000-step minimization followed by a 2-ps-long molecular dynamics run under NpT conditions (p = 1 atm, T = 298.15 K). Then, the side chains were relaxed by several consequent minimizations with decreasing force constants applied to the backbone atoms. After the relaxation, the system was heated to 250 K for 10 ps and then up to 298.15 K for 40 ps. The particle-mesh Ewald (PME) (Darden et al. 1993) method for treating electrostatic interactions was used. All simulations were run under periodic boundary conditions in the NpT ensemble at 298.16 K by Berendsen temperature coupling (Berendsen et al. 1984) and a constant pressure of 1 atm using a 2-fs time integration step. The SHAKE algorithm (Ryckaert et al. 1977) with a tolerance of 10−5 Å was applied to fix all bonds containing hydrogen atoms. A 10.0 Å cutoff was applied to nonbonding interactions. Coordinates were stored every 2 ps. The total duration of all production phases for all studied systems was 0.11 μs. The size of the studied systems ranged from 30,000 to 70,000 atoms.
MD trajectories were analyzed by the essential dynamics (ED) technique (Amadei et al. 1996; de Groot et al. 1996; van Aalten et al. 1997). The ED method separates large concerted structural rearrangements from irrelevant fluctuations in a multiparticle system. From the MD trajectory the covariance matrix of the positional fluctuations of the Cα carbon atoms is built up and diagonalized. The procedure yields new axes (eigenvectors), representing the directions of the concerted motions, and eigenvalues representing the displacement variance of the respective eigenvectors (Amadei et al. 1993). In other words, the eigenvectors are directions in a 3N-dimensional space (where N is the number of atoms), and the motion along a single eigenvector corresponds to the concerted displacement of groups of atoms in Cartesian space. This characterizes the essential subspace of the internal dynamics of the studied protein. The motions in the essential space may be linked to the biological function(s) of the protein.
The normal modes for CDK2 and its complexes were computed using the oGNM tool. The oGNM is a web-based system developed by Bahar and coworkers capable of calculating online a protein dynamics employing the Gaussian Network Model (GNM) (Yang et al. 2005, 2006). The GNM model is built on the statistical mechanical theory for describing the fluctuation dynamics of polymer networks (Flory 1976). Accordingly, the structure is modeled as an elastic network with the nodes being the Cα carbon of amino acids, and uniform springs of force constant γ connect the pairs of Cα carbon atoms located within an interaction cutoff distance r c. The calculations were done on structures taken from the PDB database (PDB codes 1HCK, 1FIN, 1JST, and 1QMZ), and an r c = 20.0 Å cutoff was applied. The 1FIN, 1JST, and 1QMZ unique monomers have been used for calculation to avoid crystal contacts.
Temperature B-factors were calculated from the MD simulations using the ptraj module of the AMBER package. B-factors, also known as Debye–Weller factors or temperature factors, describe the reduction in X-ray scattering intensity due to the thermal motion of the atoms, or crystal disorder. A B-factor indicates the true static or dynamic flexibility of an atom and is given by
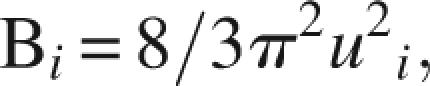 |
where u 2 i is the mean square displacement of atom i.
Essential dynamics analyses of MD trajectories were performed using the GROMACS suite of programs (http://www.gromacs.org), and porcupine plots of essential motions were acquired using the Dynamite web server (Barrett et al. 2004). In the porcupine plots, needles were drawn for all residues corresponding to the implied movement of the respective residues for a given eigenvector. Visualization of system geometries and evaluation of protein secondary structure were performed using VMD (Humphrey et al. 1996). Parameters of the phosphorylated tyrosine and phosphorylated threonine residues were taken from a previous study (Bártová et al. 2004).
Acknowledgments
We thank the Meta Center (http://meta.cesnet.cz) for computer time and Sees-Editing Ltd. (U.K.) for language corrections. The Czech Ministry of Education is acknowledged for financial support (grants MSM6198959216, MSM0021622413, and LC512).
Footnotes
Reprint requests to: Michal Otyepka, Department of Physical Chemistry and Center for Biomolecular and Complex Molecular Systems, Palacký University, třída Svobody 26, 771 46 Olomouc, Czech Republic; e-mail: otyepka@aix.upol.cz; fax: +420-58-5634756.
Article published online ahead of print. Article and publication date are at http://www.proteinscience.org/cgi/doi/10.1110/ps.072951208.
References
- Amadei, A., Linssen, A.B.M., Berendsen, J.C. Essential dynamics of proteins. Proteins. 1993;17:412–425. doi: 10.1002/prot.340170408. [DOI] [PubMed] [Google Scholar]
- Amadei, A., Linssen, A.B.M., de Groot, B.L., van Aalten, D.M.F., Berendsen, H.J.C. An efficient method for sampling the essential subspace of proteins. J. Biomol. Struct. Dyn. 1996;13:615–625. doi: 10.1080/07391102.1996.10508874. [DOI] [PubMed] [Google Scholar]
- Barrett, C.P., Hall, B.A., Noble, M.E.M. Dynamite: A simple way to gain insight into protein motions. Acta Crystallogr. 2004;60:2280–2287. doi: 10.1107/S0907444904019171. [DOI] [PubMed] [Google Scholar]
- Barrett, C.P., Noble, M.E.M. Molecular motions of human cyclin-dependent kinase-2. J. Biol. Chem. 2005;280:13993–14005. doi: 10.1074/jbc.M407371200. [DOI] [PubMed] [Google Scholar]
- Bártová, I., Otyepka, M., Kříž, Z., Koča, J. Activation and inhibition of cyclin-dependent kinase-2 by phosphorylation; A molecular dynamics study reveals the functional importance of the glycine-rich loop. Protein Sci. 2004;13:1449–1457. doi: 10.1110/ps.03578504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bártová, I., Otyepka, M., Kříž, Z., Koča, J. The mechanism of inhibition of the cyclin-dependent kinase-2 as revealed by the molecular dynamics study on the complex CDK2 with the peptide substrate HHASPRK. Protein Sci. 2005;14:445–451. doi: 10.1110/ps.04959705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berendsen, H.J.C., Postma, J.P.M., van Gunsteren, W.F., DiNola, A., Haak, J.R. Molecular-dynamics with coupling to an external bath. J. Chem. Phys. 1984;81:3684–3690. [Google Scholar]
- Bossemeyer, D. The glycine-rich sequence of protein kinases: A multifunctional element. Trends Biochem. Sci. 1994;19:201–205. doi: 10.1016/0968-0004(94)90022-1. [DOI] [PubMed] [Google Scholar]
- Brown, N.R., Noble, M.E.M., Endicott, J.A., Garman, E.F., Wakatsuki, S., Mitchell, E., Rasmussen, B., Hunt, T., Johnson, L.N. The crystal structure of cyclin A. Structure. 1995;3:1235–1247. doi: 10.1016/s0969-2126(01)00259-3. [DOI] [PubMed] [Google Scholar]
- Brown, N.R., Noble, M.E.M., Lawrie, A.M., Morris, M.C., Tunnah, P., Divita, G., Johnson, L.N., Endicott, J.A. Effects of phosphorylation of threonine 160 on cyclin-dependent kinase-2 structure and activity. J. Biol. Chem. 1999;274:8746–8756. doi: 10.1074/jbc.274.13.8746. [DOI] [PubMed] [Google Scholar]
- Chen, C.J., Xiao, Y., Zhang, L.S. A directed essential dynamics simulation of peptide folding. Biophys. J. 2005;88:3276–3285. doi: 10.1529/biophysj.104.046904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chothia, C., Lesk, A.M. The relation between the divergence of sequence and structure in proteins. EMBO J. 1986;5:823–826. doi: 10.1002/j.1460-2075.1986.tb04288.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cui, Q., Bahar, I. Normal mode analysis: Theory and applications to biological and chemical systems. Chapman & Hall/CRC; Boca Raton, FL: 2006. [Google Scholar]
- Daidone, I., Amadei, A., Roccatano, D., Di Nola, A. Molecular dynamics simulation of protein folding by essential dynamics sampling: Folding landscape of horse heart cytochrome c . Biophys. J. 2003;85:2865–2871. doi: 10.1016/S0006-3495(03)74709-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daniel, R.M., Dunn, R.V., Finney, J.L., Smith, J.C. The role of dynamics in enzyme activity. Annu. Rev. Biophys. Biomol. Struct. 2003;32:69–92. doi: 10.1146/annurev.biophys.32.110601.142445. [DOI] [PubMed] [Google Scholar]
- Darden, T., York, D., Pedersen, L. Particle mesh Ewald: An N·Log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993;98:10089–10092. [Google Scholar]
- De Azevedo, W.F., Leclerc, S., Meijer, L., Havlíček, L., Strnad, M., Kim, S.H. Inhibition of cyclin-dependent kinases by purine analogues—Crystal structure of human cdk2 complexed with roscovitine. Eur. J. Biochem. 1997;243:518–526. doi: 10.1111/j.1432-1033.1997.0518a.x. [DOI] [PubMed] [Google Scholar]
- De Bondt, H.L., Rosenblatt, J., Jancarik, J., Jones, H.D., Morgan, D.O., Kim, S.H. Crystal structure of cyclin-dependent kinase-2. Nature. 1993;363:595–602. doi: 10.1038/363595a0. [DOI] [PubMed] [Google Scholar]
- de Groot, B.L., Amadei, A., van Aalten, D.M.F., Berendsen, H.J.C. Towards an exhaustive sampling of the configurational spaces of the two forms of the peptide hormone guanylin. J. Biomol. Struct. Dyn. 1996;13:741–751. doi: 10.1080/07391102.1996.10508888. [DOI] [PubMed] [Google Scholar]
- De Vivo, M., Cavalli, A., Bottegoni, G., Carloni, P., Recanatini, M. Role of phosphorylated Thr160 for the activation of the CDK2/cyclin A complex. Proteins. 2006;62:89–98. doi: 10.1002/prot.20697. [DOI] [PubMed] [Google Scholar]
- Dhavan, R., Tsai, L.H. A decade of CDK5. Nat. Rev. Mol. Cell Biol. 2001;2:749–759. doi: 10.1038/35096019. [DOI] [PubMed] [Google Scholar]
- Eisenmesser, E.Z., Millet, O., Labeikovsky, W., Korzhnev, D.M., Wolf-Watz, M., Bosco, D.A., Skalicky, J.J., Kay, L.E., Kern, D. Intrinsic dynamics of an enzyme underlies catalysis. Nature. 2005;438:117–121. doi: 10.1038/nature04105. [DOI] [PubMed] [Google Scholar]
- Elber, R., Karplus, M. Enhanced sampling in molecular-dynamics—Use of the time-dependent Hartree approximation for a simulation of carbon-monoxide diffusion through myoglobin. J. Am. Chem. Soc. 1990;112:9161–9175. [Google Scholar]
- Fischer, P.M., Endicott, J., Meijer, L. Cyclin-dependent kinase inhibitors. Prog. Cell Cycle Res. 2003;5:235–248. [PubMed] [Google Scholar]
- Flory, P.J. Statistical thermodynamics of random networks. Proc. R. Soc. London A, Mater. 1976;351:351–380. [Google Scholar]
- Garcia, A.E. Large-amplitude nonlinear motions in proteins. Phys. Rev. Lett. 1992;68:2696–2699. doi: 10.1103/PhysRevLett.68.2696. [DOI] [PubMed] [Google Scholar]
- Grant, B.D., Tsigelny, I., Adams, J.A., Taylor, S.S. Examination of an active-site electrostatic node in the cAMP-dependent protein kinase catalytic subunit. Protein Sci. 1996;5:1316–1324. doi: 10.1002/pro.5560050710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanks, S., Quinn, A.M. Protein kinase catalytic domain sequence database: Identification of conserved features of primary structure and classification of family members. Methods Enzymol. 1991;200:38–62. doi: 10.1016/0076-6879(91)00126-h. [DOI] [PubMed] [Google Scholar]
- Hemmer, W., McGlone, M., Tsigelny, I., Taylor, S.S. Role of the glycine triad in the ATP-binding site of cAMP-dependent protein kinase. J. Biol. Chem. 1997;272:16946–16954. doi: 10.1074/jbc.272.27.16946. [DOI] [PubMed] [Google Scholar]
- Humphrey, W., Dalke, A., Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- Hung, A., Tai, K., Sansom, M.S.P. Molecular dynamics simulation of the M2 helices within the nicotinic acetylcholine receptor transmembrane domain: Structure and collective motions. Biophys. J. 2005;88:3321–3333. doi: 10.1529/biophysj.104.052878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iakoucheva, L.M., Brown, C.J., Lawson, J.D., Obradovic, Z., Dunker, A.K. Intrinsic disorder in cell-signaling and cancer-associated proteins. J. Mol. Biol. 2002;323:573–584. doi: 10.1016/s0022-2836(02)00969-5. [DOI] [PubMed] [Google Scholar]
- Jeffrey, P.D., Russo, A.A., Polyak, K., Gibbs, E., Hurwitz, J., Massague, J., Pavletich, N.P. Mechanism of cdk activation revealed by the structure of a cyclin A–cdk2 complex. Nature. 1995;376:313–320. doi: 10.1038/376313a0. [DOI] [PubMed] [Google Scholar]
- Johnson, L.N., Lewis, R.J. Structural basis for control by phosphorylation. Chem. Rev. 2001;101:2209–2242. doi: 10.1021/cr000225s. [DOI] [PubMed] [Google Scholar]
- Johnson, L.N., Lowe, E.D., Noble, M.E.M., Owen, D.J. The structural basis for substrate recognition and control by protein kinases. FEBS Lett. 1998;430:1–11. doi: 10.1016/s0014-5793(98)00606-1. [DOI] [PubMed] [Google Scholar]
- Kannan, N., Neuwald, A.F. Evolutionary constraints associated with functional specificity of the CMGC protein kinases MAPK, CDK, GSK, SRPK, DYRK, and CK2α. Protein Sci. 2004;13:2059–2077. doi: 10.1110/ps.04637904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kannan, N., Neuwald, A.F. Did protein kinase regulatory mechanisms evolve through elaboration of a simple structural component? J. Mol. Biol. 2005;351:956–972. doi: 10.1016/j.jmb.2005.06.057. [DOI] [PubMed] [Google Scholar]
- Knockaert, M., Greengard, P., Meijer, L. Pharmacological inhibitors of cyclin-dependent kinases. Trends Pharmacol. Sci. 2002;23:417–425. doi: 10.1016/s0165-6147(02)02071-0. [DOI] [PubMed] [Google Scholar]
- Lesk, A.M., Chothia, C. How different amino-acid sequences determine similar protein structures—Structure and evolutionary dynamics of the globins. J. Mol. Biol. 1980;136:225–270. doi: 10.1016/0022-2836(80)90373-3. [DOI] [PubMed] [Google Scholar]
- Lu, B.Z., Wong, C.F., McCammon, J.A. Release of ADP from the catalytic subunit of protein kinase A: A molecular dynamics simulation study. Protein Sci. 2005;14:159–168. doi: 10.1110/ps.04894605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malumbres, M., Barbacid, M. Mammalian cyclin-dependent kinases. Trends Biochem. Sci. 2005;30:630–641. doi: 10.1016/j.tibs.2005.09.005. [DOI] [PubMed] [Google Scholar]
- Manning, G., Whyte, D.B., Martinez, R., Hunter, T., Sudarsanam, S. The protein kinase complement of the human genome. Science. 2002;298:1912–1934. doi: 10.1126/science.1075762. [DOI] [PubMed] [Google Scholar]
- Mapelli, M., Musacchio, A. The structural perspective on CDK5. Neurosignals. 2003;12:164–172. doi: 10.1159/000074617. [DOI] [PubMed] [Google Scholar]
- Meijer, L., Raymond, E. Roscovitine and other purines as kinase inhibitors. From starfish oocytes to clinical trials. Acc. Chem. Res. 2003;36:417–425. doi: 10.1021/ar0201198. [DOI] [PubMed] [Google Scholar]
- Morgan, D.O. Principles of CDK regulation. Nature. 1995;374:131–134. doi: 10.1038/374131a0. [DOI] [PubMed] [Google Scholar]
- Morgan, D.O. The dynamics of cyclin-dependent kinase structure. Curr. Opin. Struct. Biol. 1996;8:767–772. doi: 10.1016/s0955-0674(96)80076-7. [DOI] [PubMed] [Google Scholar]
- Morgan, D.O. Cyclin-dependent kinases: Engines, clocks, and microprocessors. Annu. Rev. Cell Dev. Biol. 1997;13:261–291. doi: 10.1146/annurev.cellbio.13.1.261. [DOI] [PubMed] [Google Scholar]
- Olsson, M.H.M., Parson, W.W., Warshel, A. Dynamical contributions to enzyme catalysis: Critical tests of a popular hypothesis. Chem. Rev. 2006;106:1737–1756. doi: 10.1021/cr040427e. [DOI] [PubMed] [Google Scholar]
- Otyepka, M., Kříž, Z., Koča, J. Dynamics and binding modes of free cdk2 and its two complexes with inhibitors studied by computer simulations. J. Biomol. Struct. Dyn. 2002;20:141–154. doi: 10.1080/07391102.2002.10506830. [DOI] [PubMed] [Google Scholar]
- Otyepka, M., Bártová, I., Kříž, Z., Koča, J. Different mechanisms of CDK5 and CDK2 activation as revealed by CDK5/p25 and CDK2/cyclin A dynamics. J. Biol. Chem. 2006;281:7271–7281. doi: 10.1074/jbc.M509699200. [DOI] [PubMed] [Google Scholar]
- Park, H., Yeom, M.S., Lee, S. Loop flexibility and solvent dynamics as determinants for the selective inhibition of cyclin-dependent kinase 4: Comparative molecular dynamics simulation studies of CDK2 and CDK4. ChemBioChem. 2004;5:1662–1672. doi: 10.1002/cbic.200400214. [DOI] [PubMed] [Google Scholar]
- Russell, R.B., Saqi, M.A.S., Sayle, R.A., Bates, P.A., Sternberg, M.J.E. Recognition of analogous and homologous protein folds: Analysis of sequence and structure conservation. J. Mol. Biol. 1997;269:423–439. doi: 10.1006/jmbi.1997.1019. [DOI] [PubMed] [Google Scholar]
- Russo, A.A., Jeffrey, P.D., Patten, A.K., Massagué, J., Pavletich, N.P. Crystal structure of the p27Kip1 cyclin-dependent kinase inhibitor bound to the cyclin A–CDK2 complex. Nature. 1996a;382:325–331. doi: 10.1038/382325a0. [DOI] [PubMed] [Google Scholar]
- Russo, A.A., Jeffrey, P.D., Pavletich, N.P. Structural basis of cyclin-dependent kinase activation by phosphorylation. Nat. Struct. Biol. 1996b;3:696–700. doi: 10.1038/nsb0896-696. [DOI] [PubMed] [Google Scholar]
- Ryckaert, J.P., Ciccotti, G., Berendsen, H.J.C. Numerical integration of Cartesian equations of motion of a system with constraints—Molecular dynamics of n-alkanes. J. Comput. Phys. 1977;23:327–341. [Google Scholar]
- Schlessinger, A., Rost, B. Protein flexibility and rigidity predicted from sequence. Proteins. 2005;61:115–126. doi: 10.1002/prot.20587. [DOI] [PubMed] [Google Scholar]
- Sen, T.Z., Jernigan, R.L. Optimizing the parameters of the Gaussian network for ATP-binding proteins. In: Cui Q., Bahar I., editors. Normal mode analysis: Theory and applications to biological and chemical systems. Chapman and Hall; Boca Raton, Florida: 2006. pp. 171–186. [Google Scholar]
- Sharma, P., Steinbach, P.J., Sharma, M., Amin, N.D., Barchi, J.J., Pant, H.C. Identification of substrate binding site of cyclin-dependent kinase 5. J. Biol. Chem. 1999;274:9600–9606. doi: 10.1074/jbc.274.14.9600. [DOI] [PubMed] [Google Scholar]
- Sielecki, T.M., Boylan, J.F., Benfield, P.A., Trainor, G.L. Cyclin-dependent kinase inhibitors, useful targets in cell cycle regulation. J. Med. Chem. 2000;43:1–18. [PubMed] [Google Scholar]
- Teague, S.J. Implications of protein flexibility for drug discovery. Nat. Rev. Drug Discov. 2003;2:527–541. doi: 10.1038/nrd1129. [DOI] [PubMed] [Google Scholar]
- Tobi, D., Bahar, I. Structural changes involved in protein binding correlate with intrinsic motions of proteins in the unbound state. Proc. Natl. Acad. Sci. 2005;102:18908–18913. doi: 10.1073/pnas.0507603102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Aalten, D.M., de Groot, B.L., Findlay, J.B.C., Berendsen, H.J.C., Amadei, A. A comparison of techniques for calculating protein essential dynamics. J. Comput. Chem. 1997;18:169–181. [Google Scholar]
- Wang, J.M., Cieplak, P., Kollman, P.A. How well does a restrained electrostatic potential (RESP) model perform in calculating conformational energies of organic and biological molecules? J. Comput. Chem. 2000;21:1049–1074. [Google Scholar]
- Wood, T.C., Pearson, W.R. Evolution of protein sequences and structures. J. Mol. Biol. 1999;291:977–995. doi: 10.1006/jmbi.1999.2972. [DOI] [PubMed] [Google Scholar]
- Yang, L.W., Liu, X., Jursa, C.J., Holliman, M., Rader, A., Karimi, H.A., Bahar, I. iGNM: A database of protein functional motions based on Gaussian Network Model. Bioinformatics. 2005;21:2978–2987. doi: 10.1093/bioinformatics/bti469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang, L.W., Rader, A.J., Liu, X., Jursa, C.J., Chen, S.C., Karimi, H.A., Bahar, I. oGNM: Online computation of structural dynamics using the Gaussian Network Model. Nucleic Acids Res. 2006;34:W24–W31. doi: 10.1093/nar/gkl084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan, Z., Zhao, J., Wang, Z.X. Flexibility analysis of enzyme active sites by crystallographic temperature factors. Protein Eng. 2003;16:109–114. doi: 10.1093/proeng/gzg014. [DOI] [PubMed] [Google Scholar]
- Zhang, B., Tan, V.B.C., Lim, K.M., Tay, T.E. Molecular dynamics simulations on the inhibition of cyclin-dependent kinases 2 and 5 in the presence of activators. J. Comput. Aided Mol. Des. 2006;20:395–404. doi: 10.1007/s10822-006-9081-z. [DOI] [PubMed] [Google Scholar]