A tensor higher-order singular value decomposition for integrative analysis of DNA microarray data from different studies

Abstract

We describe the use of a higher-order singular value decomposition (HOSVD) in transforming a data tensor of genes × “x-settings,” that is, different settings of the experimental variable x × “y-settings,” which tabulates DNA microarray data from different studies, to a “core tensor” of “eigenarrays” × “x-eigengenes” × “y-eigengenes.” Reformulating this multilinear HOSVD such that it decomposes the data tensor into a linear superposition of all outer products of an eigenarray, an x- and a y-eigengene, that is, rank-1 “subtensors,” we define the significance of each subtensor in terms of the fraction of the overall information in the data tensor that it captures. We illustrate this HOSVD with an integration of genome-scale mRNA expression data from three yeast cell cycle time courses, two of which are under exposure to either hydrogen peroxide or menadione. We find that significant subtensors represent independent biological programs or experimental phenomena. The picture that emerges suggests that the conserved genes YKU70, MRE11, AIF1, and ZWF1, and the processes of retrotransposition, apoptosis, and the oxidative pentose phosphate pathway that these genes are involved in, may play significant, yet previously unrecognized, roles in the differential effects of hydrogen peroxide and menadione on cell cycle progression. A genome-scale correlation between DNA replication initiation and RNA transcription, which is equivalent to a recently discovered correlation and might be due to a previously unknown mechanism of regulation, is independently uncovered.

DNA microarrays make it possible to record the genome-scale signals, for example, mRNA expression levels (1–4) and proteins' DNA-binding occupancy levels (5–7), that guide the progression of cellular processes. Future discovery and control in biology and medicine will come from the mathematical modeling of these data, where the mathematical variables and operations represent biological reality: The variables, patterns uncovered in the data, might correlate with activities of cellular elements, such as regulators or transcription factors, that drive the measured signals. The operations, such as data classification and reconstruction in subspaces of selected patterns, might simulate experimental observation of the correlations and possibly also causal coordination of these activities (8). Comparative analyses of these data among two or more organisms might give insights into the universality and specialization of evolutionary, biochemical, and genetic pathways (9). Integrative analyses of different types of signals from the same organism might reveal cellular mechanisms of regulation (10).

The structure of DNA microarray data integrated from different studies is of an order higher than that of a matrix. Each of the multiple biological and experimental settings under which the data are measured represents a degree of freedom in a tensor (11). Unfolded into a matrix, these degrees of freedom are lost and much of the information in the data tensor might also be lost.

We describe the use of a higher-order singular value decomposition (HOSVD) (12–14) in transforming a data tensor of genes × “x-settings,” that is, different settings of the experimental variable x × “y-settings,” which tabulates DNA microarray data from different studies, to a “core tensor” of “eigenarrays” × “x-eigengenes” × “y-eigengenes.” The eigenarrays and x- and y-eigengenes are unique orthonormal superpositions of the arrays and the genes across the x- and y-settings, respectively. Reformulating this multilinear HOSVD, also known as the N-mode singular value decomposition (SVD) (15–17), such that it decomposes the data tensor into a linear superposition of all outer products of an eigenarray, an x- and a y-eigengene, that is, rank-1 “subtensors” (12), the superposition coefficients of which are the “higher-order singular values” tabulated in the core tensor, we define the significance of each subtensor in terms of the fraction of the overall information in the data tensor that it captures.

We illustrate this HOSVD with an integration of genome-scale mRNA expression data from three yeast cell cycle time courses, two of which are exposed to either hydrogen peroxide (HP) or menadione (MD) (1, 2). We find that significant subtensors represent independent biological programs or experimental phenomena common to all three studies or exclusive to either one or two of the studies (18), including the subtle differential effects of HP and MD on cell cycle progression. We also find that this subtensor interpretation is robust to variations in the data selection cutoffs.

The picture that emerges from this data-driven analysis suggests that the conserved genes YKU70, MRE11, AIF1, and ZWF1, and the processes of retrotransposition, apoptosis, and the oxidative pentose phosphate pathway, that these genes are involved in, may play significant, yet previously unrecognized, roles in the differential effects of HP and MD on cell cycle progression (1, 19–27). A genome-scale correlation between DNA replication initiation and RNA transcription, which is equivalent to a recently discovered correlation (10), is consistent with the current understanding of replication initiation (28–31) and recent experimental results (32–36), and might be due to a previously unknown mechanism of regulation, is independently uncovered.

Mathematical Methods: HOSVD

A single DNA microarray probes the genome-scale signal of K genes of a cellular system in a single sample. A series of L arrays probes L different samples under L different settings of the experimental variable x, that is, x-settings. A series of M arrays probes the genome-scale signal under M different y-settings for each given x-setting. Let the third-order tensor 𝒯, of size K-genes × L-x-settings × M-y-settings, tabulate the genome-scale signal for all genes and under all x- and y-settings, assuming that LM < K. Each element of 𝒯, that is, 𝒯_klm, is the signal measured for the kth gene under the lth x- and mth y-settings. Each column vector of 𝒯, that is, 𝒯:_lm, lists the genome-scale signal measured under the lth x- and mth y-settings. The x- and y-row vectors, 𝒯_k:m and 𝒯_kl:, list the signal measured for the kth gene under the mth y-setting across all x-settings, and under the lth x-setting across all y-settings, respectively.

The N = 3-mode SVD, a HOSVD (12–14) of the third-order data tensor, is then a transformation of the data tensor from the space of K-genes × L-x-settings × M-y-settings to the reduced space of LM < K-eigenarrays × L-x-eigengenes × M-y-eigengenes [supporting information (SI) Fig. 4],

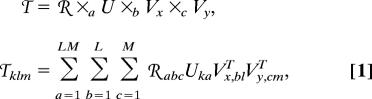where ×_a U, ×_b V_x, and ×_c V_y denote multiplications of the tensor ℛ and the matrices U, V_x, and V_y, which contract the first, second, and third indices of ℛ with the second indices of U, V_x, and V_y or, equivalently, the first indices of U^T, V_x^T, and V_y^T, respectively. In this space the data tensor is represented by the third-order core tensor ℛ, which in general, is full. The transformation matrix U defines the K-genes × LM-eigenarrays basis set. The vector in the ath column of U, U:_a, lists the genome-scale signal of the ath eigenarray. The transformation matrices V_x^T and V_y^T define the L-x-eigengenes × L-x-settings and M-y-eigengenes × M-y-settings basis sets, respectively. The vectors in the bth and cth rows of V_x^T and V_y^T, V_x,b:^T and V_y,c:^T, list the signal of the bth x-eigengene across all y-settings and that of the cth y- eigengene across all x-settings, respectively. The eigenarrays and the x- and y-eigengenes are orthonormal superpositions of the arrays and the genes across the x- and y-settings, respectively.

The multilinear HOSVD of Eq. 1 can be reformulated such that it decomposes the data tensor 𝒯 into a linear superposition of ≤ (LM)² rank-1 subtensors, the superposition coefficients of which are the higher-order singular values, tabulated in the core tensor ℛ (12), that is,

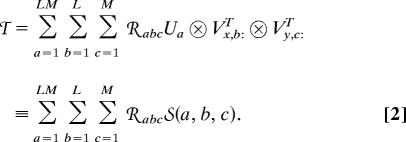where the subtensor 𝒮(a, b, c) is the outer product, denoted by ⊗, of the ath eigenarray U:_a and the bth x- and cth y-eigengenes, V_x,b:^T and V_y,c:^T (SI Fig. 5). Following Eq. 2, we define the significance of a subtensor 𝒮(a, b, c) relative to all other subtensors in terms of the “fraction” 𝒫_abc,

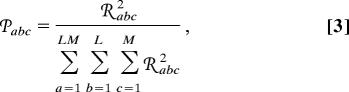which measures the fraction of the overall information in the data tensor that this subtensor captures. The “Shannon entropy” d,

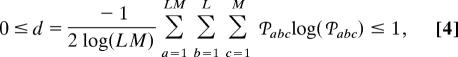measures the complexity of the data tensor from the distribution of the overall information among the different subtensors. This HOSVD holds for a tensor 𝒯 of any order N. For a second-order tensor, that is, a matrix, this HOSVD reduces to the matrix SVD (15).

HOSVD Computation.

We compute the transformation matrix U from the SVD of the matrix T_k ≡ (𝒯_:11, …, 𝒯_:1M, …, 𝒯_:LM) = UDV^T, which is obtained by appending all column vectors {𝒯_:LM} along the K-genes axis. Note that U is independent of the order of the appended arrays. The singular values, which are tabulated in the diagonal matrix D, are ordered in decreasing order, such that the eigenarrays, the column vectors of U, are ordered in decreasing order of their relative significance in terms of the fraction of the overall information in the data tensor that each eigenarray captures (SI Fig. 6). Similarly, we compute the transformation matrices V_x and V_y from the SVD of the matrices T_l = U_xD_xV_x^T and T_m = U_yD_yV_y^T, which are obtained by appending all x-row vectors {𝒯_k:m} along the L-x-settings axis and all y-row vectors {𝒯_kl:} along the M-y-settings axis, respectively (SI Figs. 7 and 8). For a real data tensor, the eigenarrays and the x- and y- eigengenes are unique up to phase factors of ±1, such that each eigenarray and each x- and y-eigengene capture both parallel and antiparallel data patterns, except in degenerate subspaces, defined by equal corresponding singular values in the diagonal matrices D, D_x, or D_y, respectively. For example, the y-eigengenes V_y,c:^T and V_y,m:^T, which satisfy D_y,cc ≈ D_y,mm, span an approximately degenerate subspace. We reformulate the HOSVD of Eqs. 1 and 2 with a unique orthogonal rotation of these two y- eigengenes, which is selected by subjecting the rotated y-eigengenes to a constraint, that may be advantageous in the interpretation and visualization of the data (SI Fig. 9). We then compute the core tensor by multiplying the data tensor 𝒯 and the transformation matrices U, V_x, and V_y, that is, ℛ = 𝒯 ×_k U^T ×_l V_x^T ×_m V_y^T (SI Fig. 10).

Approximately Degenerate Subtensor Space Rotation.

We define a subset of subtensors as approximately degenerate if their corresponding higher-order singular values are approximately equal in magnitude and if N − 1 = 2 of their N = 3 indices are equal, such that they are listed in a single vector in the core tensor ℛ. For example, the subtensors 𝒮(a, b, c) and 𝒮(k, b, c), which satisfy |ℛ_abc| ≈ |ℛ_kbc|, span an “approximately degenerate subtensor space.” We reformulate the HOSVD of Eq. 2 with a single rank-1 subtensor 𝒮(a + k, b, c) unique to the data tensor, which is composed of these two subtensors, with the corresponding higher-order singular value ℛ_a+k,b,c, that is, ℛ_abc𝒮(a, b, c) + ℛ_kbc𝒮(k, b, c) = ℛ_a+k,b,c𝒮(a + k, b, c). The subtensor 𝒮(a + k, b, c) ≡ U_:,a+k ⊗V_x,b:^T ⊗ V_y,c:^T is computed from the outer product of U_:,a+k ≡ ℛ_a+k,b,c⁻¹ (ℛ_abcU:_a + ℛ_kbcU_:k), a normalized superposition of the eigenarrays U:_a and U_:k, and the shared x- and y- eigengenes, V_x,b:^T and V_y,c:^T (Fig. 1). This subtensor is unique to the data tensor, because it is defined by a unique rotation in the space spanned by 𝒮 (a, b, c) and 𝒮 (k, b, c).

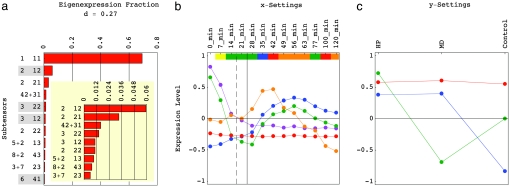
Fig. 1.

Significant HOSVD subtensors, after rotation of the approximately degenerate subtensor spaces 𝒮(4, 2+3, 1), 𝒮(5+2, 1, 3), 𝒮(8+2, 4, 3), and 𝒮(3+7, 2, 3). (a) Bar chart of the fractions of the 11 most significant subtensors. The higher-order singular values corresponding to subtensors highlighted in gray are <0. The entropy of the data tensor is 0.27. (b) Line-joined graphs of the first (red), second (blue), third (green), and fourth (orange) x-eigengenes and the superposition of the second and third x-eigengenes (violet), which define the expression variation across time in these subtensors. The time points are color-coded according to their cell cycle classification in the control time course: M/G₁ (yellow), G₁ (green), S (blue), S/G₂ (red), and G₂/M (orange). The grid lines mark the dissipation of the response to α-factor in the control time course (dashed) and the start of exposure to either HP or MD, at ≈20 and 25 min, respectively. (c) Line-joined graphs of the first y-eigengene (red), and the second (blue) and third (green) rotated y-eigengenes, which define the expression variation across the oxidative stress conditions.

Subtensor Interpretation.

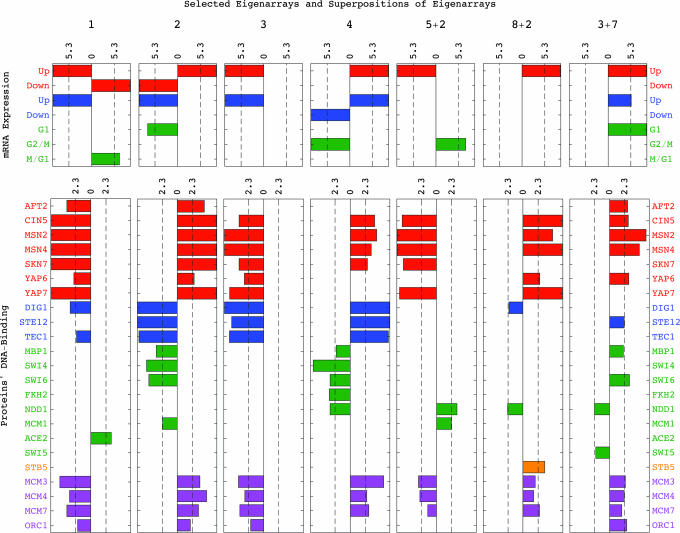
We associate a subtensor with an independent biological program or experimental phenomenon when a consistent biological or experimental theme is reflected in the interpretations of the patterns of the eigenarray, or superposition of eigenarrays, and the x- and y-eigengenes, which outer product defines the subtensor mathematically, taking into account the sign of the superposition coefficient of this subtensor, that is, the sign of the corresponding higher-order singular value. We parallel- and antiparallel-associate an eigenarray with the most likely parallel and antiparallel cellular states according to the annotations of the two groups of k genes, one with largest and one with smallest levels of biological signal in this eigenarray among all K genes, respectively. The P value of a given association is calculated assuming hypergeometric probability distribution of the J annotations among the K genes, and of the subset of j ⊆ J annotations among the subset of k genes, P(j; k, K, J) = (_k^K)⁻¹ Σ_i=j^k (_i^J) (_{k − i}^{K − J}) (18). We associate the x- and y-eigengenes with a biological or experimental process when their patterns of variation across the x- and y-settings, respectively, are interpretable (Fig. 2). For visualization, we set the average of each array across the genes and of each gene across the x- and y-settings to zero, such that the signal of each array and gene is centered at its gene- or x- and y-setting-invariant level, respectively.

Fig. 2.

Associations by annotations of the eigenarrays and superpositions of eigenarrays that define expression variation across genes in all ten most significant subtensors. Bar chart of −log₁₀(P value) for parallel (Right) and antiparallel (Left) enrichments of genes, which are expressed in response to environmental stress (red) or the pheromone (blue) or during the cell cycle (green), or of genes that are binding targets of oxidative stress activators (red), pheromone response (blue), or cell cycle (green) transcription factors, Stb5 (orange) or replication initiation proteins (violet).

Biological Results: Integrative Analysis of mRNA Expression from Yeast Cell Cycle Time Courses Under Different Oxidative Stress Conditions

The data tensor we analyze (SI Dataset 1) tabulates relative mRNA expression levels of K = 4,329 yeast Saccharomyces cerevisiae genes across L = 13 time points sampled from each of M = 3 cell cycle time courses of cultures synchronized by the pheromone α-factor, under different oxidative stress conditions: Exposures to (i) ≈0.2 mM HP, and (ii) ≈2 mM MD, starting at 25 min after 90 min of incubation in ≈7 nM α-factor, monitored by Shapira et al. (1) and (iii) a control time course, synchronized by 120 min of incubation in ≈7 nM α-factor, monitored by Spellman et al. (2). The time points sample approximately two cell cycle periods in the control culture. The first period of 63 min is sampled at 7-min intervals. The second period is sampled at 77, 98, and 119 ± 2 min. Each relative expression level is presumed valid when the signal-to-background ratio is >1.1 for both the synchronized culture and asynchronous reference, and each of the 4,329 genes has valid data in at least eight time points in each course, and at least 32 of the LM = 39 arrays.

We use SVD to estimate the missing data in each time course separately (9). After normalizing each array by its norm ‖𝒯_:LM‖, and computing the transformation matrices U, V_x, and V_y (SI Figs. 6–8), we rotate the approximately degenerate second and third y-eigengenes, V_y,2:^T and V_y,3:^T, such that the rotated V_y,3:^T describes over- and underexpression in response to HP and MD, respectively, and steady-state expression in the control time course (SI Mathematica Notebook). We then compute the HOSVD of the data tensor (SI Fig. 9), and rotate the approximately degenerate subtensor spaces 𝒮(4, 2+3, 1), 𝒮(5+2, 1, 3), 𝒮(8+2, 4, 3), and 𝒮(3+7, 2, 3) (Fig. 1).

Of the 4,329 genes, the mRNA expression of 579 was traditionally or microarray-classified as cell cycle-regulated (2). The expression of 312 and 680 genes was microarray-classified as regulated by pheromone (3) or environmental stress (4), respectively (SI Dataset 2). We annotate each of the genes as a DNA-binding target of either one of 19 transcription factors and four replication initiation proteins if the microarray-assigned P value for the binding of that protein to at least one of the probes that maps to that gene is <0.02 (5–7) (SI Datasets 3–6). The DNA-binding occupancy levels of the oxidative stress response activators and the pheromone response factors were measured after a 30-min exposure to ≈4 mM HP or 3 nM α-factor, respectively. The cell cycle factors, Stb5 and the replication initiation proteins were measured at steady growth conditions (Fig. 2).

We find that significant subtensors represent independent biological programs or experimental phenomena common to all three studies or exclusive to either one or two of the studies, including the subtle differential effects of HP and MD on cell cycle progression. We also find that this subtensor interpretation is robust to variations in the data selection cutoffs.

Significant Subtensors Represent Independent Biological Programs or Experimental Phenomena.

Steady state.

The first and most significant subtensor 𝒮(1, 1, 1) captures 𝒫₁₁₁ ≈70% of the overall expression information in the data tensor, with the corresponding higher-order singular value ℛ₁₁₁ > 0 (Fig. 1a). Following the P values for the distribution of the genes among each of the subsets of k = 200 genes with largest and smallest levels of expression in the first eigenarray U_:1 (SI Dataset 7), which defines the expression variation across the genes in this subtensor, this eigenarray is antiparallel-associated with mRNA expression in response to environmental stress and the pheromone, and is parallel-associated with overexpression during the cell cycle stage M/G₁ (Fig. 2). Consistently, this eigenarray is also antiparallel-associated with the expression of genes bound by oxidative stress response activators and the pheromone response factors Dig1 and Tec1, and is parallel-associated with the expression of genes bound by the M/G₁ factor Ace2. The first x-eigengene V_x,1:^T, which defines the expression variation across time in this subtensor, describes time-invariant underexpression (Fig. 1b). The first y-eigengene V_y,1:^T, which defines the expression variation across the oxidative stress conditions, describes condition-invariant overexpression (Fig. 1c). Taken together, the first subtensor is inferred to represent the steady state of mRNA expression in response to HP, MD, or α-factor, averaged over time and conditions.

Oxidative stress responses.

The second, third, and seventh subtensors, 𝒮 (2, 1, 2), 𝒮 (2, 2, 1), and 𝒮 (2, 2, 2), capture ≈6%, 3.3%, and 1% of the overall information, respectively, with ℛ₂₁₂ < 0 and ℛ₂₂₁, ℛ₂₂₂ > 0. The second eigenarray is parallel-associated with expression in response to environmental stress and is antiparallel-associated with pheromone response and G₁. The second x-eigengene describes a transition from under- to overexpression at ≈35 min. The second y-eigengene describes overexpression in the HP- and MD-treated cultures and underexpression in the control culture. These subtensors are inferred to represent expression in response to oxidative stress: The second subtensor represents time-averaged response to the oxidative stress induced by HP and MD vs. the time-averaged response induced by α-factor. The third subtensor represents condition-averaged expression variation across time in response to HP or MD exposure starting at 25 min, or in response to α-factor, which in the control culture dissipates at ≈20 min. The seventh subtensor represents oxidative stress response that varies across both time and conditions.

Pheromone responses.

The fourth, fifth, and sixth subtensors, 𝒮(4, 2+3, 1), 𝒮 (3, 2, 2), and 𝒮(3, 1, 2), capture ≈1.6%, 1.4%, and 1% of the overall information, with ℛ_4,2+3,1 > 0 and ℛ₃₂₂, ℛ₃₁₂ < 0. The superposition of the second and third x-eigengenes describes a time-decaying transition from over- to underexpression at ≈20 min. Both third and fourth eigenarrays are antiparallel- and parallel-associated with expression in response to environmental stress and the pheromone, respectively. These subtensors are inferred to represent pheromone and pheromone-induced oxidative stress responses: The fourth subtensor represents a condition-averaged, time-decaying response. The fifth subtensor represents an α-factor response that varies across time and conditions. The sixth subtensor represents a time-averaged response to the α-factor in the HP- and MD-treated cultures vs. that in the control culture.

HP- vs. MD-Induced Expression.

The eighth, ninth, and tenth subtensors, S(5+2, 1, 3), S(8+2, 4, 3), and S(3+7, 2, 3), capture ≈0.9%, 0.75%, and 0.6% of the overall information, with the corresponding higher-order singular values > 0. Of the corresponding superpositions of eigenarrays, U_:,5+2 is antiparallel- and U_:,8+2 and U_:,3+7 are parallel-associated with expression in response to environmental stress and of oxidative stress activator-bound genes. Also, U_:,5+2 is parallel- and U_:,8+2 and U_:,3+7 are antiparallel-associated with expression activated by the G₂/M factor Ndd1. These subtensors are inferred to represent responses to the HP- vs. MD-induced oxidative stress: The eighth subtensor represents time-averaged underexpression. The ninth and tenth subtensors represent overexpression, starting at ≈25 and 35 min and peaking at ≈40 and 55 min, when the control culture is at S/G₂ and G₂/M, respectively (Fig. 3a). Taken together, oxidative stress-induced and G₁ genes are over- and G₂/M genes are underexpressed in the HP- vs. the MD-treated time course. These results are in agreement with the current understanding of the differences in the response to HP vs. the response to MD: The HP-treated culture arrests in G₂/M after extended G₁ and S stages in a manner that depends on inactivation of the Mcm1-Fkh2-Ndd1 transcription regulatory complex (1) and the DNA damage-induced RAD9 checkpoint, whereas the MD-treated culture continues through G₂/M and M/G₁ and arrests in G₁ because of underexpression of the G₁ cyclin-encoding CLN1 and CLN2 (19).

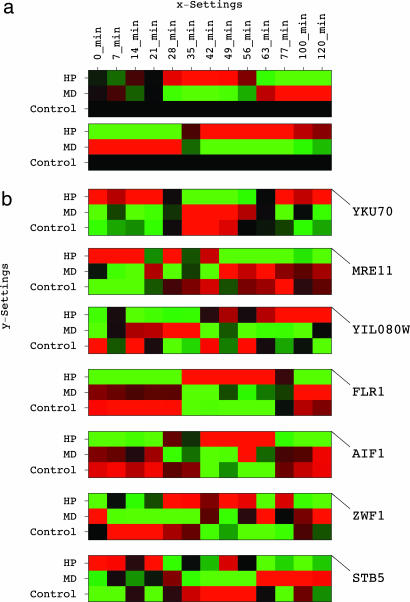
Fig. 3.

Eigengenes and genes that are significant in the HP vs. MD-induced responses. (a) Raster display of the outer products of the fourth and second x- eigengenes with the third y-eigengene, V_x,4:^T ⊗ V_y,3:^T and V_x,2:^T ⊗ V_y,3:^T, which define the expression variations across time and oxidative stress conditions in the ninth and tenth subtensors, 𝒮(8+2, 4, 3) and 𝒮(3+7, 2, 3), respectively. (b) Raster display of the expression of significant genes centered at the time- and condition-invariant expression levels of each gene.

The eighth, ninth, and tenth subtensors classify the yeast genes according to the time dependence of their differential expression and identify the subsets of genes with largest and smallest expression in each subtensor as significant in the HP- vs. MD-induced responses in terms of the fraction of the information in either subtensor that they capture. The genome-scale picture that emerges from this data-driven analysis suggests that the evolutionarily highly conserved genes YKU70, MRE11, AIF1, and ZWF1, and the processes of retrotransposition, apoptosis, and the oxidative pentose phosphate pathway, that they are involved in, may play significant, yet previously unrecognized, roles in the difference between the effects of HP and MD on cell cycle progression in yeast.

Retrotransposition.

Overexpression in the eighth subtensor and underexpression in the ninth and tenth subtensors define genes of which time-averaged expression is greater in the MD- than the HP-treated culture and is modulated by a peak in the MD- and a trough in the HP-treated culture at ≈50 min, when the control culture is at G₂/M. The most significant of these genes in terms of the fraction of the information in the eighth, ninth, and tenth subtensors that it captures is the yeast Ku protein-encoding YKU70 (Fig. 3b). Yku70 is a telomere maintenance protein, which is necessary for escape from the RAD9 checkpoint arrest in G₂/M. In this process, Yku70 and the meiotic recombination protein Mre11 play antagonistic roles, even though deletion of YKU70 is similar to that of MRE11 in its effect on nonhomologous end joining of DNA double-strand breaks (20). Yku70 was shown to potentiate retrotransposition (21), whereas disruption of MRE11 was shown to increases retrotransposition levels (22). We find MRE11 the 40th most significant gene with underexpression in the eighth and tenth subtensors and overexpression in the ninth subtensor. Consistently, the subset of the 200 most significant genes, which are anticorrelated with MRE11 in these subtensors, includes 16 of the 20 retrotransposon nucleocapsid genes in this data tensor, such as YIL080W, an enrichment that corresponds to a P value of ≈10⁻¹⁸.

Apoptosis.

Among genes anticorrelated with YKU70 in the eighth, ninth, and tenth subtensors, the second most significant gene is FLR1, a multidrug transporter. This differential expression of FLR1 is consistent with the observation that its transcription is regulated by the oxidative stress factor YAP1 and is induced by HP but not by MD (23). The 19th most significant gene is AIF1, which encodes the yeast apoptosis-inducing factor. Overexpression of AIF1, which with SKN7, SNQ2, and YAP1, constitutes the gene ontology “response to singlet oxygen” core (24), stimulates HP-induced apoptopic cell death (25). This differential expression of AIF1 is consistent with the inactivation of the frog Xenopus laevis Ku70 during apoptosis (26).

Oxidative pentose phosphate pathway.

Among genes correlated with AIF1 and anticorrelated with YKU70, the 18th most significant is ZWF1, which encodes the yeast glucose-6-phosphate dehydrogenase. Glucose-6-phosphate dehydrogenase catalyzes the first step of the pentose phosphate pathway, that is, the oxidative utilization of glucose, and is involved in response to HP. ZWF1 is among the 200 genes with the smallest expression in the ninth subtensor, together with GND1 and SOL3, the two other genes in the gene ontology “oxidative brunch of the pentose-phosphate shunt” core in this data tensor, and STB5, an S/G₂ gene that encodes a transcription factor required for the regulation of the pentose phosphate pathway (27). Consistently, the ninth subtensor is parallel-associated with expression of Stb5-bound genes (Fig. 2).

Oxidative Stress Response Is Correlated with Overexpression of Binding Targets of Replication Initiation Proteins.

Recently, we discovered a genome-scale correlation between the DNA binding of the replication initiation proteins Mcm3, Mcm4, and Mcm7 and underexpression of adjacent genes during G₁ (16). Replication initiation requires G₁ binding of these proteins, which are involved in transcriptional silencing (28), at replication origins (29). Therefore, we suggested that this correlation might be explained by a previously unknown mechanism of regulation.

Now we uncover independently an equivalent genome-scale correlation: In all ten most significant subtensors and the corresponding seven eigenarrays and superpositions of eigenarrays, overexpression of binding targets of Mcm3, Mcm4, and Mcm7 correlates with expression in response to environmental stress and with overexpression of oxidative stress activator-bound genes. DNA damage as caused by oxidative stress is known to inhibit binding of origins by targeted degradation of the essential prereplicative complex protein Cdc6 (30, 31). Taken together, we find that overexpression of binding targets of replication initiation proteins correlates with reduced, or even inhibited, binding of the origins. This correlation is in agreement with the recent observation that reduced efficiency of activation of origins correlates with local transcription (32, 33).

As with the correlation between the DNA binding of Mcm3, Mcm4, and Mcm7 and underexpression of adjacent genes during G₁, this equivalent correlation between overexpression of binding targets of Mcm3, Mcm4, and Mcm7 and expression in response to stress may be due to either one of at least two mechanisms of regulation: Stress-induced transcription of genes that are located near origins (34, 35) may reduce the binding efficiency of the adjacent origins. Or, reduced or even inhibited binding of origins by replication initiation proteins caused by degradation of Cdc6 may release genes that are located near origins for transcription. For example, the promoter region of the stress-induced FLR1, which includes Cin5 and Yap7 binding sites, overlaps with the yeast autonomously replicating sequence ARS209, and the stress-induced ZWF1 is transcribed in the direction of ARS1412 (36).

Conclusions

We have shown that this multilinear HOSVD, reformulated to decompose a data tensor into a linear superposition of rank-1 subtensors, provides an integrative framework for analysis of DNA microarray data from different studies, where significant subtensors represent independent biological programs or experimental phenomena. By using this HOSVD in an integration of genome-scale mRNA expression data from three yeast cell cycle time courses, two of which are exposed to either HP or MD, we were able to find that the conserved genes YKU70, MRE11, AIF1, and ZWF1, and the processes of retrotransposition, apoptosis, and the oxidative pentose phosphate pathway that these genes are involved in, may play significant, yet previously unrecognized, roles in the differential effects of HP and MD on cell cycle progression. A genome-scale correlation between DNA replication initiation and RNA transcription, which is equivalent to a recently discovered correlation and might be due to a previously unknown mechanism of regulation, has been independently uncovered.

Abbreviations

HOSVD

higher-order singular value decomposition

HP

hydrogen peroxide

MD

menadione

SVD

singular value decomposition.