On anti-portfolio effects in science and technology with application to reaction kinetics, chemical synthesis, and molecular biology

Abstract

The portfolio effect is the increase of the stability of a system to random fluctuations with the increase of the number of random state variables due to spreading the risk among these variables; many examples exist in various areas of science and technology. We report the existence of an opposite effect, the decrease of stability to random fluctuations due to an increase of the number of random state variables. For successive industrial or biochemical processes of independent, random efficiencies, the stability of the total efficiency decreases with the increase of the number of processes. Depending on the variables considered, the same process may display both a portfolio as well as an anti-portfolio behavior. In disordered kinetics, the activation energy of a reaction or transport process is the result of a sum of random components. Although the total activation energy displays a portfolio effect, the rate coefficient displays an anti-portfolio effect. For random-channel kinetics, the stability of the total rate coefficient increases with the average number of reaction pathways, whereas the stability of the survival function has an opposite behavior: it decreases exponentially with the increase of the average number of reaction pathways (anti-portfolio effect). In molecular biology, the total rate of a nucleotide substitution displays a portfolio effect, whereas the probability that no substitutions occur displays an anti-portfolio effect, resulting in faster evolutionary processes due to fluctuations. The anti-portfolio effect emerges for products of random variables or equations involving multiplicative convolution products.

An old and popular idea is that the use of a variety of resources for a given asset increases the stability of the supply of the asset by spreading the risk among the resources. For example, it is expected that a diversified investment portfolio would provide a small, but stable, low-risk profit stream; reducing the numbers of resources opens the way for possible higher profits but at a higher risk (1). Similarly, in agriculture, increasing biodiversity, that is, using different genetic varieties of a plant, is expected to increase the stability of the harvest with respect to environmental fluctuations (2–4). For example, if only a high-yield crop that is sensitive to bad weather is cultivated, then it is likely to have either a good harvest (good weather) or none at all (bad weather). The loss risk is reduced by growing different varieties of the plant and spreading the risk among these varieties.

Many other similar examples can be given from various areas of science and technology, which suggests the existence of a generic mechanism for the occurrence of the portfolio effect; it is usually assumed that the fluctuations of various resources are (almost) independent and the variations of their contributions tend to compensate each other. This statement can be easily formulated in a quantitative way. For example, we consider the simple situation of a sum X = x₁ + … + x_m of a variable number m of random variables x₁, …, x_m, independently and randomly selected from the same probability density p(x). The probability P(X) of the sum X is the m-fold repeated additive convolution product of p(x), P(X) = p(x)⊕ … ⊕p(x), and thus the characteristic function G(k) = ∫ exp(ikX)P(X)dX is the mth power of the characteristic function g(k) = ∫ exp(ikx)p(x)dx of the probability density p(x). If we assume that the cumulants 〈〈x^q〉〉, q = 1, 2, … of p(x) exist and are finite, then it follows that all cumulants 〈〈X^q〉〉, q = 1, 2, … also exist and are proportional to the number m of the random variables 〈〈X^q〉〉 = m〈〈x^q〉〉, q = 1, 2, … In the literature the stability with respect to fluctuations is measured by the stability coefficient (2, 5):

that is, the ratio of the cumulant of the first order of the random variable (that is, the average value) and the square root of the cumulant of the second order (the square root of the dispersion). According to Eq. 1, the bigger the stability coefficient, the smaller the fluctuations are compared with the average value of the total random variable. In the particular case of a sum of independent random variables selected from the same probability law, we have ϑ(m) = ϑ(1)$\sqrt{m}$, where ϑ(1) = 〈〈x〉〉/[〈〈x²〉〉]^1/2 is the stability coefficient of a random variable corresponding to the probability density p(x); that is, the stability coefficient of the sum is proportional to the square root of the sum of random variables. This is a simple illustration of the portfolio effect, which can be easily extended to more complicated situations such as independent contributions selected from different probability densities, p_u(x_u), or even nonindependent contributions that are weakly correlated, or yet more complicated cases where the fluctuations of the contributions, x_u, are described by various stochastic models. Despite the popularity of the idea that many systems from natural and social sciences and technology display the portfolio effect, there are various objections regarding its claimed occurrence in some specific cases. For example, in ecology some stochastic models and sets of experimental data suggest that there are systems for which the portfolio effect does not exist (2–5).

The purpose of this article is to show that some systems may display an anti-portfolio effect for which the combination of different resources reduces the stability of the systems with respect to fluctuations. We investigate various systems displaying the anti-portfolio effect and show that it generally occurs as the various resources combine in a multiplicative way rather than in an additive way. Based on the examination of different systems, we come up with a set of rules for identifying systems that may display the anti-portfolio effect. Strictly speaking, the fluctuations of a given variable can display a portfolio or anti-portfolio effect; however, to simplify the language throughout this article we refer to the variables themselves, not to their fluctuations. Regarding the definition of the portfolio or anti-portfolio effect, throughout this article we use the following convention: if, by increasing the number of variables the stability function increases one or more times and remains constant all other times, we have a portfolio effect. Similarly, if, by increasing the number of variables the stability function decreases one or more times and remains constant all other times, we have an anti-portfolio effect. Typically, the stability function remains constant if the added variables are nonrandom.

The structure of the article is the following. In section 1 we show that the anti-portfolio effect occurs whenever the observable of interest is the product of many independent random factors; in particular, we discuss the total yield of a chemical synthesis involving a variable number of successive operations. As an illustration of the general result derived in section 1, in section 2 we show that the random activation energy model (random rate) may display an anti-portfolio effect. In section 3 we show that reaction, transport, or relaxation systems that obey random-channel kinetics have a similar behavior. In section 4 we present a continuous time generalization of the anti-portfolio effect, with application to chemical kinetics, reliability theory, and vital statistics.

1. Anti-Portfolio Effect, Chemical Synthesis and Beyond

In this section we consider a simple, generic mechanism that leads to the anti-portfolio effect. We are interested in the behavior of a product of nonnegative, independent random factors

Expressions of type 2 describe many situations. For example the synthesis of a chemical compound often involves a succession of various chemical and physical (separation) processes. The total yield ζ_m of the process is the product of the yields η₁, …, η_m of the individual processes. In an ideal world the technologies are strictly respected and the yields η₁, …, η_m are constant and reproducible. In the real world, however, accidents do happen and the yields η₁, …, η_m are in general random variables. Similarly, the transmission of a biological signal by an m-step process is described by an equation of the type 2, where η₁, …, η_m are individual amplification factors of the signal and ζ_m is the total amplification factor of the signal. Drake's equation from astrobiology has the same structure (6, 7). Similarly, in economics the ratio ζ_m = 𝒱_m/𝒱₀ (total interest) between the value 𝒱_m of an asset at time m and its value 𝒱₀ at time 0, is given by Eq. 2, where η_m′ = 1 + r_m′^%/100, m′ = 1, …, m, and r_m′^% are the interest percent rates of the asset for different time periods. In this section we show that in all these cases the fluctuations of the product (total yield, total amplification, total compound interest, etc.) have an anti-portfolio behavior.

In this article we limit ourselves to the case where the fluctuations of the factors η₁, …, η_m are independent of each other and described by arbitrary probability densities p_m′(η_m′). The only restriction we impose on p_m′(η_m′) is that their positive moments 〈(η_m′)^β〉 = ∫(η_m′)^βp_m′(η_m′)d_m′, β > 0, exist and are finite. These assumptions are reasonable in many cases. In the case of chemical synthesis, the assumption of independence means that the accidents that lead to the fluctuations of the efficiencies of different steps are independent of each other. Similarly, in economics, we assume that the fluctuations of the interest rates for different time periods are produced by independent causes.

The positive moments of the total factor, ζ_m, can be easily evaluated. We have 〈(ζ_m)^β〉 = ∏_m′=1^m [〈(η_m′)^β〉], β > 0. In particular, we obtain the following expression for the stability function of the total factor:

As the dispersions of the individual multiplicative factors η₁, …, η_m are nonnegative, 〈(η_m′ − 〈η_m′〉)²〉 = 〈(η_m′)²〉 − 〈η_m′〉² ≥ 0, the product in Eq. 3, is made up of terms bigger than or at least equal to one, and therefore this product never decreases as m increases and the stability function ϑ_ζm is nonincreasing. Strictly speaking, the equality 〈(η_m′)²〉 = 〈η_m′〉² holds only for deterministic η_m′, and thus, for random η_m′ the stability ϑ_ζm of the total factor is decreasing with m, whereas for nonrandom random η_m′ it remains constant. It follows that, for at least one random η_m′, the fluctuations of the product ζ_m display an anti-portfolio behavior. In particular, if the probability densities p_m′(η_m′) are identical, p₁(η) = … = p₁(η) = p(η), then Eq. 3 turns into a simpler form: ϑ_ζm ≈ (〈η²〉/〈η〉²)−m^/2 for m ≫ 1, that is, the stability of the total factor ζ_m is decreasing exponentially with m.

These results are consistent with what is intuitively known in the chemical industry. Accidental violations of procedures for technologies involving long successions of transformation processes are very dangerous. For example, if a technology involves 12 processes, each needing one month to complete, a serious accident taking place at step 6 may mean wasting six months of work. From step to step, the danger is increasing multiplicatively.

In conclusion, in this section we have shown that the anti-portfolio effect may occur for any process described by variables given by products of independent random factors. This formulation covers a large class of processes from physics, chemistry, biology, and technology, including the random activation energy model discussed in the next section.

2. Anti-Portfolio Effect in Random Activation Energy Kinetics

The random activation energy model (8–12) has various applications in physics, chemistry, and biology. We consider a transport or transformation process that involves transitions over many energy barriers. The total transition rate is given by the Arrhenius law:

where 𝒜 is a preexponential amplitude factor; E_u = E_u⁰ + ΔE_u are the activation energies corresponding to the different barriers; u = 1, …, m, E_u⁰, and ΔE_u are deterministic and random components of the activation energies, respectively; v = 𝒜 ∏_u=1^m exp(−E_u⁰/k_BT) is a nonrandom universal frequency; χ_u = exp(−ΔE_u/k_BT) are transparence factors corresponding to the random components ΔE_u of the activation energies; T is the temperature of the system; and k_B is Boltzmann's constant. According to the random activation energy model, the random components ΔE_u of the activation energies are independent random variables selected from a set of Maxwell–Boltzmann probability densities:

with

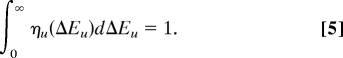Here T_u* > T are characteristic temperatures attached to the different energy barriers that are related to the history of the system: the probability densities (5) are equilibrium Maxwell–Boltzmann distributions “frozen” at the temperatures T_u* > T, u = 1, …, m. Here, we assume finite lower limits for the total activation energies, E_u, and denote them by E_u⁰. As a result, by definition, the random components of the activation energies, ΔE_u = E_u − E_u⁰, are nonnegative. The activation energies, E_u = E_u⁰ + ΔE_u, however, can be either positive or negative. It is convenient to evaluate the probability densities of the transparence factors χ_u, p_u(χ_u), with ∫₀¹ p_u(χ_u)dχ_u = 1. We have

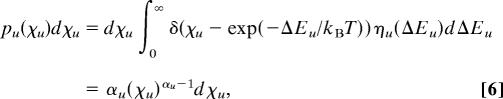where α_u = T/T_u* are fractal exponents between zero and unity 1 > α_u > 0.

We can define a total activation energy E = Σ_u=1^m E_u + E⁰ = ΔE, where E⁰ = Σ_u=1^m E_u⁰ and ΔE = Σ_u=1^m ΔE_u are deterministic and random components, respectively. We have W = 𝒜 exp(−E/k_BT) = v exp(−ΔE/k_BT). Since ΔE is the sum of m independent random variables distributed according to the Maxwell–Boltzmann probability laws (5), its cumulants and the stability function ϑΔ_E = 〈〈ΔE〉〉/〈〈ΔE²〉〉^1/2 can be easily evaluated. We have

where (T*_u)^q|_m = Σ_u=1^m(T_u*)^q/m, q > 0, are moments of the characteristic temperature. As m → ∞ it is reasonable to assume that the averages Σ_u=1^m(T_u*)^q/m, q = 1,2, tend toward constant values and, thus, for large m, the stability function ϑ_ΔE increases as ϑ_ΔE ∼ m^1/2 and, thus, ΔE displays the portfolio effect. In particular, if all characteristic temperatures are the same T₁* = … = T_m* = T*, then the scaling law ϑ_ΔE ∼ m^1/2 holds for any values of m, small or large.

The total rate coefficient, however, has an anti-portfolio behavior. The moments 〈W^q〉, q > 0, can be easily evaluated by averaging W^q over all possible values of the random components ΔE_u, u = 1, …, m. We obtain

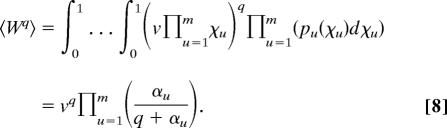The cumulants, 〈〈W^q〉〉, can be computed, step by step, from the moments, 〈W^q〉. From the expressions for the cumulants of first and second order we can derive the stability function ϑ_W of the total rate coefficient:

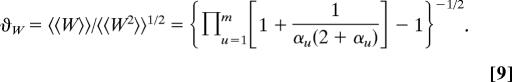As 1 > α_u > 0, it follows that the product in Eq. 9 is made up of terms >1, and therefore the product increases as m increases and the stability function ϑ_W decreases; that is, W displays an anti-portfolio behavior. In particular, for T₁* = … = T_m* = T*, we have α₁ = … = α_m = α, and Eq. 7 leads to ϑ_W ≈ [1 + 1/[α(2 + α)]]^−m/2 for m ≫ 1; that is, the stability is decreasing exponentially with m. Eq. 9 is a particular case of the general Eq. 3 derived in section 1. By comparing Eqs. 4 and 2, we notice that the transparence factors χ_u from Eq. 2 play the same role as the factors η_u from Eq. 2. From the general theory presented in section 1, it follows that the total rate coefficient displays an anti-portfolio behavior even if the random components ΔE_u of the activation energies do not obey Maxwell–Boltzmann statistics; for the anti-portfolio effect to occur, it is enough that the fluctuations of the different random components ΔE_u are independent of each other.

In conclusion, in this section we have shown that the random activation energy model displays both a portfolio as well as an anti-portfolio behavior, depending on the variable studied. The fluctuations of the total activation energy, which is the sum of many random contributions, tend to decrease with the increase of the number of contributions. The fluctuations of the rate coefficient, however, increase with the increase of the number of contributions to the total activation energy. The type of model considered here includes as a special case the old multiple trapping model for charge transport in disordered systems suggested by Schmidlin (12), but it also has other applications (8–11).

3. Anti-Portfolio Effect in Random-Channel Kinetics

Random rates are frequently used for describing various phenomena in physics, chemistry, and biology, such as rate or transport processes in disordered systems, single-molecule kinetics, or the fluctuations of the evolution rates measured by the time frequency of the nucleotide or amino acid substitution events in molecular biology (9–11, 13–16). In this section we focus on random-channel kinetics, for which the fluctuations of the rate coefficients are due to the individual contributions of different reaction channels (pathways) and show that it may display an anti-portfolio behavior. For illustration we consider rate or transport processes with static or dynamic disorder or the process of nucleotide substitution in molecular biology. The total rate of transformation W is the sum of a random number m of components w_u, u = 1, …, m, which describes the contributions of various transport, relaxation, or transformation channels (pathways), W = Σ_uw_u. We introduce a set of grand canonical probability density functionals for the number m and the values w_u, u = 1, …, m, of the components attached to the different channels at various times: Q₀, …, Q_m[w₁(t′), …, w_m(t′)] 𝒟[w₁(t′)] … 𝒟[w_m(t′)], which obey a normalization condition of the Gibbs type: Q₀ + Σ_m=1^∞(m!)⁻¹ ∫∫ Q_m𝒟[w₁(t′)], …, 𝒟[w_m(t′)] = 1 and where 𝒟[w₁(t′)], …, 𝒟[w_m(t′)] are integration measures over the space of functions w₁(t′), …, w_m(t′), respectively, and ∫∫ stands for the operation of path integration.

For many problems of random-channel kinetics, the experimental observables are the positive moments 〈ℓ^q(t)〉, q ≥ 0, of the survival function of the process, ℓ(t) = exp(−∫₀^t W(t′)dt′). These moments can be easily evaluated in terms of the characteristic functional,

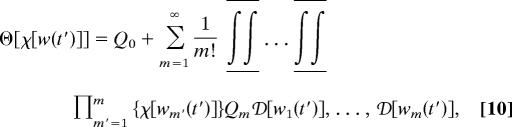of the grand canonical probability density functionals Q_m; here, χ[w_m′(t′)] are a suitable set of test functionals. We have

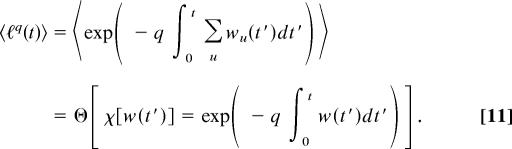In a similar way we can evaluate the statistical properties of the total rate W, which can be described in terms of a characteristic functional 𝒢[ξ(t′)] = 〈exp(i ∫ ξ(t′)W(t′)dt′)〉, where ξ(t′) is a test function conjugated to the total rate and the average is taken over all possible numbers of channels m and the corresponding rates and over all possible values of the contributions w_u(t′) of different channels to the total transformation rate W(t′). We have

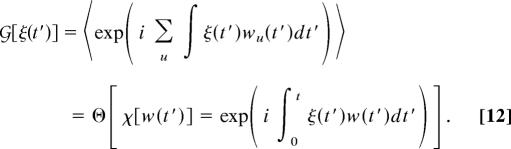In this article, we consider only the case of independent (Poissonian) channels for which

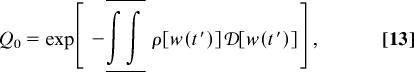where ρ[w(t′)] is the average functional density of channels. We have shown that the Poissonian Eqs. 13 and 14 emerge as a universality class for a limit of the thermodynamic type for weakly interacting channels (17). For independent channels we obtain

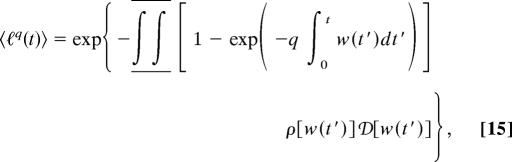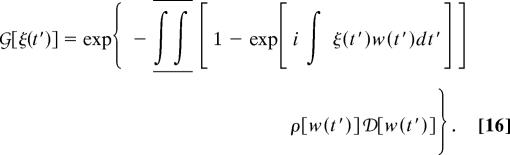Eqs. 15 and 16 characterize the stochastic properties of the survival function, ℓ(t), and of the total rate, W(t), respectively. The cumulants of the survival function ℓ(t) can be computed step by step from Eq. 15 for the moments. Similarly, the cumulants of the total rate, W(t), can be computed from Eq. 16 by expanding ln 𝒢[ξ(t′)] in a functional Taylor series in the test function and evaluating the coefficients of this expansion. After some calculations we obtain the following expressions for the stability functions of the total rate and for the survival function, respectively:

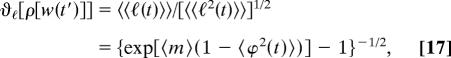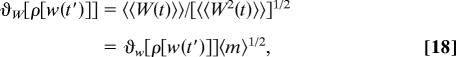where 〈ϕ²(t)〉 = 〈exp(−2∫₀^t w(t′)dt′)〉 is the dynamic average of the square of the decay (survival function) ϕ(t) = exp(−∫₀^t w(t′)dt′), corresponding to a given channel, over all possible values of the contribution of the channel to the total rate; 〈m〉 = ∫∫ρ[w(t′)] 𝒟[w(t′] is the total average number of channels; and ϑ_w[ρ[w(t′)]] = 〈〈w(t)〉〉/[〈〈w²(t)〉〉]^1/2 is the stability function of the contribution of a channel to the total rate. The cumulants 〈〈w^q(t)〉〉 of the contribution w(t) are evaluated by expanding the logarithm of its characteristic functional,

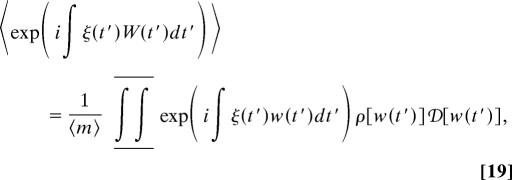in a functional Taylor series.

From Eqs. 17 and 18, we notice that, although the increase of the average number of channels, 〈m〉, leads to the increase of the stability with respect to fluctuations of the total rate coefficient, W(t) (portfolio effect), it has the opposite effect on the survival function ℓ(t), for which the increase of the average number of channels, 〈m〉, leads to the decrease of the stability with respect to fluctuations. The anti-portfolio effect on ℓ(t) is much stronger than the portfolio effect on W(t): ϑ_W[ρ[w(t′)]] ≈ 〈m〉^1/2 increases slowly with 〈m〉, whereas the decrease of ϑ_ℓ[ρ[w(t′)]] ∼ exp[−½ 〈m〉(1 − 〈ϕ²(t)〉)] for 〈m〉 ≫ 1 is practically exponential. A naïve analysis based on the portfolio effect for W(t) would suggest that, if the average number of channels is large, 〈m〉 ≫ 1, then the fluctuations of the total rate W(t) can be neglected, and thus W(t) and therefore ℓ(t) are practically deterministic. This result is obviously incorrect: for 〈m〉 ≫ 1, the fluctuations of ℓ(t) increase exponentially with 〈m〉.

To clarify the origin of the anti-portfolio effect in random-channel kinetics, we express the total survival function, ℓ(t), in terms of the survival functions ϕ_u(t) = exp(−∫₀^t w_u(t′)dt′), u = 1, 2, …, attached to different channels. For a given number m of channels, we have ℓ(t) = ∏_u=1^m ϕ_u(t). The multiplicative structure of ℓ(t) leads to the accumulation of fluctuations of the individual terms ϕ_u(t) (compare with sections 1 and 2).

In conclusion, in this section, we have shown that the independent (Poissonian) version of random-channel kinetics with dynamical disorder leads both to a portfolio as well as an anti-portfolio effect for different random parameters of the systems. The total rate W(t) is made up of additive random contributions and displays a portfolio effect, whereas the total survival function displays an anti-portfolio effect.

4. Anti-Portfolio Effect and Field Theory with Applications to Chemical Kinetics, Reliability Theory, and Vital Statistics

The anti-portfolio effect occurs whenever a variable of interest is the product of a variable number of random factors, like in Eq. 2. This observation suggests that the anti-portfolio effect may occur for continuous systems, described by field variables. As a starting point, we rewrite Eq. 2 as an exponential of a sum, ζ_m = exp(Σ_m′=1^m ln η_m′), and replace the discrete variables η_m′ by a scalar field ξ(ρ), where ρ is a state vector such as a position vector, ρ = (r), in real space; the time, ρ = (t); the space-time continuum, ρ = (r, t); or even an abstract state space vector. We consider observables that have a structure similar to Eq. 2 and are functionals of the field ξ(ρ),

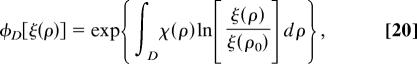where ρ₀ is a reference position vector, χ(ρ) is a real, scalar function of the state vector, and D is an integration domain in the state space. Various experimental observables can be described by a functional of type 20; for example, the relaxation function of an oscillator in the theory of line shape in spectroscopy (18), of survival functions in disordered kinetics, of reliability theory, and of vital statistics (19, 20).

We can define a stability functional for Φ_D[ξ(ρ)], which is given by an expression similar to Eq. 1:

We start out from the domain D₀ and we extend it by adding additional domains, D₁, …, D_m, …, which do not overlap with D₀ and each other: D_u ∩ D_u′ = , for any u ≠ u′. If the stability functionals ϑΦ_DuΣ[ξ(ρ)], u = 1, 2, …, m, … attached to the total domains D_u^Σ = D₀ ∪ D₁∪ … ∪D_u, u = 1, 2, …, m … increase or do not decrease as new domains are added, then we have a portfolio effect. In the opposite situation where the stability functionals ϑΦ_DuΣ[ξ(ρ)] decrease or do not increase as new domains are added, then we have an anti-portfolio effect.

For computing the stability function ϑΦ_Du[ξ(ρ)], we introduce the transformed scalar field ψ[ξ(ρ)] = ln[ξ(ρ)/ξ(ρ₀)] and assume that its stochastic properties are described in terms of a suitable characteristic functional

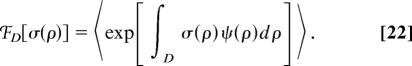We notice that the moments of the functional Φ_D[ξ(ρ)] can be easily expressed in terms of the characteristic functional ℱ_D[σ(ρ)]. We have 〈{Φ_D[ξ(ρ)]}^m〉 = ℱ_D[mχ(ρ)], m > 0. By applying this equation we obtain

In this article we limit ourselves to the case where the random field, ξ(ρ), is independent; that is, the fluctuations of ξ(ρ) are independent of fluctuations of ξ(ρ′) for ρ ≠ ρ′. Under these circumstances we have ℱ_{D0∪D1∪…}D_m[σ(ρ)] = ∏_u=0^m ℱ_Du[σ(ρ)] if D_u ∩ D_u′ = 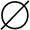, for any u ≠ u′ and, therefore,

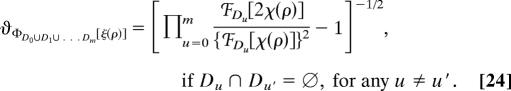We apply Eq. 23 for different nonoverlapping domains, D₀, …, D_m., and eliminate the characteristic functionals from the two resulting equations and Eq. 24. We obtain the following composition law for the stability functional:

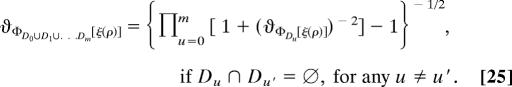Since by definition both Φ and ϑ are nonnegative, it follows that in the product in Eq. 25 each term is bigger or at least equal to one; the equality to one occurs if and only if on a domain D_u the field is not fluctuating. It follows that, as new domains are added the stability functional ϑΦ_D0∪_D1∪_Dm[ξ(ρ)] is nonincreasing and thus we have an anti-portfolio effect.

As a simple illustration of this theory we consider the fluctuations of a relative survival function due to independent random variation of the decay (mortality) rate, ℓ(a|a₀) = exp[−∫_a0^a μ(x)dx], which describes different problems from various areas of science and technology. In disordered chemical kinetics μ(x) is a random rate coefficient, which in general is independent of age. In reliability theory, μ(x) is the rate of occurrence of a defect for a product of age between x and x + dx. Similarly, in demography and biostatistics, μ(x) is the mortality force for an individual of age between x and x + dx. In all of the cases the survival function ℓ(a|a₀) is the probability that a species (molecule, product, individual) alive at age a₀ survives up to age a; the absolute survival function ℓ(a) = exp[−∫₀^a μ(x)dx] corresponds to a₀ = 0, ℓ(a) = ℓ(a|0). The relative survival function ℓ(a|a₀) is a particular case of the functional Φ_D[ξ(ρ)], where the state vector is the age a, and the mortality force μ(x) plays a similar role to the field ψ[ξ(ρ)]. We consider a succession of age windows, delimited by the values a₀, a₁, …, a_m = a. According to its definition, the relative survival function ℓ(a|a₀) can be expressed as a product of relative survival functions ℓ(a|a₀) = ℓ(a|a_m−1) … ℓ(a₁|a₀). From the general theory presented in this section it follows that, as the age a increases, the stability function of the relative survival function decreases, that is, ℓ(a|a₀) displays an anti-portfolio effect.

In conclusion, in this section we have shown that the anti-portfolio theory can be easily extended to functionals that depend multiplicatively on independent random fields. In particular, this field approach covers various problems from science and technology described in terms of random survival functions produced by independent, random mortality forces, in disordered kinetics, technological reliability, and survival statistics. In all these applications, as age increases, the survival functions display an anti-portfolio effect.

Conclusions

The anti-portfolio effect may occur whenever we deal with variables that are products of independent random factors, Eq. 2, or the corresponding field generalization, Eq. 20. Very often the multiplicative structure of the equations of a model is not obvious; this happens in the case of the model of random-channel kinetics presented in section 2. A hint for the occurrence of the anti-portfolio effect is the presence of the multiplicative convolution product in the evolution equations of the process. For example, in the case of product 2, we consider two successive total variables, ζ_m−1 and ζ_m = ζ_m−1η_m, and express p_ζm(ζ_m) as the average of a delta function:

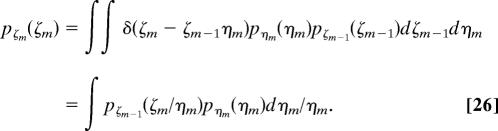The last integral in Eq. 26 is the multiplicative convolution product of p_ζm−1 to p_ηm. Multiplicative convolution products appear in the evolution equations of different growth and transport phenomena, for example, in the theory of dilution in environmental chemistry or in the theory of radiative transfer. It is likely that such processes display an anti-portfolio effect.

In the past two decades, interest in the study of multiplicative random processes has been growing; it has been shown that they display many unexpected features, such as stochastic intermittency. The anti-portfolio effect, pointed out in this article, is another example of an unexpected effect displayed by a multiplicative random process. The anti-portfolio effect is due to the fact that, in multiplying a variable by a succession of random factors, there is no mechanism in place for the compensation of fluctuations. Instead of canceling each other out, the fluctuations are accumulating in the system.

As pointed out by a referee, the derivation for independent multiplicative random variables presented in section 1 is generic and can be applied to many processes displaying the anti-portfolio effect, including the random activation energy model studied in section 2. The study of random-channel kinetics and the field generalization discussed in sections 2 and 3, are more complicated and go beyond the derivation from section 1. Moreover, it is possible to study anti-portfolio effect for certain classes of nonindependent, multiplicative random variables or fields described by multiplicative log-normal processes. Work on a general theory of the anti-portfolio effect should be performed.

Our theory can be applied to a large class of processes from science and technology involving growth and/or amplification. We are especially interested in applications regarding signal transmission and amplification in biology as well as genetic and genomic applications.