A Mixed-Model Quantitative Trait Loci (QTL) Analysis for Multiple-Environment Trial Data Using Environmental Covariables for QTL-by-Environment Interactions, With an Example in Maize

Abstract

Complex quantitative traits of plants as measured on collections of genotypes across multiple environments are the outcome of processes that depend in intricate ways on genotype and environment simultaneously. For a better understanding of the genetic architecture of such traits as observed across environments, genotype-by-environment interaction should be modeled with statistical models that use explicit information on genotypes and environments. The modeling approach we propose explains genotype-by-environment interaction by differential quantitative trait locus (QTL) expression in relation to environmental variables. We analyzed grain yield and grain moisture for an experimental data set composed of 976 F₅ maize testcross progenies evaluated across 12 environments in the U.S. corn belt during 1994 and 1995. The strategy we used was based on mixed models and started with a phenotypic analysis of multi-environment data, modeling genotype-by-environment interactions and associated genetic correlations between environments, while taking into account intraenvironmental error structures. The phenotypic mixed models were then extended to QTL models via the incorporation of marker information as genotypic covariables. A majority of the detected QTL showed significant QTL-by-environment interactions (QEI). The QEI were further analyzed by including environmental covariates into the mixed model. Most QEI could be understood as differential QTL expression conditional on longitude or year, both consequences of temperature differences during critical stages of the growth.

THE incidence of genotype-by-environment interactions (GEI) for quantitative traits has important implications for any attempts to understand the genetic architecture of these traits by mapping quantitative trait loci (QTL) and also for the effectiveness of attempts to improve these traits by both conventional and marker-assisted selection (MAS) breeding strategies. The literature on GEI and QTL-by-environment interactions (QEI) for quantitative traits in maize is ambiguous, with evidence in favor (Moreau et al. 2004) and against (Ledeaux et al. 2006) their importance. The diversity of the results for the importance of QEI for quantitative traits in crop plants observed in the literature strongly suggests that explicit testing for their presence, magnitude, and form is a critical step in any attempt to understand the genetic architecture of these traits. Further, theoretical considerations of the impact of different forms of QEI on the outcomes of MAS in plant breeding (Podlich et al. 2004; Cooper et al. 2002, 2005, 2006) motivate the development of methods for explicitly studying the importance of QEI as a component of the genetic architecture of quantitative traits.

When QEI occurs and environmental covariables derived from geographical and weather information are available, QTL effects across environments can be tested for dependence on particular environmental covariables (Crossa et al. 1999; Malosetti et al. 2004; Vargas et al. 2006). More generally, the phenotypic behavior can be modeled in the form of QTL-dependent response curves to the environmental characterizations (Hammer et al. 2006; Malosetti et al. 2006; Van Eeuwijk et al. 2007). These response curves are expected to have nonlinear forms, but limited environmental information will typically allow only linear approximations to these curves.

In this article, we develop a mixed-model framework that can be used to explicitly test for the presence of QEI and investigate its structure for quantitative traits in multiple-environment trials (MET). Our strategy for the analysis of MET is a bottom-up approach, starting with a phenotypic analysis per trial, using no further genotypic and environmental information. This preliminary step serves to select a model for the intraenvironment error structure for each trial, for later use in the MET analysis. We start the MET analysis at the phenotypic level with a genotype-by-environment analysis, with the aim to model genetic variances for each environment and genetic correlations between environments. In the next step we search for QTL main and QEI effects, by including genotypic covariables in the model that represent the marker information. In the final step of our analysis, we include both genotypic and environmental covariables, with the intention to model QTL responses on specific environmental covariables. It is especially this last step that distinguishes our mixed-model QTL approach to MET data from other, comparable mixed-model proposals (Piepho 2000, 2005; Verbyla et al. 2003).

For a serious study of QEI large populations are needed. Therefore, we applied our mixed-model analysis to a large maize experiment, for two quantitative traits, grain moisture and grain yield. The experiment was designed as a MET, with a biparental cross consisting of almost 1000 F₅ testcrosses, evaluated in several locations across the U.S. corn belt in 1994 and 1995. This data set was analyzed previously by Openshaw and Frascaroli (1997), Melchinger et al. (2004), and Schön et al. (2004). However, there are major differences between these previous approaches and our methodology. We used a mixed-model approach in which we modeled genetic correlations between environments and allowed for trial-specific error structures in the phenotypic and genetic model for the MET data. Furthermore, we incorporated explicit environmental information, such as weather conditions and geographical information, in our analysis.

MATERIALS AND METHODS

We briefly summarize the main features of the data, and for further details we refer to descriptions in Openshaw and Frascaroli (1997) and Schön et al. (2004).

Plant materials:

Two elite maize inbred lines, subsequently referred to as A and B, were used as parents. The two parents belonged to the same heterotic group and were chosen because of their eliteness and because the coefficient of coancestry was relatively low, namely 0.21 (Openshaw and Frascaroli 1997). F₂ plants from the cross A × B were selfed to produce 990 independently derived F₅ (F₄:F₅) lines. Testcross seed was produced by crossing to an unrelated inbred tester line from a complementary heterotic pool. Check inbreds including parents A and B, as well as the F₁ between A and B, were also crossed to the inbred tester. All plant materials used in this study are proprietary to Pioneer Hi-Bred International.

Field experiments:

Yield trial data on the testcrosses were obtained from 17 environments located in the U.S. corn belt, with 6 locations in 1994 and 11 locations in 1995. We removed five of the environments due to low observed heritabilities. The reduced data set analyzed in this article consists of 5 locations in 1994 and 7 locations in 1995 (see Table 1). In each of the environments the experimental design consisted of 18 incomplete blocks with 60 entries each. Each incomplete block contained a random sample of testcrosses of 55 F₅ lines, augmented by the two parents A and B, their F₁, and two checks. The same block grouping of the lines was applied in all environments with a different randomization of the blocks and lines within the blocks. Thus, within each trial there were randomized multiple replicates of the parent, the F₁, and two check testcross entries, referred to collectively as repeated checks. The within-trial replication of these check entries enabled modeling of the intraenvironmental trial error variances. Trials were performed with one replication of each of the F₅ testcross progeny per environment.

TABLE 1.

The 12 environments used in the MET analysis

Environment	Location	Year	Irrigation	Latitude	Longitude
AD94	Johnston, Iowa	1994	No	41.68	−93.71
CI95	Champaign, Illinois	1995	No	40.11	−88.43
GC95	Garden City, Kansas	1995	Yes	37.83	−100.86
MR95	Marion, Iowa	1995	No	42.10	−91.62
NP94	North Platte, Nebraska	1994	Yes	41.10	−100.79
NP95	North Platte, Nebraska	1995	Yes	41.10	−100.79
PR95	Princeton, Illinois	1995	No	41.44	−89.48
SV94	Shelbyville, Illinois	1994	No	39.72	−89.10
SV95	Shelbyville, Illinois	1995	No	39.72	−89.10
WN94	Windfall, Indiana	1994	No	40.33	−85.84
YA95	Princeton, Indiana	1995	No	38.11	−87.78
YK94	York, Nebraska	1994	Yes	40.85	−97.53

All these environments were located in the U.S. corn belt and evaluated in 1994 and 1995. The first column gives the name of the environment (corresponding to each location, year combination) that is used in the text and the figures. The irrigation column indicates whether or not there was irrigation at a particular location. Finally, the geographical positions of the trials are defined in the latitude and longitude columns.

Data were recorded and analyzed for grain yield in megagrams per hectare, adjusted to 155 g kg⁻¹ grain moisture, and grain moisture in grams per kilogram at harvest.

Environmental classification:

A modified CERES-maize model (Löffler et al. 2005) was used to characterize the environments, using the input data of nearby weather stations. Average maximum (TMXA) and minimum (TMNA) temperatures and water stress (WS) were calculated for the following four developmental periods simulated by CERES-maize: (1) planting–V7 (seven leaf collars visible), (2) V7–R1 (silks visible outside the husks), (3) R1–R3 (kernels' inner fluid milky white due to development of starch), and (4) R3–R6 (physiological maturity). For further details about the growth stages of maize we refer to the maize page of Iowa State University (http://maize.agron.iastate.edu). In the analysis of the MET data we calculated the QTL responses to the following environmental covariates: year (1994/1995), latitude, longitude, TMNA_d, TMXA_d, and WS_d, where d = 1, … , 4 indicates the development periods as defined above.

Linkage map:

A linkage map was constructed from 172 restriction fragment length polymorphism (RLFP) markers produced for 976 of the 990 analyzed F₄ plants.

Construction of genetic predictors:

Genetic predictors, or regressors, for the additive genetic QTL effects were constructed for a grid of evaluation points, q, along the genome (q = 1, … , Q). These genetic predictors were introduced as explanatory variables in the mixed models (see below). The genetic predictor for individual i and evaluation point q is denoted by 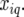At positions with a fully informative marker the genetic predictors for the additive QTL effect had the value 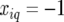when both alleles stemmed from the first parent (A), while they had the value 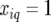when both alleles stemmed from the second parent (B). For heterozygous individuals we had 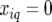More generally, for an individual i and evaluation point q we had

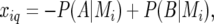(1)

meaning that 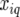is the expected value of the explanatory variable for the additive QTL effect at position q, given all the marker information for individual i, the latter denoted by 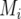(Haley and Knott 1992; Martínez and Curnow 1992; Lynch and Walsh 1998). The QTL probabilities, conditional on all the marker data, 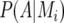and 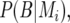were calculated by a hidden Markov chain method (Lander and Green 1987; Jiang and Zeng 1997).

Genetic predictors were calculated at all the marker positions and at an additional grid of points with a maximum step size of 2.5 cM, resulting in 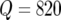evaluation points along the genome.

Single-environment phenotypic analysis for yield:

For the trait yield we started our analysis of the MET data with a phenotypic analysis of the individual environments. Obvious outliers were removed, that is, the values that we could identity as representing faulty data, for example, if there was a clear indication of mixing up seed between neighboring plots.

For the mathematical description of the model for the data, with the data containing both repeated checks and F₅ individuals in each trial, we use a notation similar to that of Eckermann et al. (2001) and Verbyla et al. (2003). Let 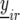denote the phenotype of the rth replicate observation on the ith genotype (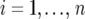), where the underline indicates a random variable. The statistical model is given by

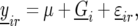(2)

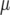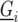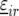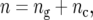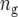where is the general mean, represents the genetic effect of genotype i expressed as a deviation from the general mean, and represents nongenetic effect r for genotype i. The genotypes can be separated into two groups, where is the number of testcross lines derived from the cross between parents A and B (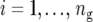), and 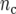is the number of check entries (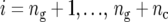). The model for 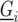reads

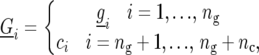(3)

where 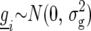is a random variable for the genetic effect of line i derived from the parental cross, and 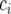represents a fixed effect for check i. Although the check entries are not relevant to the detection of QTL, these entries are important in providing information on the nongenetic variation that may be present (Verbyla et al. 2003).

We started the trial analysis with the following model for the nongenetic term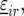

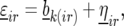(4)

where 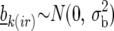is the effect of incomplete block k, appropriate for the replicate r observation on genotype i. The term 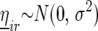represents a residual error term. Next, we added random row and columns effects, denoted by 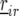and 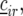to the model for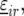

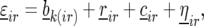(5)

and used these extra terms in later analyses if these effects were found significant. In contrast to the block effects, the row and column effects did not follow from randomization theory: in the field design, row and columns did not represent a restriction on the allocation of genotypes to experimental plots. Instead, inclusion of random row and column effects should be interpreted as an attempt to control local variation along the lines discussed in Gilmour et al. (1997) and Cullis et al. (1998, 2006).

Preliminary investigations showed linear and quadratic relationships between yield and stalk count across locations. Therefore, linear and quadratic terms for stalk count were included in the model for 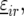where these terms were significant. The model with all the random and fixed effects for 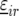reads

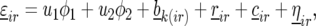(6)

where 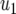is the centered covariate for stalk count with parameter 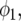and 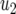is the centered covariate for squared stalk count with parameter 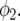We included stalk count as an extra explanatory variable because it gives a measure for the environmental quality of the plots. For each environment, nonsignificant terms in this full model were omitted.

Multi-environment phenotypic and QTL analysis for yield:

Our mixed-model strategy consisted of three steps, which we first describe in words. In the first step, a phenotypic mixed model was fitted to genotype-by-environment data, where the aim was to identify a variance–covariance (VCOV) model with the possibility of heterogeneity of genetic variances across individual environments and heterogeneity of genetic correlations between pairs of environments. At this stage, no marker information was included in the model, nor were environmental characterizations. In the second step of our procedure, we performed a repeated genome scan for the detection of environment-specific QTL effects. The mixed model that we used to test for environment-specific QTL contained marker-related information in the fixed part of the model, combined with the VCOV structure between environments identified in the previous phenotypic analysis. The marker-related information entered the model in the form of genetic predictors, linear functions of QTL genotype probabilities given flanking marker genotypes, and chromosome position. A first genome scan for QTL corresponded to simple interval mapping (Lander and Botstein 1989), in which a putative QTL is moved along the genome and at each position a test for environment-specific QTL is performed. In a second scan, the genetic predictors of identified QTL of the first scan were used as cofactors. This second scan was performed by multi-environment composite interval mapping. Jiang and Zeng (1997) proposed a comparable procedure in a mixture model context. In the final step of our procedure, for the identified QTL positions in the genome scan of step two, QTL expression across environments is regressed on environmental covariables in an attempt to identify the driving environmental forces behind QEI.

We now describe our mixed-model strategy in a more formal way, starting with the first step. Let 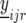denote the phenotype of the rth replicate observation on the ith genotype (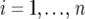) in environment j (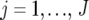). The statistical model is given by

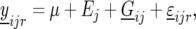(7)

where 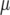is the general mean, 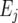is the environmental main effect expressed as a deviation from the general mean, 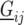represents the genetic effect of genotype i at environment j, and 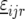is a nongenetic effect. Using a vector–matrix notation, the nongenetic variation within an environment j can be further decomposed as

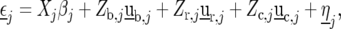(8)

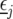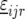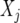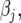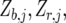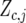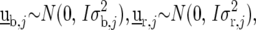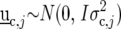where is a vector with elements ; is the design matrix for fixed effects to be defined shortly; and are the design matrices for the random blocks, rows, and columns effects and ; and 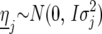is a residual error term. For the trait yield the number of fixed and random effects depended on a model selection process per environment. If a random block, row, or column effect was not selected in the single-environment analysis, we put the corresponding variance component equal to zero in the MET analysis. Stalk count and squared stalk count were used as candidates for fixed effects. For the trait moisture we used only incomplete blocks as a random effect to account for nongenetic variation within the environments.

The model for 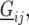in the absence of genetic predictors, is given by

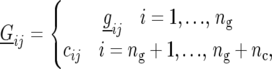(9)

where 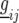is a random variable for the genetic effect of line i derived from the parental cross in environment j, and 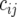represents a fixed effect for check i in environment j. We assume that the vectors 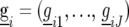have a multivariate normal distribution with zero mean and a VCOV matrix 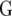: 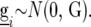In this article we analyzed and compared seven models for the VCOV matrix 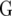(Table 2). The simplest model is homogeneous (residual) variation (ID), for which there are no genetic correlations between environments and for which the genetic variances are homogeneous across the environments. These assumptions are rarely realistic. For the well-known compound symmetry (CS) model, the genetic covariances between environments are modeled by an extra parameter 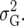The heterogeneous (residual) genetic variation (DG) model allows for heterogeneous genetic variances (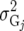) but assumes there are no genetic correlations between environments. The uniform covariance, heterogeneous variance (UCH) model is an extension of model DG with a common covariance parameter 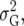assumed uniform between all pairs of environments. Again, the latter assumption is usually not realistic, and model UCH can be improved by using a first-order or a second-order factor analytic (FA1 or FA2, respectively) model (Piepho 1997, 1998; Smith et al. 2001). The most flexible model is to choose the VCOV matrix 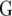unstructured (UN) model, with a total number of 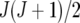parameters. More details are given in Table 2. We used the Bayesian information criterion (BIC) (Hastie et al. 2001; Broman and Speed 2002) to select the optimal model, i.e., the model that gives the right balance between fit to the data and model complexity,

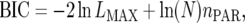(10)

where 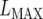is the maximum (residual) likelihood, N is the total number of observations, and 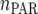is the number of parameters in the VCOV matrix 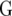(Table 4; Piepho 2000).

TABLE 2.

Models for the VCOV structure

Model		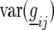		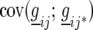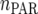Description
ID		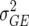0	1	Identical (residual) genetic variation
CS		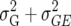	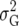2	Compound symmetry
DG		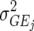0	J	Heterogeneous (residual) genetic variation
UCH		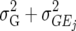		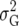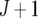Uniform covariance, heterogeneous variance
FA1		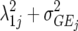	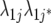2J	First-order factor analytic model
FA2		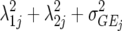	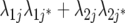3J−1	Second-order factor analytic model ()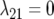
UN		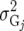		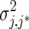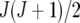Unstructured model

For a further explanation see text.

TABLE 4.

Comparison of the VCOV models for yield and moisture

Model	NPAR	BIC yld	BIC mst	Deviance yld	Deviance mst
ID	1	785.5	6888.7	776.0	6879.2
CS	2	277.5	1459.7	258.6	1440.8
DG	12	872.3	6768.9	758.7	6655.3
UCH	13	364.7	1533.2	241.6	1410.1
FA1	24	389.2	645.9	161.9	418.7
FA2	35	418.8	495.3	87.3	163.8
UN	78	738.6	738.6	0.0	0.0

The first column refers to the particular model, N_PAR is the number of parameters, and BIC yld and BIC mst give the BIC for yield and moisture, respectively. The last two columns give the deviances for yield and moisture. Both BIC and deviance are given relative to the most complex model, the unstructured (UN) model.

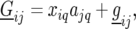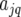In the following step of the analysis of the MET data, a putative QTL is moved along the genome. This corresponds to the simple-interval-mapping (SIM) approach developed by Lander and Botstein (1989) in a mixture model framework. The model for the genotypic effect of the F₅ lines becomes where is the environment-specific effect of the additive genetic predictor at evaluation point q. The complete model for the individuals derived from the biparental cross reads

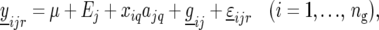(11)

where we use the VCOV matrix for 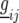that was selected in the previous phenotypic modeling step. Under the null hypothesis, i.e., assuming that the putative QTL has no effect at all across environments, we have H₀: a_1q = a_2q = … = a_Jq = 0. The Wald test (Verbeke and Molenberghs 2000) can be used to test for the fixed terms in mixed models. Under the null hypothesis, the Wald test statistic has an approximate 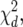where d is the number of degrees of freedom. The degrees of freedom are equal to the difference in the number of parameters between the null and the alternative hypothesis, which means in this case that it is equal to the number of environments, d = J.

For completeness, we also performed a test for QTL main effects along the genome, in which case the model reads

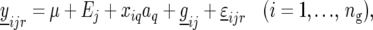(12)

where a_q is the QTL main effect.

Now, significant peaks in the QTL profile produced by model (11) are selected, with successive QTL being separated from each other by at least 30 cM. The genetic predictors corresponding to the selected QTL positions are subsequently used as cofactors, to correct for genetic background effects, while a putative QTL is moved along the genome. This method is a multi-environment case of the composite-interval-mapping (CIM) approach by Zeng (1994) and the multiple-QTL-mapping (MQM) approach by Jansen and Stam (1994), using mixed models instead of mixture models. The model for the genotypic effects of the F₅ lines reads

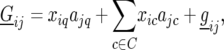(13)

where C is the set of cofactors used to model QTL on other chromosomes. The complete model is given by

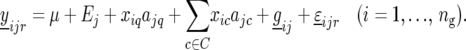(14)

Subsequently, the significant peaks of the profile produced by (14) are selected as QTL, with again successive QTL on the same chromosome being separated by at least 30 cM. The selected QTL obtained from the CIM scan are denoted by S. Environment-specific QTL effects are estimated from the model:

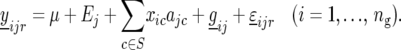(15)

In the next step we determine which QTL have a significant QTL × E effect, by splitting the environment-specific QTL effects into two parts, namely main effects for each QTL (a_c) and environment-specific deviations from the main effects ():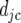

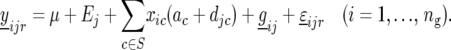(16)

We test for the significance of the deviations 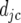by using a Wald test.

Finally, we calculate QTL responses to environmental covariables. For each QTL with a significant QTL × E effect and for each environmental covariable we use

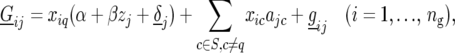(17)

where 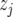is the value of an environmental covariable in environment j, 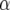is a QTL main effect, 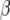is the slope parameter, which expresses the response of the selected QTL to the environmental covariable, and 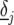is a residual environment-specific QTL effect.

Genomewide significance threshold:

In this article we use a Bonferonni correction (e.g., Lynch and Walsh 1998) for the Q = 820 evaluation points along the genome. For a 5% genomewide significance threshold we obtain T = 4.2 for the −log₁₀ of the P-values. Instead of using a genomewide significance threshold we also considered using the idea of false discovery rate (FDR) control, introduced by Benjamini and Hochberg (1995). However, Chen and Storey (2006) showed that FDR suffers from several problems when applied to linkage analysis, and therefore we decided to use a simple Bonferonni correction.

Software:

For the calculation of the genetic predictors we implemented the hidden Markov model methodology in C++. These genetic predictors can also be calculated using software packages like Grafgen (Servin et al. 2002) and R/QTL (Broman et al. 2003). For the statistical analysis we used Genstat (Payne et al. 2006).

RESULTS

Single environment analysis:

We analyzed the phenotypic data per environment (trial), to select appropriate models for the error structure. The models for the error structures were retained in the later MET analyses. Initially only the obvious outliers were removed, that is, the values that we could identify as representing faulty data. Additionally, a number of plots had extremely low stand counts; as plots with very low stands do not contain reliable yield data, these plots were omitted.

For grain moisture we used only incomplete block effects (see materials and methods) in the models for the single trials, since the spatial variation within environments was relatively low. For yield we used a more elaborate approach: we compared several models, starting with a model with only (incomplete) block effects. Block effects were used for all the environments. Next, postblocking effects, rows and columns, were added to the model when significant. Table 3 shows that in all environments, except NP94, columns were included in the final model. Row effects were included in four of the environments. In the next step quadratic regressions on stalk count were added to the model, because preliminary investigations of stalk count indicated significant relationships between stalk count and yield. Linear and quadratic effects for stalk count were added to the model only when significant. Linear effects for stalk count were used in nine environments, and the quadratic effects were used in three environments.

TABLE 3.

Selected environments used in the QTL × E analyses and the spatial models for yield for each environment

Environment	Stalk count	Stalk count squared	Row	Column
AD94	x	x		x
CI95	x	x	x	x
GC95			x	x
MR95			x	x
NP94	x	x
NP95				x
PR95	x			x
SV94	x			x
SV95	x		x	x
WN94	x			x
YA95	x			x
YK94	x			x

x's indicate that the model term in the column heading was included in the within-trial error model for that specific trial. For the definition of the environments see Table 1.

We have checked for the necessity of including first-order autoregressive (AR1) processes on rows and columns, but found that effects corresponding to AR1 processes were small. Such processes were therefore omitted from further analyses. Fitting of autoregressive processes increased computation times substantially in the multiple-environment analyses. In addition, convergence problems occurred with these models.

Multi-environment analysis:

First, we compared VCOV structures for the modeling of genetic correlations between environments (Table 4) for both yield and moisture. The models were compared using BIC. As can be seen in Equation 10, lower BIC values indicate a better balance between model complexity and model fit. The results are summarized in Table 4.

For moisture, exclusion of genetic correlations from the model produced very high BIC values (Table 2). BIC decreased substantially if we used a (heterogeneous) compound symmetry model. The BIC decreased further for a factor analytic model. FA2 was selected as the optimal model.

For yield, the difference between BIC values for the different models was less pronounced. Three models, those without genetic correlations and the unstructured model, with a different correlation coefficient for each pair of environments, were inferior to the other four. The best model in terms of BIC was model CS, the compound symmetry model. However, the differences were small and we decided to select the FA1 model, because it is more flexible in modeling different genetic correlations between environments.

QTL genome scans:

First, we discuss the main features of the genome scan, and then we discuss QTL positions and QTL effects in more detail. The CIM genome scans for moisture and yield are given in Figures 1 and 2, respectively. In the analysis we only used cofactors on other chromosomes, so this means that cofactors on the chromosome with the putative QTL were excluded from the model.

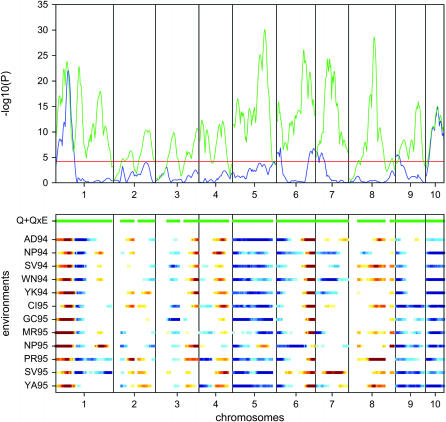
Figure 1.—

Genome scan for moisture. (Top) The P-values for the test for main effects (blue) and the test for environment-specific effects (green) are shown. The red horizontal line is the 5% genomewide significance threshold. The green horizontal lines in the bottom section indicate significant environment-specific effects. (Bottom) The environment-specific QTL effects are shown. Blue (red) indicates that parent A (B) has significantly higher moisture values. For the VCOV structure we used the second-order factor analytic model.

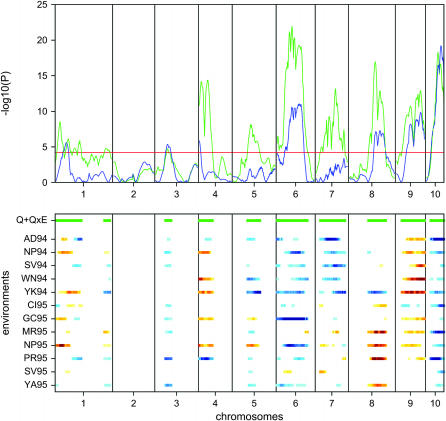
Figure 2.—

Genome scan for yield. (Top) The P-values for the test for main effects (blue) and the test for environment-specific effects (green) are shown. The red horizontal line is the 5% genomewide significance threshold. The green horizontal lines in the bottom section indicate significant environment-specific effects. (Bottom) The environment-specific QTL effects are shown. Blue (red) indicates that parent A (B) has significantly higher yield values. For the VCOV structure we used the first-order factor analytic model.

The top sections of Figures 1 and 2 show the P-values of tests for QTL main effects and for environment-specific QTL effects. The bottom sections show heat maps along the genome for each environment, where red means that the A allele had a significant positive effect, and blue means that the B allele had a significant positive effect in that environment. An effect was called significant when the P-value was below the significance level 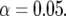The P-values were determined from squared z-ratios, with z-ratios being calculated as estimates divided by standard errors.

The analysis for moisture shows that the −log₁₀(P-values) were very high, pointing to a very strong signal along the whole of the genome (Figure 1). Further, it can be seen that there were strong QEI effects. Most of the interactions were noncrossovers; i.e., the effects had the same sign in each environment. Examples of crossover interactions were found on chromosomes 1, 4, 5, 7, and 8. On chromosome 10 there was a QTL with a strong main effect. For this QTL the allele from parent A had significantly higher moisture values than the allele from parent B. Chromosome 1 shows three types of QTL: the first QTL had a strong main effect, the second QTL showed changes in magnitude across the environments, and the third QTL exhibited strong crossover interactions. A large year effect was present for QTL on the second part of chromosome 9; only in 1995 did the alleles from parent A have a significantly higher moisture value.

The genome scan for yield is given in Figure 2. The QTL on chromosome 10 had a strong main effect, where the A allele resulted in higher yields. Other QTL with a relatively strong main effect were found on chromosomes 6, 8, and 9. There were also several QTL with strong QEI interactions; examples can be found on chromosome 4 and 7. The heat maps show that there were chromosome regions with strong year effects. One example can be found on chromosome 7, where the allele from parent A had a positive effect only in 1994. Another example of a segment with a year effect was located on the second part of chromosome 8, where parent B had a positive effect only in 1995.

QTL positions and effect:

QTL positions were estimated on the basis of the genome profile given in Figures 1 and 2, where we further assumed that the minimum distance between significant QTL should be at least 30 cM. In this large population with strong signals along the whole genome for both grain moisture and grain yield, it is difficult to decide what should be considered a single QTL effect. One of the possible reasons that we found such strong QTL main and QEI effects is that many QTL, both directly and indirectly, were involved in the complex traits yield and moisture.

The QTL positions and effects for grain moisture and grain yield are summarized in Tables 5 and 6, respectively. The given estimated effects are the estimates for the B allele. Suppose the estimated allele effect for B at a particular QTL position is a, then the estimated allele effect for A should be −a, and the estimated phenotypic difference between two individuals differing at only this particular QTL position amounts to 2a.

TABLE 5.

Environment-specific QTL effects for moisture

		Chromosome no.
Environment name	Position (cM):	1	1	1	2	2	2	3	3	4	4	5	5	6	6	7	8	8	9	9	10
				54	113	218	41	81	156	86	200	9	110	21	152	5	128	54	122	208	4	107	53
AD94		50	−49	10	−6	26	−15	−10	20	−1	18	−26	−32	−25	24	10	11	5	−13	8	−14
NP94		27	−30	14	−11	14	1	−8	13	−4	9	−16	−13	−14	−1	−10	−5	6	−11	−2	−20
SV94		39	−41	12	−10	16	−4	−21	17	−9	8	−22	−23	−13	14	−4	19	10	−12	1	−17
WN94		44	−45	15	−10	15	−11	−13	22	−12	12	−27	−18	−18	7	−20	14	8	−16	2	−24
YK94		19	−12	2	−6	7	6	−3	9	−1	5	−7	−9	−7	5	−5	−1	3	−7	−1	−13
CI95		34	−26	5	−10	20	5	−15	12	−10	14	−17	−26	−9	11	9	14	5	−11	−19	−21
GC95		38	−22	7	−7	2	8	−23	4	−3	7	−29	−23	−8	−1	1	0	6	−7	−10	−15
MR95		32	−18	7	−10	8	−1	−6	1	−4	4	−4	−14	−9	0	0	6	6	−7	−7	−14
NP95		36	−23	22	−17	14	−9	−8	17	7	−9	−19	16	−12	−15	0	−2	17	−12	−12	−16
PR95		24	−23	−5	−14	20	0	−7	11	−15	8	−16	−14	−19	−1	2	26	2	−7	−6	−11
SV95		33	−36	−11	−14	17	6	−2	0	−5	15	−25	−33	−5	15	18	10	9	−12	−16	−15
YA95		28	−15	1	−16	10	14	−6	4	−19	10	−23	−17	−21	6	−7	16	3	−8	−15	−23

The effects given are multiplied by a factor of 100. Negative QTL effects mean that the A allele gives higher moisture values than the B allele, and positive QTL effects mean that the B allele gives higher moisture values. The italic (underlined) values are significant negative (positive) QTL effects. For the VCOV structure we used the second-order factor analytic model.

TABLE 6.

Environment-specific QTL effects for yield in kg ha⁻¹

		Chromosome no.
Environment name	Position (cM):	1	1	1	3	4	5	6	7	8	9	10
				25	121	250	59	41	86	73	96	127	119	57
AD94		28.6	−101.3	−11.2	−42.1	−69.4	−73.0	−40.7	−107.8	−1.3	86.8	−183.8
NP94		96.7	−40.6	79.0	−87.4	111.4	−26.9	−138.0	−87.7	−12.2	109.0	−108.2
SV94		−26.6	−58.7	−41.2	−67.2	25.3	−35.8	−73.8	−143.8	43.9	147.0	−0.4
WN94		−6.3	17.0	−10.9	−1.5	100.8	−113.2	−58.2	−101.3	26.2	169.9	−62.2
YK94		81.8	84.6	−194.1	69.5	208.4	−150.6	−158.0	−168.2	−197.5	225.6	−181.2
CI95		−37.0	56.2	9.2	−65.6	−23.2	−20.5	−48.0	31.2	62.8	−33.5	−83.6
GC95		99.5	−60.5	71.2	−69.1	98.3	70.9	−294.8	−61.9	17.1	110.0	−44.9
MR95		7.2	−8.9	79.3	−54.6	−16.0	−60.1	−6.8	76.6	121.3	84.3	−130.8
NP95		160.3	−2.0	70.2	−44.9	105.4	115.6	−158.3	−10.8	145.6	68.4	−85.4
PR95		−1.2	−76.1	−49.3	−102.5	−133.5	−62.7	−47.8	−7.5	163.5	82.1	−151.9
SV95		−25.9	26.2	12.3	−30.9	−22.8	−56.2	34.7	7.9	37.0	36.2	−53.4
YA95		−33.0	2.6	−70.2	−109.9	−21.0	−84.2	−63.6	−45.7	125.1	35.0	−73.3

Negative QTL effects point to superiority of the A allele, and positive QTL effects point to superiority of the B allele. The italic (underlined) values are significant negative (positive) QTL effects. For the VCOV structure we used the second-order factor analytic model.

For moisture 20 QTL were detected (Table 5). The most consistent QTL effects across environments were found on chromosome 1 at ∼54 cM and on chromosome 10 at ∼53 cM. Crossover effects, with both significant positive and significant negative effects, were found on chromosomes 1 (∼218 cM), 2 (∼156 cM), 4 (∼9 cM, ∼110 cM), 5 (∼152 cM), 6(∼128 cM), and 7(∼54 cM). A year effect was observed for the QTL on chromosome 9 at ∼107 cM. Some of the estimated QTL effects at the location North Platte in 1995 (NP95) were quite different from those at other locations, which can also be observed in Figure 1. For example, the QTL effects for this environment are opposite in sign to the other locations with a significant effect for the QTL on chromosome 4 (∼9 cM, ∼110 cM), the second QTL on chromosome 5 (∼152 cM), and the second QTL on chromosome 6 (∼128 cM).

For yield we detected in total 11 QTL or chromosome segments with a strong signal (Table 6). There were two QTL with strong main effects, one on chromosome 9 (∼119 cM) with a positive effect and one on chromosome 10 (∼57 cM) with a negative effect. Significant crossover interactions were found for 6 QTL. A year effect was observed for the QTL on chromosome 8 (∼127 cM). The strongest QTL effects were found for the irrigated environments NP94, YK94, GC95, and NP95 (see Table 1 for definitions of environments).

Environmental covariates:

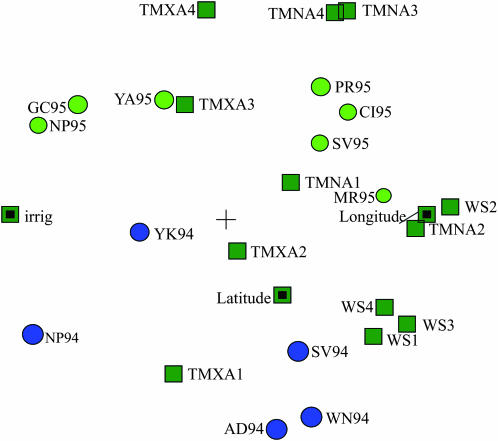
A further decomposition of the QTL with significant QEI effects was obtained by introducing environmental covariates as explanatory variables. Before we describe the QTL responses to environmental covariables, we investigate the relations between the environmental covariables and the trials. Figure 3 shows a biplot for the environments and the environmental covariates following a principal components analysis on the standardized environmental covariates. The representation in the plane of covariates was generally good as most of them were located close to or on the unit circle typical of perfect representation (Gabriel 1971). The vertical axis represents a year contrast, and the horizontal axis is related to longitude. The year 1995 had higher average minimum and maximum temperature in the reproductive stages 3 and 4 (TMNA3, TMNA4, TMXA3, TMXA4) than the year 1994. Longitude had a highly positive correlation with both water stress and minimum temperature in the second stage (WS2, TMNA2) and was negatively correlated with irrigation.

Figure 3.—

Biplot for environmental classification data. The circles are the environments, with 1994 in blue and 1995 in light green. The environmental covariates are indicated by squares. For a further description of the environments and the environmental covariates see materials and methods and Table 1.

The QTL responses for moisture are given in Table 7. Most QTL had a strong response to temperature and water stress in the reproductive stage (stages 3 and 4). These environmental covariates were positively (TMXA3, TMXA4, TMNA3, TMNA4) or negatively (WS3) correlated with year (Figure 3). QTL on chromosomes 4 and 8 responded to longitude, which was related to differences in climate and management practices: in the western parts of the U.S. corn belt differences between mean daily minimum and maximum temperatures are higher, while rainfall is lower than in the eastern parts (National Climatic Data Center, http://gis.ncdc.noaa.gov). Because of the higher likelihood of drought stress, the environments in the western parts of the U.S. corn belt are more likely to be irrigated (Table 1).

TABLE 7.

QTL responses for moisture

Chromosome	Position (cM)	First	Second	−log10(P)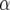
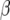1	113	WS3	WS1	4.2	−27.18	−36.20
1	218	TMNA4	TMNA3	2.8	6.33	−1.90
3	200	TMXA4	TMNA4	3.7	9.23	−2.39
4	9	Longitude	TMXA3	3.8	−6.66	−0.99
6	5	TMXA2	WS1	3.2	−11.57	4.76
6	128	WS3	WS1	3.0	5.39	28.69
8	122	Longitude	WS1	6.3	8.68	1.46
8	208	TMXA3	TMNA2	3.0	5.35	1.53
9	107	TMXA4	Year	5.9	−5.58	−2.93

First and second refer to the two environmental covariates that gave the best explanation for the Q × E effect. The P-value, QTL main effect α, and slope parameter β are given for the first covariate.

The QTL responses for yield are given in Table 8. Most of the QTL responses can be explained in terms of spatial (longitude, latitude) and temporal (year) effects. The QTL on chromosome 5 at ∼86 cM had the highest response to TMXA3, but this environmental covariate had a high positive correlation with year (Figure 3). The QTL on chromosome 1 at ∼25 cM had a strong response to longitude, which can also be seen in Table 6: only the environments in the western part of the U.S. corn belt (NP94, NP95, GC95) had positive effects.

TABLE 8.

QTL responses for yield

Chromosome	Position (cM)	First	Second	−log10(P)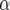
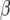1	25	Longitude	TMNA2	11.7	0.46	−0.17
4	41	Longitude	WS2	1.5	0.44	0.15
5	86	TMXA3	TMNA2	6.6	−0.65	0.49
6	73	Longitude	WS2	3.6	−1.35	0.19
7	96	Year	TMNA4	5.9	−0.75	0.95
9	119	Year	TMNA4	2.6	1.47	−0.69
10	57	Latitude	TMXA2	2.7	−1.48	−0.46

First and second refer to the two environmental covariates that gave the best explanation for the Q × E effect. The P-value, QTL main effect α, and slope parameter β are given for the first covariate.

DISCUSSION

Statistical models:

In this article we used mixed models to analyze the data, because of their flexibility and the possibility of modeling genetic correlations between environments and error structure within environments. Within this mixed-model framework choices have to be made; in particular, we have to choose which terms should be considered random and which ones fixed. Here, we assumed the genotypes to be random and environments, the QTL main effects, and environment-specific QTL effects to be fixed. The same type of model was also used by Malosetti et al. (2004). Piepho (2000) assumed random environments, fixed QTL main effects, and random effects for environment-specific deviations from the QTL main effects. Verbyla et al. (2003) did not include a separate parameter for QTL main effects and assumed that the environment-specific effects were random. The discussion on whether to take particular terms as fixed or random often reinforces dogmatic stands. We prefer a pragmatic attitude for this question. Thus, we also analyzed the present data set with a model assuming random effects for the QTL effects, upon which we found similar profiles for the genome scans and identified very comparable QTL, showing that our analysis, for this data set at least, is robust with regard to the choice of fixed or random QTL effects. Maybe the most important difference between a random- and a fixed-effect model for environment-specific QTL effects or deviations from the QTL main effect is that the estimates in a random-effect model are shrunken, making us less optimistic and more realistic about their impact in marker-assisted selection applications.

Instead of the mixed-models methodology, other statistical techniques would have been possible too, at least in principle. An elegant method would be a Bayesian approach. Within a Bayesian framework, several approaches have been developed for QTL analysis. One example of such a Bayesian method is a multiple-QTL approach. QTL are added or removed from the model by using a reversible-jump Markov chain Monte Carlo method; see, e.g., Sorensen and Gianola (2002) for an overview. Another example of a Bayesian method includes all the markers of the entire genome, where each marker effect has its own variance parameter, which in turn has its own prior distribution so that the variance can be estimated from the data (Meuwissen et al. 2001; Xu 2003; Ter Braak et al. 2005). These Bayesian methods have the advantage that they automatically select QTL or cofactors (in terms of our methodology) and give a credibility interval for the positions of the QTL. Possible disadvantages of these methods, when applied to the data set discussed in this article, are the computation time and problems related to the convergence of the Markov chain. Another point, which can be seen both as an advantage and as a disadvantage of a Bayesian analysis, is that we need to choose prior distributions for the parameters.

Another alternative for a mixed-model approach is penalized regression (Boer et al. 2002; Zhang and Xu 2005) and the use of regularization paths (e.g., Hastie et al. 2001; Friedman and Popescu 2004). Penalized regression is strongly related to the mixed-model approach. In mixed models, the ratios of the variance components can be regarded as penalties, where strong penalties result in small ratios of variance components. Penalized regression is an example of the broader class of regularization path methods, in which a set of candidate models is defined by a path through the space of parameter values, starting from the simplest model where the parameter values are shrunk to zero and ending at the most complex model, where there is no shrinkage of the parameters. The goal is to find an optimal point along this path, for example, by using cross-validation (Friedman and Popescu 2004). We think that the idea of regularization paths can form an interesting bridge between mixed-model methods and Bayesian techniques. However, these regularization path techniques have to be further developed for QTL analysis both in single-environment and in multiple-environment situations.

QTL analysis in MET:

We found that QEI effects were important for both grain yield and grain moisture and that most of the QEI effects could be decomposed as QTL responses to spatial and temporal environmental covariables. The temporal effects were related to differences in weather conditions between years. The spatial (longitude, latitude) effects were related to differences in climate, soil type, and management practices, particularly the use of irrigation. A number of the QTL responses to spatial and temporal variations very probably reflect responses to temperature effects and in some cases associated water-stress effects.

Also in other METs evidence for QTL responses to temperature has been found. In a MET of tropical maize consisting of 211 F_3:4 lines tested in eight environments, QTL responses to both maximum and minimum temperature during flowering time were reported (Crossa et al. 1999; Vargas et al. 2006). In wheat QEI effects were explained by the temperature during pre-anthesis growth (Campbell et al. 2004). In barley QEI effects for yield could be described as QTL expression in relation to the magnitude of the temperature during heading (Malosetti et al. 2004). In all these cases the environmental variable temperature in a critical stage of the development of the crop could explain the QEI effects, but this still is not proof that there is a causal relationship between QTL response and the environmental variable, because many environmental covariables are correlated in a complex way, and not all environmental variables are observed.

In this article we analyzed a biparental cross, in which the two parents were elite inbreds from a heterotic group developed during the course of a long-term commercial breeding program (Openshaw and Frascaroli 1997). Since we found several QTL sensitivities to environmental covariables in this experiment, it can be expected that also in other crosses, with two or more parents with high genetic diversity, QEI interactions will play an important role. Furthermore, it is important to note that the QTL main effects and QEI effects are observed in a given genetic background. Simulation results show that epistatic interactions between QTL and the genetic background in combination with QEI are expected to be important for the outcomes of MAS (Podlich et al. 2004; Cooper et al. 2005).

Our mixed-model analyses resulted in the detection of many QTL, both for grain moisture and for grain yield, which is consistent with earlier analyses (Openshaw and Frascaroli 1997; Melchinger et al. 2004; Schön et al. 2004). However, it is difficult to compare the results in much detail, because in these earlier analyses no information about the positions of the QTL for grain yield and grain moisture was given. An important difference with these earlier analyses is that we also found strong evidence for QEI interactions, and, even more important, we found that most of these QEI interactions could be explained in terms of QTL responses to environmental covariates. In the U.S. corn belt, one of the most productive maize regions of the world, and an important target population of environments, both spatial and temporal environmental variations were strongly related to QTL expression. On the basis of their analyses of the current data, in relation to power of QTL detection and estimation of QTL effects, Schön et al. (2004) advised to increase the population size rather than the number of test environments, unless plot heritabilities are very low. We qualify that conclusion. We think that the statistical model used by Schön et al. (2004), being a kind of regression model with simple assumptions on error structure and no genetic correlations between environments, was not flexible enough to cope with all the complexities of the present data set, and therefore the environmental dependency of QTL expression received insufficient attention. Thus, Schön et al. (2004) concentrated exclusively on QTL main effects and treated environments as exchangeable. In the light of our findings on the omnipresence of structured QEI in the current data, we would not subscribe to the view that an increase in population size is more important than an increase in the number of test environments. Even when one wants to focus on main-effect QTL expression, it is still worthwhile to collect information across enough test environments for modeling QEI, because the quantification of the error attached to the main-effect QTL estimate will be improved by explicit modeling of the QEI. So, we would not opt for the choice of just a few test environments to favor a larger population. Beyond population sizes of 500 there probably is not very much to gain and it would then be wise to consider a fuller sampling of the target population of environments.

Biological models for predicting gene-to-phenotype associations:

We used linear mixed models to analyze the data and searched for linear QTL responses to environmental covariates. Upon the collection of additional genotypic information in the form of measurements describing plant development or information relating to gene and metabolic expression, a next step in modeling could be the fitting of statistical models containing increased biological realism. Such models would immediately become nonlinear (Ma et al. 2002; Malosetti et al. 2006; Van Eeuwijk et al. 2007). Of course, from a biological point of view, nonlinear QTL models are still simplified representations of the interacting biological and environmental components of the dynamic plant system (Hammer et al. 2006), but for most applied prediction purposes, like marker-assisted breeding, such nonlinear models would represent an improvement over the present linear models. Another promising approach would be to combine mathematical models, using differential equations to model plant growth and gene expressions in time (Welch et al. 2005), with advanced statistical methods.