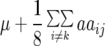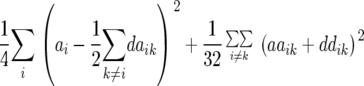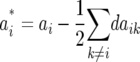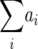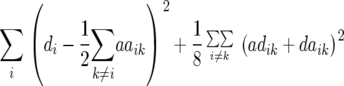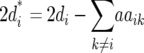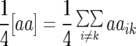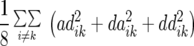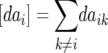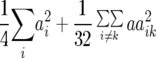Heterosis for Biomass-Related Traits in Arabidopsis Investigated by Quantitative Trait Loci Analysis of the Triple Testcross Design With Recombinant Inbred Lines

Abstract

Arabidopsis thaliana has emerged as a leading model species in plant genetics and functional genomics including research on the genetic causes of heterosis. We applied a triple testcross (TTC) design and a novel biometrical approach to identify and characterize quantitative trait loci (QTL) for heterosis of five biomass-related traits by (i) estimating the number, genomic positions, and genetic effects of heterotic QTL, (ii) characterizing their mode of gene action, and (iii) testing for presence of epistatic effects by a genomewide scan and marker × marker interactions. In total, 234 recombinant inbred lines (RILs) of Arabidopsis hybrid C24 × Col-0 were crossed to both parental lines and their F₁ and analyzed with 110 single-nucleotide polymorphism (SNP) markers. QTL analyses were conducted using linear transformations Z₁, Z₂, and Z₃ calculated from the adjusted entry means of TTC progenies. With Z₁, we detected 12 QTL displaying augmented additive effects. With Z₂, we mapped six QTL for augmented dominance effects. A one-dimensional genome scan with Z₃ revealed two genomic regions with significantly negative dominance × additive epistatic effects. Two-way analyses of variance between marker pairs revealed nine digenic epistatic interactions: six reflecting dominance × dominance effects with variable sign and three reflecting additive × additive effects with positive sign. We conclude that heterosis for biomass-related traits in Arabidopsis has a polygenic basis with overdominance and/or epistasis being presumably the main types of gene action.

THE improved vigor of F₁ hybrids in comparison with their parental homozygous lines, defined as heterosis (Shull 1922), is a widely exploited phenomenon in plant breeding (Schnell 1982; Duvick 1999). In general, heterosis is largest in allogamous and smallest in strictly autogamous crops. Furthermore, its relative amount usually increases with the complexity of a trait and can exceed 100% for traits such as grain yield in maize (Becker 1993).

Ever since its discovery at the beginning of the 20th century (East 1908; Shull 1908), heterosis has attracted the attention of geneticists and breeders because of its poorly understood genetic nature. The first hypotheses on the genetic causes underlying heterosis are based on dominance and overdominance gene action. Regarding the former, superiority of hybrids results from the accumulation of dominant favorable alleles from both homozygous parents (Davenport 1908; Bruce 1910; Jones 1917). In contrast, the overdominance hypothesis suggests the superiority of the heterozygous state over either homozygote (Hull 1945; Crow 1948). A third hypothesis implies that heterosis results from epistatic interactions among alleles at different loci (Powers 1944; Williams 1959).

Quantitative trait loci (QTL) mapping approaches have proven to be powerful in dissecting the genetic basis of complex traits and heterosis in crops. In a pioneer QTL study with maize, Stuber et al. (1992) detected 11 QTL for grain yield, mostly with a strong tendency toward dominance and overdominance. A reanalysis of their data set with a different biometrical model (Cockerham and Zeng 1996) led to the conclusion that heterosis in the maize hybrid B73 × Mo17 was attributable not only to dominance of favorable alleles but also to epistatic effects between linked QTL. Contradictory results were reported in studies on heterosis in rice. Findings of several authors (Xiao et al. 1995; Li et al. 2001; Luo et al. 2001) indicated that heterozygotes were superior to both parental homozygotes at most QTL, suggesting the presence of overdominance or pseudo-overdominance. In contrast, a study by Yu et al. (1997) as well as more recent investigations with an immortalized F₂ population (Hua et al. 2002, 2003) showed that heterozygosity was not necessarily advantageous for trait performance in genotypes derived from a highly heterotic hybrid.

To determine the contribution of different genetic effects to midparent heterosis (MPH) of quantitative traits, Melchinger et al. (2007, accompanying article in this issue) developed a novel theory based on classical quantitative genetic approaches utilizing design III (Comstock and Robinson 1952) and the triple testcross (TTC) design (Kearsey and Jinks 1968). They developed a generalized derivation of the relative contributions of different genetic effects to MPH for multiple QTL and all types of higher-order epistasis and derived genetic expectations of heterotic QTL identified by QTL mapping. Furthermore, they devised a joint likelihood-ratio test for detecting QTL involved in heterosis.

Arabidopsis has emerged as a leading model species in plant genetics and functional genomics. It possesses considerable advantages for studies on the causes underlying heterosis such as the ease with which appropriate large mapping populations can be established, genotyped, and phenotyped. However, only few investigations on heterosis for biomass-related traits have been published up to now (Barth et al. 2003; Kearsey et al. 2003; Meyer et al. 2004; Kroymann and Mitchell-Olds 2005). In a previous study (Kusterer et al. 2007), we used a TTC design to estimate the relative contribution of dominance and epistatic effects to heterosis by biometric analyses of first- and second-degree statistics.

The goals of this study were to apply the novel approach of Melchinger et al. (2007) to detect and characterize QTL for heterosis of biomass-related traits in Arabidopsis hybrid C24 × Col-0, using the TTC design. In particular, our objectives were to (i) estimate the number, genomic positions, and genetic effects of QTL contributing to heterosis, (ii) characterize their mode of gene action, and (iii) elucidate the role of epistasis in the manifestation of heterosis.

MATERIALS AND METHODS

Plant materials, experimental design, and traits measured:

Plant materials and phenotypic data were described in detail in our previous article (Kusterer et al. 2007). Briefly, of 409 recombinant inbred lines (RILs) derived from the cross between Col-0 (parent P1) and C24 (parent P2), we studied a randomly chosen subset of 234 RILs together with their TTC progenies. Performance of testcross progenies of the nth RIL with testers P1, P2, and F₁ is denoted by H_1n, H_2n, and H_3n (n = 1, 2, … , 234), respectively. Owing to the large number of entries to be tested, the entire set of 234 RILs and their 702 TTC progenies was subdivided into three experiments, each with 78 RILs plus their corresponding TTC progenies and six checks. Each experiment was arranged in a split-plot design with three replicates. Checks and RILs with their TTC progenies were grown in different main plots. Main plots were arranged in a 12 × 7 α-design. Each main plot comprised four entries: 1 RIL and its 3 TTC progenies. The main plots of checks also comprised four entries: parents P1 and P2, as well as the F₁ and F₂ generations from one of the two reciprocal forms P1 × P2 and P2 × P1. In all instances, the entries within each main plot were randomly assigned to the subplots. We recorded rosette diameter (in millimeters) of individual plants 22 days after sowing (RD22) and 29 days after sowing (RD29) and calculated the absolute growth rate per day (GR) (in millimeters per day) as GR = (RD29 − RD22)/7. Biomass yield above ground (BY) (in milligrams) was recorded for the bulk of 10 plants from each subplot after drying in an oven to practically 0% moisture content. Dry matter content (DMC) (in percentage) was calculated as the ratio between dry and fresh biomass, multiplied by 100.

Molecular markers and linkage maps:

Single-nucleotide polymorphism (SNP) analyses were performed according to Törjék et al. (2003) for 110 SNP markers across the 409 RILs. A linkage map was constructed as described in detail by Törjék et al. (2006). Deviation of marker allele frequencies from 0.5 was tested with a χ²-test statistic using a sequential Bonferroni correction of P-values (Holm 1979).

Data analysis:

For each RIL, we calculated the linear transformations Z₁ = (H₁ + H₂)/2, Z₂ = H₁ − H₂, and Z₃ = H₁ + H₂ − 2H₃ at the main plot level. These transformations provided the basis for all further biometric and quantitative genetic analyses. The checks were not included in the analysis.

Entry means adjusted for incomplete blocks and experiments were calculated for each transformation Z_s (s = 1, 2, 3) by a mixed-model analysis across experiments. Following Kearsey and Jinks (1968), presence of additive × additive epistasis at the level of the entire genome was examined by testing the average of adjusted-entry means of Z₃ across RILs for deviation from zero using an appropriate χ²-test. Genotypic (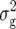) and error variances (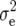) as well as phenotypic and genotypic correlations between Z_s and Z_u (s ≠ u) were estimated by established procedures (Mode and Robinson 1959; Searle 1971) from analyses of variance and covariance of the transformed observations. In addition, heritability (h²) on an entry-mean basis was computed for each Z_s from variance components as 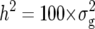/(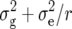), where r corresponds to the number of replicates. Significance of variance components estimated by restricted maximum likelihood (REML) was tested by Wald statistics. This test is approximate and asymptotically equivalent to a likelihood-ratio test (Rao 1973). The Wald statistic was compared with a chi-square distribution with 1 d.f. and the P-value was halved to account for the fact that the null hypothesis places the parameter on the boundary of the parameter space (Stram and Lee 1994). All computations were performed with SAS PROC MIXED (Sas Institute 2004).

QTL analyses:

QTL analyses were carried out by using adjusted entry means of Z₁, Z₂, Z₃, and H₃ of each RIL as well as their SNP data and the linkage map. Composite-interval mapping (CIM) (Jansen and Stam 1994; Zeng 1994) was used for the detection, mapping, and characterization of QTL. For all Z_s as well as H₃, a genetic model fitting only one genetic effect (corresponding to the additive effect in conventional QTL mapping) was chosen for QTL mapping, as described by Utz et al. (2000), because the SNP marker data referred to RILs. LOD threshold levels for QTL detection were determined by a permutation test (Churchill and Doerge 1994) using 2000 permutations. For Z_s and H₃ of each trait, the LOD threshold ranged between 1.7 and 1.9 for an experimentwise error rate of 30%. Therefore, a LOD threshold value of 1.8 was used to declare presence of a QTL for every Z_s and H₃. Estimates of QTL positions and effects for Z_s as well as H₃ were obtained at the position where the corresponding LOD score reached a global maximum in the region under consideration. In addition, genetic effects of QTL for the other transformations Z_u (u ≠ s) were determined at the position of Z_s to obtain estimates of the augmented dominance ratio (ratio of augmented dominance effect d_i* to augmented additive effect a_i* estimated by Z₂ and Z₁, respectively, see below for definitions) and also potential QTL × genetic background interactions revealed by Z₃ (Table 1). The proportion of the genotypic variance explained (p) was determined according to the procedure described by Utz et al. (2000) from the ratio 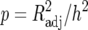, where h² is the heritability and 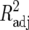is the adjusted partial correlation coefficient of a putative QTL or the multiple correlation coefficient of a set of QTL in the simultaneous fit. It must be noted that partial R² values for the detected QTL do not add up to the R² of the multiple-QTL model due to linkage disequilibrium between markers and corresponding multicollinearity of the regression problem.

TABLE 1.

Expectation (ɛ(X)), variance (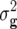(X)), and conditional expectation (ɛ(X | QTL i)) of the contrast between the two homozygous marker classes at the position of QTL i and conditional expectation (ɛ(X | QTL i × QTL j)) of the interaction between the two homozygous marker classes at the positions i and j for X = Z₁, Z₂, Z₃, and H₃ in terms of genetic effects of the F₂-metric under digenic epistasis in the absence of linkage

	Statistica
Variable X	ɛ(X)		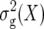ɛ(X | QTL i)	ɛ(X | QTL i × QTL j)
Z1				aaij + ddij
Z2				adij + daij
Z3				2ddij
H3	μ		ai	aaij

For description of Z₁, Z₂, Z₃, and H₃ and for notation of genetic effects see materials and methods.

^aSummation is over the entire set of QTL involved in the trait expression.

In addition to one-dimensional genome scans for epistasis with Z₃, we also tested Z₃ and H₃ for presence of digenic epistatic effects by two-way analyses of variance between all pairs of marker loci. As a modification of the procedure described by Holland (1998), in this search for significant marker pairs we included the same set of markers as cofactors as used in CIM for QTL mapping of main effects, to eliminate their influence on the detection of epistatic QTL. Marker pairs were selected on the basis of the Bayesian information criterion (BIC) (Piepho and Gauch 2001), if the BIC value for the model with epistasis was at least 2 units below the BIC value for the model without epistasis, following Raftery (1995). Finally, all selected epistatic marker pairs as well as the positions of QTL from CIM for a given trait and Z₃ or H₃ were subjected to a further step of backward elimination in multiple regression based on the BIC. For those marker × marker interactions remaining in the final model, epistatic effects were estimated simultaneously with the QTL main effects.

In addition to separate QTL scans for each transformation Z_s, we followed for each trait the method of Jiang and Zeng (1995) to conduct a joint mapping for all three transformations Z_s, as proposed by Melchinger et al. (2007) for QTL mapping with design III. Using the permutation test (Churchill and Doerge 1994), we obtained the following LOD threshold values (corresponding to an experimentwise error rate of 30%) to declare presence of a QTL in the joint analysis: 3.1 for RD22, RD29, and GR; 3.3 for DMC; and 3.4 for BY.

All QTL computations were performed with the software package PLABQTL (Utz and Melchinger 1996), with an extension for calculation of the BIC according to the method of Burnham and Anderson (2004) to accommodate selection of cofactors and comparison of the models with and without digenic epistatic interactions.

Quantitative genetic expectations:

Melchinger et al. (2007) provided general formulas for first- and second-degree statistics as well as QTL parameters for the transformations Z_s under the F₂-metric model with arbitrary linkage and digenic epistasis. Quantitative genetic expectations of the statistics most relevant to our further analyses, ignoring linkage, are given in Table 1, using the following notation: a_i and d_i denote the additive and the dominance effect at QTL i, respectively; and aa_ij, ad_ij, da_ij, and dd_ij denote the additive × additive, additive × dominance, dominance × additive, and dominance × dominance epistatic effects between loci i and j, respectively. QTL detected by genome scans with Z₁ reflect augmented additive effects a_i* = a_i − 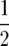[da_i] that, apart from the additive effect a_i, also include [da_i], i.e., the sum of dominance × additive effects of QTL i with all other QTL in the genetic background. QTL detected with Z₂ capture augmented dominance effects d_i* = d_i − 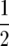[aa_i], which include the dominance effect d_i and [aa_i], i.e., the sum of additive × additive effects of QTL i with all other QTL in the genetic background. Finally, QTL mapping with Z₃ provides a one-dimensional genome scan for QTL × genetic background interactions of type dominance × additive [da_i]. Interactions between marker pairs linked to QTL i and j depend for Z₃ only on dominance × dominance effects (dd_ij) and for H₃ only on additive × additive effects (aa_ij) (Table 1). In contrast, different types of epistatic effects are confounded in interactions between marker pairs for Z₁ and Z₂ and, hence, the latter were not considered in our study.

RESULTS

Linkage map construction:

The SNP assays of the 409 RILs yielded an almost complete data set with <0.1% missing data points. The complete linkage map with 110 markers covered all five Arabidopsis chromosomes uniformly and spanned in total 425.7 cM, with an average interval length of 3.9 cM between markers (Figure 1). The maximum distance between markers was 13 cM. Altogether, the total length of our map was within the range of other crosses with Arabidopsis (Loudet et al. 2002; Malmberg et al. 2005). Allele frequencies on one chromosomal region of chromosomes 1, 4, and 5, as well as on two chromosomal regions of chromosome 3 deviated significantly (P < 0.05) from Mendelian expectations. On chromosomes 1, 3 (position 3/52–3/57), and 5, there were excesses of Col-0 alleles of 10, 20, and 10% over genomic regions of 8, 5, and 11 cM, respectively. On chromosomes 3 (position 3/0–3/2) and 4, predomination of C24 alleles reached ∼10 and 20% over genomic regions of 2 and 5 cM, respectively. A detailed description of the segregation distortion was given by Törjék et al. (2006). Heterozygosity across the 110 SNP markers in each RIL averaged 1.8%, with a maximum of 8.2%.

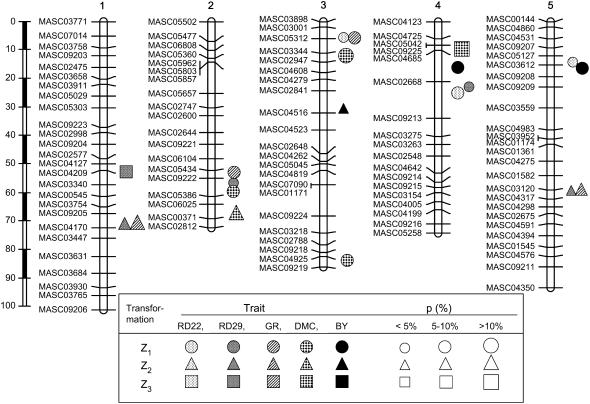
Figure 1.—

Genomic locations and proportion (p) of the genetic variance (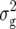(Z_s)) explained by QTL detected for linear transformations Z₁, Z₂, Z₃ for five biomass-related traits in Arabidopsis hybrid C24 × Col-0. For description of linear transformations and traits see materials and methods.

Trait means, variances, and heritability:

Means, genetic variances, and heritabilities of the original observations H₁, H₂, and H₃ for the TTC progenies were presented in our previous article (Kusterer et al. 2007). Means and genetic variances for the transformation Z₁ were significantly (P < 0.01) greater than zero for all traits (Table 2). Heritability of Z₁ ranged between 59% for DMC and 80% for RD29. For Z₂, the mean deviated significantly (P < 0.01) from zero for all traits except RD22. Estimates of 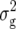(Z₂) were always highly significant (P < 0.01) and almost twice as large as 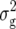(Z₁) for RD22 and BY. Heritability of Z₂ ranged between 45% for GR and 78% for RD22 and BY. For Z₃, the mean deviated significantly (P < 0.05) from zero only for RD29. Estimates of 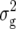(Z₃) were highly significant (P < 0.01) for all traits and approximately twice the corresponding values of 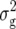(Z₂) for RD22, RD29, and BY. For GR and DMC, estimates of 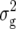(Z_s) were of similar size for Z_1, Z₂, and Z₃. Estimates of 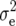(Z_s) differed for Z_1, Z₂, and Z₃, because (i) Z₁ refers to the mean of H₁ and H₂, whereas Z₂ and Z₃ refer to contrasts of H₁, H₂ and H₃, and (ii) the error of main plots contributes to 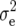(Z₁) but cancels in the model equation of Z₂ and Z₃. Heritability of Z₃ ranged from 30% for GR and DMC to 81% for BY. Genotypic correlations between Z₁ and Z₂ were mostly close to zero, as expected from theory (Melchinger et al. 2007) and the small differences between parents C24 and Col-0 in comparison with the range between RILs for per se performance of all traits reported in our previous study (Kusterer et al. 2007). By comparison, moderately positive correlations were observed between Z₁ and Z₃.

TABLE 2.

Summary statistics (mean, genotypic variance 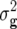, error variance 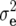, heritability h², phenotypic correlation r_p, genotypic correlation r_g) with associated standard errors for linear transformations Z₁, Z₂, and Z₃ of five biomass-related traits in Arabidopsis hybrid C24 × Col-0

Linear transformation		Trait
		Statistic	RD22 (mm)	RD29 (mm)	GR (mm/day)	DMC (%)	BY (mg)
Z1	Mean	30.3 ± 0.3**	77.5 ± 0.5**	6.78 ± 0.04**	7.79 ± 0.03**	98.6 ± 1.6**
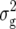		34.1 ± 4.2**	99.0 ± 11.9**	0.42 ± 0.07**	0.24 ± 0.04**	776.3 ± 109.8**
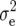		27.1 ± 1.8**	75.0 ± 5.2**	0.71 ± 0.05**	0.49 ± 0.03**	1084.4 ± 72.6**
	h2	79.1 ± 2.5	79.8 ± 2.4	64.00 ± 4.37	59.10 ± 5.06	68.2 ± 3.7
Z2	Mean	0.7 ± 0.4	2.5 ± 0.7**	0.26 ± 0.06**	0.57 ± 0.04**	9.6 ± 2.0**
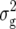		51.2 ± 6.3**	124.2 ± 17.5**	0.46 ± 0.11**	0.25 ± 0.06**	1513.5 ± 186.0**
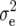		44.6 ± 3.0**	163.6 ± 11.4**	1.73 ± 0.12**	0.73 ± 0.05**	1296.7 ± 87.0**
	h2	77.5 ± 2.6	69.5 ± 3.6	44.56 ± 6.83	50.36 ± 6.69	77.8 ± 2.6
Z3	Mean	−1.0 ± 0.6	−2.0 ± 1.0*	−0.13 ± 0.09	−0.05 ± 0.05	1.4 ± 3.3
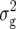		124.6 ± 15.8**	211.9 ± 33.6**	0.61 ± 0.23**	0.25 ± 0.09**	4421.2 ± 523.1**
		119.5 ± 8.0**	370.7 ± 26.0**	4.18 ± 0.29**	1.72 ± 0.12**	3058.7 ± 206.8**
	h2	75.8 ± 2.8	63.2 ± 4.4	30.60 ± 8.60	29.77 ± 8.78	81.3 ± 2.2
rp (Z1, Z2)		−0.02	0.11	0.16*	−0.04	−0.09
rp (Z1, Z3)		0.37**	0.30**	0.23**	0.16*	0.41**
rp (Z2, Z3)		−0.05	0.03	−0.07	0.01**	−0.15*
rg (Z1, Z2)		−0.04	0.11*	0.24**	0.09	−0.12*
rg (Z1, Z3)		0.38**	0.27**	0.13	0.24*	0.42**
rg (Z2, Z3)		−0.06	0.00	−0.21*	−0.05	−0.14*

Phenotypic correlation was significant at *P < 0.05 and **P < 0.01, respectively, and the genotypic correlation exceeded twice and three times its standard error, respectively. For description of the linear transformations and traits see materials and methods.

Identification of QTL affecting biomass-related traits:

We detected a total of 20 QTL for the five biomass-related traits in Arabidopsis hybrid C24 × Col-0 (Table 3 and Figure 1). Several of these QTL regions affected more than one trait. However, each QTL position was declared significant only for one of the three transformations Z_s, on the basis of the LOD thresholds determined by permutation tests. In the joint QTL analysis of all three transformations, 7 of the 20 QTL detected in the separate analyses of Z₁, Z₂, or Z₃ were also found, but no additional QTL could be detected.

TABLE 3.

QTL positions and effects for linear transformations Z₁, Z₂, and Z₃ as well as dominance ratio d_i*/|a_i*| and joint mapping of five biomass-related traits in Arabidopsis hybrid C24 × Col-0

		Z1			Z2				Z3
Chromosome	Position (cM)a	LOD scoreb	Effect ai*	p (%)c	LOD score	Effect 2di*	p (%)	di*/|ai*|	LOD score	Effect [dai]	p (%)	Joint LOD scored
RD22 (mm)
3	6	1.85	−2.03**	3.9	0.23	−0.55	0.5	−0.13	0.02	0.18	0.0	2.08
4	24	3.10	2.87**	6.3	0.03	0.17	0.0	0.03	0.24	−0.78	0.4	4.24
5	14	1.87	2.14**	4.2	0.08	−0.19	0.1	−0.04	0.78	1.43	1.4	2.87
Total				12.6			0.6				1.8
RD29 (mm)
1	52	0.38	−3.13	1.2	0.00	−0.46	0.1	−0.07	2.11	−3.92**	5.4	2.30
1	70	0.02	2.04	0.5	2.12	3.20**	5.8	0.78	0.01	0.33	0.0	2.17
2	58	2.02	−5.89**	4.9	0.28	0.99	0.7	0.08	0.32	1.50	0.9	2.85
4	20	2.10	5.92**	5.3	0.34	1.13	1.0	0.09	0.00	0.19	0.0	2.53
5	60	0.54	−2.28	0.7	1.82	2.55**	4.6	0.56	0.01	0.43	0.0	2.23
Total				10.4			12.5				7.1
GR (mm/day)
1	70	0.0	−0.03	0.0	3.95	0.31**	15.3	5.17	0.03	0.00	0.0	3.99
2	50	2.02	−0.31**	5.0	0.12	0.14	3.6	0.22	0.02	0.04	0.0	0.40
3	6	2.23	−0.34**	6.4	0.01	−0.01	0.0	−0.01	0.06	−0.13	0.3	0.22
5	60	0.10	−0.04	0.0	2.38	0.26**	11.4	3.25	0.00	0.06	0.0	2.46
Total				10.5			28.0				0.6
DMC (%)
2	60	4.59	0.29**	6.6	0.23	0.13	1.1	0.22	0.51	−0.02	0.0	5.79
2	68	0.06	0.02	0.0	2.92	−0.30**	11.1	−7.50	0.06	0.00	0.0	4.68
3	14	3.58	0.23**	10.5	0.01	−0.01	0.0	−0.02	0.26	0.11	2.7	6.55
3	84	2.17	0.20**	6.6	0.02	−0.01	0.0	−0.02	0.26	0.04	0.3	2.48
4	8	0.02	0.02	0.0	0.06	0.02	0.2	0.50	3.41	−0.31**	16.4	3.47
Total				31.1			13.7				20.5
BY (mg)
3	30	0.40	−3.25	1.0	2.41	6.59*	3.2	1.01	0.02	0.96	0.0	2.64
4	16	3.43	10.69**	9.8	0.01	−0.82	0.0	−0.04	0.03	2.32	0.2	4.38
5	16	2.69	9.33**	8.9	0.21	−2.80	0.6	−0.15	0.50	5.87	1.5	3.24
Total				17.4			3.6				1.7

For description of linear transformations and traits see materials and methods.

^aPosition on chromosome according to the map published by Törjék et al. (2006).

^bEstimates of QTL, for which the LOD score surpassed the threshold level, are given in italics.

^cProportion of genotypic variance explained by the QTL in a simultaneous fit.

^dJoint mapping over all linear transformations Z₁, Z₂, and Z₃.

For RD22, we revealed three QTL, all by QTL mapping with Z₁ (Table 3). They were located on chromosomes 3, 4, and 5 and explained individually from 3.9 to 6.3% and simultaneously 12.6% of 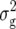(Z₁). Effects of these QTL for Z₂ and Z₃ were practically zero.

For RD29, we detected five QTL (Table 3). Two of them were found for Z₁, one located on chromosome 2 and the other on chromosome 4 at the same marker interval as the QTL for RD22, each explaining ∼5% of 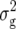(Z₁). Two QTL were detected for Z₂, one located on chromosome 1 and one on chromosome 5, explaining 6 and 5% of 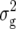(Z₂), respectively. For Z₃, we found one QTL on chromosome 1, explaining ∼5% of 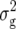(Z₃).

For GR, we detected four QTL (Table 3). For Z₁, we found two QTL, one located on chromosome 2 in the same region as the Z₁ QTL for RD29 and DMC and the other on chromosome 3, explaining individually 5 and 6% of 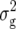(Z₁). For Z₂, two QTL, explaining 15 and 11% of 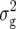(Z₂), were detected on chromosomes 1 and 5, respectively, at exactly the same positions as Z₂ QTL for RD29. In a simultaneous fit, these QTL accounted for 28% of 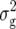(Z₂).

For DMC, we detected five QTL (Table 3). Three of them were found for Z₁, located on chromosomes 2 and 3, explaining between 7 and 11% of 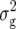. The simultaneous fit of all five QTL explained 31.1% of 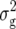(Z₁). Only one QTL was detected for Z₂, located on chromosome 2 and explaining 11% of 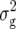(Z₂). Likewise, for Z₃ we detected only one QTL located on chromosome 4, which accounted for 16% of 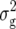(Z₃).

For BY, we detected three QTL (Table 3). Two of these were found for Z₁ on chromosomes 4 and 5 and explained ∼9% of 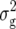(Z₁). One QTL was detected for Z₂ on chromosome 3, which explained only 3.2% of 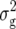(Z₂).

We detected a total of six marker pairs with significant epistatic effects for Z₃ across all traits (Table 4). Three of these marker pairs were found for RD22 with variable sign of the estimated effect dd_ij, explaining between 4.6 and 6.5% of 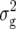(Z₃). Likewise, three marker pairs displaying epistatic effects dd_ij with variable sign were detected with Z₃ for BY, explaining between 3.0 and 6.7% of 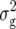(Z₃); one of the markers involved in significant interactions was always located on the long arm of chromosome 5. For H₃, we detected consistently one epistatic marker pair with a positive sign of the estimated effect aa_ij for RD29, GR, and DMC, explaining between 5.6 and 10.7% of 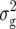(H₃). Each of these marker pairs involved the same marker on the long arm of chromosome 5; for RD29 and GR, the other marker was also identical.

TABLE 4.

Marker positions and estimated digenic epistatic effects dd_ij and aa_ij determined by two-way analyses of variance with variables Z₃ and H₃ of five biomass-related traits in Arabidopsis hybrid C24 × Col-0

	Marker i		Marker j		ddij
Trait	Chromosome	Positiona	Chromosome	Positiona	LOD score	Effect	p (%)b
Variable Z3
RD22	1	81	2	55	1.96	−2.68	5.06
RD22	2	24	5	37	1.77	2.53	4.57
RD22	4	24	5	14	2.54	−3.30	6.53
BY	2	10	5	53	1.96	10.48	5.1
BY	2	70	5	53	2.57	−12.16	6.7
BY	3	30	5	70	1.14	8.44	3.0
	Marker i		Marker j		aaij
Trait	Chromosome	Positiona	Chromosome	Positiona	LOD score	Effect	p (%)b
Variable H3
RD29	1	8	5	92	2.15	6.62	5.63
GR	1	8	5	92	2.56	0.57	9.1
DMC	2	29	5	92	2.30	0.23	10.7

For description of Z₃ and H₃ and traits see materials and methods.

^aPosition on chromosome according to the map published by Törjék et al. (2006).

^bProportion of genotypic variance explained by the marker pair interaction.

DISCUSSION

Composition of heterosis under epistasis:

Melchinger et al. (2007) provided a general formula for MPH under the F₂-metric model. According to this formula, with digenic epistasis, MPH depends on both dominance and additive × additive effects. Moreover, the contribution of individual QTL to MPH corresponds exactly to their augmented dominance effects d_i*.

Usefulness of the TTC design for heterosis studies:

Hua et al. (2003) pointed out that most of the previous molecular-marker-based genetic analyses of heterosis were based on performance measurements of traits rather than on heterosis itself and that the genetic basis of heterosis was inferred from the genetic components of trait performance. To obtain a better picture of the genetic components underlying heterosis, these authors advocated the use of direct measurements of heterosis in data analysis, as provided, for example, by the immortalized F₂ design. Even though design III and the TTC design do not fulfill this criterion, we believe they are ideal designs for unraveling the basis of heterosis because QTL mapping with Z₂ provides estimates of augmented dominance effects d_i*, the contribution of a QTL to MPH. Since QTL mapping with Z₁ also provides estimates of the augmented additive effect a_i*, which enters the expression for the parental difference in the presence of epistasis, design III and the TTC design allow us also to determine the augmented dominance ratio d_i*/|a_i*| at each QTL. The TTC design for QTL mapping with Z₃ has a further advantage in that it permits a one-dimensional genome scan for epistatic effects [da_i] contributing to a_i*.

Interpretation of first- and second-degree statistics:

As pointed out by Kearsey and Jinks (1968), the transformation Z₃ provides a test for [aa], the sum of aa_ij epistatic effects averaged over all pairs of QTL (Table 1). In our study, this test was significant only for RD29. By comparison, a generation means analysis that included the checks (P1, P2, F₁, F₂) and RILs in addition to the TTC progenies yielded significantly (P < 0.05) positive estimates of [aa] for BY (Kusterer et al. 2007). Compared with Z₃, the latter approach has a higher statistical power to detect epistasis owing to a smaller coefficient in the error variance for the estimate of [aa].

Table 1 also provides a quantitative genetic interpretation of 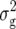(Z_s). Using the F₂-metric, the genetic variance can be partitioned into independent components of the genetic effects with no genetic covariance among them (Kao and Zeng 2002). Thus, we obtain 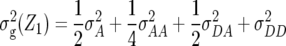, , 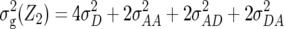and 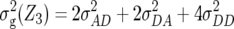, where 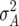, , 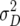, , , 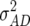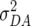and 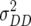denote the variances of a_i, d_i, aa_ij, ad_ij, da_ij, and dd_ij effects summed over all loci or loci pairs, respectively, as defined for the F₂-metric by Yang (2004). This demonstrates that in a TTC design with RILs, 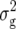(Z_s) for s = 1, 2, and 3 can be strongly influenced by epistatic effects. In particular, the significant estimates of 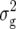(Z₃) for all traits observed in our study reveal the presence of epistasis of type a × d and d × a and/or d × d or even higher-order epistasis. Estimates of 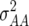and 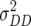reported in our previous study (Kusterer et al. 2007) on the analysis of variance of the original observations H_s (s = 1, 2, 3) support this conclusion.

Interpretation of QTL-mapping results:

Until recently, QTL analyses of heterosis with design III (e.g., Stuber et al. 1992) were performed with (i) marker data of the candidates (e.g., F₃ lines or RILs) from a segregating population of cross P1 × P2 and (ii) phenotypic data (H₁ and H₂) of their testcross progenies. QTL effects determined with this approach have expectations d_i* + a_i* and d_i* − a_i* (Melchinger et al. 2007) and gene action at each QTL must be deduced from these estimates. By comparison, the novel QTL-mapping approach devised by Melchinger et al. (2007) also uses marker data of the candidates, but employs linear transformations Z₁, Z₂, and Z₃ of the performance of TTC progenies. The advantages of this approach are that (i) estimates of the detected QTL reflect directly a_i* and d_i* and (ii) the joint analysis of Z₁ and Z₂ enables testing of hypotheses on the type of gene action.

Across all five biomass-related traits, we detected a total of 20 QTL with main effects. This number compares favorably with the 38 QTL reported for 22 traits in a design III study of Arabidopsis hybrid Col × Ler (Kearsey et al. 2003) but is lower than that in crops like maize (Stuber et al. 1992; Cockerham and Zeng 1996) and rice (Li et al. 2001; Luo et al. 2001; Hua et al. 2002, 2003). However, the studies with maize and rice investigated grain yield and yield components. These traits display much larger MPH than forage yield in maize (Melchinger et al. 1992) or biomass-related traits in Arabidopsis, where MPH was largest for BY but still <66% except under extremely high light intensities and at an earlier time of evaluation (Meyer et al. 2004). Altogether, the number of detected QTL was at the lower end of our expectations because the conditions for QTL mapping were benign in our study. First, we used replicated experiments with a total of 30 plants per entry and heritabilities for all Z_s were moderately high for all traits except GR and DMC for Z₃ (Table 2). Thus, experimental errors in the phenotypic measurements most likely did not hamper QTL detection. Second, we chose a sufficiently large population size (N = 234). On the basis of theoretical results (Charcosset and Gallais 1996), the power of QTL detection with this population size is >90% for a QTL explaining 10% of for a trait with h² = 50%. Third, QTL mapping was performed with marker data from RILs, where the heterozygous marker class is empty. As a consequence, under a purely additive genetic model, as applies to testcross progenies, RILs have the highest power for detection of QTL in comparison with F_2, F₃, or backcross populations (Moreno-Gonzalez 1993; Charcosset and Gallais 1996). Fourth, we used a high-density linkage map with an average marker distance of 3.9 cM and a maximum interval length of 13 cM, which favors QTL detection and improves the resolution of separating closely linked QTL (Luo et al. 2001).

Segregation distortion observed for four genomic regions may have reduced the power of QTL detection in our study, because of unequal size of marker classes (Crane and Crane 2005). Nevertheless, according to the theoretical results of Cockerham and Zeng (1996), this effect on power of QTL detection is presumably of secondary importance with the degree of distortion observed in our RIL population. Likewise, errors in the assignment of marker genotypes of RILs to the phenotypic observations of their TTC progenies would reduce the power of QTL detection. To avoid such mistakes, we used the same seed lot of each RIL for producing the TTC progenies, as well as propagating the RILs and sampling of plant materials for the SNP assays.

Given the large number of entries evaluated in our study (N = 936), we had to subdivide the entire set of 234 RILs and their TTC progenies into three separate experiments. Even though utmost care was exercised to warrant uniform temperature, light, and moisture conditions, a perfect control of the environmental conditions across the experiments was not possible. However, an analysis of variance of the checks that were included as multiple entries in each experiment revealed only minor genotype × experiment interactions. Nevertheless, if genotype × experiment interactions affected biomass-related traits in the TTC progenies, our mapping procedure would favor the detection of those QTL that displayed no or little QTL × environment interactions. Moreover, h² calculated from pooled values of individual experiments would tend to overestimate the heritabilities across experiments. Consequently, estimates of p given in Table 3 represent a lower limit for the proportion of 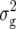across experiments explained by the detected QTL.

Twelve of the 20 QTL were detected for Z₁ with significant augmented additive effects a_i* (Table 3). Eight of these 12 QTL colocalized with QTL detected for H₃ (data not shown), which reflect additive effects a_i without any confounding by digenic epistatic effects (Table 1). This is in agreement with the findings from our previous study (Kusterer et al. 2007) showing that 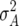was the predominant variance component compared with 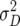and the epistatic variances. Three QTL were detected for DMC, which explained altogether about one-third of 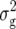(Z₁). Since DMC is related to the developmental stage, we compared the QTL detected for this trait with the 12 QTL for flowering time in Arabidopsis revealed by El-Lithy et al. (2006). Two QTL for DMC, on chromosomes 3 (position 3/14) and 4 (position 4/8), mapped to genomic regions reported for flowering time, thus suggesting that the underlying genes have a pleiotropic effect on these two traits.

Five of six QTL detected for transformation Z₂ displayed a positive augmented dominance effect d_i*, which is in agreement with the positive MPH for the underlying traits. A QTL with negative d_i* effect was revealed only for DMC, as expected from the negative MPH for this trait. The two largest QTL for d_i*, explaining simultaneously 28% of 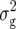(Z₂), were found for GR, the trait with the highest average squared degree of dominance in our previous study (Kusterer et al. 2007).

Altogether, it is difficult to conclude whether the small number of QTL detected in our study was due to the low level of heterosis for all traits except BY or a lack of statistical power in detecting QTL or a combination of both.

Comparison of individual and joint QTL mapping:

We found no common QTL positions between Z₁, Z₂, and Z_3. This implies that the QTL detected displayed either only significant augmented additive effects a_i* detected by Z₁, or significant augmented dominance effects d_i* detected by Z₂, or significant epistatic effects [da_i] detected by Z₃. Consequently, the dominance ratio d_i*/|a_i*| shown in Table 3 was either close to zero or extremely high. The only exception was the QTL for BY on chromosome 3, where a_i* and d_i* were of equal size. This result is in harmony with the findings of Cockerham and Zeng (1996) and Frascaroli et al. (2007), who reported only a small overlap between QTL for Z₁ and Z₂ in single-marker analyses of design III progenies of maize hybrid B73 × Mo17 and in CIM of TTC progenies of maize hybrid B73 × H99, respectively. Likewise, most QTL detected for heterosis of grain yield in rice displayed either a dominance ratio well above 1.0 or close to zero (Yu et al. 1997; Hua et al. 2002, 2003). Altogether, these findings imply that estimates of the average degree of dominance 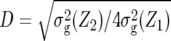are not very informative for drawing conclusions on the primary mode of gene action involved in heterosis at individual QTL because a mixture of QTL with additive and overdominance would result in an estimate of D that would suggest partial dominance at most QTL.

The joint QTL analysis across all three transformations Z_s did not improve the power of QTL detection in our study (Table 3). In most instances, the LOD score of the joint analysis was approximately equal to the sum of the LOD scores for the individual transformations. This result is in accordance with theory (Jiang and Zeng 1995) and was expected on the basis of the low phenotypic and genotypic correlations between Z₁, Z₂, and Z₃ (Table 2). However, since the LOD threshold was much higher for the joint mapping (corresponding to a χ²-distribution with 4 d.f. according to Jiang and Zeng 1995) than that of individual Z_s (corresponding to a χ²-distribution with 2 d.f.), only 7 of the 20 QTL found with the latter approach could be confirmed by the joint analysis. Nevertheless, joint mapping was instrumental in dissecting the two closely linked QTL on chromosome 2 using the procedure described by Jiang and Zeng (1995).

Detection of epistatic QTL:

We used two approaches to detect epistasis among QTL. First, a one-dimensional genome scan was performed by QTL mapping with Z₃ to detect QTL × genetic background interactions (Table 1). This test revealed two genomic regions with significantly negative [da_i] effects, one for GR and one for DMC. Since a_i* = a_i − 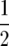[da_i], it follows that the additive effect a_i is smaller than the augmented additive effect a_i* estimated at these positions by QTL mapping with Z₁. This conclusion was confirmed by comparison with additive effects a_i determined by QTL mapping with H₃ (data not shown).

Second, we performed two-way ANOVAs with all marker pairs (using cofactors determined by CIM and subsequent backward elimination) for Z₃ and H₃. This yields statistical tests for epistatic effects of types dd_ij and aa_ij (Table 1), respectively, but because Z₃ and H₃ are correlated, the statistical tests for Z₃ and H₃ are not stochastically independent. Very few significant digenic epistatic effects were found with this approach (Table 4), presumably because of its low statistical power as a consequence of the aggravated multiple-test problem associated with two-dimensional genome scans. Interestingly, none of the markers contributing to significant aa_ij effects, identified with H₃, colocalized with main-effect QTL detected with Z₂, despite the fact that augmented dominance effects d_i* reflect not only d_i but also minus half the sum of aa_ik effects. Two explanations can be given for this observation: (1) positive d_i effects counterbalanced the effects of the detected positive aa_ij effects and/or (2) [aa_i], the sum of aa_ik interactions of QTL i with all other QTL k, contributing to d_i*, was smaller than the aa_ij effect estimated from H₃ due to other interactions aa_ik (k ≠ j) with a negative sign that were too small to be detected by marker × marker contrasts with H₃ in our approach. Hence, if the goal is to determine the relative contribution of epistatic vs. dominant gene action to MPH, investigating only pairwise interactions aa_ij is not sufficient to obtain a realistic picture of the role of epistasis in heterosis. What is needed are new designs that for each QTL allow separate estimation of d_i and [aa_i], as pointed out by Melchinger et al. (2007).

Comparison of QTL for different traits:

In agreement with the significant correlations among biomass-related traits in the TTC progenies reported in our previous study (Kusterer et al. 2007), we also found common QTL positions for different traits (Figure 1). All QTL detected for GR were found either for RD22 (one QTL) or for RD29 (three QTL) with the same type of gene action. Likewise, two QTL regions for RD22 were also identified as QTL for BY with the same type of gene action. However, with the limited sample size (N = 234) and moderate size of the detected genetic effects, confidence intervals for QTL positions were still in the order of 10–15 cM (see Manichaikul et al. 2006) in spite of our high-density map. Thus, we were not able to distinguish pleiotropic or closely linked QTL regions. Hence, fine-mapping approaches with introgression libraries or near-isogenic lines and, subsequently, comparison of DNA sequences between the parents in regions of candidate genes are required to solve this problem.

Genetic basis of heterosis:

In our previous article (Kusterer et al. 2007), MPH was highest (49%) for BY, medium (23–28%) for RD22, RD29, and GR, and negative (−2%) for DMC. By QTL mapping for augmented dominance effects d_i* with Z₂, we detected one QTL explaining 11% of MPH for BY and two QTL explaining 18% of MPH for GR. This suggests that heterosis for BY and GR has a truly polygenic mode-of-inheritance with a large number of underlying QTL, each with only a small contribution. The small number of QTL detected in our study in comparison with similar investigations in maize (Stuber et al. 1992; Lu et al. 2003) and rice (Hua et al. 2002, 2003) is most likely attributable to the moderate level of MPH for biomass-related traits in Arabidopsis hybrid C24 × Col-0. However, our analyses allow only inferences on augmented dominance effects d_i* and not on dominance effects d_i themselves. If positive effects d_i were counterbalanced by positive effects aa_ij, as suggested by positive estimates of [aa] in our previous article (Kusterer et al. 2007) as well as positive estimates of aa_ij detected by marker × marker interactions for H₃ (Table 4), this has resulted in smaller values for d_i* in comparison with d_i and has prevented their detection by QTL mapping with Z₂. This hypothesis is supported by results from rice (Yu et al. 1997; Hua et al. 2002, 2003) showing that additive × additive epistasis is a major component of heterosis for yield and yield components in autogamous species. In the past, inferences on the primary mode of gene action at QTL involved in heterosis have been drawn from the average degree of dominance D, estimated from the ratio 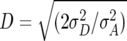. For the materials and traits investigated in this study, Kusterer et al. (2007) reported D values between 0.54 and 0.74, close to the ratio . Following the arguments of previous studies (Comstock and Robinson 1952; Moll and Robinson 1967), one would conclude that most QTL contributing to heterosis display partial to complete dominance. However, our results on the augmented dominance ratio d_i*/|a_i*| suggest that the majority of QTL display either additive gene action or overdominance, but owing to the limited power of QTL detection in our study and lack of a statistical test for testing |a_i*| = d_i*, further research is warranted to substantiate this conclusion. Nevertheless, our results demonstrate that considering only D can be rather misleading concerning the type of gene action at the majority of loci contributing to heterosis.

Our observation of overdominant gene action at one-quarter of the detected QTL is in harmony with recent findings in tomato (Semel et al. 2006). In a population of introgression lines, which carried defined chromosome segments of a wild relative, these authors reported prevalence of overdominant QTL for fitness-related traits. Likewise, most QTL detected for heterosis of grain yield in the maize hybrid B73 × H99 were in the overdominance range (Frascaroli et al. 2007). Nevertheless, pseudo-overdominance of closely linked loci with dominant genes in repulsion phase could be an alternative explanation. This hypothesis would also be consistent with DNA sequence comparisons of maize inbred lines, which differed in their gene content in a given genomic region as a result of transposon-induced gene shuffling (Fu and Dooner 2002). If the different sets of genes in each parent complement each other in their action, this would result in pseudo-overdominance. The Arabidopsis hybrid C24 × Col-0 represents an ideal model system to study this hypothesis, because the DNA sequence of Col-0 is completely known (Lin et al. 1999; Mayer et al. 1999; Salanoubat et al. 2000; Tabata et al. 2000; Theologis et al. 2000) and very detailed knowledge of C24 vs. Col-0 polymorphisms will soon become available from resequencing by hybridization (Clark et al. 2007). Furthermore, introgression libraries of Col-0 genome segments in C24 genetic background and vice versa have been constructed (O. Törjek, R. C. Meyer, M. Zehnsdorf, M. Teltow, G. Strompen, H. Witucka-Wall, A. Blacha and T. Altmann, unpublished results), which allow mapping of heterosis to defined genomic regions, eliminating a major part of genomewide epistasis.