Skip to main content
PMC home page
Genetics logoLink to Genetics
. 2007 Nov;177(3):1941–1949. doi: 10.1534/genetics.107.080077

Accelerated Rate of Gene Gain and Loss in Primates

Matthew W Hahn 1,1, Jeffery P Demuth 1, Sang-Gook Han 1
PMCID: PMC2147951  PMID: 17947411

Abstract

The molecular changes responsible for the evolution of modern humans have primarily been discussed in terms of individual nucleotide substitutions in regulatory or protein coding sequences. However, rates of nucleotide substitution are slowed in primates, and thus humans and chimpanzees are highly similar at the nucleotide level. We find that a third source of molecular evolution, gene gain and loss, is accelerated in primates relative to other mammals. Using a novel method that allows estimation of rate heterogeneity among lineages, we find that the rate of gene turnover in humans is more than 2.5 times faster than in other mammals and may be due to both mutational and selective forces. By reconciling the gene trees for all of the gene families included in the analysis, we are able to independently verify the numbers of inferred duplications. We also use two methods based on the genome assembly of rhesus macaque to further verify our results. Our analyses identify several gene families that have expanded or contracted more rapidly than is expected even after accounting for an overall rate acceleration in primates, including brain-related families that have more than doubled in size in humans. Many of the families showing large expansions also show evidence for positive selection on their nucleotide sequences, suggesting that selection has been important in shaping copy-number differences among mammals. These findings may help explain why humans and chimpanzees show high similarity between orthologous nucleotides yet great morphological and behavioral differences.

GIVEN the low nucleotide divergence between humans and chimpanzees, King and Wilson (1975) proposed that regulatory changes must explain the large number of morphological differences between these species. While the importance of cis-regulatory change as a general source of adaptive evolution has been championed in recent years (e.g., Carroll 2005), few human regulatory regions have been identified that demonstrate signatures of positive selection (reviewed in Hahn 2007b). Furthermore, analyses of nucleotide substitutions have provided evidence for a slower rate of molecular evolution in primates relative to rodents, and an even greater “hominoid slowdown” in humans and chimpanzees relative to other primates (Wu and Li 1985; Yi et al. 2002; Elango et al. 2006). This slowdown in substitution rate means that humans and chimpanzees are extremely similar at orthologous nucleotides. In contrast, studies of both gene duplication (Lynch and Conery 2003; Goodstadt and Ponting 2006) and segmental duplication (Cheng et al. 2005; She et al. 2006) have found higher rates of change in the primates, with humans showing a greater frequency of gene duplication among the hominoid lineages (Fortna et al. 2004). Observations such as these stimulate controversy over whether sufficient evidence is available to judge the relative contributions of different forms of molecular evolution to organismal adaptation (Hoekstra and Coyne 2007). Our study focuses on one area where evidence is particularly inadequate—the rate at which genes are gained and lost from genomes.

Incomplete accounting of changes in gene copy number is partially due to the fact that comparisons of orthologous nucleotides among species ignore genes that are not universally present among taxa. Furthermore, providing evidence of gene absence is difficult and requires deep whole-genome sequencing for all organisms being compared. Analyses of change in the size of gene families among several prokaryote and viral genomes shows that copy-number changes can be substantial (Daubin et al. 2003; Mclysaght et al. 2003). A limitation of these previous studies has been the absence of a statistical framework necessary for making probabilistic statements about the causes of change in gene family size (such as are well developed for the evolution of nucleotide substitutions) (Li 1997). The completion of several mammalian genomes in recent years as well as improved statistical methods now offer the possibility of a more complete accounting of the molecular changes important to human evolution.

In the following we apply a likelihood model for studying gene family evolution (Hahn et al. 2005) that estimates the rate of gene turnover—including both gene gain and loss—across the phylogenetic tree of the deeply sequenced mammals: dog, rat, mouse, macaque, chimpanzee, and human. The current study improves on our previous efforts to account for gene family evolution (Demuth et al. 2006) by incorporating a novel method that allows for lineage-specific rates of gene turnover. We find that there is a highly significant acceleration in the rate of gene turnover in both the primates as a whole as well as in the two hominoid species relative to macaque. We also use multiple alternative methods for analyzing gene gain and loss to demonstrate the robustness of our results.

MATERIALS AND METHODS

Data collection:

We used the genomes of Macaca mulatta (rhesus macaque; Mmul 1.0 assembly), Canis familiaris (dog; CanFam 1.0 assembly), Rattus norvegicus (rat; RGSC 3.4 assembly), Mus musculus (mouse; NCBI m36 assembly), Pan troglodytes (chimpanzee; PanTro 2.1 assembly), and Homo sapiens (human; NCBI 36 assembly). Each of these genomes has been shotgun sequenced to at least 6× coverage and has been estimated to be at least 96% complete. To avoid problems associated with recognizing different splice variants in different species, we included only the longest isoform for each gene in each genome. We used gene families as defined in the Ensembl database (v.41; www.ensembl.org). After excluding transposable elements and pseudogenes the resulting data set includes 119,746 genes in 9990 gene families across all six species (supplemental Table 1 at http://www.genetics.org/supplemental/).

The phylogenetic tree and estimates of most of the divergence times are from Springer et al. (2003), as they contained the largest number of relevant dates based on a single data set (16,397 aligned nucleotides from 19 nuclear and 3 mitochondrial genes). These divergence times are broadly consistent with other estimates (Adkins et al. 2003; Douzery et al. 2003; Steppan et al. 2004). Divergence times for human, chimpanzee, and macaque were taken from other studies (Nei and Glazko 2002; Kumar et al. 2005; Patterson et al. 2006), as both chimpanzee and macaque were not included in the Springer et al. study. Reanalysis of the data using the most extreme value for mouse–rat divergence in the literature (33 MY) (Nei and Glazko 2002) or increasing the human–chimpanzee split to 10 MY does not qualitatively affect our conclusions (supplemental Table 2 at http://www.genetics.org/supplemental/).

Estimating rates of gene gain and loss:

To estimate rates of gene gain and loss, we applied an updated version of the likelihood model developed by Hahn et al. (2005; De Bie et al. 2006). This method models gene family evolution as a stochastic birth-and-death process, where genes are gained and lost independently along each branch of a phylogenetic tree (note that this probabilistic model is not related to the verbal “birth-and-death” model of Nei et al. 1997 that aims to explain the high similarity among some tandemly arranged duplicates). A parameter, λ, describes the rate of change as the probability that a gene family either expands (via gene gain) or contracts (via gene loss) per gene per million years. The new implementation of this model allows for the λ parameter to be estimated separately for independent branches of the phylogenetic tree as well as allowing for a wider range of simulations. The model assumes that gene gain and loss occur with equal probability for each rate λ. Note that this equilibrium assumption implies only that genomes are neither consistently expanding nor contracting within our limited phylogenetic context, not that any particular gene family must experience equal numbers of gains and losses. Furthermore, stochastic birth-and-death models have been shown to reproduce the distribution of gene family sizes within taxa across a wide range of organisms when gene birth and death occur at equal rates (Karev et al. 2002).

The probability of going from an initial number of genes, X0 = s, to size c during time t, Xt = c, is given by

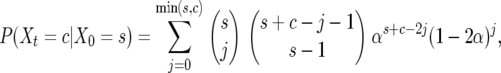graphic file with name M1.gif

where 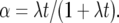Inline graphic If X0 = 0, then there is no chance of birth or death, as 0 is an absorbing boundary. We therefore include only families inferred by parsimony to have been present in the mammalian MRCA (Demuth et al. 2006).

For gene families inferred to be present in the MRCA of mammals (n = 9990), parameters are estimated by maximizing the likelihood of the observed family sizes. Starting from the hypothesis that primates show an accelerated rate of gene gain and loss, we tested a range of models with local parameters for one or more primate lineages (supplemental Table 2 at http://www.genetics.org/supplemental/). The likelihood of models with >1 rate parameter were compared to nested models in a likelihood-ratio test assuming that the negative of twice the difference in log likelihoods between nested models is χ2-distributed with degrees of freedom equal to the number of excess parameters. Nonnested models were compared using Akaike's information criterion (Burnham and Anderson 2002). The updated version of our software package used to conduct this analysis (CAFE v2.0) is available at http://www.bio.indiana.edu/∼hahnlab/Software.html.

Gene tree analysis:

To build gene trees for the 9990 gene families considered, we downloaded the protein alignments for each family from Ensembl. We then generated neighbor-joining trees in PHYLIP (Felsenstein 1989) using JTT protein distances for 9920 of the 9990 gene families (PHYLIP could not handle trees with >284 genes). We reconciled the resulting gene tree with the species tree using the NOTUNG software package (Chen et al. 2000); the bootstrap threshold for uncertainty in the gene tree was set to 90%. We considered informative branches to be the six external branches leading to extant taxa, as well as the [human, chimp] and [mouse, rat] ancestral branches. This was done to minimize the number of inappropriate duplications inferred when the gene tree is inaccurate—extraneous duplications will not be placed on these branches (Hahn 2007a). We estimated the number of duplications via the likelihood method by inferring the size of each gene family in ancestral nodes and comparing these numbers to current family sizes. Larger daughter node sizes imply gains of genes, and total gains are the number summed across all 9990 families for each branch.

Significant changes in individual families:

To identify individual families that have had expansions or contractions larger than expected after accounting for overall rate variation among the mammals, we ran Monte Carlo simulations for all 9990 families included in the full analysis (Hahn et al. 2005). These simulations provide P-values for the hypothesis that each family is evolving according to the null birth-and-death process. A low P-value for a given family implies that the observed differences in size among lineages are too large to be explained by chance.

To calculate P-values, rate estimates from the best-fit model (see Rate of gene gain and loss below) were used to generate likelihoods for each family. This likelihood was then compared to a null distribution of likelihoods generated by randomly evolving gene families over the phylogenetic tree with the same best-fit model 10,000 times. The P-value for each family is taken as the position of the observed likelihood in this null distribution (see Hahn et al. 2005 for additional details). At P < 0.0001, <1 significant result is expected by chance among the 9990 gene families tested.

For the families significant at P < 0.0001, we determined which branches of the phylogenetic tree had the most significant expansions or contractions. To do this we calculated the exact P-value of the transition from the inferred parental node to the observed daughter node (Hahn et al. 2005). For the [human, chimp] and [macaque [human, chimp]] ancestors, we used the numbers of gains and losses from gene tree reconciliation to infer the size of each of the significant families at these nodes.

Analysis of positive selection:

For the 29 smallest families identified to have significant expansions in macaque, we looked for positive selection on the nucleotide sequences of the member genes using the ratio of nonsynonymous to synonymous substitutions per site. The ratio dN/dS measures the rate of nonsynonymous substitutions compared to synonymous substitutions per site. If this ratio is >1, then adaptive natural selection must be acting to fix nonsynonymous mutations. We asked whether this ratio was significantly >1 by taking the aligned macaque, human, and chimp sequences for the 29 rapidly expanding macaque families and comparing the likelihood of models with no positive selection (M1a) to the likelihood of models with positive selection (M2a) in the program PAML (Yang 1997). The likelihood-ratio test conservatively assumes 2 d.f. for the extra positive selection parameter; this is due to boundary effects on the parameter estimates of positive selection (Wong et al. 2004).

RESULTS AND DISCUSSION

Rate of gene gain and loss:

Estimation of rates via maximum likelihood:

Due to differential gene gain and loss along individual lineages the size of gene families can differ among species, from zero to hundreds of copies. We used the sizes of 9990 gene families in the genomes of macaque, human, chimpanzee, rat, mouse, and dog (supplemental Table 1 at http://www.genetics.org/supplemental/) to estimate the rate of gene turnover. Previous studies of both gene duplication (Lynch and Conery 2003; Goodstadt and Ponting 2006) and segmental duplication (Cheng et al. 2005; She et al. 2006) have suggested higher rates of change in primates relative to rodents. However, these results have relied on simple comparisons of individual genomes, and have not been able to accurately estimate the magnitude or significance of differences observed. We updated our previously published method (Hahn et al. 2005; De Bie et al. 2006) to allow for estimation of rates independently along individual branches of the phylogenetic tree. This updated method allows us to assign independent λ-parameters to different branches of a phylogenetic tree and to explicitly test hypotheses of heterogeneous rates among different lineages (materials and methods).

Comparing a model with a single, global-rate parameter to models with local parameters for the primate branches of the phylogenetic tree (see Figure 1 and supplemental Table 2 at http://www.genetics.org/supplemental/), we find strong evidence for a higher rate of gene gain and loss in the primate lineages. The best-fit model (Figure 1) has one rate for the human and chimpanzee lineages (λ3 = 0.0039), one for the macaque and great ape ancestor (λ2 = 0.0024), and a third for the rest of the tree (λ1 = 0.0014). The one-parameter (1-p) model estimates the global value of λ as 0.0017. The difference in likelihoods between the models is highly significant (P < 1.0 × 10−16). Individual parameter estimates from the three-parameter (3-p) model are consistent with the rate of gene duplication per million years estimated previously for mouse (Waterston et al. 2002), rat (Gibbs et al. 2004), and human (Lynch and Conery 2003) using different methods.

Figure 1.—

Figure 1.—

Open in a new tab

Rates of gene gain and loss across the mammals. The species tree of the six mammalian genomes considered is shown, shaded according to the estimated rates of gene gain and loss.

We conducted several checks to ensure the accuracy and significance of rate estimates via our likelihood method. To examine the influence of heterogeneity in genome annotation among species, we removed each species, one at a time, and re-estimated branch-specific rates (supplemental Table 2 at http://www.genetics.org/supplemental/). Importantly, the observed acceleration remains significant when the chimpanzee or human genomes are removed from the analysis, indicating that the results are not due to an incomplete assembly of the chimpanzee genome or to the relatively high-quality human annotation. The results are also significant after removal of any of the other individual genomes. To examine the effect of any outlying data, we tested models after removing the potentially disproportionate influence of the largest gene families, including olfactory receptors and zinc fingers (supplemental Table 2). The accelerated rates of change in the primates remained significant after removal of these families (supplemental Table 2).

To test the assumption that the negative of twice the difference in log-likelihoods between our nested models is χ2-distributed, we used a one-parameter model to simulate data and then estimated the likelihood of this data under both 1-p and 3-p models (where the 3-p model corresponds to the best-fit 3-p model from above). The likelihood ratio between these two estimates can then be used as a null distribution for comparison to the ratio in the observed data. Supplemental Figure 1 at http://www.genetics.org/supplemental/ shows that the observed ratio is still highly significant using the simulated data (P ≪ 0.002). This figure also shows that the χ2-distribution is overly liberal for the tests being conducted: only 5% of simulated data sets should have a likelihood ratio >6 with 2 d.f., while ∼95% of simulated values are above this threshold.

Given that the three-parameter model provides the best fit to the data, we also used simulations to assess the accuracy of our rate estimates. Using the estimated rate for the 1-p model (λ = 0.0017), we simulated data over the mammalian phylogeny for each of the 9990 families, setting the root sizes equal to the maximum-likelihood sizes estimated for each family in our data set. For 500 simulated data sets, we estimated λ-values under both the 1-p and 3-p models. For none of the 500 simulated data sets did we find the estimated primate rate to be as high as in the observed data (maximum simulated λ3 = 0.0019; observed λ3 = 0.0039; supplemental Figure 2 at http://www.genetics.org/supplemental/), nor was this value ever as great relative to the rest of the tree as in the observed data (maximum simulated λ3/λ1 = 1.3; observed λ3/λ1 = 2.79; supplemental Figure 3 at http://www.genetics.org/supplemental/). These results indicate that the likelihood method does not show a bias that would result in overestimating rates of evolution on the primate branches (P ≪ 0.002). However, it does appear as though there is a slight bias toward underestimation of rates on very long branches of the phylogenetic tree (supplemental Figure 2). This is most likely due to multiple gains and losses in the same family masking one another (Hahn et al. 2005).

Finally, we used simulations to test the robustness of the assumption in our model that there are equal probabilities of birth (gain) and death (loss). In particular, we asked whether we were more likely to reject the null hypothesis of one global rate parameter if birth is much greater than death on a branch of the tree (such as is observed in humans). To test this assumption we simulated 1000 data sets for the three primate species under a 1-p model (λ = 0.0017); we then also made 1000 identical data sets, except that all losses on the human branch of the tree were made into gains (so that 1 loss = 1 gain, 2 losses = 2 gains, etc.). This simulation method should maintain the overall rate of change, but shift the changes in family size from births equaling deaths to births much greater than deaths along the human branch of the tree. We calculated the likelihood ratios for each data set of a model with one parameter vs. a model with two parameters, one for the human branch and one for all other branches. Our results clearly indicate that we were no more likely to reject the null when birth is much greater than death (supplemental Figure 4 at http://www.genetics.org/supplemental/). The λ-parameter estimate for the human branch was also not higher using the birth is much greater than death data set.

Corroborating evidence:

To further determine the robustness of our results, we used three independent methods for inferring gene duplications: gene tree-species tree reconciliation (Durand et al. 2005), whole-genome assembly comparison (WGAC) (Bailey et al. 2001), and whole-genome shotgun sequence detection (WSSD) (Bailey et al. 2002). Each of these methods uses slightly different assumptions or data than our likelihood method and should provide independent evidence for gene duplications or losses.

The total number of genes gained via duplication and loss can be estimated by reconciling gene trees for each family with the underlying species tree (e.g., Zmasek and Eddy 2001). This method does not assume a specific probability model for changes in gene family size and therefore represents an independent method for assessing differences in the rate of gene gain and loss. To carry out this analysis we built gene trees for 9920 of the 9990 gene families (see materials and methods). We then reconciled the gene tree for each family with the species tree using the NOTUNG software package (Durand et al. 2005). Over all informative branches, there is a highly significant correlation between the number of duplications inferred via the gene tree and likelihood methods (r = 0.96, P < 0.0001) (supplemental Figure 5 at http://www.genetics.org/supplemental/). Numbers of losses cannot accurately be estimated by tree reconciliation methods (Hahn 2007a). The results from this analysis also indicate that gene conversion among paralogs is not a common occurrence. If there were high rates of gene conversion, paralogs within a genome would be most closely related to one another and gene trees would therefore show many recent duplicates along tip branches even without changes in overall copy number. The high correspondence between the number of duplicates inferred by our likelihood method, which considers only copy number, and the tree reconciliation method indicates that rampant gene conversion is not occurring.

Because the previous analyses are based on gene models contained within the assembled macaque genome, we expect there to be a good correlation between the gene duplications we have identified via likelihood and those identified by the WGAC method (Bailey et al. 2001). WGAC identifies large DNA-mediated duplications (“segmental duplications”) that may or may not contain genes. We used WGAC results from the rhesus macaque genome (Gibbs et al. 2007) to compare the two sets of results. Of the 1358 macaque-specific duplicates identified by the likelihood method, 911 are found in segmental duplications using the WGAC method. As WGAC only finds duplicated regions larger than 20 kb in assembled genomes, it may therefore miss smaller duplications. Overall, there is a highly significant correlation between the number of duplications in each family inferred via likelihood and the number of genes from those families found in segmental duplications (r = 0.79, P < 0.0001).

In contrast to WGAC, the WSSD method (Bailey et al. 2002) identifies duplicates on the basis of unincorporated reads from whole genome shotgun assemblies; it therefore identifies duplicates that are too similar to be split apart in the assembly process. These highly similar sequences may be either very young duplicates or older duplicates that have undergone recent gene conversion. If the latter case is true, then families in which we have inferred gene losses will appear as duplicates in the WSSD analysis. We used WSSD results from the rhesus macaque genome (Gibbs et al. 2007) to ensure that losses inferred via likelihood are true losses and not recent conversion events. We identify 666 gene losses in the lineage leading to macaque, but we find no association between losses in our likelihood analysis and duplications in the WSSD analysis (r = 0.14, P = 0.51). Further, we find that only 10% of families with inferred losses contain a gene that overlaps with a WSSD region; by comparison, 12% of families where we infer gains overlap with WSSD regions. There should not be a correlation between duplications in our analysis and WSSD as the latter explicitly addresses duplications not included in genome assembles. We conclude that gene conversion has not played a major role in apparent gene losses. The congruence of our likelihood results with results from the WGAC, WSSD, and gene-tree/species-tree reconciliation methods suggests that the observed increase in the rate of gene turnover in primates is not an artifact of either our analysis or of genome assembly.

Possible mechansims of rate acceleration:

Both mutational (Bailey et al. 2003) and selective (Spofford 1969; Lynch et al. 2001) forces have been proposed as mechanisms of increased rates of gene duplication. Increased levels of unequal crossover during meiosis due to nonallelic homologous recombination among transposable elements (TEs) may result in more gain and loss of DNA. An explosion of transposable elements in the primate lineage ∼35 MYA (Shen et al. 1991) could explain the lineage-specific differences in mutational input (Bailey et al. 2003). An increase in the rate of fixation of gene duplicates in species with smaller effective population sizes (Lynch et al. 2001) could further accelerate the overall rate of gene gain. Taken together, these two mechanisms may be sufficient to explain the patterns observed here. If an increase in mutational input from TEs predates the split of the macaque and great ape lineages, then all descendant species may show a slight acceleration in the rate of DNA gain and loss. Decreased population sizes in the hominoids then further contribute to rates of gene turnover, leading to even more gene gain and loss in these lineages. Further work into the mutational and selective forces that result in increased rates of turnover will need to be done to clarify the exact processes responsible.

Accelerated rate of change in individual gene families:

In addition to the proposed nonadaptive explanations for gene gain and loss, natural selection may have acted on individual gene families to promote expansion or contraction. Using our likelihood method, we identified individual gene families that have undergone large enough changes in any of the primate lineages to suggest evidence for adaptive evolution (materials and methods). Over the whole tree, 180 families show expansions or contractions that are extremely unlikely to be due to random gain and loss of genes (all P < 0.0001). Among these families, 108 have individually significant changes (P < 0.01) along at least one of the four primate lineages (human, chimp, great ape [human–chimp ancestor], and macaque) even after accounting for the lineage-specific rate acceleration in the primates. The number of changes inferred on each of these lineages was also confirmed by examining the gene tree for each family. These changes may therefore represent instances where natural selection has acted to increase or decrease the copy number of genes underlying a particular biological function. Figure 2 presents the families with significant changes in human, chimpanzee, and macaque.

Figure 2.—

Figure 2.—

Open in a new tab

Rapidly evolving gene families. Individual families showing significantly accelerated rates of evolution along the human, chimpanzee, and macaque lineages are shown. Each row is a single gene family, with the relative rate of evolution along the human (red), chimpanzee (green), and macaque (blue) lineages given by the width of the colored bars. The size of the family in each of the three species is shown to the right; italicized numbers indicate significance in that lineage.

Several gene families have undergone significant expansions in the lineage leading to modern humans, including previously identified families (Shannon et al. 2003; Birtle et al. 2005; Goodstadt and Ponting 2006; Popesco et al. 2006). Of particular note is the gain of nine genes in the centaurin gamma family (humans have 15 copies, and none of the other mammals has >7). Centaurin gamma 2 is a member of this family and is a brain-related gene thought to play a major role in the etiology of autism (Wassink et al. 2005; Sebat et al. 2007); an otherwise conserved noncoding sequence in Centaurin gamma 2 also shows an accelerated rate of evolution in humans (Prabhakar et al. 2006). A gene tree for the centaurin gamma family is shown in Figure 3. A BLAST search of the chimpanzee genome revealed two unannotated, possibly functional centaurin gamma genes (data not shown); the total number of genes gained in humans would still be significant even if the existence of these putative genes is confirmed in the future. Other biologically interesting families with expansions in humans include a double homeobox transcription factor family, a golgin subfamily involved in multiple autoimmune disorders, and an immunoglobulin heavy-chain variable-region gene family with 10 gains in humans.

Figure 3.—

Figure 3.—

Open in a new tab

Gene tree for centaurin gamma. The relationships among the members of the centaurin gamma gene family are shown, including gene copies from human, chimpanzee, macaque, mouse, and rat. The numbers for each protein correspond to Ensembl protein identification numbers.

We also find remarkable expansions in multiple gene families in macaque (Figure 2). The largest expansions identified in macaque are in HLA genes: at least 22 gene duplicates have been gained independently along this lineage alone. This result is further supported by aCGH data showing a large expansion in this family along the macaque lineage (Gibbs et al. 2007). A number of additional immunity-related gene families have expanded in macaque, including immunoglobulin κ chain variable regions, T cell receptors, and killer cell immunoglobulins. Intriguingly, these expansions are accompanied by macaque-specific expansions in several nuclear-encoded viral proteins, including the envelope and gag polyproteins. This may indicate a coevolutionary arms race between viral invaders and the macaque host immune system.

Because the rate of segmental duplication (i.e., duplicates >20 kb in length) appears to be accelerated in the primates (Cheng et al. 2005), it may be that there are more duplication events that individually encompass multiple members of the same gene family. This would lead to larger overall numbers of gene gains per mutational event in these species and spurious inferences of natural selection on large expansions. To look for an association between segmental duplications and multiple gene gains, we asked whether individual segmental duplications in the macaque genome inferred by the WGAC method contain multiple members of a gene family with macaque-specific duplications. Overall, only 6% of duplicated genes are found in the same segmental duplication as another member of the same family, with only four segmental duplications containing three members of the same gene family. There are no segmental duplications with more than three copies from a single gene family. Of the 42 gene families that show an accelerated rate of evolution in macaque, only 3 families have multiple genes in the same segmental duplication (keratin type II proteins, aldo/keto reductase, and prohibitin). In each of these cases, there are at most two genes contained within a single segmental duplication. These results imply that large segmental duplications are not responsible for large gains in numbers of genes, and consequently that natural selection likely plays a larger role in significant expansions of individual gene families than does mutation.

Previous results (Shannon et al. 2003; Birtle et al. 2005; Demuth et al. 2006; Popesco et al. 2006) suggest that adaptive natural selection may act simultaneously to both increase the number of copies of a gene and change the amino acid sequence of the new gene duplicates. As similar functional categories appear to be evolving rapidly at the level of nucleotide and gene number across mammals (Demuth et al. 2006), it may be that those genes under recurrent positive selection for amino acid changes are simply more likely to fix gene duplicates with alternative sequences (Spofford 1969). To examine the generality of this relationship, we tested for the action of positive selection on the nucleotide sequences of a subset of families that we identified as exhibiting rapid expansions in macaque. Overall, 19 of the 29 families examined (65.5%) had significant evidence for positive selection in a subset of codons after correcting for multiple tests (P < 0.001; supplemental Table 3 at http://www.genetics.org/supplemental/). A further 6/29 families examined (20.7%) have dN/dS > 1 over the entire coding region. A comparison with the analysis of positive selection among single-copy orthologous genes in the primates (Gibbs et al. 2007) reveals that only 1.7% (178/10,376) of these genes showed evidence for positive selection. Though there may be differences in power to detect selection between these two data sets because of unequal sample sizes, we have used a more conservative method for detecting positive selection (materials and methods). These results therefore support the idea that natural selection acts at a multiplicity of levels in molecular evolution and suggest that adaptive processes responsible for the maintenance of gene duplicates (e.g., Hughes 1994) may be more prevalent than previously appreciated.

Conclusions:

In their original hypothesis for the role of cis-regulatory changes in human evolution, King and Wilson (1975) offered no evidence that regulatory changes occurred at a higher rate, or had a larger effect per mutation, in primates relative to other species. In contrast, we have shown here that a disproportionate amount of gene gain and loss has occurred between humans and chimpanzees. Our analyses demonstrate that there has been an acceleration in the rate of gene gain and loss along the primate lineage, especially among the great apes. We have also identified several gene families that have undergone copy-number changes large enough to suggest the influence of natural selection. These results are an illustrative example of the novel insights that only become available with multiple, whole-genome sequences. Summing across all families, we infer the gain of at least 678 genes in the human genome and the loss of 740 genes in the chimpanzee genome since their split 5–6 MYA; these results imply that 6.4% (1418/22,000) of all human genes do not have a one-to-one ortholog in chimpanzee. This genomic revolving door (Demuth et al. 2006) must certainly account for human adaptations due to both recent gene duplications (e.g., Fortna et al. 2004) and recent gene losses (e.g., Olson 1999; Wang et al. 2006). The accelerated rate of evolution in primates further suggests that duplication and loss of genes has played at least as great a role in the evolution of modern humans as the modification of existing genes.

Acknowledgments

We thank R. Gibbs, J. Sikela, E. Eichler, W. Miller, M. Batzer, A. Siepel, T. Vinar, A. Harris, A. Vilella, A. Ureta-Vidal, and all the members of the Rhesus Macaque Genome Consortium for making this work possible. We also thank L. Moyle, M. Rockman, M. Lynch, D. Scofield, D. Durand, J. Stajich, D. Begun, and two reviewers for comments on the manuscript and W. Li for help in making the figures. This work was supported by a grant from the National Science Foundation (DBI-0543586) to M.W.H.

References

  1. Adkins, R. M., A. H. Walton and R. L. Honeycutt, 2003. Higher-level systematics of rodents and divergence time estimates based on two congruent nuclear genes. Mol. Phylogenet. Evol. 26: 409–420. [DOI] [PubMed] [Google Scholar]
  2. Bailey, J. A., Z. P. Gu, R. A. Clark, K. Reinert, R. V. Samonte et al., 2002. Recent segmental duplications in the human genome. Science 297: 1003–1007. [DOI] [PubMed] [Google Scholar]
  3. Bailey, J. A., G. Liu and E. E. Eichler, 2003. An Alu transposition model for the origin and expansion of human segmental duplications. Am. J. Hum. Genet. 73: 823–834. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bailey, J. A., A. M. Yavor, H. F. Massa, B. J. Trask and E. E. Eichler, 2001. Segmental duplications: Organization and impact within the current Human Genome Project assembly. Genome Res. 11: 1005–1017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Birtle, Z., L. Goodstadt and C. P. Ponting, 2005. Duplication and positive selection among hominin-specific PRAME genes. BMC Genomics 6: 120. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Burnham, K. P., and D. R. Anderson, 2002. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach. Springer-Verlag, New York.
  7. Carroll, S. B., 2005. Evolution at two levels: on genes and form. PLoS Biol. 3: e245. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Chen, K., D. Durand and M. Farach-Colton, 2000. NOTUNG: A program for dating gene duplications and optimizing gene family trees. J. Comput. Biol. 7: 429–447. [DOI] [PubMed] [Google Scholar]
  9. Cheng, Z., M. Ventura, X. She, P. Khaitovich, T. Graves et al., 2005. A genome-wide comparison of recent chimpanzee and human segmental duplications. Nature 437: 88–93. [DOI] [PubMed] [Google Scholar]
  10. Daubin, V., N. A. Moran and H. Ochman, 2003. Phylogenetics and the cohesion of bacterial genomes. Science 301: 829–832. [DOI] [PubMed] [Google Scholar]
  11. De Bie, T., J. P. Demuth, N. Cristianini and M. W. Hahn, 2006. CAFE: a computational tool for the study of gene family evolution. Bioinformatics 22: 1269–1271. [DOI] [PubMed] [Google Scholar]
  12. Demuth, J. P., T. De Bie, J. E. Stajich, N. Cristianini and M. W. Hahn, 2006. The evolution of mammalian gene families. PLoS ONE 1: e85. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Douzery, E. J. P., F. Delsuc, M. J. Stanhope and D. Huchon, 2003. Local molecular clocks in three nuclear genes: Divergence times for rodents and other mammals and incompatibility among fossil calibrations. J. Mol. Evol. 57: S201–S213. [DOI] [PubMed] [Google Scholar]
  14. Durand, D., B. V. Halldorsson and B. Vernot, 2005. A hybrid micro-macroevolutionary approach to gene tree reconstruction. J. Comput. Biol. 13: 320–335. [DOI] [PubMed] [Google Scholar]
  15. Elango, N., J. W. Thomas and S. V. Yi, 2006. Variable molecular clocks in hominoids. Proc. Natl. Acad. Sci. USA 103: 1370–1375. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Felsenstein, J., 1989. PHYLIP–hylogeny Inference Package (Version 3.2). Cladistics 5: 164–166. [Google Scholar]
  17. Fortna, A., Y. Kim, E. MacLaren, K. Marshall, G. Hahn et al., 2004. Lineage-specific gene duplication and loss in human and great ape evolution. PLoS Biol. 2: e207. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Gibbs, R., J. Rogers, M. Katze, R. Bumgarner, G. Weinstock et al., 2007. Evolutionary and biomedical insights from the rhesus macaque genome. Science 316: 222–234. [DOI] [PubMed] [Google Scholar]
  19. Gibbs, R. A., G. M. Weinstock, M. L. Metzker, D. M. Muzny, E. J. Sodergren et al., 2004. Genome sequence of the Brown Norway rat yields insights into mammalian evolution. Nature 428: 493–521. [DOI] [PubMed] [Google Scholar]
  20. Goodstadt, L., and C. P. Ponting, 2006. Phylogenetic reconstruction of orthology, paralogy, and conserved synteny for dog and human. PLoS Comput. Biol. 2: e133. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Hahn, M. W., 2007. a Bias in phylogenetic tree reconciliation methods: implications for vertebrate genome evolution. Genome Biol. 8: R141. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Hahn, M. W., 2007. b Detecting natural selection on cis-regulatory DNA. Genetica 129: 7–18. [DOI] [PubMed] [Google Scholar]
  23. Hahn, M. W., T. De Bie, J. E. Stajich, C. Nguyen and N. Cristianini, 2005. Estimating the tempo and mode of gene family evolution from comparative genomic data. Genome Res. 15: 1153–1160. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Hoekstra, H. E., and J. A. Coyne, 2007. The locus of evolution: evo devo and the genetics of adaptation. Evolution 61: 995–1016. [DOI] [PubMed] [Google Scholar]
  25. Hughes, A. L., 1994. The evolution of functionally novel proteins after gene duplication. Proc. R. Soc. Lond. B Biol. Sci. 256: 119–124. [DOI] [PubMed] [Google Scholar]
  26. Karev, G. P., Y. I. Wolf, A. Y. Rzhetsky, F. S. Berezovskaya and E. V. Koonin, 2002. Birth and death of protein domains: A simple model of evolution explains power law behavior. BMC Evol. Biol. 2: 18. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. King, M.-C., and A. C. Wilson, 1975. Evolution at two levels in humans and chimpanzees. Science 188: 107–116. [DOI] [PubMed] [Google Scholar]
  28. Kumar, S., A. Filipski, V. Swarna, A. Walker and S. B. Hedges, 2005. Placing confidence limits on the molecular age of the human-chimpanzee divergence. Proc. Natl. Acad. Sci. USA 102: 18842–18847. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Li, W.-H., 1997. Molecular Evolution. Sinaur Associates, Sunderland, MA.
  30. Lynch, M., and J. S. Conery, 2003. The evolutionary demography of duplicate genes. J. Struct. Funct. Genomics 3: 35–44. [PubMed] [Google Scholar]
  31. Lynch, M., M. O'Hely, B. Walsh and A. Force, 2001. The probability of preservation of a newly arisen gene duplicate. Genetics 159: 1789–1804. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. McLysaght, A., P. F. Baldi and B. S. Gaut, 2003. Extensive gene gain associated with adaptive evolution of poxviruses. Proc. Natl. Acad. Sci. USA 100: 15655–15660. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Nei, M., and G. V. Glazko, 2002. Estimation of divergence times for a few mammalian and several primate species. J. Hered. 93: 157–164. [DOI] [PubMed] [Google Scholar]
  34. Nei, M., X. Gu and T. Sitnikova, 1997. Evolution by the birth-and-death process in multigene families of the vertebrate immune system. Proc. Natl. Acad. Sci. USA 94: 7799–7806. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Olson, M. V., 1999. When less is more: gene loss as an engine of evolutionary change. Amer. J. Hum. Genet. 64: 18–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Patterson, N., D. J. Richter, S. Gnerre, E. S. Lander and D. Reich, 2006. Genetic evidence for complex speciation of humans and chimpanzees. Nature 441: 1103–1108. [DOI] [PubMed] [Google Scholar]
  37. Popesco, M. C., E. J. MacLaren, J. Hopkins, L. Dumas, M. Cox et al., 2006. Human lineage-specific amplification, selection, and neuronal expression of DUF1220 domains. Science 313: 1304–1307. [DOI] [PubMed] [Google Scholar]
  38. Prabhakar, S., J. P. Noonan, S. Paabo and E. M. Rubin, 2006. Accelerated evolution of conserved noncoding sequences in humans. Science 315: 786. [DOI] [PubMed] [Google Scholar]
  39. Sebat, J., B. Lakshmi, D. Malhotra, J. Troge, C. Lese-Martin et al., 2007. Strong association of de novo copy number mutations with autism. Science 316: 445–449. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Shannon, M., A. T. Hamilton, L. Gordon, E. Branscomb and L. Stubbs, 2003. Differential expansion of zinc-finger transcription factor loci in homologous human and mouse gene clusters. Genome Res. 13: 1097–1110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. She, X., G. Liu, M. Ventura, S. Zhao, D. Misceo et al., 2006. A preliminary comparative analysis of primate segmental duplications shows elevated substitution rates and a great-ape expansion of intrachromosomal duplications. Genome Res. 16: 576–583. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Shen, M. R., M. A. Batzer and P. L. Deininger, 1991. Evolution of the master Alu gene(s). J. Mol. Evol. 33: 311–320. [DOI] [PubMed] [Google Scholar]
  43. Spofford, J. B., 1969. Heterosis and evolution of duplications. Am. Nat. 103: 407–432. [Google Scholar]
  44. Springer, M. S., W. J. Murphy, E. Eizirik and S. J. O'Brien, 2003. Placental mammal diversification and the cretaceous-tertiary boundary. Proc. Natl. Acad. Sci. USA 100: 1056–1061. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Steppan, S. J., R. M. Adkins and J. Anderson, 2004. Phylogeny and divergence-date estimates of rapid radiations in muroid rodents based on multiple nuclear genes. Syst. Biol. 53: 533–553. [DOI] [PubMed] [Google Scholar]
  46. Wang, X., W. E. Grus and J. Zhang, 2006. Gene losses during human origins. PLoS Biol. 4: e52. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Wassink, T. H., J. Piven, V. J. Vieland, L. Jenkins, R. Frantz et al., 2005. Evaluation of the chromosome 2q37.3 gene CENTG2 as an autism susceptibility gene. Am. J. Med. Genet. B Neuropsychiatr. Genet. 136B: 36–44. [DOI] [PubMed] [Google Scholar]
  48. Waterston, R. H., K. Lindblad-Toh, E. Birney, J. Rogers, J. F. Abril et al., 2002. Initial sequencing and comparative analysis of the mouse genome. Nature 420: 520–562. [DOI] [PubMed] [Google Scholar]
  49. Wong, W. S. W., Z. Yang, N. Goldman and R. Nielsen, 2004. Accuracy and power of statistical methods for detecting adaptive evolution in protein coding sequences and for identifying positively selected sites. Genetics 168: 1041–1051. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Wu, C. I., and W. H. Li, 1985. Evidence for higher rates of nucleotide substitution in rodents than in man. Proc. Natl. Acad. Sci. USA 82: 1741–1745. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Yang, Z., 1997. PAML: a program package for phylogenetic analysis by maximum likelihood. Comput. Appl. Biosci. 13: 555–556. [DOI] [PubMed] [Google Scholar]
  52. Yi, S. J., D. L. Ellsworth and W. H. Li, 2002. Slow molecular clocks in Old World monkeys, apes, and humans. Mol. Biol. Evol. 19: 2191–2198. [DOI] [PubMed] [Google Scholar]
  53. Zmasek, C. M., and S. R. Eddy, 2001. A simple algorithm to infer gene duplication and speciation events on a gene tree. Bioinformatics 17: 821–828. [DOI] [PubMed] [Google Scholar]

Articles from Genetics are provided here courtesy of Oxford University Press

RESOURCES