Significance Thresholds for Quantitative Trait Locus Mapping Under Selective Genotyping

Abstract

In the case of selective genotyping, the usual permutation test to establish statistical significance for quantitative trait locus (QTL) mapping can give inappropriate significance thresholds, especially when the phenotype distribution is skewed. A stratified permutation test should be used, with phenotypes shuffled separately within the genotyped and ungenotyped individuals.

IN the mapping of quantitative trait loci (QTL) in an experimental cross, selective genotyping (in which only the individuals at the extremes of the phenotype distribution are genotyped) can provide nearly equivalent power to complete genotyping at a reduced cost (Lander and Botstein 1989; Darvasi and Soller 1992).

Interval mapping with selectively genotyped data is best performed with consideration of all individuals, even those that were not genotyped (Lander and Botstein 1989). Consideration of only the genotyped individuals results in a biased estimate of the QTL effect. Haley–Knott regression (Haley and Knott 1992) generally provides a good approximation to standard interval mapping, but should be avoided in the case of selective genotyping, as it tends to produce inflated evidence for linkage (Feenstra et al. 2006).

Despite the common use of selective genotyping for QTL mapping and the extensive literature on significance thresholds for QTL mapping, we are not aware of any discussion of the derivation of appropriate thresholds for statistical significance in the case of selective genotyping. In the usual approach for establishing statistical significance in QTL mapping experiments, one considers the distribution of the genomewide maximum LOD score under the global null hypothesis that there are no segregating QTL. This distribution is best derived via a permutation test (Churchill and Doerge 1994).

The permutation test is attractive because of its applicability to a wide range of settings. It provides the correct genomewide P-value regardless of the phenotype distribution, marker density, and statistical test. The usual permutation test makes an important assumption that all individuals in the cross are exchangeable, under the null hypothesis of no QTL. In other words, validity of the standard permutation procedure requires that all orderings of phenotypes relative to genotypes are equally likely, under the null hypothesis (that is, that there is no association between the phenotypes and the pattern of missing genotypes).

When selective genotyping is used, the exchangability condition is violated, and application of the usual permutation test may give rise to inappropriate significance thresholds, as we show below. When using standard interval mapping (Lander and Botstein 1989), significance thresholds tend to be too large, especially in the case that the phenotype distribution is skewed, and so are overly conservative. In contrast, with the multiple-imputation approach (Sen and Churchill 2001), the usual permutation test yields thresholds that are too small, making them excessively liberal in declaring evidence for a QTL.

The usual permutation test is not justified in the presence of selective genotyping because individuals with different genotyping patterns are not exchangeable under the null hypothesis (Welch 1990). Under selective genotyping, the genotype data for all individuals at a particular marker can be represented by a vector of actual genotypes, g = (g₁,…, g_n), combined with a vector of response indicators, r = (r₁,…, r_n), denoting whether or not each particular individual was genotyped. When employing selective genotyping, the genotype data, represented by the pair (g, r), are associated with the phenotypes, y = (y₁,…, y_n), by design. Specifically, the response indicator, r, is equal to 1 for extreme individuals only and 0 for everyone else. Thus, even under the null hypothesis, we cannot permute phenotypes completely at random relative to genotypes. Rather, we must permute in a way that maintains the relationship between the phenotypes, y, and the missing data pattern, r, in which genotypes are available only for the phenotypic extremes.

We propose the use of a stratified permutation test: shuffle the phenotype data within similarly genotyped individuals. One thus conditions on the genotyping pattern. When selective genotyping is used, we need permute the phenotype data only within genotyped individuals. If the ungenotyped individuals were subsequently genotyped at markers in regions exhibiting initial evidence for a QTL, separate individuals into strata according to the amount of genotyping performed and permute phenotypes relative to genotypes separately within the different strata. The estimated significance thresholds obtained by a stratified permutation test do not suffer from the problems seen with the unstratified permutation test.

To illustrate the problems, we performed simulations to study the behavior of (1) permutation with complete genotyping, (2) unstratified permutation in the case of selective genotyping, and (3) stratified permutation with selective genotyping. With this comparison in mind, one possible simulation strategy would be to generate many data sets and perform permutations using each of the three scenarios described. For each simulation replicate, permutation would give the null distribution of the LOD score under a particular genotyping strategy, conditional on the observed distributions of genotypes and phenotypes. Rather than performing permutation repeatedly for many unique data sets, we investigated the null distributions by direct simulation. The key idea is that, if a complete permutation is applied to selectively genotyped data, one obtains data in which a random subset of individuals has been genotyped. Thus the behavior of the usual permutation test, when applied to selectively genotyped data, may be determined via the simulation of data with genotypes on a random subset of individuals. Similarly, behavior of a stratified permutation is seen by examining data simulated with genotypes on the phenotypic extremes only.

We simulated an intercross of 250 individuals having a skewed phenotype distribution, with phenotypes following a 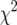-distribution with 7 d.f. (The need for the stratified permutation test was most apparent in the case of a skewed phenotype distribution; this particular distribution is skewed but not extremely so.) We considered three scenarios: (1) complete genotype data on all individuals, (2) genotype data on a random 100 individuals and no genotype data on the remaining 150 individuals (as would occur after an unstratified permutation test was applied to selectively genotyped data), and (3) genotype data on the top 50 and bottom 50 individuals (phenotypically) and no genotype data on the remaining 150 individuals. In all scenarios, the available phenotype data for all individuals were considered in the analysis, regardless of whether or not those individuals were genotyped. The null distribution of the genomewide maximum LOD score was estimated for each scenario for each of three methods: standard interval mapping via the EM algorithm (Dempster et al. 1977), multiple imputation (Sen and Churchill 2001), and the extended Haley–Knott method (Feenstra et al. 2006). (We omitted the original Haley–Knott regression method, as it is inappropriate in the context of selective genotyping.) We used 10,000 simulation replicates for standard interval mapping and the extended Haley–Knott method and 2000 replicates for the imputation method.

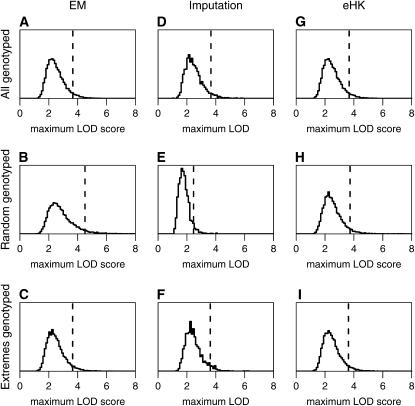
The results are displayed in Figure 1. For standard interval mapping (via the EM algorithm), the null distribution in the case of selective genotyping (Figure 1C) was similar to that for complete genotyping (Figure 1A), but in the case that a random 100 individuals were genotyped but all individuals were included in the analysis (Figure 1B), greater LOD scores often resulted, and the 95th percentile of the distribution was 4.5 rather than the expected 3.7. For the multiple-imputation method, the null distribution in the case of selective genotyping (Figure 1F) closely matched that from complete genotyping (Figure 1D), but smaller LOD values were often seen with random genotyping (Figure 1E). The resulting 95th percentile was 2.5 rather than 3.7. Finally, for the extended Haley–Knott method, the null distribution was very similar for the three genotyping schemes (Figure 1, G–I), with 95th percentiles of 3.7, 3.7, and 3.6 for complete, random, and selective genotyping.

Figure 1.—

Estimated null distribution of the genomewide maximum LOD score for the EM algorithm (A–C), multiple imputation (D–F), and the extended Haley–Knott (eHK) method (G–I), for an intercross with 250 individuals and with the phenotypes following a 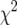-distribution with 7 d.f. A, D, and G correspond to the case of complete genotype data; B, E, and H correspond to the case that a random 100 individuals were genotyped; and C, F, and I correspond to the case that 100 individuals with extreme phenotypes (the top and bottom 50 individuals) were genotyped. Simulations were conducted in R/qtl (Broman et al. 2003), an add-on package to the general statistical software R (Ihaka and Gentleman 1996). We used 10,000 simulation replicates for the EM and eHK methods and 2000 replicates for the multiple-imputation method. The dashed vertical lines indicate the 95th percentiles of the distributions.

Our results demonstrate that a stratified permutation test yields an appropriate threshold value regardless of whether standard interval mapping, multiple imputation, or extended Haley–Knott was used for analysis. In contrast, an unstratified permutation test in the presence of selective genotyping gives excessively large thresholds under standard interval mapping, making the test too conservative. With multiple imputation, the thresholds from an unstratified permutation test are too small, making the procedure too liberal in declaring evidence for QTL.

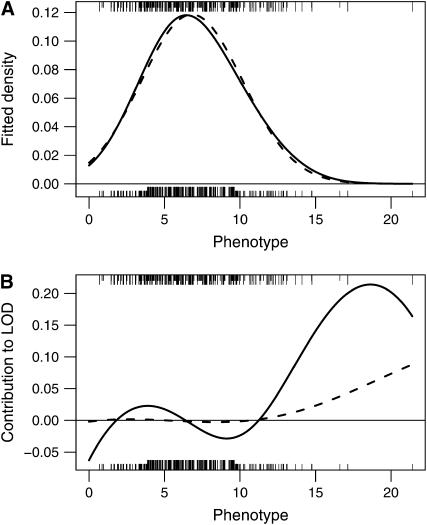
While theoretical considerations support the need for the stratified permutation test, the inflation in LOD scores in the unstratified permutation test for standard interval mapping and the deflation in LOD scores for the multiple-imputation method were not anticipated and deserve explanation. In the application of an unstratified permutation test to selectively genotyped data, the genotypes are attached to a random subset of the phenotypes, rather than remaining with the extreme phenotypes. When a random portion of the phenotyped individuals have been genotyped but all individuals are included in the analysis, the use of standard interval mapping (Lander and Botstein 1989) can inflate evidence for a QTL through improved fit in the tails of the phenotype distribution. Consider, for example, Figure 2A: under random genotyping (solid curve), the mixture modeling performed in standard interval mapping provides a moderately improved fit to the right tail of the phenotype distribution. Since the null model is constrained to be normal, phenotypically extreme individuals with no genotype data have a large contribution to the LOD score (Figure 2B) and so can inflate the evidence for a QTL. If the extremes are genotyped and the ungenotyped individuals come only from the center of the phenotype distribution, this inflation of evidence for a QTL does not occur.

Figure 2.—

The fitted phenotype distributions (A) and the individual contributions to the LOD score for individuals with no genotype data (B), from maximum-likelihood estimation via the EM algorithm (Dempster et al. 1977) under the usual normal mixture model, for simulated intercross data with 250 individuals, phenotype following a 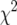-distribution with 7 d.f., markers at a 10-cM spacing, and under the null hypothesis of no QTL. The solid curves correspond to the case that a random 100 individuals were genotyped; the dashed curves correspond to the case that 100 individuals with extreme phenotypes were genotyped. Tick marks indicate the observed phenotypes, with longer tick marks corresponding to individuals with no genotype data. The top tick marks are for the case that a random 100 individuals were genotyped; the bottom tick markers are for the case that 100 individuals with extreme phenotypes were genotyped.

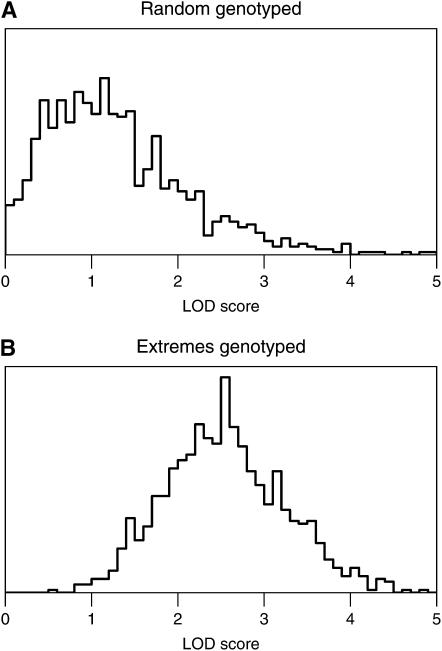
Phenotypically extreme observations also play a role in shaping the null distributions of LOD values obtained by multiple imputation (Sen and Churchill 2001). In the case of random genotyping (Figure 3A), the distribution of LOD scores across imputations at the position of maximum LOD has a large spread, reflecting the variability seen in attaching different sets of imputed genotypes to phenotypically extreme individuals with more influence on the LOD score. When the extremes are genotyped (Figure 3B), only individuals in the center of the phenotype distribution lack genotype information, and so the LOD scores across imputations are less variable. The distribution is symmetric, with a higher median that is derived principally from the genotyped extreme observations. Since the imputation method performs an averaging operation over genetic model parameters, the LOD under random genotyping, in which there is lower information, is smaller than the LOD under complete genotyping. On the other hand, the LOD under selective genotyping is close to the LOD under complete genotyping, since they have approximately equal information.

Figure 3.—

The distribution of LOD scores from the multiple imputations obtained at the position of the maximum overall LOD score, for simulated intercross data with 250 individuals, phenotype following a 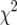-distribution with 7 d.f., markers at a 10-cM spacing, and under the null hypothesis of no QTL, analyzed by the multiple-imputation approach (Sen and Churchill 2001), in the case that a random 100 individuals were genotyped (A) or that 100 individuals with extreme phenotypes were genotyped (B).

The null distribution of the genomewide maximum LOD score from the extended Haley–Knott method was seen to be largely unchanged by the presence of random ungenotyped individuals (Figure 1H). This is due to the fact that individuals are weighted by the inverse of the variance of their phenotype given the available marker data, and so the ungenotyped individuals, having high variance, are given low weight and are essentially ignored in the analysis.

The problem with the unstratified permutation test is similar to the phenomenon of spuriously large LOD scores in regions of low genotype information (Broman 2003). In standard interval mapping, the problem with the unstratified permutation test is more pronounced in the case of a skewed or multimodal phenotype distribution, which is better approximated by a normal mixture model than by a single normal distribution. Further, the problem is more pronounced in an intercross than in a backcross, because the two homozygotes have smaller frequencies and allow asymmetry in the mixture modeling of the phenotype distribution.

In summary, selective genotyping can be an efficient method for mapping QTL. In the analysis of selectively genotyped data, all phenotyped individuals should be included, Haley–Knott regression should be avoided, and a stratified permutation test should be used to establish the statistical significance of the results. The proposed procedures have been implemented in R/qtl (Broman et al. 2003).