Axial ligand tuning of a nonheme iron(IV)–oxo unit for hydrogen atom abstraction

Abstract

The reactivities of mononuclear nonheme iron(IV)–oxo complexes bearing different axial ligands, [Fe^IV(O)(TMC)(X)]ⁿ⁺ [where TMC is 1,4,8,11-tetramethyl-1,4,8,11-tetraazacyclotetradecane and X is NCCH₃ (1-NCCH₃), CF₃COO⁻ (1-OOCCF₃), or N₃⁻ (1-N₃)], and [Fe^IV(O)(TMCS)]⁺ (1′-SR) (where TMCS is 1-mercaptoethyl-4,8,11-trimethyl-1,4,8,11-tetraazacyclotetradecane), have been investigated with respect to oxo-transfer to PPh₃ and hydrogen atom abstraction from phenol OH and alkylaromatic CH bonds. These reactivities were significantly affected by the identity of the axial ligands, but the reactivity trends differed markedly. In the oxidation of PPh₃, the reactivity order of 1-NCCH₃ > 1-OOCCF₃ > 1-N₃ > 1′-SR was observed, reflecting a decrease in the electrophilicity of iron(IV)–oxo unit upon replacement of CH₃CN with an anionic axial ligand. Surprisingly, the reactivity order was inverted in the oxidation of alkylaromatic CH and phenol OH bonds, i.e., 1′-SR > 1-N₃ > 1-OOCCF₃ > 1-NCCH₃. Furthermore, a good correlation was observed between the reactivities of iron(IV)–oxo species in H atom abstraction reactions and their reduction potentials, E_p,c, with the most reactive 1′-SR complex exhibiting the lowest potential. In other words, the more electron-donating the axial ligand is, the more reactive the iron(IV)–oxo species becomes in H atom abstraction. Quantum mechanical calculations show that a two-state reactivity model applies to this series of complexes, in which a triplet ground state and a nearby quintet excited-state both contribute to the reactivity of the complexes. The inverted reactivity order in H atom abstraction can be rationalized by a decreased triplet-quintet gap with the more electron-donating axial ligand, which increases the contribution of the much more reactive quintet state and enhances the overall reactivity.

High-valent iron(IV)–oxo species have been implicated as the key reactive intermediates in the catalytic cycles of oxygen-activating iron enzymes (1–6). In heme enzymes, proximal ligands are proposed to tune the reactivity of the iron(IV)–oxo porphyrin π-cation radical intermediates, collectively designated as Compounds I (Cpd I) (7, 8). In particular, the role of the axial cysteinate ligand of cytochrome P450 has received much attention because of the enzyme's ability to hydroxylate unactivated CH bonds (7–10). In recent reports, Ogliaro et al. (10) and Green and coworkers (11–14) demonstrated that the thiolate ligand in closely related chloroperoxidase increases the basicity of the iron(IV)–oxo moiety such that the Fe–O unit becomes protonated at neutral pH upon reduction by one electron to the Cpd II state. Green speculated that this increased basicity is a strategy that allows hydrogen atom abstraction by Cpd I to occur at a lower redox potential so that the surrounding enzyme environment can be protected from oxidative destruction.

What is required to test this intriguing hypothesis is more direct experimental evidence that systematically shows the effect of axial ligands on the reactivity of a high-valent iron–oxo species. Although there are several studies demonstrating that axial ligands affect the reactivities of iron(IV)–oxo centers in biomimetic Cpd I analogs (15, 16), only one of these studies reported the effect of a range of ligands on reaction rates (15), but no clear correlation between reactivity and some property of the axial ligand was discerned. More recently, with the synthesis of the first nonheme iron(IV)–oxo complex, [Fe^IV(O)(TMC)(NCCH₃)]²⁺ (where TMC is 1,4,8,11-tetramethyl-1,4,8,11-tetraazacyclotetradecane) (17), we found that the axial CH₃CN ligand can be replaced with anions and that these anions affected the reactivity of the iron(IV)–oxo unit (18–20). In this article, we report a systematic study that documents a dramatic axial ligand effect on the ability of a nonheme iron(IV)–oxo unit to carry out oxygen atom transfer to PPh₃ versus its ability to effect hydrogen atom abstraction of CH and OH bonds. These observations are interpreted in light of theoretical results that shed light on how high-valent iron(IV)–oxo species can activate CH bonds.

Results and Discussion

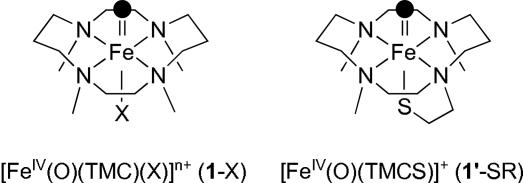
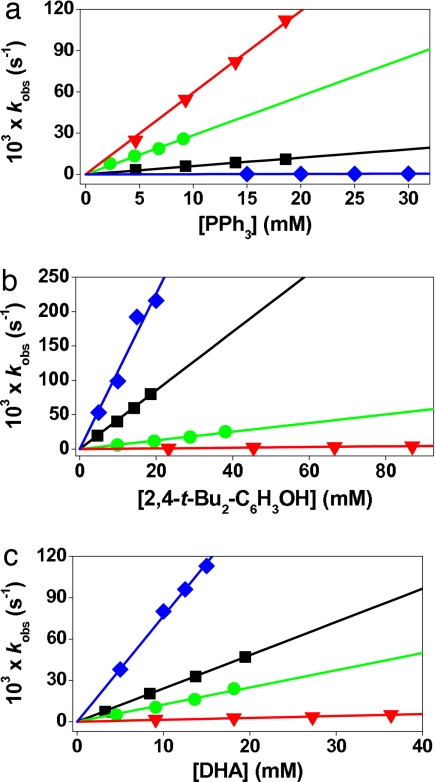
Mononuclear nonheme iron(IV)–oxo complexes bearing different axial ligands, [Fe^IV(O)(TMC)(X)]ⁿ⁺ (1-X) [where X is NCCH₃ (1-NCCH₃), CF₃COO⁻ (1-OOCCF₃), or N₃⁻ (1-N₃)] (see the structure in Fig. 1), were prepared by reacting their iron(II) complexes, [Fe^II(TMC)(X)]ⁿ⁺, with 1.2 eq of PhIO in CH₃CN at 25°C and characterized as previously reported (17–19). Upon addition of PPh₃ to the solutions, the intermediates reverted back to the starting iron(II) complexes [supporting information (SI) Fig. 7], yielding Ph₃PO quantitatively. Second-order rate constants extracted from these experiments afforded the reactivity order of 1-NCCH₃ > 1-OOCCF₃ > 1-N₃ (Table 1 and Fig. 2a), suggesting that the axial ligand modulates the reactivity of the FeO unit in oxygen atom transfer in a systematic fashion.

Fig. 1.

Schematic structures of [Fe^IV(O)(TMC)(X)]ⁿ⁺ (1-X) and [Fe^IV(O)(TMCS)]⁺ (1′-SR).

Table 1.

Second-order rate constants and KIE values determined in substrate oxidations by [Fe^IV(O)(TMC)(X)]ⁿ⁺ (1-X) and [Fe^IV(O)(TMCS)]⁺ (1′-SR)

Substrate	CH BDE,† kcal/mol	k2, M−1·s−1
		1-NCCH3	1-OOCCF3	1-N3	1′-SR
PPh3	N/A	5.9	2.9	0.61	[0.016]
2,4-t-Bu2C6H3OH	N/A	0.050	0.63	4.3	[12]
Xanthene	75.5	0.39	7.6	9.6
(KIE)‡		(16)	(20)	(17)
DHA	77	0.14 [0.20]	1.3	2.4 [4.9]	[7.5]
(KIE)‡		(10)	(19)	(17)
CHD	78	0.12	1.2	1.4
Fluorene	80	n.d.§	0.051	0.15
Ep,c in CH3CN at 25°C		−0.32	−0.50	−0.60
(1:1 CH3CN/CH3OH at −30°C)		(−0.44)	(−0.62)	(−0.66)	(−1.00)

Rate constants were determined at 0°C in CH₃CN for 1-X or 1:1 CH₃CN/MeOH for 1′-SR. Square brackets designate values obtained in 1:1 CH₃CN/CH₃OH at 0°C. The spectral changes were monitored at 820 nm for 1-NCCH₃, 835 nm for 1-OOCCF₃ and 850 nm for 1-N₃ and 1′-SR. Rate constants are averaged by three determinations, and standard deviation is <10% of the given values. N/A, not applicable.

^†BDE of CH bonds are from refs. 29 and 30.

^‡KIE values were determined at 25°C for 1-NCCH₃ and at 0°C for 1-OOCCF₃ and 1-N₃. See SI Table 3 for k_obs constants determined in the reactions.

^§Not determined due to the low reactivity of the intermediates in the oxidation of fluorene.

Fig. 2.

Second-order rate constants determined in the reactions of [Fe^IV(O)(TMC)(X)]ⁿ⁺ (0.5 mM) at 0°C with PPh₃ (a), 2,4-t-Bu₂C₆H₃OH (b), and DHA (c). Blue diamonds indicate 1′-SR; black squares indicate 1-N₃; green circles indicate 1-OOCCF₃; and red inverted triangles indicate 1-NCCH₃.

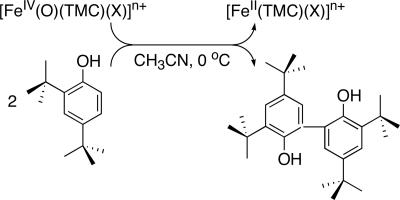
The effect of the axial ligands on hydrogen atom abstraction by 1-X also was investigated in the oxidation of CH and OH bonds. Addition of 2,4,6-tri-tert-butylphenol to 1-X caused the decay of the intermediates with the concurrent formation of the corresponding phenoxyl radical as detected by UV–visible and EPR spectroscopies (data not shown) (21, 22). In the case of 2,4-di-tert-butylphenol (2,4-t-Bu₂C₆H₃OH) as substrate, we observed the formation of 2,2′-dihydroxy-3,3′,5,5′-tetra-tert-butylphenol (≈100% based on the intermediates used) (Scheme 1); 2 eq of phenol are oxidized per molecule of 1-X to give the starting [Fe^II(TMC)(X)]ⁿ⁺ complex and the coupling product from the 2,4-di-tert-butylphenoxyl radical (23). Pseudo-first-order fitting of the kinetic data allowed us to determine k_obs values, and second-order rate constants were determined by plotting first-order rate constants against phenol concentration (Table 1 and Fig. 2b). This analysis also revealed a significant axial ligand effect, resulting in a reactivity order of 1-N₃ > 1-OOCCF₃ > 1-NCCH₃, which is opposite to that observed for PPh₃ oxidation.

Scheme 1.

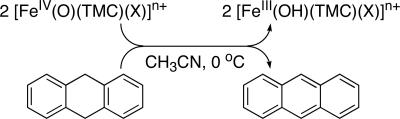
9,10-Dihydroanthracene (DHA) also was oxidized by 1-X to form anthracene as the sole product in ≈80% yield based on the stoichiometry shown in Scheme 2. The product yield was not dependent on the axial ligands, as observed in the 2,4-t-Bu₂C₆H₃OH oxidation reactions. Unlike for the phenol oxidation, two molecules of 1-X are required to oxidize one molecule of DHA, so 1-X acts as an one-electron oxidant in this case, and the hydroxoiron(III) species that is formed is apparently not a powerful enough oxidant to abstract a hydrogen atom from DHA (19, 20). That an iron(III) species is the iron product of DHA oxidation was indicated by the oxidation of 2,4-t-Bu₂C₆H₃OH added after the reactions of 1-X with DHA were completed, affording half as much biphenol product as the reactions of 1-X with 2,4-t-Bu₂C₆H₃OH in the absence of DHA. The second-order rate constants derived from an analysis of the DHA oxidation reactions exhibited a reactivity order similar to that for phenol oxidation (Table 1 and Fig. 2c). Taken together, the above results demonstrate that the reactivity of 1-X is significantly affected by the axial ligands, X. Interestingly, the effect of X is opposite in H atom abstraction with respect to oxo-transfer reactions, i.e., 1 e⁻ vs. 2 e⁻ oxidations. Thus, more detailed investigations were carried out to understand the mechanism(s) and the origin of the axial ligand effect(s) in the oxidation of CH and OH bonds by mononuclear nonheme iron(IV)–oxo complexes.

Scheme 2.

Oxidation of Phenol OH Bonds.

The oxidation of phenols can in principle occur via an H atom abstraction pathway or by a proton-coupled electron transfer mechanism (24, 25). The latter is disfavored by a comparison of two substrates having similar OH bond strengths and pK_a values but different steric demands, namely 2,6-t-Bu₂C₆H₃OH [OH bond dissociation energy (BDE) = 81.65 kcal/mol; pK_a = 11.70 in aqueous solution] and 2,4-t-Bu₂C₆H₃OH (OH BDE = 81.85 kcal/mol; pK_a = 11.64 in aqueous solution) (25, 26). We observed a 175-fold rate difference in their reactions with 1-N₃, 3.6 × 10⁻⁴ s⁻¹ for 2,6-t-Bu₂C₆H₃OH and 6.3 × 10⁻² s⁻¹ for 2,4-t-Bu₂C₆H₃OH at 0°C. We interpret this large difference in reactivity to reflect a steric effect that implicates OH bond cleavage as the rate-determining step (23–25, 27).

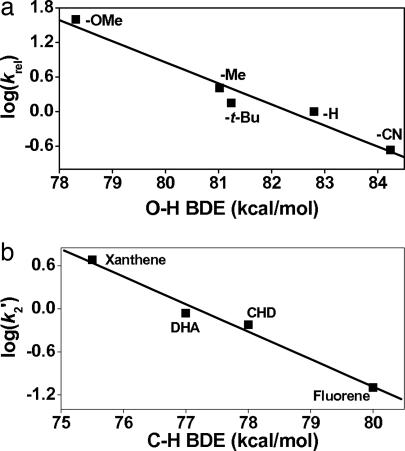
Further mechanistic studies with various para-substituted 2,6-di-tert-butylphenols (p-Y-2,6-t-Bu₂-C₆H₂OH) revealed that the electronegativity of the para-substituents influences the reaction rates significantly as well (SI Table 2). A plot of the relative rates as a function of σ_p⁺ shows a good Hammett correlation with ρ values of −1.5 for 1-N₃, −2.3 for 1-OOCCF₃, and −3.2 for 1-NCCH₃ (SI Fig. 8). Such a linear relationship has been used as evidence for an H atom abstraction mechanism in the oxidations of phenol OH bonds by [Mn^V(O)(Cz)] (where Cz is corrolazine) (23) and [(L)Ru^VI(O)₂]²⁺ (25). Further support for this notion derives from the plot of log k_rel against phenol OH BDE, which also afforded a good linear correlation with slopes of −0.36 for 1-N₃, −0.42 for 1-OOCCF₃, and −0.55 for 1-NCCH₃ (Fig. 3a for 1-N₃; SI Fig. 9 for 1-OOCCF₃ and 1-NCCH₃) (23, 25, 28).

Fig. 3.

Correlations of reaction rates with BDE. (a) Plot of log k_rel of [Fe^IV(O)(TMC)(N₃)]⁺ (1-N₃) against OH BDE of p-Y-2,6-t- Bu₂C₆H₃OH in CH₃CN at 25°C. (b) Plot of log k′₂ of [Fe^IV(O)(TMC)(N₃)]⁺ (1-N₃) against CH BDE of substrates. Second-order rate constants, k₂, were determined at 25°C and then adjusted for reaction stoichiometry to yield k′₂ based on the number of equivalent target CH bonds of substrates (e.g., four for DHA and CHD and two for xanthene and fluorene).

Oxidation of Activated CH Bonds.

Further insight into the mechanism of CH bond activation by nonheme iron(IV)–oxo complexes was obtained by investigating the reactions of 1-X with a range of substrates having weak CH bonds, specifically xanthene (75.5 kcal/mol), DHA (77 kcal/mol), 1,4-cyclohexadiene (78 kcal/mol), and fluorene (80 kcal/mol) (29, 30), from which second-order rate constants were determined. For these reactions, the reactivity order was found to be 1-N₃ > 1-OOCCF₃ > 1-NCCH₃ (Table 1 and SI Fig. 10), as found for DHA oxidation (Fig. 2c). The log (k′₂) values also correlated linearly with the CH BDE values of the substrates, giving a slope of approximately −0.4 for each iron(IV)–oxo complex studied (Fig. 3b for 1-N₃ and SI Fig. 11 for 1-OOCCF₃ and 1-NCCH₃). As expected, the rate constants decrease with the increase of the CH BDE of substrates; this linear relationship between the reaction rates and the BDE of substrates implicates an H atom abstraction as the rate-determining step for the oxidation (31–39).

Further evidence for an H atom abstraction mechanism was obtained from a measurement of kinetic isotope effects (KIE) in the oxidation of DHA and xanthene. KIE values of 10–20 (average 17) were obtained in all of the reactions, consistent with CH bond cleavage being the rate-determining step (Table 1 and SI Table 3) (33–37). These large KIE values exceed the semiclassical limit (i.e., KIE < 7) and suggest a tunneling behavior in the reaction mechanism or another phenomenon that creates these high values (see below). For comparison, even larger KIE values of 30–50 were reported in the oxidations of ethylbenzene and benzyl alcohol by [Fe^IV(O)(N4Py)]²⁺ [where N4Py is N,N-bis(2-pyridylmethyl)-N-bis(2-pyridyl)methylamine] (38, 39) and in the cleavage of the target CH bond of taurine by the Fe^IVO intermediate of taurine:α-ketoglutarate dioxygenase (40). The good correlation between reaction rates and BDE of substrates and large KIE values in the oxidation of alkylaromatics support the notion that the CH bond oxidation by 1-X occurs via an H atom abstraction mechanism.

The Reactivity of [Fe(IV)(O)(TMCS)]⁺ (1′-SR).

The reactivity trends noted above were further tested by extending the series in some experiments to include [Fe^IV(O)(TMCS)]⁺ (1′-SR) (where TMCS is 1-mercaptoethyl-4,8,11-trimethyl-1,4,8,11-tetraazacyclotetradecane) (see the structure in Fig. 1) (20), because 1′-SR has an axial thiolate, the most electron-donating ligand thus far shown to coordinate to an iron(IV)–oxo center. However, 1′-SR differs from the 1-X series in having its axial ligand introduced as a mercaptoethyl tail that replaces one of the TMC methyl groups. Furthermore, the generation of the iron(IV)–oxo complex requires different reaction conditions, mainly the use of CH₃OH as solvent and a requirement for lower temperature due to the greater instability of 1′-SR (20). To be able to compare the reactivity of 1′-SR with the 1-X series, 1′-SR was first generated in CH₃OH solvent as previously described (20), and the resulting solution was then diluted by an equal volume of CH₃CN before the addition of substrates. Reaction of 1′-SR with PPh₃ afforded a k₂ of 0.016 M⁻¹·s⁻¹, a value that is clearly the smallest of any found in the 1-X series (Table 1 and Fig. 2a). In contrast, the reactions of 1′-SR with 2,4-t-Bu₂C₆H₃OH and DHA afforded k₂ values of 12 and 7.5 M⁻¹·s⁻¹, respectively, values that are larger than any found in the 1-X series (Table 1 and Fig. 2c). As a control, DHA oxidations were carried out for 1-NCCH₃ and 1-N₃ in 1:1 CH₃OH/CH₃CN, and the second-order rate constants obtained did not differ significantly from those obtained in pure CH₃CN solvent (Table 1). These results corroborate the electrophilicity trend for phosphine oxidation observed in the 1-X series and the opposite trend for H atom abstraction.

Electrochemical Measurements.

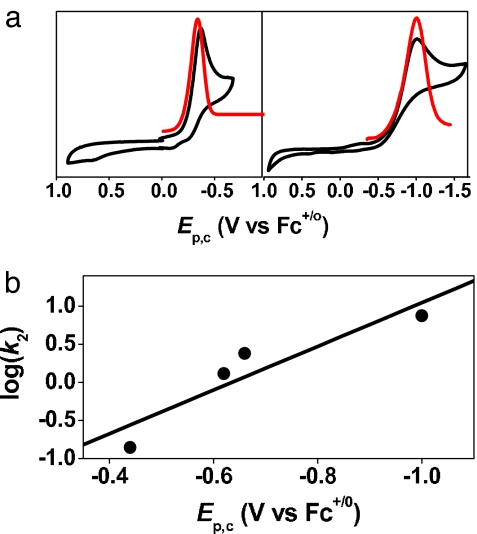
The electrochemistry of the 1-X series was investigated as a means to gain insight into the observed reactivity and provide a more quantitative basis for the effect of the anionic ligands on the iron(IV)–oxo center. Cyclic and differential pulse voltammetry of 1-NCCH₃ revealed only one feature, a reductive wave with E_p,c at −0.32 V vs. ferrocene (Fc)^+/o (Fig. 4a Left). This wave shifted cathodically upon replacement of CH₃CN with anionic ligands to −0.50 V for 1-OOCCF₃ and −0.60 V for 1-N₃ in CH₃CN at 25°C and to −1.00 V for 1′-SR in 1:1 CH₃OH/CH₃CN at −30°C (Table 1, Fig. 4a Right, and SI Fig. 12). The negative shifts observed are consistent with the introduction of anionic ligands trans to the oxo group, which are more basic than CH₃CN and would thus be expected to decrease the redox potential of the iron(IV)–oxo center. Very interestingly, there is a linear correlation between the E_p,c values of the 1-X series and the reaction rates of phenol and DHA oxidation by the intermediates [Fig. 4b for the reaction of DHA and SI Fig. 13 for the reactions of 1,4-cyclohexadiene (CHD), xanthene, and 2,4-t-Bu₂C₆H₃OH]. Strikingly, the complex having the most negative potential exhibits the fastest rates of oxidation within the series.

Fig. 4.

Electrochemical comparisons. (a) Cyclic and differential pulse voltamograms of [Fe^IV(O)(TMC)(NCCH₃)]²⁺ (1-NCCH₃) in CH₃CN at 25°C (Left) and [Fe^IV(O)(TMCS)]⁺ (1′-SR) in 1:1 CH₃OH/CH₃CN at −30°C (Right). (b) Plot of log k₂ determined in the oxidation of DHA at 0°C against E_p,c values of [Fe^IV(O)(TMC)(X)]ⁿ⁺ complexes and [Fe^IV(O)(TMCS)]⁺ in 1:1 CH₃CN/CH₃OH measured at −30°C.

The observed E_p,c values for the 1-X series, however, are surprisingly quite negative for oxidants that can carry out the reactions described in the previous sections. However, the electrochemical behavior of nonheme iron(IV)–oxo complexes exhibits some complexity that is not straightforward to interpret. For example, a reduction wave with an E_p,c value of −0.44 V vs. Fc^+/o has been observed in the cyclic voltammetry of the closely related [Fe^IV(O)(N4Py)]²⁺ complex (41), which has been shown to be reactive enough to oxidize cyclohexane at room temperature (38). However, subsequent spectropotentiometric experiments established its actual redox potential to be significantly more positive, 0.9 V vs. Fc^+/o (42). This unusual electrochemical behavior for the Fe^IV/III couple was in fact first noted by Wieghardt and coworkers (43) in their study of a series of [M^IIIFe^III(μ-O)(O₂CR)(L)₂] complexes (where M is Fe or Cr and L is a tridentate N3 ligand), and was attributed to “strongly kinetically inhibited heterogeneous electron transfer processes at the working electrode (glassy carbon).” Establishing whether this explanation applies to the 1-X series will require an in-depth electrochemical investigation supported by spectroscopic experiments. For the purposes of this study, we focus on the observation that the redox potentials of the 1-X complexes decrease in an order that follows the increase in the basicity of the X ligand. Despite the more negative potentials, the iron(IV)–oxo complexes with more electron donating axial ligands are more reactive in the activation of CH and OH bonds. This reactivity trend is opposite to that observed for PPh₃ oxidation by the 1-X series and requires a compelling rationale, which is provided by DFT calculations discussed in the next section.

DFT Calculations.

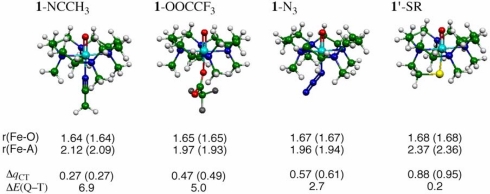
To understand the effect of the axial ligands on the properties of the [Fe^IV(O)(TMC)(X)]ⁿ⁺ complexes, we carried out DFT calculations using the hybrid functional, B3LYP, and the double-zeta basis set, LACVP (44) (see SI Materials and Methods for details). The so computed geometric features of these complexes are shown in Fig. 5, along with the amount of charge transferred (Δq_CT) from the axial ligand X to the [Fe^IV(O)(TMC)]²⁺ moiety. Inspection of the Δq_CT values shows that the DFT calculations support the axial ligand effect as reflected by the experimental E_p,c values. Thus, the DFT results demonstrate that the poorest electron donor among the axial ligands is CH₃CN and the strongest is RS⁻ followed by N₃⁻. As such, the organizing quantity of the CH and OH oxidation reactivities appears to be the electron-releasing property of X, as quantified by Δq_CT in Fig. 5 and the experimental E_p,c quantity in Table 1.

Fig. 5.

Key geometric features of 1-NCCH₃, 1-OOCCF₃, 1-N₃, and 1′-SR optimized at the B3LYP/LACVP level (bond lengths in angstroms) in the triplet (quintet) states, along with the amounts of charge shifted from ligand to the (TMC)FeO moiety (Δq_CT) and the quintet–triplet energy gap (ΔE_Q-T, in kcal/mol).

Recent discussions on the reactions of metal-oxo species with CH bonds, particularly the seminal work of Mayer (30, 31), have focused on the notion that the key determinant of the hydrogen atom abstraction rate is the hydrogen affinity of a metal–oxo reagent. This property is equivalent to the BDE of the OH bond that is formed, which is a function of both the redox potential of the MO oxidant and the pK_a of the nascent OH bond based on a thermochemical cycle developed by Bordwell et al. (45) and others (46–48). Thus, a less favorable redox potential can be energetically compensated for by a higher pK_a. To address this question directly, we have calculated the BDE (OH) values for all of the [Fe^III(OH)(TMC)(X)]ⁿ⁺ complexes and find that BDE(OH) is essentially independent of the ligand X at 84 ± 1 kcal/mol (see SI Table 4). Therefore, the counterintuitive reactivity trend in H atom abstraction from DHA and CHD does not originate in bond strength effects in the series, and the explanation must be found elsewhere.

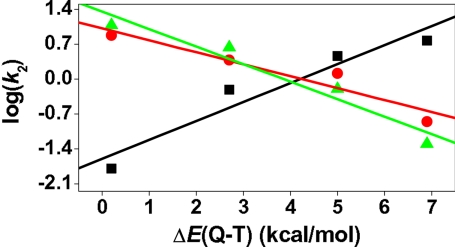
Note that all of the [Fe^IV(O)(TMC)(X)]ⁿ⁺ complexes (Fig. 5) possess two adjacently lying states: a ground state with a triplet spin quantum number (T) and a low-lying state with a quintet (Q) spin state (44). The two states are very close in energy for all of the complexes, lying within <7 kcal/mol; as X becomes a better electron donor, the ΔE_Q-T gap decreases (Fig. 5) and the quintet state becomes more accessible along the reaction trajectory. As explained previously (44), this trend is rooted in the greater destabilizing effect on the localized δ orbital compared with the delocalized σ∗_xy orbital as the donor ability of X increases from the neutral to the anionic ligands. Indeed, this tuning of reactivity by the ΔE_Q-T parameter is apparent from Fig. 6, which plots the log k₂ values for the oxidations of PPh₃, DHA, and 2,4-t-Bu₂C₆H₃OH against this quantity. Thus, it is seen that PPh₃ oxidation exhibits a reactivity pattern opposite of those of DHA and phenol oxidation. In the P-oxidation series, the reactivity follows the electrophilicity of the reagents; the rate constant is small when X is a good electron donor (e.g., where X is RS⁻) and large when X is a poor electron donor (e.g., where X is CH₃CN). In sharp contrast, the CH and OH activation rate constants increase as ΔE_Q-T decreases, indicating that the greater accessibility of the quintet state enhances the CH and OH activation rates. Indeed, as shown and rationalized in a previous theoretical study (44), the quintet transition state lies below the triplet one and has much smaller barriers for CH bond activation (SI Figs. 14 and 15). Therefore, the participation of the quintet species in the overall reaction is expected to increase progressively as X becomes a better electron donor, and the net barrier for CH activation will now decrease with the increased accessibility of the quintet state.

Fig. 6.

Plots of log k₂ values for the reactions of 1-X and 1′-SR with DHA (red open circles), 2,4-t-Bu₂C₆H₃OH (green filled triangles), and PPh₃ (black filled squares) against the computed quintet-triplet energy gaps (ΔE_Q-T) for 1-X and 1′-SR.

A simple way to understand the effect is to write the free-energy barrier of the combined triplet-quintet reaction (44) as a weighted blend of the individual barriers (Eq. 1),

where w_Q is the weight of the quintet reaction in the total reaction and this weight should increase as the quintet-triplet energy gap decreases. The lowering of the barrier due to the participation of the quintet reaction is given by Eq. 2.

It is seen that the blended barrier, ΔG^≠, decreases (compared with the large triplet barrier) in proportion to w_Q, which depends on the accessibility of the quintet state. It follows therefore that, as the ligand changes from when X is CH₃CN to when X is RS⁻, the quintet reaction will become more important (higher w_Q) and the blended barrier will be increasingly reduced compared with the triplet barrier. In this manner, the participation of the quintet state in the CH activation can in principle reverse the reactivity order of 1-X to become an antielectrophilic trend as observed in this study. In a case where the blending coefficient w_Q is 1, the relative reactivity will obey the electrophilicity of 1-X, because the barriers on the quintet surface should behave normally and follow electrophilicity. This appears to be the case for oxo-transfer to triphenylphosphine, where the reaction crosses over and proceeds mostly via the transition state of the quintet surface. An alternative two-state reactivity (TSR) scenario is one in which the reaction proceeds by crossover from the triplet ground state to the quintet state where the bond activation takes place. In such a scenario, with a slow spin crossover, the rate of the reaction will be given by the rate constant for the quintet reaction times the spin-inversion probability (τ_TQ) from the triplet to the quintet, namely,

Here k_Q is the rate constant according to transition state theory, and it increases with the increase of the electrophilicity of 1-X. In contrast, τ_TQ depends on the Q–T energy gap and increases as this gap decreases; namely, it is the largest for the worst electrophilie in the series 1′-SR, and smallest for the best one, 1-CH₃CN. The combination of the two factors can lead to the observed reversal of reactivity and generation of a counterintuitive trend in H atom abstraction.

Clearly, therefore, although the correlations found here are fundamentally important in the connection that they make with the ligand control of reactivity in heme enzymes, theory and spectroscopy suggest that the reactivity scenario might be more complex and more intriguing because of the availability of two closely lying spin states for all of the 1-X reagents (44). The two-state picture does not affect the correlations found here (49) but may provide rationale for other observations, such as the observed KIEs and the stereoselectivity of the reactions with substrates containing stereochemical probes.

Summary

We have demonstrated that the behavior of [Fe^IV(O)(TMC)(X)]ⁿ⁺ and [Fe^IV(O)(TMCS)]⁺ complexes in both oxo-transfer and H atom abstraction reactions depends systematically on the electron-donating ability of the axial ligands, as measured by the electrochemical properties of the complexes. Interestingly, whereas oxo-transfer reactivity follows a trend expected of the electrophilicity of the oxidant, H atom abstraction reactivity follows the opposite trend, which is counterintuitive. DFT calculations provide a plausible framework within which to rationalize these reactivity patterns. It is postulated that the observed reactivity reflects the availability of two closely lying spin states for all of the 1-X reagents, the so-called TSR hypothesis fully detailed in ref. 44, wherein the excited quintet state has a much lower reaction barrier than the ground triplet state. Thus, increasing the electron-donating character of the axial ligand results in a decrease in the triplet-quintet gap and an increased participation of the quintet state in determining the rate of reaction. With respect to the role of the thiolate ligand in cytochrome P450, our studies suggest that the thiolate ligand may serve not only to reduce the redox potential of the high-valent iron center to mitigate unwanted electron transfer events but also to maintain and perhaps even enhance the H atom abstraction ability of the iron–oxo unit for the catalysis of alkane hydroxylation.

Materials and Methods

Preparation and handling of air-sensitive materials were done under an inert atmosphere either on a Schlenk line or in a glove box with solvents dried according to published procedures (50). Iron(II) complexes [Fe^II(TMC)(X)]ⁿ⁺ (where X is NCCH₃, CF₃COO⁻, or N₃⁻) were prepared by adding 1.2 eq of appropriate tetraalkylammonium salts to Fe^II(TMC)(CF₃SO₃)₂ (17–19). Iron(IV)–oxo complexes [Fe(O)(TMC)(X)]ⁿ⁺ (1-X) were prepared by reacting [Fe^II(TMC)(X)]ⁿ⁺ (0.5 mM) with 1.2 eq of PhIO (0.6 mM) in CH₃CN at ambient temperature (17–19). The salt [Fe^II(TMCS)](PF₆) was prepared as previously described (20, 51). The corresponding iron(IV)–oxo complex [Fe^IV(O)(TMCS)]⁺ (1′-SR) was generated by treating a methanol solution of [Fe^II(TMCS)](PF₆) (1 mM) with 1.1 eq of m-chloroperbenzoic acid in the presence of 6 eq of potassium tert-butoxide (20). For reactivity studies of 1′-SR, 1 ml of 1′-SR (1 mM) was generated at 0°C and immediately diluted with chilled acetonitrile to bring the concentration of 1′-SR to 0.5 mM. An appropriate amount of substrate was then added to this solution, and the resulting reaction was monitored by a UV–visible spectrophotometer.

Kinetic studies were performed by adding appropriate amounts of substrates to the solutions of 1-X and 1′-SR, and spectral changes of the intermediates were directly monitored by a UV–visible spectrophotometer. Rate constants, k_obs, were determined by pseudo-first-order fitting of the decrease of absorption bands at 820 nm for 1-NCCH₃, 835 nm for 1-OOCCF₃, and 850 nm for 1-N₃ and 1′-SR. Product analysis for the oxidation of PPh₃ was performed by injecting reaction solutions directly into HPLC. Product analysis for the oxidation of 2,4-t-Bu₂C₆H₃OH and DHA by 1-X was performed by injecting reaction solutions directly into GC and GC–MS, by following procedures reported by Lansky and Goldberg (23).

All of the geometries were optimized with Jaguar 5.5 (52) at the UB3LYP/LACVP level (UB3LYP/B1) (53, 54).

Complete materials, instrumentation, and methods are provided in SI Materials and Methods, SI Figs. 8–15, and SI Tables 2–4.