Observational evidence for volcanic impact on sea level and the global water cycle

Abstract

It has previously been noted that there are drops in global sea level (GSL) after some major volcanic eruptions. However, observational evidence has not been convincing because there is substantial variability in the global sea level record over periods similar to those at which we expect volcanoes to have an impact. To quantify the impact of volcanic eruptions we average monthly GSL data from 830 tide gauge records around five major volcanic eruptions. Surprisingly, we find that the initial response to a volcanic eruption is a significant rise in sea level of 9 ± 3 mm in the first year after the eruption. This rise is followed by a drop of 7 ± 3 mm in the period 2–3 years after the eruption relative to preeruption sea level. These results are statistically robust and no particular volcanic eruption or ocean region dominates the signature we find. Neither the drop nor especially the rise in GSL can be explained by models of lower oceanic heat content. We suggest that the mechanism is a transient disturbance of the water cycle with a delayed response of land river runoff relative to ocean evaporation and global precipitation that affects global sea level. The volcanic impact on the water cycle and sea levels is comparable in magnitude to that of a large El Niño–La Niña cycle, amounting to ≈5% of global land precipitation.

Volcanic eruptions inject scattering aerosol into the stratosphere and thus impose a significant radiative cooling of the atmosphere (1). In the years after major eruptions it has been reported that there is a drop in global oceanic heat content (GOHC) (2, 3). A colder ocean is denser and an associated drop in global mean sea level of ≈5 mm during the 1–4 years after a major eruption has been modeled (2). However, observational evidence for the impact on global sea level (GSL) has so far not been convincing (4, 5) because there is substantial variability in the GSL record over periods similar to those at which we expect volcanoes to have an impact (6). Stenchikov et al. (7) found by modeling that large-scale atmospheric circulation patterns such as the Arctic Oscillation (AO) were affected by the Pinatubo eruption. We have previously shown a link between AO and European sea level (6), which is best explained by a redistribution of water driven by shifts in surface air pressure.

Producing a GSL curve with valid confidence intervals from the observational database is not a trivial job (see Methods). We reconstruct GSL over the past 150 years by using all available time series (830) of monthly mean relative sea level (RSL) from the Permanent Service for Mean Sea Level (PSMSL) database (ref. 8 and Fig. 1). Sea level records do not cover the same time period and there is therefore no common reference level (Fig. 2). The time-varying geographical distribution of tide gauge records along the coastline is more convoluted in some regions than others, which will cause time-varying geographical bias if care is not taken to avoid this (9). Because there is no common reference level for the tide gauge data (10), it makes sense to look at the rate of change in sea level rather than sea level itself. Our approach for creating a GSL curve is therefore to integrate the rate of change in GSL (dGSL), which we obtain by making a geographically weighted average (see Methods) of the sea level rates from individual tide gauge stations, using the “virtual station” method (9). We apply an inverse barometer correction to the individual RSL records, correct them for postglacial rebound, and use a statistical scheme to detect and remove data affected by earthquake-related vertical land movement (see Methods) before stacking.

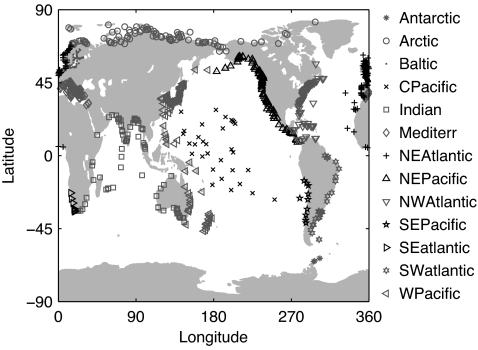
Fig. 1.

Location of tide gauges and their distribution into 13 regions. Symbols indicate the designated region.

Fig. 2.

Data coverage of the regional sea level rates calculated by using the virtual station method. Vertical lines indicate the volcanic eruption dates used in the study.

Only the largest volcanic eruptions produce a stratospheric aerosol loading large enough to alter global climate to a degree we can hope to detect in GSL. There were nine eruptions since 1890 that produced a stratospheric aerosol loading at least ≈10% as big as Pinatubo in 1991 (1) [see supporting information (SI)]. Only eruptions located in the tropics affect both hemispheres, and the five largest eruptions are all tropical, with only one of the nine located at high latitudes (1). The GSL curve shows considerable variability over periods comparable to the time scale at which we expect volcanoes to have an impact, and any significant change before and after a particular volcanic eruption could be argued to be caused by natural variability such as, e.g., El Niño. We therefore examine the average impact from the five eruptions with the largest stratospheric aerosol loading since 1890 (Colima, February 1890; Santa Maria, October 1902; Agung, March 1963; El Chichón, April 1982; Pinatubo, June 1991), which have been previously modeled to have an impact on GSL (2). To isolate the volcanic impact from the long-term climatic trend we detrend the GSL record by subtracting a low-pass-filtered version of the series. From the detrended GSL we calculate the average impact of the eruptions. Because the interannual variability in GSL is very large compared with the signals plausibly produced by volcanic eruptions, estimating the significance in a low signal-to-noise ratio environment is critical. Hence we develop robust bespoke bootstrap methods for dependent data (see Methods) for the significance and confidence intervals of the results, and we verify them with less conservative but more traditional statistical methods.

Results and Discussion

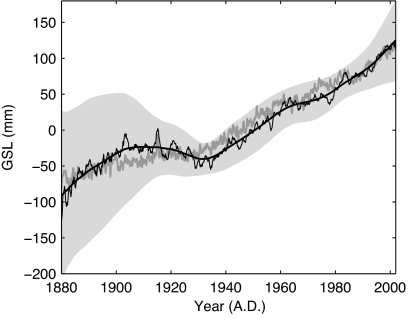
We first present the smoothed GSL curve from our virtual station sea level reconstruction method in comparison with the Church and White (5) GSL reconstruction in Fig. 3. The curves are generated by using two completely different methods; however, the reconstructions generally agree within confidence limits, but they diverge before ≈1930, where the trend variability in the Church and White reconstruction is insignificant (5). It is essentially the low-frequency trend in Fig. 3 that must be removed to isolate the year-to-year variability needed to show the volcanic influence on GSL.

Fig. 3.

GSL relative to the 20th-century mean. The reconstruction of this study (thin black line) and the reconstruction of Church and White (5) (gray line) are shown for comparison. The nonlinear trend (10-year lag) of the present GSL reconstruction and its 2σ confidence interval (a region-based jack-knife estimate) are shown as a thick black line and a gray shaded area.

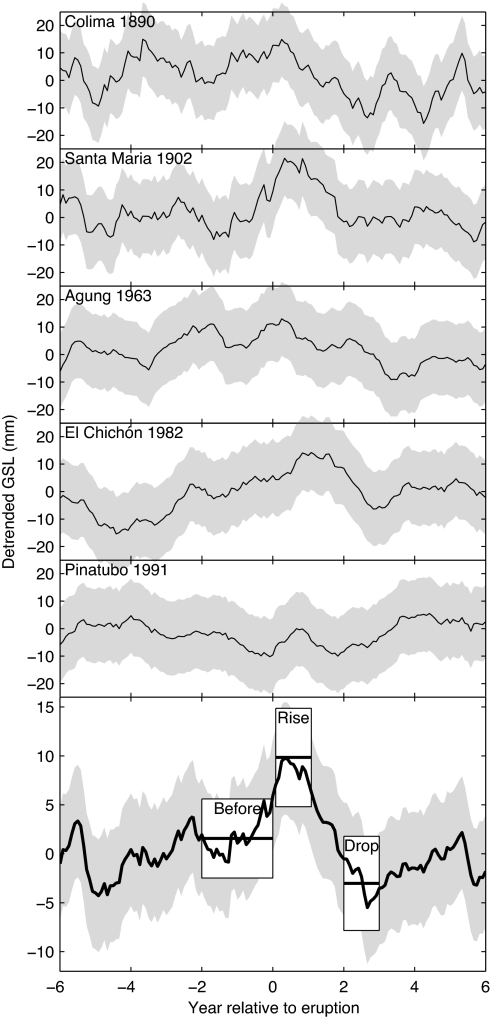
After removing the low-frequency trend, we compute the response of GSL to the five largest eruptions and also the average response (Fig. 4), an initial rise in GSL in the first year followed by a drop in the period 2–4 years after the eruption (Fig. 4). GSL reaches background levels ≈5 years after an eruption. As expected, the entire preeruption period is not significantly different from zero. The maximal rise of 9 ± 3 mm occurs 4 months after the eruption, which coincides with the timing of the maximal radiative forcing (1), and the maximal drop of 7 ± 3 mm occurs after 32 months. To asses the significance of the rise and drop, we compare the median GSL in windows representing preeruption GSL (0–2 years before eruption), the rise (the first year after eruption), and the drop (2–3 years after eruption). We label these three windows Before, Rise, and Drop (Fig. 4). We find that the median Before–Rise difference of 8 ± 3 mm is significant at the 99% confidence level, whereas the Before–Drop difference of 5 ± 3 mm is significant only at the 84% level. The Rise appears more significant than the Drop both because it is a larger absolute difference and also because it is less separated in time from the Before period and so the autocorrelation of errors makes the difference less likely to be caused by chance. The Rise to Drop median difference of 13 ± 3 mm is significant at the 99% level.

Fig. 4.

Sea level surrounding five major volcanic eruptions and the average sea level in these five periods. The solid black curves show nonlinearly detrended (10-year lag) (see ref. 12) GSL as observed in tide gauge records (gray shows 95% confidence interval). Boxes show the median sea level (center line of box) of the “Before,” “Rise,” and “Drop” windows. Top and bottom edges of the boxes show the 95% confidence interval of the median.

To gain confidence in the bootstrap estimates of the statistical significance of the results we also tested them against a traditional Student's t test. It is necessary to consider both natural nonvolcanic variability and geophysical noise as sources of error in the volcanic impact plot (Fig. 4). A simple method of determining the combined error magnitude is to simply look at the distribution of the monthly detrended GSL in the preeruption period because this should be zero except for the short periods influenced by eruptions. The empirical cumulative distribution function (CDF) of the preeruption period is shown in SI. The standard error in the mean curve is therefore $5.8/\sqrt{5}=2.6$ mm because there are 5 values in each mean. This indicates that the noise is within ±5 mm of zero 95% of the time. This can also be interpreted as the 95% confidence interval of the mean impact curve. Hence, Student's t test shows that the both the maximal rise (9 mm) and the maximal drop (7 mm) are significantly different from zero. The window median differences are also significant when traditional statistical methods are used (see SI).

The Santa Maria 1902 eruption is the largest contributor to the rise in sea level (Fig. 4). Because this period has relatively poor data coverage we may ask whether the hitherto unappreciated rise in sea level appears significant only because of large errors around this eruption. In the SI we calculate the average impact excluding the 1902 Santa Maria eruption (see SI). We find that both the maximal rise and the maximal drop are significantly different from zero. Further, the Before–Rise median difference is significant at the 86% level and the Before–Drop median difference is significant at the 96% level. Hence, we conclude that even when arbitrarily removing the eruption with the largest impact, we can still be reasonably confident that volcanic eruptions cause a rise in sea level. We also investigated the volcanic impact on regional sea level (see SI). Most regions naturally show the same pattern of behavior as the GSL (see SI). However, some regions (Antarctic, Mediterranean, SE Pacific, SW Atlantic, W Pacific) have a different pattern, e.g., the “Drop” is actually a rise or the “Rise” is actually a lower sea level. Several of these regions have rather poor data coverage (Fig. 2), whereas others such as the Mediterranean are relatively disconnected from the global ocean. Pacific variability is also strongly affected by El Niño–Southern Oscillation (ENSO)-induced sea level changes that can dominate the volcanic signal. The Rise and Drop features are robust and not dominated by any particular region or volcanic eruption.

Because ENSO has a large impact on sea level (6, 9), especially in the tropics (1), it is fortunate that these eruptions occurred in both El Niño and La Niña years, so that the volcanic signal is maximized at the expense of nonvolcanic variability. However, El Niño prevailed slightly more often than the expectation value. We may therefore ask whether the apparent average volcanic response in Fig. 4 is really caused by residual ENSO variability. We note that our bootstrap confidence intervals take this into account by design. In the SI we show that our conclusions are robust against removing ENSO variability from GSL before analysis, and also that using nine eruptions results in a GSL response similar to that with the five we discuss here.

In the SI we examine the average impact of the five volcanic eruptions on the detrended GSL reconstruction by Church and White (5), following the same procedure used for our virtual station reconstruction. The window location of the Drop window was chosen to match the modeled drop in GOHC seen after Pinatubo (2). We find that Before and Drop medians are significantly different only at the 65% confidence level. Moving the Drop window further away from the Before window does not improve the significance. We therefore conclude that the predicted drop in sea level does not appear significant for these five volcanoes when the Church and White (5) reconstruction is used. The possible reasons for this are discussed in the SI.

The timing of the largest drop in GSL ≈3 years after the eruption agrees with modeling and observations of GOHC (3, 11); however, its magnitude of ≈7 ± 3 mm is ≈40% larger than modeled (2). Furthermore, we unexpectedly find a significant rise of ≈9 ± 3 mm in GSL in the first year immediately after an eruption. These differences between modeled and observed volcanic impact on sea level suggests that, in addition to lowering the GOHC and thus reducing ocean volume, major volcanic eruptions also change ocean mass. Mass changes in the oceans may be mediated by variation in glacier mass balance, river discharge, and precipitation–evaporation (P-E) (12).

Volcanic eruptions reduce atmospheric water vapor (13). However, Pinatubo caused a decrease of only ≈0.5 mm (13) and the ≈9 ± 3 mm peak in GSL can therefore not be explained by drying of the atmosphere. There is both observational and modeling evidence for less precipitation over land after volcanic eruptions (1, 14, 15). This reduction in precipitation has previously been tied to reduced evaporation (1, 2). The reduced land precipitation after an eruption is accompanied by an observable reduction in continental discharge (15). We propose that the initial peak and the larger than expected drop in sea level may be explained by lower evaporation from the oceans and a delayed response of river discharge to the associated lower precipitation. Interannual changes in land precipitation entail changes in modeled terrestrial water storage equivalent to a few millimeters of GSL (16). The volcanic radiative forcing will have an immediate cooling effect at the ocean surface. Oceanic evaporation rate is strongly determined by ocean skin temperature (17), which can respond very fast to changes in incoming radiation and has a very short memory of past forcing because mixing quickly dilutes temperature anomalies. It is therefore expected that ocean evaporation tracks the radiative forcing rather than the integrated forcing. The observed peak in sea level occurs 4 months after the eruption, which agrees well with the timing of the maximal radiative forcing after a large eruption (3) and the timing of maximal reduction in global land precipitation after Pinatubo (16). In contrast, a steric drop in sea level would be caused by a reduced GOHC and would largely depend on the integrated radiative forcing and hence be delayed and of longer duration (18). The observation that GSL first rises and then drops thus agrees with our hypothesis. To summarize, initially there is lower ocean evaporation but river discharge does not respond immediately to the consequent lower precipitation and therefore sea level rises. After 1–2 years P-E returns to normal, but river discharge is now relatively low because of the reduced land precipitation in the preceding years. Additionally the global cooling caused by the eruption reduces runoff from ice masses, effectively lowering sea level. Whereas the volcanic impact on the water cycle is transient, the steric drop in GSL may persist for many years (2, 18). We note that the proposed mechanisms are consistent with the observation (see SI) that the initial rise in sea level is especially evident in regions where the steric change is relatively small, such as in the Baltic and Northeast Pacific (19, 20).

The magnitude of the impact on the water cycle may be seen by comparison with natural changes in global river discharge (21) where a 5% change corresponds to a change in GSL of 5.5 mm/year. The initial 9 ± 3 mm rise in sea level is equivalent to a 2.5% change in global lake and river reservoirs (22). This rise corresponds to an imbalance in ocean surface water fluxes of ≈0.02 mm/day for a year, which translates into a reduction in land P-E of ≈0.06 mm/day or ≈3% of mean land precipitation. This is in the range of modeled natural variability (23). The magnitude of this change is similar to the ≈4% variations in global land precipitation associated with El Niño–Southern Oscillation (24). The volcano-induced changes in water cycle may, depending on relative timing, act in the opposite sense to those that occur in a normal El Niño–La Niña cycle, thus supporting observations that the El Niño coincident with eruptions of El Chichón (1982/3) and Pinatubo (1991/2) were rather atypical in their oceanic precipitation/temperature behavior (1, 24).

Conclusion

Here we examine the average impact on observed GSL of the five volcanic eruptions with the largest stratospheric aerosol loading since 1890. Earlier modeling work found that GSL drops after major volcanic eruptions as the oceans cool because of the radiative forcing of the volcanic stratospheric aerosol. We find that GSL does indeed drop by 7 ± 3 mm in the period 2–3 years after the eruption relative to preeruption sea level. However, the initial response is a significant rise in sea level of 9 ± 3 mm in the first year after the eruption. We propose that this hitherto-unappreciated sea level rise is caused by an imbalance in ocean mass fluxes due to a transient disturbance of the global water cycle, where the radiative forcing initially reduces ocean evaporation. This interpretation is supported by observations of large reductions in both land precipitation and continental discharge after major volcanic eruptions (15) and modeled reductions in terrestrial storage caused by reductions in precipitation (16). The volcanic impact on the water cycle is comparable in magnitude to that of a large El Niño–La Niña cycle, amounting to ≈5% of global land precipitation. The respective roles that heat content, evaporation, and interoceanic redistribution of water play in the regional response of sea level need further study. The proposed mechanism for the initial rise in sea level can be tested by modeling the volcanic impact on ocean evaporation, ocean precipitation, and river discharge.

Methods

We use 830 time series of monthly mean relative sea level (RSL) from the Permanent Service for Mean Sea Level (PSMSL) database (8). Detailed descriptions of these time series are available from www.pol.ac.uk/psmsl. We applied an inverted barometer correction to the records by using sea level pressure from the HadSLP2 dataset (25), taking care to adjust the atmospheric pressure so that the over-ocean pressure integral is constant. RSL data sets were further corrected for local datum changes and glacial isostatic adjustment (GIA) of the solid Earth (26). However, because we are interested in the transient response of GSL to volcanic eruptions we will be detrending GSL before analysis and therefore the choice of GIA corrections is not critical to this study.

The average detrended GSL is shown in Fig. 4 and its qualitative shape (the initial peak followed by a drop) is robust to excluding any particular volcano from the analysis. In the SI we show that results are robust against removing ENSO variability from GSL before analysis, and that there is no detectable link between GSL and the decadal solar cycle. Further, an alternative method of calculating average impact from nine volcanic eruptions may be seen in the SI.

We isolate the transient response from long-term climatic changes in GSL by subtracting the nonlinear trend obtained from singular spectrum analysis (with 10-year lag) by using the minimum roughness criterion at the data boundaries (27, 28). This procedure effectively applies a data-adaptive high-pass filter to the GSL curve that corresponds very closely to a 239-month-wide Bartlett window (29). We note that the average curve in Fig. 4 is qualitatively unchanged when even the simplest trend removal procedure possible is used. That is, removing a constant 3.2 mm/year, ensuring that the 6-year preeruption slope is zero.

There is usually a strong seasonal component of a given tide gauge record, especially in extratropical regions, and many stations have been routinely measured only during some parts of the year (mostly during summer months). First differences may therefore be severely biased, e.g., if only the rising part of the cycle is covered. To circumvent seasonal bias while maximizing data usage, we calculate the mean annual rate for a given month over a whole year (e.g., the rate in January is calculated as the July to July difference). The resulting GSL reconstruction will therefore represent 12-month averages. Using this approach, we calculate the sea level rate for all stations in the PSMSL database. Data gaps shorter than 1 year in the final rate series are filled by linear interpolation.

Earthquake-related vertical land movement can cause sudden shifts in a tide gauge record. Earthquakes will not directly influence GSL. For example, tsunamis are only a short-lived redistribution of sea level; as such, they do not affect the global average. The sudden vertical land movement, however, will appear in the tide gauge records as a step change in sea level. The sea level rate will hence be anomalously large/small at the time of the earthquake. We detect and remove such outliers before stacking by using the following scheme. For each tide gauge we first find the trimmed mean (m_trim) and the trimmed standard deviation (σ_trim) of the local sea level rates between the 10th and the 90th percentiles. We then discard all sea level rates that are within 6 months from a value that is more than 5σ_trim away from m_trim. Additionally we discard all stations that after this treatment have a rate distribution with skewness >0.8. Statistics for these preprocessing steps can be found in the SI and the resulting data coverage for each region can be seen in Fig. 2.

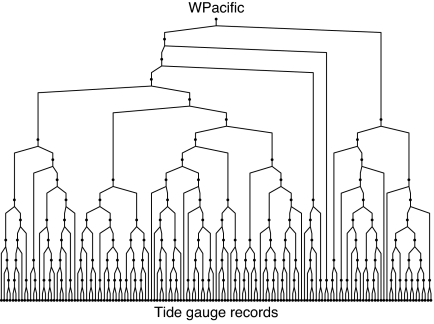
While we have corrected the tide gauge records for pressure and therefore they should not be very sensitive to shifts in atmospheric pressure patterns, it is still necessary to minimize geographical bias. We have developed a “virtual station” method for this purpose that can quantify the uncertainties because of representativeness of the stations used (9). We first assign each station to 1 of 13 regions (Fig. 1). We then recursively collapse the two closest stations within a region (by averaging their records) into a new virtual station half-way between them until only one station remains. This last remaining virtual station represents the average for the entire region. The method is illustrated in Fig. 5. This ensures that isolated tide gauge records are given more weight. Whenever a virtual station is created the uncertainty due to representativity can be calculated by looking at the deviation from the mean of the source stations over the period of common overlap. This uncertainty can be combined with the underlying uncertainty of the two source records (9). We calculate GSL by integrating the rate of change in GSL (dGSL), with the dGSL curve as the arithmetic average of the sea level rates for the following regions: Northeast Pacific, Southeast Pacific, West Pacific, Central Pacific, Indian, Arctic, Antarctic, Mediterranean, Northeast Atlantic, Northwest Atlantic, Southeast Atlantic, and Southwest Atlantic. A comparison of the resulting GSL reconstruction with other reconstructions (4, 5, 9) can be found in the SI.

Fig. 5.

Binomial tree illustrating the virtual station stacking method. The top node represents the regional average, the bottom nodes represent the tide gauge records, and the remaining nodes are virtual stations.

The detrended GSL curve is far from spectrally white, and conventional tests overestimate the significance of the features in Fig. 4 because there are far fewer degrees of freedom than data points. For that reason, we test the significance and evaluate confidence intervals of the main features in Fig. 4 by using much more conservative bootstrap methods. A robust estimate of the 95% confidence interval of the mean impact (Fig. 4) can be obtained from the distribution of 10,000 means of five random values selected from the detrended GSL series. The five random values will predominantly be picked from periods with little or no volcanic influence and the distribution of the means is used to estimate the magnitude of nonvolcanic variability. This reveals a 95% confidence interval of ±5.7 mm, which is shown as a gray band in Fig. 4. Similarly, we estimate the confidence interval of the median sea level in a window (center line of boxes in Fig. 4) by using a conservative bootstrap technique for dependent data. That is, we estimate the range of natural variability of a window median by calculating 10,000 such window medians. Each median in this ensemble is calculated over the all of the samples from five random continuous sections from the detrended GSL of the same length as the window in question. From the ensemble distribution of the window medians we find the 95% confidence interval (boxes in Fig. 4).

We expect a drop in sea level because of the expected volcanic reduction in GOHC. The Singular Spectrum Analysis (SSA) nonlinear trend would tend to smoothly follow this drop and as a result we may observe a slight artificial rise in detrended GSL in the periods immediately next to Drop. It is therefore not sufficient to check whether the Rise and the Drop are significantly different from zero, as the Rise would appear more significant in the presence of a Drop and vice versa. However, the artifact will affect all windows almost equally due to the relatively long length of the detrending filter compared with the window separation. Hence, we can deal with this problem by testing whether the difference between two window medians of a given width and separation are significantly different from zero. This testing is accomplished by using a bootstrap procedure analogous to that of the previous tests. The ensemble of window median differences is based on windows with the same length and separation as the difference in question. Each window median difference in the ensemble is based on the values in five continuous sections randomly picked from the detrended GSL series. In the SI we validate the above bootstrap statistical inferential scheme and find that the bootstrap error estimates have <10% error and that they have a tendency to be conservatively biased. A comparison of the bootstrap and traditional confidence interval estimates can also be found in the SI.