Localizing frustration in native proteins and protein assemblies

Abstract

We propose a method of quantifying the degree of frustration manifested by spatially local interactions in protein biomolecules. This method of localization smoothly generalizes the global criterion for an energy landscape to be funneled to the native state, which is in keeping with the principle of minimal frustration. A survey of the structural database shows that natural proteins are multiply connected by a web of local interactions that are individually minimally frustrated. In contrast, highly frustrated interactions are found clustered on the surface, often near binding sites. These binding sites become less frustrated upon complex formation.

The complexity of protein sequences suggests they may contain conflicting signals encoding separately folding and function. Yet searching the immense energy landscape of a protein for the native structure would be slow if the landscape were very rugged due to many conflicting local interactions (1, 2). Experimental folding kinetics suggests that proteins indeed do not possess the many traps that such conflicts would cause but instead are “minimally frustrated” (1). The notion of minimal frustration has been made quantitatively precise by using the statistical mechanics of spin glasses (3). A global criterion for the landscape to be funneled to the native state emerges from this theory, which hinges on a ratio of the energy difference between the native structure from alternatives to the magnitude of the fluctuations of the decoy energies (3). This global Z-score criterion provides a practical, quantitative route to decoding effective energy functions for predicting protein structure from sequence (3, 4), predicting folding intermediates (5, 6), and designing de novo foldable proteins (7, 8).

Minimal frustration implies protein structure also is robust to mutation. However, neither the proteins' kinetic foldability nor their mutational robustness deny the possibility that some frustration from conflicting signals may be present locally in some proteins. Such local frustration, being tolerable, might naturally arise from random neutral evolution. Local frustration also could be a functionally useful adaptation. The possible adaptive value for a molecule to have spatially localized frustration arises from the way such frustration may sculpt protein dynamics for specific functions. In a monomeric protein the alternate configurations caused by locally frustrating an otherwise largely unfrustrated structure could provide specific control of the thermal motions, so the protein can function much like a macroscopic machine having only a few moving parts. Alternatively, a site frustrated in a monomeric protein may become less frustrated in the final larger assembly containing that protein, thus guiding specific association (9, 10). Thermodynamic folding studies of enzymes also show that catalytic sites exhibit signs of frustration (31, 32). These arguments suggest that quantitative methods for localizing frustration in proteins can give insights into the functional constraints on the evolution of protein energy landscapes. Protein engineering studies of folding kinetics provide such a way of localizing where frustration occurs through ϕ value analysis (11, 12). Negative ϕ values or ϕ values exceeding 1 identify frustrated sites. It appears that frustrated sites identified by anomalous kinetics are indeed often implicated in function (11, 33). In the absence of such experiments, finding sites of frustration requires the availability of a sufficiently reliable energy function, because significant error in the energy function could lead to the appearance of spurious frustration even where true frustration is absent. Beyond requiring an accurate energy function, spatially localizing frustration also requires a mathematical scheme to generalize the global aspects of energy landscape theory so as to apply to only local parts of the protein. Because folding is a collective process, ultimately locking most of the molecule together, the manner we choose of breaking the energy into parts may not be operationally unique. Nevertheless, in this paper we will provide a heuristic but quantitative approach to localizing frustration in folded protein structures that seems both to be reasonable and to provide useful structural insights.

We develop a spatially local version of the global gap criterion formulation of the minimal frustration principle. To be precise, we compare the contribution to the extra stabilization energy ascribed to a given pair of amino acids in the native protein to the statistics of the energies that would be found by placing different residues in the same native location or by creating a different environment for the pair. If there is a sufficient additional stabilization for an individual native pair as normalized by the typical energy fluctuation (in accord with the global Z-score criterion for minimal frustration) the local interaction can be called minimally frustrated. The precise magnitude of the threshold to be designated minimally frustrated depends on the configurational entropy that must be overcome when the protein folds. If the stabilization of the native pair lies in the middle of the distribution of alternatives, the interaction can be considered “neutral.” On the other hand, if the native pair is sufficiently destabilizing compared with the other possibilities we will call the pair interaction “frustrated.” Such a high level of local frustration may be the result of an evolutionary constraint that conflicts with robust folding. Because of the nonlinearity of entropy loss on assembly, not all of the individual pair interactions in a protein need to be minimally frustrated for the landscape as a whole to be funneled. Indeed, we find that this localized version of the landscape folding criterion, when combined with a reasonably accurate water-mediated potential inferred for structure prediction by a energy landscape optimization strategy (10), suggests that 40% of interactions individually can be considered minimally frustrated, 45% are neutral, and only a small fraction can be called highly frustrated.

We find frustrated interactions form clusters that mainly reside on the protein surface. These frustrated clusters turn out to be near binding sites in proteins known to form complexes, although some may have other adaptive value, such as facilitating allostery. Hydrophobically and electrostatically destabilized patches have been previously proposed to be functionally relevant to binding (13–15).

Results and Discussion

Definition of Local Frustration.

To locate frustrated interactions, we systematically perturb the protein sequence, evaluating the resulting total energy change according to the Associative Memory Hamiltonian water-mediated potential (AMW) energy function (10). The amino acids forming a particular contact are changed to other amino acids generating a set of decoys for which the total energy of the protein is recomputed. Sequence space is randomly sampled according to the native amino acid frequency distribution of the particular protein under consideration, giving 1,000 appropriately distributed decoys for each contact. We construct a histogram of the energy of the decoys and compare the distribution to the native energy, E⁰. The “frustration index” for the contact between the amino acids i, j is defined as a Z score of the energy of the native pair compared with the N decoys:

where E_i′j′^U is the energy of the decoy. The frustration index measures how favorable a particular native contact is relative to the set of all possible contacts in that location and is normalized by using the variance of that distribution. We may classify the individual contacts with regard to their frustration level. For a protein to be minimally frustrated, the global energy landscape theory indicates that its folding temperature (T_f) must exceed its glass transition temperature (T_g). The energy gap of the protein and variance in energy of decoy are related to T_f and T_g through the configurational entropy (16):

Here E⁰ is the native energy, E^U is the unfolded state energy, S_c is the configurational entropy loss upon folding from a compact molten globule, where 〈δE〉² = 1/NΣ_k=1^N (E_ij⁰ − 〈E_i′j′^U〉)². For the global energy landscape of a protein to be funneled, the global Z score must exceed a value that depends on the entropy loss because T_f must exceed T_g:

The entropy change for forming a single pairwise contact depends on the sequence separation between the residues (loop entropy) and on the degree of consolidation of neighboring interactions, giving rise to cooperative folding. Ignoring these complexities, we crudely estimate the configurational entropy change S_i,j as the sum of the entropic cost for fixing individual residues. Using a theory of helix–coil transition in molten globules, Luthey–Schulten et al. (17) estimated this entropy to be ≈0.6k_b per residue. This estimate has been used in many quantitative descriptions of folding funnel topography (18). To be minimally frustrated and fold at T_f, a given contact cannot be too unstable:

For the entire protein to be minimally frustrated, one must have T_f/T_g > 1. By using this minimal value and the entropy estimate above for the single pair, a contact will now be defined as minimally frustrated if its native energy is at the higher end of the distribution of decoy energies, having a frustration index as measured with a Z score of 0.78 or higher magnitude; that is, the majority (but by no means all) of other amino acid pairs in that position would be unfavorable. The fact that many variants of that pair also would lead to minimally frustrated interactions is consistent with the known sequence degeneracy of proteins (7). Conversely, a contact will be defined as highly frustrated if E⁰ is at the other end of the distribution with a local frustration index lower than −1; that is, unlike for a minimally frustrated pair, most other amino acid pairs at that location would be more favorable for folding than the native ones by more than one standard deviation of that distribution. If the native energy is in between these limits, we will equivocate and define the contact as neutral. Of course, the precise values of these local Z score boundaries should depend on other factors, such as protein size, contact order, or the actual T_f/T_g ratio for the native protein, factors that will vary among individual proteins. The T_f/T_g ratio for helical proteins has been estimated as 1.6 but may be larger (19). We have found that the suggested limits are generous enough to make the frustration index robust between samples and gives reasonable local frustration distributions. Indeed, we have made parallel studies requiring the T_f/T_g ratio to be the estimated typical 1.6 value and find that this change gives only mildly different results from those we discuss below.

In its early incarnation in the theory of magnetic spin glasses, frustration was easy to define locally because of the binary nature of Ising spins (20). In the existing quantitative theory of protein folding, where configurations are not digital but analog, the precise notion of minimal frustration is strictly applicable only to an entire folding domain. A localized frustration index may depend on the choice of parts in which the whole energy is divided. It therefore becomes natural for us to divide the energy up in a way that is at least roughly comparable with what natural selection can do: We computationally examine the changes in energy upon making mutations. We propose two related but complementary ways for localizing frustration. These methods differ in how the set of decoys is constructed. In one choice, the decoy set is made randomizing the identities of the interacting amino acids i, j, keeping all other interaction parameters at their native value. This scheme effectively evaluates every possible mutation of the amino acid pair that forms a particular contact in a robustly fixed structure. We call the resulting index the “mutational frustration.” It is worth noting that the energy change upon pair mutation not only comes directly from the particular contact probed but also changes through interactions of each residue with other residues not in the pair, and those contributions also will vary upon mutation. One advantage of the mutational frustration index is that, in principle, this local measure of frustration also can be experimentally probed by (unfortunately tedious) combinatorial protein engineering. A second way of measuring frustration more suitable to the ideas of polymer physics theory imagines that the residues are not only changed but are also displaced in location. The energy variance thus reflects contributions to different energies of the molten globule conformations. For this index, suitable for examining alternative structures, the decoy set involves randomizing not just the identities but also the distance and densities of the interacting amino acids i, j. This scheme effectively evaluates the native pair with respect to a set of structural decoys that might be encountered in the folding process. We call the frustration index computed in this way the “configurational frustration.”

A similar analysis can be carried out by mutating single residues. This separate frustration index is useful when there are nonadditive forces in the model. In this case, the set of decoys is constructed by shuffling the identities only of the single amino acid i, keeping all other parameters and neighboring residues in the native state, and evaluating the total energy change upon mutation. We call the resulting local ratio the “single-residue-level frustration index.”

Distribution of the Frustration Index in Natural Proteins.

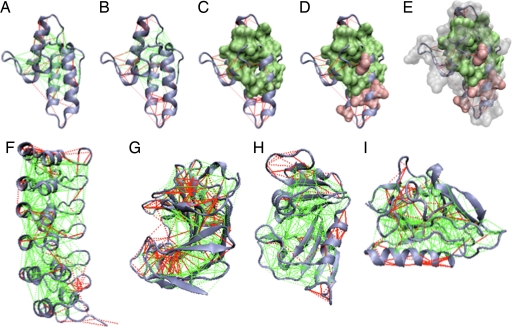
To study the distribution of the frustrated regions in natural proteins, we analyzed an extensive nonredundant set of 314 monomeric protein domains having high-resolution structures (21). For each protein, the frustration pattern can be visualized on the structure as shown in Fig. 1. For clarity, in the three-dimensional structure, only the minimally frustrated (green lines) and highly frustrated (red lines) interactions are depicted. The remainder are neutral. In general, it becomes apparent that individual domains are highly connected by minimally frustrated interactions. The small minority of highly frustrated contacts is preferentially located at the protein surface. Examining several proteins with known functional sites, we observed that the highly frustrated regions often correspond to regions that bind other macromolecules or small ligands. This anecdotal survey also suggests some frustrated regions colocate with regions that are known to undergo structural changes. In some other cases, the frustrated interactions look scattered on the surface or were hardly present at all. Clearly, local frustration is not randomly nor uniformly distributed in the protein structure space. Some structures or functions may lead to a greater propensity of a region to be frustrated. To quantify the spatial distribution of the frustration indices in a statistically meaningful way, we analyze the distribution of local frustration indices over an extensive nonredundant monomeric protein database.

Fig. 1.

Examples of the localized frustration and minimally frustrated networks in protein structures. The protein backbone, direct interresidue interactions, and water-mediated interactions are displayed as blue ribbons, solid lines, and dashed lines, respectively. Minimally frustrated interactions and highly frustrated ones are shown in green and red, respectively; neutral contacts are not drawn. The surfaces indicate the single-residue-level frustration index, using a corresponding coloring scheme. (A) Im7 protein [Protein Data Bank (PDB) ID code 7CEI] mutational frustration index. (B) Configurational frustration index. (C–E) Single-residue frustration index surfaces overlaid. (F–I) Configurational frustration index of IκBα (PDB ID code 1NFI) (F), Streptomyces Endoglucanase (PDB ID code 1OA4) (G), dihydrofolate reductase (PDB ID code 1RX2) (H), and Endostatin (PDB ID code 1KOE) (I).

Frustration Index Distribution in Contact Types.

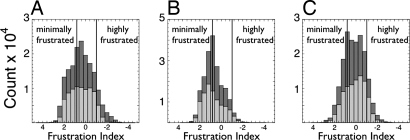
Fig. 2 shows the distribution of the frustration index for contact pairs in the three separate categories. These data are also summarized in supporting information (SI) Table 1. According to the mutational frustration index, 48% of the direct contacts turn out to be minimally frustrated, 46% are neutral, and 6% lie in the highly frustrated region. The water-mediated interactions are divided thusly: 26% minimally frustrated, 61% neutral, and 13% highly frustrated. Taking into account that the direct contacts are more abundant than the water-mediated ones, a typical natural globular domain has ≈40% of contacts that can individually be considered minimally frustrated, 50% that are neutral, and only 10% of the contacts that can be considered highly frustrated. The configurational frustration index has a narrower distribution for direct interactions, leading to an increase in the fraction of neutral contacts. For the configurational frustration index, 35% of the contacts are found to be strictly minimally frustrated, 55% are neutral, and only 10% are highly frustrated. The single-residue level frustration distribution suggests there are ≈40% minimally frustrated residues and >10% in the highly frustrated region. These overall distributions are independent of the protein size (see SI Fig. 6).

Fig. 2.

Histograms showing the distribution of the mutational frustration index (light gray) and the configurational frustration index (dark gray) in the three different contact classes considered. These frustration indices were computed for every native contact present in a database of 314 monomeric protein domains. (A) Short-range contacts. (B) Long-range contacts. (C) Water-mediated contacts. The vertical lines indicate the energy landscape theory-based cutoff used to define minimally frustrated interactions as well as the cutoff for neutral or highly frustrated interactions.

Are there chemical or structural patterns of the localized frustration? Minimally frustrated residues do tend to have lower solvent accessibility than do the highly frustrated or the neutral ones (SI Fig 6A), but there is little bias in the computed frustration index for residues in different secondary structure elements. There is a rather slight increase in the propensity of minimally frustrated residues to be found in α-helices and β-sheets, as compared with being in coils, turns, or bends, consistent with their greater structural conservation (SI Fig. 7B). Large aliphatic and aromatic residues are most likely to be minimally frustrated, whereas acidic and charged residues are more likely to be highly frustrated in protein structures (SI Fig 7C). Some amino acids, like Thr, Ser, or Gly are almost always neutral. These patterns can be related to the three-dimensional location of the minimally frustrated interactions at the “hydrophobic core,” as opposed to the more frustrated ones preferentially located at the surface.

Spatial Distribution of the Frustration Index.

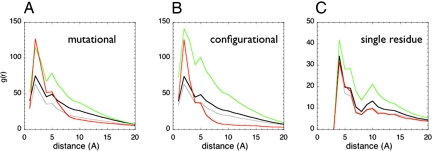
Minimally frustrated contacts are typically closer to the center of mass of a globular domain than the neutral ones are, whereas the frustrated contacts are preferentially clustered near the surface (Fig. 1). To quantify the degree of clustering we computed pair distribution functions between all of the contacts over the whole set (Fig. 3, black lines) and for contact classes having different frustration indices. These reveal that interactions with different frustration indices have different patterns of spatial distribution (Fig. 3a). The neutral contacts are randomly distributed over all of the protein molecule, having a pair distribution function following the average protein topology (Fig. 3, gray and black lines). The highly frustrated contacts do indeed tend to be closer to each other than expected from a random distribution (Fig. 3, red lines) for distances up to 6 Å for the mutational frustration definition. Most interestingly, for both the mutational and the configurational criteria, the minimally frustrated contacts correlate over longer ranges. This long-range correlation indicates they form a three-dimensionally connected contact network spanning over 5–15 Å. In the cases we examined, the globular domains are internally connected by an extensive minimally frustrated contact network allowing the assumption of uniformly unfrustrated models to be sufficient for treating many problems in folding kinetics (22, 23). This observation is paralleled at the single-residue frustration level, when a similar comparative analysis is done on the single-residue frustration index (Fig. 3c).

Fig. 3.

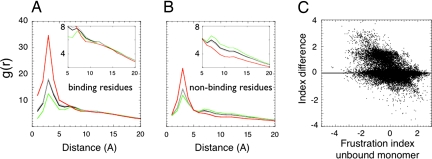
The pair distribution functions between the centers of mass of the contacts was calculated for a database of 314 monomeric proteins (black). The distributions for minimally frustrated (green), neutral (gray), or highly frustrated contacts (red) are shown both for each class using the mutational frustration index (A), the configurational frustration index (B), or the single-residue-level frustration index (C). For the single-residue-level frustration index, the distance between C^α atoms was used.

We see the application of quantitative landscape theory (with even its crude entropy estimates) provides reasonable values for the thresholds to be relevant for spatially localizing frustration in a structurally sensible way. We see the frustration distribution in native proteins is fairly robust to the different ways of localization proposed here, as the configurational-, mutational-, or residue-level indices show similar trends.

Frustration in Protein Assemblies.

Landscape theory has already proven useful for describing protein–protein interaction (9, 10). From the point of view of the localized frustration index, a natural question is whether and how often the residues that conflict with folding are specific for protein association. To test this hypothesis, we analyze the distribution of frustration index in the networks of interactions of protein assemblies, just as we did for the monomeric protein database. Our survey used a recently curated set of nonredundant dimeric complexes solved to high resolution (24).

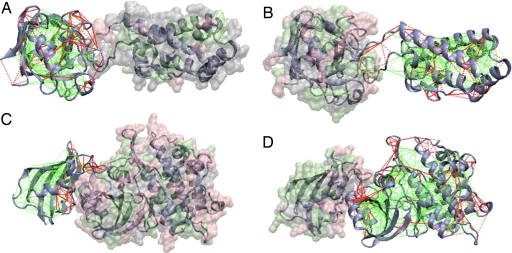
We first analyze the localization of the frustration in the individual binding partners and correlate the frustration indices to the known binding sites. Fig. 4 shows the configurational frustration indices of the contacts and residues in some of the complexes of the database. One sees in these and other cases that there is an enriched distribution of frustrated interactions near the binding sites. Not all of the highly frustrated regions are strictly close to the known binding partner found in the database; however, we confirmed this observation by comparing the pair distribution function of the contacts in the different frustration classes relative to the locations of the annotated binding residues (the surface residues that contact the partner when in complex) to the pair distribution function of the same contacts to the rest of the surface, the nonbinding residues (Fig. 5). We see the highly frustrated contacts both cluster and tend to be closer to the binding residues than they are to the nonbinders (Fig. 5a). On the other hand, minimally frustrated interactions are particularly excluded from the vicinity of binding residues. The neutral interactions follow the native topological distribution (Fig. 5a). Interestingly, when the nonbinding surface is examined, some clusters of highly frustrated interactions still appear (Fig. 5b). Whereas many of the highly frustrated interactions are close to the annotated binding residues, these additional frustrated patches on the protein surface not corresponding to the annotated binding site may be involved in binding to other partners not found in the crystal structure or, perhaps, are sites relevant for allostery.

Fig. 4.

Examples of localized frustration patterns in protein assemblies. The interactions in one monomeric partner are colored according to the contact configurational frustration index, whereas the other partner's surface is colored according to the single-residue-level frustration index, as described for Fig. 1. The frustration indices are shown as calculated for the unbound monomers. Complementary views of the same complexes are shown and correspond to the database members cyclophilin bound to the N-terminal domain of HIV-1 capsid (PDB ID code 1AK4) (A and B) and cytoplasmic domain of the type 1 TGF-β receptor in complex with fkbp12 (PDB ID code 1B6C) (C and D).

Fig. 5.

Frustration distribution in protein assemblies. (A and B) The pair distribution functions between the center of mass of contacts classified by their frustration index (minimally frustrated in green, neutral in gray, or highly frustrated in red) to the C^α of either binding (A) or the surface residues not involved in binding (B) are shown. (C) The change of the configurational frustration index upon binding for the contacts close to the binding site in all of the complexes analyzed.

To understand how the local frustration distribution changes upon binding, we calculated the frustration indices for proteins in the complexes and for the unbound monomers. Upon binding, the newly formed contacts have a distribution similar to that for contacts in single domains, implying that specific association can as well be accounted by the principle of minimal frustration. Fig. 5c depicts the change in the configurational frustration index of the individual contacts close to the binding site. Approximately 25% of the single contacts became less frustrated upon association, whereas a minor fraction, ≈7%, do change in the opposite direction. Interestingly, the decrement in frustration is nearly constant being ≈1.5 units of the frustration index. This comes from the change in the solvent accessibility upon binding, captured by the burial term and the contact type in the AMW energy function. In summary, the frustration index of the regions close to the binding site changes upon association, often becoming very much less frustrated in the complex, and the newly formed interfaces have a similar distribution of local frustration to the interiors of unbound domains.

Concluding Remarks.

Natural proteins as we observe them today are highly evolved complex systems (25). Self-assembly and mutual recognition of these polypeptides into defined structural ensembles is a fundamental aspect of the biology of macromolecules, the specificity of which is physically captured by the principle of minimal frustration (26). This principle, however, does not rule out that some energetic frustration may be present in a folded protein. Moreover, the remaining frustration facilitates motion of the protein around its native basin and, as such, the residual frustration may be fundamental to protein function (26). Rooted in folding landscape theory, this work has presented methods for spatially localizing and quantifying the energetic frustration present in native protein structures. We find that the single protein domains are strongly cross-linked by a minimally frustrated contact network. Our localization procedure shows that the minority of the interactions that are highly frustrated typically cluster at the protein surface. Moreover, these frustrated interactions that, in principle, might conflict with the robust folding of the domain, seem to reflect evolutionary constraints other than folding and often correspond to physiologically relevant sites. Our statistical survey has shown that these sites do colocalize with regions involved in the formation of heterodimeric protein assemblies. An accompanying article in this issue of PNAS (27) describes in detail a particularly interesting application of these concepts highlighting the role played by local frustration in the folding mechanism of the Im7 protein.

Folding-upon-binding, allostery, switching, and gating are examples of conformational transitions associated with the biological functions of proteins that are deeply connected to the energy landscape that biological polypeptides explore. Quantitative methods for localizing frustration can give insights into the functional constraints on the evolution of those landscapes. Protein function and local protein dynamics have long been thought to be related (28). Quantitative NMR methods can provide an experimental picture of how function emerges from a dynamic protein system (29). Computationally localizing frustration may also provide a useful view of such local protein dynamics. Lastly, we wish to point out that the scheme we propose for localizing frustration can be used with any sufficiently accurate force field or energy function. By making “alchemical” transformations (30) of amino acid pairs in all-atom models of proteins and solvent, the localized frustration can be computed from accurate first principles. In addition, the mutational frustration index can be directly probed in the laboratory by appropriate high-throughput experimental studies of protein stability changes.

Methods

To evaluate the statistics of the frustration indices, we used the non-backbone terms of the water-mediated AMW energy function (10), details of which can found in SI Text. The references for the structural databases used can also be found in SI Text.