Abstract
Rotating waves (rotors) of cellular activity were observed in nonconfluent cultures of embryonic chick heart cells by using a macroscopic imaging system that detected fluorescence from intracellular Ca2+. Unlike previous observations of rotors or spiral waves in other systems, the rotors did not persist but exhibited a repetitive pattern of spontaneous onset and offset leading to a bursting rhythm. Similar dynamics were observed in a cellular automaton model of excitable media that incorporates spontaneous initiation of activity, and a decrease of excitability as a consequence of rapid activity (fatigue). These results provide a mechanism for bursting dynamics in normal and pathological biological processes.
Since early studies demonstrated that bursting rhythms could originate from single cells (1), theoretical analyses of bursting have focused on cellular ionic mechanisms (2–5). It has been difficult to assess what contribution spatial patterns of activation within groups of participating cells have on the dynamics of a burst. This work was initiated to determine the spatial patterns of activation occuring in dispersed cultures of heart cells. Previous studies of excised slices of cardiac tissue demonstrated sustained rotors initiated by electrical stimulation and proposed that rotors might be a mechanism for abnormally rapid cardiac arrhythmias (tachycardias) (6, 7). Although tachycardias in people can be initiated by electrical stimulation, they usually start spontaneously. In most instances, the rhythms also terminate spontaneously. On occasion there is a repeated spontaneous paroxysmal initiation and termination of tachycardias (8, 9). In this paper, we demonstrate repeated spontaneous initiation and termination of rotors in cultured cardiac myocytes.
These phenomena are modeled by using a cellular automaton. In a cellular automaton, there is a lattice of sites with discrete states and a synchronous updating rule that is identical for all sites. Cellular automata have been used as simplified models for a large range of phenomena, including neural networks (10), cardiac arrhythmias (11), oscillating chemical reactions (12), and forest fires (13). However, none of these previous formulations display the repeated onset and offset of rotors observed here.
METHODS
Cell Culture.
Ventricular cells from 7-day embryonic chick ventricular myocytes were isolated as described (14). Cells were plated at just under confluent densities of 7.0–14.0 × 103 cells per cm2 within 12-mm diameter glass retaining rings on lysine-coated plastic cell culture dishes. Cells were kept in maintenance medium 818a at 5% CO2 at 36°C for 1–2 days before experiments. Monolayers were loaded with calcium-sensitive dye fluo-3 (5 μM, Molecular Probes) (15) in Hanks’ balanced salt solution (HBSS, 1.3 mM K) for 25–30 min, washed with fresh HBSS to remove excess dye, and then transferred to the imaging setup. Experiments were conducted at 36° ± 1°C.
Fluorescent Imaging.
A macroscope was constructed (16) to allow low light level measurements at low magnification scales (objective, Nikon 80 mm; imaging lens, Chromicar Zoom 130; excitation filter, 460 nm; dichroic beamsplitter, 510 nm; imaging filter, 540 nm). The macroscope was mounted on top of an inverted microscope (Zeiss Axiovert 125M) to allow for simultaneous monitoring of the monolayer at macroscopic and microscopic scales. Images were collected by using a cooled CCD camera (Princeton Instruments, Model TE CCD 576). Adjacent pixels in the CCD were binned (5 × 5), and up to 30,000 consecutive images were transferred directly to computer (Pentium 90) for storage and analysis. Image data from each binned pixel are scaled based on its maximal range over 20 frames, the image is spatially averaged, and the background is subtracted. The image is viewed by using custom-written software.
Cellular Automaton.
We adapt the Greenberg–Hastings model of excitable media (17, 18) to account for the physiological properties of spontaneous activity and fatigue (see Results).
Each site of a two-dimensional lattice at time (t) is assigned a state, uij(t) and a level of fatigue φij(t), where the subscripts refer to the location in the lattice. The neighborhood of a given site corresponds to its N nearest neighbors. The state is an integer: 0 is a rest state; states 1, 2, … , E are excited states; states E + 1, E + 2, … , E + R are refractory states; and state (E + R + 1) is identified with the rest state 0.
The update rule for the state of a site is as follows: if 1 ≤ uij(t) ≤ (E + R), then uij(t + 1) = uij(t) + 1. If uij(t) = 0, then uij(t + 1) = 0, unless one of two conditions hold: (i) the number of sites with an excited state at time (t) in the neighborhood of a site at (ij) is greater than θij(t) = θ + φij(t), where θ is a positive number indicating the threshold for excitation in the absence of fatigue and φij(t) is a fatigue term defined below; or (ii) ξij(t) < p, where ξij(t) is a random number uniformly distributed on the interval [0, 1], and p is a positive number representing the probability for spontaneous activation of a site.
The update rule for φij(t) is as follows. If uij(t) = 0 and uij(t + 1) = 1, then φij(t + 1) = φij(t) + δ; otherwise φij(t + 1) = γφij(t), where γ is a positive constant, 0 < γ < 1. Thus, there is an increment of the fatigue term associated with excitation of a site, and exponential decay of the fatigue at other times.
By setting p, φ, and δ equal to 0, we recover the Greenberg–Hastings model (17, 18) of excitable systems.
To carry out the simulations, we need to set E, R, θ, δ, γ, p, and the neighborhood size. This is a rich array of parameters, and we have not systematically investigated behaviors throughout parameter space. For simplicity, we assume that the neighborhood consists of the eight nearest neighbors of a given site. For this neighborhood, planar wave propagation requires that θ ≤ 2, and we set θ = 2. By choosing θ at the maximum value that allows planar wave propagation, we increase the likelihood for block and the initiation of rotors. We require that broken wave fronts curve to generate rotors as observed in the experiments. With θ = 2, rotors will form if E ≥ 5 and we select E = 5. R is set equal to E + 1 = 6 to prevent a wave from exciting sites directly in its refractory wake. Simulations with the above parameters with no fatigue give a rotor with a period of about 36 iterations. If φij > 1, then site (ij) will not be excited by a planar wave. For these parameters, a rotor of period N will not persist if (1 + δ)γN > 1. To obtain long burst, we need a slow buildup of fatigue. We arbitrarily set δ = 0.05 and γ = 0.999 based on the above equation. The probability of random firing at a site is 7.5 × 10−4 per iteration. The mean burst time and time between bursts increases as p decreases. Although we report the results with this set of parameters, we have carried out many other simulations with the same model, or other variants of cellular automata models (12), and obtained similar results in all cases.
RESULTS
Fluorescent Imaging.
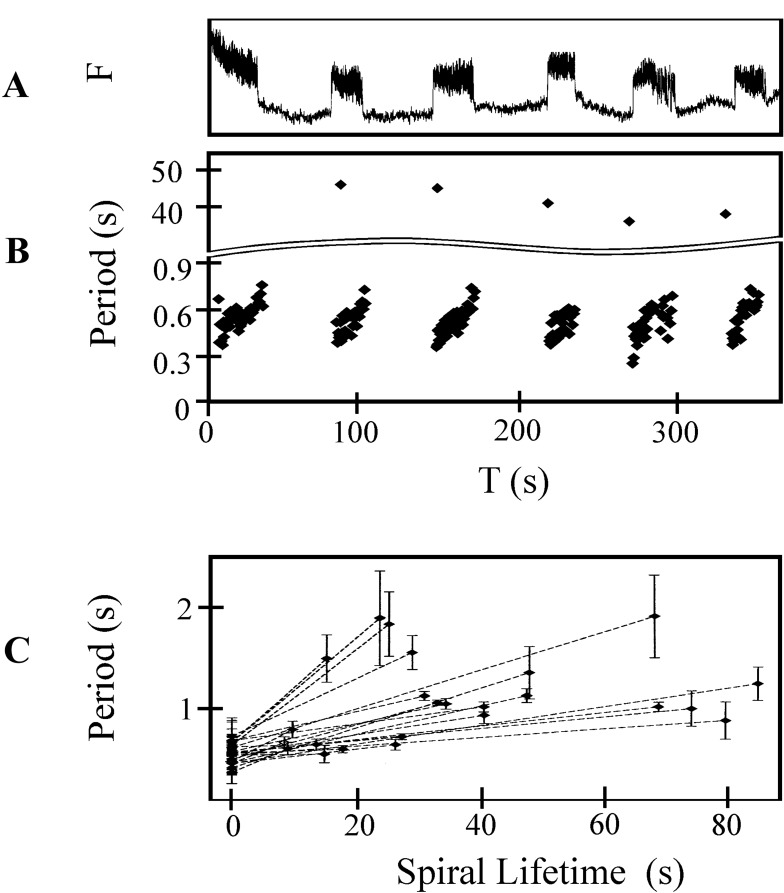
Bursting dynamics were observed in 14/17 different preparations. Fig. 1A shows fluorescent intensity over a duration of 6 min recorded from an area of 1 mm2 in a single preparation. Six bursts of fluorescence were recorded. During each burst, there were distinct fluorescent peaks. The period between the peaks increased from 450 ms to 700 ms during a single burst. Fig. 1B shows the period recorded over six consecutive bursts plotted against time by using the data in Fig. 1A. The time between bursts remained relatively constant (40 ± 15 s). Fig. 1C summarizes data from 30 bursts recorded in 6 different preparations. The mean period for the first five peaks of each burst is given at time 0. Each dashed line represents a single burst, where the abscissa and ordinate of the right end point give the burst duration and mean period of the last five peaks, respectively. In six preparations the mean period within a single burst increased by 20–80%.
Figure 1.
Dynamics of burst generation. (A) Calcium fluorescence for six consecutive bursts from a 1 mm2 area. (B) The interbeat period measured from calcium fluorescence during rotor bursting as a function of time. During each burst duration increases from about 0.4 s to 0.8 s. The interburst duration ranges from 36 s to 44 s. (C) Average period of rotor rotation for 24 representative rotor bursts taken from 6 different preparations. The average period, calculated for the first and last five rotations of each rotor during a burst, is plotted as a function of burst duration. The error bars show the standard deviation of the period over the five averaged periods.
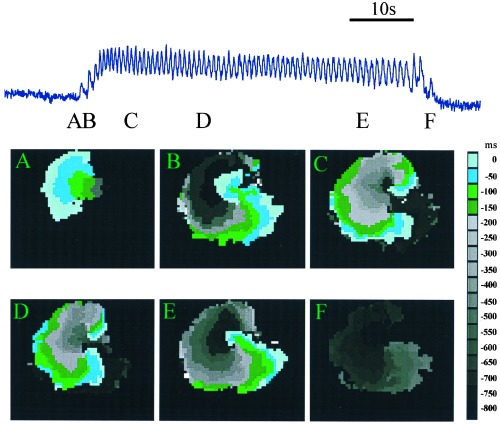
To determine the spatio-temporal patterns of activity underlying the burst, fluorescent activity was recorded from a 1-cm2 area. These recordings demonstrated the presence of a spontaneously initiated rotor associated with the burst (Fig. 2). The top trace in Fig. 2 shows a 25-s burst of increased Ca2+ recorded from a 1-mm2 region. A peak in activity is created every time the activation front passes through the 1-mm2 recording region. To study the activation sequences leading to the initiation and the termination of the burst, contour plots of activation times were constructed. A wave of activity was spontaneously initiated (Fig. 2A) but did not propagate uniformly. The wave was blocked at a point near the site of initiation leading to unidirectional propagation to the left. After the wave propagated about 2 mm (Fig. 2B), it doubled back, invading the previously blocked regions leading to two mirror-image rotors, with a common pathway in between them. For the initial 14 rotations, the top rotor excited the common pathway first (Fig. 2C). Then the top and bottom rotors simultaneously excited the common pathway (Fig. 2D). After 44 rotations, the top rotor was blocked, after which there remains only a single rotor (Fig. 2E). This wave was eventually blocked, leading to termination of the burst (Fig. 2F).
Figure 2.
Anatomy of a typical burst. The upper trace shows fluorescence intensity during a single burst. The width of each panel is 1 cm. The colored images show contour plots of activation times at several different times during the burst indicated by the labels. Contour maps are constructed by determining the location of the activation front at 50-ms intervals. The location of the activation front at a given time is plotted in a color given by the key. This format allows for the representation of a number of consecutive raw data frames onto a single composite image. Activation front detection is determined by a threshold set at half maximum fluoresence. (A) Unidirectional block. The wave is initiated at a single site and propagates only to the left. (B) Formation of two mirror-image rotor waves. The excitation doubles back, to invade the tissue forming a mirror-image pair or rotors. (C and D) Contour plots of the mirror-image pair of rotors. (E) Destruction of one of the rotors leaves a single rotor (F) Termination of the remaining rotor.
The sequence shown in Fig. 2 was observed in 72/120 bursts. In another 24/120 cases, there was a similar initiation to a pair of mirror-image rotors, but there was no evolution to a single rotor before termination. In the remaining 24/120 rotor bursts, unidirectional propagation evolved directly to a single rotor and then terminated.
Cellular Automaton.
Tissue culture of embryonic chick myocytes display intrinsic spontaneous oscillation (14, 19). In addition, in many cardiac preparations (20, 21), including cultured cardiac myocytes (22), there is a decrease in excitability, or fatigue, caused by rapid stimulation. We model the dynamics observed experimentally by implementing a cellular automaton (see Methods). Briefly, a site can be excited, refractory (unable to become excited), or in a rest state (able to become excited). An excitable site becomes excited because of spontaneous activity, which we assume to be random, or by spread of activity from neighboring sites if a sufficient number of neighbors are excited at the previous time step. A site remains in the excited state for a constant time and then becomes refractory for a constant time before reaching the rest state.
Waves are initiated by the chance random activation of a sufficient number of sites in a given neighborhood. Once initiated, a wave can be blocked from propagating in all directions, it can propagate as a broken wave in one direction, or it can propagate symmetrically to generate a target. Waves of high curvature are blocked more easily by refractory sites than waves of low curvature are. As high curvature activation fronts advance, they become less curved and less vulnerable to block. These properties of the model allow stable rotors to be generated from broken activation fronts created at initiation sites.
To model fatigue, the number of active sites needed to excite a given site is increased as a consequence of excitation. At the termination of a burst, fatigue decays exponentially. Rapid activity results in a buildup of fatigue that reduces excitability of the site. Spontaneous activity was modeled by assuming a random excitation of sites in the rest state.
The model shows initiation and annihilation of bursting rotors similar to experimental observations (Fig. 3). Impulses are initiated by the chance simultaneous firing of several sites in close proximity to each other, so that additional sites in the neighborhood fire. In the example shown (Fig. 3), local heterogeneity prevents spread of excitation in all directions, resulting in unidirectional propagation upward (Fig. 3A). The wave advances and doubles back to excite the region previously blocked (Fig. 3B), resulting in reentrant excitation in the form of two mirror-image rotors (Fig. 3C). Heterogeneity, induced by random firing in the model, breaks the symmetry (Fig. 3D) leading to a single rotor (Fig. 3E). The buildup of fatigue eventually makes propagation impossible and the rotor is annihilated (Fig. 3F). These features are similar to experimental observations (Fig. 2).
Figure 3.
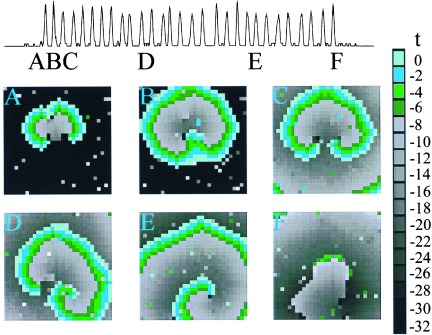
Simulation of a single burst in a 30 × 30 array. Contour maps of activation times for the cellular automaton model during a rotor burst. (A) Unidirectional block. The wave is initiated from the random firing of more than two neighboring sites. Heterogeneity results in unidirectional propagation upward. (B and C) Formation of two mirror-image rotors. The excitation doubles back and invades the site of block to form a rotor. (D and E) Rotation of the mirror-image pair of rotors. The rightmost rotor dominates and the leftmost rotor dies out first. (F) Termination of the remaining rotor.
In the cellular automaton model, each site corresponds to approximately 0.1 mm2, or 7–14 cells in the biological preparation. During the burst, the period of rotation of the rotor is approximately 36 iterations, so each iteration step corresponds to approximately 20 ms. With this scaling, the time interval between bursts in the cellular automaton model is about 1,000 iterations or 20 s, which is comparable experimental observations (Fig. 1).
DISCUSSION
Rotors are well known from experimental (6, 7, 15, 23–28) and theoretical studies (11, 12, 29, 30). However, this earlier work does not describe the repeated spontaneous onset and offset of rotors that we observe here.
The current work demonstrates bursting rotors and provides a mechanism for bursting behavior in diverse settings. Bursting arises because of local interactions of nonbursting elements. An alternative mechanism is that the individual cells display bursting dynamics and that the rotors are a secondary phenomenon. The current experiments cannot distinguish between these two possibilities. However, by changing the parameters in the theoretical model, other types of nonbursting dynamics could be observed, including localized activity with no macroscopic wave propagation, and wave propagation in plane waves or target patterns. Similar dynamics were observed in the cultured myocytes as the plating densities and media conditions were modified. The current parameters in the model were selected to demonstrate the feasibility of obtaining bursting dynamics in a model with elements that do not burst themselves.
These results should be applicable to cardiology where the paroxysmal onset and offset of reentrant cardiac arrhythmias presents significant clinical management problems (8, 9). Other potential applications involve bursting in neural systems (31, 32) and in pancreatic β cells (33), but more work is needed to determine the actual patterns of spatio-temporal activation in these systems. The current work underscores the delicate factors that lead to the stabilization and destabilization of rotating waves of activity independent of external interventions. Moreover, because biological systems are spatially extended, patterns of spatial activation must necessarily be investigated before the mechanism of bursting behavior can be assessed.
Acknowledgments
We thank Johanne Ouellette for expert technical assistance with the biological preparation and A. T. Winfree and N. Kopell for helpful comments. This work has been supported by funds from the Medical Research Council (Canada), the Heart and Stroke Foundation (Québec), the Natural Sciences Engineering and Research Council (Canada), Fonds pour la Formation de Chercheurs et l’Aide à la Recherche (Québec), and the National Institutes of Health (USA).
References
- 1.Frazier W T, Kandel E C, Kupfermann I, Waziri R, Coggeshall R E. J Neurophysiol. 1967;30:1288–1351. doi: 10.1152/jn.1967.30.6.1352. [DOI] [PubMed] [Google Scholar]
- 2.Canavier C C, Clark J W, Byrne J H. J Neurophysiol. 1991;66:2107–2124. doi: 10.1152/jn.1991.66.6.2107. [DOI] [PubMed] [Google Scholar]
- 3.Cook D L, Satin L S, Hopkins W F. Trends Neurosci. 1991;14:411–414. doi: 10.1016/0166-2236(91)90033-q. [DOI] [PubMed] [Google Scholar]
- 4.Wang X-J, Rinzel J. In: The Handbook of Brain Theory and Neural Networks. Arbib M A, editor. Cambridge, MA: MIT Press; 1995. pp. 686–691. [Google Scholar]
- 5.Sherman A, Rinzel J. Biophys J. 1991;59:547–559. doi: 10.1016/S0006-3495(91)82271-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Allessie M A, Bonke F I M, Schopman F J C. Circ Res. 1976;39:168–177. doi: 10.1161/01.res.39.2.168. [DOI] [PubMed] [Google Scholar]
- 7.Davidenko J M, Pertsov A V, Salomonsz R, Baxter W, Jalife J. Nature (London) 1992;355:349–351. doi: 10.1038/355349a0. [DOI] [PubMed] [Google Scholar]
- 8.Parkinson J, Papp C. Br Heart J. 1947;9:241–262. doi: 10.1136/hrt.9.4.241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Coumel P, Leclercq J-F, Slama R. In: Cardiac Electrophysiology and Arrhythmias. Zipes D P, Jalife J, editors. Orlando, FL: Grune & Stratton; 1985. , Chap. 50. [Google Scholar]
- 10.Farley B G. Comput Biomed Res. 1965;1:265–294. [Google Scholar]
- 11.Moe G K, Rheinboldt W C, Abildskov J A. Am Heart J. 1964;67:200–220. doi: 10.1016/0002-8703(64)90371-0. [DOI] [PubMed] [Google Scholar]
- 12.Gerhardt M, Schuster J, Tyson J J. Science. 1990;247:1563–1566. doi: 10.1126/science.2321017. [DOI] [PubMed] [Google Scholar]
- 13.Bak P, Chen K, Tang C. Phys Lett A. 1990;147:297–300. [Google Scholar]
- 14.Koidl B, Tritthart H A, Erkinger S. J Mol Cell Cardiol. 1980;12:165–178. doi: 10.1016/0022-2828(80)90086-3. [DOI] [PubMed] [Google Scholar]
- 15.Lechleiter J, Girard S, Peralta E, Clapham D. Science. 1991;252:123–126. doi: 10.1126/science.2011747. [DOI] [PubMed] [Google Scholar]
- 16.Ratzlaff E H, Grinvald A. J Neurosci Methods. 1991;36:127–137. doi: 10.1016/0165-0270(91)90038-2. [DOI] [PubMed] [Google Scholar]
- 17.Greenberg J, Hassard B, Hastings S. SIAM J Appl Math. 1978;34:515–523. [Google Scholar]
- 18.Fisch R, Gravner J, Griffeath D. Stat Comput. 1991;1:23–29. [Google Scholar]
- 19.Guevara M, Glass L, Shrier A. Science. 1981;214:1350–1353. doi: 10.1126/science.7313693. [DOI] [PubMed] [Google Scholar]
- 20.Noma A, Tsuboi N. J Physiol. 1987;382:193–211. doi: 10.1113/jphysiol.1987.sp016363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Billette J, Métayer R, St. Vincent M. Circ Res. 1988;62:790–799. doi: 10.1161/01.res.62.4.790. [DOI] [PubMed] [Google Scholar]
- 22.Kunysz A M, Shrier A, Glass L. Am J Physiol. 1997;273(Cell Physiol. 42):C331–C346. doi: 10.1152/ajpcell.1997.273.1.C331. [DOI] [PubMed] [Google Scholar]
- 23.Gerisch G. In: Current Topics in Developmental Biology, Vol. 3. Moscona A, Monroy A, editors. New York: Academic; 1968. , Chap. 6. [Google Scholar]
- 24.Winfree A T. Science. 1972;175:634–636. doi: 10.1126/science.175.4022.634. [DOI] [PubMed] [Google Scholar]
- 25.Schoels W, Gough W B, Restivo M, El-Sherif N. Circ Res. 1990;67:35–50. doi: 10.1161/01.res.67.1.35. [DOI] [PubMed] [Google Scholar]
- 26.Gómez-Gesteira M, Fernández-García G, Muñuzuri A P, Pérez-Muñuzuri V, Krinsky V I, Starmer C F, Pérez-Villar V. Physica D. 1994;76:359–368. [Google Scholar]
- 27.Steinbock O, Kettunen P, Showalter K. Science. 1995;269:1857–1860. doi: 10.1126/science.269.5232.1857. [DOI] [PubMed] [Google Scholar]
- 28.Palsson E, Cox E C. Proc Natl Acad Sci USA. 1996;93:1151–1155. doi: 10.1073/pnas.93.3.1151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kopell N, Howard L N. Adv Appl Math. 1981;2:417–449. [Google Scholar]
- 30.Winfree A T. When Time Breaks Down: The Three-Dimensional Dynamics of Electrochemical Waves and Cardiac Arrhythmias. Princeton, NJ: Princeton Univ. Press; 1987. [Google Scholar]
- 31.Misgeld U, Swandulla D. J Basic Clin Physiol Pharmacol. 1990;1:57–63. doi: 10.1515/jbcpp.1990.1.1-4.57. [DOI] [PubMed] [Google Scholar]
- 32.Destexhe A, Contreras D, Sejnowski T J, Steriade M. J Neurophysiol. 1994;72:803–818. doi: 10.1152/jn.1994.72.2.803. [DOI] [PubMed] [Google Scholar]
- 33.Mears D, Sheppard N F, Atwater I, Rojas E. J Membr Biol. 1995;146:163–176. doi: 10.1007/BF00238006. [DOI] [PubMed] [Google Scholar]