3D Ultrasound Elastography for Early Detection of Lesions. Evaluation on a Pressure Ulcer Mimicking Phantom

Abstract

A pressure ulcer is a damaged tissue area induced by an unrelieved pressure compressing the tissue during a prolonged period of immobility. The lack of information and studies on the development of this pathology makes its prevention difficult However, it is both acknowledged that lesions initiate in the deep muscular tissues before they expand to the skin, and that lesions are harder than healthy tissues. Elastography is therefore an interesting tool for an early detection of the pathology. A 3D strain estimation algorithm is presented and evaluated on a PVA-cryogel phantom, mimicking a pressure ulcer at an early stage.

I. Introduction

Pressure ulcers, also known as bedsores, are lesions of the skin and underlying tissues, caused by a high and prolonged pressure at the body interface. This pathology concerns any people with weakened sensitivity or limited mobility. But it mostly strikes elders and spinal cord injury patients. This disease is painful, handicapping and becomes a growing issue, as life expectancy increases in western countries. Yet, it has been neglected till now, and there is still little consensus about the pathological process that triggers the formation of bedsores.

It is now acknowledged that pressure ulcers appear after a prolonged period of immobility, during which the body interface lying on a support (either a bed or a wheelchair) undergoes a high and unrelieved pressure. During a short time, biological soft tissues can tolerate relatively high pressures. However, a weaker but continuous pressure can result in severe injuries and a pressure ulcer can therefore appear anywhere in the body as soon as it is subjected to a significant pressure. Nevertheless, thin layered tissues in regard to a bony prominence are privileged regions, as a high stress is focused on a small volume. This pattern is met for sacrum or heels. These are privileged regions and 80 % of bedsores affect these two locations.

Above a threshold, compression results in local occlusions of blood capillaries. This shortage of blood supply, called ischemia, prevents the natural exchanges of oxygen and nutrients between the blood and body cells to occur. These ischemic conditions may lead to cell death and severe tissue damages. Besides, skin and muscle have different metabolisms: skin metabolism is anaerobic, while muscle has an aerobic metabolism, requiring much more oxygen [1]. Muscles are therefore more vulnerable to ischemia than the skin and surrounding fat tissues. Thus, lesions first initiate in the deep muscle tissue before expanding to the skin, making difficult their early detection. This explains why the sore is already at a severe stage when it appears on the skin surface.

In the literature, few studies are available on pressure ulcer mechanical properties. The main reference in this area is given by Gefen et al. [2], who showed that tissues damaged by pressure ulcer are harder than healthy tissues. By applying a prolonged compression on rat muscle tissues in vivo, they observed a significant increase of tissue elastic modulus with time and pressure level.

Because of this process of hardening of damaged areas and the deep origin of the ulcer, ultrasound elastography seems especially appropriate for the early detection of pressure ulcer formation.

Elastography is a promising technique, which aim is to provide information about the mechanical properties of soft biological tissues, by investigating their deformation under an external load. Pre- and post-compression ultrasonic (US) radio-frequency (RF) signals are first acquired. Then, changes within the signals induced by the stress are analyzed to compute a map of local strains.

Since static elastography has appeared in the early 90s [3], mainly ID methods were developed. A few 2D methods have also been worked out [4]–[10]. These techniques are adapted to current clinical equipment since ultrasound scanners essentially provides 2D data. However they may lead to noisy elastograms if significant out-of plane motion occurs, since it represents a source of decorrelation between pre- and post-compression signals. To overcome this decorrelation problem, and with the development of 2D transducer arrays, we use in this study a 3D estimator, which computes the axial strain while considering lateral and azimuthal motions. This strain estimation model is further detailed in the following section. Pressure ulcer early detection is then investigated with the proposed method.

II. Method

The proposed 3D strain estimator is based on an adaptive and iterative constrained optimization process. For each elementary RF region R₁ selected in the pre-compression volume V_1, its deformed version R₂ is searched in the post-compression volume V₂ and the corresponding local strain is then estimated. In the axial direction (see directions in fig. 1), R₂ is considered as a time-delayed (parameter d) and scaled (parameter α) replica of R₁. Because lateral and azimuthal resolutions are much coarser than the axial resolution, R₂ is only considered to be a shifted version of R₁ in these directions (parameters τ and ν). The axial delay d results from the accumulation of axial deformations of the regions located between the probe and the region of interest. After having compensated for this axial delay, three parameters remain to be calculated: the axial scaling factor α, the lateral shift τ and the azimuthal shift ν. They are estimated as the arguments that minimize an objective function f, defined as the opposite of the correlation coefficient between R₁ and its deformed version R₂ compensated for the three parameters. Since this objective function f may suffer from multiple local minima, and could therefore yield to incorrect estimations, strong constraints are introduced on the different arguments. An admissible set of values is thus defined.

Fig. 1.

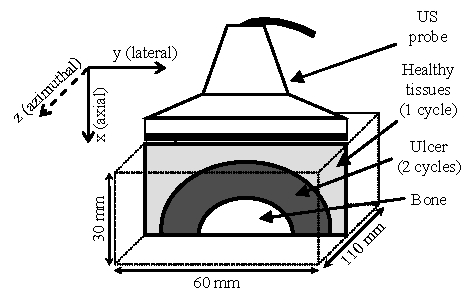
Phantom scheme.

A three step process is applied to compute the strains. First, an adaptive windowing of the region of study is used, followed by the joint estimation of the three parameters α, τ and ν. The strain map is finally computed.

A-. Adaptive windowing of the region of study

The axial tissue compression yields also to lateral and out-of-plane motion in the region of interest, resulting in a transformation of the acoustical footprint of the pre-compression signal. To overcome the subsequent loss of correlation, an adaptive displacement of the 3D region of study is considered. It allows tracking the motion of the scatterers due to the compression and enables to work on corresponding tissue regions, and therefore equivalent US data in both volumes. To cover the whole US volume V₁, the pre-compression region of study R₁ is regularly moved by constant steps of Δ_ax, Δ_lat, and Δ_azim in the axial, lateral and azimuthal directions, respectively. An adaptive displacement is considered for R₂: its axial displacement results from the accumulation of axial deformations of the regions located between the probe and the region of interest, and the lateral and azimuthal displacements are directly linked to those estimated over adjacent regions. u_R1 and u_R2, the positions of R₁ in V₁ and R₂ in V₂, respectively, are then given by:

$$\begin{array}{l}{u}_{R_1}(m,n,q)=m·{\mathrm{\Delta }}_{ax}·\overrightarrow{i}+n·{\mathrm{\Delta }}_{\mathit{lat}}·\overrightarrow{j}+q·{\mathrm{\Delta }}_{\mathit{azim}}·\overrightarrow{k}\\ u_{R_2}(m,n,q)=\sum _{k=0}^{m-1}(1/{\alpha }_k)·{\mathrm{\Delta }}_{ax}·\overrightarrow{i}+\sum _{k=0}^{n-1}{\tau }_k·\overrightarrow{j}+\sum _{k=0}^{q-1}{\nu }_k·\overrightarrow{k}\end{array}$$ (1)

where α_k is the axial scaling factor at position u_R1(m,n,q), τ_k the lateral displacement and ν_k the azimuthal displacement, estimated on step k. The axial time-delay (parameter d) is directly linked to the axial coordinate of u_R2. Hence, with such an initialization for the location of R₂ in V₂, the parameter d is already determined, and the three parameters α, τ and ν remain to be estimated, the two latter being of small magnitude.

B-. Joint estimation of the parameters α, τ and ν

A joint estimation of the parameters α, τ and ν is then performed. The region of interest R₂ is searched within V₂, as an axially scaled, laterally and azimuthally shifted replica of R₁, noted R₂(αx,y+τ,z+ν). This is done thanks to the minimization of the objective function f, which computes the opposite of the normalized correlation coefficient between R₁ and R₂, when R₂ is compensated for the three searched parameters:

$$[\widehat{\alpha },\widehat{\tau },\widehat{\nu }]=\underset{\alpha ,\tau ,\nu }{argmin}f(\alpha ,\tau ,\nu ),$$ (2)

with:

$$f(\alpha ,\tau ,\nu )=\frac{-{\displaystyle \sum _{x,y,z}}{\stackrel{\sim }{R}}_1(x,y,z)·{\stackrel{\sim }{R}}_2(\alpha x,y+\tau ,z+\nu )}{\sqrt{{\displaystyle \sum _{x,y,z}}{({\stackrel{\sim }{R}}_1(x,y,z))}^2}·\sqrt{{\displaystyle \sum _{x,y,z}}{({\stackrel{\sim }{R}}_2(\alpha x,y+\tau ,z+\nu ))}^2}},$$ (3)

where

$$\text{where\hspace{0.17em}}{\stackrel{\sim }{R}}_i(x,y,z)=R_i(x,y,z)-{\overline{R}}_i(x,y,z).$$ (4)

R̄_i(x, y, z) is the mean value of the region R_i. In elastography, deformations are of small magnitude (a few %). The optimization is therefore submitted to a set of linear inequalities constraints, drastically limiting the occurrence of local minima:

$${\alpha }_{min}\le \alpha \le {\alpha }_{max},\mathrm{\hspace{0.17em} }{\tau }_{min}\le \tau \le {\tau }_{max},\mathrm{\hspace{0.17em} }{\nu }_{min}\le \nu \le {\nu }_{max}.$$ (5)

Reducing the parameter domain also saves calculation time. The algorithm is implemented as a descent method, following the scheme:

$$(\begin{array}{lll}{\alpha }_{k+1}\hfill & {\tau }_{k+1}\hfill & {\nu }_{k+1}\hfill \end{array})=(\begin{array}{lll}{\alpha }_k\hfill & {\tau }_k\hfill & {\nu }_k\hfill \end{array})+{\rho }_k·S_k$$ (6)

where ρ_k is the descent step computed by a linear search, and S_k is the descent direction.

The first iteration is chosen as the middle of the admissible set K={(α,τ,ν) | α_min ≤ α ≤ α_max, τ_min ≤ τ ≤ τ_max, ν_min ≤ ν ≤ ν_max}, and a sequence of admissible iterations is then generated, until a stop criteria is met.

C-. Strain computation

Strain maps are then computed thanks to the set of parameters calculated for the whole US volume. We focus here on the axial strain, which is directly linked to the estimated parameter α_k according to the relation:

$${\widehat{\epsilon }}_{ax,k}=1/{\widehat{\alpha }}_k-1.$$ (7)

III. Experimental Results

A polyvinyl alcohol (PVA) cryogel phantom was designed to mimic a pressure ulcer at an early stage. Since PVA cryogel is a material whose acoustical properties are very close to those of soft biological tissues, it can easily be imaged with an ultrasound device. Moreover its stiffness increases with the number of freeze-thaw cycles applied. This typically allows encompassing the range of elasticity values commonly met in soft biological tissues [11].

As previously mentioned, pressure ulcers are found on sites where thin layered tissues are in regard to a bony prominence. Therefore, the phantom is designed as a parallelepiped of dimensions 30 mm × 60 mm × 110 mm, with three distinct areas: a bone, a region mimicking the pressure ulcer at an early stage and healthy tissues surrounding it. The geometry is further detailed in figure 1. The bone, taken from the forward limb of a dog, measured 10 mm in diameter. The pathological area underwent 2 freeze-thaw cycles, which is one more than the healthy region. This led to a harder material for the pressure ulcer mimicking area [12].

Acquisitions of RF US data were performed with an Ultrasonix - Sonix RP device. The probe and sampling frequencies were 7 MHz and 40 MHz, respectively. Each image was composed of 128 RF A-lines, with a line interdistance of 0.29 mm. A linear stepper motor was used to move the probe azimuthally and to acquire regularly spaced 2D scans (by steps of 0.2 mm). A first set of scans was performed with the phantom in a pre-compression state. The corresponding RF data volume was built by stacking the images. Then a flat plate was used to uniformly compress the phantom and achieve a global axial deformation of 2%, and the same protocol was once again applied to compute the post-compression volume.

The ability of our algorithm to detect the pathological area was evaluated on these data. The size of the region of interest R₁ was 60 axial points × 3 RF lines × 3 azimuthal slides, and the overlap was 80 %, both axially and laterally (no azimuthal overlap). The results for an area centered on the middle of the phantom are presented in fig. 2. A B-mode image of the region is shown in fig. 2e. Even if the bone is visible because of its echogenicity, the echography does not exhibit any mechanical information. On the contrary, the axial strain map (fig. 2a) is of great help for distinction between the lesion, the healthy tissues and the bone. Due to the low compression level, strain values remain within a small range. However, the deformation of the bone is almost zero, while the mean axial strain of the pathological area is about half that of surrounding tissues (0.75% vs. 1.5%). Moreover, the boundary between the healthy region and the ulcer is recognizable, which could allow a diagnostic about the stage of the illness. The lateral displacement map (fig. 2b) displays this limit too, especially in the top corners of the image. Azimuthal displacement estimations are shown fig. 2c. Surprisingly, there are large displacements for tissues immediately surrounding the bone. This might be due to slippery conditions at the bone/cryogel interface and to a weak link between them when the phantom was built. Because of the poor resolution in the azimuthal direction, this map is also noisy. But it especially demonstrates the interest of considering the 3D motion of soft tissues. The objective function of our algorithm is based on the normalized correlation coefficient, that’s why it is also interesting to consider the correlation coefficient map (fig. 2d). Its mean value over the image reaches a satisfying level of 0.93, which means that the estimations can be trusted.

Fig. 2.

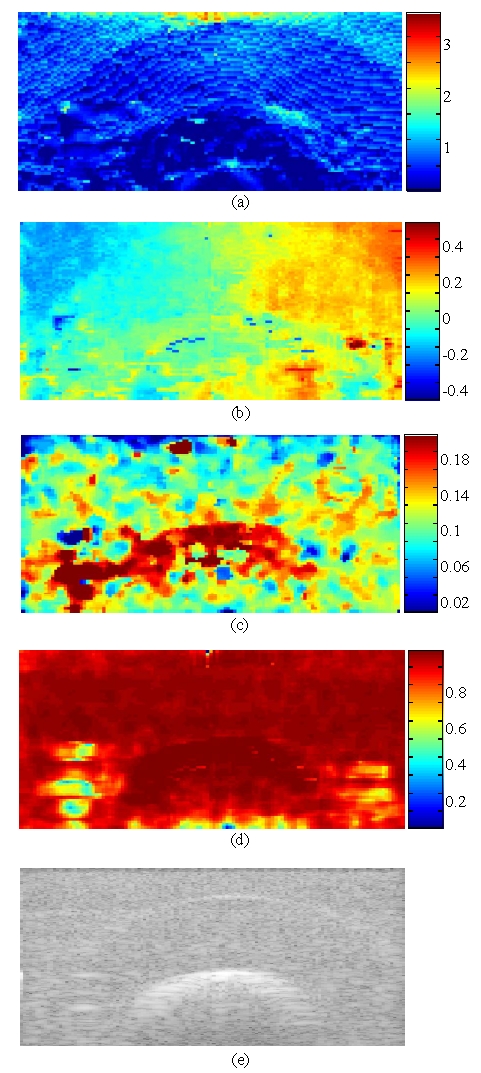
Results for a volume centered on the middle of the phantom. (a) is the axial strain (%). (b) is the lateral displacement (mm). (c) is the azimuthal displacement (mm). (d) is the correlation coefficient map. (e) is a B-mode image.

Since the algorithm is three-dimensional, these information (axial strain, lateral and azimuthal displacements) are available for the whole scanned volume. For clinical purpose, the desired parameter could be displayed like a movie (with the z axis corresponding to time), to see its evolution along the azimuth and to provide the physician with a better understanding of the imaged area. We chose here to present the axial strain along the z axis (perpendicular to the US scan) for two different positions (fig. 3). The axial strain for the middle slice (corresponding to the axe of the bone axis) is shown fig. 3a. Here again, the coarse resolution is a limitation. Yet, it is still possible to distinguish the 3 regions. Fig. 3b exhibits the axial strain for an off-centered slice. The bone is not visible at this position, but the healthy and pathological regions can clearly be differentiated, since the deformation of healthy tissues is approximately twice the deformation of the diseased region.

Fig. 3.

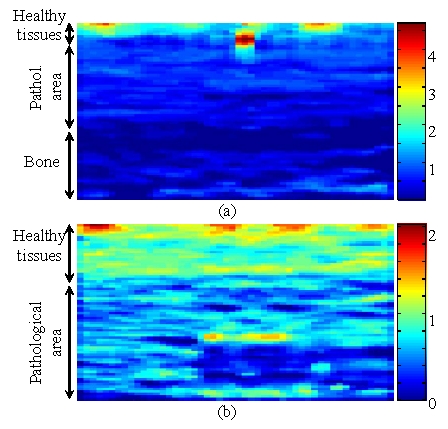
Axial strain along the z axis, for a slice centered on the middle of the phantom (a), and for an off-centered slice (b).

IV. Conclusion

A 3D strain estimator has been described in this paper. Thanks to an optimized adaptive and iterative process, it enables accurate estimations of the axial strain distribution, while considering lateral and azimuthal motion. The strain estimation technique was evaluated on a PVA-cryogel phantom mimicking a pressure ulcer at an early stage. Results are very encouraging, both for the potential of our 3D elastographic method, and for the possibility of detecting this pathology at an early stage. Complementary tests on in vitro and in vivo biological tissues are now planed.