STATISTICAL PROPERTIES OF ION CHANNEL RECORDS: II. ESTIMATION FROM THE MACROSCOPIC CURRENT

Abstract

Macroscopic ion channel current is the summation of the stochastic records of individual channel currents and therefore relates to their statistical properties. As a consequence of this relationship, it may be possible to derive certain statistical properties of single channel records or even generate some estimates of the records themselves from the macroscopic current when the direct measurement of single channel currents is not applicable.

We present a procedure for generating the single channel records of an ion channel from its macroscopic current when the stochastic process of channel gating has the following two properties: (I) the open duration is independent of the time of opening event and has a single exponential probability density function (pdf), (II) all the channels have the same probability to open at time t. The application of this procedure is considered for cases where direct measurement of single channel records is difficult or impossible. First, the probability density function (pdf) of opening events, a statistical property of single channel records, is derived from the normalized macroscopic current and mean channel open duration. Second, it is shown that under the conditions (I) and (II), a non-stationary Markov model can represent the stochastic process of channel gating. Third, the nonstationary Markov model is calibrated using the results of the first step.

The non-stationary formulation increases the model ability to generate a variety of different single channel records compared to common stationary Markov models. The model is then used to generate single channel records and to obtain other statistical properties of the records. Experimental single channel records of inactivating BK potassium channels are used to evaluate how accurately this procedure reconstructs measured single channel sweeps.

INTRODUCTION

Recording of single ion channel current using the patch clamp technique [1] revealed that the ion channels exhibit discrete conductance levels, typically fully open or fully closed [1, 2]. Recordings of the same ion channel under the same test conditions exhibit different opening and closing patterns, suggesting that they should be characterized using statistical methods. Fractal models [3–6] and Markov models [7] are two types of models used for modeling ion channel kinetics. However, Markov models have been shown to predict experimental data better than fractal models [8–13] and are the accepted statistical models commonly used in the scientific literature. Statistical analysis of single channel records has been used to construct and calibrate appropriate Markov models [14–21] and also to relate macroscopic current fluctuations to single channel properties [22–25]. Effects of different environmental conditions (e.g. temperature, inhibitors and other biochemical modulators) on single channel data and their statistical properties have also been of great interest [26, 27].

For many channels under particular test conditions, the direct measurement of single channel currents is difficult to perform or even impossible. For example, if the membrane voltage is close to the Nernst potential (small driving force) or if the single channel conductance is small (e.g. I_Kr, the cardiac rapid delayed rectifier K⁺ current), then the amplitude of the single channel current will be small and indistinguishable from the measurement noise. In certain cases, ion channels form a cluster or reside very close to each other (e.g. I_Ks, the cardiac slow delayed rectifier K⁺ current), making it extremely difficult or impossible to clamp a single channel to measure its current [28].

When the amplitude of single channel current is small, it may be possible to increase the current to a distinguishable level by increasing the driving force through changing the ion concentration to a non-physiological level. This way, the voltage dependent properties remain unaffected. In some cases, the open channel conductance depends on the ion concentration (e.g. I_Kr) and changing the ion concentration may increase single channel conductance as well [29]. Single channel currents under physiological conditions can then be estimated by adjusting the parameters of the stochastic model that was calibrated initially to the non-physiological conditions [30]. In cases where direct measurement of single channel currents is not possible, various single channel properties can still be derived from macroscopic current measurements. Fluctuation analysis is one such example, used to derive the amplitude of single channel current and the channel open probability [22]. Fluctuation analysis, however, does not provide information about the statistics of channel gating.

The goal of this work is to formulate a method for estimating statistical properties of single channel sweeps and for generating these sweeps from the (measurable) macroscopic current. Clearly, it is not possible to derive every statistical property of single channel records and to construct the records solely from the macroscopic current. In this paper we present a method for estimating single channel records from the macroscopic current assuming that the stochastic process of channel gating has certain properties. For the purpose of analysis presented here, we use recorded single-channel data from inactivating BK potassium channels [31].

METHODS

We first describe the derivation of statistical properties of single channel sweeps from macroscopic current using the results of the accompanying paper [32]. Then, we introduce a non-stationary Markov model which can be calibrated using these derived statistical properties and the macroscopic current. We use this model to generate single channel sweeps and to derive additional statistical properties. Finally, we use experimental single channel data recorded from inactivating BK potassium channels to validate the analysis and evaluate accuracy with which the non-stationary Markov model reconstructs the single-channel data.

Macroscopic current is defined as the summation of many single channel records of either an individual channel in repetitive tests or different channels of the same type in the same test. In this definition, we implicitly assume that all the channels of the same type have similar properties. The amplitude of single channel current, I_os, scales the macroscopic current. Similarly, the number of records, N, or number of channels, N_ch, which contribute to the macroscopic current scale the current linearly (for sufficiently large N or N_ch). Normalized macroscopic current, G(t), is defined by dividing the macroscopic current by I_os and N_ch (or N) [32]. The following distribution functions are chosen to represent the statistical properties of single channel records: H(t), the probability density function (pdf) of opening events; D(t), the pdf of the open duration; F(t), the pdf of latency to first opening; E(n), the distribution of the number of openings per record; R(t), the cumulative density function (cdf) of closed duration (including the closed duration before the first opening). In our analysis, we sometimes use the cumulative density function of opening events, P(t), and of open duration, Q(t), which are the time integrals of H(t) and D(t), respectively. Table 1 provides definitions and abbreviations of the parameters used in this paper. In this study the generation of single channel records from the macroscopic current is achieved by assuming two properties for the underlying stochastic process of channel gating. (I): The duration of openings is assumed to be independent of the time that the channel has opened and can be represented with a single exponential pdf. This behavior has been validated experimentally for many channels (including sodium channels, many types of potassium channels and of calcium channels) and can be represented by a single open-state Markov model for channel kinetics [8, 16, 30, 33–35].

Table 1.

DEFINITIONS AND ABBREVIATIONS

D(t)	pdf of open duration
Q(t)	cdf of open duration
H(t)	pdf of opening events
P(t)	cdf of opening events
R(t)	cdf of closed duration
E(n)	Distribution of the No. of openings per record
F(t)	pdf of latency to first opening
G(t)	Normalized macroscopic current
Imac(t)	Macroscopic current
η(t)	Probability of transition from closed to open state
α	Probability of transition from open to closed state
L(t)	Probability of the channel staying closed until time t
L*(t1, t2)	Probability of the channel staying closed between times t1 and t2
φ(t;n)	probability of n openings after time t if the channel is closed at t
τ	Mean open duration
τcap	The cap value of mean open duration
Ios	Amplitude of single channel current
N	Number of single channel records
Nch	Number of channels contributing to the macroscopic current

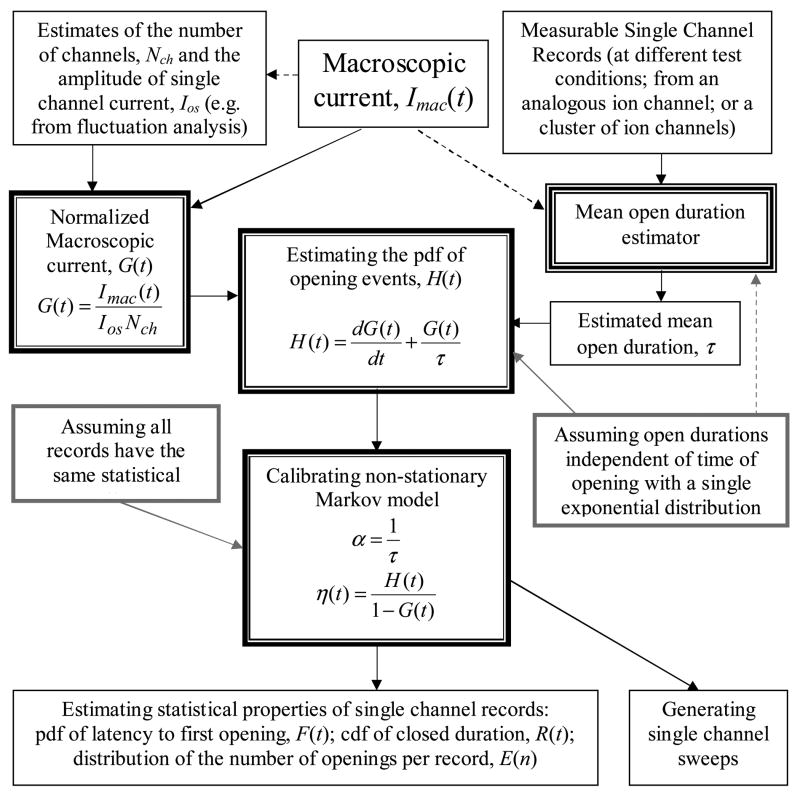
For the inverse procedure presented here for generating single channel sweeps from macroscopic current, the following parameters are required: the number of channels that generates the macroscopic current, N_ch, the amplitude of single channel current, I_os, and the mean channel open duration, τ. Estimates of these parameters can be found using fluctuation analysis of the macroscopic current or through other indirect measurement techniques [36]. Using these three parameters subject to the open-duration independence assumption, we derive the probability density function of opening events, H(t), from the macroscopic current. H(t) is the probability of an opening event in all sweeps and does not include information about how these openings are distributed among different sweeps. Generating the single channel records requires an additional assumption. We assume that (II): all sweeps have the same statistical pattern; in particular, the channel has the same probability to open between any t and t+dt in all the records. Figure 1 provides a flowchart of the procedure.

Figure 1.

Flowchart of the procedure for generating single channel sweeps and statistical properties from macroscopic current. Arrows indicate the direction of flow; grey boxes and arrows indicate assumptions; dashed arrows indicate steps that may or may not be necessary.

In order to test and validate our analysis, we use a set of 100 sweeps of single channel records from inactivating BK potassium channels. Recording and processing of these data and derivation of their statistical properties are explained in the accompanying paper [32]. The macroscopic current is calculated by summation of all sweeps in the set. The parameters I_os, and τ are measured directly from the data and N_ch is given by N, the number of records.

RESULTS

Calculating Statistical Properties of Channel Gating from Macroscopic Current

In the accompanying paper we showed that the normalized macroscopic current G(t) can be determined through the following equation:

$$G(t)=P(t)-H(t)\ast Q(t)=H(t)\ast (1-Q(t))$$ (1)

where * indicates convolution, H(t) is the pdf of opening events, and P(t) and Q(t) are time integrals of H(t) and D(t) (the pdf of open duration), respectively.

This relationship indicates that the two statistical properties of single channel records: the pdf of opening events, H(t) and the pdf of open duration, D(t), uniquely determine the normalized macroscopic current. Assuming a single-term exponential distribution for open duration, Q(t) becomes:

$$Q(t)=1-e^{-t/\tau }$$ (2)

where τ is the mean channel open duration and Equation (1) simplifies to:

$$G(t)=e^{-t/\tau }\underset{0}{\overset{t}{\int }}H(\zeta )e^{\zeta /\tau }d\zeta$$ (3)

Equation (3) can be used to find a closed form expression for H(t) in terms of G(t) and mean channel open duration, τ. Taking derivative of both sides of Equation (3) and performing algebraic simplifications provides the following expression for H(t):

$$H(t)=\frac{dG(t)}{dt}+\frac{G(t)}{\tau }$$ (4)

Therefore, knowing the mean channel open duration, τ, the probability density function of opening events, H(t), can be derived from the normalized macroscopic current. H(t) is a statistical property of single channel data that can be derived from the macroscopic current. This derivation is based on the reasonable assumption that the pdf of open duration is a single exponential function, independent of the time of opening event.

Constructing a Non-Stationary Markov Model for Generating Single Channel Sweeps from Macroscopic Current

Single channel records can be treated as the ensembles of a stochastic process. From quantitative knowledge of this process, one can generate single channel sweeps. In order to do so using some known statistical properties of channel gating, a suitable stochastic model should be calibrated to these properties. This calibrated model can be assumed to represent the underlying stochastic process of the single channel data and can be used to generate the single channel sweeps. Of course, if calibration were accurate, the statistical properties used to calibrate the model should appear in the generated data. In addition, other statistical properties of channel gating (not used to calibrate the model) can be derived from the generated sweeps.

The stochastic model we implement for generating the single channel sweeps is a nonstationary model that incorporates the Markov assumptions for transitions between closed (nonconducting) and open (conducting) states. In this model, opening and closing of the ion channel obey the following rules:

1. After applying a sudden voltage change or change in environmental conditions there is a transient change in the opening and closing patterns of the ion channel that finally settles to a steady state behavior.

2. Transition from a closed sate to an open state is a nonstationary Markov process. It does not depend on the behavior (history) of the channel from the beginning of the test, but it does depend on the time from the beginning of the test.

3. Probability of transition from an open state to a closed state is a stationary Markov process. It does not depend on the previous channel behavior, or on time. It depends on the membrane voltage or other environmental conditions.

Here we study the model for a particular voltage clamp test, a sudden change of membrane voltage from the resting potential to a given test potential. How the model behavior varies with membrane voltage and other environmental conditions is reserved for future studies. Consistent with our experimental data, where the initial current (at resting potential) is zero, we perform our analysis for the case of zero initial current.

Assume that η(t) is the probability of channel opening at time t (if it is closed) and α is the probability of channel closing at any time (if it is open). In other words, the probability of a channel transition from the closed state to the open state between times t and t+dt is η(t)dt and the probability of reverse transition during this time is αdt. Figure 2 shows a schematic diagram of this model. Note that this is not a common (stationary) two state Markov model. Allowing the transition rates to be any function of time changes the nature of the model equations and enables the model to generate a variety of different single channel records.

Figure 2.

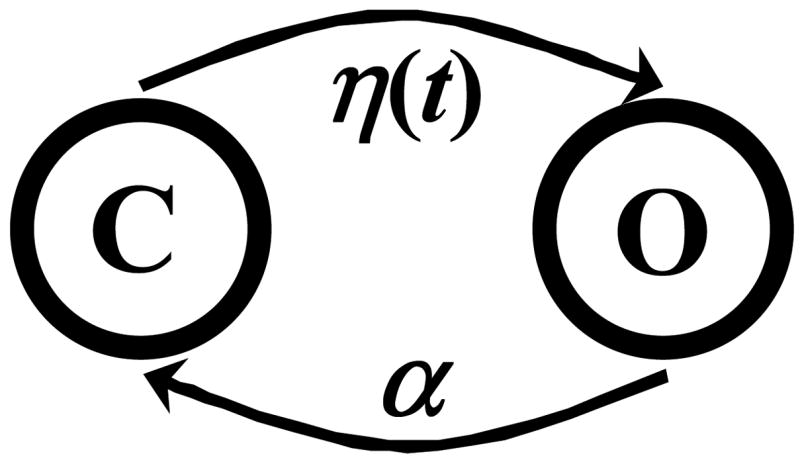
Schematic representation of the nonstationary Markov model. C is the closed state and O is the open state. η(t) is the transition rate from closed to open state at time t and α is the transition rate from open to closed state at any time.

In order to calibrate this model we must express the model parameters η(t) and α in terms of some statistical properties of single channel records. The assumption that the probability of transitions from the open to the closed state is constant leads to a single exponential pdf for open duration with a mean channel open duration of τ =1/α [37]. Therefore, α is the reciprocal of the (known or estimated) mean open duration. In order for an opening event to occur between t and t+dt, the channel must be in the closed state at time t and transition to the open state between t and t+dt. Therefore η(t) and H(t) are related through:

$$H(t)=\mathbf{P}(\text{Channel\hspace{0.17em}is\hspace{0.17em}in\hspace{0.17em}closed\hspace{0.17em}state})•\eta (t)$$ (5)

where P indicates probability. We can write:

$$\mathbf{P}(\text{Channel\hspace{0.17em}is\hspace{0.17em}in\hspace{0.17em}closed\hspace{0.17em}state})=1-\mathbf{P}(\text{Channel\hspace{0.17em}is\hspace{0.17em}in}\hspace{0.17em}\text{open\hspace{0.17em}state})=1-G(t)$$ (6)

Substituting G(t) from equation (1):

$$\eta (t)=\frac{H(t)}{1-G(t)}=\frac{H(t)}{1-P(t)+H(t)\ast Q(t)}$$ (7)

η(t) can be calculated from the normalized macroscopic current G(t) using Equation (7). Note that H(t) is expressed in terms of G(t) and τ (Equation (4)) so given an estimate of τ, η(t) can be computed from G(t). Knowing α and η(t), the stochastic model is calibrated and then used to generate single channel currents. The generated sweeps have the same pdf of open duration, D(t), and the same pdf of opening events, H(t), used for the calibration.

Deriving Model Generated Statistical Properties of Single Channel–Sweeps

We choose three statistical properties not used for calibration, to evaluate the model and above procedure; these are the pdf of the latency to first opening, F(t); the distribution of the number of openings per records, E(n); the cdf of closed duration. In the following we explain how to derive these statistical functions analytically for the single channel sweeps generated by the stochastic model.

In order for the first channel opening to occur between t and t+dt, the channel should remain closed until t and transition to the open state between t and t+dt. As the opening is a Markov process in the model, we can write:

$$\begin{array}{l}\mathbf{P}(\text{First\hspace{0.17em}opening\hspace{0.17em}happens\hspace{0.17em}between\hspace{0.17em}}t\hspace{0.17em}\text{and\hspace{0.17em}}t+dt)=\mathbf{P}(\text{Channel\hspace{0.17em}remains\hspace{0.17em}closed}\hspace{0.17em}\text{until\hspace{0.17em}}t)•\\ \mathbf{P}(\text{Channel\hspace{0.17em}opens\hspace{0.17em}between\hspace{0.17em}}t\hspace{0.17em}\text{and\hspace{0.17em}}t+dt)\end{array}$$ (8)

Defining L(t) as the probability of channel remaining closed until t, (8) becomes:

$$F(t)\hspace{0.17em}dt=L(t)\hspace{0.17em}\eta (t)\hspace{0.17em}dt$$ (9)

To find F(t) we need to find L(t). L(t) can be found in terms of η(t) using a simple analysis as follows:

$$L(t+dt)=L(t)•\mathbf{P}(\text{Channel\hspace{0.17em}remains\hspace{0.17em}closed\hspace{0.17em}between\hspace{0.17em}}t\hspace{0.17em}\text{and}\hspace{0.17em}t+dt)$$ (10)

but we know:

$$\mathbf{P}(\text{Channel}\hspace{0.17em}\text{remains\hspace{0.17em}closed\hspace{0.17em}between\hspace{0.17em}}t\hspace{0.17em}\text{and\hspace{0.17em}}t+dt)=1-\eta (t)\hspace{0.17em}dt$$ (11)

Combining these two equations provides:

$$\begin{array}{l}L(t+dt)=L(t)(1-\eta (t)dt)\to L(t+dt)-L(t)=-\eta (t)L(t)dt\\ \Rightarrow \frac{dL(t)}{L(t)}=-\eta (t)dt\end{array}$$ (12)

This differential equation can be solved with initial condition L(0) = 1 to provide:

$$L(t)=e^{-\underset{0}{\overset{t}{\int }}\eta (\zeta )d\zeta }$$ (13)

and:

$$F(t)=\eta (t)e^{-\underset{0}{\overset{t}{\int }}\eta (\zeta )d\zeta }$$ (14)

Note that F(t)dt is the probability that the first opening of the channel (if any) occurs between t and t+dt, which is a scale of the pdf of the time of first openings; the scaling factor is the proportion of records with at least one opening. The associated statistical parameter is the time of first opening (a random variable). For a finite time interval of the length Δt between t and t+Δt, F(t)Δt (in our definition) is the number of first openings during this interval in all the records, divided by the number of records. The pdf of the time of first opening is the number of first openings during this interval in all records, divided by the total number of first openings. The distribution of the number of openings per record is basically the probability of a channel opening n times, where n = 0, 1, 2, 3…. n = 0 is the probability that the channel never opens and remains closed; it equals L(∞).

We define φ(t;n) as the probability of n openings after time t if the channel is closed at t. For n = 1 the channel should open once after time t, at an arbitrary time t_o. The channel should remain closed between t and t_o, transition to open state between t_o and t_o+dt and stays open for an arbitrary period d, then remain closed until t =∞. This probability can be found by integrating over all possible combinations of t_o and d. The probability that a channel stays closed between two arbitrary times, t₁ and t₂ is a generalized form of Equation (13) and is given by:

P (Channel stays closed between times t₁ and t₂) =

$$L^{\ast }(t_1,t_2)=e^{-\underset{t_1}{\overset{t_2}{\int }}\eta (\zeta )d\zeta }=e^{-\left(\underset{0}{\overset{t_2}{\int }}\eta (\zeta )d\zeta -\underset{0}{\overset{t_1}{\int }}\eta (\zeta )d\zeta \right)}=\frac{L(t_2)}{L(t_1)}$$ (15)

And so φ(t;1) will be:

$$\phi (t;1)=\underset{t}{\overset{\infty }{\int }}\underset{0}{\overset{\infty }{\int }}\frac{L(\xi )}{L(t)}\eta (\xi )D(\zeta )\frac{L(\infty )}{L(\xi +\zeta )}d\zeta d\xi =\frac{L(\infty )}{L(t)}\underset{t}{\overset{\infty }{\int }}\underset{0}{\overset{\infty }{\int }}\frac{L(\xi )\eta (\xi )D(\zeta )}{L(\xi +\zeta )}d\zeta d\xi$$ (16)

For n>1 we can obtain each φ(t;n+1) function in terms of the φ(t;n) function. For a channel to have n+1 openings after time t it should open first at an arbitrary time t_o> t with a duration d and experience n additional openings after time t_o+d. Integrating over all possible combinations of t_o and d yields:

$$\phi (t;n+1)=\frac{1}{L(t)}\underset{t}{\overset{\infty }{\int }}\underset{0}{\overset{\infty }{\int }}L(\xi )\eta (\xi )D(\zeta )\phi (\xi +\zeta ;n)d\zeta d\xi$$ (17)

Clearly, the probability of a channel experiencing n openings during a recording is:

$$E(n)=\phi (0;n)$$ (18)

The pdf of closed duration can be found using a similar derivation and is given by:

$$R(t)=\frac{1-L(t)+\underset{0}{\overset{\infty }{\int }}(1-L^{\ast }(\zeta ,t+\zeta ))J(\zeta )d\zeta }{1-L(\infty )+\underset{0}{\overset{\infty }{\int }}(1-L^{\ast }(\zeta ,\infty ))J(\zeta )d\zeta }$$ (19)

where

$$J(t)=H(t)\ast D(t)$$ (20)

Computing a Cap Value for Mean Channel Open Duration

For inactivating channels, Equation (4) also provides a cap value on the possible range of mean channel open duration based on the shape of the macroscopic current. For inactivating channel data there exists a region in the time domain where G(t) decreases and its derivative is negative. But as H(t) can not become negative, in any region where the derivative of G(t) is negative the term G(t)/τ (which is always a positive term) should be greater than the magnitude of the derivative of G(t) (Equation (4)). The smallest value of τ that makes H(t) zero on at least one point, t_o, is the cap value of the mean open duration, τ_cap; for any τ greater than this cap there is a region in the time domain where H(t) is negative, a non physical behavior. At the critical τ = τ_cap the derivative of H(t) is zero at t = t_o and so:

$$\begin{array}{l}H(t)=G^{\prime }(t_o)+\frac{G(t_o)}{{\tau }_{\mathit{cap}}}=0\\ H^{\prime }(t)=G^{″}(t_o)+\frac{G^{\prime }(t_o)}{{\tau }_{\mathit{cap}}}=0\end{array}$$ (21)

Therefore the magnitudes of τ_cap and t_o can be found from the intersection of the following two curves:

$$\begin{array}{l}\frac{1}{\tau (t)}=-\frac{G^{\prime }(t)}{G(t)}=\mathrm{\Psi }(t)\\ \frac{1}{\tau (t)}=-\frac{G^{″}(t)}{G^{\prime }(t)}=\mathrm{\Gamma }(t)\end{array}$$ (22)

Application to Measured Data

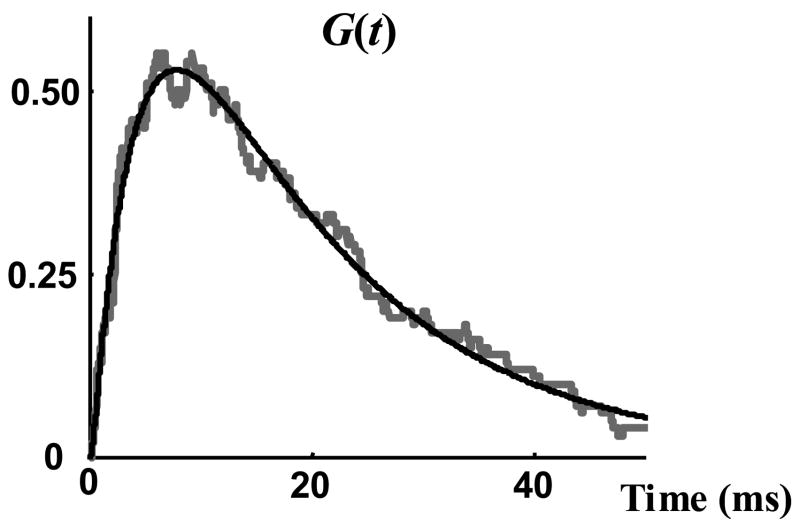
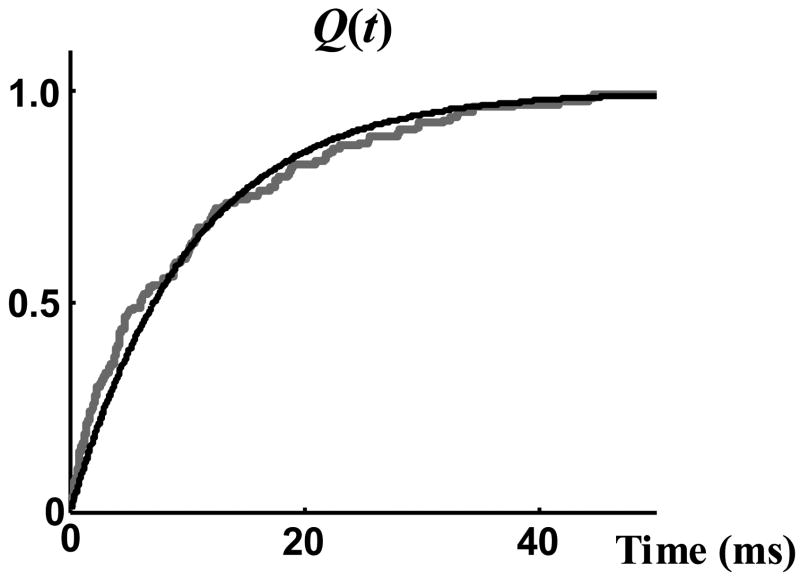
The single channel data used to evaluate the analysis and modeling approach and their statistical properties have been described in the accompanying paper [32]. Normalized macroscopic current, G(t), was derived by dividing the average of all 100 sweeps by the amplitude of single channel current. This amplitude, I_os, was 19.5 pA as measured directly from the single channel records. G(t) was fitted by a three-term exponential function (Figure 3) and this continuous function was used to represent G(t) in all computations. In order to find τ, a single exponential curve in the form of Equation (2) was fitted optimally to the measured cdf of open duration, Q(t) (Figure 4). The close fit of Q(t) by a single exponential function confirms that Equation (4) can be used to obtain the pdf of opening events, H(t), from the normalized macroscopic current, G(t). The time constant of this curve is the mean channel open duration τ = 10.3 ms; the same value is obtained through direct measurement.

Figure 3.

Normalized macroscopic current, G(t). Grey curve is the macroscopic current derived from experimental single channel records. Black curve is a three time constant exponential curve fitted to the macroscopic current.

Figure 4.

Cumulative density function (cdf) of open duration, Q(t). Grey curve is the cdf measured from the data and black curve is a single exponential fitted to the measured cdf.

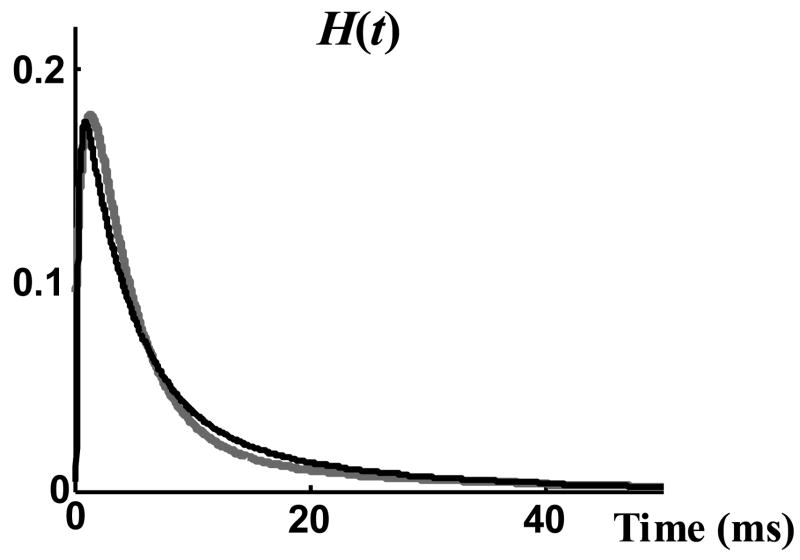
Figure 5 shows H(t) calculated through Equation (4) (black curve) and measured directly from the data (grey curve). This figure shows how close Equation (4) can predict the pdf of opening events. The small differences between the prediction of Equation (4) for H(t) and the actual measured H(t) is related to the small imperfections of fitting Q(t) by a single exponential curve (Figure 4). Insightful information about the kinetics of channel gating can be deduced by comparing H(t) and G(t). Comparing Figures 3 and 5, it can be seen that channel opening reaches its fastest rate (maximum of H(t)) about 1 ms after the beginning of test, but the number of channels in the open state reaches its maximum (maximum G(t)) only 7 ms later. After about 20 ms there are very few opening events (Figure 5). By that time the macroscopic current (Figure 3) has declined to about 50% of its maximum value; it decreases to zero exponentially due to the closure of channels that are already in the open state. Therefore, during the increasing phase of the macroscopic current both opening and closing of ion channels shape the current, but the decreasing tail of the macroscopic current is shaped only by the closure of open channels.

Figure 5.

pdf of opening events, H(t). The measured pdf of opening events (grey) is compared with the prediction of Equation (4) (black).

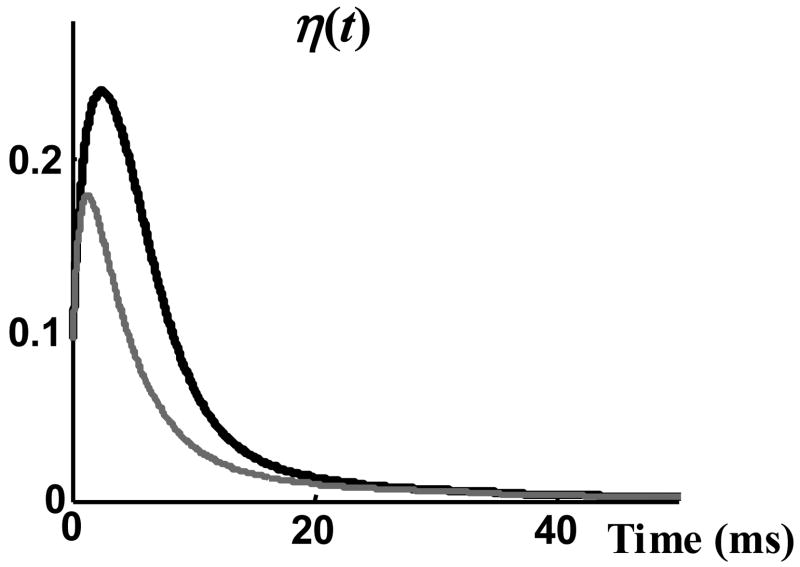
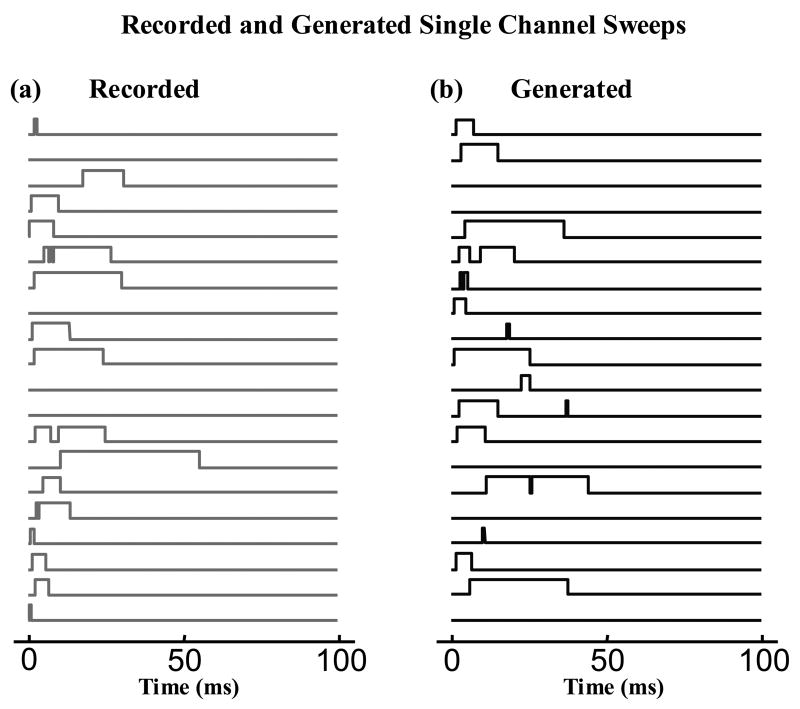
The nonstationary Markov model was calibrated by finding its parameters, α and η(t). α was found simply by inverting the $\tau :\alpha =\frac{1}{\tau }\approx 97\hspace{0.17em}{\text{s}}^{-1}·\eta (t)$ was found through Equation (7) from the measured function H(t) (Figure 6). Figure 7a shows samples of square pulse representation of experimentally recorded single channel currents and Figure 7b shows a set of single channel sweeps generated using the calibrated stochastic model. Both sets of sweeps appear similar, but because of their stochastic nature, it is difficult to determine how similar they are based on observation alone. In order to compare two sets of single channel records (recorded and generated) quantitatively, one can compare their statistical properties (e.g. pdf of the latency to first opening, of open duration, of closed duration, and the number of openings per record). But, it can not be concluded that if certain statistical properties of two data sets are the same, the data sets are identical and therefore their other statistical properties are the same. Obviously, the likelihood that two data sets have been generated by similar stochastic processes increases with the number of independent statistical properties that are similar between the two sets.

Figure 6.

Model parameter η(t). η(t), the probability of channel opening (black), is compared with H(t), the probability of an opening event (grey).

Figure 7.

Samples of single channel sweeps. a) Square-pulse representation of experimentally recorded single channel currents. b) Single channel sweeps generated with the calibrated nonstationary Markov model.

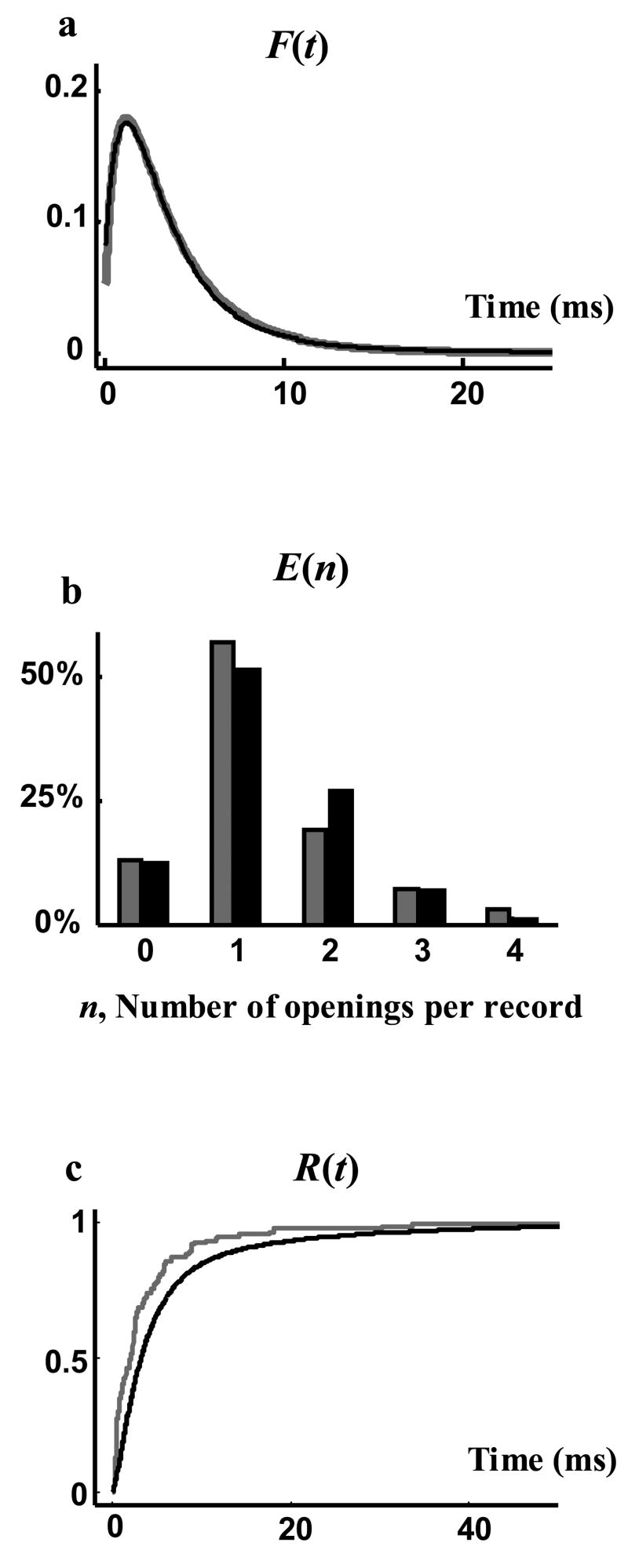
Because the nonstationary Markov model was calibrated to the pdf of opening events and pdf of open duration of the recorded data, these two pdf and consequently the macroscopic current are the same in both recorded and generated data. However, other statistical properties of recorded and generated data could be different. To evaluate how closely the calibrated non-stationary Markov model represents the stochastic process of channel gating and generates the statistics of single-channel records, we compare other independent statistical properties of single channel sweeps, not used for calibration: the pdf of the latency to first opening, F(t), the cdf of closed duration, R(t), and the distribution of the number of openings per record, E(n). The prediction of the model for F(t), E(n) and R(t) is calculated using Equations (14), (18) and (19) respectively, where the φ function is defined by Equations (16) and (17). These three statistical properties are measured from the data and compared with the model prediction. As shown in Figure 8a, the model prediction for F(t) (black curve) is superimposed on the measured F(t) (grey curve). Figure 8b shows the prediction of the model for E(n) (black bars) compared to the measured values (grey bars). The close agreement between the model predictions and the actual values of the functions F(t) and E(n) indicates that the nonstationary Markov representation is an appropriate stochastic model for predicting these two statistical properties from the macroscopic current. Figure 8c shows that the cdf of closed duration, R(t), can also be approximated by its model estimate.

Figure 8.

Evaluating the ability of the estimation procedure to generate statistical properties of single-channel sweeps from macroscopic current. a) Latency to first opening density function, F(t), of the single channel records (grey) compared with the one estimated from Equation (14) (black). b) Distribution of the number of openings per record; grey is the measured and black is the analytical estimation of Equations (15)–(18).

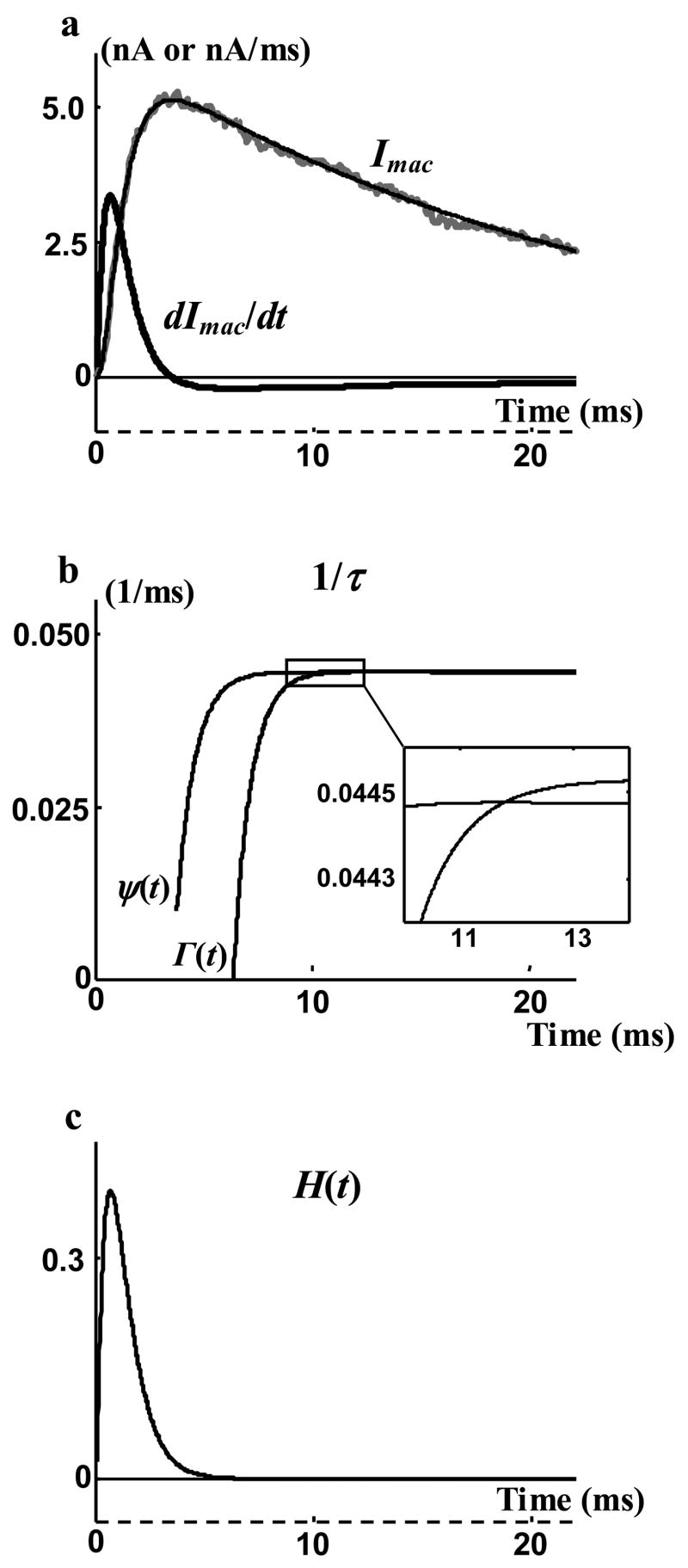
The macroscopic current of BK potassium channels (presented in Figure 3 of the accompanying paper [32]) was used to find the cap value of channel mean open duration using Equation (4). Figure 9a shows this macroscopic current and its derivative. First, the experimentally measured macroscopic current (grey curve) was fitted with a smooth curve (thin black curve) and then the derivative of this smooth curve was used as the derivative of the macroscopic current (thick black curve). The unit of the vertical axis for macroscopic current is nA and for its derivative is nA/ms. The two curves of Equation (22) and their intersection is shown in Figure 9b. At the intersection t_o=11.8 ms and 1/τ is 0.04444 (ms)⁻¹ resulting in τ_cap = 22.5 ms. Figure 9c shows the H(t) calculated for τ = τ_cap. Although mathematically H(t) becomes zero at t =11.8 ms, H(t) is very small 5 ms after beginning of the test and can practically be assumed zero at all later times.

Figure 9.

Finding a cap value for mean channel open duration, τ_cap. a) Macroscopic current and its derivative. b) The two curves of Equation (22) over the range where the derivative of the macroscopic current is negative. Inset magnifies the intersection region. c) The pdf of opening events, H(t), for the cap value of mean channel open duration.

DISCUSSION

For many ion channels, measurement of single channel current is very difficult or even impossible. For these channels, however, the macroscopic current (through a large patch or in the whole cell) can be measured with much less difficulty in most cases. Therefore, it is highly desirable to be able to obtain information about single-channel recordings from the macroscopic current (an “inverse problem”). In this paper we present a procedure to approximate single channel sweeps and their statistical properties from the macroscopic current when the stochastic process of channel gating has certain properties (mentioned in the METHOD section). We introduce a non-stationary Markov model with two parameters η(t) and α that represents the stochastic process of channel gating with these properties. This model is calibrated using the normalized macroscopic current and the mean channel open duration. Therefore, it can be used to generate approximate single channel records from the macroscopic current when the mean channel open duration is known. This procedure assumes that three channel properties are known: the number of channels, the amplitude of single channel current and the mean channel open duration. Fluctuation analysis can be used to find estimates of the number of channels and amplitude of single channel current [22]. Alternatively, the number of channels can be estimated from labeling procedures [36]. For completely inactivating channels, the mean channel open duration can be estimated from the time constant of the decaying tail current or from the power density spectrum of the current [24, 38, 39] (Note that by decaying tail we mean the end portion of the decreasing phase of current, not the entire decreasing phase.). Anderson and Stevens first mentioned this possibility for a situation where all the openings occur at the beginning of the test with an exponentially (single term) distributed duration [24]. This estimate is accurate only if the open duration obeys a single exponential distribution and its average is not much shorter than the duration of H(t) over which the opening events occur (e.g. sodium channels). It is not applicable to channels that show burst openings and variable burst length (e.g. L-type calcium channels) as in this case the open duration is much shorter than the duration of H(t). Therefore, for the inverse procedure introduced in this paper, this estimate can be used if it is known that the mean open duration of the single channel is not much shorter than the duration of the macroscopic current. We formulate a method for finding the maximum possible mean open duration, τ_cap, from the macroscopic current, assuming a single exponential pdf for open duration. This cap value is always less than the time constant of the decaying tail of macroscopic current if it decays exponentially. The difference between the time constant of the decaying tail of macroscopic current and τ_cap is not significant for the experimental macroscopic current presented in this paper. However, this difference can be significantly larger as shown in Figure 10. Figure 10a shows a hypothetical macroscopic current with an exponentially decaying tail. The time constant of the decaying tail (grey part of the curve) is 19.0 ms. In Figure 10b the two Γ and Ψ functions of this macroscopic current are drawn. The intersection of these two curves predicts a cap value of 10.8 ms for the mean open duration which is considerably shorter than the time constant of the tail of the macroscopic current. This happens when there are some opening events in the tail portion of the macroscopic current, or when the pdf of open duration is not a single-term exponential function.

Figure 10.

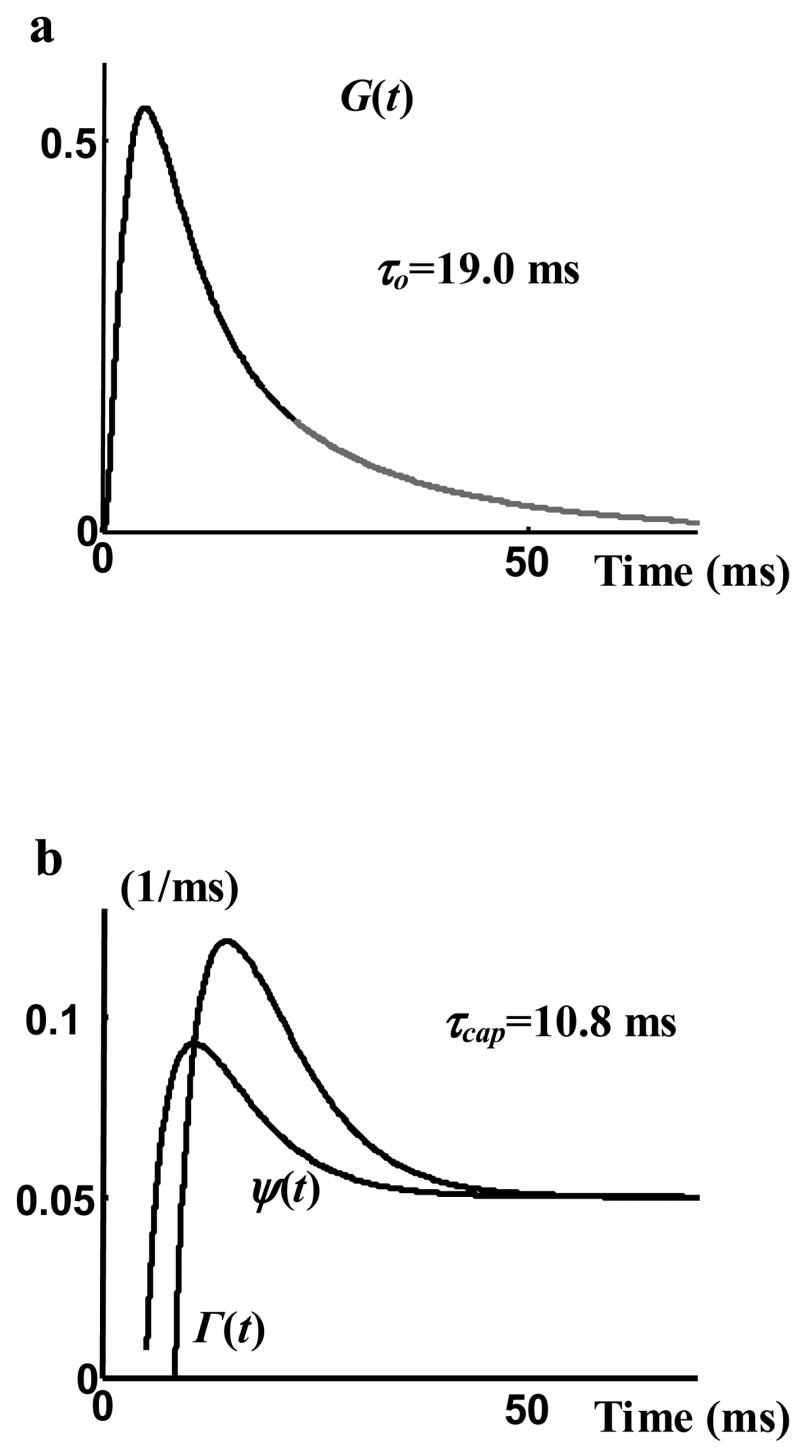
a) A curve assumed to represent a macroscopic current. The grey portion was chosen as the decaying tail and could be fitted accurately by a single exponential curve with time constant of 19.0 ms. b) The two curves of Equation (22) over the range where the derivative of the macroscopic current is negative. The intersection predicts a much smaller cap value of 10.8 ms.

Mean open duration can be estimated using alternative methods as well. One situation where the recording of a single channel current is extremely difficult or not possible is for ion channels that form clusters or reside very close to each other (e.g. I_Ks, the cardiac slow delayed rectifier K⁺ current). In such cases the current recorded from a micro-patch that contains a few channels still exhibits distinguishable transitions between open and closed states, making it possible to measure the mean open duration (even if there are intervals with more than one channel in the open state, and the number of channels in the patch is not known). Another scenario where single channel recoding is difficult or impossible is when the amplitude of single channel current is too small and indistinguishable from the measurement noise (either because of small ion channel conductance (e.g. cardiac I_Kr) or a small driving force). In this case, the channel mean open duration can be estimated from measurements at different membrane potentials or ion concentrations that augment the single channel current. For many ion channels, the variation of mean open duration with membrane potential and ion concentration is small compared to the variation of the macroscopic current [14, 26, 29, 30, 33, 40], making this estimate adequate for the procedure presented here.

The effect of mean open duration on the prediction of single channel statistics is illustrated in Figure 11 by comparing three H(t) functions resulting from three different mean channel open durations: 7, 14 and 21 ms, for the macroscopic current shown in Figure 9a. It should be mentioned that the time constant of the decaying tail of the current (after 30 ms) is 24.0 ms, greater than the 22.5 ms cap for the mean open duration, and so τ = 21 is a reasonable estimate for the mean channel open duration. The resultant H(t) for τ = 14 (dark grey) and τ = 21 (light grey) are very close to each other, the only difference is that for τ = 14 there is a very small probability for channel openings during the decaying tail of macroscopic current. Therefore, for this macroscopic current, reducing the mean channel open duration to two thirds its estimated value does not have a significant effect on prediction of the pdf of opening events. This is because the two estimated τ values are both much larger than the 0 to 5 ms range over which H(t) is significantly greater than zero.

Figure 11.

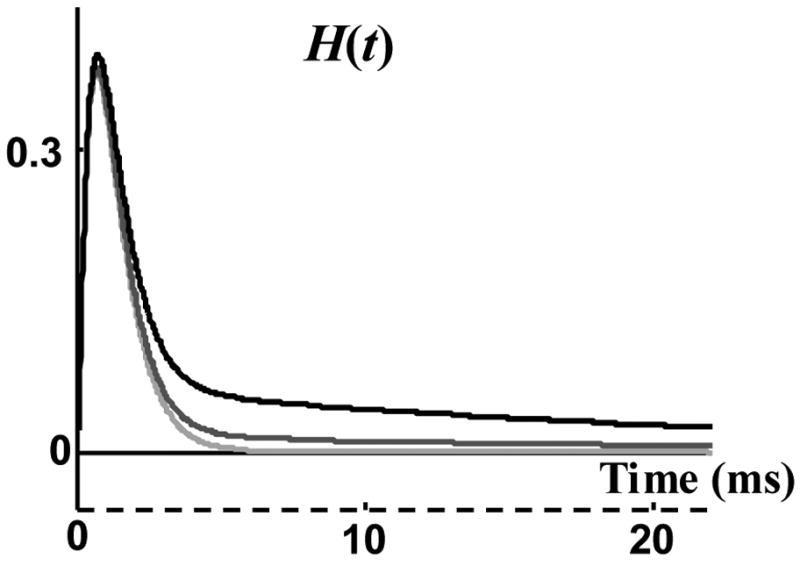
pdf of opening events, H(t), for three different mean channel open durations: 7 ms (black), 14 ms (dark grey), and 21 ms (light grey).

The multiplication of the number of channels and the amplitude of the single channel current is the factor used to normalize the macroscopic current. The estimate of the number of channels in the macroscopic patch or whole-cell may deviate from the actual number. As the measurement of macroscopic current is considered accurate, the relative error of the normalized macroscopic current, G(t), is equal to the relative error of the normalization factor which leads to the same relative error for H(t) through Equation (4). For example, if the estimated normalization factor is 1.05 times the accurate value, G(t) and H(t) will be 0.95 of their values computed with the accurate normalization factor. As a consequence, the estimation of η(t) will also differ from its estimation based on an accurate normalization factor. Unlike H(t), the error is not a constant fraction of η(t); it depends on the magnitude of G(t) and increases for G(t) close to one (Equation (7)). However, η(t) is the probability of channel opening at time t, if the channel is closed at that time. For G(t) close to one, most channels are in the open state and their behavior (next transition) is determined by α (probability of closing), which is a constant that does not depend on t or the normalization factor. Hence, the increased error in η(t) for large G(t) (e.g. G(t)=0.8) will have only a small effect on the statistical properties of the generated single channel records.

Accuracy of the generated records also depends on the validity of the underlying assumptions for the stochastic process of channel gating. In the accompanying paper it has been verified that for the BK channel records used here, the open duration (or equivalently the event of channel closure) is independent of the opening time and does not depend on previous openings [32]. In addition, the single exponential distribution of open duration (Figure 4) shows that the underlying assumptions of Equation (4) are valid and so the estimate of H(t) through this equation should be accurate (Figure 5). Clearly, this stochastic model generates single channel sweeps with mean channel open duration, pdf of opening events and macroscopic current similar to the experimental data, as it is calibrated to these properties. In addition to these statistical properties, this model accurately predicts other independent statistical properties of BK single channel records that are not used in calibrating the model, including pdf of latency to first opening, F(t), and the distribution of the number of openings per record, E(n) (Figure 8). The estimation of the model for the cdf of closed duration is not as accurate; however, it is still a reasonable estimate that provides a useful approximation when direct measurement is not possible. The difference in the distribution of closed duration between model and experiment suggests that the probability of channel opening at time t may not be equal among all records and depends to some extent on the history of channel behavior.

For the common stationary Markov structures, theoretically, there are infinite arbitrary choices of Markov structures, and infinite combinations of transition rates that can generate the same macroscopic current and mean open duration. However, the statistical properties of the single channel sweeps generated by these models can be very different. In the procedure of this paper, the non-stationary Markov model is not an arbitrary choice of a stochastic model. It is the unique stochastic model of channel gating subject to the constraints (I) and (II), determine a statistically unique set of single channel records which can be reconstructed by the inverse procedure presented here.