Effects of Multiple Metal Binding Sites on Calcium and Magnesium-dependent Activation of BK Channels

Abstract

BK channels are activated by physiological concentrations of intracellular Ca²⁺ and Mg²⁺ in a variety of cells. Previous studies have identified two sites important for high-affinity Ca²⁺ sensing between [Ca²⁺]_i of 0.1–100 μM and a site important for Mg²⁺ sensing between [Mg²⁺]_i of 0.1–10 mM. BK channels can be also activated by Ca²⁺ and Mg²⁺ at concentrations >10 mM so that the steady-state conductance and voltage (G-V) relation continuously shifts to more negative voltage ranges when [Mg²⁺]_i increases from 0.1–100 mM. We demonstrate that a novel site is responsible for metal sensing at concentrations ≥10 mM, and all four sites affect channel activation independently. As a result, the contributions of these sites to channel activation are complex, depending on the combination of Ca²⁺ and Mg²⁺ concentrations. Here we examined the effects of each of these sites on Ca²⁺ and Mg²⁺-dependent activation and the data are consistent with the suggestion that these sites are responsible for metal binding. We provide an allosteric model for quantitative estimation of the contributions that each of these putative binding sites makes to channel activation at any [Ca²⁺]_i and [Mg²⁺]_i.

INTRODUCTION

BK type large conductance K⁺ channels contain multiple binding sites for divalent cations that allow intracellular Ca²⁺ and Mg²⁺ to activate the channel at physiological concentrations ([Ca²⁺]_i, 0.1–100 μM; [Mg²⁺]_i, 0.4–3 mM) (Marty, 1981; Pallotta et al., 1981; Flatman, 1984; Gupta et al., 1984; Corkey et al., 1986; Golowasch et al., 1986; Flatman, 1991). Ca²⁺-dependent activation of the BK channel is key to its functions in a variety of physiological processes including neural excitation (Adams et al., 1982; Lancaster and Nicoll, 1987; Storm, 1987; Roberts et al., 1990; Robitaille and Charlton, 1992; Robitaille et al., 1993; Raffaelli et al., 2004; Sun et al., 2004), muscle contraction (Nelson et al., 1995; Tanaka et al., 1997; Perez et al., 1999; Brenner et al., 2000b; Pluger et al., 2000; Wellman and Nelson, 2003), hearing (Hudspeth and Lewis, 1988a, 1988b; Wu et al., 1995; Fettiplace and Fuchs, 1999; Ricci et al., 2000; Samaranayake et al., 2004), and immunity (Ahluwalia et al., 2004). The physiological function of Mg²⁺ dependence in BK channel activation has not been explored extensively. However, pharmacological studies have shown that Mg²⁺ may be an effective therapeutic agent following neurotrauma to improve survival and motor outcome and to alleviate cognitive deficits (Vink and Cernak, 2000). Magnesium supplements are also important in the prevention and management of cardiovascular diseases that predispose to hypertension or congestive heart failure (Laurant and Touyz, 2000; Seelig, 2000; Delva, 2003a,b,c; Touyz, 2003). Given the importance of BK channels in neurotransmitter release and vessel tone (Petersen and Maruyama, 1984; Stretton et al., 1992; Robitaille et al., 1993; Perez and Toro, 1994; Wang et al., 1994; Kume et al., 1995; Yazejian et al., 1997), Mg²⁺ modulation of BK channels may play a significant role in these pathophysiological processes.

Two sites important for Ca²⁺ sensing and one site important for Mg²⁺ sensing have been identified in the intracellular domain of the α subunit of BK channels, which is encoded by slo1 genes (Atkinson et al., 1991; Adelman et al., 1992; Butler et al., 1993; Dworetzky et al., 1994; Pallanck and Ganetzky, 1994; Tseng-Crank et al., 1994; Moss et al., 1996a,b; Schreiber and Salkoff, 1997; Schreiber et al., 1999; Bian et al., 2001; Braun and Sy, 2001; Zhang et al., 2001; Bao et al., 2002, 2004; Shi et al., 2002; Xia et al., 2002, 2004; Zeng et al., 2005). One site important for Ca²⁺ sensing is located in “Ca²⁺ bowl,” a motif that contains many Asp residues (Moss et al., 1996a,b; Schreiber and Salkoff, 1997; Schreiber et al., 1999; Bian et al., 2001; Braun and Sy, 2001; Xia et al., 2002; Bao et al., 2004). The other is located in the RCK1 domain (Bao et al., 2002; Xia et al., 2002), which is similar to a structural domain found in prokaryotic K⁺ channels important for regulating K⁺ conductance (Jiang et al., 2001, 2002). Mutations in Ca²⁺ bowl, such as the change of five consecutive Asp residues (D898 –902) into Asn, known as 5D5N and mutations in RCK1 such as M513I or D367A each reduces part of Ca²⁺ sensitivity of the channel (Schreiber and Salkoff, 1997; Bao et al., 2002; Shi et al., 2002; Xia et al., 2002). The site important for Mg²⁺ sensing was identified to contain E374, Q397, and E399 in the RCK1 domain of mslo1 (Shi et al., 2002; Xia et al., 2002). These previous results, primarily derived from mutational studies, suggest that these sites may be the candidates for metal binding sites. Previous studies have revealed complex effects of Ca²⁺ or Mg²⁺ binding on channel activation. Ca²⁺ at concentrations beyond physiological conditions can bind to the Mg²⁺ site, with a similar affinity as Mg²⁺, to activate the channel (Shi and Cui, 2001; Zhang et al., 2001); while Mg²⁺ at physiological concentrations can bind to Ca²⁺ sites and compete with Ca²⁺ (Shi and Cui, 2001). These complex effects of Ca²⁺ and Mg²⁺ on BK channel activation determine physiological functions of the channel and have been a major subject of structure–function studies in recent years (Bian et al., 2001; Braun and Sy, 2001; Shi and Cui, 2001; Zhang et al., 2001; Bao et al., 2002, 2004; Piskorowski and Aldrich, 2002; Shi et al., 2002; Xia et al., 2002; Qian and Magleby, 2003; Zeng et al., 2005). However, uncertainties regarding metal-binding sites and the effects of Ca²⁺ and Mg²⁺ binding still exist. Among these uncertainties, it was reported that the channel with a triple mutation 5D5N + D362A:D367A + E399A, which should have destroyed the three candidate metal binding sites, can be activated by high [Mg²⁺]_i (≥10 mM) (Xia et al., 2002).

In this paper we investigate BK channel activation at various [Mg²⁺]_i, [Ca²⁺]_i, and voltages in order to examine the effects of this novel Mg²⁺ dependence on channel activation at physiological [Mg²⁺]_i and [Ca²⁺]_i. We find that the effects of the two Mg²⁺-dependent activation at [Mg²⁺]_i around 10 mM overlap, and thus this novel Mg²⁺ dependence interferes with the study of Mg²⁺-dependent activation at physiological concentrations. On the other hand, we found that an additional metal binding site may contribute to this activation and residue D362 may be involved in channel activation at high metal concentrations. The mechanism of this novel Mg²⁺-dependent activation is independent from channel activation due to metal binding to other sites.

An abstract of this work has been presented at the 49th Annual Meeting of Biophysical Society.

MATERIALS AND METHODS

Clones, Mutagenesis, and Channel Expression

All channel constructs were made from the mbr5 clone of mslo1 (Cui et al., 1997) by using PCR with Pfu polymerase (Stratagene). The PCR-amplified regions of all mutants were verified by sequencing. RNA was transcribed in vitro with T3 polymerase (Ambion). We injected 0.05–50 ng of RNA into each Xenopus laevis oocyte 2–6 d before recording.

Electrophysiology

Macroscopic currents were recorded from inside-out patches formed with borosilicate pipettes of 1∼2 MΩ resistance. Data were acquired using an Axopatch 200-B patch-clamp amplifier (Axon Instruments, Inc.) and Pulse acquisition software (HEKA Electronik). Records were digitized at 20-μs intervals and low-pass filtered at 10 kHz with the 4-pole Bessel filter built in the amplifier. The pipette solution contained the following (in mM): 140 potassium methanesulfonic acid, 20 HEPES, 2 KCl, and 2 MgCl₂, pH 7.20. The basal internal solution (with buffer) contains the following (in mM): 140 potassium methanesulfonic acid, 20 HEPES, 2 KCl and 1 EGTA, pH 7.20. The basal internal solution (without buffer) contains the following (in mM): 140 potassium methanesulfonic acid, 2 KCl, pH 7.20. Methanesulfonic acid was purchased from Sigma-Aldrich. The “0 [Ca²⁺]_i” solution was the same as the basal internal solution (with buffer) except that it contained 5 mM EGTA (Fabiato and Fabiato, 1979). MgCl₂ was added to these internal solution (with buffer) to give the appropriate free [Mg²⁺]_i. For solutions with [Ca²⁺]_i < 100 μM, CaCl₂ was added to the basal internal solutions (with buffer) with amounts calculated using a program similar to published (Cox et al., 1997b; Shi and Cui, 2001) to give rise various free [Ca²⁺]_i. For solutions with [Ca²⁺]_i ≥ 100 μM, CaCl₂ was added to the basal internal solutions (without buffer) with calculated amounts. The free [Ca²⁺]_i was measured with a calcium-sensitive electrode (Orion Research Inc.) with the same procedure as previously described (Shi et al., 2002; Xia et al., 2002). The calcium-sensitive electrode was always calibrated right before measurements, and then recalibrated immediately after measurements. The results of calibration and recalibration were the same, indicating that the electrode was stable during measurements. 18-crown-6-tetracarboxylic acid (18-C-6-T; Sigma-Aldrich) was added to internal solutions to prevent Ba²⁺ block. For solutions with [Ca²⁺]_i ≤ 100 μM, 50 μM 18-C-6-T was added; for solutions with higher [Ca²⁺]_i, 100–150 μM 18-C-6-T was added. Experiments were conducted at room temperature (22°C–24°C).

Analysis and Model Fitting

Relative conductance was determined by measuring tail current amplitudes at −50 mV for WT and E374A:E399N mutant channels and at −120 mV for 5D5N + D367A + E399N and 5D5N + D362A:D367A + E399N mutant channels. The conductance–voltage (G-V) relations of the WT and mutant mslo1 channels were fitted with Boltzmann equation:

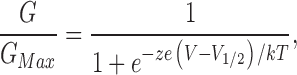(1)

where z is the number of equivalent charges, V_1/2 is the voltage for channel in half activation, e is the elementary charge, k is Boltzmann's constant, and T is the absolute temperature.

Eqs. 2, 3, and 4 are derived from the MWC models based on hypotheses 1, 2, and 3 respectively.

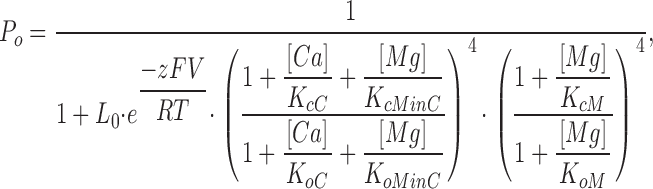(2)

where P_o is the probability of the channel being open; L₀ is the equilibrium constant between the closed and open states at the voltage of 0 mV when no Ca²⁺ or Mg²⁺ is bound (L₀ = [C₀]/[O₀]); z is the number of equivalent gating charges; K_cC and K_oC are the dissociation constants of Ca²⁺ binding to the Ca²⁺ site on each subunit when the channel is at closed and open states, respectively; K_cMinC and K_oMinC are the dissociation constants of Mg²⁺ binding to the Ca²⁺ site on each subunit when the channel is at closed and open states, respectively; K_cM and K_oM are the dissociation constants of Mg²⁺ binding to the Mg²⁺ site on each subunit when the channel is at closed and open states, respectively; and V, T, F, and R have their usual meanings.

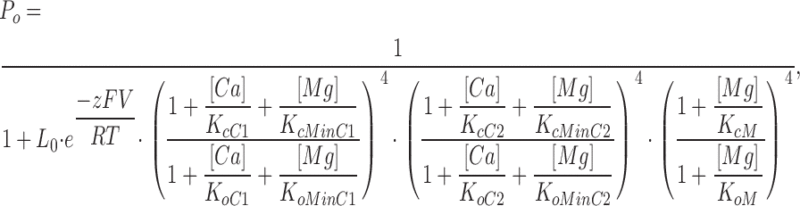(3)

where K_cC1, K_cC2, K_oC1, and K_oC2 are the dissociation constants of Ca²⁺ binding to the first and second Ca²⁺ sites on each subunit when the channel is at closed and open states, respectively; K_cMinC1, K_cMinC2, K_oMinC1, and K_oMinC2 are the dissociation constants of Mg²⁺ binding to the first and second Ca²⁺ sites on each subunit when the channel is at closed and open states, respectively, and K_cMinC1 = K_oMinC1; and other parameters have the same meaning as in Eq. 2.

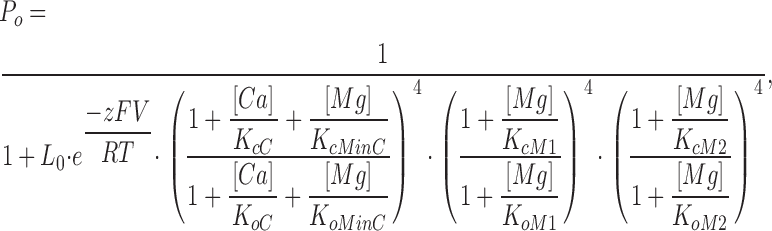(4)

where K_cM1, K_cM2, K_oM1, and K_oM2 are the dissociation constants of Mg²⁺ binding to the first and second Mg²⁺ sites on each subunit when the channel is at closed and open states, respectively, and other parameters have the same meaning as in Eq. 2 (K_cMinC = K_oMinC).

In fitting these models, the G-V relations of the WT and E374A:E399N mutant channels at various [Ca²⁺]_i and [Mg²⁺]_i were fitted with Eqs. 2–4 respectively using LSQCURVEFIT program in Matlab 6.1 (the MathWorks, Inc.). The parameters defining the models were acquired step by step through the model fittings as described in RESULTS. Rational lower and upper bounds of the parameters were set during model fitting. The equivalent charge, z, was assumed to be the same for both the WT and E374A:E399N mutant channels under all ionic conditions. The means of the data were obtained by averaging from 4 to 16 patches and error bars represent SEMs.

RESULTS

Activation of BK Channels at High (≥10 mM) and Low (0–10 mM) [Mg²⁺]_i

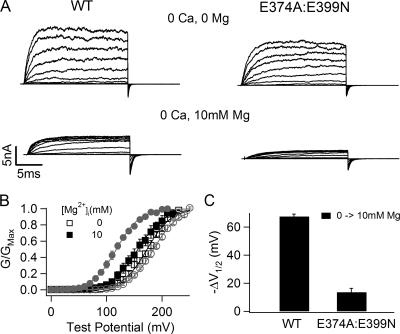
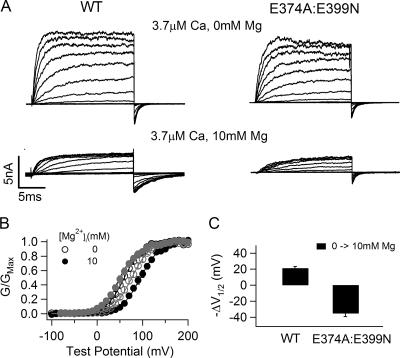
Previous studies have suggested that the residues E374 and E399 in the RCK1 domain of the mslo1 BK channels are important for Mg²⁺ sensing in the RCK1 domain of the mslo1 BK channels (Shi et al., 2002; Xia et al., 2002). Consistent with these studies, the double mutation E374A:E399N dramatically reduced the Mg²⁺ sensitivity when [Mg²⁺]_i increased from 0 to 10 mM (Fig. 1), indicating that the mutation has destroyed the ability of Mg²⁺ sensing mediated by this site. Fig. 1 A shows the WT and E374A:E399N mutant channel macroscopic currents recorded in inside-out patches with and without 10 mM [Mg²⁺]_i. The outward currents at positive voltages decreased in 10 mM [Mg²⁺]_i due to a fast, voltage dependent block of the channel (Ferguson, 1991; Laver, 1992; Shi and Cui, 2001). Upon the return of membrane potential to −50 mV, the block is relieved rapidly and the tail current of the WT mslo1 channel has a slower time course and a larger maximum amplitude in the presence of 10 mM [Mg²⁺]_i than at 0 [Mg²⁺]_i (5.5 vs. 3.7 nA), revealing that the channel is activated by Mg²⁺ (Shi and Cui, 2001). To the contrary, for the mutant channel, 10 mM [Mg²⁺]_i did not have obvious effects on the tail current. The effect of the mutation on Mg²⁺-dependent activation is more obviously shown by the conductance–voltage relation (G-V relation). Fig. 1 (B and C) shows that 10 mM [Mg²⁺]_i shifts the G-V relation for the WT channel by about −67 mV, indicating that the channels can be activated in more negative voltages with Mg²⁺ binding. However, for the mutant channel the shift of the G-V relation is reduced to about −14 mV.

Figure 1.

Mutation E374A:E399N reduces Mg²⁺ sensitivity. (A) Current traces of WT mslo1 channels (left) and E374A:E399N mutant channels (right) recorded at indicated [Mg²⁺]_i and [Ca²⁺]_i. Testing potentials were −20 to 240 mV with 20-mV increments. The holding and repolarizing potentials were −80 and −50 mV, respectively. (B) Mean G-V relations of WT mslo1 (gray symbols) and the mutant channels (black symbols) at 0 or 10 mM [Mg²⁺]_i and 0 [Ca²⁺]_i. G-V relations of these channels are fitted with the Boltzmann relation (solid lines, see MATERIALS AND METHODS). (C) Shift of G-V relations from 0 to 10 mM [Mg²⁺]_i at 0 [Ca²⁺]_i for WT mslo1 and the mutant channels. V_1/2 is the voltage where the G-V relation is at half maximum.

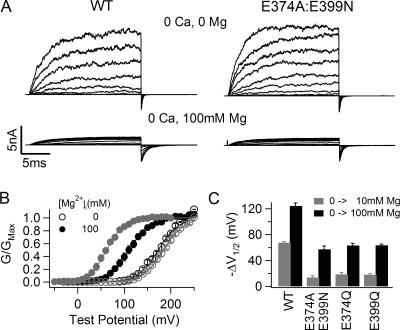
Although the destruction of the site at E374 and E399 reduces Mg²⁺ sensitivity of channel activation dramatically, a leftward shift of G-V relation is consistently observed in response to 10 mM [Mg²⁺]_i as shown in Fig. 1 C, indicating that the mutant channel remains Mg²⁺ sensitive. The remaining Mg²⁺ sensitivity of channel activation becomes more prominent when [Mg²⁺]_i increases to 100 mM (Fig. 2). Fig. 2 B shows G-V relations of the WT and E374A:E399N mutant channels at 0 and 100 mM [Mg²⁺]_i. Consistent with the previous observation (Shi and Cui, 2001), 100 mM [Mg²⁺]_i shifts the G-V relation of the WT channel by about −124 mV, −57 mV more than the leftward shift caused by 10 mM [Mg²⁺]_i (Fig. 2 C). For the mutant channel, 100 mM [Mg²⁺]_i shifts the G-V relation by about −57 mV, −43 mV more than the leftward shift by 10 mM [Mg²⁺]_i. The large G-V shift caused by 100 mM Mg²⁺ on the E374A:E399N mutant channel suggests that Mg²⁺ is still able to affect channel activation even though the mutation abolishes the ability of Mg²⁺ sensing mediated by this site. This result is consistent with a previous report that when E399 was mutated the channel was still sensitive to high concentrations of Mg²⁺ (Xia et al., 2002).

Figure 2.

Mg²⁺ sensitivity of WT mslo1 and mutant channels at high [Mg²⁺]_i. (A) Current traces of WT mslo1 channels (left) and E374A:E399N mutant channels (right) recorded at indicated [Mg²⁺]_i and [Ca²⁺]_i. Testing potentials were −70 to 190 mV with 20-mV increments for WT mslo1 channels at 100 mM [Mg²⁺]_i and 0 [Ca²⁺]_i; and were −20 to 240 mV with 20-mV increments for others. The holding and repolarizing potentials were −80 and −50 mV, respectively. (B) Mean G-V relations of WT mslo1 (gray symbols) and E374A:E399N mutant channels (black symbols) at 0 or 100 mM [Mg²⁺]_i and 0 [Ca²⁺]_i, and fits with the Boltzmann relation (solid lines). (C) G-V shifts at 0 [Ca²⁺]_i from 0 to 10 mM [Mg²⁺]_i (gray bars) and from 0 to 100 mM [Mg²⁺]_i (black bars) of WT mslo1 and mutant channels E374A:E399N, E374Q and E399Q.

We considered the possibility that the mutation might not have fully removed the ability of this site in mediating Mg²⁺ sensing so that Mg²⁺ in high concentration could still activate the channel. Fig. 2 C compares Mg²⁺ sensitivity of the double mutant E374A:E399N with two single mutants E374Q and E399Q. If the double mutant could not completely destroy Mg²⁺ sensing and left some residual Mg²⁺ sensitivity then each single mutant may destroy the site to a less extent and leave a higher Mg²⁺ sensitivity. However, contrary to this prediction, ΔV_1/2 (V_1/2 is the voltage where the G-V relation is half maximum) caused by 10 and 100 mM [Mg²⁺]_i are similar for both single mutations and the double mutation. In addition, although the activation of all mutant channels by Mg²⁺ at low concentration of 0–10 mM is largely reduced (Fig. 1), ΔV_1/2 between 10 and 100 mM [Mg²⁺]_i is similar among the WT and mutant channels (Fig. 2 C, subtracting gray bars from the black bars), indicating that the mutations affect Mg²⁺ sensitivity primarily in the concentration range between 0 and 10 mM but not between 10 and 100 mM. These results suggest that the ability of mediating Mg²⁺ sensing by the site at E374 and E399 may have been fully removed by the double and single mutations and the remaining Mg²⁺ sensitivity must be the consequence of some other mechanism.

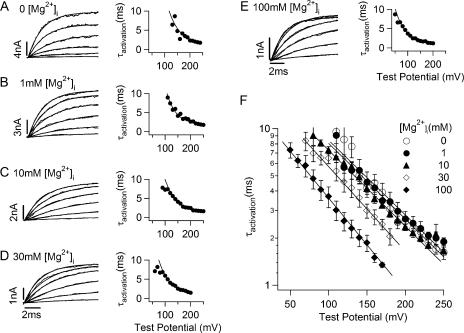
The differences between Mg²⁺-dependent activation at low (0–10 mM) and high [Mg²⁺]_i (10–100 mM) are also reflected on the kinetics of the channel gating. The left panels in Fig. 3 (A–E) show the current traces of the WT channel elicited by depolarization testing pulses in different [Mg²⁺]_is. Although the steady-state currents were reduced by Mg²⁺ block of the channel pore, the blocking was so fast as compared with the time course of channel activation (Ferguson, 1991; Laver, 1992; Shi and Cui, 2001) that the current trace could still be fitted with a single exponential function (Fig. 3, A–E). The corresponding activation constants as the function of testing voltages (τ-V relations) are shown on the right panels. The averaged τ-V curves at various [Mg²⁺]_i are plotted in Fig. 3 F. Unlike the shift of G-V relations caused by [Mg²⁺]_i changes from 0 to 10 mM, the τ-V relation does not shift as much (Fig. 3 F) (Horrigan, 2005; Zeng et al., 2005). However, τ-V relation shifts to the left as [Mg²⁺]_i increases to 30 and 100 mM (Fig. 3 F), similar to the shift of G-V relations in response to the same [Mg²⁺]_i changes (Fig. 2).

Figure 3.

Voltage and Mg²⁺ dependence of activation time courses of mslo1 channels. (A–E) Left panels, current traces recorded from a single membrane patch in response to depolarizing membrane voltages of 20 mM increments, and fitted with a single exponential function (thin curves). [Mg²⁺]_i was as indicated. Right panels, activation time constants as a function of test potential, and fits with the function τ = Ae ^−qFV/RT + b (solid curves). (F) Semi-log plots of mean activation time constants as a function of both voltage and [Mg²⁺]_i. Solid lines represent fits to the same function as in A–E.

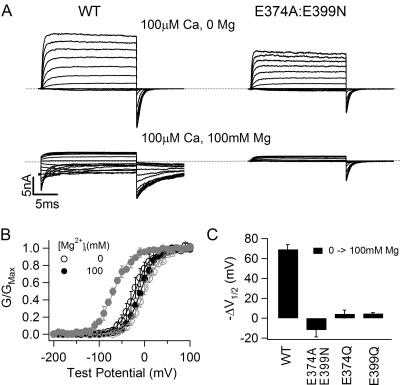
The effects of high [Mg²⁺]_i on channel activation appear differently at different [Ca²⁺]_i. Fig. 4 shows that in the presence of 100 μM [Ca²⁺]_i, the shift of G-V relations by 100 mM [Mg²⁺]_i is reduced for both WT and E374A:E399N mslo1 channels as compared with the shift at 0 [Ca²⁺]_i (Fig. 2). For WT channels, 100 mM [Mg²⁺]_i shifts the G-V relation to a more negative voltage range by about −70 mV. However, for the mutant channel, the G-V does not shift to more negative voltages at all, or even shifts slightly to more positive voltages (Fig. 4, B and C). The lack of G-V shift in response to 100 mM [Mg²⁺]_i at 100 μM [Ca²⁺]_i is the same for both single mutants E374Q and E399Q and the double mutant E374A:E399N (Fig. 4 C).

Figure 4.

Effects of 100 μM [Ca²⁺]_i on channel activation at high [Mg²⁺]_i. (A) Current traces of WT mslo1 channels (left) and E374A:E399N mutant channels (right) recorded at indicated [Mg²⁺]_i and [Ca²⁺]_i. Dashed lines indicate zero current. Testing potentials were −200 to 140 mV with 20-mV increments. The holding and repolarizing potentials were −80 and −100 mV, respectively. (B) Mean G-V relations of WT mslo1 (gray symbols) and E374A:E399N mutant channels (black symbols) at 0 or 100 mM [Mg²⁺]_i and 100 μM [Ca²⁺]_i, and fits with the Boltzmann relation (solid lines). (C) G-V shifts from 0 to 100 mM [Mg²⁺]_i at 100 μM [Ca²⁺]_i of WT mslo1 and mutant channels E374A:E399N, E374Q, and E399Q.

Activation of BK Channels at High [Mg²⁺]_i and Physiological [Ca²⁺]_i

In this section, we examine if a high affinity Ca²⁺ binding site may contribute to channel activation at high [Mg²⁺]_i. Although two sites important for high affinity Ca²⁺ sensing have been suggested as candidates for Ca²⁺ binding sites by mutational studies, the ultimate identification of the binding sites may rely on additional structural data that are not yet available. Further, it is not clear whether any unidentified Ca²⁺ binding sites besides the two candidates also contribute to BK channel activation at physiological [Ca²⁺]_i (Piskorowski and Aldrich, 2002; Qian and Magleby, 2003). Therefore, here we address this question by studying BK channels at various [Ca²⁺]_i and [Mg²⁺]_i without presuming the identity of Ca²⁺ binding sites.

It has been previously demonstrated that Mg²⁺ can bind to high affinity Ca²⁺ binding sites and compete with Ca²⁺ (Shi and Cui, 2001). An increase of [Mg²⁺]_i from 0 to 10 mM shifts the G-V relation of the WT mslo1 by about −60 mV at 0 or 100 μM [Ca²⁺]_i (Fig. 1) but much less at 3.7 μM [Ca²⁺]_i (Fig. 5) because the activation due to Mg²⁺ binding to its site is compensated by the loss of Ca²⁺-dependent activation due to such competition (Shi and Cui, 2001). We examined such competition further by measuring the G-V shift of E374A:E399N mutant channels under the same ionic conditions (Fig. 5). Since this mutation destroys Mg²⁺ sensitivity at low concentrations, an increase of [Mg²⁺]_i from 0 to 10 mM should only result in a small activation of the channel (see Fig. 1) but the loss of Ca²⁺-dependent activation due to competition should remain the same as in the WT mslo1. Therefore, instead of activating the channel, a [Mg²⁺]_i increase from 0 to 10 mM should make the channel less active. This prediction is confirmed in Fig. 5 (B and C), which shows that the G-V relation of the mutant channel shifted to a more positive voltage range in response to [Mg²⁺]_i increase, demonstrating that Mg²⁺ can bind to high affinity Ca²⁺ binding sites. These experiments, however, do not show if the binding of Mg²⁺ to Ca²⁺ binding sites can also activate the channel.

Figure 5.

Mg²⁺ competes with Ca²⁺ by binding to Ca²⁺ binding sites. (A) Current traces of WT mslo1 channels (left) and E374A:E399N mutant channels (right) recorded at indicated [Mg²⁺]_i and [Ca²⁺]_i. Testing potentials were −140 to 180 mV with 20-mV increments. The holding and repolarizing potential were −80 and −50 mV, respectively. (B) Mean G-V relations of WT mslo1 (gray symbols) and the mutant channels (black symbols) at 0 or 10 mM [Mg²⁺]_i and 3.7 μM [Ca²⁺]_i, and fits with the Boltzmann relation (solid lines). (C) G-V shifts from 0 to 10 mM [Mg²⁺]_i at 3.7 μM [Ca²⁺]_i of WT mslo1 and the mutant channels.

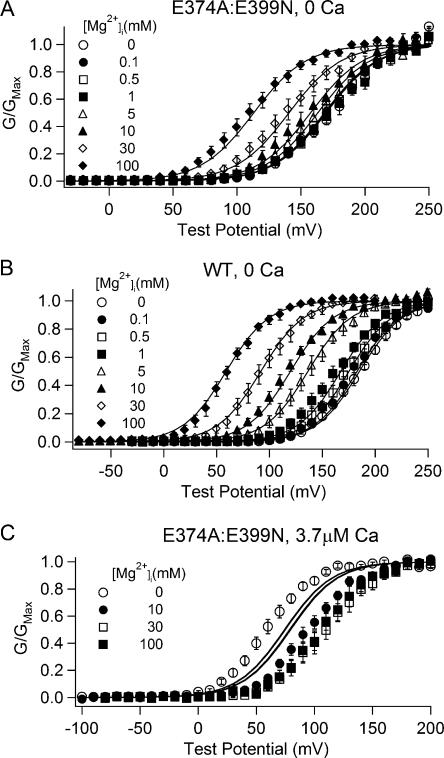
To answer this question we measured the activation of the WT and mutant E374A:E399N mslo1 channels at various [Ca²⁺]_i and [Mg²⁺]_i (Figs. 6–8). We then fit these data with MWC models of channel activation, which have been successfully used to describe Ca²⁺ and Mg²⁺-dependent activation of BK channels in previous studies (McManus and Magleby, 1991; Cox et al., 1997a; Shi and Cui, 2001; Zhang et al., 2001; Xia et al., 2002). The fitting was based on the general hypothesis that each subunit of the channel contains two high affinity Ca²⁺ binding sites (Schreiber and Salkoff, 1997; Bao et al., 2002, 2004; Xia et al., 2002; Zeng et al., 2005), which have similar Ca²⁺ affinities (Bao et al., 2002). We then assume in the following hypotheses two, one, or none of the high affinity Ca²⁺ binding sites are responsible for channel activation at high [Mg²⁺]_i to examine if any hypothesis results in a good fit of all the data.

Figure 6.

Voltage, Ca²⁺, and Mg²⁺-dependent activation of WT and E374A:E399N mutant channels and fittings with the hypothesis 1 model. (A–C) G-V relations of WT mslo1 and E374A:E399N mutant channels at indicated [Mg²⁺]_i and [Ca²⁺]_i. The data were fitted (solid lines) with Eq. 2. The parameters obtained from fittings in A and B are listed in Table I. In the fits in C, K_cC = 8 μM and K_oC = 1 μM.

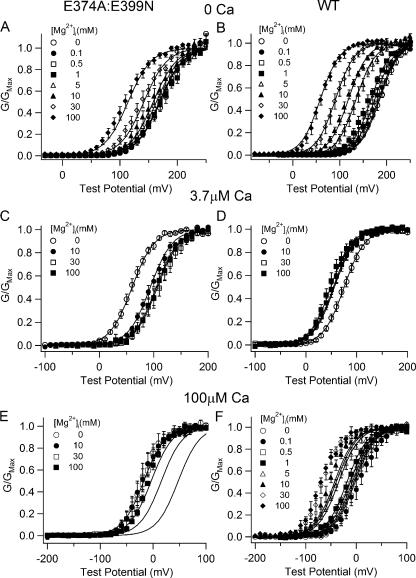
Figure 8.

Voltage, Ca²⁺, and Mg²⁺-dependent activation of WT and E374A:E399N mutant channels and fittings with the hypothesis 3 model. (A–F) G-V relations of WT mslo1 and E374A:E399N mutant channels at indicated [Mg²⁺]_i and [Ca²⁺]_i. The data were fitted (solid lines) with Eq. 4. The parameters obtained from fittings in A-C are listed in Table III.

Hypothesis 1

Mg²⁺ at high concentration activates the channel by binding to both Ca²⁺ binding sites. Since the two Ca²⁺ binding sites are similar, for simplicity, we assume that each BK channel subunit contains one Ca²⁺ binding site and one Mg²⁺ binding site. Ca²⁺ at our experimental concentrations (0, 3.7, and 100 μM) can cause little activation by binding to the Mg²⁺ binding site (Shi and Cui, 2001) so that it is assumed to only bind to the Ca²⁺ binding site to activate the channel. Mg²⁺ can bind to both Ca²⁺ and Mg²⁺ binding sites to activate the channel.

Hypothesis 2

Mg²⁺ at high concentration activates the channel by binding to one of the Ca²⁺ binding sites, but cannot activate the channel by binding to the other Ca²⁺ binding site. In this model, Ca²⁺ binds to the two Ca²⁺ binding sites to activate the channel. Mg²⁺ can bind to all three binding sites but only one of the Ca²⁺ binding sites can contribute to channel activation by Mg²⁺ binding. Mg²⁺ binds to the other Ca²⁺ site with the same affinity at open and closed states and thus cannot activate the channel.

Hypothesis 3

Mg²⁺ at high concentration activates the channel by binding to a novel low affinity Mg²⁺ binding site. In this model, we assume that each BK channel subunit contains one Ca²⁺ binding site since the two Ca²⁺ binding sites are similar, and two Mg²⁺ binding sites including the novel low affinity site. Ca²⁺ binds to the Ca²⁺ site to activate the channel. Mg²⁺ can bind to all three sites, but it binds to the Ca²⁺ site with the same affinity at open and closed states and thus cannot activate the channel. Eqs. 2, 3, and 4 based on these hypotheses are given in MATERIALS AND METHODS. The model fitting proceeded in four steps and is described as follows.

Step 1

The models are fitted to the data from E374A:E399N mutant channels at 0 [Ca²⁺]_i, with [Mg²⁺]_i of 0, 0.1, 0.5, 1, 5, 10, 30, and 100 mM. Under these conditions there is no activation due to Ca²⁺ binding to the Ca²⁺ binding site(s) or Mg²⁺ sensing at low [Mg²⁺]_i. Therefore, the fitting generates parameters for channel activation only at high [Mg²⁺]_i. The experimental data show that at 0 [Mg²⁺]_i and all [Ca²⁺]_i tested (0, 3.7, and 100 μM) the G-V relation of E374A:E399N mutant channels is similar to that of the WT mslo1 (Fig. 7 or 8), indicating that the mutation only destroys Mg²⁺ sensing at low [Mg²⁺]_i without affecting Ca²⁺-dependent activation significantly. The mutation does not significantly affect Mg²⁺ sensing at high [Mg²⁺]_i either (Fig. 2). Therefore, the parameters obtained in this step for channel gating at high [Mg²⁺]_i are also used for the WT mslo1 channel.

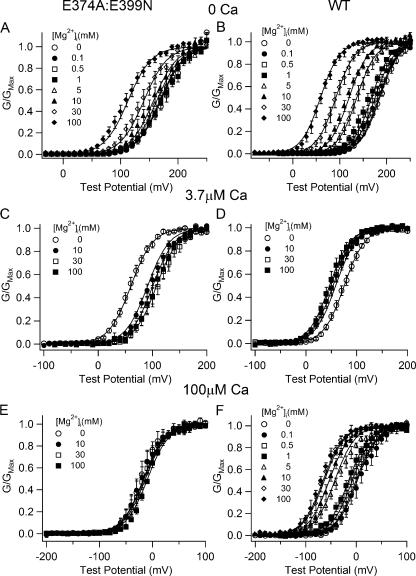
Figure 7.

Voltage, Ca²⁺, and Mg²⁺-dependent activation of WT and E374A:E399N mutant channels and fittings with the hypothesis 2 model. (A–F) G-V relations of WT mslo1 and E374A:E399N mutant channels at indicated [Mg²⁺]_i and [Ca²⁺]_i. The data were fitted (solid lines) with Eq. 3. The parameters obtained from fittings in A–C are listed in Table II.

Step 2

The models are fitted to the data from the WT channel at 0 [Ca²⁺]_i, with [Mg²⁺]_i of 0, 0.1, 0.5, 1, 5, 10, 30, and 100 mM. Under these conditions the channel is activated by Mg²⁺ at both low and high concentrations, but without Ca²⁺ binding to the Ca²⁺ site(s). The parameters obtained in step 1 for channel gating at high [Mg²⁺]_i will be used in the fitting, which allows us to obtain the parameters for channel gating at low [Mg²⁺]_i.

Step 3

The models are fitted to the data from E374A:E399N mutant channels at 3.7 μM [Ca²⁺]_i, with [Mg²⁺]_i of 0, 10, 30, and 100 mM. Under these conditions the channel is activated by Mg²⁺ at high concentrations, and by Ca²⁺ binding to the Ca²⁺ site(s). The parameters obtained in step 1 will be used in the fitting, which allows us to obtain the parameters for Mg²⁺ and Ca²⁺ binding to the Ca²⁺ site(s). The fittings in steps 1–3 have allowed us to obtain all the parameters needed to define the models.

Step 4

With all the parameters acquired in steps 1–3, we examine if the models can fit the rest of data to verify the validity of each hypothesis. The data fitted in this step include (a) WT channels at 3.7 μM [Ca²⁺]_i, with [Mg²⁺]_i of 0, 10, 30, and 100 mM; (b) E374A:E399N mutant channels at 100 μM [Ca²⁺]_i, with [Mg²⁺]_i of 0, 10, 30, and 100 mM; and (c) WT channels at 100 μM [Ca²⁺]_i, with [Mg²⁺]_i of 0, 0.1, 0.5, 1, 5, 10, 30, and 100 mM.

Fig. 6 shows the model fitting of data based on hypothesis 1, i.e., each subunit contains one Ca²⁺ and one Mg²⁺ binding site for Ca²⁺ and Mg²⁺-dependent activation at all concentrations. During the step 1 and step 2 fittings, the data of the WT and mutant channels at 0 [Ca²⁺]_i and various [Mg²⁺]_i can be well fitted by the model (Fig. 6, A and B). The parameters generated from these fittings are listed in Table I. However, in the step 3 fitting, the model cannot fit the data of the mutant channel at 3.7 μM [Ca²⁺]_i (Fig. 6 C). This result can be understood by the analysis as follows. The experimental results demonstrate that Mg²⁺ at 10 mM can bind to the Ca²⁺ binding site(s) and effectively compete with Ca²⁺ to reduce the activation of the channel, shifting the G-V relation to the right by ∼35 mV (Fig. 5 and Fig. 6 C). This result indicates that the affinity of the Ca²⁺ binding site for Mg²⁺ should be high enough to allow a significant binding of Mg²⁺ at 10 mM. This requirement is contradictory to the model fitting in Fig. 6 A, in which the affinity of the Ca²⁺ binding site for Mg²⁺ is low, being 136 mM at closed states and 40 mM at open states (Table I), in order to allow Mg²⁺ binding at high concentrations to open the channel. Because a single Ca²⁺ binding site or two Ca²⁺ binding sites with similar properties cannot satisfy the requirements of both activation and competition results (Fig. 6, A and C) hypothesis 1 is not valid.

TABLE I.

Parameters for Model Fitting of Hypothesis 1

	WT mslo1	E374A:E399N
L0	9334	4360
z	1.25	1.25
KcMinC	136.1	136.1
KoMinC	40.1	40.1
KcM	5.46	–
KoM	2.25	–

Unlike hypothesis 1, hypothesis 2 assumes that the two Ca²⁺ binding sites are not equal in their affinity for Mg²⁺. Fig. 7 shows the model fitting of data based on hypothesis 2, i.e., each subunit contains two Ca²⁺ and one Mg²⁺ binding site for Ca²⁺ and Mg²⁺-dependent activation at all concentrations. During step 1–3 fittings, we limited the affinity of the first Ca²⁺ site for Mg²⁺ binding (K_cMinC1 and K_oMinC1) between 1 and 30 mM and the affinity of the second Ca²⁺ site for Mg²⁺ binding (K_cMinC2 and K_oMinC2) between 30 and 200 mM. The data of the WT and mutant channels at 0 and 3.7 μM [Ca²⁺]_i and various [Mg²⁺]_i can be well fitted by the model (Fig. 7, A–D). The parameters generated from these fittings are listed in Table II. However, the model fails to fit the data of both WT and mutant channels at 100 μM [Ca²⁺]_i (Fig. 7, E and F). It happens because in the model Mg²⁺ competes with Ca²⁺ at both Ca²⁺ binding sites and causes too much loss of Ca²⁺-dependent activation. On one hand the binding of Mg²⁺ to the second Ca²⁺ binding site activates the channel, but on the other hand the channels lose activation due to less Ca²⁺ binding to both Ca²⁺ sites. The loss of Ca²⁺-dependent activation is larger than the activation by Mg²⁺ binding, thus at high [Mg²⁺]_i (≥10 mM) the model predicts a larger right shift of G-V than the experimental data (Fig. 7, E and F). The adverse effects of Mg²⁺-dependent activation and loss of Ca²⁺-dependent activation due to Mg²⁺ binding to Ca²⁺ sites also happen at 3.7 μM [Ca²⁺]_i, which can be accounted for by the model during the step 3 fitting (Fig. 7 C). However, the parameters obtained from the fitting at 3.7 μM [Ca²⁺]_i cannot be used to fit the data at 100 μM [Ca²⁺]_i. Thus, hypothesis 2 is not valid.

TABLE II.

Parameters for Model Fitting of Hypothesis 2

	WT mslo1	E374A:E399N
L0	9334	4360
z	1.25	1.25
KcM	5.24	–
KoM	2.12	–
KcMinC1	3.18	3.18
KoMinC1	3.18	3.18
KcMinC2	142.43	142.43
KoMinC2	42.02	42.02
KcC1	9.04	9.04
KoC1	1.95	1.95
KcC2	1.90	1.90
KoC2	0.84	0.84

The above results indicate that Mg²⁺ at high concentrations cannot activate the channel by binding to Ca²⁺ binding sites. Fig. 8 shows the model fitting of data based on hypothesis 3, i.e., a novel low affinity Mg²⁺ binding site is responsible for such activation. The parameters generated from the step 1–3 fittings (Fig. 8, A–C) are listed in Table III. These parameters are then used in the step 4 fittings (Fig. 8, D–F). Under all ionic conditions the model fits well to the experimental data of both the WT and mutant channels (Fig. 8), supporting the hypothesis that a novel low affinity Mg²⁺ binding site is responsible for channel activation at high [Mg²⁺]_i. These results also suggest that Mg²⁺ can bind to Ca²⁺ binding sites and compete with Ca²⁺ but the binding does not activate the channel. Due to Mg²⁺ competition both WT and E374A:E399N mutant channels lose Ca²⁺-dependent activation at 3.7 or 100 μM [Ca²⁺]_i and high [Mg²⁺]_i (Fig. 8, C–F). Such competition may explain the results in Fig. 4 such that at 100 μM [Ca²⁺]_i and 100 mM [Mg²⁺]_i the loss of Ca²⁺-dependent activation due to Mg²⁺ competitive binding to the Ca²⁺ sites is compensated by Mg²⁺-dependent activation through the novel low affinity Mg²⁺ site. Therefore, for the E374A:E399N mutant channels, in which Mg²⁺ sensing at low [Mg²⁺]_i is destroyed, 100 mM [Mg²⁺]_i does not change the G-V relation, while the WT mslo1 100 mM [Mg²⁺]_i shifts the G-V relation to more negative voltage ranges due to Mg²⁺ sensing mediated by the site at E374/E399.

TABLE III.

Parameters for Model Fitting of Hypothesis 3

	WT mslo1	E374A:E399N
L0	9334	4360
z	1.25	1.25
KcM1	5.46	–
KoM1	2.25	–
KcM2	136.1	136.1
KoM2	40.1	40.1
KcMinC	5.36	5.36
KoMinC	5.36	5.36
KcC	8.38	8.38
KoC	0.81	0.81

BK Channel Activation at High [Mg²⁺]_i Is Independent from Activation at Low [Ca²⁺]_i and [Mg²⁺]_i

In above fittings we use an independent MWC model to describe channel activation due to each metal binding site (Eqs. 2–4). The fitting results in Fig. 8 are reasonably good, suggesting that channel activation mediated by the novel low affinity Mg²⁺ binding site is independent from that mediated by metal binding at high affinity Ca²⁺ binding sites and Mg²⁺ sensing mediated by the site at E374/E399. To verify this conclusion we studied two triple mutations 5D5N + D367A + E399N and 5D5N + D367A:D362A + E399N, which destroy metal sensing at low concentrations of Ca²⁺ and Mg²⁺ (Xia et al., 2002). If BK channel activation at high [Mg²⁺]_i is independent from activation at low [Ca²⁺]_i and [Mg²⁺]_i the remaining activation of these mutant channels by high Mg²⁺ should be mediated only by the novel low affinity Mg²⁺ binding site, which should be intact from the mutations, and consequently, the above model should still be able to fit the Mg²⁺ dependence of channel activation.

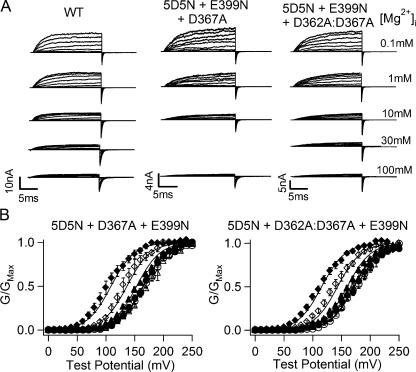
This prediction is confirmed as shown in Fig. 9. For both mutant channels, the G-V relations do not change much between 0 and 1 mM [Mg²⁺]_i. However, at high [Mg²⁺]_i (10–100 mM), the G-V relation of both mutants shifts to more negative voltage ranges (Fig. 9 B), a total of about −50 mV. Such shift is comparable to the G-V shift of the WT mslo1 in response to the same [Mg²⁺]_i increase (Fig. 2). The G-V relations of both mutants can be fitted (Fig. 9 B, solid curves) by the MWC model with only the low affinity Mg²⁺ binding site being intact and the same parameters as listed in Table III except for L₀.

Figure 9.

Voltage and Mg²⁺-dependent activation of WT, 5D5N + D367A + E399N, and 5D5N + D362A:D367A + E399N mutant channels. (A) Current traces of WT mslo1 channels (left), 5D5N + D367A + E399N mutant channels (middle), and 5D5N + D362A:D367A + E399N mutant channels (right) recorded at indicated [Mg²⁺]_i. Testing potentials were −200 to 140 mV with 20-mV increments. The holding and repolarizing potentials were −80 and −120 mV, respectively. (B) Mean G-V relations of 5D5N + D367A + E399N (left) and 5D5N + D362A:D367A + E399N mutant channels (right) in the presence of 0–100 mM [Mg²⁺]_i and fittings with the hypothesis 3 model. The symbols represent [Mg²⁺]_i (in mM) at 0 (open circle), 0.1 (closed circle), 1 (open triangle), 10 (closed triangle), 30 (open diamond), and 100 (closed diamond). The data were fitted (solid lines) with Eq. 4. The parameters were fixed with the numbers in Table III, except L₀, which were set free. In the fits, L₀ for 5D5N + D367A + E399N and 5D5N + D362A:D367A + E399N is 3516 and 4908, respectively.

DISCUSSION

Previous studies have identified three sites in mslo1 BK channels important for metal sensing, which are located in Ca²⁺ bowl (Schreiber and Salkoff, 1997; Bian et al., 2001; Braun and Sy, 2001; Bao et al., 2004), RCK1 domain (Bao et al., 2002; Xia et al., 2002), and at E374/E399/Q397 (Shi et al., 2002; Xia et al., 2002). These sites mediate metal-dependent activation at physiological Ca²⁺ and Mg²⁺ concentrations. In this paper we have studied steady-state and kinetic properties of WT and mutant mslo1 channels in various voltage ranges, Ca²⁺ and Mg²⁺ concentrations, and demonstrated that a novel low affinity metal binding site is responsible for channel activation at metal concentrations beyond normal physiological conditions (Figs. 1–3 and 6–8). Metal sensing mediated by any of these sites independently activates the channel (Fig. 8 and 9). Nevertheless, the contributions of these sites to channel activation are complex, depending on the combination of [Ca²⁺]_i and [Mg²⁺]_i (Figs. 1, 2, 4, 5, and 8). The reason, as our results demonstrated, is that both Ca²⁺ and Mg²⁺ can bind to all metal binding sites to modulate channel activation (Figs. 5, 8, 9, and 10). We examined the effects of Ca²⁺ and Mg²⁺ binding to each of metal binding sites on channel activation and provide an allosteric model for quantitative estimation of the contributions that each binding site makes to channel activation at any [Ca²⁺]_i and [Mg²⁺]_i (Eq. 4).

Figure 10.

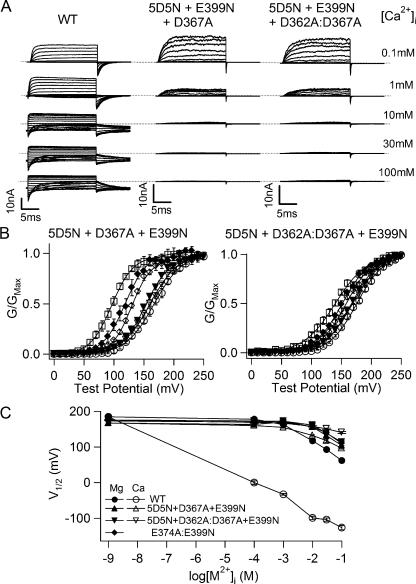
Voltage and Ca²⁺-dependent activation of WT, 5D5N + D367A + E399N, and 5D5N + D362A:D367A + E399N mutant channels. (A) Current traces of WT mslo1 channels (left), 5D5N + D367A + E399N mutant channels (middle), and 5D5N + D362A:D367A + E399N mutant channels (right) recorded at indicated [Ca²⁺]_i. Dashed lines indicate zero current. Testing potentials for WT at 0.1 mM [Ca²⁺]_i were −150 to 190 mV with 20-mV increments. Testing potentials for WT at 1, 10, 30, and 100 mM [Ca²⁺]_i were −200 to 140 mV with 20-mV increments. Testing potentials for WT at 0 [Ca²⁺]_i and 5D5N + D367A + E399N and 5D5N + D362A:D367A + E399N mutant channels were −20 to 240 mV with 20-mV increments. The holding and repolarizing potentials were −80 and −120 mV, respectively. (B) Mean G-V relations of 5D5N + D367A + E399N mutant channels (left) and 5D5N + D362A:D367A + E399N mutant channels (right) in the presence of 0–100 mM [Ca²⁺]_i The symbols represent [Ca²⁺]_i (in mM) at 0 (open circle), 0.1 (inverted open triangle), 1 (inverted closed triangle), 10 (open diamond), 30 (closed diamond) and 100 (open square). G-V relations of these channels are fitted with the Boltzmann relation (solid lines, see MATERIALS AND METHODS). (C) V_1/2 versus [Mg²⁺]_i (closed symbols) or [Ca²⁺]_i (open symbols) for WT (circle), E374A:E399N (diamond), 5D5N + D367A + E399N (triangle), and 5D5N + D362A:D367A + E399N (inverted triangle) mutant channels.

Based on this model, we calculated the contribution of the novel low affinity metal binding site to the mslo1 channel activation at physiological [Mg²⁺]_i between 0.3 and 3 mM (Flatman, 1984, 1991; Gupta et al., 1984; Corkey et al., 1986). At the physiological [Ca²⁺]_i between 0.1 and 100 μM (Roberts et al., 1990; Robitaille et al., 1993; Roberts, 1994; Yazejian et al., 1997; Marrion and Tavalin, 1998; Berridge et al., 2000; Yazejian et al., 2000), 3 mM [Mg²⁺]_i only shifts the V_1/2 for about −4.1 mV due to Mg²⁺ binding to this site, indicating that the contribution of this site is quite small. However, the physiological relevance of this binding site is not fully understood because the effects of β subunits on the function of this site are not explored yet. Since slo1 proteins often associate with various β subunits to form BK channels in vivo (Tseng-Crank et al., 1996; Cox et al., 1997a; Jiang et al., 1999; Riazi et al., 1999; Wallner et al., 1999; Behrens et al., 2000; Brenner et al., 2000b; Meera et al., 2000; Weiger et al., 2000) and it is known that β1 and β2 subunits affect apparent Ca²⁺ sensitivity of the channel (McManus et al., 1995; Meera et al., 1996, 2000; Tseng-Crank et al., 1996; Jiang et al., 1999; Nimigean and Magleby, 1999; Wallner et al., 1999; Brenner et al., 2000a,b; Cox and Aldrich, 2000; Weiger et al., 2000; Orio and Latorre, 2005), it will be interesting to examine if Mg²⁺-dependent activation is also affected by β subunits. The studies here provide a useful basis for such future studies.

The identity of this novel low affinity Mg²⁺ binding site is still unknown. A previous study reported that a triple mutation 5D5N + D362A:D367A + E399A not only destroyed Ca²⁺ and Mg²⁺-dependent activation at low concentrations (0–10 mM) but also significantly altered Ca²⁺-dependent activation at high concentrations (10–100 mM) (Xia et al., 2002). We noticed that among the mutated residues in the triple mutation D362 might not be important in either Ca²⁺ or Mg²⁺-dependent activation at low concentrations, because Ca²⁺ and Mg²⁺ sensitivity of mslo1 channels changed little when it was mutated individually (Xia et al., 2002). Therefore, this result seems to suggest that D362 is important for channel activation at high [Ca²⁺]_i.

To verify this suggestion we compared Ca²⁺ dependence of the triple mutation 5D5N + D367A:D362A + E399N with 5D5N + D367A + E399N that left D362 intact (Fig. 10). At [Ca²⁺]_i ≥ 1 mM, the currents at depolarized voltages are smaller than the currents at lower [Ca²⁺]_i, probably due to a rapid block of the channel pore by Ca²⁺ (Oberhauser et al., 1988; Cox et al., 1997a), and the current reduction is more prominent in mutant channels than in the WT mslo1 (Fig. 10 A). For the WT mslo1 channels, the block by Ca²⁺ and Mg²⁺ is voltage dependent, and the rate of unblock is very rapid at voltages more negative than the K⁺ equilibrium potential such that the inward macroscopic tail current upon repolarization is not affected by the block (Cox et al., 1997b; Shi and Cui, 2001). However, at 100 mM [Ca²⁺]_i, most mutant channels are blocked not only at depolarized voltages but also at the repolarization of −120 mV (also see Xia et al., 2002), possibly due to a more rapid deactivation time course (Fig. 10 A). Fig. 10 B shows the G-V relations of the two mutant channels at various [Ca²⁺]_i from 0 to 100 mM. The mutations destroy channel activation at low [Ca²⁺]_i so that the G-V relations do not differ much between 0 and 1 mM [Ca²⁺]_i for both mutant channels. However, at high [Ca²⁺]_i (10–100 mM) the G-V relation of 5D5N + D367A + E399N shifts to more negative voltage ranges, and at 100 mM [Ca²⁺]_i the shift is about −36 mV from the G-V at 10 mM [Ca²⁺]_i, comparable to the G-V shift of the WT mslo1 caused by the same [Ca²⁺]_i increase (Fig. 10 C). On the other hand, the G-V relation of 5D5N + D362A:D367A + E399N is not shifted as much, only −17 mV when [Ca²⁺]_i increases from 10 to 100 mM. These results indicate that D362 may be involved in channel activation at high [Ca²⁺]_i.

However, Fig. 9 shows that neither of the triple mutations 5D5N + D367A + E399N or 5D5N + D367A:D362A + E399N affected Mg²⁺ dependence at high concentration, indicating that D362A is not part of the Mg²⁺ binding site. The different effects of D362A on Ca²⁺ and Mg²⁺-dependent activation at high concentrations is striking that the mutation 5D5N + D362A:D367A + E399N reduces the leftward shift of G-V relations at high [Ca²⁺]_i but does not affect channel activation at high [Mg²⁺]_i (Figs. 9 and 10). This result may suggest that Mg²⁺ at high concentrations binds to a different site than Ca²⁺ at high concentrations in activating the channel and D362 may only affect Ca²⁺ binding. However, this possibility seems unlikely because for 5D5N + D367A + E399N mutant channels, Ca²⁺ and Mg²⁺ at high concentrations have similar effects on channel activation (Fig. 10 C), suggesting that they may bind to the same site. Since other higher affinity metal sites bind both Mg²⁺ and Ca²⁺ in mslo1 (Figs. 4 and 8), it is hard to imagine that the low affinity binding site can have a high selectivity to distinguish between Mg²⁺ and Ca²⁺. Therefore, an alternative possibility is that D362 may not be part of the metal binding site but be part of the structure that links metal binding to channel opening. The mutation D362A may affect Mg²⁺ and Ca²⁺-dependent activation differently because the two ions have different sizes and hence cause different conformational changes at the binding site.

As shown in Figs. 9 and 10, 5D5N + D362A:D367A + E399N mutant channels are mostly blocked at high [Ca²⁺]_i and [Mg²⁺]_i. Such block was observed previously in a similar triple mutant channel (Xia et al., 2002). The nature of the block is not studied in detail here. It is possible that the block may interfere with our measurements of channel activation so that the observed mutational effects on channel activation in Figs. 9 and 10 may derive from this block but not the intrinsic property of channel activation. However, 5D5N + D367A + E399N and 5D5N + D362A:D367A + E399N mutant channels are similarly blocked by high [Ca²⁺]_i but Ca²⁺-dependent activation of these mutant channels is different (Fig. 10). This result gave us some confidence to believe that D362A may indeed affect channel activation at high [Ca²⁺]_i. We also notice that although the triple mutation 5D5N + D362A:D367A + E399N reduces the leftward shift of G-V relations at high [Ca²⁺]_i it is unlike another very similar triple mutation 5D5N + D362A:D367A + E399A that reversed Ca²⁺ dependence of channel activation by causing rightward G-V shifts at high [Ca²⁺]_i (Xia et al., 2002). The cause of this discrepancy is not known.

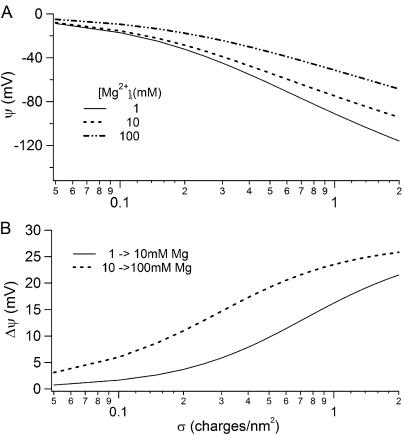
It has been shown that extracellular Mg²⁺ can shift the G-V relation of BK channels by screening electric charges on the channel protein (MacKinnon et al., 1989). While the mechanism of D362A in reducing G-V shift at high [Ca²⁺]_i (Fig. 10) is not clear, the different effects of D362A on Ca²⁺ and Mg²⁺-dependent activation at high concentrations suggest that D362 may not be responsible for any screening effect of intracellular cations on BK channels, because Ca²⁺ and Mg²⁺ should have caused a similar screening effect had the mutation D362A reduced the surface charge. However, D362A does not completely abolish the G-V shift induced by the [Ca²⁺]_i increase from 10 to 100 mM, leaving a residual ∼−17 mV shift (Fig. 10) as compared with a ∼−40 mV shift in the WT channels induced by a similar [Mg²⁺]_i increase (Fig. 2). This residual G-V shift can be caused by Ca²⁺ or Mg²⁺ screening some other charges on the surface of the channel protein or the inner membrane lipids. To estimate possible contributions of the screening effect to G-V shifts induced by increases of [Ca²⁺]_i or [Mg²⁺]_i, we calculated surface potentials under our experimental conditions using the Gouy-Chapman model (Grahame, 1947; Hille et al., 1975; McLaughlin, 1977; MacKinnon et al., 1989) (Fig. 11). The surface potential depends on charge densities on the surface of the channel protein or the inner membrane lipids (Fig. 11). The charge density on the inner surface of the plasma membrane is ∼0.14 charges/nm² (Chandler and Meves, 1965; Hille et al., 1975). The charge density on the intracellular surface of the BK channel protein that affects its voltage-dependent gating is not known. It would be ∼0.02 charges/nm² if we assume a similar charge density at both extracellular and intracellular surface (MacKinnon et al., 1989). Hence, the screening effect may contribute ∼−9 mV to the shift in G-V relations due to increases of [Ca²⁺]_i or [Mg²⁺]_i from 10 to 100 mM (Fig. 11 B). Therefore, the −40 mV shift in G-V relations in response to increases of [Ca²⁺]_i or [Mg²⁺]_i from 10 to 100 mM largely resulted from these ions' binding to the novel metal binding site. Even if the charge density at the intracellular surface of BK channels is 20 times higher than at the extracellular surface half of the G-V shift is contributed by ions' binding to the novel metal binding site.

Figure 11.

Effects of Mg²⁺ on the membrane surface potential due to surface charge screening. (A) Surface potentials at 1, 10, and 100 mM [Mg²⁺]_i as a function of surface charge density. The calculation is based on the Grahame equation (Grahame, 1947). The solution contains 140 mM K⁺. (B) Change of surface potential as [Mg²⁺]_i increases from 1 to 10 mM and from 10 to 100 mM.

We use MWC models to describe channel activation due to metal binding. The MWC model is chosen because it is the simplest kinetic scheme that represents the allosteric mechanism of metal-dependent BK channel activation and it described experimental data very well in various studies (McManus and Magleby, 1991; Cox et al., 1997a; Shi and Cui, 2001; Zhang et al., 2001; Xia et al., 2002). A more complex model has been proposed to describe the dual-allosteric mechanism of both voltage and Ca²⁺-dependent activation of BK channels (Horrigan and Aldrich, 2002). This model includes an allosteric interaction between voltage and Ca²⁺-dependent activation mechanisms (described by the E factor) that accounts for the change of G-V slopes and shifts at various [Ca²⁺]_i that slightly differ from the prediction of the MWC model (Horrigan and Aldrich, 2002). However, the primary difference between the two models lies at the description of voltage-dependent mechanism while their descriptions on Ca²⁺ dependence of channel activation are similar. Both models predict a dissociation constant of Ca²⁺ binding at the closed conformation around 10 μM and an allosteric factor C around 10 (Cox et al., 1997a; Horrigan and Aldrich, 2002). In the dual-allosteric model the coupling between voltage and Ca²⁺-dependent mechanism is weak (E is small) (Horrigan and Aldrich, 2002). Previous experimental results also demonstrated that the mechanisms of voltage and Ca²⁺-dependent activation do not affect each other significantly (Cui and Aldrich, 2000; Shi et al., 2002; Qian and Magleby, 2003). Therefore, among existing models, the MWC model is not only the simplest but also adequate in describing metal-dependent activation of BK channels. In this study the MWC model is able to fit experimental data under a broad range of ionic and voltage conditions although only a subset of the data is required to define the parameters of the model (Fig. 8). The conclusion based on model fittings (Fig. 8) is consistent with mutational studies (Fig. 9). These results indicate that the model provides a quite precise description for mslo1 channel activation within our tested experimental conditions.