Mechanism of β4 Subunit Modulation of BK Channels

Abstract

Large-conductance (BK-type) Ca²⁺-activated potassium channels are activated by membrane depolarization and cytoplasmic Ca²⁺. BK channels are expressed in a broad variety of cells and have a corresponding diversity in properties. Underlying much of the functional diversity is a family of four tissue-specific accessory subunits (β1–β4). Biophysical characterization has shown that the β4 subunit confers properties of the so-called “type II” BK channel isotypes seen in brain. These properties include slow gating kinetics and resistance to iberiotoxin and charybdotoxin blockade. In addition, the β4 subunit reduces the apparent voltage sensitivity of channel activation and has complex effects on apparent Ca²⁺ sensitivity. Specifically, channel activity at low Ca²⁺ is inhibited, while at high Ca²⁺, activity is enhanced. The goal of this study is to understand the mechanism underlying β4 subunit action in the context of a dual allosteric model for BK channel gating. We observed that β4's most profound effect is a decrease in P_o (at least 11-fold) in the absence of calcium binding and voltage sensor activation. However, β4 promotes channel opening by increasing voltage dependence of P_o-V relations at negative membrane potentials. In the context of the dual allosteric model for BK channels, we find these properties are explained by distinct and opposing actions of β4 on BK channels. β4 reduces channel opening by decreasing the intrinsic gating equilibrium (L₀), and decreasing the allosteric coupling between calcium binding and voltage sensor activation (E). However, β4 has a compensatory effect on channel opening following depolarization by shifting open channel voltage sensor activation (Vh_o) to more negative membrane potentials. The consequence is that β4 causes a net positive shift of the G-V relationship (relative to α subunit alone) at low calcium. At higher calcium, the contribution by Vh_o and an increase in allosteric coupling to Ca²⁺ binding (C) promotes a negative G-V shift of α+β4 channels as compared to α subunits alone. This manner of modulation predicts that type II BK channels are downregulated by β4 at resting voltages through effects on L₀. However, β4 confers a compensatory effect on voltage sensor activation that increases channel opening during depolarization.

INTRODUCTION

BK channels are members of the voltage-dependent potassium channel family that are activated by membrane depolarization as well as increases in cytoplasmic Ca²⁺. These two stimuli appear to open the channel's gate via allosteric mechanisms (Horrigan and Aldrich, 1999; Horrigan et. al, 1999; Rothberg and Magleby, 1999, 2000; Horrigan and Aldrich, 2002; for review see Rothberg, 2004). Voltage sensor activation and Ca²⁺ binding act independently, in an energetically additive fashion, to stabilize the channel's open conformation; as [Ca²⁺] is increased, less membrane depolarization is required to open the channel (Cox et al., 1997a; Cui et al., 1997). In different cell types, these channels display diverse functional properties, despite having a pore-forming subunit that is encoded by only a single gene (slo or KCNMA). Numerous mechanisms contribute to BK channel functional diversity, including alternative splicing, channel phosphorylation, and assembly with a family of four accessory subunits, β1–β4 (Stockand and Sansom, 1998; Xie and McCobb, 1998; Fettiplace and Fuchs, 1999; Schubert and Nelson, 2001; Fury et al., 2002; Orio et al., 2002).

The accessory β4 subunit is a component of neuronal BK channels and confers properties mediating the so-called type II BK channels. These channels were originally identified in bilayer recordings from synaptosomal membrane preparations from brain (Reinhart et al., 1989, 1991; Reinhart and Levitan, 1995; Behrens et al., 2000; Brenner et al., 2000; Meera et al., 2000; Weiger et al., 2000; Lippiat et al., 2003). Type II BK channels have slow gating kinetics, decreased sensitivity to Ca²⁺ compared with type I channels, and are insensitive to block by charybdotoxin, consistent with the properties of BK channels coexpressed with the β4 subunit in heterologous cells (Reinhart et al., 1989; Reinhart et al., 1991; Reinhart and Levitan, 1995; Behrens et al., 2000; Brenner et al., 2000; Meera et al., 2000; Weiger et al., 2000; Lippiat et al., 2003). β4 knockout mice display abnormal neuronal firing properties and temporal lobe seizures, indicating that the gating properties conferred by the β4 subunits are essential to normal neuronal function (Brenner et al., 2005).

More detailed analysis of BK channel β4 subunit has been performed by coexpression of the cloned channels in heterologous expression systems. The β4 subunit was proposed to be a “downregulator of BK channels” due to dramatic slowing of activation and a positive voltage shift of the conductance–voltage relationship (Weiger et al., 2000). However, although β4 reduces BK channels opening at low Ca²⁺, it increases channel opening at high Ca²⁺ (Brenner et al., 2000; Ha et al., 2004). In addition, the β4 subunit reduces the voltage dependence (slope) of the macroscopic conductance–voltage (G-V) relationship. These properties are unique among the β subunit family members and the mechanisms underlying these effects are not known.

Here we provide a detailed analysis of the functional properties of BK α+β4 subunit channels. To understand how the β4 subunit modulates BK channels we have employed an allosteric modeling framework for BK channels (Horrigan and Aldrich, 2002), which enables us to ascribe kinetic changes to specific gating transitions. Our results demonstrate that β4 subunit effects can be accounted for by two opposing actions: β4 inhibits BK channel activation mainly by increasing the energetic barrier to opening by decreasing L₀. This effect is countered by a negative voltage shift in voltage sensor activation for channels in the open state (parameter Vh_o in the model) and an increase in the allosteric coupling of Ca²⁺ binding to channel opening (parameter C in the model).

MATERIALS AND METHODS

Channel Expression

Experiments were performed with the mouse α subunit cDNA expression vector in pcDNA3 (GenBank/EMBL/DDBJ accession no. MMU09383), and mouse β4 in the Invitrogen vector pcDNA3.1Hygro(+). Expression constructs were transfected at a ratio of 1:10 α to β4 subunit using 2–3 μg total DNA and 10 μl lipofectamine reagent per 35 mm dish of HEK293 cells. After 5 h of incubation, the cells were replated on glass coverslips and analyzed by electrophysiology for the following 1–3 d. GFP expression from cotransfection (0.2 μg) of the CLONTECH Laboratories, Inc. EGFP-N1 vector was used to identify channel-expressing cells.

Patch Clamp Recording

Macropatch recordings were made using the excised inside-out patch clamp configuration. To limit series resistance errors, currents 5 nA or less were used for steady-state G-V. For 0 Ca²⁺ experiment determination of limiting P_o, larger currents were used but estimates of maximal conductance was determined at high Ca²⁺ and using small tail-current voltage steps. Experiments were performed at 22°C. Data were sampled at 10–30-μs intervals and low-pass filtered at 8.4 kHz using the HEKA EPC8 four-pole bessel filter. Data were analyzed without further filtering. Leak currents were subtracted after the test pulse using P/5 negative pulses from a holding potential of −120 mV. In the presence of β4 at ≥60 μM Ca²⁺, leak subtraction was not performed. Patch pipettes (borosilicate glass VWR micropipettes) were coated with Sticky Wax (Kerr Corp.) and fire polished to ∼1.5–3 MΩ resistance.

The external recording solution (electrode solution) was composed of 20 mM HEPES, 140 mM KMeSO₃, 2 mM KCl, 2 mM MgCl₂, pH 7.2. Internal solutions were composed of a pH 7.2 solution of 20 mM HEPES, 140 mM KMeSO₃, 2 mM KCl, and buffered with 5 mM HEDTA and CaCl₂ to the appropriate concentrations to give 1.7, 7, and 18.5 μM buffered Ca²⁺ solutions. Higher Ca²⁺ solutions were buffered with 5 mM NTA. Low Ca²⁺ solutions (0.3 μM and 0 Ca²⁺) were buffered with 5 mM EGTA and Ba²⁺ was chelated with 40 μM (+)-18-crown-6-tetracarboxylic acid (Cox et al., 1997b). Conductance–voltage (G-V) relationships were obtained using a test pulse to positive potentials followed by a step to a negative voltage (−80 at low Ca²⁺, −120 at high Ca²⁺), and then measuring instantaneous tail current 200 μs after the test pulse. V_1/2 and Q values were determined by fitting G-V curves to Boltzmann function (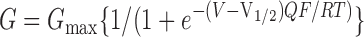) and then normalized to the maximum of the fit. At 0 and 0.3 μM Ca²⁺, where maximum conductance could not be obtained in the presence of β4, conductance was normalized to maximal conductance at high Ca²⁺.

Single Channel Analysis

Single channel opening events were obtained from patches containing one to hundreds of channels. Recordings were of 20 s to hundreds of seconds duration. Analysis was performed using TAC and TACFIT programs (Bruxton Corporations). NP_o was determined using either all-point amplitude histogram or by event detection using a 50% amplitude criteria. The probability (P_k) of occupying each open level (k) gives rise to NP_o: 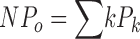. P_o was then determined by normalizing NP_o values by channel number (N). N was obtained from the instantaneous tail current amplitude (−80 mV) during maximal opening at saturating [Ca²⁺] divided by the unitary conductance for each channel at the tail voltage. β4 caused a reduced single channel conductance at negative voltages for BK channels as compared with α subunits alone. At −80 mV the conductance was 175 ± 7 pS for α+β4, and 250 ± 13 pS for α alone. Positive voltages did not show a significant change in single channel conductance. At +80 mV, single channel current was 214 ± 7 pS for α+β4 and 225 ± 14 pS for α alone.

RESULTS

Effects of β4 on Channel Steady-state G-V Relations and P_o

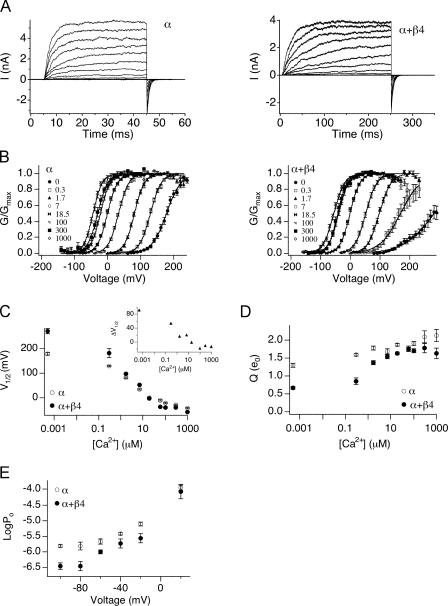
BK channel properties in the absence of the β4 subunit (α alone) or in the presence of saturating amounts of β4 (α+β4) were characterized in transiently transfected HEK293 cells. Currents were recorded in the inside-out configuration over a range of [Ca²⁺] at the intracellular face of the membrane patch ([Ca²⁺]_i). Fig. 1 A shows representative current traces of α alone and α+β4 recorded at 7 μM [Ca²⁺]_i. In Fig. 1 B, mean steady-state conductance–voltage (G-V) relations are plotted as a function of [Ca²⁺]_i. To better quantify effects of β4 on channel steady-state gating properties, G-V curves of individual recordings were fit with single Boltzmann functions (see MATERIALS AND METHODS) to derive the voltage for half-maximal activation (V_1/2) and equivalent gating charge Q (slope of G-V relationship or “voltage dependence”). Mean V_1/2 and Q values for α alone and α+β4 as a function of [Ca²⁺]_i are listed in Table I and plotted in Fig. 1 (C and D), respectively. Our data, consistent with previous results obtained with heterologous expression in Xenopus oocytes, show that the β4 subunit affects the steady-state conductance–voltage relationship (Brenner et al., 2000; Ha et al., 2004). At [Ca²⁺] <18 μM, V_1/2 is shifted toward more depolarized voltages in the presence of β4 (Fig. 1 C, inset). However, at [Ca²⁺] >18 μM, V_1/2 is shifted toward more negative voltages in the presence of β4. In addition, we also saw that at all [Ca²⁺], β4 has a dramatic effect on the apparent voltage dependence of BK channels (Fig. 1 D). This is particularly prominent at [Ca²⁺] <1.7 μM and becomes incrementally more steep as [Ca²⁺] is increased.

Figure 1.

The effects of β4 on the mslo steady-state G-V relation vary with [Ca²⁺]. (A) Examples of currents evoked by voltage steps in 7 μM [Ca²⁺]. α alone is shown in the left panel, α+β4 is shown in the right panel. (B) Mean G-V relations at different [Ca²⁺] for α alone and α+β4. Each point represents mean data from 8 to 44 experiments. Solid curves represent fits to the Boltzmann function. (C) Mean V_1/2 values plotted as a function of [Ca²⁺]. β4 shifts V_1/2 toward more positive voltages <18.5 μM [Ca²⁺], and toward more negative voltages >18.5 μM [Ca²⁺]. Inset, α+β4 V_1/2 subtracted from mean α alone values. (D) Mean effective gating charge, Q, plotted as a function of [Ca²⁺]. In the presence of β4 there is a decrease in Q, and a more dramatic increase in Q can be observed as [Ca²⁺] increases. (E) Mean P_o as a function of voltage in the absence (5–7 patches) and presence (2–6 patches) of β4 in 300 nM Ca²⁺. Error bars represent SEM.

TABLE I.

Comparing G-V Parameters

[Ca2+]	α			α+β4
	V1/2	Q	N	V1/2	Q	N
μM	mV	e0		mV	e0
0.0005	177.6 ± 4.0	1.29 ± 0.06	12	269.1 ± 11.9	0.66 ± 0.04	17
0.3	128.7 ± 1.9	1.58 ± 0.04	20	181.8 ± 17.7	0.85 ± 0.09	10
1.7	80.9 ± 1.6	1.76 ± 0.05	24	97.0 ± 2.5	1.36 ± 0.05	14
7	33.1 ± 1.7	1.68 ± 0.06	13	52.8 ± 2.6	1.57 ± 0.06	24
18.5	−0.6 ± 1.5	1.86 ± 0.03	44	−2.0 ± 1.6	1.62 ± 0.04	26
60	−10.6 ± 3.1	1.76 ± 0.07	8	−36.5 ± 2.4	1.73 ± 0.06	17
100	−21.0 ± 1.8	1.91 ± 0.05	30	−38.9 ± 2.4	1.67 ± 0.06	26
300	−29.6 ± 3.4	2.09 ± 0.16	14	−40.4 ± 3.2	1.77 ± 0.13	13
1000	−43.7 ± 2.1	2.13 ± 0.17	12	−57.4 ± 3.6	1.62 ± 0.15	12

The values shown are Boltzmann-fit parameters. They indicate mean ± SEM.

The relative change in the V_1/2 by β4 is between −26 and +90 mV, depending on the calcium concentration (Fig. 1 C, inset). However, the V_1/2 may not reflect the relative changes in P_o at physiological voltages. To determine effects on open probability, we measured channel P_o in 300 nM [Ca²⁺] at the physiological voltages of −100 to +20 mV. The results indicate that at negative voltages, α+β4 channels show a large reduction in P_o as compared with α subunits alone (Fig. 1 E). For example, at −80 mV α+β4 channels have a 4.3-fold reduction in P_o relative to α subunits alone (average P_o α+β4 is 3.5 e⁻⁷ ± 1.9 e⁻⁷, α alone is 1.5 e⁻⁶ ± 3.3 e⁻⁷). However, at +20 mV, there is no significant difference in P_o between channel types (Fig. 1 E).

Effects of β4 on Gating through the Low Affinity Ca²⁺ Binding Site

In considering the calcium-dependent effect of β4 on the V_1/2, it is important to note that BK channels are modulated over a wide range of Ca²⁺, from the submicromolar range up to ∼1 mM. The fact that Ca²⁺ does not appear to saturate channel activation (in the absence of β4) is attributed to the existence of both high and low affinity Ca²⁺ binding sites (Zhang et al., 2001; Shi et al., 2002). This is apparent in Fig. 1 C (open symbols) as increasing Ca²⁺ shifts the V_1/2 strongly at [Ca²⁺]_i <60 μM, consistent with activation at a high affinity site, then shifts the V_1/2 weakly at [Ca²⁺]_i >100 μM, consistent with activation at a low affinity site.

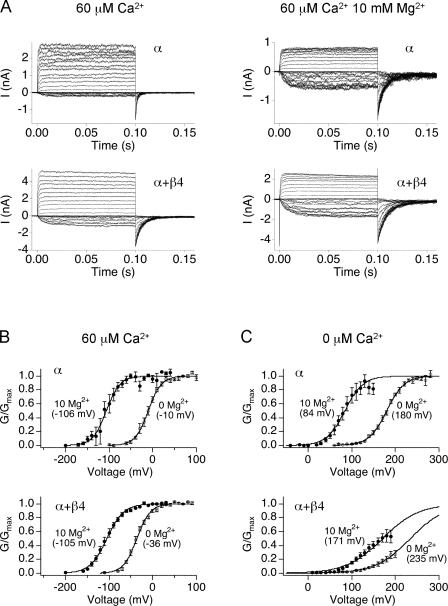
The β4 subunit promotes a negative voltage shift of the G-V curve only at high [Ca²⁺] (Fig. 1 C, inset). A possible explanation for this is that β4 may specifically affect Ca²⁺ binding to low affinity sites to promote activation at high calcium; either its affinity or coupling between Ca²⁺ binding and gating. We examined whether the β4 subunits promote activation through low affinity Ca²⁺ binding sites by measuring activation by millimolar concentrations of Mg²⁺, which acts only at low affinity sites (Shi et al., 2002). If the leftward shift in V_1/2 induced by the β4 subunits is due to increased activation at the low affinity site, then addition of Mg²⁺ should produce a larger leftward shift in the presence of β4 compared with α alone channels.

Steady-state G-V relations with and without 10 mM Mg²⁺ were obtained in the presence and absence of β4. Fig. 2 shows currents activated in 60 μM Ca²⁺, (Fig. 2 A, left, and Fig. 2 B, open symbols) and then channels are further activated through low affinity sites with 10 mM Mg²⁺ (Fig. 2 A, right, and Fig. 2 B, closed symbols). Mg²⁺ actually yielded a smaller G-V shift for α+β4 channels (by −69 mV) compared with α alone (by −96 mV), suggesting that β4 does not increase gating through Ca²⁺ binding at the low affinity site. A flaw of this interpretation is that inferring effects of Ca²⁺ binding to the low affinity sites using 10 mM Mg²⁺ may be inappropriate in the presence of Ca²⁺. At 60 μM Ca²⁺, it is possible that 10 mM Mg²⁺ can compete with Ca²⁺ for the low affinity site and therefore confer some inhibitory effects on gating. To rule out such possibility, effect of β4 on G-V shift by 10 mM Mg²⁺ was also examined at 0 Ca²⁺. Again, 10 mM Mg²⁺ produced a smaller shift in V_1/2 for α+β4 channels compared with α alone (−64 vs. −96 mV, respectively; Fig. 2 C). Together, these results suggest that activation at high Ca²⁺ cannot be explained by changes involving the low-affinity Ca²⁺ binding site.

Figure 2.

Ability of 10 mM Mg²⁺ to promote channel gating is decreased in the presence of β4. (A) BK α (top) and α+β4 (bottom) currents are recorded in 60 μM Ca²⁺/0 Mg²⁺ (left) and 60 μM Ca²⁺/10 mM Mg²⁺ (right). (B) Conductance–voltage relationships in 60 μM Ca²⁺ with (5 patches for α and 9 patches α+β4) and without 10 mM MgCl₂ (9 patches for α and 17 patches α+β4) or (C) nominally 0 Ca²⁺ with (7 patches for α and 6 patches α+β4) and without (12 patches for α and 6 patches α+β4) 10 mM MgCl₂. Error bars represent SEM.

Understanding Effects of β4 on Channel Gating in the Context of an Allosteric Model

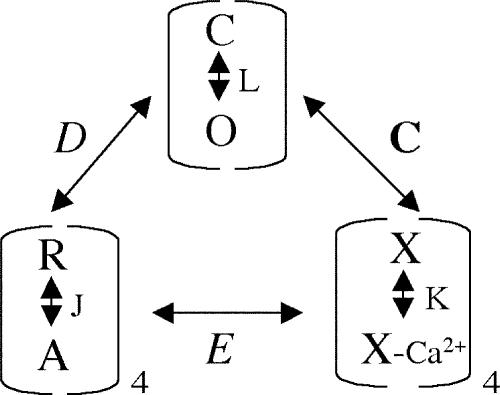
BK channel gating can be understood in terms of a dual allosteric model in which activation of a voltage sensor and a Ca²⁺ sensor each facilitate opening of the channel (Scheme 1) (Rothberg and Magleby, 1999; Horrigan and Aldrich, 2002).

(SCHEME 1).

In this model, channel opening is governed by three equilibrium constants, L (closed-to-open transition), J (voltage sensor activation), K (Ca²⁺ binding), and three allosteric factors D (coupling of voltage sensor movement to channel opening), C (coupling of Ca²⁺ binding to opening), and E (interaction between Ca²⁺ binding and voltage sensor movement). Detailed descriptions of these parameters are listed in Table II. Open probability can be described by Eq. 1:

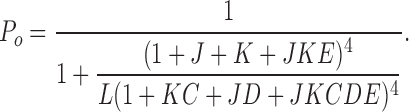(1)

TABLE II.

70-state Model Gating Parameters (Horrigan and Aldrich, 2002)

L	C–O equilibrium constant (unliganded channel, resting voltage sensors)
	L = L0exp(zLV/kT)
	L0 and zL, the zero voltage value of L and its partial charge, respectively
J	R–A equilibrium constant (closed, unliganded channel)
	J = J0exp(−zJV/kT)
	J0 and zJ, the zero voltage value of J and its partial charge, respectively
K	Equilibrium constant for Ca2+ binding (closed channel, resting voltage sensors)
	K = [Ca2+]/Kc
	Kc, calcium dissociation constant (closed channel, resting voltage sensors)
C	Allosteric factor describing interaction between channel opening and Ca2+ binding
	C = Kc/Ko
	Ko, calcium dissociation constant (open channel, resting voltage sensors)
D	Allosteric factor describing interaction between channel opening and voltage sensor activation
	D = exp[−zJ(Vho − Vhc)/kT]
	Vho and Vhc, half-activating voltage of Qc and Qo, respectively.
	Qc and Qo, steady-state gating charge distribution for closed or open channels
E	Allosteric factor describing interaction between Ca2+ binding and voltage sensor activation

To understand the mechanism underlying β4 modulation of the channel, we examined how individual gating parameters are altered by β4. Our experimental approach was to measure P_o under conditions that reduce the number of occupied states and thereby constrain a number of gating parameters. For example, to observe effects on voltage dependence, we measured P_o-V relations in the virtual absence of calcium. To observe effects of β4 on calcium dependence, we measured P_o-V relations at very negative voltages where voltage sensors are in the resting state. These experiments are presented below. The remaining gating parameters were then estimated by fitting all data using Eq. 1.

The β4 Subunit Shifts Voltage Sensor Activation to Negative Voltages and Increases the Intrinsic Energetic Barrier for Channel Opening

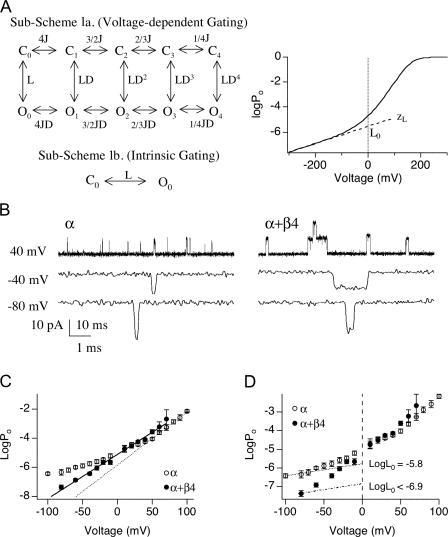
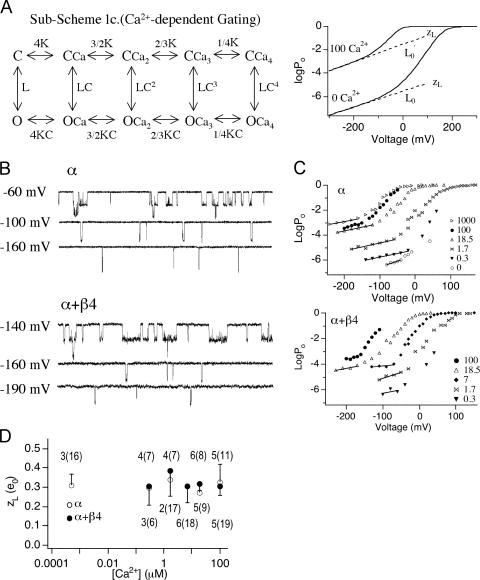
Our first aim was to measure β4 effects on the closed-to-open equilibrium and its voltage dependence (L₀ and z_L, respectively). Based on the dual allosteric model (Horrigan and Aldrich, 2002) this can be accomplished by measuring P_o-V relations in the virtual absence of Ca²⁺ (Horrigan and Aldrich, 1999). This effectively reduces the number of occupied states to 10 (Fig. 3 A, Sub-Scheme 1a) and P_o is determined by the equilibrium of intrinsic gating, L (where L = L ₀exp(z_LV/kT)), voltage sensor activation, J, and the allosteric interaction between them, D (Horrigan et al., 2002):

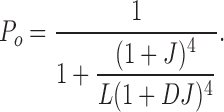(2)

Figure 3.

β4 increases the intrinsic energetic barrier for channel to open. (A, left) According to the dual-allosteric mechanism (Horrigan and Aldrich, 1999, 2002), BK channel transitions between closed (C) and open (O) conformation is allosterically regulated by the state of four independent and identical voltage sensors. Sub-Scheme 1a represents BK channel's gating scheme at 0 Ca²⁺. Channel resides in either open or closed conformation, with 0–4 voltage sensors in the activated state. Equilibrium between C-O transitions is allosterically regulated by the states of the voltage sensors. Sub-Scheme 1b represents BK channel's gating scheme at 0 Ca²⁺ and very negative voltages. With all voltage sensors in the resting state, channel resides in one of two conformations, C₀ and O₀. Equilibrium between the C₀–O₀ transition is described by L, the intrinsic equilibrium for channel opening in the absence of Ca²⁺ and voltage sensor activation. (A, right) Illustration of how two components of L (L₀ and z_L) can be estimated by logPo-V data at 0 Ca²⁺ and negative voltages. Curve represents simulated logPo vs. voltage curve in nominally 0 Ca²⁺. Gating parameters used for simulation are as follows; L₀ = 2.5 × 10⁻⁶, z_L = 0.39 e₀, z_J = 0.54 e₀, Vh_c = 173 mV, Vh_o = 25 mV. Dashed line represents fit for logPo-V at limiting slope using Eq. 4. L₀ and z_L can be derived from the fit. (B) Single-channel BK currents recorded in nominally 0 Ca²⁺ at indicated voltages. At −80 mV, α alone data was obtained from a patch containing ∼706 channels, and α+β4 data was obtained from a patch containing estimated ∼730 channels. At both −40 and +40 mV, α alone data was obtained from a patch with estimated ∼123 channels, and α+β4 data was obtained from a patch with estimated ∼411 channels. All traces were low-pass filtered at 3 kHz, except for α alone at −80 mV, which was filtered at 8.4 kHz. (C) Limiting slope is not reached for the logP_o-V data in the presence of β4. Mean logP_o as a function of voltage in the absence and presence of β4 in nominally 0 Ca²⁺ (3–12 patches for α and 4–11 patches for α+β4). Error bars represent SEM. The voltage dependence (slope) for α alone channels shows an apparent decrease at approximately +30 mV. For α+β4 channels, no apparent change in slope is observed over the voltage range between −80 and +70 mV. (D) β4 decreases L₀ by at least 11-fold. Data from C replotted to show that estimates of L₀ for α alone channels obtained by extrapolating logP_o-V relations from limiting slope to 0 mV. An upper limit of L₀ for α+β4 channels was estimated using Eq. 4, based on the mean P_o value at −80 mV and a z_L value of 0.3 e₀.

A simulated P_o-V relation predicted by Eq. 2 is shown in Fig. 3 A (right). At very negative membrane potentials, the slope of the P_o-V relation is very shallow (limiting slope), reflecting the weak voltage dependence (z_L) of the closed-to-open transition independent of voltage sensor movement. This is followed by a steeper voltage dependence at high voltages where voltage sensors start to activate and contribute to voltage sensor–dependent channel gating. By confining our analysis to very negative voltages, channel occupancy can be further reduced to two states, C₀ and O₀ (Fig. 3 A, Sub-Scheme 1b). Because J is small (J ≪ 1/D), Eq. 1 reduces to

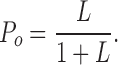(3)

Where P_o is also small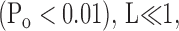

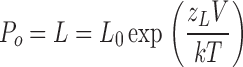(4)

Thus parameters describing channel intrinsic gating properties (L₀ and z_L) can be estimated by fitting logP_o-V relation at very negative potentials using Eq. 4. The slope of the fit is a function of voltage dependence of the closed-to-open transition (z_L), and the 0 mV value of the fit is a measure of the closed-to-open equilibrium of intrinsic channel gating (L₀).

To evaluate effects of β4 on channel intrinsic gating parameters (i.e., independent of Ca²⁺ or voltage sensor activation) using Eq. 4, BK currents were measured in 0 Ca²⁺ at negative membrane potentials. Because channel open probabilities are very low under these conditions, recordings were obtained from patches containing hundreds of channels and analyzed using single-channel analysis techniques to estimate P_o (the number of channels in each patch was estimated by measuring the maximal current amplitude at higher Ca²⁺ and dividing by the unitary current amplitude, see MATERIALS AND METHODS). Examples of recordings in the absence and presence of β4 are displayed in Fig. 3 B.

In the presence of β4, channel openings are less frequent but display longer durations, consistent with previous observations (Ha et al., 2004). Mean logP_o-V relations (between −80 and +100 mV) are displayed in Fig. 3 C. These data demonstrate effects of β4 on two aspects of channel gating. First, although the slope of logP_o-V relation shows a clear decrease for the α alone channels at around +30 mV, there is little change in slope for the α+β4 channels over this voltage range (+70 through −80 mV). Possible explanations are either that (a) for α+β4 channels, z_L is increased, and thus comparable to the voltage dependence of opening at higher voltages (that involves voltage sensor activation), or (b) β4 does not effect z_L, but we could not estimate z_L because voltage sensor activation occurs at voltages more negative than for α alone channels. It is difficult to propose a plausible physical mechanism that could account for an increase in z_L that would not also dramatically alter voltage dependence of P_o at high voltages. Therefore, we hypothesize that β4 shifts activation voltage for open-channel voltage sensors (Vh_o) to membrane potentials more negative than −80 mV. Direct measurements of z_L below −80 mV at 0 Ca²⁺ was not feasible because channel openings fall below our level of detection. However, this hypothesis is supported by measurement of z_L at high Ca²⁺, as discussed below.

Our data also suggest that β4 decreases the channel's intrinsic equilibrium for opening (L₀). L₀ value for α alone channels was estimated by fitting P_o-V relations between −100 and −70 mV (at limiting slope) using Eq. 4 and the estimated z_L value of 0.3 e₀. L₀ for the α alone channel is estimated to be 1.6 × 10⁻⁶ (Fig. 3 D). In the presence of β4, we did not reach the membrane potential where contribution of voltage sensors can be ignored. Measuring P_o below −80 mV is technically not feasible because channel openings for α+β4 are too few to get estimates of P_o (P_o < 1 e⁻⁸). Therefore, we estimated an upper limit for the closed-to-open equilibrium (L₀) using the mean P_o value at −80 mV and z_L value of 0.3 e₀ (Fig. 3 D). The estimated upper limit for L₀ in the presence of β4 is 1.4 × 10⁻⁷, suggesting that β4 decreases the equilibrium constant of the closed-to-open transition by at least 11-fold.

Voltage Dependence of the Closed–Open Transition (z_L) Is Not Altered by β4

We were able to evaluate effects of β4 on z_L, the gating parameter that describes the voltage dependence of the closed-to-open transition, in the presence of Ca²⁺. Ca²⁺ increases the P_o even in the absence of voltage sensor activation, which makes it feasible to obtain P_o-V relations at the limiting slope and directly estimate z_L. Based on the dual-allosteric model (Horrigan and Aldrich, 2002), Ca²⁺ should not change the voltage dependence of the closed-to-open transition. As illustrated in Fig. 4 A (Sub-Scheme 1c), at very low voltages, where voltage sensors remain in resting states, the number of occupied state reduces to 10 and P_o is described as

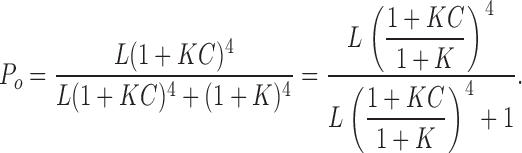(5)

When P_o is small 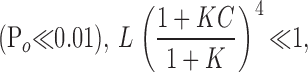Eq. 5 reduces to

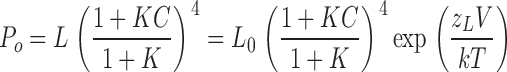(6)

Figure 4.

β4 effects on z_L in the presence of Ca²⁺. (A, left) According to the dual-allosteric mechanism (Horrigan and Aldrich, 2002), BK channel transitions between closed (C) and open (O) conformation is allosterically regulated by the state of four independent and identical Ca²⁺ binding sites. Sub-Scheme 1c represents BK channel's gating scheme at very negative voltages, where voltage sensors remain in the resting states. Channel resides in either closed or open conformations, with 0–4 Ca²⁺ binding sites occupied. Equilibrium between the C–O transitions is allosterically regulated by the states of the Ca²⁺ binding sites. In the absence of voltage sensor activation, voltage dependence of the C–O transition is entirely dependent on z_L. (A, right) Illustration of how z_L can be estimated by logP_o-V data at high Ca²⁺ and very negative voltages. Curves are simulated logP_o-V curves in nominally 0 Ca²⁺ and 100 μM Ca²⁺ according to Scheme 1c. Gating parameters used for simulation are as follows: L₀ = 2.5 × 10⁻⁶, z_L = 0.39 e₀, z_J = 0.54 e₀, Vh_c = 173 mV, Vh_o = 25 mV, K_c = 13.9 μM, and K_o = 1.4 μM. Dashed lines represent fits for logP_o-V at limiting slopes using Eq. 8. L₀′ and z_L can be derived from the fits. (B) At 100 μM Ca²⁺, currents were recorded at very negative voltages to determine logP_o vs. V relations. Currents were low-pass filtered at 20 kHz. Representative current traces at indicated voltages in the absence and presence of β4, respectively. Traces in B were all obtained from the same patch. Currents were filtered at 5 kHz for display purposes. (C) Representative logP_o-V relations at various Ca²⁺ where limiting slopes is reached. Upper limits for z_L were estimated from the apparent limiting slopes (solid lines). (D) Estimates of z_L plotted as a function of [Ca²⁺] for α subunits alone (open symbols) and α+β4 (closed symbols) for patches where limiting slope was reached. Error bars represent SEM. The number of patches where limiting slope was reached as well as total number of recordings performed (in parenthesis) at each [Ca²⁺] are indicated.

P_o-V relations predicted by the gating scheme is illustrated by simulated P_o-V relations at 0 and 100 μM [Ca²⁺] (Fig. 4 A, right). By using Eq. 6 to fit P_o-V at very negative membrane potentials in the presence of [Ca²⁺] (Fig. 4 A), z_L can be obtained since the higher P_o makes measurements more feasible.

To estimate z_L in the absence and presence of β4, we measured P_o in the presence of 0–100 μM [Ca²⁺] at decreasing membrane potentials. Examples of recordings at 100 μM Ca²⁺ at very negative membrane potentials are shown in Fig. 4 B. In a portion of recordings, logP_o-V relation appeared to have reached the “limiting slope”. Fig. 4 C illustrates how z_L was estimated using such recordings. The regions of the log(P_o)-V relations where voltage dependence of P_o is clearly reduced were fit with Eq. 6 to estimate z_L. Mean z_L values for α subunit alone at different [Ca²⁺] are summarized in Fig. 4 D. Consistent with the dual allosteric model (Horrigan and Aldrich, 2002), z_L value estimated at various [Ca²⁺] appear to be similar. The mean of all estimates of z_L for the α alone channels was 0.30 ± 0.02 e₀ (n = 26). The limiting slope was reached in a much smaller portion of α+β4 recordings, especially at low [Ca²⁺] (Fig. 4 D). Estimates of z_L at 18.5 and 100 μM Ca appeared to be better constrained than at lower Ca²⁺. The mean z_L for α+β4 channels was 0.31 ± 0.03 e₀ (n = 21). When only the best constrained data (18.5 and 100 μM) were included, the mean z_L was 0.29 ± 0.03 e (n = 10). In conclusion, β4 does not appear to alter z_L, voltage dependence associated with channel's closed-to-open transition.

Effect on Ca²⁺ Sensitivity

P_o-V relations at the limiting slope in the presence of Ca²⁺ can be used to assess effects of β4 on Ca²⁺-dependent gating (Horrigan and Aldrich, 2002). As discussed above, when P_o is low (<0.01), Eq. 5 reduces to Eq. 6. We can define L₀′ as the closed-to-open equilibrium with the allosteric contribution of calcium binding (in the absence of voltage sensor activation):

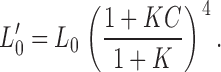(7)

Then P_o changes in the absence of voltage sensor activation becomes

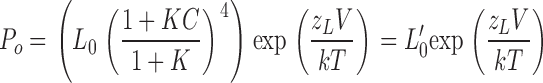(8)

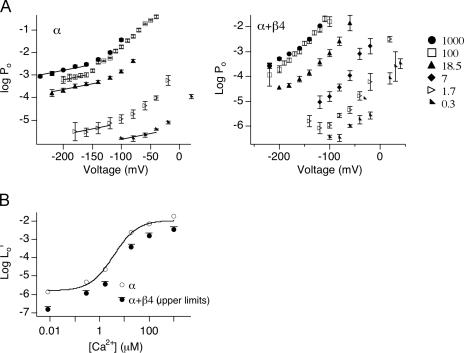
In the presence of Ca²⁺, P_o-V measured at limiting slope can be fitted by Eq. 8 to estimate L₀′. This is similar to the approach for evaluating L₀ (Fig. 3 D). L₀′-[Ca²⁺] relations can then be fitted by Eq. 7 to estimate β4 effects on calcium-dependent parameters, K_c and C.

Mean logP_o-V relations for the α alone and α+β4 channels are presented in Fig. 5 A. For the α alone channels, the limiting slopes of the logP_o-V relations were reached and fitted with Eq. 8 to estimate L₀′. Log L₀′ are plotted as a function of [Ca²⁺] (Fig. 5 B). Fitting log(L₀′) (from mean data) vs. [Ca²⁺] with Eq. 7 yielded L₀ = 1.7 × 10⁻⁶ ± 5 × 10⁻⁷, K_c = 13 ± 3 μM and C = 10 ± 1. These values are similar to previous estimates of the α alone channels based on the dual-allosteric model (L₀ = 9.8 × 10⁻⁷, K_c = 11 μM, and C = 8; Horrigan and Aldrich, 2002).

Figure 5.

Effect of β4 on Ca²⁺-dependent gating. (A) Symbols represent logP_o-V relations at various [Ca²⁺]. Error bars represent SEM. Lines are fits for mean logP_o-V at limiting slope using Eq. 8 and z_L of 0.3 e₀. L₀′ for α alone channels were derived from the fits. (B) Open symbols are logL₀′ vs. [Ca²⁺] for α alone. Curve represents fit of logL₀′-[Ca²⁺] using Eq. 7. For α+β4, only an upper limit for logL₀′ is estimated and displayed as solid symbols (solid circles with an overhanging line) and therefore were not fit with Eq. 7.

For the α+β4 channels, we again observe a negative shift in the voltage sensor activation (Vh_o). However, the limiting slope of logP_o-V relations were reached in a small percentage of recordings that allow estimation of z_L (Fig. 4 C), the limiting slope of logP_o-V relation was not reached in the majority of the patches (Fig. 4 D and Fig. 5 A). This is reflected in the logP_o-V plot in Fig. 5 A (right) where only the foot of the data points show a reduction in voltage dependence. Although L₀′ could not be obtained directly, nevertheless high limits for L₀′ at different [Ca²⁺] were determined by mean P_o value measured at the lowest membrane potentials using Eq. 8 and the mean z_L value of 0.3 e₀. The results show a plot that can be regarded as upper limits of L₀′ for the α+β4 channels (Fig. 5 B). Interestingly, L₀′ values for α+β4 were smaller than L₀′ for the α alone channels, at all [Ca²⁺]. This is an important finding in light of the fact that, at high Ca²⁺, β4 causes an increase in P_o at higher voltages (negative shift of V_1/2 at high calcium, Fig. 1 C). These findings suggest that Ca²⁺ binding (through high or low affinity sites) alone is insufficient to cause the negative G-V shift conferred by β4 in high Ca²⁺. By default, aspects of β4 modulation of voltage sensor activation must contribute to the leftward G-V shift at high Ca²⁺.

Effects of β4 in the Context of an Allosteric Model

The above analysis directly examined effects of β4 on several aspects of BK channel gating. Our analysis of open probability at limiting slope suggests that β4 increases the energetic barrier for channel opening, and causes a negative shift in the activation of voltage sensors for open channels. To understand these effects in a comprehensive framework, and whether other aspects of gating are affected by β4, families of G-V curves as well P_o-V relations obtained at low voltages were fit with the dual allosteric model (Scheme 1; Horrigan and Aldrich, 2002).

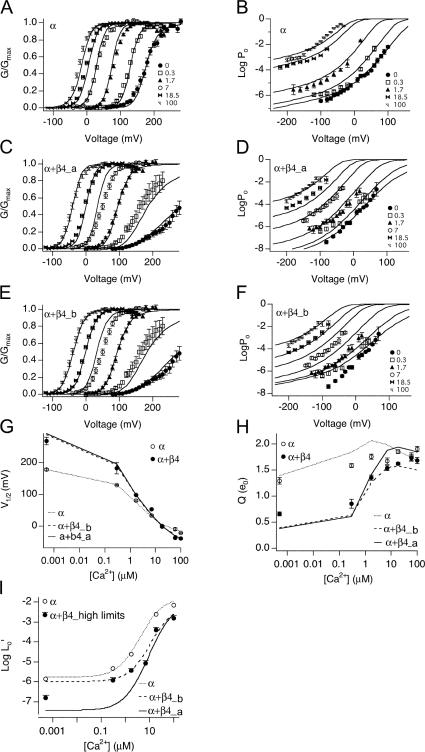
There are seven free parameters in the allosteric model (Table II). For α alone channels, four of these parameters were constrained based on analysis of our experimental data. These parameters (and range of values imposed) were z_L (0.3 e), L₀ (1.7 × 10⁻⁶), K_c (13 μM), and K_o (1.3 μM). The remaining parameters (z_J, Vh_c, Vh_o, and E) were allowed to vary freely. Although a range of parameters produce satisfactory fits for the G-V curves, we found only one set of parameters that could also reproduce P_o-V data measured at very negative voltages. These are shown in Table III. Simulated P_o with parameters in Table III reproduces reasonably well the α alone G-V curves over a wide range of Ca²⁺ (from nominally 0 through 100 μM; Fig. 6 A) as well as P_o at low voltages (Fig. 6 B), the V_1/2 vs. [Ca²⁺] relation (Fig. 6 G), the Q vs. [Ca²⁺] relation (Fig. 6 H), and the Ca²⁺-dependent shift in P_o in the absence of voltage sensor activation (Fig. 6 I). These parameters are similar to previously reported for the α alone channels (Horrigan and Aldrich, 2002).

TABLE III.

Steady-state Parameters

Best fits
	L0	zL	Kc	Ko	C	zJ	Vhc	Vho	D	E	chisq
α	1.7 e −6	0.30	13	1.3	10	0.56	187	25	35	5.9	3018
α+β4_a	3.7 e−8	0.30	44	1.9	23	0.55	110	−50	32	3.7	2157
Alternative Fits
α+β4_b	1.0 e−6	0.30	34	3.8	9	0.51	115	−18	14	8.5	15700
α+β4_c	1.8 e −7	0.30	52	3.3	16	0.57	113	−22	7.7	12.3	2298
α+β4_d	1.2 e −8	0.30	40	1.4	29	0.54	109	−68	43	2.5	2179
α+β4_e	3.0 e−7	0.30	54	3.9	14	0.57	129	0	18	13	2625
α+β4_f	1.6 e−9	0.30	37	0.8	46	0.52	109	−100	72	1.3	2256

Bold numbers indicate parameter values that were fixed during the fitting. chisq indicates Chi-square value, and was calculated based on the 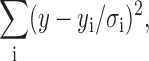where y was a fitted value for a given point, y_i is the measured data value for the point, and σ_i is an estimate of the standard deviation for y_i.

Figure 6.

Evaluation of fit parameters α, α+β4_a, and α+β4_b. P_o-V relations at 0.0005, 0.3, 1.7, 7, 18.5 and 100 μM Ca²⁺ were simulated using indicated fit parameters (Table III) and fit to the Boltzmann function. (A and B) The fit from α is superimposed on a series of G-V data for α alone channels from macroscopic recordings, and P_o-V data from single channel recordings, respectively. (C and D) The fit from α+β4_a (fit to G-V and low voltage P_o-V relations) is superimposed on G-V and P_o-V data for α+β4 channels, respectively. (E and F) The fit from α+β4_b (fit to G-V only) is superimposed on the same series of data as in C and D. (G) V_1/2 vs. [Ca²⁺], (H) Q vs. [Ca²⁺], and (I) logL₀′ vs. [Ca²⁺]. Simulations based on fit parameters (Table III) are compared with mean ± SEM of measurements (symbols).

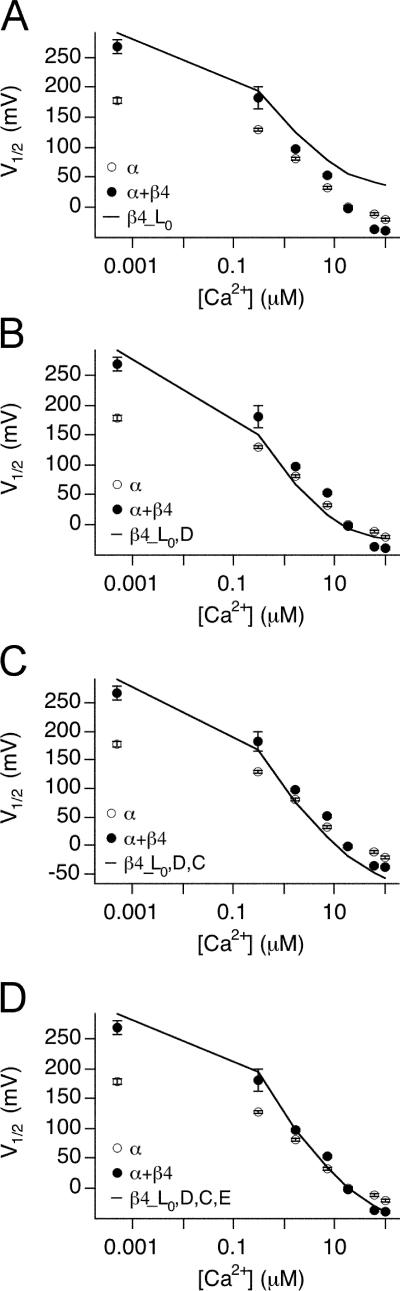
To estimate gating parameters in the presence of β4, we fit G-V data and low voltage P_o-V relations from α+β4 channels to the dual allosteric model (Horrigan and Aldrich, 2002). Based on our analysis of α+β4 channel gating at low P_o, z_L was constrained to be 0.3 e₀. Consistent with the experimental measurements in 0 calcium, the best fit (α+β4_a, Table III) suggests that major effects of β4 include decrease of L₀ (46 fold) and a −75 mV shift of voltage sensor activation (Vh_o) relative to α subunits alone. In addition, the closed channel voltage sensor equilibrium (Vh_c) is shifted to a similar extent (−77 mV), resulting in a relatively small change in voltage-dependent allosteric coupling (D). The fit indicates that there is a threefold decrease in Ca²⁺ binding affinity in the closed channel (K_c) with a smaller reduction in the open channel, resulting in an increase in calcium-dependent allosteric coupling (C). Finally, there is a small decrease in the direct allosteric coupling between Ca²⁺ binding and voltage sensor activation (E). Fit α+β4_a nicely reproduces the G-V data (Fig. 6, C and G) as well as the low voltage P_o-V relations (Fig. 6 D) and the Q vs. [Ca²⁺] relations (Fig. 6 H).

As expected, because measured logL₀′ are upper limits of the expected values, the model parameters predict a curve that falls below the α+β4 measurements (Fig. 6 I). This highlights the importance of the low voltage, single-channel P_o measurements in constraining the model. To further illustrate this, the macroscopic G-V data alone was used to fit Scheme 1 with z_L again fixed to 0.3 e₀. Although the best fit using the macroscopic G-V data alone (α+β4_b, Table III) predicts the macroscopic G-V data quite well (Fig. 6, E, G, and H), the parameters poorly predict P_o-V relations at negative voltage and low calcium (Fig. 6 F), and the predicted logL₀′ values are larger than the measured upper limits in 0 calcium (Fig. 6 I).

The Effects of β4 on L₀ and Vh_o Are Robust

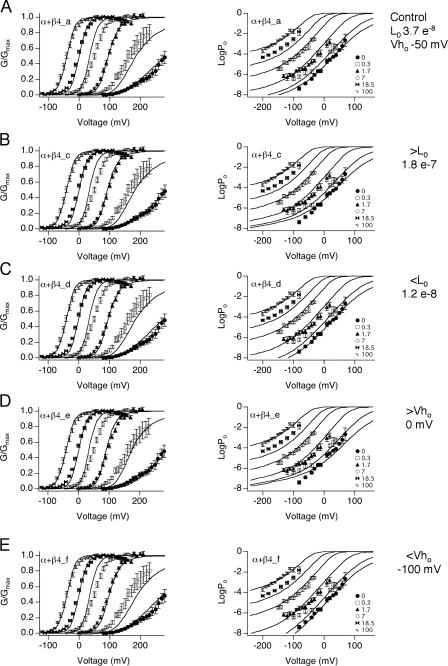
Our best fit of the α+β4 data, α+β4_a, indicates that the major effects of β4 are a decrease in L₀ and negative voltage shifts of voltage sensor equilibrium (Vh_o). To examine whether the kinetic parameters in α+β4_a are robust, we fixed L₀ or Vh_o at increased or decreased values, and then refit the other parameters to see if compensatory changes could be made in other parameters that might result in an equivalent fit.

To test if the L₀ value is robust, we obtained fits α+β4_c and α+β4_d (Table III) by fixing L₀ at values three times larger or smaller, respectively, than that predicted by α+β4_a. When L₀ is three times larger, the fit predicts the G-V data quite well (α+β4_c; Fig. 7 B, left), but does not predict the low voltage P_o-V relations at low calcium as well as α+β4_a (Fig. 7 B, right ). When L₀ is three times smaller (α+β4_d), Vh_o is shifted in the negative direction to compensate. The fit to the low voltage P_o-V relations is improved relative to α+β4_c (Fig. 7 C), although it is not improved over α+β4_a.

Figure 7.

Evaluation of fit parameters α+β4_c through α+β4_f. Fits are superimposed on the same series of G-V (left) and P_o-V data (right). Individual parameters that are fixed are shown on the right. Parameters obtained are shown in Table III. (A) Best fit (α+β4_a) from Fig. 6 (C and D) for comparison. Fixed parameters are (B) increasing L₀ threefold to 1.8 e⁻⁷, (C) decreasing L₀ threefold to 1.2 e⁻⁸, (D) 50 mV positive shift of Vh_o to 0 mV, (E) −50 mV shift of Vh_o to −100 mV.

To analyze the impact of shifting Vh_o on fitting the α+β4 data, Vh_o was fixed to a more positive value, resulting in α+β4_e (Fig. 7 D). This would correspond to a reduced contribution of voltage sensor activation to channel opening at negative voltages. Table III shows that the major compensatory effect is an increase in L₀ and E, both of which would correspond to increased channel opening at negative voltages. Although the macroscopic G-V data is predicted fairly well (Fig. 7 D, left), the low voltage P_o-V relations in low calcium are not predicted well (Fig. 7 D, right). In contrast, shifting Vh_o to more negative potentials as compared with α+β4_a (Fig. 7 E) allows fits that are comparable to α+β4_a. Because the negative shift of Vh_o has the effect of increasing P_o at negative voltages, this is compensated for by a large decrease in the L₀ value (to 1.6 e⁻⁹; Table III) and reduction in allosteric coupling between voltage sensor movement and calcium binding (E). Interestingly, the best fits (α+β4_a, α+β4_d, and α+β4_f) seem to constrain Vh_c to around 110 mV (Table III), regardless of a negative shift of the Vh_o or a reduced L₀. Consistent with this, we observed that a +50 or −50 mV shift in Vh_c produces fits that deviate significantly from the G-V data (unpublished data).

This analysis demonstrate that low voltage P_o-V relations constrain a model in which β4 mediates a negative shift of voltage sensor activation (Vh_o), and biases the intrinsic closed to open equilibrium (L₀) toward the closed state. The data can be fit by L₀ that is smaller than our estimates, if there is a corresponding negative shift in Vh_o. Independent of changes in these two parameters, this analysis indicates that β4 produces an increase in allosteric coupling to calcium binding (C), a reduction of closed channel calcium binding affinity (K_c), and a negative shift of Vh_c.

Understanding Effects of β4 on BK Channels

BK channels α+β4 currents show a positive shift of the G-V relationship at low calcium and a negative shift of the G-V relationship at high calcium. In addition, the β4 subunit causes an apparent reduction in voltage dependence at low calcium. How do the changes in individual gating parameters altered by β4 confer α+β4 properties? To address this question, the α subunit steady-state properties were simulated and compared with simulations where individual β4 gating parameters are used to replace α subunit parameters. These are shown as individual changes in Figs. 8 and 9, and as additive changes in Fig. 10.

Figure 8.

Changes in G-V relations as a consequence of β4 modulation of L₀. Simulations using α subunit parameters from Table III, with α L₀ (plus symbols) or α+β4 L₀ (closed symbols). (A) Effect of L₀ modulation on V_1/2 vs. [Ca²⁺] relationship, and (B) Q vs. [Ca²⁺] relationship. V_1/2 and Q of simulated G-V were obtained from Boltzmann fit to simulated P_o-V curves. (C–E) Illustration of how L₀ and [Ca²⁺] affect Q by influencing position of G-V curves relative to Vh_o and Vh_c. (C) Simulation of G-V curves in 7 μM (dashed line) and 0 calcium (solid line) relative to Vh_o and Vh_c (vertical dash lines) using α subunit L₀ parameter. (D) Same as C but using α+β4 L₀ parameter. (E) Q vs. V_1/2 relationships illustrates how position of V_1/2 relative to Vh_o and Vh_c affects Q values.

Figure 9.

Negative shift of Vh_o has the most significant contribution in opposing decrease in L₀ and increasing α+β4 channel opening. Data points are simulated values based on α subunit parameters in Table III with indicated parameters replaced by those of α+β4. (A and B) Effects of β4 modulation on Ca²⁺-dependent gating. (C and D) Changes in G-V relations as a consequence of β4 modulation on voltage-dependent gating. Plotted are V_1/2-[Ca²⁺] and Q-[Ca²⁺] relations when α parameters are replaced by indicated α+β4 parameters.

Figure 10.

Additive effects of β4 gating parameters on BK channel steady-state properties. Simulations with α subunit parameters incrementally replaced by those of α+β4. Panels show experimental data for α (open symbols) and α+β4 (closed symbols) V_1/2 vs. [Ca²⁺] relationship. Line shows simulations using α subunit parameters incrementally altered by β4 L₀ (A), β4 L₀ + D (B), β4 L₀ + D +C (C), β4 L₀ + D +C +E (D).

Effect on the Closed-to-Open Transition

Independent of voltage sensor movement and Ca²⁺ binding, BK channel opening is governed by an intrinsic energetic barrier (described by L₀) that has a weak intrinsic voltage dependence (z_L) (Horrigan and Aldrich, 2002). Data in Fig. 3 D suggest that the equilibrium constant L is significantly increased (at least by 11-fold) in the presence of β4. Our best fit indicates that the β4 subunit decrease (L₀ from 1.7 × 10⁻⁶ for α alone to 3.7 × 10⁻⁸ for α+β4_a, approximately by 46-fold, indeed lower than our estimated upper limits (Fig. 3 D).

Effects of a 46-fold decrease in L₀ are illustrated in Fig. 8. We first simulated G-V relations at various Ca²⁺ based on gating parameters for α (Table III) and obtained V_1/2-[Ca²⁺] and Q-[Ca²⁺] relations by fitting simulated G-V curves with Boltzmann function (Fig. 8, A and B). To see how changes in L₀ might affect BK channel gating, we simulated G-V curve using α parameters except for the L₀, which is replaced by that of β4 L₀ (Fig. 8, A and B). As expected, a 46-fold decrease in L₀ by β4 creates a positive shift of the V_1/2 at all [Ca²⁺] (Fig. 8 A, β4_L₀). Interestingly, the effect of L₀ also causes a significant decrease in the voltage dependence (Fig. 8 B).

Why does decreasing L₀ cause a decrease in voltage dependence, particularly at submicromolar [Ca²⁺]? In the dual allosteric gating scheme (Scheme 1), voltage sensors are activated around a voltage range defined by Vh_o for open channels and Vh_c for closed channels. Within this range (between Vh_o and Vh_c), the energetic difference between voltage sensor activation in closed and open channel is greatest, thus allosteric coupling between voltage sensor activation and gating is the strongest, and P_o is most voltage dependent (large Q). The effect of L₀ or calcium positions P_o-V curves along the voltage axis relative to Vh_o and Vh_c and therefore affects the voltage dependence. This is illustrated in P_o-V relations at two different [Ca²⁺] simulated with the parameter from α alone channels, in Fig. 8 C. Channel opening at 0 and 7 μM calcium falls approximately within this voltage range, and G-V curves show high voltage dependence (steep slope). Below and above these ranges, voltage sensors are either in the resting or activated state, respectively, and voltage-dependent channel openings are dependent on the weaker closed-to-open voltage dependence, z_L. In contrast, data simulated using an L₀ fixed at the value estimated for α+β4 channels (Fig. 8 D) resulted in channel openings at voltages more positive than Vh_c for the 0 Ca²⁺ data. This resulted in a reduced voltage dependence (shallower slope). However, as higher calcium (≥7 μM) contributes significantly to channel gating, openings fall within the ranges where voltage sensors contribute to channel gating and we see a greater apparent voltage dependence.

By examining apparent Q vs. V_1/2 (determined by fitting simulated data with Boltzmann equations; Fig. 8 E), we can see that the L₀ affects Q mostly by shifting the V_1/2 along the voltage axis. Where V_1/2 is similar between α and β4_L₀, the Q values are similar. At low [Ca²⁺], channel activation occurs at membrane potentials more depolarized than Vh_c, causing a decrease in apparent voltage dependence (Q). This is more dramatic in the presence of β4, since the significant decrease in L₀ requires much higher membrane potential to open the channels.

Effect on Ca²⁺ Dependence

The fits with Scheme 1 suggest that the α+β4 channels have a threefold reduction in affinity of Ca²⁺ in the closed state (K_c = 13 μM α alone; 44 μM α+β4) with little change in affinity of the open state (K_o = 1.3 α alone; 1.9 μM α+β4). Thus, the β4 subunit imparts an increase in the strength of allosteric coupling between Ca²⁺ binding and channel opening (C = 10 for α alone vs. 23 for α+β4). A reduced affinity and greater coupling to Ca²⁺ binding may contribute to the negative shift in the V_1/2 at high Ca²⁺ (Fig. 9 A). It should be noted however, that the model predicts that effects on Ca²⁺ sensitivity alone are not sufficient to offset the increased L₀, particularly at low Ca²⁺ (Fig. 9 A, open circles). This is consistent with Ca²⁺ experiments discussed previously (Fig. 5 B). In these experiments, we found that the contribution of calcium alone in the absence of voltage sensor activation does not impart sufficient energy to shift the V_1/2 more negative to α subunit. As discussed below, left shift of voltage sensor activation (Vh_o) makes an important contribution to the negative shift of the V_1/2.

Interestingly, effects on allosteric coupling to Ca²⁺ (C) appear to contribute to a slight reduction in apparent voltage sensitivity in high Ca²⁺ (Fig. 9 B). Increased Ca²⁺ coupling positions the V_1/2 at 100 μM at approximately −60 mV, below the foot of voltage sensor activation (Vh_o is +25 mV for α, see Table III). These effects are predicted to reduce apparent voltage dependence at high calcium, as indeed we see for α+β4 channels (Fig. 1 D).

Effect on Voltage Dependence

Although the fits suggest that β4 does not alter z_J (0.56 e₀ for α and 0.55 e₀ for α+β4), it causes large shifts in the equilibrium of voltage sensor activation in both the open state (Vh_o = 25 mV α alone vs. −50 mV α+β4) and closed state (Vh_c = 187 mV α alone vs. 110 mV α+β4). Although coupling between voltage sensor activation and gating (D) is slightly decreased by β4 (35 for α and 32 for α+β4), changing Vh_o and Vh_c results in a significant negative shift of the G-V curves at [Ca²⁺] >7 μM, sufficient to compensate for the increased energetic barrier (L₀) conferred by β4 (Fig. 9 C). It should be noted that the effect of changing Vh_o, besides shifting the G-V curves to more negative membrane potentials, also positions the G-V at a more optimal position relative to Vh_o and Vh_c to increase the apparent voltage dependence (Fig. 9 D). The above results and recent findings by Bao and Cox (2005) illustrate another important prediction of the dual allosteric model: channel gating is regulated not only by the coupling factor D but also by the value of Vh_o and Vh_c.

Analysis of the effects of α+β4 currents demonstrates that the change in properties contributed by the β4 subunit offset each other to produce moderate changes in the conductance–voltage relationship. A manner to consider these changes is to simulate the using the α subunit parameters, and compare these to simulated data where the α+β4 parameters are incrementally used to replace those of α subunit channels. This is shown in Fig. 10. The effect of β4 on the closed-to-open equilibrium, L, and coupling between gating and to voltage sensor movement, D, have opposing and parallel effects on the V_1/2-[Ca²⁺] relations (Fig. 10, A and B). The decrease of L₀ shifts the curve to positive potentials, and D has a compensatory shift to negative potentials at [Ca²⁺] >7 μM. Increased coupling between calcium binding and gating (C) further increases the slope of the V_1/2 vs. [Ca²⁺] curve so that at high [Ca²⁺] the V_1/2 is shifted to more negative membrane potentials relative to α subunits alone (Fig. 10 C). Model fits indicate that the β4 subunit reduces allosteric coupling between voltage sensor movement and calcium binding (E), which contributes to a positive shift of the V_1/2 at high [Ca²⁺] (Fig. 10 D).

DISCUSSION

Our analysis demonstrates that the β4 subunit alters several aspects of BK channel gating. In this respect, β4 is similar to the β1 subunit, which has been shown to modulate BK channels in a complex manner (Cox and Aldrich, 2000; Orio and Latorre, 2005). For the β4 subunit, we show that these are fairly dramatic effects on BK channel gating properties, particularly Vh_o and L₀, that seem to offset one another to produce moderate changes in the conductance–voltage relationship at micromolar [Ca²⁺]. In many regards, this too is similar to changes observed with β1 subunits. β1 and β4 both mediate a negative voltage shift of open channel voltage sensor activation, Vh_o (Cox and Aldrich, 2000; Bao and Cox, 2005; Orio and Latorre, 2005). In addition, it appears that β1 and β4 both increase the energetic barrier to opening by reducing L₀ (Orio and Latorre, 2005). This is somewhat controversial because a more recent study did not see an effect on L₀ by β1 (Bao and Cox, 2005).

What underlies the negative voltage shift of the G-V relationship at high [Ca²⁺] that is often described as an “apparent increase in Ca²⁺ sensitivity”? Orio and Latorre attribute the apparent increase in Ca²⁺ sensitivity by β1 to a decrease in z_J (Orio and Latorre, 2005). Similar to predictions by Bao and Cox (2005) for the β1 subunit, our simulations indicate that the negative shift in Vh_o by β4 has the highest contribution to increase channel opening. A very important aspect of the dual-allosteric model is that energetic contributions of voltage sensors are not equivalent over the voltage axis. Although we did not see a dramatic change in voltage-dependent allosteric coupling factor D, the negative shift of voltage sensor activation (Vh_o) contributed significantly to increase P_o. In this, the β4 and β1 are also similar (Bao and Cox, 2005).

Why would evolution alter so many properties of BK channels to produce a net effect on the V_1/2 that appears relatively moderate, particularly at higher calcium concentrations? For instance, at [Ca²⁺] between 1.7 and 18 μM, the V_1/2 is shifted by β4 to positive potentials ∼20 mV or less (Table I). At [Ca²⁺] >18 μM, there is a similar 10–30 mV negative shift. In considering the physiological role for BK α+β4 properties, one must consider the fact that the V_1/2 value often does not reflect the open probabilities at physiological voltages, particularly at resting global [Ca²⁺] where the V_1/2 is >100 mV. Instead, it may be more relevant to consider the changes in open probability in the physiological voltages between −80 and +20 mV. Although P_o values can be low, opening of even a relatively few BK channels can nevertheless have profound effects on membrane voltage. For instance in vascular smooth muscle, activation of a cluster of BK channels near a Ca²⁺ spark site can hyperpolarize the membrane by 10–20 mV (Knot et al., 1998). For β4 subunits, which are predominantly expressed in neurons, the larger energetic barrier to opening (L₀), would be expected to hold BK channels silent at resting voltages. However, the negative shift of the Vh_o means that voltage sensors are more easily activated following depolarization. Thus, appropriate with the concept that neurons respond to very transient changes in membrane potential, the opposing properties conferred by β4 subunits, increased energetic barrier to opening (L₀) and a negative shift of voltage sensor activation (Vh_o), allow BK channels to activate in a switch-like, rather than graded, fashion. For instance, at 1.7 μM calcium and resting membrane voltage of −80 mV, α+β4 L₀ confers a >10-fold lower P_o than α subunits alone (P_o α is 1.9 × 10⁻⁵, α+β4 1.6 × 10⁻⁶). However following depolarization to +20 mV, effects on Vh_o allow α+β4 BK channels to have a similar P_o to that of α subunits alone (P_o α is 4.0 × 10⁻³, α+β4 3.4 × 10⁻³). Indeed, recent findings that mutations resulting in gain of function of BK channels lead to seizure phenotypes (Du et al., 2005, Brenner et al., 2005) highlights the importance of holding BK channels silent until necessary.

The current study has focused on steady-state properties conferred by β4 subunits. Yet the β4 subunit has very profound effects on BK channel activation and deactivation kinetics that may be more physiologically important in neurons, where the β4 subunit appears to be enriched (Weiger et al., 2000). In central neurons, BK channels appear to have an important role in membrane repolarization following an action potential (Hu et al., 2001). Yet the β4 subunit slows the activation of BK channels to time scales that are incompatible with a role in shaping individual action potentials (tens to hundreds of milliseconds; Brenner et al., 2000). Further studies are warranted to understand how β4 effects on L₀ and Vh_o mediate changes in gating kinetics.