Voltage Clamp Fluorometric Measurements on a Type II Na⁺-coupled P_i Cotransporter: Shedding Light on Substrate Binding Order

Abstract

Voltage clamp fluorometry (VCF) combines conventional two-electrode voltage clamp with fluorescence measurements to detect protein conformational changes, as sensed by a fluorophore covalently attached to the protein. We have applied VCF to a type IIb Na⁺-coupled phosphate cotransporter (NaPi-IIb), in which a novel cysteine was introduced in the putative third extracellular loop and expressed in Xenopus oocytes. Labeling this cysteine (S448C) with methanethiosulfonate (MTS) reagents blocked cotransport function, however previous electrophysiological studies (Lambert G., I.C. Forster, G. Stange, J. Biber, and H. Murer. 1999. J. Gen. Physiol. 114:637–651) suggest that substrate interactions with the protein can still occur, thus permitting study of a limited subset of states. After labeling S448C with the fluorophore tetramethylrhodamine MTS, we detected voltage- and substrate-dependent changes in fluorescence (ΔF), which suggested that this site lies in an environment that is affected by conformational change in the protein. ΔF was substrate dependent (no ΔF was detectable in 0 mM Na⁺) and showed little correlation with presteady-state charge movements, indicating that the two signals provide insight into different underlying physical processes. Interpretation of ion substitution experiments indicated that the substrate binding order differs from our previous model (Forster, I., N. Hernando, J. Biber, and H. Murer. 1998. J. Gen. Physiol. 112:1–18). In the new model, two (rather than one) Na⁺ ions precede P_i binding, and only the second Na⁺ binding transition is voltage dependent. Moreover, we show that Li⁺, which does not drive cotransport, interacts with the first Na⁺ binding transition. The results were incorporated in a new model of the transport cycle of type II Na⁺/P_i cotransporters, the validity of which is supported by simulations that successfully predict the voltage and substrate dependency of the experimentally determined fluorescence changes.

INTRODUCTION

Members of the type II sodium-phosphate cotransporter family are integral membrane proteins that mediate thermodynamically coupled transport of inorganic P_i and Na⁺. In mammals, three classes of type II cotransporters (NaPi-II) are presently known. Types IIa and IIb are electrogenic and operate with a 3:1 Na:HPO₄ ²⁻ stoichiometry and translocate one net positive charge per transport cycle (for review see Murer et al., 2000; Forster et al., 2002). Type IIc is electroneutral and operates with a 2:1 Na:HPO₄ ²⁻ stoichiometry (Bacconi et al., 2005). The physiological role of these proteins is to facilitate cellular uptake of P_i by coupling it to the transmembrane electrochemical gradient. In the kidney proximal tubule, NaPi-IIa and NaPi-IIc mediate regulated reabsorption of P_i from the glomerular filtrate. NaPi-IIb has a wide tissue distribution and is expressed for example in lung, liver, and salivary gland (Hilfiker et al., 1998; Hattenhauer et al., 1999; Frei et al., 2005; Homann et al., 2005). In the intestine, NaPi-IIb is expressed at the apical membrane in enterocytes and mediates P_i absorption from the diet (Hilfiker et al., 1998; Radanovic et al., 2005). In contrast to mammals, teleosts do not express a kidney-specific NaPi-IIa isoform, instead NaPi-IIb is widely expressed including the kidney (for review see Werner and Kinne, 2001).

The transport kinetics of electrogenic type II Na⁺/P_i cotransporters have been studied in detail by electrophysiology and uptake assays (for review see Forster et al., 2002) by means of heterologous expression in Xenopus oocytes. Type IIa Na⁺/P_i cotransporters are functional monomers (Kohler et al., 2000) and we assume that this holds true for all three subtypes. A kinetic model has been developed based on analysis of substrate-induced steady-state currents and presteady-state charge movements. According to the model, the electrogenic NaPi-II transport cycle comprises ordered binding (on the extracellular side) of one Na⁺ ion, a divalent HPO₄ ²⁻, followed by two more Na⁺ ions before translocation of the fully loaded carrier to the internal side. After unloading, the empty carrier returns to an external-facing configuration via an electrogenic partial reaction, and each complete forward transport cycle transfers one positive charge to the intracellular medium (Forster et al., 1997, 1998, 2000; Virkki et al., 2005).

The documentation of substrate-dependent presteady-state charge movements for NaPi-IIa/b proteins supported the notion that voltage-dependent conformational changes accompany substrate binding/debinding and translocation. Furthermore, for NaPi-IIa/b, we have documented presteady-state charge movements in the absence of substrate (Forster et al., 1997, 1998, 2000; Virkki et al., 2005); these are assumed to reflect voltage-dependent molecular rearrangements of the empty carrier itself. In general, however, such presteady-state charge movements may arise from a global response of mobile charges distributed throughout the protein to changes in the transmembrane electric field. Moreover, electrically silent transitions are detected only indirectly through their effect on voltage-dependent events. Therefore, their usefulness as a means to localize regions or sites undergoing conformational changes may be limited.

Voltage clamp fluorometry (VCF) offers a means to overcome these limitations by allowing real-time recording of fluorescence changes of a fluorophore covalently attached to a selected site. The method relies on the property that the fluorescence of a fluorophore is sensitive to its local environment, and that conformational changes in the environment of the fluorophore may therefore effect a fluorescence change. A particular advantage of VCF is that fluorescence changes in response to changes in substrate and membrane voltage can be followed in real time; moreover, unlike presteady-state charge movement assays, detection of conformationally sensitive sites does not necessitate the movement of charged particles in an electric field. VCF was originally developed for the study of gating-induced conformational changes in K⁺ channels (Mannuzzu et al., 1996; Cha and Bezanilla, 1997). Since then, VCF has been applied to several membrane transporter systems, including the glucose transporter SGLT1 (Loo et al., 1998; Meinild et al., 2002), the glutamate transporter EAAT3 (Larsson et al., 2004), the GABA transporter GAT1 (Li et al., 2000), the serotonin transporter SERT (Li and Lester, 2002), and the Na⁺/K⁺-and H⁺/K⁺ ATPases (Geibel et al., 2003a,b). We therefore decided to apply VCF to the Na⁺/P_i cotransporter to identify parts of the protein that are involved in conformational change during substrate binding and translocation, and to shed new light on the individual kinetic steps of the transport cycle.

Wild-type (WT) NaPi-II proteins contain 13–14 cysteines, none of which is normally accessible to external methanethiosulfonate (MTS) reagents. As the first site to be investigated, we chose a previously identified mutation (S460C) in the rat NaPi-IIa isoform that appeared to show substrate-dependent changes in its MTS accessibility (Lambert et al., 1999). This mutant displays WT-like kinetics, but after modification of the cysteine, cotransport function is suppressed. However, substrate binding still appears to be intact, which would allow study of conformational changes associated with substrate binding and/or membrane voltage. An advantage of the suppression of cotransport function by MTS modification is that it gives a readily measurable readout of cysteine modification at this site, and therefore we can use this property to study the effect of membrane voltage and substrate on the accessibility of the site. Moreover, the lack of cotransport activity means that the number of distinct conformational states is reduced, thereby potentially simplifying interpretation of data in terms of kinetic schemes. Although the original mutation was created in the rat NaPi-IIa isoform, we chose the flounder NaPi-IIb isoform for VCF measurements because its expression level in oocytes is high, with P_i-induced currents up to 10 times those of the rat isoform (Forster et al., 1997).

MATERIALS AND METHODS

Reagents and Solutions

(2-aminoethyl)methane thiosulfonate hydrobromide (MTSEA), 2-(trimethylammonium)ethyl methanethiosulfonate bromide (MTSET), and sodium (2-sulfonatoethyl)methane thiosulfonate (MTSES) were obtained from Toronto Research Chemicals. 2-((5(6)-tetramethylrhodamine)carboxylamino)ethyl methanethiosulfonate (MTS-TMR) was obtained from either Toronto Research Chemicals or Biotium. All other reagents were from Sigma-Aldrich or Fluka.

The standard experimental solution (ND100) contained (in mM) 100 NaCl, 2 KCl, 1.8 CaCl₂, 1 MgCl₂, 10 HEPES, pH 7.4 (adjusted using Tris). In Na⁺ replacement experiments, NaCl was equimolarly replaced with choline Cl, LiCl, or KCl. Solutions containing the required concentrations of P_i were prepared by adding K₂HPO₄/KH₂PO₄ (pH 7.4). Modified Barth's solution for storing oocytes contained (in mM) 88 NaCl, 1 KCl, 0.41 CaCl₂, 0.82 MgSO₄, 2.5 NaHCO₃, 2 Ca(NO₃)₂, 7.5 HEPES, pH 7.5 adjusted with Tris and supplemented with 5 mg/l doxycyclin.

Oocyte Expression and Molecular Biology

cDNA encoding wild-type (WT) flounder NaPi-IIb (GenBank/EMBL/DDBJ accession no. AAB16821) was subcloned into a vector containing the 5′ and 3′ UTRs from Xenopus β-globin to improve its expression in oocytes. Mutant S448C was generated using the Quikchange site-directed mutagenesis kit from Stratagene and sequenced (Microsynth). Complementary capped RNA was synthesized using the T3 Message Machine kit (Ambion).

Adult female Xenopus laevis were purchased from Xenopus Express France or African Xenopus Facility (R. South Africa). Portions of ovaries were surgically removed from anaesthetized (0.1% Tricaine) animals and cut into small pieces. Oocytes were defolliculated using a 35–45-min treatment in ND100 solution (without Ca²⁺) containing 2 mg/ml collagenase (crude type 1A) and 0.2 mg/ml trypsin inhibitor type III-O. After extensive washing with Ca²⁺-free ND100 solution, stage V–VI oocytes were selected and maintained in modified Barth's solution at 16°C. Oocytes were injected with 50 nl of cRNA (0.2 μg/μl) and experiments performed 3–7 d after injection. Prior to fluorescence measurements, oocytes were voltage clamped to −90 mV and exposed for 5 min to 0.4 mM MTS-TMR in ND100 solution in the dark. The P_i-induced current response was recorded before and after labeling to ensure complete labeling of S448C (no significant P_i-induced currents observed after labeling). The treatment did not alter the normal P_i current response of the WT.

Conventional Two-electrode Voltage Clamp

The procedure for standard two-electrode voltage clamp has been described in detail previously (Forster et al., 1998). Membrane voltage was controlled and transmembrane current measured using a laboratory-built voltage clamp system that achieved clamping of a model oocyte (membrane capacitance 220 nF, leak resistance 200 kΩ) with a 10–90% rise time = 0.65 ms. Data were acquired using a Digidata 1322A (Molecular Devices Corp.) driven by pClamp 9 software. The oocyte was mounted in a chamber optimized for rapid solution exchange and continuously perfused at a rate of 5 ml/min. For constant voltage recordings, currents were acquired at 20 samples/s and filtered at 10 Hz. Faster sampling rates (up to 20k samples/s) were used for voltage-jump recordings, with filtering adjusted accordingly.

Steady-state and presteady-state kinetics were determined using previously described protocols (Forster et al., 1998) by applying voltage steps in the range −160 mV to +80 mV from a −60 mV holding potential (V _h). In brief, steady-state P_i activation was determined by varying the P_i concentration always in the presence of ND100 and subtracting the respective currents in ND100 from those in ND100 + P_i; steady-state Na⁺ activation was similarly determined by subtracting the respective responses in NDX from those in NDX+P_i (1 mM), where X is the test Na⁺ concentration (in mM). Steady-state P_i-induced currents (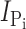) were fit with a form of the modified Hill equation:

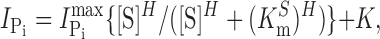(1)

where [S] is the concentration of the variable substrate (Na⁺ or P_i), 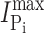is the maximum electrogenic activity, K _m ^S the apparent substrate affinity for substrate S, H the Hill coefficient, and K is a constant that takes account of uncoupled leak effects (Ehnes et al., 2004a; Virkki et al., 2005). For P_i activation, H = 1 and Eq. 1 reduces to a Michaelian form.

Presteady-state relaxations were quantitated from the records obtained in 0 mM P_i, by fitting with a two-component exponential function. The faster component was assumed to represent endogenous linear capacitive charging of the oocyte and was subtracted from the total relaxation to yield the NaPi-II–dependent component. This was numerically integrated to obtain the charge Q moved for a step from V _h to the test potential (V), as previously described (e.g., Ehnes et al., 2004a; Virkki et al., 2005). The Q-V data were fit with a Boltzmann function of the form:

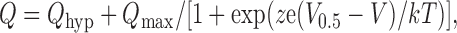(2)

where V _0.5 is the voltage at which the charge is equally distributed between two hypothetical states, z is the apparent valency of an equivalent charge that moves through the whole of the membrane field, Q _max is the total charge available to move, Q _hyp is the charge at the hyperpolarizing limit and is a function of V _h, and e, k, and T have their usual meanings.

Incubation with MTS reagents and reaction rate determinations were done as described previously (Lambert et al., 2001; Ehnes et al., 2004b). The oocyte was placed in the recording chamber and the holding current monitored continuously. After applying 1 mM P_i to determine the initial current response at −50 mV, freshly prepared MTSEA (2.5 μM) or MTSES (25 μM) in ND100 solution was applied to the oocyte for a set period of time, while the membrane voltage was held at either V _h = −90 or 0 mV. After a 1-min washout, the current response to 1 mM P_i at V _h = −50 mV was again determined and the MTS application was repeated. The MTS concentrations were optimized in preliminary experiments to allow for convenient determination of the modification rate.

The P_i-induced current remaining after each successive application of MTS reagent was extracted and plotted as a function of the cumulative exposure time, normalized to the initial P_i-induced current. The data were fit with a single decaying exponential to determine the effective second order reaction constant using an equation of the form

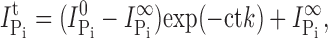(3)

where 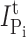is the P_i-induced current after a cumulative exposure time t, 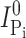is the initial P_i-induced current, 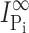is the P_i-induced current at infinity, c is the concentration of MTS reagent (assumed to be in excess), and k is the effective second order rate constant (Zhang and Karlin, 1997).

Assay for ³²P_i Uptake

P_i uptake measurements using radioactive ³²P_i on control oocytes or oocytes expressing WT or S448C NaPi-IIb were performed as follows. Groups of six to eight oocytes were preincubated in ND100 solution containing 1 mM MTSEA for 5 min. This solution was replaced with 100 μl ND100 solution containing 1 mM MTSEA, 1 mM cold P_i, and 1 μCi ³²P_i. Uptake was allowed to proceed for 10 min and then the oocytes were washed thrice with ice-cold ND0 solution containing 2 mM P_i, and finally lysed individually in 10% SDS. The amount of radioactivity trapped in each oocyte was measured using scintillation counting.

Apparatus for Simultaneous Voltage Clamp and Fluorometry

The voltage clamp hardware, data acquisition hardware, and software were the same as described above with an additional channel for fluorescence. In addition, we acquired continuous current and fluorescence signals separately with a Minidigi 1A and Axoscope software (Molecular Devices Corp). The recording chamber and arrangement of the optical components was adapted from a system originally developed by D.D.F. Loo and B. Hirayama (University of California Los Angeles, CA). The recording chamber had a volume of ∼40 μl with a 0.5-mm-thick glass coverslip as its base, upon which the oocyte was positioned and mechanically stabilized by the two microelectrodes. These were standard 3 M KCl-filled pipettes with resistances of typically 2–5 MΩ. An Ag/AgCl pellet served as the bath electrode. As noted by Meinild et al. (2002), we also found that mounting the oocyte with animal (dark) pole facing the chamber bottom resulted in lowest background fluorescence. The oocyte was continuously superfused by a gravity-feed system that allowed up to eight different solutions to be independently applied. Solution exchange in the chamber was achieved within ∼10 s.

The optical unit comprised a fluorescence objective mounted on a stable enclosure that housed the filter set and associated components. The optical unit was mounted on an X-Y translation stage (M406, Newport) that allowed centering of the oocyte within the excitation beam. Fluorescence was excited by a 100-W halogen light source powered from a stabilized DC source. For stability the light was operated continuously during the experimental session and an electronic shutter (VS252T1, Uniblitz, Vincent Assoc.) was mounted between the light source and optical unit to avoid photobleaching when not recording. The shutter controller was adapted from the manufacturer's OEM design (Vincent Assoc.) and allowed either manual control or software control by the 1322A interface. Excitation and emission wavelengths were nominally 535 and 605 nm, respectively, achieved using an XF33 filter set, which comprised a 535DF35 excitation filter, 570DRLP dichroic mirror, and 605DF50 emission filter (Omega Optical Inc.). The excitation beam was focused on the oocyte using a ×10 fluorescence objective (CFI S Fluor, 0.5 N.A., 1.2 mm W.D., Nikon), the vertical position of which could be adjusted for optimal beam focusing. The ∞-focus emission beam was reflected at 45° using a mirror (20SJ00ER.3, Newport) that was mounted below the XF33 cube. The emerging horizontal beam was focused using a convex lens (O-PCL-13, Vision GmbH) onto a Si photodiode (S1336-18BQ, Hamamatsu). The diode and lens were mounted in a separate enclosure at the side of the optical unit.

The photodiode was connected directly to the input of a CV 201 integrating headstage (Axon Instruments), and the headstage signal was processed by an Axopatch 200A patch clamp amplifier (Axon Instruments) to give an output voltage:diode current conversion ratio of 1 mV/pA (scaled output gain = 1) and a nominal bandwidth of 10 kHz. To improve the signal-to-noise ratio further when measuring voltage step-evoked fluorescence changes, the scaled output of the Axopatch 200 was processed by a differential amplifier/filter unit (LPF-8, Warner) before digitization. This allowed independent subtraction of the background fluorescence signal from the photodiode output (using a stable, low noise, adjustable voltage reference) before final amplification and filtering. The effective dark noise of the fluorescence hardware was typically ∼0.4 pA rms (5 kHz bandwidth) referred to the input of the integrating headstage, and at this bandwidth the fluorescence signal exhibited a 10–90% rise time = 0.075 ms, determined using an LED-generated light pulse coupled to the recording chamber via an optical fiber. To confirm that the VCF setup was working properly, we used oocytes expressing the Q457C mutant of human SGLT1 (a gift of E. Wright, University of California Los Angeles, CA).

Experimental Protocols

Changes in fluorescence were measured in response to changing substrate concentrations and changing membrane potential. Fluorescence signals were expressed as a percentage of the background fluorescence determined at V_h = −60 mV. For the normalized data in the voltage jump experiments, F is expressed in arbitrary units (a.u.).

In the first set of experiments (steady-state experiments) we studied the influence of changing substrate by measuring the change in steady-state F in response to an increase in the Na⁺ concentration (range: 10–125 mM), Li⁺ concentration (range: 10–100 mM) or P_i concentration (range: 0.01–1 mM in 100 mM Na⁺). Each test substrate concentration was bracketed with a control solution to allow for correction of fluorescence rundown. The fluorescence signal was acquired after the new superfusate had been applied for 1.5–2.5 min to ensure equilibration of solution also under the oocyte, from which most of the fluorescence signal was assumed to arise. After equilibration, the shutter was opened 7–10 times in succession for 230 ms at 2.23-s intervals to minimize photobleaching (see Fig. 3 A), and the signal was averaged over these openings to minimize error due to noise. During the shutter opening time, the membrane potential was stepped from V _h = −60 to −120 mV (Na⁺ and Li⁺ experiments) or from V _h = −60 to 0 mV (P_i experiments) to acquire ΔF-substrate data at two voltages. The data were corrected for fluorescence rundown (see below).

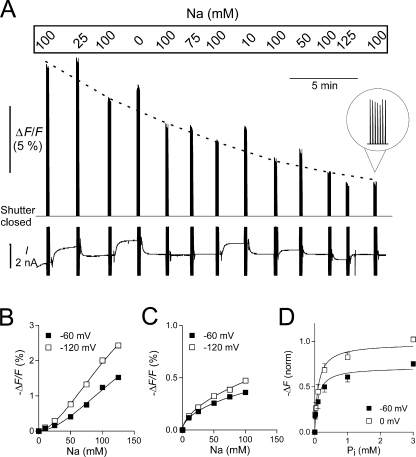
Figure 3.

Steady-state fluorescence measurements. (A) Original trace showing the fluorescence signal F and the holding current I recorded on the Minidigi 1A from an experiment in which the Na⁺ concentration was varied. The S448C-expressing and MTS-TMR–labeled oocyte was initially clamped at −60 mV and superfused with ND100 solution. After we equilibrated the oocyte with a new test solution, the shutter was opened periodically for seven successive 230-ms pulses followed by a 2-s closing time. To control for fluorescence rundown, each test solution was bracketed by ND100 solution. For better visualization of the rundown, the ND100 data is connected by a dotted line (drawn by eye). During the shutter opening, the membrane potential was stepped from −60 to −120 mV. These step changes in membrane potential are the cause of the capacitive current spikes visible in the current recording. Note the change in holding current as the Na⁺ concentration is changed. When the shutter is closed, F is outside the measurable range. (B) ΔF/F plotted as a function of Na⁺ for a representative oocyte, after correction for fluorescence rundown. Continuous lines are fits to data using the Hill equation. (C) ΔF/F plotted as a function of Li⁺ for a representative oocyte using a similar protocol as in A but with variable Li⁺ instead of Na⁺. Data were fitted with the Hill equation with H constrained to 1. (D) ΔF/F plotted as a function of P_i with Na⁺ constant at 100 mM. During the shutter opening time, the membrane potential was stepped from −60 to 0 mV. Data for individual oocytes were fit with the Hill equation (Eq. 1) with H constrained to 1, normalized to ΔF _max at 0 mV, pooled, and refit with Eq. 1 (n = 5). See text for all fit parameters.

In the second set of experiments we extended the voltage range over which voltage-dependent changes in fluorescence (ΔF) were investigated by using a voltage-step protocol. This also allowed us to follow the time course of the voltage-induced fluorescence change by matching the bandwidths of the current and fluorescent signals. Except when noted otherwise, the membrane voltage was stepped from V _h = −60 mV to test potentials ranging between −200 and +80 mV in 40-mV increments for a duration of 100 ms, and averaged over 10 sweeps. Data were acquired at different Na⁺, Li⁺, and P_i concentrations as described above. To correct for photobleaching, every third recording was done in 100 mM Na⁺ (experiments with variable Na⁺ or P_i) or 100 mM Li⁺ (experiments with variable Li⁺). ΔF data were acquired at 20k samples/s and filtered at 40 or 500 Hz for steady-state and presteady-state analysis, respectively. The F traces acquired for each substrate concentration were baseline corrected to the value at V _h = −60 mV and also corrected for photobleaching (see below). Each recording was then offset with respect to the zero-substrate condition to take into account that F at V _h = −60 mV was substrate concentration dependent. The amount of offset necessary was estimated from the data acquired using the steady-state experiments described above.

For presteady-state fluorescence measurements, the voltage jump protocol was modified by shortening the time spent at each target potential to 40 ms to reduce photobleaching and by increasing the number of averages to 64 to improve the signal-to-noise ratio without sacrificing signal bandwidth, which was set to 500 Hz for both the current and F signals.

Correcting for Fluorescence Rundown and Photobleaching

During the course of an experiment, fluorescence decreased, and this decrease fell into two categories. On the one hand, there was a slow rundown of the steady-state fluorescence that was independent of exposure to light, and which followed an exponential time course with a half time (t _1/2 ≈ 1 h). This rundown probably resulted from washout of unbound dye and/or internalization of membrane proteins covalently labeled with dye and was noticeable during the steady-state experiments even in the absence of light exposure (see Fig. 3 A). On the other hand, light-induced photobleaching of the dye proceeded with t _1/2 ≈ 5 min with the lamp set to maximum light intensity and was the dominant type of fluorescence decrease in the voltage jump experiments.

All data were corrected for the decrease in fluorescence during the experiment by normalizing to the extrapolated value at t = 0. In the voltage jump experiments, we plotted ΔF acquired in the control solutions at different voltages (after zeroing for V _h = −60 mV) as a function of cumulative light exposure time and fitted with a single decaying exponential. For the steady-state experiments, we plotted the fluorescence data acquired in the control solution as a function of time elapsed after the start of the experiment (in these experiments the contribution of photobleaching to the fluorescence decrease was minimal). We fitted the data with a single decaying exponential plus an offset, which takes into account that the fluorescence will never reach zero (even a nonlabeled oocyte gives a definite fluorescence signal when placed in the experimental chamber). In both cases, the approach was validated, because it successfully corrected the fluorescence change seen in control solutions during the course of an experiment.

Data Analysis

The fluorescence response to a change in substrate concentration, determined for different membrane voltages, was fitted with the modified Hill equation of the form

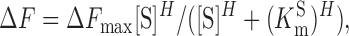(4)

where [S] is the substrate concentration (Na⁺, Li⁺, or P_i), ΔF _max is the extrapolated maximum fluorescence, K _m ^S is the concentration of S that gives a half-maximum response, and H is the Hill coefficient. Presteady-state ΔF data were fit with an exponential growth function to estimate the ON time constant (τ^ΔF) (Clampfit, v9.2, Molecular Devices Corp).

Simulations

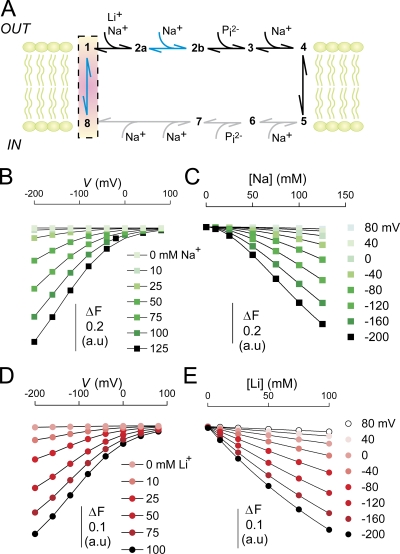
Computer simulations were performed as described earlier (Forster et al., 1998; Virkki et al., 2005). In brief, voltage- and substrate-dependent changes in fluorescence were simulated by assigning rate constants to the transitions between the states shown in Fig. 8 A. Voltage-dependent rates were formulated according to Eyring transition rate theory, assuming sharp energy barriers. We assumed that the empty carrier states (1 and 8 in Fig. 7 A) were associated with the highest fluorescence and that a reduction in the occupancy of these states resulted in a proportional decrease in fluorescence.

Figure 8.

Modeling the transport cycle of NaPi-II. (A) Kinetic scheme for the transport cycle of NaPi-II. Transitions that are influenced by voltage are indicated by blue arrows and include transition of the empty carrier (1⇔8) and the second Na⁺ binding (2a⇔2b). No information is available on the internal substrate interaction transitions, but they are depicted to mirror those taking place on the external side and are indicated with gray arrows. The highest fluorescence is associated with states 1 and 8, and is highlighted with a red box. (B) Simulated ΔF in response to membrane voltage and Na⁺ concentration. The points are joined for visualization only. (C) Data in B were replotted as a function of [Na]. The solid lines represent the fit Eq. 4. The Hill coefficient reported by the fit was 1.8 ± 0.01, in excellent agreement with experimental data. (D) Simulated ΔF in response to membrane voltage and Li⁺ concentration (data points joined for visualization only). Based on experimental data, we assumed that Li⁺ only interacts with the first Na⁺ binding step (1-2a). (E) Data in D were replotted as a function of [Li] and fitted with Eq. 4. The Hill coefficient reported by the fit was 1.0. The rate constants (in s⁻¹) used in the simulations were as follows: k_12a = 500[Na]_o or k_12a = 200[Li]_o, k_2a1 = 900(Na⁺ data) or k_2a1 = 40 (Li⁺ data), k_2a2b = 10,000[Na]_oexp(αeV/2kT), k_2b2a = 200exp(−αeV/2kT), k₈₁ = 40exp(−γeV/2kT), k₁₈ = 400exp(γeV/2kT). α and γ are the fractions of the electrical field that are sensed by the hypothetical charge moving through the membrane electrical field for transitions 2a⇔2b and 1⇔8, respectively, and were set to α = 0.13 and γ = 0.4. We assumed sharp, symmetrical energy barriers for the voltage-dependent transitions. Differential equations describing the rate of change of state occupancies (X_n) were solved for the state occupancies, where n is the state. The state occupancies were constrained such that X₈ + X₁ + X_2a + X_2b = 1, and the change in fluorescence was given by ΔF = 1 − (X_2a + X_2b). For the simulations, T = 293 K, [Na]_o varied from 0 to 0.125 M, [Li]_o varied from 0 to 0.1 M.

Figure 7.

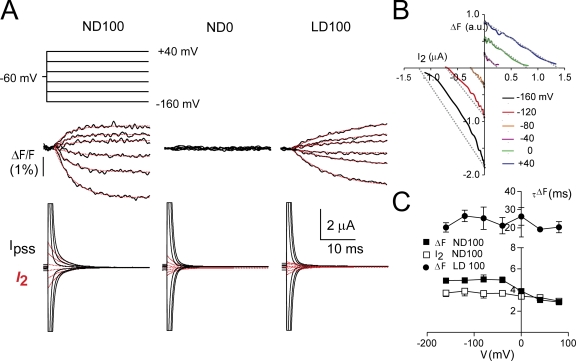
Presteady-state charge movements and fluorescence. (A) Simultaneous recordings of percent change in fluorescence (ΔF/F) for a representative oocyte in response to the voltage step protocol as shown, for superfusion in full Na⁺ (ND100), choline replacement (ND0), and Li⁺ replacement (LD100) and corresponding presteady-state currents (I _pss, black traces). For I _pss, the records were fit with a double decaying exponential and the main component (I _2, assumed to be S448C-related is shown superimposed, red traces). For the ΔF/F records, the data were fit with a single growing exponential, shown superimposed on each trace (red traces). Recording bandwidth was 500 Hz for I _pss and ΔF/F. Baseline adjustment was performed for I _pss. (B) Parametric plot of ΔF/F against I ₂ as a function of time for the cell in A at the indicated test potentials. Dotted lines indicate deviations from linear behavior for hyperpolarizing potentials. (C) Voltage dependency of the time constants associated with the decay of I ₂ (ND100) and time-dependent phase of ΔF/F (ND100, LD100). Note that the ordinate scale covers two ranges. Data pooled from n = 5 cells.

RESULTS

S448C Is Kinetically Indistinguishable from the WT and Can Be Labeled with MTS Reagents

We previously reported that the Ser to Cys substitution at site 460 in the rat NaPi-IIa isoform does not significantly alter the transport-related kinetics (Lambert et al., 1999). To establish that this was also the case for the aligned substitution in the flounder NaPi-IIb (Fig. 1 A), we profiled the steady-state voltage-dependent kinetics of S448C and compared them with those of the WT over a more extensive voltage range than previously reported (Forster et al., 1997). Oocytes expressing S448C displayed P_i-induced currents (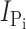) typically in the range −200 to −800 nA at V _h = −50 mV (unpublished data), depending on the oocyte batch and time after injection. As shown in Fig. 1 (B and C), the magnitude and voltage dependency of the apparent P_i and Na⁺ affinities (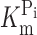 and K _m ^Na, respectively) were indistinguishable from the WT. Moreover, for Na⁺ activation at constant P_i (1 mM), the Hill coefficient (H) and predicted maximum P_i-induced current (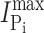) showed similar voltage dependencies (unpublished data). These data confirmed that the Ser to Cys substitution at site 448 did not alter the basic electrogenic cotransport kinetics.

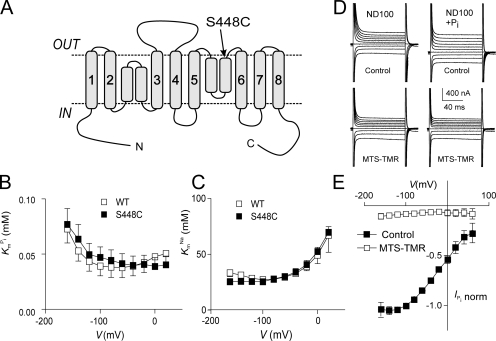
Figure 1.

Topology model and basic characterization of the S448C mutant. (A) Topology model predicting eight transmembrane segment and two reentrant loops, which dip into the membrane. N and C termini are intracellular. The site of the Ser-448-Cys mutation is indicated. (B) Voltage dependency of apparent affinity constant for P_i interaction (), determined at 100 mM Na⁺ for WT and S448C. Each data point is the mean ± SEM of the 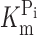estimated from n = 4 oocytes. (C) Voltage dependency of the apparent affinity constant for Na⁺ interaction (K _m ^Na), determined at 1 mM P_i for WT and S448C. Each data point is mean ± SEM of the K _m ^Na estimated from n = 3 oocytes. (D) Original current traces obtained from an oocyte expressing S448C in response to voltage jumps between −120 and +60 mV from a holding potential of −60 mV in ND100 solution (left) or ND100 + 1 mM P_i (right). Upper traces were acquired before, and lower traces after the oocyte was exposed to MTS-TMR for 5 min. (E) Current–voltage relationship of S448C obtained by subtracting recordings similar to those shown in D before and after labeling with tetramethylrhodamine-methanethiosulfonate (MTS-TMR). Data points were normalized to 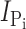at −100 mV (n = 4).

Exposure of oocytes expressing S448C to methanethiosulfonate (MTS) reagents (impermeable MTSET, MTSES, MTS-TMR, and semi-impermeable MTSEA) resulted in a distinct alteration in the voltage-dependent kinetics both in the presence and absence of P_i as illustrated in Fig. 1 D for a representative oocyte. In the control condition, superfusion in ND100 + 1 mM P_i gave a clear increase in steady-state holding current, whereas after exposure to 0.4 mM MTS-TMR, there appeared to be little change in the steady-state current after addition of P_i. We subtracted the traces in ND100 from the corresponding traces in ND100 + P_i to obtain the P_i-dependent current (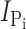) for the control and MTS-TMR conditions. Fig. 1 E shows the steady-state I-V data for 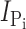at each test voltage, pooled and normalized to 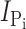at −100 mV in the control condition (n = 4). These data show that MTS exposure largely eliminated the electrogenic cotransport activity over the entire range of test potentials. We also noted that for superfusion in ND100, MTS exposure appeared to suppress the presteady-state currents that follow the step onset and are partially superimposed on the oocyte capacitive transient (Fig. 1 D, left). These currents are the subject of a more detailed analysis below. In general, this behavior was similar to that of the rat NaPi-IIa isoform (mutant S460C; Lambert et al., 1999) and indicated that the site is (a) functionally important in both type IIa and IIb Na⁺/P_i cotransporters and (b) accessible from the extracellular medium. We also confirmed by radioactive ³²P_i uptake assays that there was no significant P_i uptake in S448C-expressing oocytes after MTS exposure (unpublished data).

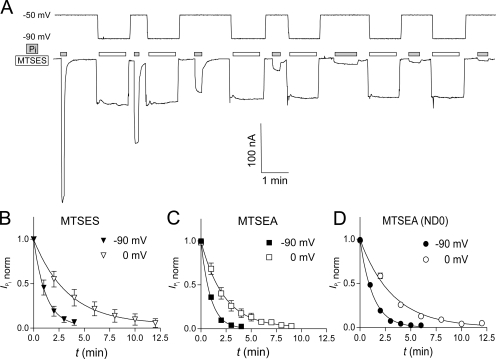
As the electrogenic cotransport function of S448C was blocked by treatment with MTS reagents, we exploited this property to determine the effect of membrane holding potential on the reaction rates of MTS reagents bearing a positive (MTSEA) or a negative (MTSES) charge. The reaction rates for MTSEA were determined both in the presence and absence of Na⁺, whereas MTSES was applied only in the presence of Na⁺. Fig. 2 A shows the progressive decrease in 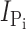with increasing cumulative MTS exposure times. We estimated the effective second-order rate constant k by fitting the data with Eq. 3, as summarized in Table I. For MTSEA (Fig. 2, C and D), the reaction rate constants were almost threefold smaller when the incubation was performed in the presence of Na⁺ (ND100) compared with incubation in 0 mM Na⁺ (ND0). Furthermore, the reaction rate constants were ∼2.5 times smaller at V _h = −90 mV, compared with 0 mV, independent of the charge of the MTS reagent or whether or not Na⁺ was present. These results indicated that (a) the reactive site Cys-448 does not lie within the membrane electrical field, (b) hyperpolarization of the membrane induced a conformational change in the NaPi-IIb protein that increased the apparent accessibility of Cys-448 for MTS reagents, and (c) accessibility to this site increased in the presence of external Na⁺. The slower reaction rate for MTSES (Fig. 2 B), compared with MTSEA, can be accounted for in part due to its overall slower reaction rate with small thiols in solution (Karlin and Akabas, 1998). Moreover, like MTSEA and MTSES, the rate of labeling with MTS-TMR showed a qualitatively similar dependency on the incubation holding potential (unpublished data).

Figure 2.

Time course of modification of Cys-448 by MTS reagents. (A) Original voltage (top) and current (bottom) trace acquired from an oocyte expressing S448C and repeatedly exposed to 25 μM MTSEA for successive 1-min intervals (white bars). During MTSES exposure, the membrane potential was held at −90 mV. After washout of MTSES, the membrane potential was changed to −50 mV and 1 mM P_i was applied (gray bars) to record the P_i-induced current. (B–D) 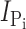, as a function of cumulative exposure time in MTSES (B), MTSEA (C), and MTSEA in the absence of Na⁺ (ND0 superfusate) (D). Abscissa is the cumulative exposure time (t) at the indicated incubation holding potential. In each panel, 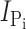(at V _h = −50 mV) after each MTS exposure was normalized to 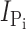at t = 0 and fitted with Eq. 3 (solid line) to obtain the effective second-order rate constant (see Table I).

TABLE I.

Effective Second Order Rate Constants (k) for MTS Modification of Cys-448

V h (mV)	MTSEA (ND100)	MTSEA (ND0)	MTSES (ND100)
0	2.9 ± 0.3	1.0 ± 0.2	0.20 ± 0.04
−90	7.1 ± 0.4	2.6 ± 0.4	0.55 ± 0.08

k (in mM⁻¹s⁻¹) was obtained by fitting time-dependent modification data using Eq. 3. Values are mean ± SEM of fit to pooled, normalized data. V _h is holding potential during labeling with given reagent. Superfusion conditions are indicated in parentheses.

Effect of Substrate on Steady-state Fluorescence in S448C

Oocytes expressing S448C and labeled with MTS-TMR showed voltage- and substrate-dependent change in fluorescence. First, we examined the effect of different substrates on steady-state F at two potentials. Fig. 3 A shows original continuous fluorescence and current traces recorded using the Minidigi 1A interface from an oocyte expressing S448C and labeled with MTS-TMR. The oocyte was initially clamped at −60 mV and perfused with ND100 solution. After a stable current baseline was reached, the shutter was opened for seven consecutive 230-ms pulses, each separated by a 2-s closing time to minimize photobleaching. The fluorescence signal within each cluster of openings appears jagged because the sampling rate of the Minidigi was very low (20 s⁻¹), but nevertheless it clearly shows how the absolute fluorescence changed over the course of the experiment.

The software-triggered opening of the shutter was synchronized with data acquisition using the Digidata 1322A interface at a sampling rate of 1 ms⁻¹. While the shutter was open, the membrane potential was stepped from V _h = −60 to −120 mV. The solution was then changed, and after equilibration to the new Na⁺ concentration, F was acquired in the new solution. Each test solution was bracketed by ND100 solution to allow correction for fluorescence rundown. As can be seen from the steady decrease in F acquired at successive applications of ND100 solutions (traced by the dotted line in Fig. 3 A), rundown proceeded independently of light exposure time and probably represents internalization of labeled membrane protein.

After correction for rundown, the Na⁺-dependent change in fluorescence (ΔF) was determined for the two potentials and plotted as a function of the Na⁺ concentration. ΔF/F data from a representative oocyte is shown in Fig. 3 B. The data were fitted with the Hill equation (Eq. 4). The Hill coefficient H reported by the fit was 1.7 ± 0.4 and 1.7 ± 0.2 for −60 and −120 mV, respectively, for the oocyte shown, and after H = 1.6 ± 0.5 for both potentials tested (n = 4). The result indicated cooperative binding of more than one Na⁺ ion. The estimate of K _m ^Na from the fit was unreliable due to lack of saturation, but suggested a K _m ^Na >150 mM.

To determine whether Li⁺ (which is physically smaller than Na⁺) can also interact with the transporter, we performed similar experiments as shown in Fig. 3 A but with Li⁺ as the variable substrate. Li⁺ produced a qualitatively similar but smaller decrease in F than Na⁺. After correction for rundown, we plotted the Li⁺-dependent change in F as a function of the Li⁺ concentration and fitted the data with Eq. 4. Fig. 3 C shows ΔF/F data from a representative oocyte. In contrast to the Na⁺ data, the Li⁺ data did not show a sigmoidal dose–response, but were best described with H in Eq. 4 constrained to 1, i.e., a Michaelis-Menten function. The K _m ^Li reported by the fit was unreliable, but indicated K _m ^Li >200 mM (n = 5). These results document, for the first time, that Li⁺ can interact with the NaPi-IIb transporter. Furthermore, the interaction differs from that of Na⁺ in that no cooperativity was evident, suggesting that the change in fluorescence occurs with the binding of only one Li⁺ ion.

Finally, we examined the effect of P_i on the steady-state fluorescence. P_i was applied in ND100 solution using a similar protocol as shown in Fig. 3 A, with the exception that during the shutter opening time, the membrane potential was stepped from −60 to 0 mV. Applying P_i decreased F in a concentration-dependent manner. The P_i-induced decrease in F was derived after correction for fluorescence rundown and plotted as a function of the P_i concentration in Fig. 3 D. In these experiments obvious saturation was obtained with increasing P_i concentrations. This allowed for normalization of the data obtained from individual oocytes to the extrapolated F _max measured at 0 mV before pooling the data. The data were refit with the Hill equation with H constrained to 1. The apparent K _m ^Pi reported by the fit was 0.097 ± 0.03 mM for −60 mV and 0.11 ± 0.02 for 0 mV (n = 5).

As a control, we repeated the above protocols on oocytes expressing WT NaPi-IIb labeled with MTS-TMR under the same conditions. No changes in F above background noise were seen after changing Na⁺, Li⁺, or P_i, indicating that the effects on F seen in the above experiments are specific to S448C (unpublished data).

S448C Shows Voltage and Na⁺-dependent Changes in Steady-state Fluorescence

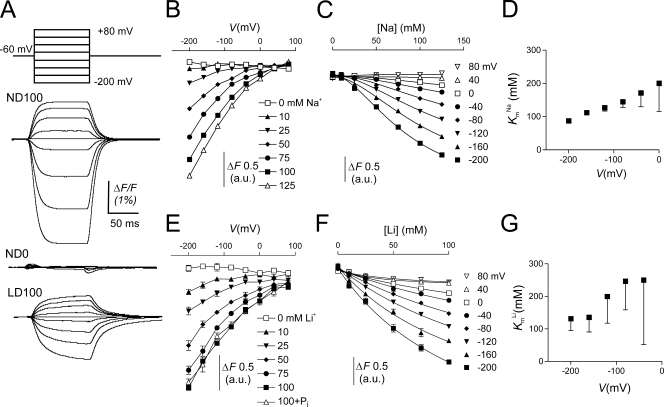
Next, we examined the voltage dependency of the S448C-dependent fluorescence signal in more detail. We obtained current recordings similar to those shown in Fig. 4 A with variable amounts of Na⁺ or Li⁺ in the bath. Each recording was initially baseline corrected for V _h = −60 mV to obtain ΔF, and then shifted with respect to the zero substrate condition using data obtained in the steady-state experiments described above (Fig. 3 B) as reference. This procedure was adopted because the fluorescence signal did not saturate at hyperpolarizing potentials precluding, for example, fitting the data with a Boltzmann function.

Figure 4.

Cation dependency of the voltage-dependent fluorescence in oocytes expressing S448C. (A) Original fluorescence trace recorded in ND100 (top), ND0 (middle), and LD100 (bottom) solutions from an oocyte labeled with MTS-TMR. The membrane voltage was stepped from V _h = −60 mV to voltages ranging between −200 and +80 mV in 40-mV increments as indicated. ΔF signals were lowpass filtered at 70 Hz (note that in these traces the relaxations are significantly distorted by the filter). (B) Na⁺ dependency of the voltage-dependent fluorescence (ΔF). Steady-state fluorescence at different membrane potentials was acquired for each Na⁺ concentration indicated on the figure. Data points are joined for visualization only. (C) Data in B were replotted as a function of the Na⁺ concentration and fitted with Eq. 4 (solid lines). (D) K _m ^Na as reported by the fit of Eq. 4 to the data in C. For the initial fit we obtained H = 1.8 ± 0.02, and then refit the data with H constrained to 1.8 to reduce the fitting error associated with K _m ^Na. (E) Li⁺ dependency of the voltage-dependent fluorescence (ΔF). Steady-state fluorescence at different membrane potentials was acquired for each Li⁺ concentration indicated in the figure. In addition, data were acquired with 1 mM P_i in 100 mM Li⁺. Symbols are joined for visualization only. (F) Data in E were replotted as a function of the Li⁺ concentration and fitted with Eq. 4 (solid lines). (G) K _m ^Li as reported by the fit of Eq. 4 (H constrained to 1) to the data in F.

Voltage-dependent ΔF was only observed in oocytes expressing S448C and labeled with MTS-TMR. No voltage-dependent ΔF was observed in noninjected oocytes or oocytes expressing WT NaPi-IIb labeled under the same conditions as S448C (unpublished data). ΔF showed saturation for jumps to more positive potentials, but no saturation was observed for negative jumps (−200 mV is the most negative command voltage possible with the voltage clamp). As a consequence, the maximum decrease in F attainable with hyperpolarization is unknown. We also established that F was independent of the starting potential by applying the same series of final test potentials for starting potentials −200, −60, and +80 mV (unpublished data). For each test potential, ΔF varied with the starting potential whereas F at the test potential depended only on the test potential. This confirmed that the fluorescence signal F represented a memoryless process.

We determined the Na⁺ dependency of F by substituting Na⁺ in the bath with equimolar choline. Fig. 4 B shows that for a given nonzero Na⁺ concentration, F decreased with hyperpolarization. The variation in F with voltage became smaller as the external Na⁺ was decreased, until at 0 mM Na⁺, F was essentially voltage independent. At depolarizing potentials, F appeared to asymptote to the same level for all Na⁺ concentrations. In contrast to the presteady-state current measurements, where saturation was observed at the limits of both hyper- and hypopolarizing voltages (see below), the lack of saturation of F at negative potentials precluded a reliable fit of a Boltzmann function (Eq. 2) to the data. Instead, we determined an apparent K _m ^Na for the Na⁺ dependency of the fluorescence signal at each potential by replotting the data in Fig. 4 B as a function of the Na⁺ concentration and fitting the data with Eq. 4 (Fig. 4 C). Fig. 4 D shows a plot of the apparent K _m ^Na as a function of the membrane potential. K _m ^Na is clearly voltage dependent and increases with depolarizing potentials, which suggested that the binding of Na⁺ is voltage dependent. The Hill coefficient did not show any apparent voltage dependency. It averaged 1.8 ± 0.2 for the different potentials, which suggested that more than one Na⁺ ion interacted with the protein. Most significantly, this showed that although the electrogenic cotransport activity of the labeled S448C mutant was suppressed (see Fig. 1 D), Na⁺ ions were still able to interact with the protein.

Effect of Other Cations on Fluorescence

Na⁺ is the only known cation that can drive P_i cotransport in the NaPi-II family, however other cations may interact with partial reactions in the transport cycle, as has been shown for H⁺ (Forster et al., 2000; Virkki et al., 2005) and for Li⁺ in the steady-state experiments (Fig. 3 C) described above. First, we replaced Na⁺ equimolarly with Li⁺ (LD100) and measured voltage-dependent ΔF in MTS-TMR–labeled S448C. F showed a qualitatively similar voltage dependency in LD100 as in ND100. The fluorescence signal saturated at positive voltages, but not at negative voltages. Compared with ND100, in LD100, ΔF (measured between +80 and −200 mV) was reduced by ∼50%. Furthermore, the time constant for ΔF in response to a voltage step was slower in LD100 than in ND100 (see below). Finally, adding 1 mM P_i to LD100 solution did not affect ΔF.

Reducing Li⁺ in the bath (replaced equimolarly with choline) led to a concomitant reduction of the voltage-dependent ΔF. As in the experiments with variable Na⁺ described above, the fluorescence traces acquired at each Li⁺ concentrations were offset with respect to the zero substrate condition using data obtained in the steady-state experiments as reference. Fig. 4 E shows the effect of changing the Li⁺ concentration on the voltage dependency of F. We replotted F as a function of the Li⁺ concentration and fitted the data with Eq. 4 (Fig. 4 F). The initial fit yielded an average Hill coefficient of 0.93 ± 0.07 over the voltage range tested. We therefore constrained H to unity to reduce the fit uncertainty. K _m ^Li ranged between 100 and 300 mM (Fig. 4 G), but the fit uncertainty was still quite large due to lack of saturation of the signal at the highest Li⁺ concentration used.

Replacing Na⁺ with K⁺ abolished the voltage dependency of F, which indicated that unlike Na⁺ and Li⁺, K⁺ ions do not interact with the transporter (unpublished data). Finally, reducing external pH from 7.4 to 6.2 did not alter the ΔF signal (unpublished data). In summary, the conformational changes reported by the fluorescence were not supported by K⁺ and unaffected by an ∼10-fold increase in the proton concentration.

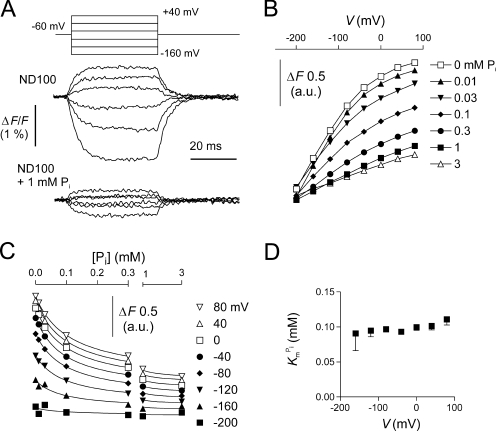
P_i Dependency of Fluorescence

Finally, we investigated the voltage dependency of F in response to P_i in MTS-TMR–labeled S448C. Adding 1 mM P_i to ND100 solution strongly suppressed ΔF over the voltage range measured (Fig. 5 A). Fig. 5 B shows the voltage dependency of F at different P_i concentrations. Each trace was offset for V _h = −60 mV with respect to the 0 mM P_i condition using data obtained in the steady-state experiments (Fig. 3 D) as reference. Increasing the P_i concentration reduced F mostly at depolarizing voltages, in a concentration-dependent manner. Like the 0 mM P_i data (Fig. 4, B and E), no saturation was observed at negative voltages, which precluded a Boltzmann analysis of the data. Instead, we replotted the data in Fig. 5 B as a function of the P_i concentration (Fig. 5 C). Fitting the data with Eq. 4 yielded a 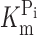of ∼100 μM, with no apparent voltage dependency (Fig. 5 D). For these fits, we constrained the Hill coefficient to unity to reduce the fit error (the initial fit with H as a variable yielded an average Hill coefficient of 1.0 ± 0.03 over the voltage range tested).

Figure 5.

P_i dependency of the voltage-dependent fluorescence in oocytes expressing S448C. (A) Original fluorescence trace recorded in ND100 (top) and ND100 + 1 mM P_i (bottom) solutions from an oocyte labeled with MTS-TMR. The membrane voltage was stepped from V _h = −60 mV to voltages in the range −200 to +80 mV in 40-mV increments, as indicated. Data were lowpass filtered at 500 Hz. (B) P_i dependency of the voltage-dependent fluorescence (ΔF). Steady-state fluorescence at different membrane potentials was acquired for each P_i concentration indicated in the figure. Data points are joined for visualization only. (C) Data in B were replotted as a function of the P_i concentration and fitted with Eq. 4 (solid lines). (D) 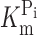, as reported by the fit of Eq. 4 to the data in C (H constrained to 1).

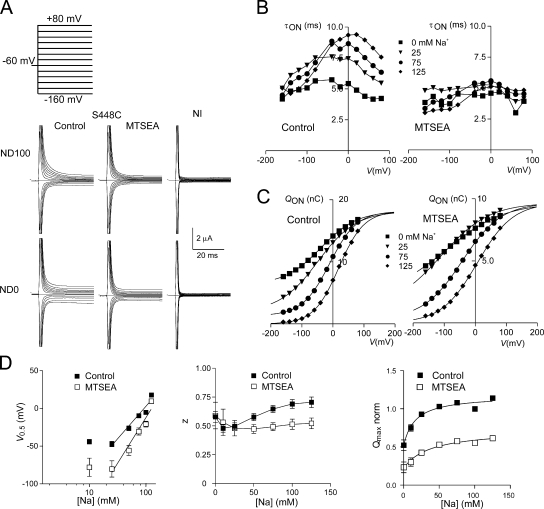
Presteady-state Charge Movements Before and After Labeling

We observed robust presteady-state currents from S448C-expressing oocytes in response to voltage steps (Fig. 6 A). Current relaxations were recorded in 100 mM Na⁺ (ND100) and in the absence of Na⁺ (ND0). In ND0, the amount of charge displaced was smaller at all potentials compared with ND100. After exposure to MTSEA, the relaxations were clearly suppressed, but were still distinguishable from the endogenous capacitive charging currents recorded from a noninjected oocyte from the same donor frog (NI, Fig. 6 A). These data established that despite a >90% reduction in the P_i-induced steady-state current after labeling (see Fig. 1 D), we were still able to detect (a) intrinsic charge movement in the absence of external Na⁺, which we assumed to be S448C related since we did not observe it in uninjected oocytes, and (b) the putative movement of Na⁺ ions within the transmembrane electric field, which contributed to the overall charge movement. The suppression of relaxations was identical for labeling with other MTS reagents (MTSES, MTSET, or MTS-TRM) (unpublished data).

Figure 6.

Presteady-state charge movements associated with S448C before and after labeling. (A) Representative current recordings from the same oocyte before (left) and after (middle) labeling with 1 mM MTSEA for 3 min for superfusion in 100 mM Na⁺ (ND100) and 0 mM Na⁺ (ND0). Voltage steps were applied from V _h = −60 mV to test potentials in the range −160 to +80 mV, as indicated. For comparison, currents from a noninjected oocyte (NI, right) from the same donor frog are also shown for the two superfusion conditions. (B) Voltage dependency of the main relaxation time constant (τ_ON) as a function of the four Na⁺ concentrations indicated, before (left) and after (right) labeling for the S448C expressing oocyte in A. (C) Corresponding voltage dependency of the ON-charge (Q _ON) associated with the main relaxation component plotted for four Na⁺ concentrations indicated before (left) and after (right) labeling. Continuous lines are fits with Eq. 2. The data were offset so that each curve superimposed at the depolarizing limit predicted for ND125, to better visualize the effect of Na⁺ on V _0.5. Note the difference in ordinate scales for the control and +MTSEA conditions. (D) Summary of the Na⁺ dependency of the Boltzmann fit parameters, V _0.5 (left), z (middle), and normalized Q _max (right). Data points are shown as mean ± SEM (n = 4). The linear regression lines for the V _0.5 data were fit to data points for Na⁺ ≥ 25 mM. The Q _max data were fit the modified Hill equation (Eq. 1) with a variable offset and H constrained to 1, and yielded K_m ^Na = 16 ± 6 mM for control and 38 ± 14 mM for +MTSEA. For z, data points are joined for visualization only.

Previously, we reported qualitatively similar charge movement suppression after MTS labeling for the equivalent mutant in the rat NaPi-IIa isoform (S460C), however in that study the poor signal-to-noise ratio precluded detailed analysis (Lambert et al., 1999). In the present case, the larger expression levels of S448C allowed us to quantify the kinetics of the charge movements before and after labeling by fitting the relaxations with a double decaying exponential. The faster time constant (typically 0.5–0.7 ms), which represents the linear charging of the oocyte capacitance, showed little voltage dependency and only a small (∼20%) increase when external Na⁺ ions were removed due to the change in conductivity of the bath solution affecting the voltage clamp response (unpublished data). On the other hand, the slower component showed an obvious voltage dependency, with a distinct maximum, as well as dependency on the external Na⁺ concentration (Fig. 6 B, left). Before labeling, the time constant showed a peak that shifted to more depolarizing potentials as Na⁺ increased and agreed with previous data for the WT NaPi-IIb (Forster et al., 1997). After labeling, the relaxations were generally faster at all nonzero Na⁺ concentrations, and approached the time constant for 0 mM Na⁺ before labeling (Fig. 6 B, right).

Fig. 6 C compares the charge obtained by numerical integration of the slow relaxation before (left) and after (right) labeling for the same representative oocyte at different external Na⁺ concentrations indicated. These data were fit with a single Boltzmann function (Eq. 2). To better visualize the effect of changing external Na⁺, the data and associated Boltzmann curve were offset so that they superimposed at the same depolarizing limit predicted from the fit for ND125. The fit parameters are shown in Fig. 6 D as a function of external Na⁺, pooled from five oocytes. The midpoint potential of the Boltzmann fit (V _0.5, Fig. 6 D, left) shifted to more hyperpolarizing potentials as we decreased external Na⁺ and showed a linear relationship when plotted against log₁₀ [Na⁺] in the 25–125 mM range. The slope of the linear regression line increased from 86 ± 12 mV/decade-[Na⁺] before labeling to 121 ± 17 mV/decade-[Na⁺] after labeling. Before labeling, the apparent valency from the Boltzmann fit (z) for S448C increased slightly with increasing Na⁺. After labeling, z was not sensitive to Na⁺ and was ∼30% smaller at high Na⁺ than before labeling. The slope and z estimates reported here for S448C were comparable with values obtained from WT NaPi-IIb cells, which yielded a linear regression slope = 111 ± 14 mV/decade [Na⁺] (n = 4) and a mean z = 0.56 for 25 mM ≤ [Na⁺] ≤ 125 mM. Finally, the predicted maximum charge available for mobilization (Q _max) was reduced by 50%, relative to unlabeled S448C, for all Na⁺ concentrations. We were able to fit the Na⁺-dependent component of the Q _max data with the Hill equation (Eq. 1) with H constrained to 1 and an offset corresponding to Q _max in ND0. The apparent K _m ^Na reported by the fit was 16 ± 6 mM and increased to 38 ± 14 mM after labeling. In addition to blocking the cotransport function, these findings established that modification of S448C resulted in altered presteady-state kinetics.

We also recorded presteady-state relaxations in Li⁺ solution (LD100) (unpublished data) and derived Boltzmann parameters from these data (Table II). For unmodified S448C-expressing oocytes, replacing Na⁺ with Li⁺ resulted in a reduction in the predicted Q _max comparable to that obtained with choline replacement (ND0). In contrast, V _0.5 was not statistically different between ND100 and LD100. The apparent equality of Q _max between ND0 and LD100 was also maintained after Cys modification, however V _0.5 for the charge distribution in LD100 was shifted toward hyperpolarizing potentials and was statistically indistinguishable from V _0.5 for ND0. These findings established that for the unmodified cotransporter, Li⁺ ions did not contribute to overall charge movement, although their presence altered the steady-state distribution of mobile charge. After modification, the invariance of the Boltzmann fit parameters within the experimental error indicated that superfusion in LD100 was indistinguishable from ND0.

TABLE II.

Comparison of Boltzmann Fit Parameters of S448C for Three Superfusion Conditions

Label	−MTSEA			+MTSEA
Superfusate	Q max	V 0.5 (mV)	z	Q max	V 0.5 (mV)	z
ND100	1.0	5 ± 4	0.6 ± 0.1	0.42 ± 0.03	−18 ± 6	0.5 ± 0.1
ND0	0.48 ± 0.05	−31 ± 8	0.6 ± 0.1	0.16 ± 0.04	−49 ± 5	0.7 ± 0.1
LD100	0.54 ± 0.03	−6 ± 5	0.5 ± 0.1	0.16 ± 0.04	−46 ± 5	0.6 ± 0.2

Data pooled from n = 5 cells. Q _max was normalized to ND100 –MTS for each cell before pooling. Labeling with 1 mM MTSEA for 3 min at −50 mV in ND100.

Comparing Presteady-state Current and Fluorescence Changes

Unlike F, which only showed saturation for V > 0 (Fig. 4), it was obvious from the presteady-state current data that saturation of the charge movement occurred at both hyperpolarizing and depolarizing potentials. To investigate if the kinetics of charge movements accompanying a change in membrane voltage were reflected in the time course of the fluorescence signal for the same change of state, we recorded ΔF at the same bandwidth as for the presteady-state relaxations (500 Hz). Fig. 7 A shows representative fluorescence (ΔF) and current (I _pss) recordings from a labeled S448C-expressing oocyte for voltage steps in the range −160 to + 40 mV for three superfusion conditions: 100 mM Na⁺ (ND100), 100 mM Choline⁺ (ND0), and 100 mM Li⁺ (LD100). S448C-related presteady-state relaxations were resolved, as described above, and the main relaxation component (I ₂) was extracted, as shown. There was a clear difference in the time course of the voltage step–induced ΔF between ND100 and LD100 superfusion. In the latter case, a steady- state ΔF was reached only after ∼50 ms (see also Fig. 4 A). For ND100, the time course of I ₂ and the rising phase of ΔF appeared qualitatively similar, whereas for LD100 superfusion, we were unable to detect a similarly slow component of charge movement. To better visualize any correlation between charge movement and fluorescence for ND100 superfusion, we plotted ΔF parametrically against I ₂ as a function of time for the same oocyte (Fig. 7 B). There was an obvious linear dependency for V > −40 mV, as would be predicted for a correlation between ΔF and I ₂, but this dependency did not hold at hyperpolarizing potentials.

We quantified the rising phase of ΔF by fitting with a single exponential function. In ND100, the fluorescence time constant (τ^ΔF) showed a weak voltage dependency (Fig. 7 C) and increased with hyperpolarizing potentials. For V > 0 mV, there was good agreement between τ^ΔF and the time constant associated with I ₂. In the hyperpolarizing region (V ≤ −40 mV), the two time constants differed significantly (P < 0.05). In contrast, for LD100, τ^ΔF was approximately fivefold larger than in ND100 and showed no clear voltage dependency in the measured range.

DISCUSSION

In this study, we have labeled a site in the type II Na⁺/P_i cotransporter with a fluorescent probe and recorded voltage-dependent and substrate-dependent changes in fluorescence (F). Labeling of the protein at the mutated S448C site blocked cotransport of substrate. However, because a change in the concentration of substrate was paralleled by a change in F, it appeared that substrate binding still occurred in the modified protein. This indicated that after Cys modification, the cotransporter can occupy a limited subset of possible conformational states within the complete cotransport cycle. Interaction of the substrates with the protein under these conditions was previously reported for the equivalent mutant of the rat NaPi-IIa isoform (S460C). For this mutant, we proposed that after Cys modification, P_i could still bind and thereby block the leak mode (Lambert et al., 1999; Kohler et al., 2002). However, based on these electrophysiological studies, we obtained no quantitative information about the substrate interactions. The voltage- and substrate-dependent changes in fluorescence reported here imply that the protein undergoes conformational changes that result in an alteration in the environment sensed by the fluorophore.

Effect of Modification on Steady-state Currents

Our current view of the location of Ser-448 is that it lies in a predicted loop region between transmembrane domains 5 and 6 (Fig. 1 A). Based on substituted cysteine accessibility studies, we believe that this loop is reentrant and contains α-helical elements (Lambert et al., 2001). Previous work showed that in the rat NaPi-IIa isoform, modification of S460C (equivalent to S448C in the flounder) by MTSEA or MTSES was less efficient at depolarized potentials in the absence of Na⁺, however, in contrast to the present study, no effect of membrane potential on the modification was observed when Na⁺ was present. For flounder S448C, we found that the reaction rates were ∼2.5 times slower at 0 mV than at −90 mV independent of Na⁺, but removing Na⁺ slowed down the reaction rates for MTSEA 2.6-fold. In the previous study, MTSEA was applied for 2 min at a higher concentration (10 μM, as compared with 2.5 μM in this study) and the effective second order rate constants were not explicitly determined (Lambert et al., 1999). The most likely explanation for the apparent discrepancy is that in the presence of Na⁺, the reaction had enough time to proceed to completion independent of membrane voltage at the higher MTS reagent concentration. Only in the absence of Na⁺ was the reaction slow enough so that the difference in reaction rates caused by membrane potential became apparent. Nevertheless, the previous study (Lambert et al., 1999) provided the first indication that Ser-460 (or Ser-448) lies in an area where voltage- and substrate-dependent conformational changes occur.

Since we did not detect any difference in the voltage dependency of the reaction rates between positively or negatively charged MTS reagents, it appears that S448C itself does not lie within the membrane electrical field. Instead, the site might be occluded by conformational changes that occur in response to membrane voltage and substrate, so that its accessibility to MTS reagents is reduced at depolarizing potentials and by removal of Na⁺.

Effect of Modification on Presteady-state Currents

Since the flounder NaPi-IIb mutant S448C gave much higher currents than the previously studied equivalent rat NaPi-IIa mutant (S460C), we were able to gain deeper insight into the effect of MTS labeling on NaPi-II kinetics than before. In agreement with our previous study, presteady-state relaxation kinetics were significantly altered by the labeling, as indicated by the systematic changes to the Boltzmann parameters obtained from the Q-V data. In an attempt to understand the behavior of these parameters in mechanistic terms, Eq. 2 was recast in the form of a field-dependent ion binding model (e.g., (Mager et al., 1996, 1998) that describes the charge movement as a function of membrane voltage and external Na⁺ concentration, [Na⁺]:

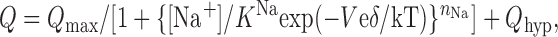(5)

where K ^Na is a zero-voltage Na⁺ binding constant, corresponding to [Na⁺] when half the charge has moved, and n _Na is the number of Na⁺ ions that bind at a hypothetical site located a fraction δ through the membrane field. This model predicts that the slope of V _0.5 vs. ln[Na⁺] = kT/eδ, from which we can estimate δ. For the −MTS case, δ = 0.63, and for the +MTS case, δ = 0.44, which suggested that the depth of the hypothetical Na⁺ binding site was reduced after labeling. Moreover, the Boltzmann fit to the Q-V data yielded an apparent valency (z) that can be expressed as z = δ n _Na. Therefore, taking z ∼ 0.7 (−MTS) and z ∼ 0.5 (+MTS) from the fit estimates (Fig. 6 D), these data would be consistent with one Na⁺ ion binding in a voltage-dependent manner, for both the unlabeled and labeled S448C, as we have previously proposed for the WT protein (Forster et al., 1997). Moreover, this predicted decrease in δ after labeling is also qualitatively consistent with the corresponding reduction in Q _max. For a constant number of cotransporters (N _t) contributing to charge movement before and after labeling, the total charge is given by Q _max = N _ten _Naδ. The 50% reduction in normalized Q _max observed (Fig. 5 D, right) is however larger than we would predict, based on the estimates of δ. This discrepancy most likely arises because of the faster presteady-state relaxations in the +MTS case (Fig. 6 B). The faster relaxation time constant obtained after labeling would result in a greater underestimation of the transporter-associated charge movement after subtraction of the endogenous charging component (see Materials and Methods). Furthermore, we note that the V _0.5 vs. log[Na⁺] data deviate from the expected behavior of this model at low Na⁺, where the charge contributed by the empty carrier (i.e., when [Na⁺] = 0) becomes more significant. This underscores the limitation of the simple two-state model implied when fitting a single Boltzmann function to the Q-V data.

In summary, based on presteady-state charge movement analysis, we conclude that at least one Na⁺ ion interacts with the protein in a voltage-dependent manner before and after labeling Cys-448, and the effect of labeling is to reduce the electrical depth of the apparent “ion binding well.”

Comparison of Electrophysiological Data and ΔF

A comparison of the apparent affinity constants for P_i and Na⁺ derived from electrophysiological data for the unmodified protein (Fig. 1, B and C) with the corresponding constants derived from the ΔF analysis of the modified protein (Fig. 4 D and Fig. 5 D) indicates that there are differences both in magnitude and voltage dependency. For example, at −100 mV, the electrogenic 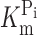is ∼0.05 mM, compared with ∼0.1 mM for ΔF. Similarly, the K _m ^Na obtained from the Na⁺ dependency of the steady-state P_i-induced current (∼25 mM) and from the Na⁺ dependency of Q _max (16 ± 6 mM) are significantly smaller than the K _m ^Na for ΔF (100–200 mM measured over −200 to 0 mV). Furthermore, K _m ^Na for ΔF was voltage dependent over the entire range measured, whereas the electrogenic K _m ^Na was voltage dependent only for potentials more positive than −60 mV. These differences are not surprising given the fact that the fluorescence data were obtained from the protein occupying a limited subset of putative conformational states (Fig. 8 A), whereas 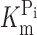and K _m ^Na obtained from steady-state current analysis of the unmodified protein are functions of all the transition rates in the cotransport cycle. Moreover, we cannot exclude that the labeling itself may alter the substrate binding kinetics. From analysis of charge movement before and after labeling, we saw that in the latter case, the apparent K _m ^Na of the Na⁺-dependent Q _max (Fig. 6 D) was doubled. This might be a consequence of the apparent reduction of the electrical depth of a putative ion binding well as discussed above.

Importantly, we also documented three obvious differences between the presteady-state current (I _pss) and corresponding fluorescence signal for the modified protein: (1) in ND0 solution, we observed no variation in ΔF with V, although we detected I _pss; (2) in LD100 solution, significant ΔF was observed, which showed a slower temporal response to changes in V compared with ND100, yet I _pss in LD100 and ND0 was indistinguishable; and (3) in ND100 solution, ΔF saturated only at positive voltages, whereas I _pss showed saturation at both the hyper- and depolarizing limits. The apparent lack of correlation between the two signals is also not surprising given that I _pss may encompass a global movement of charges possibly distributed throughout the protein, whereas ΔF reports a local phenomenon. The only agreement between the two signals occurred in ND100 solution at V > −40 mV, where ΔF and I _pss develop and decay respectively, with similar time constants in response to a voltage step (Fig. 7 C). This behavior suggests that the voltage-dependent conformational changes reported by each signal may have a common origin only for depolarizing potentials.

A Revised Model for Binding Order

Our previous model of the transport cycle of NaPi-II was based on steady-state and presteady-state electrophysiology data. In this model, one Na⁺ ion binds first, followed by a divalent HPO₄ ²⁻ and then the remaining two Na⁺ ions required for the 3:1 stoichiometry of coupled cotransport. Once the transporter is fully loaded it undergoes a conformational change that allows the release of bound substrates to the intracellular side. The cycle is completed by another conformational change that returns the empty binding sites to face the outside. The external binding order of substrates was deduced from electrophysiological evidence: (a) presteady-state charge dependency on external Na⁺ in the absence of P_i, (b) the presence of a Na⁺-dependent leak pathway with a Michaelian Na⁺ dose dependency consistent with a single Na⁺ ion interaction before P_i binding, and (c) K _m and V _max kinetics, consistent with ordered substrate binding and Na⁺ being the last substrate to bind (Forster et al. 1998).

The Na⁺ dependency of the ΔF data presented in this study provided compelling evidence that this model requires revision. A Hill coefficient of 1.6 ± 0.5 reported by the fit of the Hill equation to the ΔF-Na data in Fig. 3 B suggests that at least two Na⁺ ions are able to bind cooperatively in the absence of P_i. In addition, it appears that at least one of these sites has significant affinity for Li⁺. In the absence of Na⁺, Li⁺ supported voltage-dependent ΔF in a concentration-dependent manner. In contrast to the Na⁺ data, the Hill coefficient reported from fitting the Hill equation to the ΔF-Li data was unity, which suggested that the change in fluorescence resulted from the binding of a single Li⁺ ion. Thus, this is the first indication that Li⁺ can interact with the NaPi-II protein, because in the absence of Na⁺, Li⁺ supports neither cotransport nor presteady-state charge movement in NaPi-II. Furthermore, for superfusion in 100 mM Li⁺, no suppression of ΔF by P_i was observed. This lends further support to the idea that only one Li⁺ is able to interact with the protein, and that occupancy of the second Na⁺ binding site is required to allow for P_i interaction with NaPi-IIb.

We have incorporated these findings into the revised model presented in Fig. 8 A. The Na⁺ and Li⁺ dependency of ΔF was simulated using four of the eight states shown in the kinetic scheme, with the rate constants associated with the transitions (8⇔1⇔2a⇔2b) given in the figure legend. The transitions simulated include the transition of the empty carrier (8⇔1) and the two Na⁺ binding steps (transitions 1⇔2a and 2a⇔2b). The empty carrier (states 1 and 8) is assumed to have the highest fluorescence, as fluorescence remained high in the absence of substrate, independent of the applied voltage, but in the presence of Na⁺ or Li⁺, ΔF was suppressed at hyperpolarizing voltages. Based on our analysis of presteady-state currents, we included voltage dependency in the transition of the empty carrier (8⇔1) and the second Na⁺ binding transition (2a⇔2b). We assumed that the first Na⁺ binding transition was voltage independent because, according to our fluorescence data, Li⁺ ions can interact with the transporter (Fig. 4 A), but do not add detectable presteady-state charge movement to that of the empty carrier itself (Fig. 7 A). As the interaction of Li⁺ with the protein is noncooperative, and because Li⁺ supports neither cotransport in the unmodified NaPi-IIb protein nor P_i suppression of ΔF in the modified protein, the most intuitive interpretation is that Li⁺ is only able to interact with the first Na⁺ binding step as indicated in the model (transition 1⇔2a).

Although the model is most likely a gross oversimplification in terms of the true molecular events taking place, it satisfactorily predicts the behavior of ΔF in response to voltage and cation substrates (Na⁺ or Li⁺). For Na⁺ ion interactions, fitting the ΔF-Na data with Eq. 3 yielded a Hill coefficient of 1.8 ± 0.01, as expected for cooperative binding of the two Na⁺ ions in the simulation, which agreed with the experimental data (Fig. 4, B and C). For Li⁺ ion interaction, fitting the simulated ΔF-Li data with Eq. 1 yielded a Hill coefficient of 1.0, as expected. It is noteworthy that as we assume that the Li⁺ interaction step is voltage independent (Li⁺ ions do not enter the transmembrane electric field), the voltage dependency of ΔF in Li⁺ (Fig. 4 E) results solely from the voltage dependency of the empty carrier transition (8⇔1). This transition therefore probably still occurs in the labeled protein, although it is not sensed by the fluorophore. We also found that for best agreement between the experimental and simulated ΔF data, it was necessary to choose the empty carrier zero voltage rate constants such that occupancy of state 8 was favored. This would correspond to an inward facing conformation in accordance with an alternating access scheme for carrier-mediated transport and is consistent with the findings of our previous modeling studies (Forster et al., 1997, 1998; Ehnes et al., 2004a; Virkki et al., 2005) on the electrogenic behavior of NaPi-II cotransporters.

We drew a heartening conclusion from this modeling exercise. Although the lack of saturation of the ΔF-V data in the hyperpolarizing range (Fig. 4 B) prevented fitting with a Boltzmann-type equation, as we would have expected for a canonical saturable system, the use of the Hill equation (Eq. 4) to determine the number of Na⁺ binding sites appeared to be validated.

Conclusions

This is the first report of the application of VCF to study the kinetics of a type II Na⁺/P_i cotransporter. We note that for this revised scheme of cation interaction to be also applicable to the unmodified S448C and WT NaPi-IIb, we assume that the cooperative Na⁺ binding, as revealed by the fluorescence data, is not a result of the modification of site Cys-448. That this apparent cooperativity is not simply an artifact of labeling is supported by the result that the Li⁺ interaction did not show cooperativity. Although labeling abolished cotransport function, the protein still retained its ability to bind substrate. Our findings that P_i binding was preceded by the binding of two Na⁺ ions, that Li⁺ can interact with the first Na⁺ binding site, and that only the second Na⁺ binding was voltage dependent were incorporated into a new model of the transport cycle of electrogenic type II Na⁺/P_i cotransporters. This application of VCF has enabled us to uncover new modes of substrate interaction that would have been undetectable using electrophysiology alone.