Membrane Stretch Slows the Concerted Step prior to Opening in a Kv Channel

Abstract

In the simplest model of channel mechanosensitivity, expanded states are favored by stretch. We showed previously that stretch accelerates voltage-dependent activation and slow inactivation in a Kv channel, but whether these transitions involve expansions is unknown. Thus, while voltage-gated channels are mechanosensitive, it is not clear whether the simplest model applies. For Kv pore opening steps, however, there is excellent evidence for concerted expansion motions. To ask how these motions respond to stretch, therefore, we have used a Kv1 mutant, Shaker ILT, in which the step immediately prior to opening is rate limiting for voltage-dependent current.

Macroscopic currents were measured in oocyte patches before, during, and after stretch. Invariably, and directly counter to prediction for expansion-derived free energy, ILT current activation (which is limited by the concerted step prior to pore opening) slowed with stretch and the g(V) curve reversibly right shifted. In WTIR (wild type, inactivation removed), the g(V) (which reflects independent voltage sensor motions) is left shifted. Stretch-induced slowing of ILT activation was fully accounted for by a decreased basic forward rate, with no change of gating charge. We suggest that for the highly cooperative motions of ILT activation, stretch-induced disordering of the lipid channel interface may yield an entropy increase that dominates over any stretch facilitation of expanded states. Since tail current τ(V) reports on the opposite (closing) motions, ILT and WTIR τ(V)_tail were determined, but the stretch responses were too complex to shed much light.

Shaw is the Kv3 whose voltage sensor, introduced into Shaker, forms the chimera that ILT mimics. Since Shaw2 F335A activation was reportedly a first-order concerted transition, we thought its activation might, like ILT's, slow with stretch. However, Shaw2 F335A activation proved to be sigmoid shaped, so its rate-limiting transition was not a concerted pore-opening transition. Moreover, stretch, via an unidentified non–rate-limiting transition, augmented steady-state current in Shaw2 F335A.

Since putative area expansion and compaction during ILT pore opening and closing were not the energetically consequential determinants of stretch modulation, models incorporating fine details of bilayer structural forces will probably be needed to explain how, for Kv channels, bilayer stretch slows some transitions while accelerating others.

INTRODUCTION

Many, perhaps most, membrane channels exhibit changes in open probability (P_O) when membrane tension increases; known mechanosensitive (MS) channels include neurotransmitter-gated (NMDA) channels, gramicidin, voltage-gated channels, TRP channels, two pore domain K channels, alamethicin, diverse microbial channels (e.g., MscL and MscS) and others (e.g., see Martinac, 2004). For some, like MscL, a prokaryotic osmotic valve channel, this propensity has been exploited and enhanced during evolution (Kung and Blount, 2004). Eukaryotic channels whose P_O responds to stretch, however, typically have principal physiological stimulators other than bilayer stretch (Vandorpe et al., 1994; Chemin et al., 2005; Maroto et al., 2005). Evidently evolution has found it difficult to design multiconformation membrane proteins whose state probability distributions are inured to bilayer mechanics. An MS P_O could result if stretch changed the rates of closed–closed, closed–open, and/or open–open transitions. Thus, at any given voltage, an MS P_O for NMDA or Shaker channels, for example, may signify that stretch modulates transitions characterized primarily as voltage sensitive, ligand sensitive, temperature sensitive, and so on.

For a membrane protein, the lateral pressure profile (Cantor, 2002) at the protein–bilayer interface differs for each conformation (Gullingsrud and Schulten, 2004). It would be surprising, therefore, if external factors that alter the profile of forces at the protein–bilayer interface (see Wiggins and Phillips, 2005) in a channel had no impact on the occupancy of the available conformations and hence no impact on P_O. In this light, the ever growing list of gating responses to membrane stretch (and hence, presumably, bilayer strain) from diverse channel families is to be expected. For many channels, bilayer mechanics may be physiologically significant in allowing for modulation of P_O via membrane stretch and/or the bilayer lipid composition (e.g., raft versus nonraft lipids). The voltage-gated channels are a case in point. Studies in native cells and recombinant channel systems show that voltage-gated channels are modulated by both bilayer stretch and bilayer constituents (Langton, 1993; Jennings et al., 1999; Calabrese et al., 2002; Morris and Laitko, 2005). Voltage-gated channel modulators whose pure bilayer mechanics are broadly understood include lysophospholipids, cholesterol, and short chain alcohols like hexanol. Determining whether the actions of such surface active agents involve low-affinity binding sites (e.g., Shahidullah et al., 2003) or bilayer mechanics (e.g., Crowley et al., 2003; Lundbaek et al., 2004; Mohr et al., 2005) is difficult. Arguably, except for hydrophobic binding pockets isolated from bilayer lipids, the two interpretations should converge.

Kvs (voltage-gated K channels) are the best characterized of any channel and since the P_O of the prototypical Kv, Shaker, changes with stretch (Gu et al., 2001), Shaker is a good model system. In patch recordings (unitary and macroscopic currents), Shaker susceptibility to bilayer stretch resembles that of other eukaryotic MS channels. In recordings made near the foot of the activation curve (Gu et al., 2001), (voltage sensors partially destabilized from their rest positions but P_O(V) still near zero) stretch reversibly and in a stretch dose–dependent manner increases Shaker activity. Just as for “typical” patch recordings of MS channels (e.g., Maroto et al., 2005 for a MS TRP), the single channel amplitude is unaffected and stretch effects become evident at −20 or −30 mm Hg, though suctions as low as −10 mm Hg sometimes suffice. In Shaker mutants with most of the extracellular S3–S4 linker deleted (yielding slowed, right-shifted kinetics), stretch has the same effect on activation as it does in WTIR (wild type, fast inactivation removed), as gauged from the left shift imposed by near-lytic tension (Tabarean and Morris, 2002). The robustness of this result in conjunction with kinetic simulations supported the idea that the largely independent motions of voltage sensing are inherently stretch sensitive; stretch, we suggested, adds no new kinetic states but simply increases the net forward rate of preexisting voltage-dependent transitions (see Fig. 1). For WTIR, kinetically isolating activation transitions to test this is difficult, but the S3–S4 linker deletant, 5aa (Gonzalez et al., 2000), has an apparently identical rate-limiting voltage-dependent activation step in each homotetrameric subunit (Laitko and Morris, 2004). Slow inactivation in 5aa, too, is a single exponential process. 5aa responses proved rigorously that a voltage-dependent activation transition is stretch sensitive and that (contrary to an earlier suggestion; Tabarean and Morris, 2002) slow inactivation is also stretch sensitive. Though independently mechanosensitive, slow inactivation in 5aa undergoes the same-fold acceleration with stretch as activation, as if these two distinct Kv transitions “feel” bilayer stretch the same way.

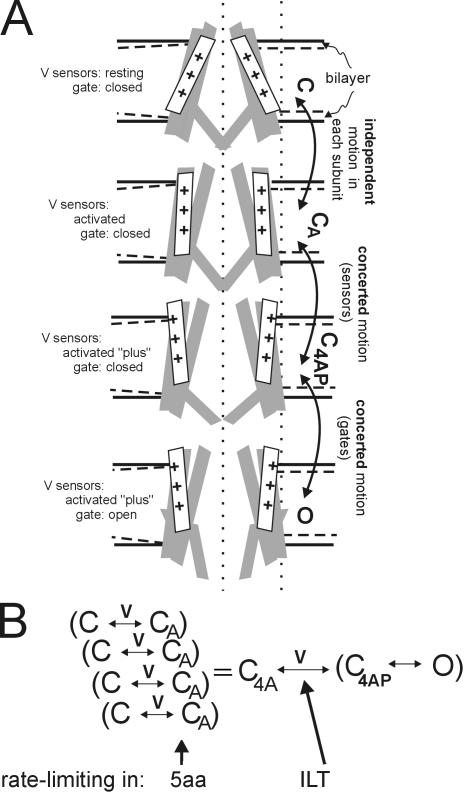
Figure 1.

Schematic for Kv motions and kinetics. (A) Section through a bilayer-embedded Shaker in conformations C, C_A, C_4AP, and O (closed, closed-but-activated, closed-4subunits-activated-plus, open). First, consider the bilayer and the bilayer-protein interface; details of the bilayer's laterally acting forces on Kv channels are unknown, but as Fig 4 of Morris and Laitko (2005) and associated references point out, bilayer forces contribute to conformational equilibria. Insofar as the bilayer thins with stretch (dashed lines in each leaflet) the channel–lipid interface will change (two possibilities are depicted: accommodation on the left, mismatch on the right). Next, the protein conformations themselves. The vertical dotted lines are for positional reference. A closed-resting state (C) is depicted with the voltage sensors in a position stabilized by hyperpolarization. In the closed-activated (C_A) states favored by depolarization, the sensors and neighboring domains repack (the motions that yield C_1A–C_4A are largely independent), but the gates remain shut. Each C→C_A subsumes greater complexity (e.g., to describe Shaker WTIR and ILT gating current, two independent steps in series are needed; Ledwell and Aldrich, 1999), which we ignore here. Next are two concerted motions. First four voltage sensors do a final motion together (yielding “activated-plus”). The next concerted step is opening of the tetrameric gate, C_4AP→O. B summarizes this as a kinetic scheme showing the voltage-dependent steps. In ILT, the concerted voltage-dependent forward rate C_4A→C_4AP is rate limiting (Del Camino et al., 2005), whereas in Shaker 5aa, we found (Laitko and Morris, 2004) that independent voltage-dependent steps that we take to be C→C_A are rate limiting. In WT channels, the two rates are similar, making it harder to distinguish activation from pore opening.

Thus, activation and slow inactivation involve MS motions, but what of the motions associated with Kv pore opening and closing? Thermodynamically, the Kv pore module (S5–S6) prefers its closed state (Yifrach and MacKinnon, 2002), so the four voltage sensors, having attained activated positions (via largely independent motions) have an additional job, namely to concertedly (Ledwell and Aldrich, 1999) apply a lateral force that couples depolarization to opening (see Fig. 1). To test the idea that stretch accelerates this (putative) expansion, a Kv is needed in which pore opening is strongly rate limiting. Here we report on the effects of stretch on just such a mutant, Shaker ILT. This channel monitors the final (cooperative) voltage-dependent step leading to Shaker opening (Ledwell and Aldrich, 1999; Webster et al., 2004; Del Camino et al., 2005). In WTIR Shaker, activation motions are tightly coupled to this last step, but not so in ILT, probably because in ILT, overly strong intersubunit S4–S5 interactions stabilize the activated state (Pathak et al., 2005).

If an open state is expanded relative to a closed state, a simple prediction is that bilayer stretch will favor the open state (Sachs and Morris, 1998) as in MscL (Sukharev and Anishkin, 2004). For bacterial MS channels, but not for Kv channels, structure-based models for closed and open conformations are available. There is, nevertheless, a wealth of structure–function information on Kv channels (Bezanilla, 2005; Horn, 2005), including, now, an open-like Kv1.2 structure (Long et al., 2005a,b). The following scenario (see Fig. 1) is thought to apply during activation: in response to a depolarizing step, the four Kv voltage sensors move independently (or largely so) along trajectories that relocate most of the gating charge with respect to the electric field. During these independent “activation” steps (C→C_A), the detailed structure (and hence forces) of the protein–bilayer interface must change, but the models lack information on whether a net expansion (in the plane of the bilayer) is expected. Activation is followed by a two-stage pore opening (Webster et al., 2004), which involves much of the Kv protein, with all four S4 voltage sensors simultaneously moving a final bit of charge(C_4A→C_4AP), exerting a lateral force to pull open the tetrameric S6 gates at its hinge (C_4AP→O) (Pathak et al., 2005). The question we ask here is whether the concerted opening steps feel and respond to membrane stretch. The answer turns out to be yes, but the polarity of the response was not as expected within the framework of the simplest model (expanded states favored by stretch): stretch slowed ILT activation and diminished steady-state ILT current.

MATERIALS AND METHODS

Oocyte Preparation, Channel Expression

Xenopus oocyte lobes with stageV–VI oocytes were collagenase treated with shaking for 50–75 min to defolliculate oocytes then washed five times (often, collagenase was stopped at 50–60 min and defolliculation was aided manually). Oocytes were injected the same day with the cRNA described below and maintained at 18°C in ND96 (96 mM NaCl, 2 mM KCl, 2 mM pyruvic acid, 1 mM MgCl2, 1.8 mM CaCl₂, 5 mM HEPES pH 7.6) supplemented with antibiotics.

Capped cRNA for expression in oocytes was produced by in vitro transcription of linearized plasmid DNA template using the T7, SP6, or T3 Message Machine kit (Ambion). RNA concentration was determined by absorbance at 260 nm and the quality of RNA by agarose gel electrophoresis.

WT Shaker H4 with its inactivation ball intact (construct ZH4-pBSTA; provided by F. Bezanilla, University of Chicago, Chicago, IL) was linearized with NotI (T7 promoter). Shaker WTIR (WT Shaker H4 with the NH₂-terminal inactivation ball removed) was provided by C. Miller (Brandeis University, Waltham, MA) with an added eight–amino acid COOH-terminal epitope. Shaker WTIR was subcloned into the “Melton” oocyte expression vector SP64TM (Gu et al.,. 2001) and linearized with EcoRI (SP6). Shaker 5aa, a WTIR Shaker H4 S3–S4 deletion mutant Δ-Δ(330–355) provided by R. Latorre (Centro de Estudios Científicos, Valdivia, Chile) (Gonzalez et al.,. 2000) was linearized with NotI (T7). Shaker ILT, which is a WT Shaker B (Δ6–46) ILT (Smith-Maxwell et al., 1998a) in the oocyte expression vector BSKS, was provided by R.W. Aldrich (University of Texas, Austin, TX). It was linearized with KpnI (T7). The Shaw2 mutant, F335A (Harris et al., 2003), was used as the “WT” by Shahidullah et al. (2003) because it expressed at higher levels than WT Shaw2, had no significantly affected biophysical properties, and, like WT, was inhibited by 1-alkanols. M. Covarrubias (Thomas Jefferson University, Philadelphia, PA) provided the Shaw2-F335A mutant in the Xenopus oocyte expression vector pBscMXT. It was linearized with SalI (T3).

Oocytes were injected with cRNA and incubated at 18°C as follows: Shaker WT (20 ng; 3 d), Shaker WTIR (14 ng; 2–4 d), Shaker 5aa (20 ng; 3 d), Shaker ILT (20–60 ng; 3–14 d), and Shaw2-F335A (50 ng; 2–3 d).

Immediately before patching, an oocyte was briefly shrunk (3–10 min) in a hyperosmotic solution and the vitelline layer was removed with forceps. For the Shaw experiments, shrinking was omitted.

Electrophysiological Recordings

Pipettes (∼2.5-5 MΩ) were pulled from thick-walled borosilicate glass (Garner; 1.15 mm inner diameter, OD 1.65) using an L/M-3P-A (List Medical). Pipettes were sylgard coated (Dow Corning) and tips were fire polished using a soda glass–covered platinum filament. Currents, filtered at 5 kHz, were recorded using an Axopatch 200B (Axon Instruments, Inc.) amplifier and digitized using pClamp6 (Axon Instruments, Inc.) software and A/D converter Digidata 1200 (Axon Instruments, Inc.). Currents were corrected for linear capacitive currents with the amplifier's compensation circuits, and residual capacitive and leakage currents were corrected by P/N linear subtraction (see pClamp; Axon Instruments, Inc.). For stretch runs, stretch was applied just before the P/N steps started. Conductance versus voltage curves (g(V)) were obtained by plotting the peak tail current amplitude at a constant post-pulse potential (20 mV for ILT) that provided a good driving force for potassium (Stefani et al., 1994; Zagotta et al., 1994).

The patch pipette solution contained (in mM) 95 NaCl, 1 KCl, 5 MgCl₂, and 5 HEPES at pH 7.2; the bath solution contained (in mM) 100 KCl, 0.8 MgCl₂, 0.5 CaCl₂, and 5 HEPES at pH 7.2. To inhibit stretch-activated endogenous cation channels, 20–40 μM gadolinium was sometimes included in the pipette. The experiments were performed at room temperature.

Mechanical Stimulation

Membrane patches were stretched by suction (negative pressure, −30 or −40 mm Hg) applied via the patch pipette sideport.The same level of suction was applied for any given patch at all voltages tested. Suction was created with a syringe (a manual valve was opened to reset to atmospheric pressure) and measured with a pneumatic transducer pressure tester (DPM-1B; Bio-Tek). Because tip diameter (and hence patch size and curvature) and mechanical properties of membranes differ among patches, and we did not image the patches, membrane tension was not quantified.

Data analysis was performed with Origin 6.0 (Microcal Software Inc.). Where shown, error bars are the standard error of the mean.

RESULTS

ILT as a Kinetic Tool

To help determine how voltage sensor movement communicates to the pore region, and whether separately moving subunits “join forces” for a concerted pore opening transition, Smith-Maxwell et al. (1998a) generated S4-based Shaker/Shaw chimeras. In the chimeric channels, opening remains voltage dependent, but g(V) slopes and positions do not correlate with the nominal charge content of the S4. Instead, in the Shaker-with-ShawS4 chimera, the rate-limiting process for activation of ionic current is a highly cooperative step: the four subunits' concerted conformation change into either the open state or one that precedes and prepares pore opening. In Shaker, this concerted step is rapid but introduction of the foreign S4 slows it dramatically. This showed that S4 participates in cooperative interactions between channel subunits as well as (noncooperatively) in voltage sensing. Strikingly, substitution of three neutral residues in Shaker S4 by the respective ones from Shaw (I, L, and T) recreated the gating changes caused by substituting into Shaker the entire Shaw S4 (Smith-Maxwell, 1998b); ILT thus reports on the final cooperative step(s) in Shaker gating (Ledwell and Aldrich, 1999). Insofar as the opening motion per se is so tightly coupled as to be nearly simultaneous with the final concerted voltage-dependent step in WT channels, C_4A→C_4AP→O (Fig. 1 B) has been modeled as one step. The kinetics of current activation in ILT (like those of Shaw; Ledwell and Aldrich, 1999) have been described as approximating a two-state voltage-dependent channel (Smith-Maxwell et al., 1998b) summarized as C↔O with voltage-dependent forward and backward rates (this would be equivalent to a lumped C_4A↔O in our Fig. 1 B).

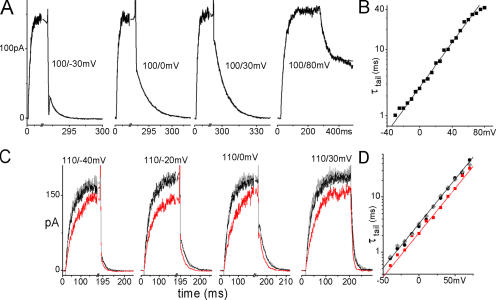
During depolarizing steps from resting voltages, ILT current activated monoexponentially, and tail currents during hyperpolarizing steps toward rest also declined monoexponentially (Fig. 2). ILT g(V) relations were single Boltzmann functions, strongly right shifted in comparison to WTIR. These properties fit with the simplest model for channel opening (Smith-Maxwell et al., 1998b): a single (simultaneous in four subunits) reversible opening transition, C_4A→O. This model's parameter set is parsimonious, comprising only two gating charges, z_α and z_β, and two basic rates, α₀ and β₀, for the voltage-dependent opening and closing transition, respectively. The opening and closing time constant τ(V) is

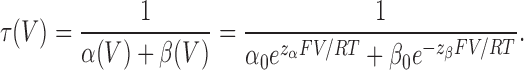(1)

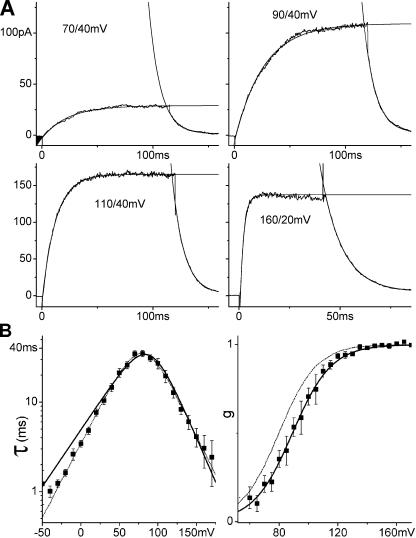
Figure 2.

ILT kinetics. (A) Averaged (n = 15 runs) currents from one patch. The membrane was stepped from −90 mV to the first and then to the second voltage indicated. Current activation and decline were fitted with single exponentials. (B) τ(V) from exponential fits and g(V) from tail current amplitudes, averaged results from 16 and 11 patches, respectively, with SEM, and fitted with Eqs. 1 and 3. Both τ(V) and g(V) can be fitted with these expressions over their entire respective voltage ranges, but with slightly different z and K₀ that cannot be brought into agreement for the two datasets. Dashed lines: best τ(V) fit (z_α = 1.0, z = 2.0, α₀ = 0.58 s⁻¹, K₀ = 740) and Eq. 3 for g(V) with these parameters. However in the voltage range of ILT activation (60–170 mV, solid lines), z and K₀ from the g(V) fit (z = 1.9, K₀ = 810) describe τ(V) very well (z_α = 1.2, α₀ = 0.25 s⁻¹).

τ(V) can be gained from exponential fits to the rising phase (or falling phase) of currents induced by depolarizing (or hyperpolarizing) steps to V,

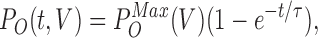(2)

and the τ(V) values determined from either phase will be identical. The relation between steady-state open probability and voltage is

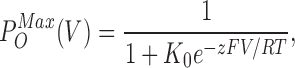(3)

with the combined parameters z = z_α + z_β and K₀ = β₀/α₀ giving a normalized g(V) relation. If the simple model is valid for ILT kinetics, a sigmoid g(V) and a bell-shaped τ(V) should be described with Eqs. 3 and 1 using the same set of z and K₀ but with the following conditions. Eqs. 2 and 3 assume P_O(V)_max = 1, whereas inspection of Shaker WTIR activity at the single channel level reveals that at P_O(V)_max the true P_O value is only ∼0.8 (Hoshi et al., 1994) (flickery voltage-independent transitions generate unitary current “bursts” whose within-burst P_O is ∼0.8). Thus, when fitted with Eq. 3, our macroscopic data yield not Po(V) values, but normalized g(V) values.

Fig. 2 A shows exponentially fitted activation and tail currents for ILT and Fig. 2 B shows averaged g(V) and τ(V) from current families. For g(V), varying activation voltages and fixed tail voltages were used, for τ(V), activation and tail voltages were both varied. g(V) and τ(V) relations were fitted with the one-step model. Best fitting total gating charge z and K₀ are close but not identical; Eq. 3 with the parameters from the τ(V) fit cannot quite reproduce the experimental g(V) and vice versa. Restricting the fit of τ(V) to the voltage range of channel activation (i.e., the same range as for g(V)), however, yields a good fit using z and K₀ from the g(V) fit. Thus, the two-state model was fully satisfactory to describe channel opening and closing kinetics between 60 and 170 mV in our cell-attached patch recordings, though an additional step may limit channel closing below 60 mV.

Effects of Stretch on g(V) in ILT

Without or with stretch, ILT current had negligible delays, indicating that ILT opening kinetics were almost unaffected by the independent S4 movements of voltage sensing. Fig. 3 A shows, for a sample patch, ILT currents (averaged responses, n = 5) for depolarizing steps before, during, and after stretch using moderate suction (tail current segments for three of these are also shown below at an expanded time scale as part of Fig. 3 B). Activation kinetics were slowed by stretch at all voltages, even where g(V)/g(V)_max = 1. Stretch decreased steady-state current amplitude at smaller depolarizations, but this decrease was not observed at the largest depolarizations, consistent with stretch slowing the rate-limiting opening transitions, but affecting neither open channel conductance nor the number of functional channels in the patch nor the value of g(V)_max. The stretch effect was completely reversible. The diminished steady-state current levels at large depolarizations (a feature unaffected by stretch; see Fig. 3 A) was evidently a property of open pore conductance (Harris and Isacoff, 1996), since tail current amplitudes at 20 mV indicated that the number of open channels remains maximal at these voltages. Fig. 3 B illustrates g(V) determined from the peak tail current amplitudes and shows that stretch produced a right shift with unaffected voltage dependence (slope). Fig. 3 C presents averaged results. In all oocytes and on all patches tested, stretch reversibly acted in this way. The critical point about these effects is their qualitative robustness, not the absolute value of the stretch induced shift, since absolute membrane tension estimates are needed to assess the energetics of the effects. Pipette suction translates into membrane tensions that vary with patch geometry, so the among-patches averages of the τ(V)s and g(V)s shown here yield an inherently conservative shift (i.e., an under-rather than an overestimate of the within-patch mean). Stretch reversibly increased τ in the voltage range of activation (n = 7 patches) and reversibly right shifted the g(V) (n = 4 patches) without affecting its slope. Although it was possible (as in Fig. 2) to fit τ(V) with Eq. 1 for the entire voltage range with and without stretch, the resulting z and K₀ do not describe g(V). Instead, we show fits confined to the activation voltage range (where τ(V) is essentially τ(V)_on, that is, α⁻¹ the inverse on-rate of Eq. 1), and in that case, the same parameter set does describe both τ(V) and g(V). Neither the voltage dependence of τ nor the maximal conductance changed with stretch; both can be described using the same gating charge with and without stretch. The stretch-induced slowing is completely accounted for by a decrease in the basic opening (forward) rate α₀, (basic closing rate remained unaffected). The lack of stretch effect at voltages below the foot of the g(V) results from averaging effects of opposite polarity, a point we return to below in the section on tail currents.

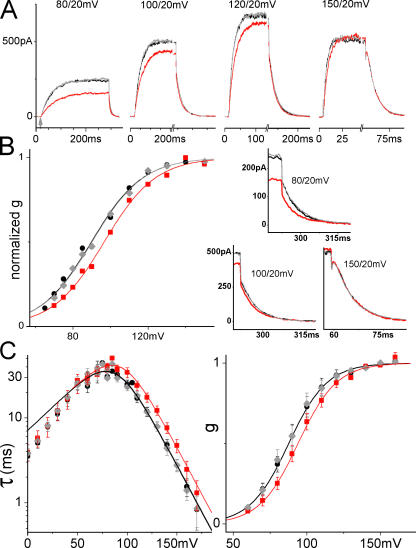
Figure 3.

Stretch and ILT currents. Here and for other figures, black (lines or filled circles) = before stretch, red (lines or squares) = during stretch, gray (lines or diamonds) = after stretch. Data from a sample patch. (A) Averaged sample currents (n = 5 runs; repeats were done in succession before moving to another voltage), for steps from −90 mV to the indicated voltage and back to 20 mV, with axis breaks to better visualize the tail. For the leftmost set of currents, an arrow marks the start of the depolarizing step. In all sets, a time scale is provided by labels at t = 0 and at the first major tick (“0” marks the start of recording, not the beginning of a step; the initial flat section is the holding current at −90 mV). Below, at right, for three voltages, tail currents are shown on expanded time scales, as indicated. (B) g(V) relation from tail current amplitudes after stepping back to 20 mV. The fit with Eq. 3 shows that gating charge is unaffected by stretch, whereas K₀ increased (z = 1.9, K₀ = 700/1170/720 for before/during/after). (C) Averaged τ(V) (seven patches) and normalized g(V) (four patches) with and without stretch, fits with Eqs. 1 and 3 in the range of activation voltages. z and K₀ from the g(V) fit (z = 2.0, K₀ = 780 without and 1260 with stretch) describe τ(V) very well (z_α = 1.3, α₀ = 0.18 s⁻¹ without and 0.11 s⁻¹ with stretch).

What about C→C_A in ILT? At V_hold (−90 mV) ILT channels would be mostly in C₍₄₎ (resting state). If stretch accelerated the C→C_A transitions in ILT several fold as it does in 5aa (Tabarean and Morris, 2002), we would not expect to detect this as a rate change, since in ILT these independent steps are substantially faster than the next concerted step (Ledwell and Aldrich, 1999).

The ILT Stretch Response Is Distinct from WT and 5aa Mutants

Since the ILT responses were unexpected, we confirmed that the right shift of the g(V) was mutant specific by obtaining the Shaker WTIR g(V) via the same method (initial tail current amplitude). We also rechecked 5aa current responses and, for completeness, tested the WT (wild type Shaker with inactivation ball present) since we had not previously done so; Fig. 4 (A–C) illustrates currents before/during/after stretch for these constructs. For WTIR g(V) data obtained from tail currents; four of four patches showed a reversible stretch-induced g(V) left shift (Fig. 4 D shows the average), in direct contrast to the reversible right shift of ILT. As previously, 5aa (Laitko and Morris, 2004) and WTIR (Tabarean and Morris, 2002) showed stretch acceleration during activation; WT currents were similarly affected. Stretch acceleration of the voltage-sensing transition revealed in 5aa could also explain WTIR responses. In WTIR (Schoppa and Sigworth,1998), unlike ILT (Ledwell and Aldrich, 1999), the voltage-sensing transition is markedly slower than the subsequent pore opening step and this could explain why the pore-related (or S4–pore interaction–related) stretch phenomenon we observed in ILT, slowing of pore opening, was not evident in WTIR (or WT and 5aa). Thus, the unexpected stretch effects on ILT, including the right shift of its g(V), made a coherent mutant-specific picture and was not an artifact of some factor such as the group of Xenopus from which oocytes were obtained.

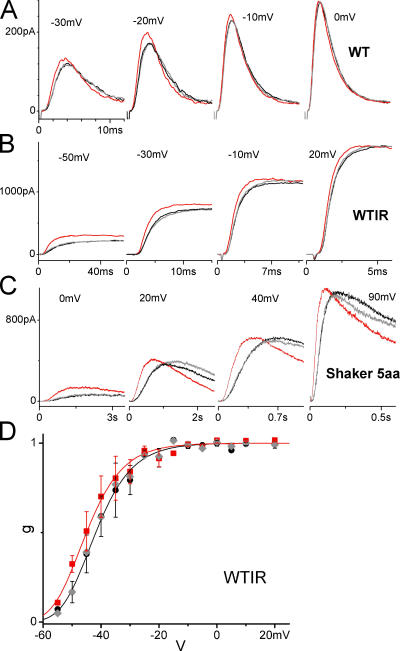
Figure 4.

Stretch and other Shaker mutants. Sample currents taken before, during, and after stretch at a range of voltages for (A) Shaker WT (fast N-type inactivation present), (B) Shaker WTIR, and (C) Shaker 5aa. (D) Average normalized g(V) (n = 4) from peak tail current amplitudes, with and without stretch, for WTIR. Fits with a fourth order Boltzmann (Eq. 3 to the fourth power). z = 3.3 for both curves, K₀ = 0.00093 and 0.00062 for without stretch and with stretch, respectively. The resulting total gating charge of ∼13 (i.e., 4 × 3.3) is in agreement with the literature. Determining the g(V) with the tail current method is problematic for WT and 5aa, as they possess similar time scales of activation and inactivation, however it is clear from the sample currents in A and C that their g(V) relations would be left shifted, too. (Colors and symbols as in Fig. 3).

Effects of Stretch on ILT Tail Currents

ILT tail current responses (exponential rate of decline toward equilibrium after a hyperpolarizing step) to stretch were obtained over a range of voltages (limited by the time resolution of the recording system at very negative voltages); simple exponentials usually sufficed (Fig. 5, A and B). Note, however, that on switching back from extremely depolarized voltages, small delays were often observed (see Figs. 2 and 3). Tail current stretch responses were reproducible in a given patch (e.g., Fig. 5, C and D) and qualitatively consistent for a given oocyte batch, but were not uniform among batches. Among batches (i.e., oocytes from different frogs), we observed stretch acceleration (e.g., Fig. 5 D), stretch slowing, and complete absence of stretch effects in the tail currents, but in all cases, as seen in Fig. 5 C, the stretch-induced slowing of activation was preserved. In all cases, including with stretch, tail τ(V) was fitted with single exponentials (e.g., Fig. 5 D), so as a first approximation, the first closing step determined ILT tail kinetics.

Figure 5.

ILT tail currents. (A) Averaged sample currents (n = 10) with exponential fits (fits and data overlap). (B) Tail current time constant vs. voltage on a logarithmic scale. Exponential fit: τ₀ = 2.7 ms, z = 1. The data would be situated on the left flank of the τ(V) relation in Fig. 2 B, z here is equivalent to z_β. (C) Averaged samples (n = 3) from a tail current family recorded from a patch with stretch-accelerated tails. (D) τ(V) for that patch, exponential fits: τ₀ = 3.3/2.3/ 3.3 ms for before/during/after stretch, z = 0.95 for all.

This spectrum of stretch effects might indicate that multiple elementary steps (with oocyte batch-dependent weights and stretch dependence) control the channel closing observed by the tail current. This view is corroborated by our inability to fit τ(V) for the entire voltage range, including voltages where contributions from activation would be negligible, with Eq. 1 derived for the two-state model (Fig. 2 B). On the other hand, whether tail decline was accelerated, unaffected, or slowed by stretch, the ILT tail τ(V) was readily fitted with single exponentials of almost indistinguishable gating charge values; either we were monitoring a single closing step or multiple steps with similar parameters. Stretch might affect a given step differently depending on the oocyte bilayer lipid composition. It is plausible that oocyte batches could vary with respect to bilayer lipids that impact gate residues in Kv channels (cf., Shahidullah et al., 2003), rendering pore closing differentially vulnerable to stretch.

Stretch and WTIR Tail Currents

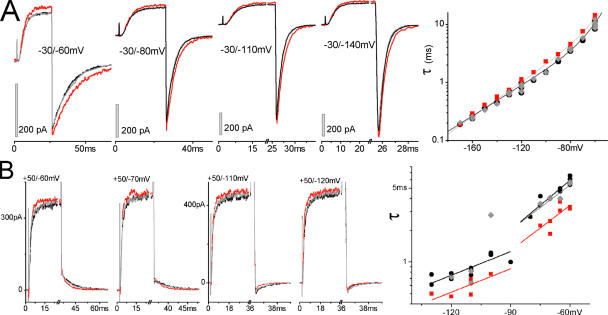
Pore closing as seen via ILT tail currents with/without stretch proved to be complicated. We hoped, nevertheless, that pore closing as seen via WTIR tail currents would show consistent stretch responses. Zagotta et al. (1994) found τ(V) to be a single exponential (z = 1.1 between −160 and −60 mV) and Schoppa and Sigworth (1998) found a multiphasic τ(V) that becomes single exponential (z = 0.5) below −120 mV where, they argue, channel closing is not contaminated by fast reopenings. In our patch recordings, WTIR tail current τ(V) showed two phases, a shallow branch at more negative voltages and a steeper one above about −50 mV (presumably due to fast reopenings) (Fig. 6). Since currents are unmeasurable near E_K (∼−80 to −90 mV for “normK” pipette solution), we also used a “hiK” pipette solution (E_K close to −40 mV) to obtain some uninterrupted τ(V) datasets (Fig. 6, WTIR hiK). HiK affected channel kinetics (see figure legend, Fig. 6) but the normK slopes (steep and shallow branch z = 1.1 and 0.67, respectively) were comparable to the hiK double exponential values (z = 1.3 and 0.46), which in turn are like those of Zagotta et al. and of Schoppa and Sigworth.

Figure 6.

Resolvable tail currents at various voltages. WTIR tail current τ(V) in normK (n = 8) (gray squares) and hiK (n = 6) (black inverted triangles) compared with the ILT tail τ(V) (n = 9) in normK (gray open circles) from Fig. 1 B. Double exponential fit for WTIR hiK: τ_0,1 = 170 ms, z₁ = 1.3, τ_0,2 = 4.2 ms, z₂ = 0.46. Due to a discontinuity near E_K, WTIR normK cannot be fitted in its entirety; the shallow and steep branches were fitted with single exponentials (shallow branch: z = 0.67, τ₀ = 25 ms, steep branch: z = 1.1, τ₀ = 300 ms). ILT tail τ(V) is from Fig. 1 B (single exponential z = 0.92, τ₀ = 3.6 ms). For net K⁺ movement being inward, WTIR closing was faster; the lack of a shallow branch or a τ(V) jump in ILT makes sense if the discontinuity (in WTIR normK) depended on a change in current direction.

As illustrated in Fig. 7 (A and B), stretch did not alter the basic character of the WTIR τ(V) relations (i.e., the WTIR-normK “jump” and the WTIR-hiK double exponentials persisted with stretch). However, WTIR tail currents showed the same spectrum of effects with stretch as in ILT. With 16 WTIR-normK experiments (different patches, mostly from different oocytes), six yielded stretch acceleration (as illustrated by Fig. 7 B), five yielded stretch slowing, two had unaffected tail currents (even though the WTIR activation was demonstrably accelerated), and three were complex. These three had either a stretch dose–dependent or voltage-dependent switch from slowing to acceleration; we sought but did not find further examples of intensified stretch eliciting a switch in stretch-effect polarity. From eight WTIR-hiK experiments, six patches showed stretch slowing and two scored as a voltage-dependent switch in effect polarity. In the latter two, the stretch effect “faded” at very negative voltages (e.g., Fig. 7 A). It is unclear if double exponential fits to WTIR-hiK τ(V) (Fig. 6; Fig. 7 A) actually reflect the closing mechanism since the stretch and no-stretch data could not always (e.g., Fig. 7 A) be fitted with the same pair of gating charges. However, it is clear for WTIR-hiK patches that above ∼−120 mV, stretch slowed the steps that dominate pore closing.

Figure 7.

WTIR and stretch. (A) Stretch-slowed tail currents (recorded in hiK) samples and τ(V) with double exponential fit: τ_0,1 = 34 ms, z₁ = 0.78, τ_0,2 = 3.6 s, z₂ = 2.8 without stretch, τ_0,1 = 62 ms, z₁ = 0.88, τ_0,2 = 3.4 s, z₂ = 2.8 with stretch. (B) Stretch-accelerated WTIR tail currents recorded in normK; τ(V) cannot be fitted with double exponentials. Fits with two separate lines: left branch (before and during [after cannot be fitted]) τ₀ = 5.9/4.0 ms, z = 0.44/0.44; right branch (before, during, after): τ₀ = 52/25/38 s, z = 0.93/0.85/0.85.

Effects of Stretch on Shaw Current

Membrane stretch increases far-field tension in bilayers, simultaneously increasing the area per headgroup in both bilayer leaflets (Gullingsrud and Schulten, 2004). Bilayer stretch is mimicked in several respects when short chain alcohols intercalate between lipid headgroups in both leaflets, thinning the bilayer, increasing the area per headgroup, and decompressing the hydrocarbon tails (Ly and Longo, 2004). We were struck by the report that short chain alcohols inhibit Shaw2 current, since Shaw activation “mainly occurs as a first-order concerted transition … that might correspond to the main late opening step in Kv channels” (i.e., to pore opening) (Shahidullah et al., 2003). As described earlier, the S4 of Shaw2 inspired the design of ILT (Shaker with three mutated S4 residues). Stretch slows ILT activation, and if Shaw2 behaved similarly, this could suggest that alcohol effects on Kvs (like stretch effects) arise from bilayer mechanics. To reiterate, our rationale was as follows: (a) short chain alcohols decrease Shaw2 steady-state current in a Traube's rule-like fashion (Shahidullah et al., 2003), (b) Shaw2 channel activation is limited by a concerted (ILT-like) transition, (c) short chain alcohols thin bilayers in accord with Traube's rule, (d) stretch thins bilayers, and (e) stretch slows ILT activation and should do likewise for Shaw2.

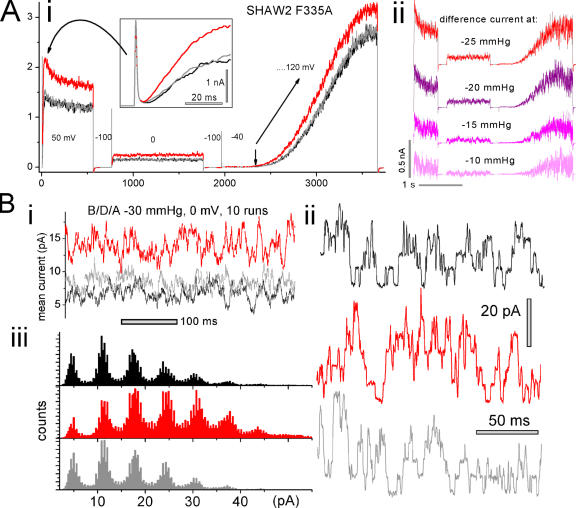
Shaw2 F335A is the mutant used as “wild type” by Shahidullah et al. (2003) and was provided by M. Covarrubias. The multistep protocol of Fig. 8 A (i and ii) is not a kind of conditioning protocol (such as that used for tail currents) but rather was used to maximize information about the effect of one and the same stretch stimulus. It controlled for possible stretch artifacts while showing responses to a given relatively brief stretch stimulus over a range of voltages. In long experiments, patches can change, so the more information gleaned from a given stretch stimulus the better. 50 mV was the holding potential of Shahidullah et al. (2003) during alcohol concentration jumps, hence our step to 50 mV (before, during, and after stretch in our case). The current response to this step revealed a voltage- and time-dependent stretch-sensitive current with, surprisingly, a sigmoid delay (see expanded inset, Fig. 8 A, i) of a few ms. As shown, Shaw2 F335A steady-state current, contrary to prediction, increased with stretch. The effect was dose dependent (see difference currents due to stretch, Fig. 8 A, ii). Scaling for amplitude (not depicted) revealed that during the onset of stretch-augmented currents, kinetics were indistinguishable from the before/after controls. The protocol included a step to 0 mV (the reversal potential for nonselective cation channels) to illustrate that outward current during that stretch-induced steady-state current was not endogenous (TRPC1-based) stretch-activated cation current (Maroto et al., 2005). (Gadolinium, added to the pipette at 40 μm for Shaw experiments, inhibits endogenous stretch current, but is unreliable.) The ramp clamp showed first that 50 mV was well below g(V)_max and second that stretch augmented current at all voltages, including at large depolarizations where, notably, control and stretch ramp currents did not converge (by contrast, such ramp currents do converge for WTIR; Tabarean and Morris, 2002).

Figure 8.

Effects of stretch on Shaw2 F335A. (A i) Shaw2 F335A macroscopic current (single traces) during a multistep protocol (voltages indicated in mV; protocol rationale is given in the text), before, during, and after stretch (using −25 mm Hg). An expanded inset reveals that current onset was sigmoid shaped. (A ii) From the same patch, stretch difference currents at the indicated levels of applied suction (difference currents = [(before + after)/2 – during]). (B) From an oocyte expressing Shaw2 F335A at a low level, (B i) current at 0 mV (10 traces averaged; membrane continuously at 0 mV, using −30 mmHg) before, during, and after stretch. From the same patch (but using −35 mm Hg), (B ii) excerpts from single traces, and (B iii) all-points amplitude histograms from eight runs per condition (i.e., before/during/after stretch) during steps from −100 to 0 mV show that the outward (=upward) unitary current jump amplitude (6.5 pA) was stretch independent. Since for this patch, linear subtraction was not done, interference from the capacitative current was avoided by omitting the first 200 ms of each run for ii and iii.

Stretch-enhanced activation of F335A was observed consistently (six of six patches from three oocyte batches). Positive (+15 mm Hg) as well as negative pipette pressure was tested in one patch, and both reversibly augmented current, as expected when stretch (i.e., far-field tension, not a bending energy) provides the MS stimulus (Sachs and Morris, 1998). Though ramp clamp yields only an approximation to a g(V) relation, the ramps verified that F335A activation was not right shifted by stretch. Another difference was that ILT g(V)_max was unaffected by stretch, but ramp currents suggested that in Shaw2 F335A, g(V)_max might increase with stretch.

Fig. 8 B shows that unitary current amplitude (the i of iNP_o, the determinants of macroscopic current) is not implicated in the stretch augmentation of Shaw2 F335A steady-state current. Recordings of outward current jumps at 0 mV (where endogenous MS current is ruled out) before, during, and after stretch show no change in unitary current amplitude. Fig. 8 B, i–iii, are ensemble currents, segments of raw current, and all-points amplitude histograms, respectively. Since it is unlikely that N (number of contributing Shaw channels) increased reversibly with each stretch episode, we conclude that stretch reversibly increased the P_O of Shaw2 channels via a transition(s) that, in this mutant was not rate limiting. If this is a “two concerted steps” channel, then a MS voltage-independent concerted transition, C_4AP↔O, could be responsible (i.e., the ratio of forward/backward rates here could increase with stretch). Alternately, given the MS sigmoidal current onset in Shaw2 F335A, the MS fast (nonrate limiting) step could be a C→C_A step. Or, it could be a partially concerted version of ILT's fully concerted final voltage-dependent step.

In any case, the plan to test if rate-limiting concerted pore opening motions in two different Kv channels would cause them to respond similarly to membrane stretch had to be abandoned. However the attempt added a Kv3 channel to the list of voltage-gated channels known to be modulated by stretch. The response pattern of Shaw2 F335A to stretch (activation kinetics unchanged with stretch, current augmented at all voltages, and no increase in unitary current amplitude) corresponded to those of N-type Cav channels (Calabrese et al., 2002) more closely than to the Kv1, Shaker. A stretch-induced increase in N might explain a stretch-induced increase in N P_O of Shaw2 F335A (and Cav) channels. Alternatively, stretch might change the ratio of forward/back rates of a fast closed–closed step (a P_O effect), increasing the occupancy of the state closer to the open state. Distinctions between P_O effects (“kinetic effects”) and N-based effects could, we note, be semantically and conceptually fuzzy if, say, stretch reversibly induced a partitioning of channels out of inhibitory lipid microdomains.

DISCUSSION

Pore Opening and Stretch

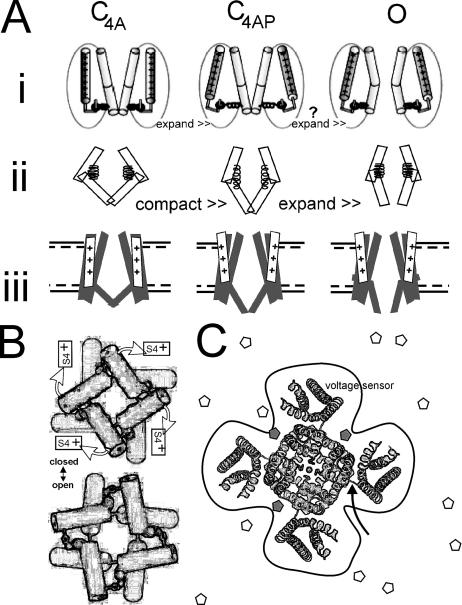
We find that, contrary to expectation, membrane stretch slowed activation of ILT current and diminished ILT steady-state current. Stretch right shifted the g(V) curve without altering the amount of charge moved or the value of g(V)_max. Tail currents, which report on pore closing, were also susceptible to stretch, but while the response sign (acceleration versus deceleration) was consistent for patches of a given oocyte batch, it differed among batches. In the framework of the simplest model (expanded states favored by membrane stretch, compacted states disfavored), our observations on ILT were in keeping with the rate-limiting concerted voltage-dependent motion producing a net compaction (hence the slowing by stretch). However, in an open-like Kv1.2 structure, the putative gate hinge has a bend (Long et al., 2005a; see the comments of Swartz, 2005), making a “pull-out” triggered gate expansion (cartooned in Fig. 9 A, i) likelier than a “pop-in” triggered gate expansion (suggested by cartoons Fig. 9 A, ii and iii). In Fig. 9 A (ii), we generically depict a compaction step (the concerted voltage-dependent step), which, as in A i, is followed by spontaneous gate expansion. Stretch effects on ILT were small (for the 30 or 40-mm Hg suction stimuli used to generate tension, the average right shift was <5 mV; see calculations relating g(V) shifts and membrane tensions to kT in Tabarean and Morris, 2002). But significantly, the small effects of stretch on ILT activation were of the “wrong” polarity to accord with the simplest model of mechanogating (assuming that A i more accurately models Shaker ILT motions than A ii). We suggest that when stretch disorders the channel lipid interface, the increased entropy (see Sigg et al., 2003) contributes more to the free energy for ILT activation than Δ-area effects. Bilayer models of stretch modulation that would implicitly capture such entropic contributions (e.g., Gullingsrud and Schulten, 2004; Wiggins and Phillips, 2005) cannot be tested without both open and closed Kv structures.

Figure 9.

Kv1 structure cartoons. (A i) A cartoon modified from Pathak et al. (2005) depicts the last concerted motion of the voltage sensor exerting a laterally acting (expansion) force within the protein. Subsequently, a concerted relaxation pulls open the channel gate (presumably this expands the hinge region). A ii suggests that the last charge concerted movements could, alternatively, couple to forces that constrict or compact the closed channel (“spring extension”) before a concerted gate region expansion (“spring relaxation”) that opens the pore. To provide context with the kinetic schemes, A iii shows the last two steps from Fig. 1 A. Note that if C_4AP is the most expanded state, this is not the factor dominating the stretch responses of ILT (this would not predict the observed stretch deceleration of ILT activation, and it would predict decreased ILT g_max with stretch, which was not observed). As explained in the text, B (modified from Webster et al., 2004) depicts the shutter-like action of the S6 pore hinge as seen from the intracellular space (rings signify the Cd bridges used to locate gating-related helix–helix interactions). The finding of Pathak et al. (2005) that a small concerted S4 movement (<15% of total sensor motion) impels an opening expansion is indicated. The cartoon in C centers on a schematic of an open-like Kv1.2 channel as seen from the extracellular side, adapted from Long et al. (2005a). A curved arrow points to the junction of sensor and pore modules in the primary structure. A perimeter line highlights the fact that the interface (i.e., amino acid residues interacting with bilayer lipid molecules on the z axis) is more extensive than for, say, a cylindrical tetramer. Bilayer stretch would alter the z axis LPP along this entire x,y perimeter. Surface active molecules (white and gray pentamers) whose mobility dropped at loci on the channel perimeter (gray molecules) could alter LPPs and hence conformational equilibria in excess of what would be predicted solely from the line tension due to bulk (white) molecules (Ly and Longo, 2004), making some distinctions between low-affinity binding effects and bilayer mechanical effects largely semantic.

ILT-based channels have recently clarified several key issues about Kv protein motions during pore opening. First, use-dependent site-specific metal bridges located the S5–S6 pore module's S6 gating hinge (Webster et al., 2004); second, residues carrying environmentally sensitive fluorophores (Pathak et al., 2005) showed that S4 movement underlies the voltage dependence of the preopening step; and third, further chemical modification studies (Del Camino et al., 2005) showed that this concerted sensor movement precedes (i.e., is demonstrably not simultaneous with) the “shutter” motion of opening. The gate model emerging from these papers is sketched in Fig. 9 B, along with a depiction (Fig. 9 C) of the crystal structure (Long et al., 2005a) of an open-like Kv1.2. Thus eight discrete channel parts (i.e., two motions of four parts each) move to take ILT from C_4A to O. The first set of motions was, we assume, the motion slowed by stretch, thereby slowing onset of macroscopic current. The same amount of charge moved with/without stretch. In Kv1.2 crystals (Long et al., 2005a,b), the S4s are not packed into four fully proteinaceous gating canals (e.g., conventional model; Horn, 2005); the voltage sensor modules are rather loosely tethered (Fig. 9 C, curved arrow) to a central pore module. The structure suggests an extensive lipid surround with parts of the S4s and possibly parts of the pore module contacting lipid. If this applies for ILT, it seems plausible that bilayer deformation by stretch would hamper (slow) the smooth orchestration of the concerted motion that is now envisaged for C_4A→C_4AP in ILT.

Tail Current Complexity with Stretch

Two general reasons for the opposing effects of stretch on Shaker tail current kinetics from different oocytes could be the following. (1) A single MS step influences channel closure and stretch affects that step with a polarity that depends on, for example, oocyte lipid composition. (2) Multiple MS steps influence tail current kinetics, some being stretch decelerated (an obvious candidate being pore opening), others stretch accelerated, with the relative weight of these steps changing with bilayer composition or some other factor. Regardless of ILT tail current response polarity (i.e., slower, faster, no change with stretch), ILT activation slowed with stretch, confirming that stretch was “felt” by the pore/gate mechanism in all tail current response polarities. Precisely how stretch reversibly alters the perichannel bilayer is not known (Fig. 1 A), but deformations/disruptions could range from hydrophobic mismatch to reversible rearrangements of lipid microdomains (see Wiggins and Phillips, 2005). If pore mechanics in ILT and WTIR conform to the model of Pathak et al., 2005 (depicted in Fig. 9 A, i), and if, in addition, some gate-related residues contact bilayer molecules, the variable-polarity stretch effects on tail current rates in both ILT and WTIR (plus reliable stretch slowing of opening in ILT) seem less disconcerting. It would fit a picture in which increased lipid disorder during stretch hampers any concerted movement, and especially a transition into an energetically unfavorable (Yifrach and MacKinnon, 2002) state, i.e., open. On the other hand, closing (O→C_4AP) as per Fig. 9 A (i) requires the open channel to acquire enough free energy to “restretch” its springs (equivalent to applying torque to the shutter-like mechanism of Fig. 9 B). With hyperpolarization, the voltage sensors move back to their C_4A position (Fig. 9 A, i and ii), but all four springs must first concertedly get restretched. Stretch would tend to slow the concerted process on entropic grounds but speed it enthalpically (the lateral force aiding spring reextension). If the balance of these free energy contributions tipped one way or the other depending on the bilayer lipids of different oocytes, this could explain our data.

Mechanically Unperturbed Filter

Although the rates of various Kv conformation changes are vulnerable to membrane stretch, the selectivity filter of Kv pore modules are evidently inured in Shaker ILT and WTIR and, it seems, in Shaw. Previously we showed that WTIR single channel amplitude with/without stretch is identical (Gu et al., 2001). Here we noted that ILT and WTIR g(V)_max were unaffected by stretch and that single channel amplitude of a Kv3 was constant when NP_O increased. Perhaps the circular domain-swapping arrangement noted by Long et al. (2005b) in the Kv1.2 tetramer contributes to the mechanical stability (Riechmann et al., 2005) of the Kv selectivity filter.

The Stressed Bilayer

A cruciform tetrameric Kv, as Fig. 9 C emphasizes, has an extensive lipid perimeter. Perhaps unavoidable disruptions of this lipid–protein interface by stretch render each kinetically isolatable Kv transition mechanosensitive. Sensor motions measured with respect to the plane of the bilayer for prokaryotic (KvAP) and eukaryotic (Shaker) Kv channels suggest a greater range of motion in the former (Ruta et al., 2005; Chanda et al., 2005). If eukaryotic Kvs have indeed evolved more damped motions, the need to minimize crosstalk from bilayer mechanics (stretch and bilayer lipid variations) may have been a selective pressure.

Kv Stretch Effects Summarized

Using Shaker channel mutants, we have now studied three MS rate-limiting (hence, kinetically isolatable) transitions. (1) A noncooperative voltage-dependent activation transition (in 5aa) is accelerated (Laitko and Morris, 2004) This is taken to be (4x)C→C_A. (2) Slow inactivation is independently accelerated in 5aa (the same-fold as no. 1; Laitko and Morris, 2004). (3) As shown here in ILT, a concerted voltage-dependent motion leading to pore opening (C_4A→C_4AP) is decelerated.

The voltage-dependent single exponential tail currents of ILT and WTIR were tested to probe closing steps, but neither provided a simple picture. It may be that variable oocyte membrane lipids (acting as surface active agents) affect the bilayer mechanics of closing. A precedent for this is Kv3, where surface active agents bind near gate residues (an interface effect?; see Fig. 9 C), modulating closed state stability (Shahidullah et al., 2003).

Wondering if concerted activation and stretch deceleration are correlated, and knowing that activation is reportedly a first-order concerted process in Kv3 Shaw2 channels, we checked Shaw2. In our patch recordings, however, the rise time of Shaw2 current was not first order but sigmoid, so a concerted motion was not rate limiting. The current was reversibly augmented by stretch with no change in kinetics; there was, therefore, an MS transition(s), albeit not a rate-limiting one. Unequivocally, however, Kv3 channels belong on the list of voltage-gated channels modulated by stretch.

Physiological Prospects for Kv Mechanosensitivity

Even small stretch effects like those of ILT could be consequential for a system operating close to the foot of the channel's g(V) relationship or curve. For example, at the smallest depolarizing step in Fig. 3 A, ILT current is almost halved by mild (i.e., comfortably nonlytic) stretch. And, as noted previously for WTIR and 5aa, several millivolts below threshold, stretch can generate “infinitely” big NP_o increases (Tabarean and Morris, 2002; Laitko and Morris, 2004). Considered over the whole voltage range, the primary stimulus (ΔV_m) is far more effective than the modulatory stimulus (Δ membrane tension). But, near the foot of its g(V), a native Kv with properties like WTIR, 5aa, or ILT could generate nontrivial mechanosignals, especially if that g(V) foot coincided with a resting, diastolic, or plateau potential.

Kv mutants can show distinctive stretch phenotypes. Shaker ILT is “stretch inactivated,” whereas WTIR and 5aa are “stretch activated.” Evolution might, therefore, have honed Kv stretch responses. In prokaryotes (e.g., KvAP; Ruta et al., 2005), stretch responses in a Kv could, say, couple K flux to osmotic compensation (Botzenhardt et al., 2004). In eukaryotes, the stretch stimuli that modulate Kv gating are no different from those that activate other channels (Chemin et al., 2005; Maroto et al., 2005; Zhou et al., 2005). Knockout organisms notwithstanding, mechanophysiological roles are still conjectural for these other MS channels, emphasizing the point that open mindedness with respect to possible mechanophysiological roles for Kv channels is warranted.