Calcium-dependent Gating of MthK, a Prokaryotic Potassium Channel

Abstract

MthK is a calcium-gated, inwardly rectifying, prokaryotic potassium channel. Although little functional information is available for MthK, its high-resolution structure is used as a model for eukaryotic Ca²⁺-dependent potassium channels. Here we characterize in detail the main gating characteristics of MthK at the single-channel level with special focus on the mechanism of Ca²⁺ activation. MthK has two distinct gating modes: slow gating affected mainly by Ca²⁺ and fast gating affected by voltage. Millimolar Ca²⁺ increases MthK open probability over 100-fold by mainly increasing the frequency of channel opening while leaving the opening durations unchanged. The Ca²⁺ dose–response curve displays an unusually high Hill coefficient (n = ∼8), suggesting strong coupling between Ca²⁺ binding and channel opening. Depolarization affects both the fast gate by dramatically reducing the fast flickers, and to a lesser extent, the slow gate, by increasing MthK open probability. We were able to capture the mechanistic features of MthK with a modified MWC model.

INTRODUCTION

Ion channel proteins open and close their pores in response to various stimuli in order to allow flow of ions in or out of cells. Ligand-gated ion channels are modulated when signaling molecules such as Ca²⁺, cAMP, cGMP, acetylcholine, and serotonin bind to specialized regions within the channel. Numerous eukaryotic ion channel proteins fall into this category, including Ca²⁺-modulated channels: BK, SK, and IK channels (for review see Vergara et al., 1998), cyclic nucleotide-gated channels (CNG and HCN channels) (Kaupp and Seifert, 2001; Kaupp and Seifert, 2002; Matulef and Zagotta, 2003; Zagotta, 1996), acetylcholine receptor channels, and serotonin receptor channels (Devillers-Thiery et al., 1993; Kotzyba-Hibert et al., 1999). Although extensive functional data has been collected for these channels and great strides have been made towards describing the mechanism of ligand gating, no high resolution structural data is yet available for eukaryotic ligand-gated channels.

The small prokaryotic channel MthK, from Methanobacterium thermoautotrophicum, is the first ligand-gated channel whose structure was determined to angstrom resolution by X-ray crystallography (Jiang et al., 2002a,b). The channel consists of a two-transmembrane region, with a GYGD-containing pore region that undoubtedly places it in the tetrameric K⁺ channel family, and contains an extended cytoplasmic Ca²⁺ binding region, called the regulator of K⁺ conductance (RCK) domain, which bears homology to a putative Ca²⁺ binding region of eukaryotic Ca²⁺-activated K⁺ (BK) channels. The functional MthK channel has a gating ring composed of eight such RCK domains, four intrinsic RCK domains integral to the channel and four identical, soluble, cytoplasmic RCK subunits. Soluble RCKs and channel RCKs are intricately connected to form the functional unit in the four fold symmetric ligand binding structure (Jiang et al., 2002a). The soluble RCK subunit is a product of the same gene that encodes the MthK channel, via an internal initiation methionine at position 107. Eight Ca²⁺ ions appear in the X-ray structure of the channel, bound specifically to the cytoplasmic RCK domains. In addition, the channel opens in the presence of millimolar Ca²⁺. Thus, MthK has served as a model for eukaryotic BK channels and as an example of an open K⁺ channel pore (Jiang et al., 2002a).

However, in some respects, MthK behavior differs from that of BK channels. The millimolar concentration of Ca²⁺ reported to open the prokaryotic MthK channel is three to four orders of magnitude larger than that required to open the eukaryotic Ca²⁺-dependent channels SK and BK (Vergara et al., 1998). Additionally, the unitary current voltage (I-V) profile of MthK (Jiang et al., 2002a) differs from BK (Barrett et al., 1982) in that the inward single-MthK channel current is several fold higher in conductance than its outward current, while for BK, the inward and outward currents have similar amplitudes. Consequently, we find ourselves with a large set of eukaryotic ligand-gated channels whose functions have been studied extensively but whose structures are unknown and, in contrast, with a prokaryotic channel whose structure has been solved but whose functional characterization lags behind.

In this article we attempt to even out the structure–function balance for MthK by investigating its gating characteristics in detail. Upon examination of purified single-MthK channels in planar lipid bilayers, we found that MthK is markedly and cooperatively activated by Ca²⁺ in the millimolar range with an unusually high Hill coefficient of ∼8. The increase in open probability (Po) of the channel is due mainly to an increase in the frequency of opening rather than an increase in the mean open time, unlike other eukaryotic Ca²⁺-activated K⁺ channels such as BK, which stay open longer and open more frequently upon Ca²⁺ application. Ca²⁺ is a specific opener of MthK channels, as Mg²⁺ does not mimic the effects of Ca²⁺ on MthK open probability. Transbilayer voltage also regulates channel opening by a different mechanism than Ca²⁺. While changing the membrane potential does not significantly alter MthK open probability (in contrast to BK channels), depolarization greatly lengthens the opening durations. In conclusion, although there must be some similarities in their mechanism of Ca²⁺ activation, as MthK is also a K⁺ channel opened by Ca²⁺ binding to RCK domains, MthK is not a faithful model for BK channel gating.

MATERIALS AND METHODS

MthK Channel Purification and Reconstitution into Liposomes

The MthK channel gene (a gift from R. MacKinnon, Rockefeller University, New York, NY), cloned in pQE70 vector (QIAGEN) with a carboxy-terminal hexahistidine tag was transformed into XL1-Blue cells and grown at 37 °C in Luria-Bertani media with ampicillin (200 μg/ml) selection. MthK expression was induced by incubating with 400 μM IPTG (Sigma-Aldrich) for 3 h at a cell density (OD₆₀₀) of 1. Protein was purified from the cell extract according to previously described protocols (Jiang et al., 2002a). In brief, bacterial pellets were resuspended and sonicated with a probe sonicator at 50–75% power in 50 ml breaking buffer (100 mM KCl, 50 mM Tris, pH 7.6) with protease inhibitors (one tablet of Complete EDTA-free Cocktail Inhibitors and 0.17 mg/ml PMSF; Roche). The membranes were extracted for 3 h at room temperature in 50 mM decyl maltoside (DM; Anatrace) and then centrifuged at 40,000 g for 45 min at room temperature. The supernatant was applied to a Co-column (Talon, 1–2 ml slurry/liter culture) pre-equilibrated in buffer B (100 mM KCl, 20 mM Tris, 5 mM DM, pH 7.6). The column was washed with 30 mM imidazole, and MthK protein was eluted with 300 mM imidazole (Fluka) in buffer B. Immediately after purification, 0.5 U Thrombin (Roche) per 3 mg of protein was added and incubated for 5 h to cleave the His tag. MthK was then further purified on a Superdex-200 (GE Healthcare) gel filtration column in buffer B and concentrated in 50,000 MWCO Amicon concentrators (Millipore). Purified MthK channels were reconstituted into liposomes (Heginbotham et al., 1999; Nimigean and Miller, 2002) made of 3:1 1-palmitoyl-2-oleoyl phosphatidylethanolamine (POPE):phosphatidylglycerol (POPG) synthetic lipids (Avanti Polar Lipids). The lipids were removed from chloroform and solubilized in 34 mM CHAPS (Anatrace) in S buffer (450 mM KCl, 20 mM HEPES, and 4 mM NMG) at a concentration of 10 mg/ml. The protein was mixed with the solubilized lipids (1–20 μg protein/mg of lipid) and applied to a 20 ml Sephadex G50-fine (GE Healthcare) column equilibrated in S buffer. The turbid eluates that contain the detergent-free protein liposomes were aliquoted, flash frozen in liquid N₂, and stored at −80 °C.

Single-channel Recording in Lipid Bilayers

For channel recording, we used a horizontal lipid bilayer setup (Chen and Miller, 1996; Heginbotham et al., 1999) with two aqueous chambers separated by a partition (transparency film, 5×5 mm) with a small hole in the middle (50–90 μm in diameter) made with a butterfly pin. The lipids, POPE:POPG 3:1 (10 mg/ml, resuspended in decane; Sigma-Aldrich) were painted on this hole to form lipid bilayers that separate the two aqueous chambers, connected by agar bridges (150 mM KCl, 2% agarose) to the recording electrodes. Formation of a bilayer was monitored electrically with a pulse protocol in Clampex (Axon Instruments). The top (cis) chamber was grounded. Using charybdotoxin (CTX), channels whose extracellular side faced the trans chamber were blocked, thus allowing the study of only the channels with extracellular side facing the cis chamber.

Single channel currents were recorded in symmetrical 200 mM K⁺ solutions (120 mM KCl, 80 mM KOH, 10mM HEPES, pH 7.0) with an Axopatch 200 (Axon Instruments) sampled at 10 kHz and low-pass filtered at 2–5 kHz. Intracellular (trans) solutions contained 100 nM charybdotoxin, a gift from C. Miller (Brandeis University, Waltham, MA), manufactured according to protocol (Park et al., 1991). The Ca²⁺ concentration was varied on the intracellular side from 0 to 10 mM, while neither Ca²⁺ nor EDTA was added to the extracellular side. Solutions deemed 0 Ca²⁺ or 0 Mg²⁺ contained no added divalents and 1 mM EDTA, a known divalent ion chelator.

Open Probability Calculations

Data were analyzed using Clampfit 9.0 (Axon Instruments). All open and closed events longer than 0.18 ms were measured using the Single Channel Search Module, and the open probability was determined. Due to uncertainty about the total number of channels per bilayer due to low open probability, we looked at the average number of open channels in the bilayer, nPo, defined as

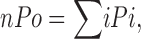(1)

where Pi is the open probability of the particular level, i, with each level corresponding to the number of open channels. In addition, due to the variable open probabilities (Po values ranging from 0.05 to 0.5) among MthK channels in identical conditions, we defined a relative activity (r_a):

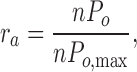(2)

where nP_o,max is the maximal open probability for a given bilayer at 5 mM Ca²⁺ (at −200 mV). We used r_a to track changes in nPo relative to this maximum activity as Ca²⁺ was varied and to average data from different channels. Each experiment began by recording in 5 mM Ca²⁺, followed by perfusion of the trans chamber with a lower Ca²⁺ concentration. For several bilayers, the chamber was re-perfused to the initial Ca²⁺ concentration to ensure no gain or loss of channels. For each bilayer, recordings at −200 mV were analyzed in detail (unless indicated otherwise). Similar results are obtained when a different negative voltage is selected (unpublished data). The dose–response data was fit with the Hill equation,

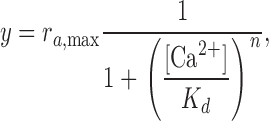(3)

where K_d is the concentration at half maximal activation, r_{a ,max} is the maximal relative activity, and n is the Hill coefficient. Parameters were free-fit, with the exception of the Hill coefficient, which was either free or constrained to 8, as described in Results (see Fig. 3).

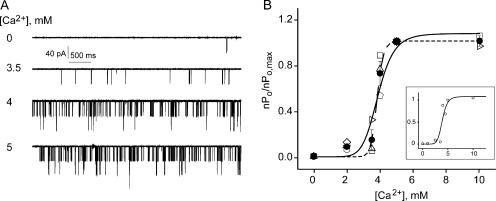
Figure 3.

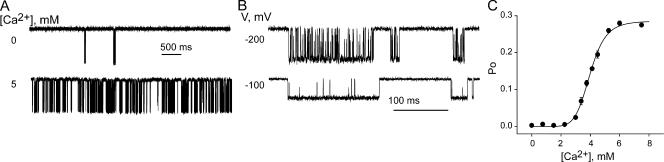
MthK is sharply activated by Ca²⁺ in the millimolar range. (A) Representative single-channel traces at 0, 3.5, 4, and 5 mM Ca²⁺. (B) Ca²⁺ dose–response of MthK. Each open symbol is a single bilayer, with 11 different bilayers analyzed. Filled symbols represent mean ± SEM from three separate bilayers with the exception of the 10 mM Ca²⁺ point with n = 2. Data points were fit with the Hill equation (Eq. 3) with n = 8 (smooth line, K_d = 3.8 ± 0.2 mM, and r_a,max = 1.07 ± 0.1) and n = 20 (dashed line, K_d = 3.8 ± 0.04 mM, and r_a,max = 1.00 ± 0.04). Inset shows a Ca²⁺ dose–response from a single representative bilayer. The data (open circles) were fit with the Hill equation with n = 8 (K_d = 3.9 ± 0.14 mM, and r_a,max = 1.08 ± 0.14). The axes are the same as in B.

Burst Kinetics

A critical time has to be determined that separates the gaps between bursts from the gaps within bursts. The closed dwell times are log-binned (McManus et al., 1987) and the distributions are plotted and fitted (maximum likelihood) with sums of exponential components:

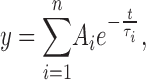(4)

where A_i is the relative number of events in each component

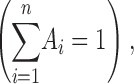and τ_i is the time constant of the exponential component (τ_i = 1/k_i, where k_i is the microscopic rate constant associated with the process). The critical time, t_c, which separates gaps between bursts and closed times within bursts has to be chosen so as to minimize the number of misclassified events (Magleby and Pallotta, 1983). Then, closures longer than t_c correspond to gaps between bursts, and closures shorter than t_c correspond to gaps within a burst. For burst duration determination, all closed intervals less than t_c were ignored during analysis. When two or more channels were open at the same time, the average burst duration was determined by adding the burst times in each level and then dividing by the total number of bursts. To determine the gap between bursts durations, all closures less than t_c were ignored and only recordings of 5 min or longer were included. When two or more channels were present, the average duration obtained for the gaps between bursts was multiplied by the number of channels visible in the bilayer. For dwell time histograms (as shown in Fig. 4 C and Fig. 5 E), only the bilayers with one channel visible were used.

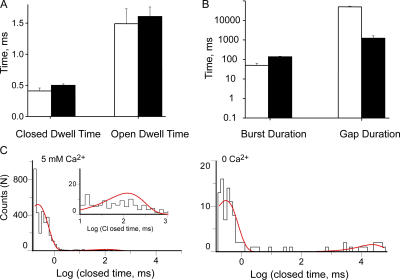
Figure 4.

Ca²⁺ increases MthK open probability by increasing burst frequency. (A) Mean closed and open dwell times within a burst in 0 and 5 mM Ca²⁺. (B) Mean gap duration and burst duration in 0 and 5 mM Ca²⁺. Bars are mean ± SEM from at least three separate bilayers (open, 0 Ca²⁺) and 10 bilayers (solid, 5 mM Ca²⁺). (C) Closed dwell time histograms for a single bilayer containing two channels. The bilayer was perfused from 5 mM Ca²⁺ to 0 Ca²⁺. The fits are with Eq. 4 with two exponential components with: A₁ = 0.97 ± 0.09, τ₁ = 0.23 ± 0.12, A₂ = 0.03 ± 0.06, and τ₂ = 118 ± 3 for 5 mM Ca²⁺, and A₁ = 0.88 ± 0.05, τ₁ = 0.30 ± 0.08, A₂ = 0.12 ± 0.04, and τ₂ = 22552 for 0 Ca²⁺. Inset shows magnification of histogram data for closures ≥10 ms; smooth line is the exponential fit.

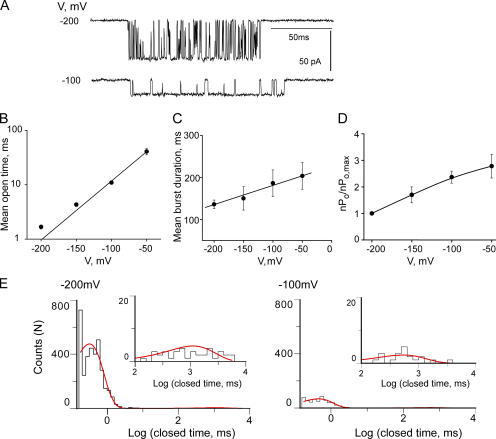
Figure 5.

MthK displays voltage-dependent gating. (A) Representative single channel traces with 5 mM Ca²⁺ at −100 and −200 mV. The open dwell time (B), burst duration (C), and relative activity (D) plotted from −200 to −50 mV. Symbols represent mean ± SEM from 10 separate bilayers for the values in B and C and three bilayers for D. Data points in B were fit with Eq. 5 (straight line) to determine the voltage dependence (z_o = 0.62 ± 0.04, n = 10) of the open durations within a burst. (E) Closed dwell time histograms from a representative bilayer at −200 and −100 mV fit with a sum of two exponentials (Materials and Methods). The fitted time constants and areas are: A₁ = 0.96 ± 0.14, τ₁ = 0.52 ± 0.11, A₂ = 0.04 ± 0.02, and τ₂ = 636 ± 3 for −100 mV, and A₁ = 0.99 ± 0.06, τ₁ = 0.36 ± 0.15, A₂ = 0.01 ± 0.045, and τ₂ = 1293 ± 11 for −200 mV. Insets show magnification of histogram data for closures ≥100 ms; smooth line is the exponential fit.

Voltage Dependence

The voltage dependence of the closing rate within a burst is given by z, the effective gating charge determined from the following equation:

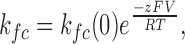(5)

where k_fc is the closing rate within a burst (k_fc = 1/o_f, where o_f is the mean open time within a burst), k_fc(0) is the closing rate at 0 mV, z is the effective gating charge and R, T, and F have their usual meanings. In order to display the effect of voltage on MthK open probability for several bilayers, the relative activity was calculated in a similar way described above for the Ca²⁺ dose–response curve (Eq. 2), only this time nP_{o ,max} is replaced by nP_{o ,−200}.

Kinetic Models

Kinetic models and simulated single-channel records were generated and analyzed using the QuB software for single-channel analysis (version 1.4.0.2, www.qub.buffalo.edu). The rates associated with each transition are in the following form: k = k ₀ × C × e^bV, where k₀ is the intrinsic rate constant, C is the Ca²⁺ concentration, V is the voltage, and b is zF/RT. The values for the rates used for the simulations in the figures in this paper were partly obtained from our data analysis (thus constrained) and the rest were assessed by eye with the trial and error method, constrained by key parameters such as the Hill coefficient for the Ca²⁺ dose–response curve and the values of the kinetic parameters in Table II. At least 60 s of continuous single-channel activity for each desired condition were simulated, sampled at 10 kHz, and filtered at 2 kHz to resemble our real data. Scaling was at 320 and the current standard deviations were 0.04 and 0.08 for the closed and open states, respectively. The open probability values for the simulated traces were calculated from all-point amplitude histograms directly in QuB and then imported into Origin (Microcal Software Inc, version 6.0) for averaging and further processing. Mean open time, mean closed time, burst duration, and gap duration were analyzed in Clampfit as above by importing lists of open and closed durations directly from QuB.

TABLE II.

Values of Kinetic Parameters, from Real and Simulated Data

		Ca2+, 0 mM	Ca2+, 5 mM	V, −200 mV	V, −100 mV
Mean open duration (ms) ± SEM	real	1.5 ± 0.2	1.6 ± 0.2	1.6 ± 0.2	11.1 ± 0.6
	simu	1.5 ± 1.3	1.4 ± 0.1	1.4 ± 0.1	12.8 ± 0.07
Mean closed duration within     bursts (ms) ± SEM	real	0.4 ± 0.05	0.50 ± 0.02	0.50 ± 0.02	0.67 ± 0.03
	simu	0.4 ± 0.2	0.4 ± 0.1	0.4 ± 0.1	0.4 ± 0.1
Mean burst duration (ms) ± SEM	real	50 ± 14	136 ± 10	136 ± 10	186 ± 32
	simu	61 ± 20	73 ± 6	73 ± 6	57 ± 3
Mean gap duration (ms) ± SEM	real	49401 ± 4529	1223 ± 392	1293 ± 11	636 ± 3
	simu	9692 ± 520	77 ± 6	77 ± 6	87 ± 2

Values are at −200 mV for the values in the first two columns and at 5 mM Ca²⁺ for the values in the last two columns. The “real” parameters are extracted from the data presented in Fig. 4 (A and B) and Fig. 5 (B and C). The “simu” parameters are from simulation and analysis of individual data sets in the required conditions.

RESULTS

MthK, an Inwardly Rectifying K⁺ Channel

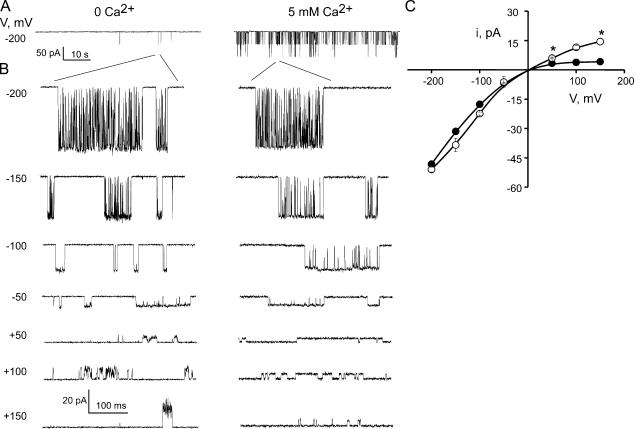
Single MthK channel current recordings are shown in Fig. 1 in symmetrical 200 mM K⁺. MthK channel gating displays bursting behavior with long periods of inactivity. We were able to detect openings, albeit infrequently, in the absence of Ca²⁺ so we can compare the MthK conduction properties in 0 Ca²⁺ with those in high Ca²⁺ (Fig. 1 A). Currents vary widely in amplitude over the range of voltages examined, with the inward current (negative voltages in Fig. 1 B) being much larger in size than the outward current (positive voltages in Fig. 1 B). The current voltage (I-V) curves in Fig. 1 C are characteristic of a classic inwardly rectifying channel. The chord conductances of the current–voltage relationship in the presence of Ca²⁺ (filled circles, Fig. 1 C) are 242 pS and 27 pS at −200 and +150 mV, respectively. It appears that some of this rectification is due to Ca²⁺ block. If Ca²⁺ is removed from the intracellular solution altogether (by replacing it with EDTA to chelate all free Ca²⁺), the current in the outward direction increases to a chord conductance of 96 pS (Fig. 1 C, open circles, value at 150 mV). This indicates that Ca²⁺ is partly responsible for the lower conductance in the outward direction either by direct fast block or by an electrostatic screening effect. This maneuver did not completely remove inward rectification and also resulted in large open channel noise (Fig. 1), as if blocking events faster than the amplifier sampling time are occurring, indicating that Ca²⁺ is not the sole culprit of channel block. Thus, we restricted our gating kinetics analysis to the negative voltage values (inward currents).

Figure 1.

MthK is an inwardly rectifying, Ca²⁺-gated channel. (A) Single MthK channel recordings in 0 and 5 mM intracellular Ca²⁺ to illustrate overall MthK gating. (B) Representative MthK channel bursts as a function of voltage in 0 and 5 mM intracellular Ca²⁺ at the indicated voltage. (C) Characteristic single-channel current voltage I-V curves where each data point represents the mean ± SEM from at least eight (5 mM Ca²⁺, filled circles) and three (0 mM Ca²⁺, open circles) separate bilayers. * indicates mean ± SEM from only two bilayers. All records are low-pass filtered at 2 kHz and sampled at 10 kHz unless specified otherwise.

Occasionally, under identical recording conditions, MthK displays a slightly lower conductance level (∼5% of the time). We constrained all our kinetic analysis to channels with the conductance properties discussed above.

Extracellular CTX Block, a MthK Orientation Tool

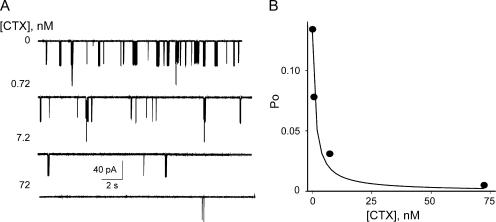
Lipid bilayer current recordings have one distinct disadvantage from patch clamp or whole cell recordings of living cells. Whereas in mammalian cells or oocytes channels are inserted in the cell membrane in a well-defined orientation, in lipid bilayers the purified channel protein will insert randomly in either of the two available orientations: with their cytoplasmic domain facing the top or bottom chamber. CTX, a well-known extracellular K⁺ channel blocker (Park et al., 1991) was shown to block MthK channels (Jiang et al., 2002a). Due to the sidedness of the block, it can be a useful orientation tool for MthK in bilayers if its blocking affinity is high enough. We investigated the CTX blocking affinity by applying increasing concentrations of the toxin to the cis chamber and examining its effect on MthK gating. As indicated in Fig. 2, CTX blocks the inward current of MthK in a concentration-dependent manner by further increasing the durations of the long gaps between bursts such that at 72 nM the current is completely blocked. The K_d of the CTX block for MthK channels as determined from Fig. 2 B is ∼1 nM, a high affinity slow block, in the same range as for other Ca²⁺-activated K⁺ channels (Miller, 1995). All data was henceforth collected in the presence of 100 nM CTX in the trans bilayer chamber to ensure that we were recording only from channels with the extracellular side facing the ground, a condition similar to normal electrophysiological conventions.

Figure 2.

Charybdotoxin as an orientation tool for MthK channels. (A) Single-channel MthK traces with 0, 0.72, 7.2, and 72 nM CTX at −200 mV. (B) MthK open probability from a representative bilayer as a function of CTX concentration. Data was fit (smooth line) with the equation

with a K_d of ∼1 nM.

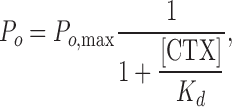Ca²⁺ Dependence of MthK

While millimolar levels of intracellular Ca²⁺ decrease outward MthK current, they also increase the open probability of the channel (Jiang et al., 2002a). Fig. 3 shows representative single MthK channel current traces at −200 mV with increasing Ca²⁺ concentrations. From 0 to 3 mM Ca²⁺ the channel is rarely open. But between 3.5 and 4 mM Ca²⁺ there is a sharp increase in Po, with maximal open probability obtained at 5 mM Ca²⁺. No further activation is observed upon raising the Ca²⁺ concentration from 5 to 10 mM. The Ca²⁺ concentrations required to open MthK channels are unusually high and have yet to be encountered among eukaryotic Ca²⁺-activated K⁺ channels (Vergara et al., 1998).

Qualitatively, as was previously reported (Jiang et al., 2002a), it is clear that Ca²⁺ increases the open probability of MthK channels. However, MthK channels are difficult to investigate quantitatively for three main reasons. First, they display variable open probability in identical conditions from bilayer to bilayer (with values ranging from 0.05 to 0.5; unpublished data) making comparisons between bilayers and averaging over several bilayers challenging. For this reason, to tame the variability in Po, for each Ca²⁺ concentration we measured the relative increase in nPo to the maximal open probability at saturating Ca²⁺ for each bilayer. Second, MthK channels display maximal open probabilities significantly less than 1 even in the presence of saturating Ca²⁺ concentrations, leading to uncertainty about the total number of channels per bilayer. To circumvent this problem, we quantified channel activity as nPo due to uncertainties in estimating the number of channels per bilayer. Third, MthK opens in bursts with relatively long periods of inactivity, thus making it necessary to record long stretches of data (minutes in each condition) to accurately sample each experimental condition investigated.

Fig. 3 B shows the plot of relative Po vs. Ca²⁺ for 11 different bilayers (the Ca²⁺ dose–response for a single representative bilayer is shown in the inset for clarity). Although channel activity and behavior showed some heterogeneity, Ca²⁺ elicited the same relative increase in activity across all experiments (the various white symbols represent separate experiments). We obtained a dose–response relation that increases extremely steeply with Ca²⁺ (Fig. 3 B, black symbols with error bars for averages and inset for a single bilayer). The open probability increases >10-fold between 2 and 5 mM Ca²⁺ (and >100-fold over a 5 mM change in Ca²⁺). This sharp increase in channel activity can be described by the Hill equation, with an n value of ≥8. If the Hill coefficient is allowed to vary freely, the dose–response data is best fit with n = 20, indicating that there are at minimum 20 cooperative binding events leading to channel opening, as shown in Fig. 3 B (dashed line). However, only eight Ca²⁺ ions were detected in the MthK structure (Jiang et al., 2002a). Hence, in the spirit of true structure–function studies, we constrained the Hill coefficient to 8 and obtained a visually satisfying fit (solid curve in Fig. 3 B). Eight, which is the lowest Hill coefficient that will satisfy both our functional and structural constraints, is the highest Hill coefficient reported for a ligand-gated channel and an indicator of highly cooperative Ca²⁺ binding interactions. In comparison, for BK channels, the highest Hill coefficient for Ca²⁺ activation is 3–4 (Nimigean and Magleby, 1999) and for Ca²⁺ activation in the presence of Mg²⁺ is 5 (Golowasch et al., 1986). MthK has the highest known cooperativity and the lowest Ca²⁺ affinity of all known Ca²⁺-activated K⁺ channels to date.

Ca²⁺ Modulation of Gating Kinetics of MthK

Through what mechanism does Ca²⁺ increase MthK's open probability? To answer this question, we examined the single-channel gating kinetics of MthK. The representative traces in Fig. 1 A and Fig. 3 A display a similar pattern; the channel is closed for long periods of time (gaps between bursts) interrupted by periods of high activity (bursts) in which the channel flickers (rapidly transitions) between the open and closed levels. Thus, the increase in channel Po with Ca²⁺ could result from any one or more of the following possibilities: (a) an increase in the duration of individual channel openings, (b) an increase in the duration of bursts, or (c) an increase in the frequency of bursting (equivalent to decreasing the durations of gaps between bursts).

In order to examine burst kinetics, we introduced a critical closed time, t_c. All closed interval durations smaller than t_c are to be classified as closings within a burst and those larger than t_c as gaps between bursts. To determine t_c, we fit the closed dwell time histograms from individual bilayers with two exponential components. For one representative bilayer, the time constants of such components were τ₁ = 0.23 and τ₂ = 117.6 ms (Fig. 4 C, 5 mM Ca²⁺). Despite some variation in the long component (due to different numbers of channels in each bilayer as well as variable open probability amongst channels), all bilayers analyzed displayed a considerable two to four orders of magnitude difference between the time constants of the short and long component, corresponding to closings within bursts and gaps between bursts, respectively. (Decreasing Ca²⁺ from 5 to 0 mM magnifies the gap between the two exponential components, as seen in Fig. 4 C.) This allows us to choose a value for t_c (10 ms) that will minimize event misclassification (Magleby and Pallotta, 1983). To test whether data analysis depends on our critical time selection, we determined the average durations of the gaps within a burst using three different critical times: 5, 10, and 20 ms. Identical results were obtained (unpublished data). Thus, we chose 10 ms as the critical time for all of our analyses.

The results of the burst analysis are shown in Fig. 4 B. The durations of the gaps between bursts decreased on average ∼40-fold as Ca²⁺ was increased from 0 to 5 mM, while the burst durations increased only threefold. As expected upon visual inspection of the channel traces in Fig. 3 A, the majority of the increase in channel activity results from an increase in burst frequency, which is determined by the duration of gaps between bursts; the shorter the gaps between bursts, the more frequent the bursts. The average open and closed times within a burst remained unchanged irrespective of the amount of Ca²⁺ present (Fig. 4 A). This is also illustrated in the bilayer represented in Fig. 4 C; the short closed duration components display identical time constants, while the gap duration components increase ∼100-fold when Ca²⁺ is increased from 0 to 5 mM. To summarize, the increase in open probability with Ca²⁺ is mainly caused by a dramatic increase in the frequency of channel openings (40-fold) and less so by a modest increase in burst durations (threefold), accounting well for the experimentally observed ∼100-fold increase in channel activity. It is noteworthy that the fast intraburst gating is Ca²⁺ independent.

Voltage Dependence of MthK

Besides the increase in open probability with Ca²⁺, MthK also displays an interesting voltage effect; as the membrane potential is made more depolarized, the frequency of the very brief closings (flickers) within the burst decreases dramatically (Fig. 5 A). This leads to a significant increase (∼24-fold for a 150-mV depolarization) in mean open time (Fig. 5 B). While this effect is apparent upon examination of single channel traces, the increase in Po resulting from this depolarization is more modest, less than threefold (Fig. 5 D) and the increase in the durations of bursts is insignificant (Fig. 5 C). To gain further insight into the mechanism of voltage gating, we examined the closed dwell time distributions for one bilayer (Fig. 5 E) at two voltages: −200 and −100 mV. These distributions were fit with the sum of two exponential components corresponding to the flickering closings within bursts and the gaps between bursts. As we depolarize the bilayer by 100 mV, the number of events comprising the “flicker” component decreases markedly while the number of gaps between bursts stays relatively constant (or, in other words, the fraction of the total number of closed events represented by fast flickers decreased approximately fivefold as the bilayer is depolarized 100 mV while their durations stayed the same; Fig. 5 E). In contrast, the durations of the long closed component decreased to about 50% their starting value and their total number did not change (Fig. 5 E). Thus it appears that the modest increase in Po with depolarization is due to a decrease in the duration of gaps between bursts. The disappearance of the flickers, while striking, contributes mainly to the large increase in mean open time and only a negligible amount to the change in open probability.

The visible lengthening of the durations of the openings within a burst (Fig. 5 B) is thus a consequence of a decrease in the flicker closing rate with depolarization. We quantified the voltage dependence (z) associated with the change in this closing rate by fitting the durations of the mean open times in Fig. 5 B with an exponential function (Eq. 5). We obtained a z value of 0.62 ± 0.04, which traditionally suggests that the flickering process is caused by a charged entity that moves one elementary charge more than halfway across the membrane on its way to occlude the pore (Woodhull, 1973).

Unlike Ca²⁺, which increases the MthK channel open probability by mainly increasing the opening frequency, voltage predominantly acts to decrease the flicker frequency within a burst with little effect on the open probability, indicating that Ca²⁺ and voltage act through separate pathways to modulate the activity of MthK channels.

Mg²⁺ Does Not Mimic Ca²⁺ in Modulating Po

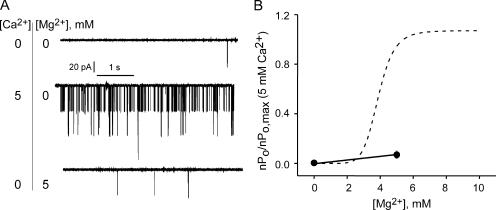
Can any divalent ion recapitulate the effects of Ca²⁺ on MthK channels or is the increase in Po Ca²⁺ specific? We investigated this issue by measuring channel activity in solutions where Mg²⁺ was substituted for Ca²⁺. Bilayers were obtained in the presence of 5 mM Ca²⁺. Then, the intracellular (trans) compartment was perfused with solutions containing 5 mM Mg²⁺ and no added Ca²⁺. The effect of removing all divalent cations was examined by perfusing with solutions containing 1 mM EDTA (and no added divalents). 5 mM Mg²⁺ has a nominal effect on the open probability of MthK as shown in Fig. 6. For comparison, in Fig. 6 B, the effect of Mg²⁺ on MthK open probability is superimposed onto the Ca²⁺ dose–response relationship for MthK (dashed line represents the fit with a Hill coefficient of 8 from Fig. 3 B). With increasing Mg²⁺ concentrations, there is a slight positive slope of the curve (Fig. 6 B), but the increase is much smaller than that seen for Ca²⁺ and is consistent with a nonspecific divalent effect. This result is in agreement with the finding that Mg²⁺ does not support the Ca²⁺-induced octameric RCK domain complexes in solution (Dong et al., 2005).

Figure 6.

The effect of Ca²⁺ on MthK open probability is not recapitulated by Mg²⁺. (A) Representative single-channel traces at 0 Ca²⁺/Mg²⁺, 5 mM Ca²⁺, and 5mM Mg²⁺ (V = −200 mV). (B) Relative channel activity as a function of Mg²⁺ (n = 3 different perfusions from two separate bilayers, solid circles). The superimposed dotted curve is the Hill fit (n = 8) from Fig. 3 B for comparison.

DISCUSSION

Calcium-activated K⁺ channels are essential players in cell physiology, as they link intracellular signaling with the electrical properties of the membrane. The mechanism of channel modulation by Ca²⁺ has been studied in detail for eukaryotic Ca²⁺-activated K⁺ channels (BK and SK channels) but an important piece of the puzzle is still missing: structural information. The structure of MthK was postulated to be a model for the structure of BK channels and a starting point for understanding the mechanism of channel opening upon Ca²⁺ modulation. However, little functional information is actually available for MthK (Jiang et al., 2003). Here, we characterize in detail the gating of MthK channels and we describe the mechanism of Ca²⁺ modulation in the framework of the available structural information.

MthK and BK Channels: Functional Comparison

What are the similarities between MthK and BK channels? They are both potassium channels with a homologous pore region and a GYG signature sequence for potassium selectivity. The COOH-terminal cytoplasmic domain of both channels is composed of two RCK domains (identical in MthK, different in BK, but homologous between the two species; Jiang et al., 2001), and calcium favors channel opening in both channel types. However, while BK channels are activated by micromolar Ca²⁺ concentrations (Latorre, 1989), MthK channels do not respond until Ca²⁺ is raised to millimolar concentrations.

One of the most intriguing features of MthK is the very steep activation by Ca²⁺. We examined MthK activation as Ca²⁺ was raised from 0 mM (with added EDTA) to 10 mM. We found that the channel activity increased sharply between 3.5 and 5 mM Ca²⁺. This jump in channel activity was well described by a Hill coefficient of at least 8. The value was constrained by the number of Ca²⁺ ions present in the high resolution structure of the channel; eight Ca²⁺ ions were found in the MthK structure, two per functional subunit and one per RCK domain. This is the highest Hill coefficient found in any ligand-gated channel; for comparison, the largest Hill coefficient found for the Ca²⁺ activation of BK channels is 4–5 (Golowasch et al., 1986; McManus and Magleby, 1991; Cox et al., 1997; Nimigean and Magleby, 1999), for cyclic nucleotide activation of CNG channels it is 2–3 (Zagotta and Siegelbaum, 1996; Ruiz et al., 1999), and for Ca²⁺ activation in SK channels it is 2–4 (Kohler et al., 1996; Vergara et al., 1998).

What does this unusually high Hill coefficient mean for the mechanism of Ca²⁺ modulation of MthK channels? The simplest answer is that MthK almost never opens unless all eight Ca²⁺ binding sites are occupied. This mechanism is different from the Ca²⁺ activation of BK channels in which the channel can open in partially Ca²⁺-occupied states and the coupling between Ca²⁺ binding and channel opening, although strong, is not as strong as we observe with MthK (McManus and Magleby, 1991; Horrigan and Aldrich, 2002). An alternative to the above simple explanation is that the extreme steepness of the Ca²⁺ dose–response is due to multiple overlapping processes that lead to channel opening from closed/dormant/blocked states (i.e., Ca²⁺ activation plus one or more additional independent processes that modulate MthK channel gating). Inactivation was recently proposed to be the cause for the apparently low open probability of KcsA channels during steady-state gating (Cordero-Morales et al., 2006). However, it is not obvious that an inactivated state exists for MthK channels (which lack the glutamate, E71, proposed to be involved in KcsA inactivation), and, in the absence of supporting data for a more complex process, we favor the simpler mechanism described above for the origin of the steep Hill slope.

The apparent all-or-none Ca²⁺ activation mechanism for MthK is also supported by our kinetic analysis of the open and closed states with Ca²⁺. First, we found that MthK activity has a “bursty” appearance at the single channel level that we catalogued as two gating modes: slow (bursts and gaps between bursts) and fast gating (flickers within a burst). We found that the durations of the open and closed intervals within a burst (the components of fast gating) are Ca²⁺ independent and that the increase in Po with Ca²⁺ (>100-fold) comes mainly from the marked decrease of the durations of the gaps between bursts (40-fold) and to a lesser extent from the increase in the duration of bursts (two to threefold). Ca²⁺ affects only the slow gating of MthK by mainly altering the frequency of opening while the fast gating is Ca²⁺ independent. For BK channels, while Ca²⁺ similarly increases the frequency of openings, it also markedly increases the durations of the open intervals (McManus and Magleby, 1991).

Therefore, while BK and MthK appear similar on the surface, as they are both activated by Ca²⁺ and possess RCK Ca²⁺ binding domains, the details of the mechanism of Ca²⁺ activation differ between the two channels. This is not surprising, as the structure of the eukaryotic BK channel is likely to be more complex than that of the more primitive MthK. BK channels have an additional five transmembrane domains upstream of the pore region, while MthK has only the two transmembrane regions that form the pore. In addition, the RCK-containing large COOH terminus of BK channels also includes other functional domains as well as other Ca²⁺ binding structures/sites (Schreiber and Salkoff, 1997; Shi and Cui, 2001; Zhang et al., 2001; Bao et al., 2002; Xia et al., 2002).

A Modified Monod-Wyman-Changeux Model Describes MthK Ca²⁺ Gating

Using our kinetic data, we derived a qualitative model to describe the Ca²⁺ activation of MthK. This model must fulfill the following conditions: (a) the channel opens in 0 Ca²⁺ (Fig.1); (b) the fast gating in 0 Ca²⁺ is identical to the fast gating in saturating Ca²⁺ (Fig. 4, durations of opening and closings within a burst are Ca²⁺ independent), and (c) the channel opens more frequently in the presence of Ca²⁺, which increases the open probability ∼100-fold (Fig. 3). The purpose of this modeling effort is not to provide an exact kinetic treatment with precisely determined rate constants, but to show that a minimal allosteric model derived from our experimental findings (with structural constraints) can reasonably reproduce our data.

We tested several allosteric schemes based on the Monod-Wyman-Changeux model (MWC; Monod et al., 1965) that were shown to be appropriate for other ligand-gated channels (Cox et al., 1997; Li et al., 1997) and the proposed model in Scheme 1

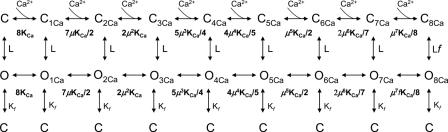is a minimal model that satisfies all the above conditions. There must be at least nine closed states and nine open states on the top two rows in order to satisfy the requirement of having a distinct kinetic state for each Ca²⁺ occupancy state (open and closed states corresponding to 0, 1, 2, 3, 4, 5, 6, 7, and 8 Ca²⁺ ions bound). These rows of states are connected by rate constants that are Ca²⁺ dependent and are involved in the slow Ca²⁺-dependent gating of MthK. The Ca²⁺ binding equilibrium constant is described by K_Ca (K_Ca = α[Ca²⁺]/β, where the forward [α] and backward [β] rate constants represent the intrinsic on and off rates of Ca²⁺ binding to both the closed and the open conformation of MthK. For simplicity, we assume that the Ca²⁺ binding constants are identical for the open and closed channel conformations (similar results are obtained if we assume they are different). L represents the equilibrium constant (L = k_o/k_c, where k_o and k_c represent the opening and closing rates, respectively, which define the vertical transitions between the top two rows). The vertical transitions between the top two rows are identical for each Ca²⁺-occupied conformation, with the exception of the eight Ca²⁺-bound conformation, which opens with a higher probability conferred by a factor f (to satisfy microscopic reversibility, f also multiplies the equilibrium constant of the final transition O_7Ca to O_8Ca). This maneuver, which distinguishes our proposed model from a classical MWC model ensures that the channel is favored to open mainly when all Ca²⁺ binding sites are occupied, as demanded by our results, and at the same time allows a nonzero open probability in the absence of Ca²⁺. The cooperativity coefficient (μ) allows each sequential Ca²⁺ binding event to occur with higher probability. In the absence of this cooperativity coefficient, we were unable to simulate a Ca²⁺ dose–response curve with Hill coefficients higher than 4. The closed states on the bottom row represent “flicker states.” This equilibrium is described by K_f (K_f = k_fo/k_fc, where k_fo and k_fc are rate constants that do not depend on Ca²⁺ and define the fast Ca²⁺-independent gating within the burst).

We were able to constrain most of these rates by examining our results; Table II lists the key parameters from our experiments that were used to determine the rate constants (“real” and “simu” denote kinetic parameters extracted from experimental and simulated data, respectively). Since the fast gating behavior is Ca²⁺ independent, k_f0 is determined by the inverse of the mean open time within the bursts (∼1.5 ms at −200 mV) and k_fc by the inverse of the mean closed time within the burst (∼0.4 ms at −200 mV). The rate of leaving the bursts (closing rate, k_c) was estimated as the inverse of the mean burst duration in 0 Ca²⁺ (∼50 ms at −200 mV). The values of these experimentally determined rate constants are in Table I.

TABLE I.

Rate Constant and Parameter Values Used To Simulate Single-channel Traces and the Dose–Response Curve in Fig. 7

α = 100 s−1	kfo = 2,500 s−1	kfc(0)= 6.5 s−1
β = 10,000 s−1	kfc = 750 s−1 (−200 mV)	k1 = 1
ko = 0.05 s−1	μ = 3	z = 0.62
kc = 20 s−1	f = 200	Q = 2.4 and 4.8 for −100 and −200 mV, respectively

K_Ca = α[Ca²⁺]/β, L = k_o/k_c, K_f = k_fo/k_fc, .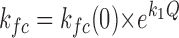

Thus, although the model in Scheme 1 may appear complex due to the total number of states presented (27), it is actually the simplest model that will satisfy all the structural and experimental constraints listed above. In addition, due to the fact that we were able to determine directly some of the microscopic rate constants from our kinetic analysis, the 27-state model in Scheme 1 has only five free parameters: the rates of Ca²⁺ association/dissociation (α and β), the opening rate k_o, the cooperativity factor, μ, and the factor f.

Using Scheme 1 and the constrained parameters, we fit by eye our data to obtain the rest of the parameters (Table I). We then simulated single channel traces (Fig.7, A and B) and a dose–response curve (Fig. 7 C) using the QuB software as detailed in Materials and Methods. The simulated data illustrates visually that Scheme 1 recapitulates the salient Ca²⁺-dependent gating features of MthK (compare simulated single-channel traces in Fig. 7 with the real traces in Figs. 1, 3, and 5). The simulated data was then analyzed to obtain the kinetic parameters (shown together for comparison with the real data in Table II). This comparison shows that using Scheme 1 we were able to capture some detailed characteristics of MthK gating as well. (a) The simulated mean open and closed times within bursts are Ca²⁺ independent and identical in values to real data. (b) Simulated burst durations are close in value to real data and change little with Ca²⁺. (c) There was a large change (>100-fold) in the durations of simulated gaps between bursts upon increasing Ca²⁺. Fig. 7 C illustrates that we also captured the steepness of the Ca²⁺ dose–response (curve in Fig. 7 C was fit with a Hill coefficient of 7.5) achieved by introducing the cooperativity coefficient, μ. A maximal open probability value <1 (0.3 in the case illustrated in Fig. 7 C) was achieved by both adjusting the open–closed equilibrium L and by varying the factor f, which multiplies the open–closed equilibrium. In Fig. 7 C, with the parameters listed in Table I, the open probability increased ∼100-fold from 0 to 5 mM Ca²⁺, as in our experimental data.

Figure 7.

The proposed kinetic scheme captures the main features of MthK Ca²⁺ and voltage-dependent gating. Simulated single-channel records using the kinetic model in Scheme 1 and the rate constants in Table I for two different Ca²⁺ concentrations (A), and two different voltages (B), for comparison with real data from Fig. 3 A and Fig. 5 A, respectively. Simulated data was filtered at 1–2 kHz and sampled at 10 kHz, just like the real data. (C) Predicted Ca²⁺ dose–response from the kinetic model in Scheme 1. Symbols represent Po values, mean ± SEM from four to seven distinct sets of 120 s of simulated single-channel data for each Ca²⁺ concentration. Solid line represents a Hill fit with Eq. 3 with n = 7.5 ± 0.5, K_d = 4 ± 0.04 mM, and P_o,max = 0.28.

Allosteric models similar to the modified MWC model proposed here for the Ca²⁺ gating of MthK have been used to describe Ca²⁺ gating in BK channels (McManus and Magleby, 1991; Cox et al., 1997; Rothberg and Magleby, 1998; Rothberg and Magleby, 2000; Horrigan and Aldrich, 2002). While our model is relatively simple, it captures the main features of MthK's Ca²⁺ activation.

Voltage-dependent Gating of MthK

For the classical voltage-gated channels (Shaker, BK channels), increasing membrane depolarization leads to a dramatic increase in the channel's open probability accompanied by an increase in the durations of the open intervals (Bezanilla and Stefani, 1994; Sigworth, 1994; Fedida and Hesketh, 2001). Since this large voltage dependence is caused by a voltage sensor domain contained within the first four to five transmembrane segments, which are absent in MthK, there is no surprise that voltage does not elicit a similar increase in open probability in MthK. At first glance, voltage appeared to only disrupt the flickering behavior of MthK channels, dramatically reducing the frequency of the short closing events within a burst. This has a strong visual impact by lengthening the amount of time the channel is open, while keeping the burst lengths constant. After further kinetic analysis, we found that the open probability also increases with voltage (to a lesser extent) but not because of the intraburst kinetics change. The open probability increased two to threefold for a 150-mV depolarization, due primarily to a twofold decrease in the durations of the gaps between bursts (Fig. 5). Thus it appears that two distinct mechanisms are responsible for the voltage effects observed here with MthK: a major one that decreases the flickering activity within the burst and a minor one that slightly increases the Po by decreasing the durations of the gaps between the burst. We will concentrate on the major voltage effect for the rest of the discussion.

Can the model described above in Scheme 1 be modified to also capture the major effect of voltage on fast gating? To do this, we assigned voltage dependence to the rate constants corresponding to the vertical flicker transitions (middle to bottom row) by assuming that only the closing rates depend on voltage (Eq. 5). We did not assign voltage dependence to the opening rates (k_fo), since the durations of the closing events within a burst do not vary with voltage (Fig. 5 E). We used z = 0.62, the value obtained from our analysis of the open duration dependence on voltage in Fig. 5 B. Using the parameters listed in Table I, we were able to simulate single-channel currents that capture the voltage effect on MthK gating (Fig. 7 B). As seen in Table II and Fig. 7 B, we succeeded in precisely capturing the increase in mean open time with depolarization by simply attaching voltage dependence (with a z value of 0.62) to the flicker closing rate. We did not attempt to capture the minor effect of voltage on the open probability using the above model.

Fast Gate and Slow Gate of MthK

What does this kinetic analysis tell us in terms of mechanism? If we examine the kinetic model proposed here, we notice that there is a clear separation between the states and transitions involved in the Ca²⁺-dependent slow gating and those involved in the voltage-dependent fast gating. This effect is not model dependent, as we showed that Ca²⁺ and voltage act on two distinct pathways because of the distinct open and closed interval populations they affect (Figs. 3 and 5).

We propose that there are two distinct gates underlying the gating of MthK. The first is the Ca²⁺-dependent gate proposed previously (Jiang et al., 2002b), located at the inverted teepee at the cytoplasmic end of the inner helices. It was suggested that when Ca²⁺ binds, the gating ring formed by eight RCK domains switches conformations and pulls on the linkers that connect the gating ring to the inner helices, mechanically opening the channel. A similar gate was proposed for the BK channels in light of recent findings that different lengths of linkers, at a homologous position to the MthK linker, affect the open–closed equilibrium in a predictable fashion for a “spring”-like model (Niu et al., 2004). This mechanism appears plausible for the slow gate of MthK channels, and our kinetic analysis is indifferent to the actual structural changes that occur upon opening the Ca²⁺ gate. However, our analysis puts some constraints on the intricacies of this mechanism. First, the Ca²⁺ gate does not open when exposed to Mg²⁺; it is a Ca²⁺ specific phenomenon. Second, voltage actually affects the slow gate as well (see above, the minor effect of voltage on the open probability). This may occur through a different mechanism than Ca²⁺, and not by modulating the binding of Ca²⁺ to open the gate if the voltage also increases the open probability and the duration of gaps between bursts in nominally 0 Ca²⁺ (we do not have sufficient data at this time to refute this possibility). Third, our very steep dose–response curve and the low affinity of the binding sites for Ca²⁺ suggest that this conformational change that “tugs” on the inner helices to open the channel is favored only when all eight Ca²⁺ ions are bound. Due to calcium's low affinity for MthK, it is also likely that the Ca²⁺ dissociation rate is very fast (as seen in Table I). If so, then in high Ca²⁺, entry into the all-eight-Ca²⁺-bound open states is favored, albeit predicted to be short lived due to the fast Ca²⁺ dissociation rate coupled with a low probability of opening in partially liganded states. However, once an open state is reached, a second gate comes into play, allowing the channel to flicker very fast between open and closed flickery states (bursting, see Scheme 1) during the time the channel has the first gate open.

The second gate is the flicker gate modulated by voltage and responsible for the fast gating behavior of MthK. No indication of such gate is visible in the structure of MthK (Jiang et al., 2002a). There are several potential candidates for an additional gate. One of them is the actual selectivity filter that was proposed to be the only gate for several other K⁺ channels (Flynn and Zagotta, 2001; Bruening-Wright et al., 2002; Kuo et al., 2003). Alternatively, these voltage-dependent flickers could represent open channel block by an external (molecules in the recording solution) or internal (protein structures/side chain residue of the channel proper) charged particle. The only external molecules present are K⁺, Cl⁻, Ca²⁺, Tris, and CTX. Tris, Cl⁻, Ca²⁺, and CTX can be disqualified from the race since the first one is uncharged, the second one is an anion that should not be able to get near the pore, and for the last two, recordings in the absence and presence of either (Figs. 1 and 2) show identical flickering behavior. That leaves K⁺ as a viable cause for the generation of fast gating behavior. Precedents exist for rapid flickery block by permeant ions in CFTR channels (Linsdell and Hanrahan, 1996).

Other possibilities include block by a flexible charged amino acid side chain that is favored to protrude into the pore when the gating ring undergoes a conformational change. We cannot identify the potential culprit side chain due to the fact that the resolution of the channel pore was only high enough to allow backbone tracing of MthK while the amino acid side chains were not resolved (Jiang et al., 2002a).

Conclusion

MthK is a low affinity Ca²⁺-gated and voltage-gated inwardly rectifying potassium channel. The MthK Ca²⁺ dose–response curve has an impressively large Hill coefficient, which suggests that the channel opens mainly when all eight sites are bound by Ca²⁺. MthK has two distinct gating modes: the slow gate, affected by Ca²⁺, and a fast gate (flickers), affected by voltage. The increase in MthK activity with Ca²⁺ is due mainly to an increase in the frequency of channel opening. While voltage does not lead to a significant increase in channel activity, it dramatically alters the frequency of flickering closures within a burst. We proposed a modified MWC kinetic model that approximates the main gating features of MthK.