Abstract
CRAC (calcium release-activated Ca2+) channels attain an extremely high selectivity for Ca2+ from the blockade of monovalent cation permeation by Ca2+ within the pore. In this study we have exploited the blockade by Ca2+ to examine the size of the CRAC channel pore, its unitary conductance for monovalent cations, and channel gating properties. The permeation of a series of methylammonium compounds under divalent cation-free conditions indicates a minimum pore diameter of 3.9 Å. Extracellular Ca2+ blocks monovalent flux in a manner consistent with a single intrapore site having an effective Ki of 20 μM at −110 mV. Block increases with hyperpolarization, but declines below −100 mV, most likely due to permeation of Ca2+. Analysis of monovalent current noise induced by increasing levels of block by extracellular Ca2+ indicates an open probability (Po) of ∼0.8. By extrapolating the variance/mean current ratio to the condition of full blockade (Po = 0), we estimate a unitary conductance of ∼0.7 pS for Na+, or three to fourfold higher than previous estimates. Removal of extracellular Ca2+ causes the monovalent current to decline over tens of seconds, a process termed depotentiation. The declining current appears to result from a reduction in the number of active channels without a change in their high open probability. Similarly, low concentrations of 2-APB that enhance ICRAC increase the number of active channels while open probability remains constant. We conclude that the slow regulation of whole-cell CRAC current by store depletion, extracellular Ca2+, and 2-APB involves the stepwise recruitment of silent channels to a high open-probability gating mode.
INTRODUCTION
In hematopoietic cells such as T cells, B cells, and mast cells, stimulation of surface receptors coupled to the generation of inositol 1,4,5-trisphosphate (IP3) promotes depletion of Ca2+ from the ER and the consequent activation of calcium release-activated Ca2+ (CRAC) channels (Lewis, 1999; Parekh and Putney, 2005). The resulting influx of Ca2+ through these store-operated channels mediates essential functions including the expression and repression of numerous genes during T cell activation (Feske et al., 2001), the secretion of histamine and serotonin from mast cells during allergic reactions, and the exocytosis of lytic granules from cytotoxic T cells during target cell killing (for reviews see Lewis, 2001; Parekh and Putney, 2005).
Much work has been done to define the biophysical and pharmacological properties of the CRAC channel, both to understand its function and to aid in testing candidates for the CRAC channel gene (Prakriya and Lewis, 2003). However, a number of uncertainties persist about the permeation and gating properties of the CRAC channel, due in large part to the difficulties of studying a channel with a conductance more than 100 times smaller than most other Ca2+-permeable channels. These uncertainties include the dimensions of the pore, the characteristics of Ca2+-dependent block, and the channel's unitary conductance and gating properties.
The CRAC channel is among the most Ca2+-selective channels known, and like voltage-gated Ca2+ (CaV) channels discriminates by >1,000:1 for Ca2+ over monovalent cations (Hoth and Penner, 1993; Hoth, 1995). Like CaV channels (Sather and McCleskey, 2003), it appears to achieve this selectivity by electrostatic repulsion of monovalent ions by Ca2+ bound within the pore. When all divalent cations are removed from the extracellular side (divalent-free [DVF] conditions), CRAC channels freely conduct a variety of small monovalent cations (Hoth and Penner, 1993; Lepple-Wienhues and Cahalan, 1996; Bakowski and Parekh, 2002; Prakriya and Lewis, 2002), and the potency of extracellular Ca2+ to block this monovalent flux increases with hyperpolarization (Bakowski and Parekh, 2002). Estimates of the dimensions of the narrowest region of the pore by measurements of the permeabilities of various monovalent cations have yielded varied results, ranging from 3.2–5.5 Å in RBL cells (Bakowski and Parekh, 2002) to 6 Å in Jurkat cells (Kerschbaum and Cahalan, 1998). By comparison, the pore diameter of CaV channels is 6 Å (McCleskey and Almers, 1985). Given the wide range of these results, the possibility that the CRAC channel pore size may be cell type specific and the extent of its similarity to CaV channels remain open questions.
Another key characteristic of the CRAC channel is its extremely small conductance of <1 pS. Because ionic throughput is too low to detect single-channel currents, past studies have relied on noise analysis to estimate the unitary current amplitude. Nonstationary fluctuation analysis typically involves measuring an ensemble of responses to a repeated activating stimulus. Assuming a homogeneous population of a fixed number of independently gated channels, theory predicts a parabolic relation between the current variance and mean that can be used to estimate the number of channels, N, their unitary current amplitude, i, and changes in their open probability, Po (Neher and Stevens, 1977; Sigworth, 1980). However, for CRAC channels, noise analysis shows a linear variance/mean current relationship (Zweifach and Lewis, 1993; Prakriya and Lewis, 2002). A linear relationship can arise from changes in Po if Po is very low (≪1), but can also reflect changes in N independently of any change in Po (Jackson and Strange, 1995). This fundamental uncertainty severely limits the accuracy of estimates of the unitary conductance, the number of active channels in the cell, their open probability, and their mode of gating, all of which are important not only for understanding the biophysics of CRAC channels but their biological roles in the cell as well.
CRAC channel activity is regulated in multiple ways on a slow time scale of seconds to tens of seconds. The best-studied types of regulation include (a) activation in response to Ca2+ store depletion, and deactivation after store refilling; (b) Ca2+-dependent potentiation (CDP) of CRAC channel activity in store-depleted cells after the readdition of extracellular Ca2+ (Christian et al., 1996; Zweifach and Lewis, 1996) and the reverse process of depotentiation after removal of divalent cations (Lepple-Wienhues and Cahalan, 1996; Prakriya and Lewis, 2002); and (c) enhancement of channel activity by low doses of 2-APB (<5 μM), and inhibition by higher doses (>10 μM; Prakriya and Lewis, 2001). Little is known about the underlying molecular mechanisms of these processes, and the inability to estimate channel Po has severely confounded any clarification of the associated changes in gating. However, their similar slow kinetics raise the possibility that they may involve a common rate-limiting step that could offer insights into how CRAC channels respond to the depletion of intracellular Ca2+ stores.
In this study, we examined monovalent CRAC currents in Jurkat T cells to determine several critical properties of the CRAC channel such as pore diameter, block by extracellular Ca2+, unitary current, and gating. We describe the time- and voltage-dependent block of monovalent current by extracellular Ca2+ and use this to assess the Po of Na+-conducting CRAC channels. The Po of CRAC channels is surprisingly high (∼0.8), leading to a significant upward revision of the unitary conductance for Na+ to ∼0.7 pS. A new variance analysis of CRAC current during depotentiation and during enhancement by 2-APB shows that Po remains constant while N, the number of active channels, changes. These new results suggest that these slow changes in CRAC channel activity are affected through abrupt transitions of channels between a silent state and a highly active state.
MATERIALS AND METHODS
Cells
Jurkat E6.1 T cells were grown in a medium consisting of RPMI 1640, supplemented with 10% FCS, 2 mM glutamine, 50 U/ml penicillin, and 50 μg/ml streptomycin. The cells were maintained in log-phase growth at 37°C in 6% CO2.
Solutions and Chemicals
The standard extracellular Ringer's solution contained (in mM) 130 NaCl, 4.5 KCl, 20 CaCl2, 1 MgCl2, 10 d-glucose, and 5 Na-HEPES (pH 7.4). Ca2+-free Ringer's was prepared by substituting 1 mM EGTA + 2 mM MgCl2 + 20 mM NaCl for CaCl2. The standard DVF Ringer's solutions contained (in mM) 155 Na methanesulfonate, 10 HEDTA, 1 EDTA, and 10 HEPES (pH 7.4). For experiments examining block of Na+-ICRAC by Ca2+, CaCl2 was added to the standard DVF solution at the appropriate amount calculated from the MaxChelator software program (WEBMAXC 2.10, available at http://www.stanford.edu/∼cpatton/webmaxc2.htm). In some experiments, the following organic compounds were substituted for Na methanesulfonate in the external solution: hydroxylamine HCl (NH2OH-HCl), hydrazine HCl (NH2NH2-HCl), methylamine HCl (CH3NH2-HCl), dimethylamine HCl ((CH3)2NH-HCl), trimethylamine HCl ((CH3)3N-HCl), and tetramethylammonium chloride ((CH3)4NCl). These chemicals were purchased from Sigma-Aldrich. pH was adjusted to 7.4 with N-methyl d-glucamine (NMDG) except in the case of hydrazine HCl (pH 6.4) and hydroxylamine HCl (pH 6.2), which were studied at acidic pH to increase the ionized concentration of the test ion. The standard internal solution contained (in mM) 150 Cs aspartate, 8 mM MgCl2, 10 BAPTA, and 10 Cs-HEPES (pH 7.2). Where indicated, Na+ was substituted for Cs+ in the internal solution.
Stock solutions of thapsigargin (Sigma-Aldrich) were prepared in DMSO at a concentration of 1 mM. All solutions were applied using a multi-barrel local perfusion pipette with a common delivery port. The time for 90% solution exchange was measured to be <1 s.
Patch-clamp Measurements
Patch-clamp experiments were conducted in the standard whole-cell recording configuration at 22–25°C using an Axopatch 200 amplifier (Axon Instruments) interfaced to an ITC-16 input/output board (Instrutech) and a Macintosh G3 computer. Recording electrodes were pulled from 100-μl pipettes coated with Sylgard and fire polished to a final resistance of 2–5 MΩ. Stimulation and data acquisition and analysis were performed using in-house routines developed on the Igor Pro platform (Wavemetrics). The holding potential was +20 mV unless otherwise indicated. Two types of stimuli were most commonly used: (1) a 100-ms step to −110 mV followed by a 100-ms ramp from −110 to +90 mV applied every 1.3 s, and (2) 200-ms sweeps collected every 0.3 s at a constant potential of −110 mV. Currents were filtered at 2 kHz with a 4-pole Bessel filter and sampled at 5 kHz. All voltages were corrected for the liquid junction potentials of the pipette solution relative to Ringer's in the bath (−10 mV) and of the bath DVF solution relative to Ringer's in the bath-ground agar bridge (+5 mV).
Noise Analysis
Noise measurements were performed on currents recorded by two methods. For variance/mean analysis, 200-ms sweeps were acquired at the rate of 3–4 Hz at a holding potential of −110 mV, digitized at 5 kHz, low-pass filtered using a 2-kHz Bessel filter, and recorded directly to hard disk. The mean current and variance were calculated from each sweep. For spectral analysis, current at a holding potential was recorded continuously at 32 kHz bandwidth to digital audio tape (Sony DTC-700 modified for DC coupling). The tape data were then low-pass filtered at 2 kHz (8-pole filter; Frequency Devices) and digitized at 5 kHz for analysis. Power spectra were computed from 2048-point sweeps using a Hanning window and averaged from 10–20 sweeps. Removal of the DC component and slowly varying drift in the data was achieved by subtracting from each trace a fourth-order polynomial fit. Application of sine wave inputs at 0.1–500 Hz confirmed that this method did not affect power at frequencies >1 Hz.
Data Analysis
Unless noted otherwise, all data were corrected for leak currents collected in either Ca2+-free Ringer's solution or in 2 mM Ca2+ + 5 μM La3+, and averaged results are presented as the mean value ± SEM. All curve fitting was done by least-squares methods using built-in functions in Igor Pro 5.0.
Relative permeabilities of the various cations were calculated from changes in the reversal potential using the Goldman-Hodgkin-Katz (GHK) voltage equation:
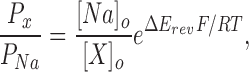 |
(1) |
where R, T, and F have their usual meanings, and Px and PNa are the permeabilities of the test ion and Na+, respectively, [X] and [Na] are the ionic concentrations, and ΔErev is the shift in reversal potential when the test cation is exchanged for Na+.
To analyze the voltage dependence of block of Na+-ICRAC by Ca2+ o, two models were considered. The first was the traditional Woodhull model (Woodhull, 1973), which assumes that the voltage dependence of block arises entirely from the movement of the charged blocker to its binding site in the pore. In this model, the voltage dependences of the association and dissociation rates are assumed to be equal and opposite and are determined solely by the valence of the blocker and the location of the binding site within the electric field. In an alternative model described by Guo and Lu (2000), these assumptions are relaxed, and association and dissociation rates are allowed to have different voltage dependences to account for movement of permeant ions that are associated with the blocker binding to its site. This model does not specify the location of the binding site within the field, but instead expresses voltage dependence in terms of an apparent valence, an empirical factor that encompasses the effects of blocker valence, binding site location, and movements of permeant ions within the field.
In both models, Ca2+ binds to a site within the pore according to the reaction:
 |
where Ch is the channel concentration, Ca2+ o and Ca2+ i are the extracellular and intracellular Ca2+ concentrations, k 1 and k −1 are the binding and unbinding rates from the extracellular side, k 2 is the unbinding rate from the intracellular side, and each zi represents the apparent valence for the corresponding transition. We assumed that block from the intracellular compartment is negligible due to nM intracellular Ca2+ concentrations.
In the Woodhull model, z 1 = z −1 = zδ and z 2 = z(1 − δ), where z is the blocker valence and δ is the fractional electrical distance through the membrane field. With these assumptions, the fraction of unblocked channels, I/I 0 is given by the relationship (Woodhull, 1973):
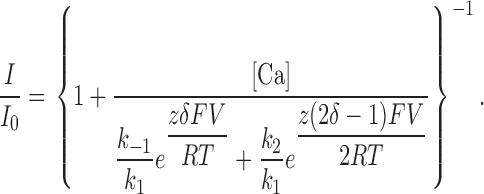 |
(2) |
In the second model, the fraction of unblocked current is given by (Guo and Lu, 2000):
 |
(3) |
where K 1 = k −1 /k 1 is the equilibrium dissociation constant at 0 applied voltage, and Z 1 and zi are the apparent valences. Z 1 (=z 1 + z −1) provides a measure of the overall voltage dependence of Ca2+ block and arises from the movement of the charged blocker (Ca2+) within the field as well as the possible displacement of permeant ions (Na+) within the pore. k 2 /k −1 is the ratio of the rates of Ca2+ escaping into the cytoplasm vs. returning to the extracellular solution from the pore, and thus provides a measure of Ca2+ permeation. The quantities k 2 /k −1, and z −1 + z 2 were treated as single adjustable parameters for fitting the data.
Online Supplemental Material
The online supplemental material (Figs. S1–S3, available at http://www.jgp.org/cgi/content/full/jgp.200609588/DC1) contains additional information on the kinetics and extent of Ca2+ block of Na+-ICRAC, and on variance changes induced by partial blockade of Na+-ICRAC by extracellular Ca2+ and Mg2+.
RESULTS
Sizing the Pore of the CRAC Channel with Monovalent Cations
To estimate the narrowest region of the CRAC channel pore, we examined its permeability to ammonium ion derivatives of increasing size. CRAC channels readily conduct monovalent cations in the absence of extracellular divalent cations (Lepple-Wienhues and Cahalan, 1996; Bakowski and Parekh, 2002; Hermosura et al., 2002; Kozak et al., 2002; Prakriya and Lewis, 2002). In the example shown in Fig. 1 A, a Jurkat T cell was treated with TG (1 μM) in Ca2+-free solution 5–10 min before seal formation to deplete stores and activate CRAC channels. Subsequent exposure to 20 mM Ca2+ o causes ICRAC to appear over ∼10 s due to Ca2+-dependent potentiation, or CDP (Christian et al., 1996; Zweifach and Lewis, 1996; Su et al., 2004). Perfusion with DVF solution elicits a large, transient Na+ current that then declines by 80–90% over tens of seconds due to the reversal of CDP, or depotentiation (Lepple-Wienhues and Cahalan, 1996; Hermosura et al., 2002; Kozak et al., 2002; Prakriya and Lewis, 2002).
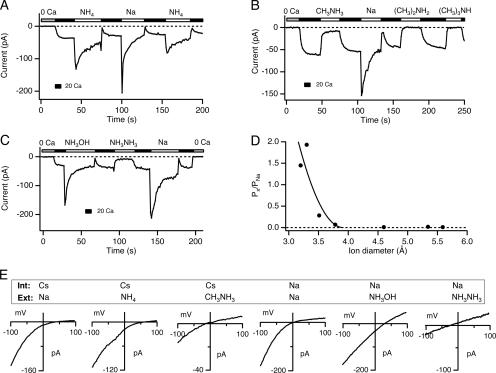
Figure 1.
Estimating the diameter of the CRAC channel pore. In A–C, cells were pretreated with 1 μM TG to deplete stores and activate CRAC channels. Leak-corrected current at −110 mV is plotted against time as the extracellular solution is periodically switched between 20 mM Ca2+ and DVF solutions containing the monovalent cation shown above the bars. (A and B) Permeation of ammonium, methylammonium, dimethylammonium, and trimethylammonium. Methylammonium carries a small current, but the larger derivatives fail to carry significant current through CRAC channels. (C) Permeation of hydroxylammonium and hydrazine. Hydroxylammonium is highly permeant through CRAC channels, whereas hydrazine is poorly permeant. (D) The permeabilities of NH4 + and its methylated derivates relative to Na+ are plotted against the size of each cation. The solid line is a least-squares fit to Eq. 4 with dpore = 3.9 Å and k = 54. (E) I-V relations of monovalent currents through CRAC channels collected near the peak of the currents in A–C. The internal and external cations are indicated in each panel. Holding potential = +20 mV.
The conductances and permeabilities of various ammonium ions were determined after substitution for Na+ in the DVF solution. NH4 + is highly permeant; both the NH4 + current amplitude and reversal potential are similar to those measured with extracellular Na+ (Fig. 1, A and E). In contrast, of the methylated ammonium derivatives, only methylammonium conducted current, which at steady state was ∼11% of the steady-state Na+ current (Fig. 1, B and E), while dimethylammonium, trimethylammonium, and tetramethylammonium failed to carry any measurable current. For the permeant cations, shifts in the reversal potential relative to Na+ current were used to measure relative permeability ratios (Fig. 1 E). Hydroxylammonium had the highest relative permeability (Px/PNa = 1.93 ± 0.14), while hydrazine, which is only slightly larger than methylammonium, was only weakly permeant (Px/PNa ∼ 0.28; Fig. 1 C). Table I summarizes the relative conductances, permeabilities, and diameters of all the cations tested.
TABLE I.
Relative Permeabilities and Conductances of Ammonium Derivatives
| Ion | Diameter(Å) | Px/PNa | n | Chord conductance (pS) | Conductance ratio (γx/γNa) |
|---|---|---|---|---|---|
| Ammonium (NH4 +) | 3.20 | 1.45 ± 0.4 | 6 | 477 ± 85 | 0.52 |
| Methylammonium (CH3NH3 +) | 3.78 | 0.07 ± 0.03 | 7 | 177 ± 35 | 0.19 |
| Dimethylammonium ((CH3)2NH2 +) | 4.60 | 0.01 ± 0.001 | 3 | ||
| Trimethylammonium ((CH3)3NH+) | 5.34 | 0.021 | 1 | ||
| Tetramethylammonium ((CH3)4N+) | 5.59 | 0.009 ± 0.003 | 3 | ||
| Hydroxylammonium (NH3OH+) | 3.30 | 1.93 ± 0.14 | 7 | 717 ± 147 | 0.79 |
| Hydrazine (NH3NH3 +) | 3.51 | 0.28 ± 0.02 | 5 | 332 ± 64 | 0.36 |
Px/PNa was calculated from the GHK equation (Eq. 1) by measuring changes in reversal potential of currents after substitution of the test cation for extracellular Na+. Ion diameters were estimated from space-filling Corey-Pauling-Koltum (CPK) models (Liu and Adams, 2001). Chord conductance was determined from the measurement of the leak-subtracted peak current after substitution of Ca2+ o with the test cation and the leak-subtracted reversal potential. Leak-subtracted currents generated by dimethylammonium, trimethylammonium, and tetramethylammanium were indistinguishable from application of a Ca2+-free medium (0 Ca + 1 mM EGTA) and were therefore not included for the chord conductance measurements. Note that the chord conductance for hydroxylammonium and hydrazine is likely underestimated as these currents were measured at acidic pH (to increase ion dissociation, see Materials and methods), which is known to inhibit CRAC current (Malayev and Nelson, 1995).
Ion permeability ratios can be used to estimate the dimensions of the narrowest region of the ion conduction pathway. Assuming that the permeability of an ion is limited primarily by steric hindrance rather than by electrostatic or chemical interactions with the walls of the pore, then the relative permeability is described by a hydrodynamic relationship:
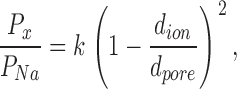 |
(4) |
where Px/PNa is the permeability ratio, k is a proportionality constant, dion is the diameter of the ion, and dpore is the pore diameter (Dwyer et al., 1980; Burnashev et al., 1996). Fitting this relation to the plot of the permeability ratio against ion diameter gives an estimate for dpore of 3.9 Å (Fig. 1 D).
Voltage-dependent Block of Monovalent Permeation by Ca2+
To characterize the Ca2+-dependent blockade of monovalent currents through CRAC channels, cells with depleted stores were exposed to Mg2+-free solution with 0–60 μM Ca2+, and current was recorded at a constant holding potential of −110 mV (Fig. 2 A). In each case, switching from 20 mM Ca2+ to the low-Ca2+ solutions elicited an initial increase in current carried by Na+ followed by depotentiation. During exposure to the low-Ca2+ solutions, the current amplitude is determined by the degree of Ca2+ block as well as by depotentiation, whose rate and extent is Ca2+ dependent (Su et al., 2004; unpublished data). Therefore, to measure the blocking effect of Ca2+ in isolation, we compared the maximum current level reached 1 s after switching to each solution, before depotentiation had a chance to develop. The results, plotted against [Ca2+]o in Fig. 2 B, are well fitted by a single-binding site model with a Ki of 19.6 μM and a Hill coefficient of 1.2.
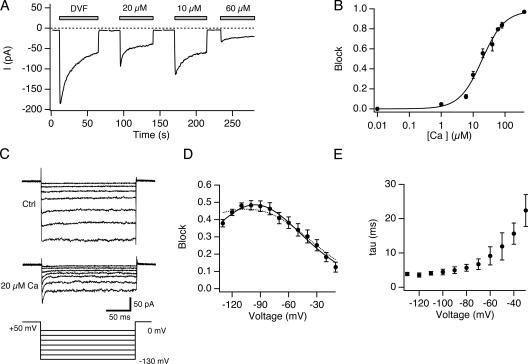
Figure 2.
Voltage-dependent blockade of Na+-ICRAC by Ca2+ o. (A) Inhibition of Na+-ICRAC by Ca2+ o. A TG-treated cell was held at a constant holding potential of −110 mV and 200-ms sweeps were collected at 3 Hz. The average current during each sweep is plotted against time. 20 mM Ca2+ o was applied between the bars. (B) Concentration dependence of Na+-ICRAC block by Ca2+ o. Block was quantified by measuring the Na+ current immediately after application of DVF solution containing the indicated [Ca2+]o as shown in A. The solid line is a least-squares fit of the Hill equation, block = 1/[1 + (Ki/[Ca])n] with Ki = 19.6 μM and n = 1.2. Holding potential = −110 mV. Each point is the mean of three to seven measurements. (C) Effects of 20 μM Ca2+ o on Na+ currents during voltage steps. After full depotentiation of the Na+ current in either DVF or 20 μM Ca2+ o, 200-ms voltage steps from −130 to 0 mV were applied from a holding potential of +50 mV. Note the time-dependent reduction in Na+ current in the presence of 20 μM Ca2+ o immediately after the voltage step. All currents were leak subtracted with a family of traces collected in 2 mM Ca2+ o + 5 μM La3+. (D) Voltage dependence of block by Ca2+ o. Block was quantified from experiments like that in C, as [1 − Iss/Ipeak], where Ipeak and Iss are the current in 20 μM Ca2+ o at the start and end of the voltage pulse, respectively. Ipeak was determined by fitting the current decay with a single exponential function and extrapolating back to the start of the voltage pulse. The solid line is a least-squares fit to Eq. 3 with Z 1 = 0.71, K 1 = 146 μM, z −1+ z 2 = 1.4, and k 2 /k −1 = 0.005. The dashed line is the best fit of the Woodull model (Eq. 2) with z = 2, δ = 0.36, k −1 /k 1 = 123 μM, and k 2 /k 1 = 5.95 μM. (E) Time constant of block obtained by fitting the current decay in the presence of the blocker (20 μM Ca2+ o) with a single exponential function. In D and E each point is the mean from four cells.
We quantified the voltage dependence of block by measuring Na+ CRAC currents (Na+-ICRAC) over a range of voltages in 0 or 20 μM Ca2+. In this case, to avoid complications from depotentiation, we measured currents after they had reached a steady value. Previous work has shown that the steady-state Na+ current under these conditions has the same reversal potential, ionic selectivity, and pharmacological sensitivity to 2-APB and SKF 96365 as the initial peak current, confirming that it represents Na+ flux through CRAC channels (Prakriya and Lewis, 2002). During voltage steps ranging from −130 to 0 mV, Na+ currents in DVF were largely time invariant (Fig. 2 C). However, Na+ currents in the presence of 20 μM Ca2+ o showed a time-dependent decline to a constant level in response to hyperpolarizing steps (Fig. 2 C). The decline at each voltage followed a single-exponential time course that accelerated with hyperpolarization (Fig. 2 E). In the example shown, peak currents in 20 μM Ca2+ were additionally reduced by a factor of 0.3 at all test voltages relative to the DVF conditions. This effect appeared to result from rundown of the current that occurred between the data collection in DVF solution and 20 μM Ca2+. In other experiments where cells were quickly changed between the two solutions, no difference in peak currents was seen (Fig. S1 A, available at http://www.jgp.org/cgi/content/full/jgp.200609588/DC1).
The data suggest that the time-dependent decline in Na+-ICRAC in Fig. 2 C reflects the development of steady-state block by Ca2+ entering the CRAC channel pore. The magnitude of block was measured by (1-Iss/Ipk), where Iss and Ipk are the steady-state and extrapolated peak currents during each voltage step. The results, plotted for four cells in Fig. 2 D, show voltage-dependent blockade that increases with hyperpolarization, reaching a peak at ∼−100 mV and declining slightly at more negative potentials. The relief of block at the most negative potentials is consistent with the exit of Ca2+ into the cytoplasm due to electrostatic pull on the ion (“punchthrough”). Importantly, the inhibition caused by 20 μM Ca2+ during the −110 mV step (48 ± 1.6%, n = 4; Fig. 2 D) agrees closely with the block measured from peak currents at a constant potential of −110 mV without depotentiation (55 ± 4%, n = 4; Fig. 2 B).
Our attempts to describe the voltage dependence of block of Na+-ICRAC by Ca2+ o using the commonly employed Woodhull model (Woodhull, 1973) (see Materials and methods) were unsuccessful; specifically, the model failed to satisfactorily account for the relief of block occurring at negative voltages (Fig. 2 D, dashed line). These shortcomings of the Woodhull model suggest that key assumptions of the model, such as assigning all of the voltage dependence to the movement of Ca2+ to its binding site and assuming equal and opposite voltage dependences for the association and dissociation rates, are not valid for the CRAC channel. However, a model that incorporates a permeant blocker without specifying the location of the Ca2+ binding site within the pore (Guo and Lu, 2000) (see Materials and methods) accounted well for both the blockade of the Na+ current by Ca2+ as well its relief at negative voltages (Fig. 2 D). The key parameters extracted from the model, the apparent valence Z 1 and the dissociation constant at 0 applied voltage, K 1, were 0.71 and 146 μM, respectively. Z 1 provides an empirical measure of the voltage dependence of Ca2+ block and represents not only the movement of the charged blocker (Ca2+) within the field but also the possible displacement of permeant ions (Na+) within the pore (Nimigean and Miller, 2002).
The kinetics of block revealed in Fig. 2 (C and E) can give information about the entry and exit rates of Ca2+ from the blocking site. With a half-blocking concentration of 20 μM, the observed time constant of block is ∼4 ms at −110 mV (Fig. 2 E). Assuming that Ca2+ accesses the site from the extracellular side at a rate kon, and exits in both directions at a combined rate koff, then it follows that
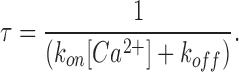 |
(5) |
The fraction of channels that are blocked is given by:
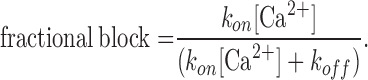 |
(6) |
Substituting the measured values of 4 ms for τ and 0.5 for fractional block (20 μM Ca2+, −110 mV) in Eqs. 5 and 6, we get koff = 125 s−1 and kon = 6.3 × 106 M−1s−1.
Noise Analysis of Na∼-CRAC Current During Depotentiation
A key property of the CRAC channel pore is its extremely small unitary conductance, which even under divalent-free conditions is too small to produce detectable single-channel currents. In previous studies, the unitary current amplitude was estimated from the changes in current noise that accompany changes in the whole-cell CRAC current (Zweifach and Lewis, 1993; Lepple-Wienhues and Cahalan, 1996; Prakriya and Lewis, 2002). Typically, nonstationary noise analysis is done by activating a constant number of independent channels (N) repeatedly by the same stimulus, and for each time point in the response calculating the mean of the ensemble of macroscopic currents (I) and the variance around the mean (σ2). Assuming stochastic transitions between a closed level and a single open level (current amplitude i), the following relations apply (Sigworth, 1980):
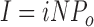 |
(7) |
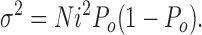 |
(8) |
N and i are generally assumed to be constant, so that the macroscopic current changes due to changes in the channels' open probability, Po (Eq. 7). Variance and Po are related by a parabolic relationship, with variance reaching a maximum when Po is 0.5 (Eq. 8). Substitution for Po in Eq. 8 yields
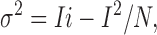 |
(9) |
from which the unitary current i can be derived simply by fitting a parabola to a plot of σ2 vs. I. Finally, combining Eqs. 7 and 9 yields
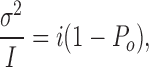 |
(10) |
which shows that the slope of the σ2/I plot approaches i when Po approaches 0.
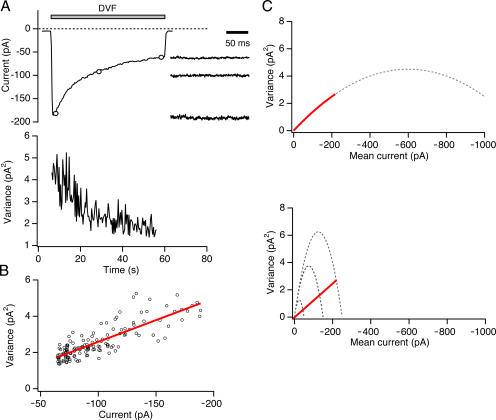
Nonstationary noise analysis was originally applied to Na+ channels that could be activated on a milliseconds time scale by repetitive voltage-clamp depolarizations (Sigworth, 1980). Unfortunately, CRAC channel activity is controlled on a time scale of tens of seconds, precluding the collection of a large ensemble of current records from repetitive stimuli. An example is shown in Fig. 3 A, in which the Na+ CRAC current declines over 60 s due to depotentiation after removal of extracellular Ca2+. To extract microscopic channel properties in this case, the current is typically divided into a sequence of short segments during which the mean current is relatively constant (<2% change in 200 ms; Fig. 3 A, right). The current variance calculated from each sweep declines during depotentiation (Fig. 3 A, bottom), producing a linear relation between variance and mean current with a slope (σ2/I) of −24 fA (Fig. 3 B; average −23 ± 2 fA, n = 10 cells). This general approach has been applied to a number of different conditions, including CRAC channel activation and deactivation, depotentiation, and enhancement and inhibition by 2-APB (Zweifach and Lewis, 1993; Lepple-Wienhues and Cahalan, 1996; Prakriya and Lewis, 2002; Spassova et al., 2006). In each case, current variance varied linearly with mean current and not by the parabolic relationship predicted by Eq. 9.
Figure 3.
Variance declines linearly with mean current during Na+ current depotentiation. (A) After substitution of DVF solution for 20 mM Ca2+, the average value (top) and variance (bottom) of the Na+ current was measured from 200-ms sweeps collected every 0.3 s at a constant holding potential of −110 mV. Example sweeps at the time points indicated by circles are shown on an expanded time scale to the right. (B) Mean–variance analysis of Na+-ICRAC from the experiment shown in A. The data are well fit by a line with slope of −24 fA. (C) Two possible explanations for the linear variance–mean current relationship seen in A. Top, an approximately linear σ2/I slope (red line) can arise during depotentiation from a decline in Po if the initial Po ≪ 1. Bottom, alternatively, a linear decline in variance (red line) can result from a reduction of the number of active channels (N) with a constant Po (in this case, Po = 0.85). In the bottom graph, the dotted lines indicate the expected parabolic σ2/I relations with N = 2,500, 1,500, and 500 channels if Po were allowed to vary.
There are two possible interpretations of the linear σ2/I relation (Fig. 3 C). Assuming that macroscopic current changes arise from changes in Po, linearity implies that the Po of CRAC channels is always ≪1 and therefore the slope (σ2/I) can be used to estimate the unitary current, i (Eq. 10). Alternatively, a change in channel number, N, at any constant value of Po would also produce a linear variance/mean relation (Eq. 8 and Fig. 3 C). If this were the case, a range of variance/mean current slopes would be possible depending on the Po. As illustrated analytically in Eq. 10 and graphically in Fig. 3 C, this would lead to an underestimate of i by a factor of 1-Po. To properly interpret the linear σ2/I plot and distinguish between the two possibilities outlined above, it is critical to determine Po. In previous studies, Po was not known, and for simplicity was assumed to be low, while recognizing that this may underestimate the true value of i.
Active CRAC Channels Have a High Open Probability
The use of Ca2+ o as a fast CRAC channel blocker provided us with a tool to estimate Po (Fig. 4). If Po is low, increasing amounts of block should cause a linear decline in variance along with the current. By contrast, if Po > 0.5, increased block should trace out a parabolic σ2/I plot. In support of the second prediction, we found that as [Ca2+]o was increased up to 20 μM, the variance increased even as the current declined (Fig. 4 B; Fig. S2). On average, although the peak Na+ current amplitude was reduced by 52 ± 5% by 20 μM Ca2+, the current variance increased by 18 ± 8% (n = 5 cells), while further increases in [Ca2+]o caused a parallel decline in current and variance (Fig. 4 B; Fig. S2). Current variance increased in response to moderate levels of blockade for both the peak currents recorded before depotentiation (as in Fig. 4 B) and the steady-state Na+ current recorded after full depotentiation (Fig. S3 A). This behavior was not specific to Ca2+; partial blockade by 100 μM Mg2+ also increased the variance, whereas 400 μM Mg2+ reduced it (Fig. S3, C and D).
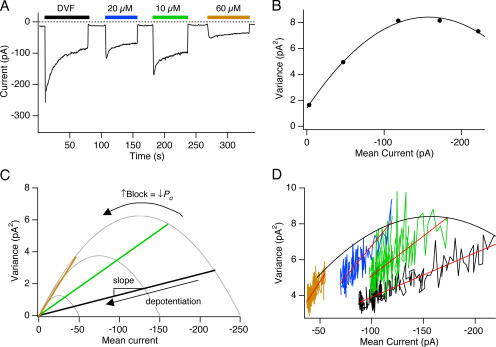
Figure 4.
Depotentiation of CRAC channels reflects a decrease in N at a constant high Po. (A) A TG-pretreated cell was held at a constant potential of −110 mV, and various [Ca2+]o indicated by the bars were applied to block the Na+ current. Each point in the plot shows the mean current during 200-ms sweeps. 20 mM Ca2+ o was applied between the bars. (B) The Po of CRAC channels is >0.5. The variance is plotted against mean current for traces collected 1 s after each solution exchange indicated by the bars in A. The point at 0 mean current shows the background variance of the leak current recorded with 2 mM Ca2+ + 5 μM La3+ in the bath. The solid line is a fit of Eq. 8 with i = 89 fA and N = 3515 channels. Given these values, the current in the absence of Ca2+ o (DVF) specifies a maximal Po of 0.7 (Eq. 7). (C) If depotentiation reflects a change in N at a constant Po, increasing block by Ca2+ will increase the slope of the σ2/I relationship. At the highest levels of block, the slope will approach the limiting slope of the parabola, providing an estimate of the unitary current. (D) Depotentiation occurs due to a change in N. Variance–mean current plots of the depotentiating Na+ current from the experiment in A. The plots for each [Ca2+]o were well fit by straight lines with slopes that progressively increased with block by Ca2+ o. The slopes are −21 fA (DVF), −44 fA (10 μM Ca2+ o), −70 fA (20 μM Ca2+ o), and −88 fA (60 μM Ca2+ o). Mean currents in D are not leak subtracted.
An increase in current variance with declining current indicates that the initial Po of unblocked CRAC channels must be >0.5. In fact, the σ2-I plot for the cell shown in Fig. 4 could be reasonably well fit with a parabola, giving a maximal Po of 0.7, N = 3515, and i = −0.09 pA (Fig. 4 B). These results demonstrate that previous assumptions of a very low Po were incorrect, and that the linear decrease in the σ2-I plot therefore cannot be explained by a simple decline in Po.
Depotentiation Reflects a Decline in the Number of Active Channels at a Constant Open Probability
The linear decline of variance with mean current observed during depotentiation could indicate a decline in the number of active channels, N, at a constant Po. As diagrammed in Fig. 4 C, this hypothesis predicts that small amounts of Ca2+ should increase the slope of the σ2/I relation during depotentiation in proportion to the extent of Ca2+-dependent block. The results shown in Fig. 4 D support this prediction; on average, the σ2/I slope increased from −23 ± 2 fA (n = 15 cells) in DVF to −107 ± 5 fA at 80 μM Ca2+ o (n = 5 cells). Power spectral analysis of the currents in DVF and in the presence of Ca2+ o, as well as of the background current in 2 mM Ca2+ + 5 μM La3+ indicated that the Na+ current power spectrum converges with the background spectrum at frequencies >1 kHz (unpublished data), confirming that no significant high frequency noise component was being missed under our experimental conditions. We conclude from these results that at every partially blocking concentration of Ca2+ o, depotentiation of the Na+ current occurs similarly through a gradual decline in channel number N at a constant value of Po.
2-APB Enhances ICRAC by Increasing the Number of Active Channels at Constant Po
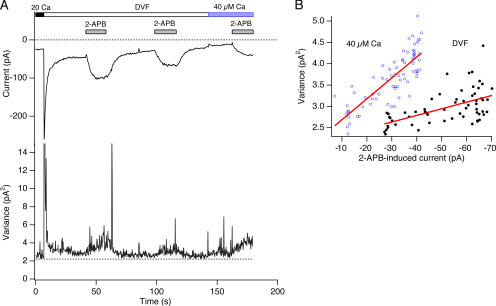
At low concentrations (2–5 μM), 2-APB strongly potentiates CRAC channels, increasing ICRAC amplitude by up to fivefold (Prakriya and Lewis, 2001). Under these conditions, current variance increases linearly with the mean current, raising the possibility that 2-APB exerts its effect by increasing N rather than Po. We tested this possibility by examining 2-APB effects in the presence of a partially blocking concentration of Ca2+. As shown in Fig. 5 A, 2-APB (5 μM) strongly enhanced steady-state Na+-ICRAC, increasing it from −29 ± 2 pA to −66 ± 3 pA (n = 5 cells). The current variance in DVF solution increased in proportion to the Na+ current, with an average σ2/I slope of −22 ± 3 fA (n = 4 cells) (Fig. 6), similar to the slope of the depotentiating Na+ current (−23 ± 2 fA). Application of 40 μM Ca2+ o caused the Na+ current variance to increase (Fig. 5 A), again indicating that the initial CRAC channel Po was >0.5. Importantly, 40 μM Ca2+ o also increased the σ2/I slope during 2-APB–induced enhancement of Na+-ICRAC to −70 ± 10 fA (n = 4 cells) (Fig. 5 B). This result suggests that 2-APB also modulates ICRAC by altering the number of activatable channels at a constant high Po, in this case by increasing N.
Figure 5.
2-APB–induced enhancement of CRAC current also results from a change in N rather than Po. (A) Mean and variance of CRAC current at a constant holding potential of −110 mV in DVF solution and in 2-APB (5 μM), measured during 200-ms sweeps. After depotentiation of the Na+ current in DVF solution, 2-APB was applied to enhance current through CRAC channels. At the indicated time points, 40 μM Ca2+ o was applied to partially block the Na+ current, and 2-APB was reapplied. (B) Mean–variance analysis of the 2-APB–induced Na+-CRAC current from the experiment in A. The σ2/I slope in DVF during enhancement by the second application of 2-APB was −16 fA. With 40 μM Ca2+ o present to partially block the Na+ current, the slope increased to −48 fA.
Figure 6.
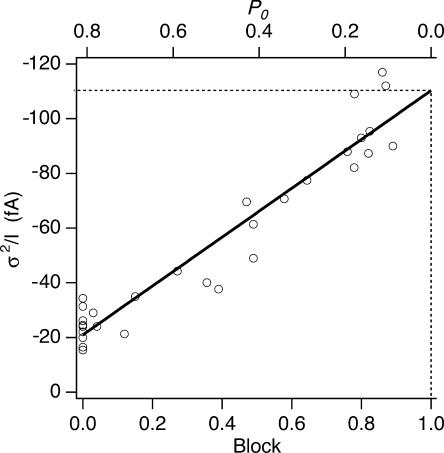
Estimating the unitary Na+ current through CRAC channels. The slope of the σ2/I relationship during depotentiation is plotted against fractional block by Ca2+ o. The data points were fit with the equation: σ2/I slope = (−89 fA) × Block − 21 fA. The plot indicates that at 100% block, the extrapolated single-channel current is −110 fA. The corresponding values of Po computed from the linear regression and Eq. 10 is shown on the top axis.
The Unitary Conductance of CRAC Channels with Na∼ as Current Carrier
As shown in Fig. 4 D, the σ2/I slope during depotentiation increased with the level of block by Ca2+. In the limit of complete block, Po = 0 and the unitary current i is given by σ2/I (Eq. 10). Fig. 6 plots the σ2/I slopes of the Na+ current during depotentiation against fractional block by 0–100 μM Ca2+ measured in individual cells. The data are well fit by a straight line, confirming the linear relation between the slope and extent of block. The linear regression indicates that the single-channel current at Po = 0 is −110 fA. With a reversal potential of +50 mV for the Na+ current (Fig. 1 E), this value corresponds to a single-channel chord conductance of 0.7 pS. The single-channel current can be used to infer the open probability of the channels in the absence of the blocker. With i = −110 fA, and an average σ2/I slope of −21.1 fA (from the linear regression) for the Na+ current in the absence of block, the average Po of Na+-conducting CRAC channels was computed from Eq. 10 to be 0.79 ± 0.02 (n = 10).
DISCUSSION
This study describes several key characteristics of the CRAC channel and its gating that significantly revise prior estimates of pore size, unitary conductance, and open probability. A surprising finding is that the open probability of active CRAC channels is high and appears to stay constant even when ICRAC is changing in response to different modulators. These results lead us to conclude that slow regulation of ICRAC under a variety of conditions reflect abrupt transitions between a silent and a highly active state rather than graded changes in Po. Together, these results further distinguish the CRAC channel from other types of Ca2+ channels and raise the possibility of a common rate-limiting step in its regulation by store depletion and several modulators.
Size of the CRAC Channel Pore
Previous studies of monovalent cation permeation through the CRAC channel have not yielded a consistent size for the pore. Based on the ability of TMA to carry significant current in the presence of low intracellular Mg2+, Kerschbaum and Cahalan (1998) concluded that the pore of the CRAC channel in Jurkat cells is physically large enough to accommodate ions up to ∼6 Å in diameter, similar to the pore of CaV channels. However, subsequent studies showed that these measurements were most likely contaminated by currents through Mg2+-inhibited cation (MIC) channels that were disinhibited by the removal of intracellular Mg2+ (Hermosura et al., 2002; Kozak et al., 2002; Prakriya and Lewis, 2002). Bakowski and Parekh (2002) examined monovalent permeation in RBL cells and found that the CRAC channel was large enough to conduct Cs+ but too small to conduct TMA, placing the CRAC channel pore size between 3.2 and 5.5 Å. They suggested that their smaller estimate of the pore size in RBL cells compared with Jurkat cells might reflect contamination of the Jurkat recordings by MIC currents, but did not rule out the possibility that CRAC channels in RBL and Jurkat T cells may also differ at the molecular level.
To size the CRAC channel pore, we measured the permeability of a sequence of cationic ammonium derivatives under conditions of high intracellular [Mg2+] that inhibit MIC channels. Ions larger than methylammonium such as TMA, trimethylammonium, and even dimethylammonium do not conduct at detectable levels, placing the pore size around 3.9 Å. Thus, the narrowest part of the CRAC channel is considerably smaller than either CaV or MIC channels. This finding argues against recent suggestions that CRAC currents in human T cells arise from L-type CaV channels operating in a voltage-independent mode (Stokes et al., 2004; Kotturi and Jefferies, 2005), as discussed below.
Ca2+ Block of Monovalent Current
We found that the Na+ current through CRAC channels is blocked by external Ca2+ in a voltage-dependent manner with a Ki of ∼20 μM at −110 mV. This apparent affinity is somewhat lower than described in previous studies. In RBL cells, Kis of 10 and 14 μM at −80 mV were reported (Bakowski and Parekh, 2002; Su et al., 2004) and in Jurkat cells the Ki was 4 μM at −80 mV (Lepple-Wienhues and Cahalan, 1996). The reasons for these discrepancies are not entirely clear, but in the Jurkat study (Lepple-Wienhues and Cahalan, 1996), only the “inactivating” component of current was measured, i.e., the difference between the peak and the fully depotentiated Na+ currents. Because Ca2+ reduces the extent of depotentiation (Su et al., 2004), the Ca2+ sensitivity of block was likely overestimated.
To avoid complications from depotentiation, we measured block by Ca2+ under two conditions. At a single voltage (−110 mV) we measured the peak Na+ current within 1 s of switching to DVF solution, before channels had a chance to depotentiate. We also measured the time-dependent decline of current during 200-ms voltage steps applied after depotentiation had reached completion; because depotentiation occurs over tens of seconds, it is not expected to change during each brief pulse. Importantly, both methods yielded a consistent value for the affinity of Ca2+ as a blocker.
Our results show that the steady-state block by Ca2+ is steeply voltage dependent in the range of 0 to −100 mV, with a slight relief of block occurring with further hyperpolarization (Fig. 2 D) that is likely to arise from the exit of bound Ca2+ into the cytosol. A previous study examined the voltage dependence of Ca2+ block of Na+-CRAC currents in RBL cells by analyzing brief (50-ms) ramp currents from −130 to +100 mV (Bakowski and Parekh, 2002). However, the time dependence of Ca2+ block during hyperpolarizations (Fig. 2 C) prevents a quantitative interpretation of ramp currents. To circumvent time-dependent effects, we measured the decline of currents from peak to steady state during voltage steps as shown in Fig. 2 (C and D). Bakowski and Parekh (2002) also reported time- and voltage-dependent decline of Na+-CRAC currents during hyperpolarization in the presence of 20 μM Ca2+ but did not interpret the results in terms of Ca2+ block. Here we conclude that the time-dependent decay arises from the entry of Ca2+ into the CRAC channel pore to block permeation by Na+ based on four lines of evidence. First, the degree of Na+ current decay caused by 20 μM Ca2+ during steps to −110 mV (∼0.48; Fig. 2 D) closely corresponds to the degree of block measured at a constant holding potential of −110 mV (∼0.5; Fig. 2 B). Second, the amplitude and kinetics of decay are voltage dependent (Fig. 2, D and E), consistent with a blocking site within the membrane field. Third, increasing concentrations of Ca2+ progressively reduce the time constant of current decay (Fig. S1 B), as expected if the Ca2+ binding rate contributes to the kinetics of reaching steady-state block (Eq. 5). Finally, a similar time-dependent decay is also elicited by Mg2+ at concentrations that are expected to block Na+ current by occluding the pore (unpublished data). Collectively, the most likely explanation is that the time-dependent decay of current reflects the time for Ca2+ to enter the pore and bind to a site that blocks permeation by Na+.
Pore Properties of the CRAC Channel Argue Against a Role for CaV1 Subunits
Several recent studies have suggested that L-type CaV1 channels operating in a voltage-independent gating mode may underlie store-operated Ca2+ influx in T cells (Stokes et al., 2004; Kotturi and Jefferies, 2005). Though CaV1 and CRAC channels both achieve an extremely high selectivity for Ca2+ by binding Ca2+ within the pore, our results reveal several significant differences in the properties of the two pores. First, the estimated CRAC pore size of 3.9 Å is much smaller than that of CaV channels (∼6 Å for CaV; McCleskey and Almers, 1985). The smaller pore size may help to explain the increased selectivity of CRAC channels for Na+ over Cs+ (PCs/PNa = 0.12 for CRAC, and 0.6 for L-type CaV channels; Hess et al., 1986). In CaV channels, hyperpolarization greatly increases the rate of Ca2+ exit from the blocking site into the cytoplasm (Lansman et al., 1986), reducing the efficacy of block at voltages negative to −30 mV. Although a qualitatively similar phenomenon occurs with CRAC channels (Fig. 2 D), it is much less pronounced; block increases with hyperpolarization and only begins to decline below ∼−100 mV. The smaller relief of block at hyperpolarized potentials suggests that blocking Ca2+ ions in CRAC channels may encounter a larger energy barrier along the permeation pathway that retards their escape into the cytoplasm, a factor that together with the smaller pore size may help explain the much smaller unitary conductance of CRAC channels.
Interestingly, the association rate of Ca2+ for its blocking site in the CRAC channel, 6.3 × 106 M−1s−1, is two orders of magnitude lower than the corresponding rate determined for L-type CaV channels from single-channel recordings (∼4.5 × 108 M−1s−1; Lansman et al., 1986). The latter rate is close to the diffusion-limited on rate. The much lower on rate of the CRAC channel suggests that access to the CRAC selectivity filter may be limited by a nonselective kinetic barrier to ion permeation between the filter and the extracellular end of the pore. The slow rate of entry of Ca2+ into the channel corresponds well with observations that the unitary conductance of CRAC channels is also two orders of magnitude lower than that of L-type channels (Hess et al., 1986). Together with the pore diameter, these findings highlight important differences between the pores of CRAC and CaV channels that are difficult to reconcile with the notion that CaV subunits line the pore of the CRAC channel.
Ca2+-dependent Noise Reveals a High-Po State and a Larger Unitary Conductance
Fluctuation analysis of CRAC currents is difficult because the slow time course of the current precludes collection of a large ensemble of responses. For this reason, variance and mean current are typically measured during a single response by analysis of short time intervals over which the current is quasi-stationary. In previous noise analysis studies, it was assumed that the number of CRAC channels (N) was constant and that changes in Po underlay changes in current amplitude (Zweifach and Lewis, 1993; Lepple-Wienhues and Cahalan, 1996; Prakriya and Lewis, 2002). To explain the linear relation between variance and mean current that was observed, Po was assumed to be low (≪1). In a previous study we attempted to test whether CRAC channels had a low Po by partially blocking the current with 1 μM Ca2+ o (Prakriya and Lewis, 2002). Under these conditions, although current declined by >50%, the σ2/I ratio did not increase, which led us to conclude that Po ≪ 0.5. In examining the discrepancy between those results and our current findings, we discovered that in the previous study, the pH had not been properly adjusted after addition of Ca2+ to DVF solution. As a result, the cells were exposed to acidic conditions, which are known to inhibit CRAC channel activity (Malayev and Nelson, 1995) and in principle could reduce the σ2/I ratio by alternate mechanisms, for example by reducing the unitary current i through protonation of the channel.
In this study, reversible blockade of monovalent CRAC current by Ca2+ has allowed us to make the first measurements of Po for the CRAC channel. Contrary to earlier assumptions, we find that Po is quite high (∼0.8). Because variance varies with the square of Po (Eq. 8), any significant change in Po during changes in ICRAC would introduce curvature into the σ2/I relation. Therefore, the linear decline of variance with mean current indicates that Po is constant as the current undergoes depotentiation, and that the current falls instead as a consequence of a decline in N. Two critical predictions of such a mechanism are that the σ2/I relation during depotentiation should be linear at all levels of Ca2+ block with a slope that varies linearly with the degree of block by Ca2+ (Eq. 10). Both of these predictions were satisfied (Fig. 6). We conclude that depotentiation occurs by a change in N without a change in Po.
The new information about Po and N leads to a more accurate estimate of the CRAC channel unitary conductance, which has fluctuated significantly in recent years. Direct single-channel measurements from T cells under Mg2+-free intracellular conditions led to a proposal of 40 pS for the monovalent CRAC current (Kerschbaum and Cahalan, 1999; Fomina et al., 2000), but these events were later shown to arise from contaminating MIC channels that were activated by the depletion of intracellular Mg2+ (Hermosura et al., 2002; Kozak et al., 2002; Prakriya and Lewis, 2002). A subsequent noise analysis study of isolated monovalent CRAC current during depotentiation yielded a unitary conductance of 0.2 pS given assumptions that N was constant and Po was ≪1 (Prakriya and Lewis, 2002). We now know these assumptions were incorrect, and Po is ∼0.8. The improved method described in this study, using progressive block by Ca2+ to extrapolate the σ2/I ratio toward the limit as Po approaches 0, indicates a single-channel conductance of 0.7 pS, three to fourfold larger than previously thought. The unitary current of −110 fA at −110 mV corresponds to a flux rate of 6.6 × 105 Na+/s, much faster than most ion carriers but compatible with a channel-type transport mechanism. This conductance may be sufficiently large to allow direct measurements of single-channel currents in patch recordings, potentially allowing studies of channel regulation and gating by more direct approaches. We estimate that there are at least 2,200 active CRAC channels per Jurkat cell, based on a peak Na+ current of −190 ± 25 pA (n = 11), a unitary current of −110 fA, and a Po of 0.8. Given that 2-APB increases the current amplitude two to fivefold by increasing N, the number of functional CRAC channels in Jurkat cells is most likely in the range of 5,000–10,000.
Is the Ca2+ current through single CRAC channels also three to fourfold larger than earlier noise-based estimates? Because the Ca2+ current is inactivated by Ca2+ (Hoth and Penner, 1993; Zweifach and Lewis, 1995), it is likely that Po is reduced when Ca2+ rather than Na+ is the current carrier. Given that the σ2/I slope underestimates the unitary current by a factor 1 − Po (Eq. 10), the error may therefore not be as severe as it is for the Na+ current. A rough estimate of the effect of inactivation on Po can be made from the effect of the holding potential on the Na+/Ca2+ current ratio after a switch from 20 mM Ca2+ to DVF solution. At +30 mV, inactivation is minimal and the ratio of the Na+/Ca2+ currents is ∼8 (Prakriya and Lewis, 2002). The current ratio increases to 22 ± 3 (n = 6) at a holding potential of −110 mV, at which Ca2+-dependent inactivation is manifest (Zweifach and Lewis, 1995). These results suggest that Po declines by ∼2/3 when Na+ is replaced by Ca2+ as the current carrier at −110 mV, in agreement with the steady-state inactivation of 0.6 measured during pulses to this voltage in 22 mM Ca2+ (Zweifach and Lewis, 1995). Thus, previous estimates of the unitary Ca2+ conductance of the CRAC channel may be underestimated by a factor of only 1/(1 − 0.8/3), or 1.4.
Implications for the Gating Mechanism of the CRAC Channel
What does a change in N mean in biological terms? N and Po are operationally defined as the number of channels contributing current during each sweep and their average open probability during the sweep. In general our data are consistent with abrupt transitions of channels between an inactive state and a highly active state with Po ∼ 0.8, both of which are much longer than the sampling period (200 ms).
It is interesting that all of the regulators of CRAC channel activity that have been studied by nonstationary fluctuation analysis produce a linear relation between variance and mean current. This phenomenon was first described for ICRAC activation by store depletion and inactivation by high levels of Ca2+ influx (Zweifach and Lewis, 1993). It is also seen during depotentiation in response to removal of extracellular Ca2+ (Prakriya and Lewis, 2002) and during enhancement by low doses of 2-APB (Prakriya and Lewis, 2002) and inactivation by high doses of 2-APB (Spassova et al., 2006). These similarities suggest that all of these processes may involve a common activation step in which channels transit abruptly between long-lived silent and highly active states. The rate at which channels transition between the two states would then determine the overall slow kinetics of ICRAC activation and modulation that are observed.
What could this common slow step be? In terms of current models of CRAC channel activation, it could represent the reversible insertion of active channels into the plasma membrane, the binding of the channel to proteins in the closely apposed ER membrane, or the action of a diffusible messenger with a slow reversal rate. Regardless of the precise mechanism, we propose that activation by store depletion, 2-APB enhancement, and Ca2+-dependent potentiation all operate by recruiting silent channels to a high-Po state. Of course, our results do not rule out other mechanisms of CRAC channel modulation, and the methods we have described may be useful for distinguishing which modulators affect the slow gating step as opposed to more frequent transitions that would be detectable as changes in Po during brief sweeps. Recently identified proteins critical for CRAC channel activation such as STIM1 (Liou et al., 2005; Roos et al., 2005) and Orai1/CRACM1 (Feske et al., 2006; Vig et al., 2006) may provide useful tools for identifying the physical basis for the silent and highly active states described here.
Supplemental Material
Acknowledgments
The authors thank members of the Lewis lab, Dr. Rick Aldrich and Dr. Zhe Lu for discussions during the work, and Dr. Merritt Maduke for a critical reading of the manuscript.
This work was supported by a post-doctoral fellowship from the Irvington Foundation for Immunological Research to M. Prakriya and grant GM45374 from the National Institutes of Health to R.S. Lewis.
Lawrence G. Palmer served as editor.
M. Prakriya's present address is Department of Molecular Pharmacology and Biological Chemistry, Northwestern University, Chicago, IL 60611.
Abbreviations used in this paper: CDP, Ca2+-dependent potentiation; CRAC, calcium release-activated Ca2+; MIC, Mg2+-inhibited cation; CaV, voltage-gated Ca2+; TG, thapsigargin; ICRAC, CRAC current; DVF, divalent free; Po, open probability; 2-APB, 2-aminoethyldiphenyl borate.
References
- Bakowski, D., and A.B. Parekh. 2002. Monovalent cation permeability and Ca2+ block of the store-operated Ca2+ current ICRAC in rat basophilic leukemia cells. Pflugers Arch. 443:892–902. [DOI] [PubMed] [Google Scholar]
- Burnashev, N., A. Villarroel, and B. Sakmann. 1996. Dimensions and ion selectivity of recombinant AMPA and kainate receptor channels and their dependence on Q/R site residues. J. Physiol. 496:165–173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christian, E.P., K.T. Spence, J.A. Togo, P.G. Dargis, and J. Patel. 1996. Calcium-dependent enhancement of depletion-activated calcium current in Jurkat T lymphocytes. J. Membr. Biol. 150:63–71. [DOI] [PubMed] [Google Scholar]
- Dwyer, T.M., D.J. Adams, and B. Hille. 1980. The permeability of the endplate channel to organic cations in frog muscle. J. Gen. Physiol. 75:469–492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feske, S., J. Giltnane, R. Dolmetsch, L.M. Staudt, and A. Rao. 2001. Gene regulation mediated by calcium signals in T lymphocytes. Nat. Immunol. 2:316–324. [DOI] [PubMed] [Google Scholar]
- Feske, S., Y. Gwack, M. Prakriya, S. Srikanth, S.H. Puppel, B. Tanasa, P.G. Hogan, R.S. Lewis, M. Daly, and A. Rao. 2006. A mutation in Orai1 causes immune deficiency by abrogating CRAC channel function. Nature. 441:179–185. [DOI] [PubMed] [Google Scholar]
- Fomina, A.F., C.M. Fanger, J.A. Kozak, and M.D. Cahalan. 2000. Single channel properties and regulated expression of Ca2+ release-activated Ca2+ (CRAC) channels in human T cells. J. Cell Biol. 150:1435–1444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo, D., and Z. Lu. 2000. Mechanism of cGMP-gated channel block by intracellular polyamines. J. Gen. Physiol. 115:783–798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hermosura, M.C., M.K. Monteilh-Zoller, A.M. Scharenberg, R. Penner, and A. Fleig. 2002. Dissociation of the store-operated calcium current ICRAC and the Mg-nucleotide-regulated metal ion current MagNuM. J. Physiol. 539:445–458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hess, P., J.B. Lansman, and R.W. Tsien. 1986. Calcium channel selectivity for divalent and monovalent cations. Voltage and concentration dependence of single channel current in ventricular heart cells. J. Gen. Physiol. 88:293–319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoth, M. 1995. Calcium and barium permeation through calcium release-activated calcium (CRAC) channels. Pflugers Arch. 430:315–322. [DOI] [PubMed] [Google Scholar]
- Hoth, M., and R. Penner. 1993. Calcium release-activated calcium current in rat mast cells. J. Physiol. 465:359–386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackson, P.S., and K. Strange. 1995. Single-channel properties of a volume-sensitive anion conductance. Current activation occurs by abrupt switching of closed channels to an open state. J. Gen. Physiol. 105:643–660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kerschbaum, H.H., and M.D. Cahalan. 1998. Monovalent permeability, rectification, and ionic block of store-operated calcium channels in Jurkat T lymphocytes. J. Gen. Physiol. 111:521–537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kerschbaum, H.H., and M.D. Cahalan. 1999. Single-channel recording of a store-operated Ca2+ channel in Jurkat T lymphocytes. Science. 283:836–839. [DOI] [PubMed] [Google Scholar]
- Kotturi, M.F., and W.A. Jefferies. 2005. Molecular characterization of L-type calcium channel splice variants expressed in human T lymphocytes. Mol. Immunol. 42:1461–1474. [DOI] [PubMed] [Google Scholar]
- Kozak, J.A., H.H. Kerschbaum, and M.D. Cahalan. 2002. Distinct properties of CRAC and MIC channels in RBL cells. J. Gen. Physiol. 120:221–235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lansman, J.B., P. Hess, and R.W. Tsien. 1986. Blockade of current through single calcium channels by Cd2+, Mg2+, and Ca2+. Voltage and concentration dependence of calcium entry into the pore. J. Gen. Physiol. 88:321–347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lepple-Wienhues, A., and M.D. Cahalan. 1996. Conductance and permeation of monovalent cations through depletion-activated Ca2+ channels (ICRAC) in Jurkat T cells. Biophys. J. 71:787–794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis, R.S. 1999. Store-operated calcium channels. Adv. Second Messenger Phosphoprotein Res. 33:279–307. [DOI] [PubMed] [Google Scholar]
- Lewis, R.S. 2001. Calcium signaling mechanisms in T lymphocytes. Annu. Rev. Immunol. 19:497–521. [DOI] [PubMed] [Google Scholar]
- Liou, J., M.L. Kim, W.D. Heo, J.T. Jones, J.W. Myers, J.E. Ferrell Jr., and T. Meyer. 2005. STIM is a Ca2+ sensor essential for Ca2+-store-depletion-triggered Ca2+ influx. Curr. Biol. 15:1235–1241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu, D.M., and D.J. Adams. 2001. Ionic selectivity of native ATP-activated (P2X) receptor channels in dissociated neurones from rat parasympathetic ganglia. J. Physiol. 534:423–435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malayev, A., and D.J. Nelson. 1995. Extracellular pH modulates the Ca2+ current activated by depletion of intracellular Ca2+ stores in human macrophages. J. Membr. Biol. 146:101–111. [DOI] [PubMed] [Google Scholar]
- McCleskey, E.W., and W. Almers. 1985. The Ca channel in skeletal muscle is a large pore. Proc. Natl. Acad. Sci. USA. 82:7149–7153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neher, E., and C.F. Stevens. 1977. Conductance fluctuations and ionic pores in membranes. Annu. Rev. Biophys. Bioeng. 6:345–381. [DOI] [PubMed] [Google Scholar]
- Nimigean, C.M., and C. Miller. 2002. Na+ block and permeation in a K+ channel of known structure. J. Gen. Physiol. 120:323–335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parekh, A.B., and J.W. Putney Jr. 2005. Store-operated calcium channels. Physiol. Rev. 85:757–810. [DOI] [PubMed] [Google Scholar]
- Prakriya, M., and R.S. Lewis. 2001. Potentiation and inhibition of Ca2+ release-activated Ca2+ channels by 2-aminoethyldiphenyl borate (2-APB) occurs independently of IP3 receptors. J. Physiol. 536:3–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prakriya, M., and R.S. Lewis. 2002. Separation and characterization of currents through store-operated CRAC channels and Mg2+-inhibited cation (MIC) channels. J. Gen. Physiol. 119:487–507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prakriya, M., and R.S. Lewis. 2003. CRAC channels: activation, permeation, and the search for a molecular identity. Cell Calcium. 33:311–321. [DOI] [PubMed] [Google Scholar]
- Roos, J., P.J. DiGregorio, A.V. Yeromin, K. Ohlsen, M. Lioudyno, S. Zhang, O. Safrina, J.A. Kozak, S.L. Wagner, M.D. Cahalan, et al. 2005. STIM1, an essential and conserved component of store-operated Ca2+ channel function. J. Cell Biol. 169:435–445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sather, W.A., and E.W. McCleskey. 2003. Permeation and selectivity in calcium channels. Annu. Rev. Physiol. 65:133–159. [DOI] [PubMed] [Google Scholar]
- Sigworth, F.J. 1980. The variance of sodium current fluctuations at the node of Ranvier. J. Physiol. 307:97–129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spassova, M.A., J. Soboloff, L.P. He, W. Xu, M.A. Dziadek, and D.L. Gill. 2006. STIM1 has a plasma membrane role in the activation of store-operated Ca2+ channels. Proc. Natl. Acad. Sci. USA. 103:4040–4045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stokes, L., J. Gordon, and G. Grafton. 2004. Non-voltage-gated L-type Ca2+ channels in human T cells: pharmacology and molecular characterization of the major alpha pore-forming and auxiliary beta-subunits. J. Biol. Chem. 279:19566–19573. [DOI] [PubMed] [Google Scholar]
- Su, Z., R.L. Shoemaker, R.B. Marchase, and J.E. Blalock. 2004. Ca2+ modulation of Ca2+ release-activated Ca2+ channels is responsible for the inactivation of its monovalent cation current. Biophys. J. 86:805–814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vig, M., C. Peinelt, A. Beck, D.L. Koomoa, D. Rabah, M. Koblan-Huberson, S. Kraft, H. Turner, A. Fleig, R. Penner, and J.P. Kinet. 2006. CRACM1 is a plasma membrane protein essential for store-operated Ca2+ entry. Science. 312:1220–1223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woodhull, A.M. 1973. Ionic blockage of sodium channels in nerve. J. Gen. Physiol. 61:687–708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zweifach, A., and R.S. Lewis. 1993. Mitogen-regulated Ca2+ current of T lymphocytes is activated by depletion of intracellular Ca2+ stores. Proc. Natl. Acad. Sci. USA. 90:6295–6299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zweifach, A., and R.S. Lewis. 1995. Rapid inactivation of depletion-activated calcium current (ICRAC) due to local calcium feedback. J. Gen. Physiol. 105:209–226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zweifach, A., and R.S. Lewis. 1996. Calcium-dependent potentiation of store-operated calcium channels in T lymphocytes. J. Gen. Physiol. 107:597–610. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.