Contributions of Stretch Activation to Length-dependent Contraction in Murine Myocardium

Abstract

The steep relationship between systolic force production and end diastolic volume (Frank-Starling relationship) in myocardium is a potentially important mechanism by which the work capacity of the heart varies on a beat-to-beat basis, but the molecular basis for the effects of myocardial fiber length on cardiac work are still not well understood. Recent studies have suggested that an intrinsic property of myocardium, stretch activation, contributes to force generation during systolic ejection in myocardium. To examine the role of stretch activation in length dependence of activation we recorded the force responses of murine skinned myocardium to sudden stretches of 1% of muscle length at both short (1.90 μm) and long (2.25 μm) sarcomere lengths (SL). Maximal Ca²⁺-activated force and Ca²⁺ sensitivity of force were greater at longer SL, such that more force was produced at a given Ca²⁺ concentration. Sudden stretch of myocardium during an otherwise isometric contraction resulted in a concomitant increase in force that quickly decayed to a minimum and was followed by a delayed development of force, i.e., stretch activation, to levels greater than prestretch force. At both maximal and submaximal activations, increased SL significantly reduced the initial rate of force decay following stretch; at submaximal activations (but not at maximal) the rate of delayed force development was accelerated. This combination of mechanical effects of increased SL would be expected to increase force generation during systolic ejection in vivo and prolong the period of ejection. These results suggest that sarcomere length dependence of stretch activation contributes to the steepness of the Frank-Starling relationship in living myocardium.

INTRODUCTION

The Frank-Starling relationship manifests an intrinsic mechanism by which cardiac performance varies on a beat-to-beat basis depending on venous return (Allen and Kentish, 1985; Lakatta, 1992; Fuchs and Smith, 2001; Fuchs and Martyn, 2005). As ventricular end diastolic volume increases, stroke volume during the next beat increases due to an increase in myocardial work capacity (Moss and Fitzsimons, 2002). The steep relationship between peak systolic pressure and end diastolic volume thus contributes to the regulation of cardiac function in vivo, but the molecular mechanisms mediating the effects of myocardial fiber length on cardiac work are still not well understood.

Several factors are likely to contribute to the length dependence of myocardial contraction. Increases in myocardial sarcomere length (SL) within the physiological working range significantly increase the Ca²⁺ sensitivity of force, i.e., the amount of force generated at a given Ca²⁺ concentration (Hibberd and Jewell, 1982; Allen and Kentish, 1985). There is some consensus that the length dependence of Ca²⁺ sensitivity is mediated or modulated by variations in the spatial relationships of thick and thin filaments such as lateral spacing between filaments (for review see Millman, 1998) and the degree of filament overlap (Gordon et al., 1966), as well as variations in Ca²⁺ binding to troponin C (TnC) (Hoffman and Fuchs, 1987, 1988) and cooperative activation of thin filaments due to strong-binding cross-bridges (Landesberg and Sideman, 1994; Fitzsimons and Moss, 1998).

Stretch activation might also play an important role in mediating length dependence of myocardial contraction (Campbell and Chandra, 2006). Similar to other oscillatory muscles, cardiac muscle exhibits a pronounced stretch activation response (Steiger, 1971, 1977), which is thought by some to contribute to ventricular ejection (Vemuri et al., 1999; Davis et al., 2001; Stelzer et al., 2006a,c). As previously suggested by Campbell and Chandra (2006), the more pronounced stretch activation response observed in cardiac muscle as compared with skeletal might account for the steeper length–force relationship in myocardium (Allen and Kentish, 1985). In this regard, we have shown that the overall rate and amplitude of the stretch activation response in skinned myocardium varies with the level of Ca²⁺ activation and is sensitive to the number of strongly bound cross-bridges (Stelzer et al., 2006c), suggesting that the response is sufficiently dynamic to significantly modulate the force and kinetics of contraction.

As proposed by Campbell and Chandra (2006), increases in SL and the corresponding increase in cross-bridge binding to the thin filament might be expected to prolong the time to peak myocardial force at submaximal Ca²⁺ concentrations as a consequence of enhanced cooperative recruitment of cross-bridges, a mechanism that would also serve to maintain force during late systole even when intracellular Ca²⁺ has decreased (Campbell and Chandra, 2006). It has been suggested that the stretch activation response is initiated by passive stretch of myofilaments during diastole before Ca²⁺ activation as the ventricle expands to accommodate an increased volume of blood (Campbell and Chandra, 2006). The small numbers of cross-bridges that remain attached to actin during the late phase of ventricular filling are strained as sarcomere length increases such that force is enhanced at the beginning of systole (Maughan, 2005). However, there is also evidence that myocytes may be actively stretched during the systolic phase of the cardiac cycle. Because the timing of electrical and mechanical activation in the heart varies across the ventricular wall, before ejection early activated regions of the ventricular wall (i.e., endocardium) contract and stretch regions that are activated later (i.e., epicardium) (Beyar and Sideman, 1985; Ashikaga et al., 2004; Sengupta et al., 2005; Buckberg et al., 2006b). It has also been observed that later in systole, late activating epicardial fibers forcibly stretch early activating endocardial fibers (Nickerson et al., 2005; Buckberg et al., 2006a). It has been proposed that the stretch of endocardial fibers later in systole is due, in part, to the enhanced force-producing ability of epicardial fibers due to greater regulatory light chain phosphorylation levels (Davis et al., 2001), and results in a delayed force response that will increase force generation during late systole. Therefore, the delayed attainment of extra force produced by stretch before ejection, whether originating during the diastolic filling phase or the systolic phase, could substantially enhance cardiac function during late systolic ejection, as has been previously observed at the whole organ level (Hunter, 1989). In this regard, the initiation of the stretch activation response from a higher force due to increased sarcomere length would be expected to significantly alter the amplitude and/or rate of the response such that delayed force development is matched to the rate of systolic force generation.

To examine possible roles of stretch activation in the length dependence of myocardial contraction, we imposed sudden stretches of 1% of muscle length on mouse skinned myocardium at short (1.90 μm) and long (2.25 μm) SL and at levels of Ca²⁺ activation between threshold and maximal for force development. When SL was increased to 2.25 μm, the responses to sudden stretch were altered, i.e., the cooperative recruitment of cross-bridges to force-generating states was accelerated while the rate of cross-bridge detachment was slowed. Taken together, these results would predict an increase in force generation in vivo and a prolongation of the systolic ejection phase when end-diastolic volume is increased, such that more blood is ejected with each beat. Thus, stretch activation may contribute to the steepness of the Frank-Starling relationship in myocardium through a cooperative mechanism that at long lengths accelerates the rate of rise of force but also slows the rate of force relaxation.

MATERIALS AND METHODS

Solutions

Solution compositions were calculated using the computer program of Fabiato (1988) and the stability constants listed by Godt and Lindley (Godt and Lindley, 1982) (corrected to pH 7.0 and 22°C). All solutions contained 100 mM N,N-bis(2 hydroxy-ethyl)-2-aminoethanesulfonic acid (BES), 15 mM creatine phosphate, 5 mM dithiothreitol, 1 mM free Mg²⁺, and 4 mM MgATP. In addition, pCa 9.0 solution contained 7 mM EGTA and 0.02 mM CaCl₂, pCa 4.5 solution contained 7 mM EGTA and 7.01 mM CaCl₂, and preactivating solution contained 0.07 mM EGTA. Ionic strength of all solutions was adjusted to 180 mM with potassium propionate. Solutions containing different amounts of [Ca²⁺]_free (i.e., pCa 6.2 to 5.5) were prepared by mixing appropriate volumes of stock solutions of pCa 9.0 and pCa 4.5.

Skinned Myocardial Preparations

Skinned ventricular myocardium for stretch activation experiments was prepared as previously described (Stelzer et al., 2004). In brief, after i.p. injection of 5,000 U heparin/kg body weight, S129 mice (3–6 mo old) were anesthetized with inhaled isoflurane (15% isoflurane in mineral oil) in accordance with institutional animal care guidelines. Their hearts were excised and right and left ventricles were dissected at room temperature in a relaxing solution containing (in mM) 100 KCl, 20 imidazole, 7 MgCl₂, 2 EGTA, and 4 MgATP (pH 7.0) and were then rapidly frozen in liquid nitrogen. To prepare skinned myocardial preparations, the frozen ventricles were thawed and homogenized in relaxing solution for ∼2 s using a Polytron, which yielded multicellular preparations of 100–250 μm × 600–900 μm. The homogenate was centrifuged at 120 g for 1 min, and the resulting pellet was washed with fresh relaxing solution and resuspended in relaxing solution containing 250 μg/ml saponin and 1% Triton X-100. After 30 min, the skinned preparations were washed with fresh relaxing solution and then dispersed in ∼50 ml relaxing solution in a glass Petri dish. The dish was kept on ice at all times except during the selection of preparations for mechanical experiments.

Experimental Apparatus

Skinned preparations with smooth, well-defined edges were transferred from the Petri dish to a stainless steel experimental chamber containing relaxing solution. The ends of each preparation were attached to the arms of a motor (model 312B; Aurora Scientific Inc.) and force transducer (model 403; Aurora Scientific Inc.), as described earlier (Stelzer et al., 2004). The chamber assembly was then placed on the stage of an inverted microscope (Carl Zeiss MicroImaging, Inc.) fitted with a 40× objective and a CCTV camera (model WV-BL600; Panasonic). Bitmap images of the preparations were acquired using an AGP 4X/2X graphics card and software (ATI Technologies Inc.) and were used to assess mean sarcomere length (SL) during the course of each experiment. Activated cardiac preparations that exhibited length changes >5% of initial sarcomere length were discarded and the data not used. Changes in force and motor position were sampled (16-bit resolution, DAP5216a; Microstar Laboratories) at rates ≥2.0 KHz using SLControl software developed in our laboratory (Campbell and Moss, 2003) and saved to computer files for later analysis. Force during the experiments was also recorded on a digital oscilloscope (Nicolet Instrument Corp.).

Experimental Protocols

Kinetics of Force Redevelopment.

The rate constant of force redevelopment (k_tr) in skinned myocardium was assessed at short (1.90 μm) and long (2.25 μm) SL using a modification of the experimental protocol originally described by Brenner and Eisenberg (1986). Each preparation was transferred from relaxing to activating solutions of varying free [Ca²⁺] (pCa 6.2–4.5) and allowed to generate steady-state force. The preparation was rapidly (<2 ms) slackened by 20% of its original length, resulting in a coincident reduction in force to near zero, i.e., <5% of steady isometric force. This was followed by a brief period of unloaded shortening (10 ms) after which the preparation was rapidly restretched to its original length. A k_tr–relative force relationship was obtained by initially activating the preparation in solution of pCa 4.5, and then in a series of submaximally activating solutions between pCa 6.2 and 5.5, and then expressing submaximal forces as a fraction of maximum force (P/P_o). The apparent rate constant of force redevelopment (k_tr) was estimated by linear transformation of the half-time of force redevelopment, i.e., k_tr = 0.693/t_1/2, as described previously (Stelzer et al., 2004).

Force–pCa Relationships.

During the recordings of force redevelopment at different SL, each preparation was allowed to develop steady force in solutions of varying free [Ca²⁺]. The difference between steady-state force and the force baseline obtained after the 20% slack step was measured as the total force at that pCa. Active force was then calculated by subtracting Ca²⁺-independent force in solution of pCa 9.0 from the total force and was normalized to the cross-sectional area of the preparation, which was calculated from the width of the preparations assuming a cylindrical cross section. Force–pCa relationships were derived by expressing submaximal force (P) at each pCa as a fraction of maximal force (P_o) determined at pCa 4.5 (P/P_o) in the same preparation. Apparent cooperativity in the activation of force was inferred from the steepness of the force–pCa relationship and was quantified using a Hill plot transformation of the force–pCa data (Stelzer et al., 2006b). The data were fit with an equation, P/P_o = [Ca²⁺]ⁿ/(kⁿ + [Ca²⁺]ⁿ), where n is the Hill coefficient and k is the [Ca²⁺] required for half-maximal force (pCa₅₀).

Stretch Activation Experiments.

At the beginning of the experiment, preparation length was set to an SL of ∼1.90 μm or ∼2.25 μm for measuring initial isometric force and for subsequent imposition of stretch. The preparations were first activated at pCa 4.5 to establish maximum force (P_o). Ca²⁺-activated forces (P) at maximum and submaximal pCa's were determined as the difference between total force in the activating solution and resting force measured in solution of pCa 9.0. Fibers were activated at short and long SL at pCa's that yielded maximal force, and submaximal forces of ∼80%, ∼60%, ∼40%, and ∼20% maximal. When the fiber achieved steady-state force, a sudden stretch of 1% (complete in <1ms) was imposed and held for 5 s before returning to solution of pCa 9.0. The speed of stretches imposed in these experiments was designed to minimize changes in cross-bridge populations during stretch, such that the initial increase in force was presumably due to the elastic strain of the cross-bridges bound before the stretch was imposed (Stelzer et al., 2006c).

The method used for measuring the stretch activation variables have been described in detail (Stelzer et al., 2006c). In brief, amplitudes were measured as follows: P₁, measured from prestretch steady-state force to the peak of phase 1; P₂, measured from prestretch steady-state force to the minimum force decay; P₃, measured from prestretch steady-state force to the peak value of delayed force; and P_df, difference between P₃ and P₂.

All amplitudes were normalized to prestretch Ca²⁺-activated isometric force to allow comparisons at different SL and Ca²⁺ activation levels. Apparent rate constants were derived for phase 2 (k _rel, s⁻¹) from the peak of phase 1 to the minimum of phase 2 and for phase 3 (k _df, s⁻¹) from the point of force reuptake after phase 2 to the completion of delayed force development.

Data Analysis

Analysis of stretch activation data was performed as previously described (Stelzer et al., 2006c). In brief, rate constants of force decay (k _rel) were obtained by fitting a single exponential to the time course of decay, i.e., y = a (1 − exp(−k ₁·x)), where “a” is the amplitude of the single exponential phase and k ₁ is the rate constant of decay. Rate constants of delayed force development in phase 3 were estimated either with a double exponential fit, y = a·exp(−k ₁·x) + b·exp(−k ₂·x), where “a” is the amplitude of the first exponential phase rising with rate constant k ₁ and “b” is the amplitude of the second exponential phase rising with rate constant k ₂, or were estimated as a single composite rate constant by linear transformation of the half-time of force redevelopment, i.e., [k _df = −ln0.5 × (t _1/2)⁻¹] (Stelzer et al., 2006c).

All data are reported as means ± SEM. Comparisons of steady-state force, k _tr, and stretch activation at different levels of activation and SL were done using a one-way analysis of variance (ANOVA) with a Tukey post-hoc test for significance (P < 0.05).

RESULTS

SL Dependence of Steady-state Isometric Force

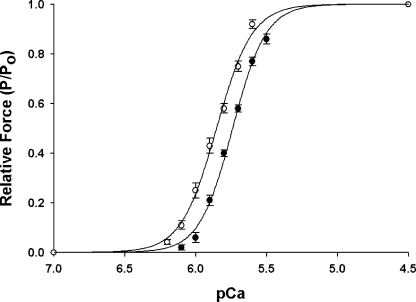
As shown in Fig. 1, increasing SL from 1.90 μm to 2.25 μm resulted in significant increases in maximal Ca²⁺ activated force (Table I) and the Ca²⁺ sensitivity of force (ΔpCa₅₀ = 0.10 ± 0.01 pCa units) such that less Ca²⁺ was required to achieve a given submaximal force (Table I). The steepness of the force–pCa relationship (Hill coefficient, n _H), which provides an index of the apparent molecular cooperativity of force development, was not significantly affected by increased SL (Table I).

Figure 1.

Effects of SL on force–pCa relationship in skinned myocardium. Force-pCa relationships were measured at short (1.90 μm, •, n = 10) and long (2.25 μm, ◯, n = 10) SL. Forces at submaximal Ca²⁺ concentration ([Ca²⁺]_free) are expressed relative to the maximum force at pCa 4.5. The smooth lines were fit using the Hill equation: P/P_o = [Ca²⁺]ⁿ/(k ⁿ + [Ca²⁺]ⁿ)], where P is the force at each [Ca²⁺]_free, P_o is the force pCa 4.5, n _H is the Hill coefficient, and k is the [Ca²⁺] required for half-maximal activation. Data points are means ± SEM.

TABLE I.

Effects of SL on Steady-state Force in Murine Myocardium

Sarcomere length	Fmax	Fmin	pCa50	nH
μm	mN/mm2	mN/mm2
1.90	15.0 ± 0.9	0.5 ± 0.2	5.71 ± 0.01	3.95 ± 0.29
2.25	21.1 ± 1.3a	1.1 ± 0.3a	5.81 ± 0.01a	3.62 ± 0.26

Data are means ± SEM, from 10 preparations. F_max, maximum Ca²⁺-activated force at pCa 4.5; F_min, Ca²⁺-independent force at pCa 9.0; pCa₅₀, pCa at half-maximal force; n _H, Hill coefficient.

^aSignificantly different from data obtained at SL of 1.90 μm, P < 0.05.

SL Dependence of the Kinetics of Force Redevelopment

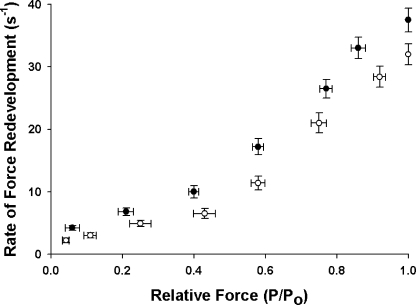
We measured the effects of [Ca²⁺] on the rate constant of force redevelopment (k _tr) (Brenner and Eisenberg, 1986) at both short and long SL. k _tr was plotted against steady-state isometric force (P/P_o) to assess variations as a function of thin filament activation (Fig. 2). k _tr increased with increasing [Ca²⁺] at both short and long SL, with the increase being more gradual at low [Ca²⁺] and steeper at high [Ca²⁺] until an apparent maximum was reached at pCa 4.5 (Fitzsimons et al., 2001a; Stelzer et al., 2004, 2006b). The relationships between k _tr and relative force at short (1.90 μm) and long (2.25 μm) SL (Fig. 2) demonstrate that despite a decrease in absolute force production at short SL, i.e., less absolute force was produced at a given Ca²⁺ concentration (Table I), there was a significant acceleration of k _tr. These results are in agreement with Adhikari et al. (2004) who also found that k _tr is accelerated at short SL. Since decreasing the SL reduced the Ca²⁺ sensitivity of force, the [Ca²⁺] of submaximal activating solutions in experiments done at short SL were increased in order to achieve activation levels (P/P_o) similar to those at long SL. The greater concentration of Ca²⁺ in activating solutions required to achieve a given submaximal activation level at short SL certainly contributed to greater k _tr, since more regulatory units would be activated in the thin filament (Gordon et al., 2000). However, k _tr was slightly accelerated at high activation levels at short SL even when the data were plotted as a function of pCa (unpublished data), suggesting that factors in addition to [Ca²⁺] contributed to the differences in k _tr at short and long SL at these activation levels.

Figure 2.

Effects of SL on the rate constant of force redevelopment in skinned myocardium. The rate constant of force redevelopment (k _tr) was measured as a function of isometric force (P/P_o) at short (1.90 μm, •, n = 10) and long (2.25 μm, ◯, n = 10) SL. Data are means ± SEM.

Effect of SL on Stretch Activation

The effects of SL on the stretch activation response in mouse skinned myocardium was studied by imposing stretches of 1% of initial muscle length during maximal and submaximal Ca²⁺ activations at short (1.90 μm) and long (2.25 μm) SL. Sudden stretch of an isometrically contracting preparation to a new length produces a multiphasic force response. There is a rapid spike in force coincident with the stretch (phase 1) due to strain of attached cross-bridges, followed by a rapid decay in force (phase 2) to a minimum, and finally a delayed increase in force (phase 3, stretch activation) that is sustained for several seconds before relaxing back to the original isometric value. As shown in the records of Fig. 3 in which a stretch of 1% of initial muscle length was imposed during an activation that was ∼50% maximal, increased SL produced an increase in prestretch isometric force that increased the overall amplitude of the stretch activation response. To facilitate comparisons of stretch activation at different activation levels and SL, the phases of the stretch activation response were normalized to prestretch isometric force, which is indicated as an arbitrary “zero” baseline: P₂, the minimum force at the end of phase 2; P_df, the peak to trough excursion of force in phase 3; and P₃, the amplitude of phase 3 measured from the prestretch isometric force. The amplitude of phase 1 (P₁) was not studied in this work.

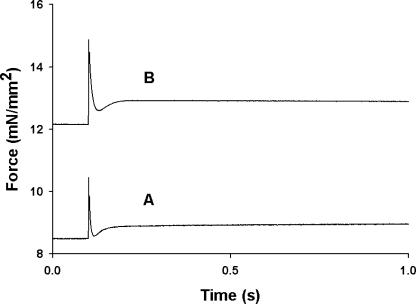
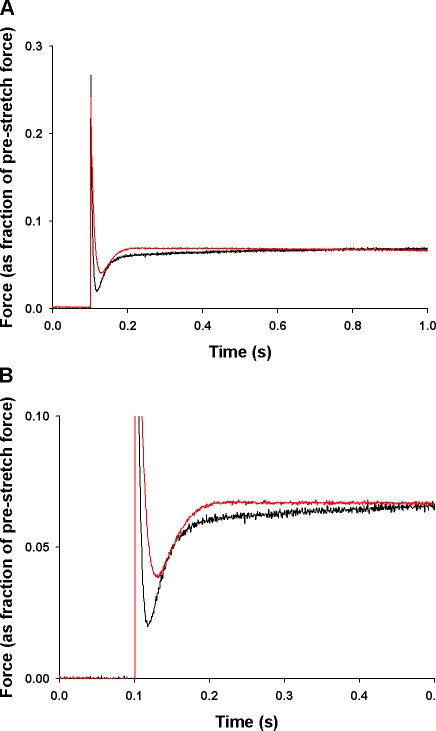
Figure 3.

Effect of SL on the force transients produced by stretch. Force responses of skinned myocardium to a stretch of 1% of muscle length applied during isometric contractions (∼50% of maximal) were recorded at (A) SL = 1.90 μm and (B) SL = 2.25 μm. Increasing SL increased the Ca²⁺-activated isometric force (from 8.5 mN/mm² to12.2 mN/mm²) and increased the absolute amplitude of the stretch activation response.

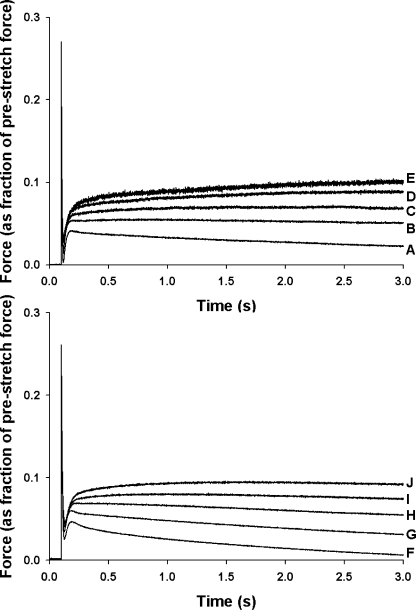
Increasing SL from 1.90 μm to 2.25 μm resulted in significant changes in the stretch activation response, as shown in the records of Fig. 4 in which a stretch of 1% of initial muscle length was imposed during activations at various Ca²⁺ concentrations. As reported previously (Stelzer, et al., 2006a,c), increases in [Ca²⁺] accelerated the overall rate of stretch activation and reduced its amplitude (normalized to prestretch isometric force) (Stelzer et al., 2006a,c). Increased SL also accelerated the stretch activation response and reduced its amplitude, with the most pronounced effects at submaximal activations (Fig. 4). The effects of SL on stretch activation can be better appreciated from Fig. 5 in which traces recorded at short and long SL at an activation level of ∼50% maximal are superimposed.

Figure 4.

Effects of SL on the stretch activation responses of skinned myocardium at varied levels of Ca²⁺ activation. Force responses to a stretch of 1% of muscle length were recorded at short (1.90 μm, top) and long (2.25 μm, bottom) SL. The force responses were normalized to prestretch isometric force (corresponding to zero baseline) at the same level of activation, i.e., the prestretch force baseline corresponds to similar relative forces (P/P_o). Relative forces (P/P_o) at short SL were A, 1.00; B, 0.80; C, 0.59; D, 0.42; E, 0.21. Relative forces (P/P_o) at long SL were F, 1.00; G, 0.75; H, 0.55; I, 0.40; J, 0.25.

Figure 5.

Effects of SL on the stretch activation responses of skinned myocardium. (A) Force responses to a stretch of 1% of muscle length were recorded at short (1.90 μm, black trace) and long (2.25 μm, red trace) SL. The force responses were normalized to the prestretch isometric force (corresponding to the zero baseline) and were recorded at similar activation levels, i.e., 0.57 P_o and 0.54 P_o at SL of 1.90 μm and 2.25 μm, respectively. (B) An amplified time scale of the traces in A show the effect of SL on phase 3 rate of delayed force development.

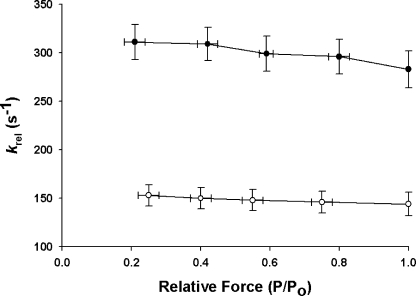
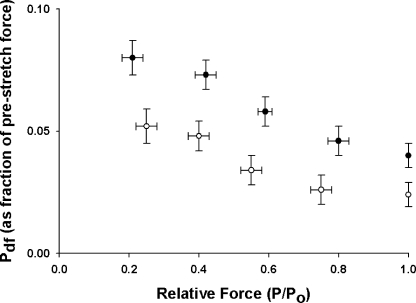
At both SL studied here, decreased prestretch activation slightly accelerated the rapid force decay in phase 2 (k _rel) (Fig. 6) and decreased the amount of force decay, i.e., increased P₂ (Fig. 7), following stretch. k _rel, which is thought to represent detachment of cross-bridges that are strained by stretch and their rapid replacement by unstrained cross-bridges (Davis and Rodgers, 1995; Piazzesi et al., 1997), was accelerated approximately twofold at all levels of activation at short SL (Fig. 6). This result is consistent with earlier reports (Kentish and Stienen; 1994; Holmes et al., 2002; Chandra et al., 2006) showing that rates of cross-bridge detachment are accelerated at shorter SL. The increase in P₂ at longer SL is consistent with a decrease in the rate of cross-bridge detachment and can also be interpreted as a decrease in the probability of reversal of force-producing steps in response to stretch (Davis et al., 2002) so that the reversal of steps such as the phosphate release step are less favored (Cooke, 1997) and forward force generating steps are more favored.

Figure 6.

Effects of SL on k _rel at different levels of activation. k _rel was estimated at short (1.90 μm, •, n = 10) and long (2.25 μm, ◯, n = 10) SL and at different levels of prestretch isometric force (P/P_o). The data shown were obtained from force responses to stretches of 1% of muscle length. Data are means ± SEM.

Figure 7.

Effects of SL on P₂ at different levels of activation. P₂ values normalized to prestretch isometric force were measured at short (1.90 μm, •, n = 10) and long (2.25 μm, ◯, n = 10) SL and at different levels of prestretch isometric force (P/P_o). The data shown were obtained from force responses to stretches of 1% of muscle length. Data are means ± SEM.

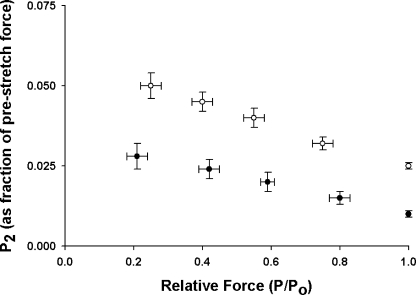
The amplitude of the delayed force response (phase 3) varies with prestretch isometric force (Linari et al., 2004; Stelzer et al., 2006c), so that the number of cross-bridges recruited by stretch can be inferred from the amplitude of the delayed force response (P_df). When activation is increased by increasing the [Ca²⁺], the amplitude (normalized to prestretch isometric force) of the delayed force response decreases because a greater number of cross-bridges are initially bound to actin, leaving fewer cross-bridges available for recruitment by stretch (Fig. 8). At all levels of activation, P_df was decreased when SL was increased (Fig. 8), in part because P₂ was increased (Fig. 6), thereby reducing the overall peak-to-trough amplitude of phase 3.

Figure 8.

Effects of SL on P_df at different levels of activation. P_df values normalized to prestretch isometric force were recorded at short (1.90 μm, •, n = 10) and long (2.25 μm, ◯, n = 10) SL and at different levels of prestretch isometric force (P/P_o). The data shown were obtained from force responses to stretches of 1% of muscle length. Data are means ± SEM.

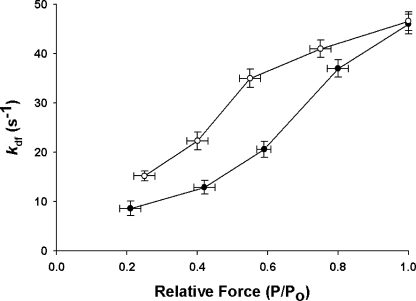
The rate constant of delayed force development (k _df) after stretch is thought to manifest the kinetics of recruitment of cross-bridges into strongly bound states (Lombardi and Piazzesi, 1990; Piazzesi et al., 1997; Campbell et al., 2004; Stelzer et al., 2006c) and, as previously reported (Linari et al., 2004; Stelzer et al., 2006c), is not well fit with a single exponential equation, especially at low levels of activation. To facilitate comparisons of phase 3 rates of force development at different levels of activation, a composite apparent rate constant (k _df) of delayed force development was calculated from the half-time of force development. Consistent with earlier reports, (Stelzer et al., 2006a,c), k _df in murine myocardium was accelerated by increasing the level of activation (Fig. 9). SL had no effect on k _df during maximal activation, but at submaximal activations, k _df was accelerated at long SL, with the most pronounced effects observed at the lowest levels of activation (Fig. 9).

Figure 9.

Effects of SL on k _df at different levels of activation. k _df values at short (1.90 μm, •, n = 10) and long (2.25 μm, ◯, n = 10) SL were recorded at different levels of prestretch isometric force and are plotted as a function of prestretch isometric force (P/P_o). The data shown were obtained from force responses to stretches of 1% of muscle length. Data are means ± SEM.

Further analysis of the kinetics of delayed force development using a double exponential fit yielded fast and slow rate constants (k ₁ and k ₂) and their corresponding amplitudes (a and b), as shown in Table II. As previously reported (Stelzer et al., 2006a,c), increasing the level of activation progressively diminished the amplitude (b) of the slower rate process (thought to represent cooperative recruitment of cross-bridges) and increased its apparent rate (k ₂) (Stelzer et al., 2006a,c). The progressive reduction in the amplitude of the slow phase (b) with increasing levels of activation culminated in its complete absence at near-maximal activations, so that delayed force development after stretch proceeded as a single process with amplitude (a). At short SL, the slow phase of force development (b) was detectable at activation levels as great as ∼80% of maximal and comprised a significantly greater proportion of the delayed force response at all submaximal levels of activation compared with long SL (Table II). At long SL, the slow phase of delayed force development (b) was completely absent at activations above ∼40% of maximal, so that only the fast component (a) was evident (Table II). During activations at long SL in which both the fast and slow components of force development were present (below ∼40% of maximal), the slow component occurred at an accelerated rate (k ₂) compared with similar activations at short SL (Table II). SL had little effect on the kinetics of the fast phase of delayed force development (k ₁) at all activation levels, suggesting that the increase in submaximal k _df at increased SL was mainly due to a decrease in amplitude (b) and an acceleration of the kinetics (k ₂) of the slow phase of delayed force development (Fig. 5).

TABLE II.

Effects of SL on the Activation Dependence of Phase 3 Delayed Force Development in Murine Myocardium

Sarcomere length	Activation level	a	k 1	b	k 2
μm	P/Po		s −1		s −1
1.90	1.00 ± 0.00	1.00	46.8 ± 2.4	–	–
2.25	1.00 ± 0.00	1.00	46.0 ± 2.3	–	–
1.90	0.80 ± 0.03	0.90 ± 0.04	42.0 ± 2.1	0.10 ± 0.02	4.6 ± 0.5
2.25	0.75 ± 0.03	1.00a	41.4 ± 2.0	–	–
1.90	0.59 ± 0.02	0.70 ± 0.04	36.8 ± 2.0	0.30 ± 0.03	2.9 ± 0.4
2.25	0.55 ± 0.03	1.00a	34.4 ± 1.8	–	–
1.90	0.42 ± 0.03	0.55 ± 0.03	28.1 ± 1.7	0.45 ± 0.03	2.6 ± 0.3
2.25	0.40 ± 0.03	0.77 ± 0.04a	29.8 ± 1.7	0.23 ± 0.02a	4.3 ± 0.4a
1.90	0.21 ± 0.03	0.45 ± 0.03	19.7 ± 1.4	0.55 ± 0.03	1.5 ± 0.1
2.25	0.25 ± 0.03	0.73 ± 0.03a	21.4 ± 1.5	0.27 ± 0.02a	3.3 ± 0.3a

Data are means ± SEM from 10 preparations subjected to a sudden stretch of 1% of muscle length. Apparent rate constants for phase 3 delayed force development were obtained by fitting a double exponential to each record, y = a·exp(−k ₁·x) + b·exp(−k ₂·x), where a and b are the amplitudes of the fast and slow phases, respectively.

^aSignificantly different from value obtained at SL of 1.90 μm, P < 0.05.

DISCUSSION

Effect of SL on Steady-state Force

The variations in SL that occur on a beat-to-beat basis as ventricular end diastolic volumes vary substantially affect contractile function in myocardium. Increasing the SL along the ascending limb of the length–force relationship increases myocardial twitch force and Ca²⁺ sensitivity of force (Allen and Kentish, 1985; Lakatta, 1992), but the mechanism by which these changes occur is still being debated. Increased Ca²⁺ sensitivity of force at long SL has been associated with an increased affinity of cardiac TnC (cTnC) for Ca²⁺, (Hoffman and Fuchs, 1987, 1988), which acts to increase cross-bridge binding and force production. As SL is increased, there is a decrease in the lateral separation of thick and thin filaments (Millman, 1998), which increases force both by increasing the probability of cross-bridge binding to actin and by increasing the Ca²⁺ binding affinity of cTnC (Fuchs and Smith, 2001). The majority of evidence (for review see Fuchs and Martyn, 2005) suggests that increased probability of myosin binding to actin is the predominant mechanism, since perturbations that increase the number of strongly bound cross-bridges (and thereby increase force) have been shown to reduce the increase in Ca²⁺ sensitivity of force when SL is increased (Fitzsimons and Moss, 1998; Fukuda et al., 2000; Adhikari et al., 2004). Conversely, the lower force and Ca²⁺ sensitivity of force at short SL is presumably due to reduced probability of cross-bridge binding as a result of increased lateral separation of thick and thin filaments (McDonald and Moss, 1995). These ideas are supported by X-ray diffraction studies showing that reducing myofilament lattice spacing by osmotic compression or increased SL both increase cross-bridge binding to the thin filament (Martyn et al., 2004; Yagi et al., 2004).

Effect of SL on Stretch Activation

Recently, Campbell and Chandra (2006) suggested that stretch activation plays an important role in length-dependent activation of cardiac muscle by determining the steepness of the Frank-Starling relationship. This idea is based on earlier observations that when cardiac muscle shortens (and SL decreases), force remains elevated for some time due to delayed force development initiated at the original muscle length before muscle activation (Hunter, 1989). The residual force produced by recruitment of strongly bound cross-bridges when SL increases during diastolic ventricular filling (Campbell and Chandra, 2006), or early systole (Davis et al., 2001), can act to prolong the systolic ejection period of the same heart beat as the muscle shortens during the period of Ca²⁺ reuptake (Hunter, 2000), possibly by cooperatively sustaining activation even as Ca²⁺ dissociates from the thin filament (Janssen and Hunter, 1997). In this regard, we have previously shown that the amplitude and rate constant of delayed force development in response to stretch varies with prestretch force (preload) (Stelzer et al., 2006c), which implies that the delayed force response is modulated to match the afterload against which the heart must work.

Since the lateral spacing of thick and thin filaments changes as a function of SL, the delayed force response due to stretch-induced cooperative cross-bridge recruitment would be expected to vary with SL. In this regard, increasing SL from 1.90 to 2.25 μm markedly altered both the magnitude and kinetics of the delayed force response. At a given SL, the amplitude of the delayed force response (P₃) normalized to prestretch force manifests the number of cross-bridges recruited by stretch, and is inversely related to level of activation (Linari et al., 2004; Stelzer et al., 2006c). Therefore, at high levels of activation where larger fractions of cross-bridges are bound to actin and fewer unbound cross-bridges are available for recruitment, P₃ is diminished. In the present study, SL did not significantly alter P₃ when normalized to prestretch force, i.e., when [Ca²⁺] in the activating solution was adjusted to account for the decreased Ca²⁺ sensitivity of force at short SL. However, as shown in Fig. 3, the amplitude of the delayed force response expressed in absolute force units is proportional to prestretch force such that greater prestretch forces produce stretch activation responses of greater amplitude. Thus, the increased Ca²⁺ sensitivity of force at longer SL would produce a proportionally greater stretch activation response than at short SL for a given Ca²⁺ activation and thus would be expected to contribute to the in vivo enhancement of twitch force with increased SL (Allen and Kentish, 1985).

Increased SL accelerated the rate constant of delayed force development (k _df) at all levels of submaximal activation but not at maximal activation (Fig. 9). These results can be explained in the context of the high degree of cooperativity in cross-bridge binding to cardiac thin filaments and contributions of cooperation to the delayed force response, particularly at submaximal levels of activation. At maximal activation, the greater proximity of myosin heads with actin at long SL (Moss and Fitzsimons, 2002; Fuchs and Martyn, 2005) would not significantly accelerate cross-bridge recruitment and force generation because cooperation in cross-bridge recruitment into force-generating states is negligible due to the large fraction of cross-bridges already bound to actin before the muscle is stretched. However, at submaximal activations where cooperative cross-bridge recruitment is more prominent in the stretch activation response, the increased proximity of cross-bridges to actin at long SL significantly accelerated k _df, with the largest effects seen at the lowest activations, i.e., below ∼50% maximal. The acceleration of k _df at long SL and submaximal activation is mediated by both a reduced amplitude and accelerated kinetics of the slower (cooperative) phase of delayed force development (Table II), suggesting that cooperative cross-bridge recruitment by stretch was either reduced (as indicated by the reduced amplitude of P_df) or accelerated. These results are in good agreement with recent studies in myocardium showing that cooperative cross-bridge recruitment during oscillatory work is slowed when SL is reduced (Levy et al., 2005; Chandra et al., 2006).

The duration of the Ca²⁺ transient that initiates cardiac muscle contraction is short in relation to the twitch duration (Backx et al., 1995), i.e., relaxation of force lags Ca²⁺ sequestration, suggesting that the relaxation process is limited by the myofilaments (Hunter, 2000). The time course of force relaxation appears to be related to the number of cross-bridges bound to actin at the onset of relaxation (Fitzsimons et al., 2001b) such that more attached cross-bridges (and force) cause a greater delay in relaxation, presumably because cooperative activation by strongly bound cross-bridges offsets the inhibiting effects of Ca²⁺ dissociation from thin filament sites (Bremel and Weber, 1972; Janssen and Hunter, 1997) or prolongs the binding of Ca²⁺ to TnC (Hoffman and Fuchs, 1987). In the present study the rate of force decay (k _rel) during phase 2 of the stretch activation response was dramatically accelerated at short SL at all levels of activation (Fig. 6). This finding is consistent with recent studies showing that the rate of cross-bridge detachment during oscillatory work is accelerated at short SL (Chandra et al., 2006), and the tension cost of cardiac contraction, which is an index of the rate of cross-bridge detachment is also increased (Kentish and Stienen, 1994; Holmes et al., 2002; Chandra et al., 2006), perhaps as a result of increased radial strain due to increased surface-to-surface distance between myosin and actin filaments as SL decreases (Brenner et al., 1996; Adhikari et al., 2004).

Because of the increased Ca²⁺ sensitivity of force at long SL, more cross-bridges are cooperatively recruited by stretch activation during the early phases of systole and more force is generated during systolic ejection, which slows the relaxation of force and prolongs the period of ejection. Conversely, at short SL, decreased stretch-induced cross-bridge recruitment and force generation cause force to relax at an accelerated rate. Accelerated k _rel at short SL (along with decreased P₂ amplitude) indicates that the transition of cross-bridges from the high-force strongly bound state to the weakly bound state is accelerated. This result is consistent with the previous suggestion that acceleration of the rate of reversal of the force-producing power stroke could contribute to accelerated rates of cross-bridge detachment at short SL (Palmer and Kentish, 1998).

Effect of SL on the Rate Constant of Force Redevelopment

Although not the primary focus of this study, we also examined the effects of SL on the rate constant of force redevelopment (k _tr) induced using a modified stretch and release protocol (Brenner and Eisenberg, 1986). Consistent with recent studies (Adhikari et al., 2004; Chandra et al., 2006), we found that k _tr was accelerated with decreased SL at all levels of activation. At first glance, these data appear to contradict our finding that k _df is accelerated at long SL, but this is not the case. k _tr is thought to be the sum of the forward (f _app) and reverse (g _app) rate constants describing the transitions between force-generating and nonforce-generating states (Brenner and Eisenberg, 1986), and thus, acceleration of k _tr is due to an increase in one or both rate constants. Our stretch activation results show that with increased SL, the rate of cross-bridge recruitment and force generation (as indicated by k _df) is accelerated but force relaxation and the transition to nonforce-generating states (as indicated by k _rel) is slowed. However, increased SL had a disproportionately greater effect on k _rel than on k _df, as indicated by the twofold increase in k _rel at short SL at all activation levels (Fig. 6). Thus, at short SL, cross-bridge transitions from weakly bound to strongly bound states (f _app) are decelerated while transitions from strongly bound to weakly bound states (g _app) are accelerated likely because of the decreased probability of interaction between cross-bridges and actin. Because k _tr is the sum of the forward and reverse processes of force generation, the disproportionately greater acceleration of g _app at short SL causes an overall acceleration of k _tr despite a decrease in f _app.

Decreased SL slows cross-bridge recruitment because of an increased lateral separation of thick and thin filaments that decreases the probability of interaction between myosin and actin filaments (Millman, 1998). Conversely, increased SL increases force production and accelerates cooperative cross-bridge recruitment because more cross-bridges are already strongly bound to actin, leaving fewer cross-bridges to recruit into strong-binding states, and also by decreasing the lateral separation of the thick and thin filaments such that the interaction between myosin and actin filaments is enhanced, thereby accelerating cross-bridge transitions from weakly bound to strongly bound states. As discussed above, accelerated rates of cross-bridge recruitment (as indicated by increased k _df) with increased SL slowed k _tr while the overall rate of the stretch activation response was accelerated. The dramatic deceleration of the rate of cross-bridge detachment with increased SL dominated the k _tr response such that the overall rate was slowed. In contrast, accelerated rates of cross-bridge detachment with increased SL during the stretch activation response are tempered by a reduction in the number of detached cross-bridges (increased P₂) such that fewer cross-bridges are recruited by stretch (decreased P_df) and cooperative recruitment of cross-bridges into force-generating states is accelerated and the overall rate of the response is accelerated.

Possible Roles of Stretch Activation in the Activation Dependence of Myocardium

Previous studies have shown that stretch activation is an intrinsic property of myocardium (Steiger, 1971, 1977) and plays an important role in the regulation of cardiac contractility (Vemuri et al., 1999; Davis et al., 2001; Stelzer et al., 2006c) by mediating oscillatory work production during ventricular systolic ejection. Here we show that the myocardial stretch activation response is altered by changes in SL, such that as SL increases and force increases, the rate of stretch-induced recruitment of force is accelerated while the rate of force relaxation is slowed. Based on these results and as suggested by Campbell and Chandra (2006), stretch-induced delayed force development enhances systolic force generation at longer muscle lengths and delays force relaxation so that the period of ejection is prolonged and stroke volume is increased. While the stretch-induced delayed force development is likely initiated before systolic ejection, the additional force due to stretch augments force and power output during the latter part of systolic ejection when the Ca²⁺ transient has already decayed to resting levels. Since up to half of the stroke volume may be ejected during late systole (Hunter, 1989), the delayed force response produced will significantly enhance systolic ejection if the delay in the stretch-induced force development is timed appropriately.

The importance of stretch activation is evident in studies that have shown that mutations in sarcomeric proteins that alter the stretch activation response and disrupt the timing of oscillatory work production can compromise systolic function and lead to hypertrophic cardiomyopathy (Vemuri et al., 1999; Stelzer et al., 2006a). Furthermore, it has been shown that in some pathological conditions such as ventricular arrhythmia, the asynchronous electrical activation of the ventricles disrupts in the timing of mechanical activation across the ventricular wall such that some regions of the ventricle become significantly “prestretched” before activation, resulting in compromised cardiac function due to regional mismatches in fiber shortening and force generation during systolic ejection (Prinzen et al., 1999). In the healthy heart, appropriate timing of the stretch activation response is achieved by matching the amplitude and rate of delayed force development to preload, i.e., when SL (and force generation) is increased, an enhanced, longer lasting delayed force response of accelerated rate is also produced. In this way, stretch activation acts as an intrinsic length-sensing mechanism and contributes to the steepness of the Frank-Starling relationship in myocardium. Furthermore, the finding that length-dependent cross-bridge recruitment during oscillatory work is reduced in end-stage human heart failure (Brixius et al., 2003) suggests that disruptions in the mechanisms of force enhancement at long SL, including stretch-induced delayed force development, may contribute to depressed systolic function in this disease.