Skip to main content
PMC home page
The Journal of General Physiology logoLink to The Journal of General Physiology
. 2007 Dec;130(6):547–558. doi: 10.1085/jgp.200709856

Acetylcholine Receptor Gating at Extracellular Transmembrane Domain Interface: the Cys-Loop and M2–M3 Linker

Archana Jha 1, David J Cadugan 1, Prasad Purohit 1, Anthony Auerbach 1
PMCID: PMC2151658  PMID: 18040057

Abstract

Acetylcholine receptor channel gating is a propagated conformational cascade that links changes in structure and function at the transmitter binding sites in the extracellular domain (ECD) with those at a “gate” in the transmembrane domain (TMD). We used Φ-value analysis to probe the relative timing of the gating motions of α-subunit residues located near the ECD–TMD interface. Mutation of four of the seven amino acids in the M2–M3 linker (which connects the pore-lining M2 helix with the M3 helix), including three of the four residues in the core of the linker, changed the diliganded gating equilibrium constant (Keq) by up to 10,000-fold (P272 > I274 > A270 > G275). The average Φ-value for the whole linker was ∼0.64. One interpretation of this result is that the gating motions of the M2–M3 linker are approximately synchronous with those of much of M2 (∼0.64), but occur after those of the transmitter binding site region (∼0.93) and loops 2 and 7 (∼0.77). We also examined mutants of six cys-loop residues (V132, T133, H134, F135, P136, and F137). Mutation of V132, H134, and F135 changed Keq by 2800-, 10-, and 18-fold, respectively, and with an average Φ-value of 0.74, similar to those of other cys-loop residues. Even though V132 and I274 are close, the energetic coupling between I and V mutants of these positions was small (≤0.51 kcal mol−1). The M2–M3 linker appears to be the key moving part that couples gating motions at the base of the ECD with those in TMD. These interactions are distributed along an ∼16-Å border and involve about a dozen residues.

INTRODUCTION

The acetylcholine receptor (AChR) is a large, five-subunit membrane protein that isomerizes between C(losed)- and O(pen)-channel conformations (Edelstein and Changeux, 1998; Unwin, 2000; Karlin, 2002; Lester et al., 2004; Sine and Engel, 2006). This “gating” reaction, which couples a change in structure (and affinity) at two transmitter binding sites with a change in structure (and conductance) at a narrow region of pore, involves the motions of hundreds of residues spread throughout this ∼300-kD protein. The diliganded C↔O transition can occur in ∼1 μs (Maconochie et al., 1995; Chakrapani and Auerbach, 2005), a time scale that is shorter than the resolution of the patch clamp but long compared with many different kinds of protein motion (Jardetzky, 1996; Karplus and Kuriyan, 2005; Boehr et al., 2006). To understand this complex and relatively slow chemical reaction it is useful to illuminate the dynamics of the short-lived intermediate states that link stable C with stable O. We will refer to this ensemble of brief intermediates as the transition region (TR) of the reaction.

Although the structure or function of the TR cannot be probed directly, it is possible to infer its characteristics from the rate constants of the diliganded gating reaction. A rate-equilibrium free energy relationship (REFER) is a log-log plot of the opening rate constant vs. the equilibrium constant (opening rate constant/closing rate constant) for a mutational series. This relationship is often approximately linear with a slope (Φ) that is a fraction between 0 and 1. Φ values for diliganded gating have been measured for >100 different AChR residues, and the emergent map, although incomplete, shows a distinct pattern. There is, approximately, a coarse-grained and decreasing gradient in Φ between the transmitter binding site and gate (Grosman et al., 2000b; Purohit et al., 2007).

Although there are likely to be many possible conformational trajectories through the TR ensemble, a simple model that assumes a single pathway through a one-dimensional, sequential series of intermediate-state transitions accounts surprisingly well for the map of Φ (Zhou et al., 2005). With this model, Φ values provide the relative timing of the gating motion of individual residues, with the limits 1 and 0 marking “early” and “late” (Auerbach, 2007). Alternative interpretations have been proposed, namely that fractional Φ values reflect fractional structures (C-like vs. O-like) of individual side chains at the TR, or heterogeneous structures in the TR arising from multiple pathways. With the interpretation that Φ provides temporal information, the clustering of Φ values in the AChR implies that there are about a dozen nanometer-sized domains comprising residues that exhibit temporally correlated gating motions (“Φ blocks”), and that these domains move back and forth (on ∼50-ns time scales) to link the structural changes at the transmitter binding sites that regulate affinity for agonists with those at a distant “gate” that regulate ion flux. We use this conceptual framework, namely that of brownian movement along a linear sequence of intermediate steps (a “brownian conformational wave”; Auerbach, 2005) for understanding the detailed mechanism of AChR gating.

TR structural transitions occurring near the interface of the ECD and the TMD (mainly in the α subunits) are components of this “wave.” Unwin (2005) proposed that there is an isomerization of backbone bonds in the M2–M3 linker at residue G275, and Lummis et al. (2005) suggested that in the related 5HT3A receptor an isomerization of a proline in this linker is essential for efficient gating. Lee and Sine (2005) provided evidence that the perturbation of a salt bridge at this interface, between R209 in the “preM1” segment and E45 in loop 2, is an important dynamic gating event. Based on cryo-EM analyses of unliganded-closed Torpedo AChRs, Unwin et al. (2002) hypothesized that in diliganded C↔O gating the α subunits undergo a rotation of the inner β sheets of the ECD, which then perturbs loop 2, the top of the M2 (pore-lining) helix, and the gate. Here, we describe the results of Φ-value analyses of residues in the M2–M3 linker and the cys-loop (loop 7), both of which are located at the ECD–TMD interface region. In two companion papers, we describe related observations regarding the effects of mutations of residues in the preM1 (β10–M1) linker, the site of the putative salt bridge (Purohit and Auerbach, 2007a), and residues in the β-core of the ECD (Purohit and Auerbach, 2007b).

The 4-Å structure of Torpedo AChRs (Unwin, 2005) shows that in the α subunits the linker between the M2 and M3 helices consists of four amino acids: P272-L273-I274-G275. Mutation of the homologous proline in 5HT3A receptors (to six different side chains) yields nonfunctional channels that are trafficked normally to the membrane and have wild-type antagonist-binding properties (Lummis et al., 2005), but the substitutions of unnatural amino acids that can undergo a backbone cis–trans isomerization are functional. This suggests that a change in the angle of the M2–M3 backbone is necessary for efficient gating. In AChRs, a full cis–trans isomerization of P272 is not essential for gating because a serine substitution only modestly alters the gating equilibrium constant (Keq; Lee and Sine, 2005). Nonetheless, these same studies show that AChR residue P272 moves in the TR (because a glycine substitution reduces Keq by ∼150-fold) and interacts energetically with V46 in loop 2 (by ∼1.6 kcal/mol).

The flanking regions of the M2–M3 linker, which include residues S269 and A270 in M2 and residues K276 and Y277 in M3, also participate in the gating reaction. Mutation of αS269 increases Keq mainly by increasing the channel opening rate constant (Grosman et al., 2000a; Mitra et al., 2005), and mutation of αY277 increases Keq mainly by decreasing the channel closing rate constant (Cadugan and Auerbach, 2007). This suggests that the gating motions in the α subunit at the top of M2 occur before those at the top of M3. Below, we describe the consequences of αA270 and αK276 mutations.

The M2–M3 linker has also been shown to participate in diliganded gating of various neuronal AChRs (Campos-Caro et al., 1996; Rovira et al., 1998), glycine receptor α1 homomers (Lynch et al., 1997), and GABAC receptor ρ1 homomers (Kusama et al., 1994). In chimeric α7-5HT3A receptors, whole-cell current amplitudes are increased when an Asp side chain is inserted in the flanking M2 region, probably because of an increase in Keq (Castillo et al., 2006). In GABAA receptors, a charge reversal at K279 (αS266 in AChRs, in M2) decreases Keq, and energetic coupling is apparent between this residue and D57 in loop 2 (Kash et al., 2003). Further evidence of the importance of the M2–M3 linker (plus flanking regions) in gating is that mutation causes human disease (Shiang et al., 1993, 1995; Elmslie et al., 1996; Croxen et al., 1997).

The “cys-loop” (β6-β7 linker, or loop 7) is composed of 13 residues bracketed by a disulfide bond (αC128- αC142). In the mouse α-subunit, the cys-loop sequence is: EIIVTHFPFDEQN. Previously, it was shown that mutations of several cys-loop residues (H134, F135, F137, D138, and Q140) increase or decrease Keq, mainly by changing the channel-opening rate (Chakrapani et al., 2004). This Φ-value places the gating motion of the cys-loop before that of M2, and approximately synchronous with that of loop 2. The cys-loop myasthenic mutation V132L reduces the Kd for ACh (by ∼30-fold) at one transmitter binding site but has only a small effect on Keq (Shen et al., 2003). Mutation of residue D138 (to K and A) yields nonfunctional AChRs, whereas an E substitution generates only a small (less than fivefold) change in Keq (Chakrapani et al., 2004; Xiu et al., 2005). In other receptors, it has been shown that the fast activation of whole cell currents from chimeras of α7 (ECD) and glycine (TMD) receptor increases when the α7 cys-loop residues are changed to their glycine receptor counterparts, or when the glycine receptor M2–M3 linker residues are changed to their α7 counterparts (Grutter et al., 2005). An interaction between F135 in the cys-loop and L270/I271 in the M2–M3 linker has been predicted from MD simulations (Cheng et al., 2007). Mutation of D149 in GABAA receptors decreases the amplitudes of whole cell currents, and the mutation of D148 in glycine receptors increases the response EC50, in both cases by charge-dependent mechanisms (Kash et al., 2003; Schofield et al., 2003).

We have quantified the effects of mutations on the diliganded AChR opening and closing rate constants for every residue in the α-subunit M2–M3 linker (positions 270–276) plus six cys-loop residues. The results add to the map of AChR Φ values and shed light on some of the structural transitions of the TR. We conclude that at the ECD–TMD interface the transfer of energy between adjacent Φ blocks occurs along a broad, ∼16-Å boundary and requires the motion of multiple residues.

MATERIALS AND METHODS

Mutagenesis and Expression

Mutants of mouse AChR subunit cDNAs were made by using the QuickChange Site-directed Mutagenesis Kit (Stratagene) and were verified by nucleotide sequencing. Human embryonic kidney fibroblast cells (HEK 293) were transiently transfected using calcium phosphate precipitation. HEK cells were treated with 0.875 mg DNA per 35-mm culture dish in the ratio of 2:1:1:1 (α:β:δ:ɛ) for ∼16 h. Most electrophysiological recordings were made ∼24 h later. We quantified the gating rate constants for a total of 37 different mutants, at 11 different amino acid positions in the M2–M3 linker region and cys-loop.

Electrophysiology

Recordings were performed in cell-attached patch configuration at 22°C. The bath and pipette solutions were Dulbecco's phosphate-buffered saline containing (in mM): 137 NaCl, 0.9 CaCl2, 2.7 KCl, 1.5 KH2PO4, 0.5 MgCl2, and 8.1 Na2HPO4 (pH 7.3). Pipettes made from borosilicate capillaries were coated with Sylgard (Dow Corning Corp.). The average pipette resistance was 10 MΩ. The pipette potential was held at +70 mV, which corresponds to a membrane potential of approximately −100 mV. Single-channel currents were recorded using a PC-505 amplifier (Warner Instrument Corp.) with low-pass filtering at 20 kHz. The currents were digitized at a sampling frequency of 50 kHz using a SCB-68 acquisition board (National Instruments Corp.) and QUB software (www.qub.buffalo.edu).

Agonist (acetylcholine or choline) was added to the pipette solution at a concentration that is approximately five times the closed-conformation equilibrium dissociation constant (Kd; 500 μM or 20 mM, respectively). The choice of agonist was determined by the effect of the mutation. To estimate the gating rate constants it is necessary to identify clusters of openings that arise from a single AChR (see below) and then to measure the lifetimes of open and shut intervals within those clusters. At high agonist concentration, the ability to satisfy both of these criteria depends on the gating equilibrium constant Keq. More specifically, because the closing rate constant (kc) is approximately the same for all agonists (Grosman et al., 2000b), the magnitude of Keq depends mainly on the magnitude of the opening rate constant (ko). In wild-type (wt) AChRs under our experimental conditions, ko with choline (∼120 s−1; see below) or ACh (∼48,000 s−1) is near the lower or upper limit of our estimation capability, respectively. Thus, choline was used to activate constructs in which Keq was larger than in the wt (gain-of-function mutants) and ACh was used to activate constructs in which Keq was smaller than in the wt (loss-of-function mutants). The opening rate constants for un- and monoliganded AChRs are much smaller than that for diliganded AChRs, so even though the concentration of agonist was only five times the Kd, essentially all of the openings were from fully liganded receptors.

Rate Constant Determination

The analyses were done by using QUB software. At 500 μM ACh or 20 mM choline openings occur in clusters with long gaps between clusters reflecting epochs when all of the AChRs in the patch are “desensitized.” Clusters of individual-channel, diliganded C↔O activity were usually selected by eye. We sometimes tested the eye-selection procedure by using a critical time (tcrit) of 50 ms to define a cluster, with equivalent results. Clusters were idealized into noise-free intervals after filtering digitally (12 kHz) by using the segmental k-means algorithm (Qin, 2004) with a C↔O model (starting rate = 100 s−1). The opening and closing rate constants were estimated from the interval durations by using a maximum-interval likelihood algorithm (Qin et al., 1997) after imposing a dead time correction of 25 μs. Usually, the rate constants were estimated by using a two-state, C↔O model because the log likelihood of the fit did not increase after adding additional C or O states. In ∼25% of patches a second closed state was connected to the O state to accommodate a relatively rare (<5% of closed intervals within clusters) and short-lived (∼2 ms) nonconducting state (Elenes and Auerbach, 2002).

Historical reports from our lab of ko for wt AChRs activated by choline range from 53 ± 8 s−1 (mean ± SEM; Zhou et al., 1999) to 257 s−1 (in 140 mM KCl; Grosman and Auerbach, 2000). This degree of variance is larger than typical for other constructs (Table III). More recently, Mitra et al. (2004) report 120 ± 6 s−1 (mean ± SEM) and Corradi et al. (2007) report 95 s−1 (no error given) for ko of wt AChRs activated by 20 mM choline. We suspect that some of the variance in the ko estimate with choline arises from difficulties in identifying single-channel, low open probability clusters, which may be contaminated by sojourns in desensitized states or by openings from overlapping clusters (see above). In support of this hypothesis, we note that mutant constructs showing higher cluster open probabilities have similar variances for ko regardless of whether ACh or choline was used as the agonist. For example, the ko estimates in three patches for αA270F activated by choline were 1601, 1846, and 1706 s−1 (1717 ± 70 s−1; mean ± SEM), whereas those for G275P activated by ACh were 3217, 3756, and 3195 s−1 (3380 ± 183). Regardless of the source, the effect of the uncertainty in ko for the wt/choline construct on the Φ estimate is not major. For instance, normalizing ko for mutants of αA270, a residue that has a “typical” REFER (150-fold range in Keq), using 53, 120, and 250 s−1 as the wt/choline value yields Φ estimates of 0.69 ± 0.05, 0.65 ± 0.07, and 0.56 ± 0.08, respectively.

TABLE III.

Rate and Equilibrium Constants

Construct ko (s−1) kc obs (s−1) kc cor (s−1) Keq Agonist Fold-change in Keq (mut/wt) n
wta 120 834 2583 0.046 Cho 1
wtb 48000 1700 28.2 ACh 1
A270T 25332 (1645) 2692 (611) 3365 (764) 7.53 (1.8) ACh 0.27 3
A270W 591 (38) 319 (79) 852 (212) 0.69 (0.18) Cho 15.0 4
A270F 1717 (70) 346 (36) 924 (96) 1.86 (0.15) Cho 40.4 3
V271W 58 (5.2) 532 (36) 1420 (97) 0.04 (0.002) Cho 0.87 3
V271I 160 (13) 988 (72) 2638 (193) 0.06 (0.007) Cho 1.3 3
V271T 36283 (3899) 972 (71) 1215 (89) 29.9 (5.4) ACh 1.06 2
V271F 36 (2) 161 (9) 430 (25) 0.08 (0.006) Cho 1.73 3
P272G 2737 (274) 4821 (141) 6026 (364) 0.45 (0.03) ACh 0.02 4
P272S 29600 (1751) 3252 (141) 4065 (995) 7.28 (2.2) ACh 0.26 4
P272A 2431 (42) 83 (131) 222 (46) 10.9 (1.3) Cho 237 4
L273V 20967 (931) 2649 (146) 3311 (182) 6.3 (1.0) ACh 0.22 3
L273T 32496 (1345) 2486 (313) 3108 (391) 10.45 (2.0) ACh 0.37 3
L273Y 25825 (3001) 1791 (586) 2239 (732) 11.53 (4.0) ACh 0.40 3
I274V 16057 (455) 1770 (278) 2213 (347) 7.25 (1.2) ACh 0.25 3
I274L 26707 (1291) 3494 (257) 4368 (321) 6.11(0.68) ACh 0.21 3
I274F 6210 (499) 4608 (448) 5760 (561) 1.07 (0.18) ACh 0.04 3
I274T 439 (59) 25085 (1093) 31354 (1366) 0.014 (0.002) ACh 0.0005 5
G275L 36716 (1028) 3189 (293) 3986 (366) 9.21 (0.60) ACh 0.32 3
G275S 28365 (3174) 3915 (710) 4894 (888) 5.79 (0.52) ACh 0.21 2
G275P 3380 (183) 8510 (439) 10638 (549) 0.32 (0.03) ACh 0.01 3
K276D 35 (3) 492 (43) 1314 (116) 0.03 (0.004) Cho 0.65 2
K276A 31689 (4998) 2778 (219) 3473 (273) 9.12 (0.83) ACh 0.33 3
K276W 16628 (2353) 1942 (35) 2428 (43) 6.84 (0.88) ACh 0.24 3
K276I 42316 (4227) 5985 (418) 7481 (522) 5.65 (0.69) ACh 0.20 3
V132A 11949 (1755) 2658 (192) 3322 (240) 3.59 (0.79) ACh 0.13 2
V132I 3093 (263) 1579 (270) 1973 (337) 1.57 (0.14) ACh 0.06 3
V132H 1436 (232) 1860 (201) 2325 (252) 0.62 (0.05) ACh 0.20 3
V132F 135 (38.5) 10250 (795) 12812 (994) 0.01 (0.004) ACh 0.0004 2
T133A 16211 (1320) 1940 (143) 2425 (178) 6.68 (0.59) ACh 0.24 3
T133F 7321 (776) 1364 (117) 1705 (146) 4.3 (0.50) ACh 0.15 3
T133V 15793 (1971) 2259 (1190) 2824 (1488) 5.59 (3.11) ACh 0.20 2
T133H 16751 1915 2394 6.99 ACh 0.25 1
T133I 17257 (1666) 2127 (312) 2659 (390) 6.5 (1.61) ACh 0.23 2
T133S 21966 1658 2072 10.6 ACh 0.37 1
H134Sc 18474 2506 7.37 ACh 0.26
H134R 14730 (385) 2496 (172) 3120 (215) 4.79 (0.4) ACh 0.17 4
H134Q 8884 (659) 2599 (248) 3249 (310) 2.79 (0.3) ACh 0.1 3
F135T 8978 (1227) 2833 (784) 3541 (980) 2.53 (0.32) ACh 0.09 3
F135Y 99 669 1786 0.05 Cho 1.08 1
F135L 7080 (794) 3552 (331) 4441 (413) 1.59 (0.33) ACh 0.06 2
F137L 248 (44) 875 (165) 2336 (441) 0.11 (0.04) Cho 2.4 3
F137Y 69 (5) 783 (57) 2091 (152) 0.03 (0.004) Cho 0.66 3
Open in a new tab

ko, apparent opening rate constant; kc obs, apparent closing rate constant; kc cor, closing rate constant after correction for channel block; n, number of patches. Values are mean (±SEM). No rate constants are reported for P136G, A, S, and Y because no currents were detected for these constructs (5 patches each, 10 min/patch).

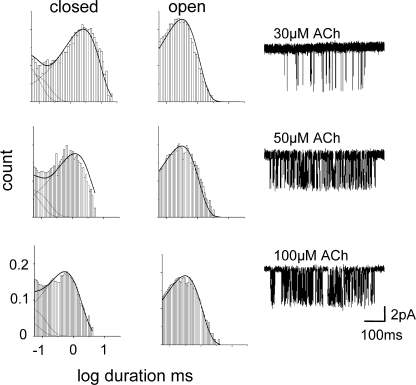
The Kd for acetylcholine was estimated only for the αI274F construct (Fig. 4). Open and closed interval durations were obtained at three different ACh concentrations (30, 50, and 100 μM). The two agonist binding sites were assumed to be equivalent and independent (Salamone et al., 1999), and the interval durations at all three concentrations were fitted together by using a C↔AC↔A2C↔A2O kinetic model (A = agonist; dead time = 35, 75, and 35 μs, respectively) that had four rate constants as free parameters: single-site association (k+, scaled by [A]), single-site dissociation (k-), ko, and kc.

Figure 4.

Figure 4.

Open in a new tab

The mutation I274 shows wild-type binding properties. Interval durations were obtained at three different ACh concentrations (30, 50, and 100 μM) and the association and dissociation rate constants were estimated by fitting with a kinetic scheme that assumed two equal and independent transmitter binding steps followed by a single gating step (dead time = 35, 75, and 35 μs, respectively). Left, interval duration histograms and square-root probability density functions (solid lines) calculated from the globally optimized rate constants. Right, an example cluster at each concentration. Total number of events analyzed were 48,776. The optimal rate constants were: k+ (single-site association) = 141 μM−1s−1, k- (single-site dissociation) = 14,781 s−1. We calculate Kd (k−/k+) = 105 μM. For comparison, one estimate for wild-type AChRs is k+ = 169 μM−1s−1 and k− = 16,904 s−1, Kd= 100 μM (Akk et al., 1996). There is no significant effect of this mutation on ACh binding to closed AChRs.

REFER Analysis

Φ was estimated as the slope of the rate-equilibrium free energy relationship (REFER), which is a plot of log ko vs. log Keq (see Figs. 3 and 5).

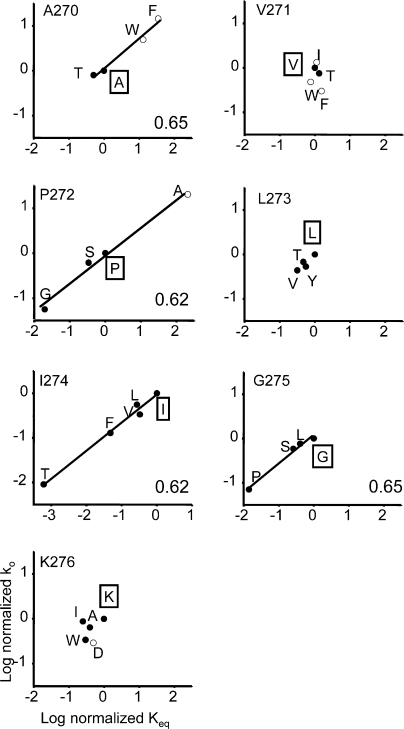
Figure 3.

Figure 3.

Open in a new tab

Rate-equilibrium free energy relationships (REFERs) for all seven M2–M3 linker residues. Φ (indicated in the lower right corner of each plot; see Table II) is estimated as slope of a linear fit. The wild-type side chain is boxed. The agonist was either ACh (500 μM, closed circles) or choline (20 mM, open circles). Both the opening rate and equilibrium constants have been normalized (mutant/wt). Φ values could not be determined for positions V271, L273, and K276 because the change in Keq was too small. The average Φ-value for the M2–M3 linker is ∼0.64.

Figure 5.

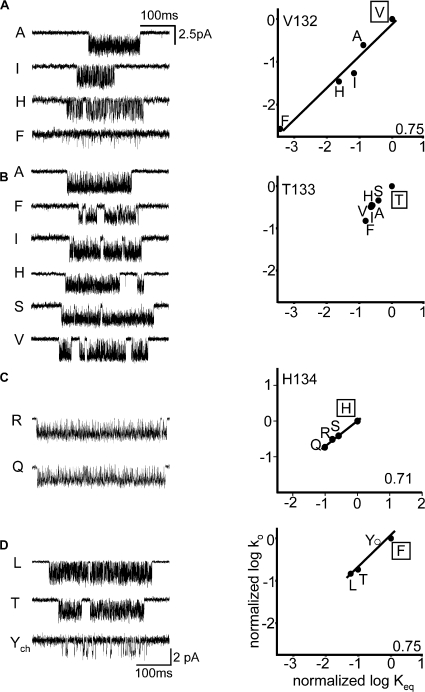
Figure 5.

Open in a new tab

Kinetic analysis of cys-loop residues. (A) Example clusters and REFER for αV132. The Φ-value was 0.75. (B) Example clusters and REFER for αT133. The change in Keq was too small to allow an estimation of Φ. (C) Example clusters and REFER for αH134. The Φ-value was 0.71. (D) Example clusters and REFER for αF135. The Φ-value was 0.75. The wild-type side chain is boxed. The agonist was either ACh (500 μM, closed circles) or choline (20 mM, open circles).

The apparent values of ko and kc both underestimate the true opening and closing rate constants. ko is underestimated because the binding sites are not fully saturated. The factor by which ko is underestimated (F) is a function of the agonist concentration ([A]) and the equilibrium dissociation constant (Kd; Colquhoun and Hawkes, 1981): F = ([A]/2Kd)/(1 + ([A]/2Kd)). In our experiments [A]/Kd = 5 for both ACh and choline, hence F ≈ 0.71 for both agonists. Assuming that the mutations did not alter Kd, the normalized (wt/mut) apparent ko values for both agonists could therefore combined without correction in the REFER without adding bias to the Φ estimate.

The observed closing rate constant (kc obs) underestimates the true value because of channel block by the agonist. The equilibrium dissociation constant for this block (KB) is ∼12 mM for choline (Purohit and Grosman, 2006) and ∼2 mM for ACh (Auerbach and Akk, 1998), thus the value [A]/KB was different for 20 mM choline (∼1.67) vs. 0.5 mM ACh (∼0.25). Using the approximation that unblock from the closed channel is negligible (Purohit and Grosman, 2006), we calculate the underestimation factor as (1 + [A]/KB). Thus, kc obs underestimates kc by a factor of ∼2.67 in the choline experiments but only by 1.25 in the ACh experiments. To eliminate this agonist bias in the Keq estimate and the REFER slope, kc obs was multiplied by the appropriate factor in order obtain a corrected estimate, kc cor. Note that because the lifetime of the agonist-blocked channel is shorter than our time resolution, the apparent amplitudes of the choline- vs. ACh-induced currents were reduced approximately by the same factor as the underestimation of kc.

For residues that showed both an increase and a decrease in Keq upon mutation, the rate constants for AChRs activated by choline or by ACh were combined into the same REFER after normalizing both ko and Keq by the corresponding wt values. In our REFERs, the wt values used for ko and Keq were 120 s-1 and 0.046 for AChRs activated by choline and 48,000 s-1 and 28.2 for AChRs activated by ACh. The normalized rate and equilibrium constants with either agonist fall approximately on the same line. Similarly, Φ values for the δS268 mutant family were the same regardless of whether the AChRs were activated by choline or acetylthiocholine (Grosman et al., 2000a), and the Φ-value for M4 residue T422 was the same with choline (on an δS268N background, 0.54+0.02; Mitra et al. 2004) and ACh (Bouzat et al., 2000). These results strongly support the notion that a change in agonist (or an independent background mutation) is like a primary mutation insofar as it can be treated as a simple perturbation in the energy landscape of the gating reaction (rather than as something that creates an entirely new reaction pathway). We document this observation further in Purohit and Auerbach (2007b).

The slope of the REFER was estimated by an unweighted, linear fit in OriginPro 7.0. We did not weight the residuals by using the errors on either axis because it was previously shown that for REFERs of M2 residues, this procedure changed only the standard deviation of the Φ estimate and not the mean (Purohit et al., 2007). For a linear, sequential, bounded reaction mechanism, Φ provides relative temporal information regarding the movement of the perturbed side chain in the gating reaction (1 is “early,” 0 is “late,” and the same is “synchronous”) (Auerbach, 2007).

We used a weighted, k-means cluster analysis algorithm (in QUB) to determine the number (n) of distinct populations of Φ-value and to assign each residue to one of these populations (Fig. 6). Φ values were segregated into populations and a minimum sum squared deviation (SSQ) was computed. We tested values of n up to and including 6, and, in order to find the global minimum SSQ, for each trial we used 50 different random starting assignments. The weight for each Φ-value was the inverse of the SEM obtained from the unweighted linear fit of the REFER.

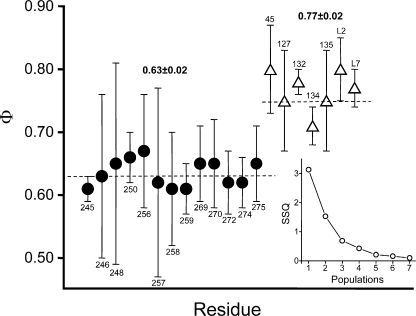
Figure 6.

Figure 6.

Open in a new tab

Cluster analysis of Φ values. The Φ values for the indicated α-subunit residues (in the M2 helix, M2–M3 linker, cys-loop, and loop 2) were grouped into populations by using a segmental k-mean algorithm (see Materials and methods). Inset, the sum squared deviation (SSQ) decreases sharply between 1 and 2 populations and gradually thereafter, indicating that the most likely number of Φ populations is two. The mean ± SEM values for these populations (dashed lines) are shown. Each residue was assigned either to the Φ = 0.77 population (open triangles) or the Φ = 0.63 population (filled circles). The error bars on Φ are ±SD. Y127 and residues in loop 2 and the cys-loop belong to the 0.77 population, and many residues in M2 and the M2–M3 linker belong to the 0.63 population. L2 and L7 are the mean Φ values for loop 2 and cys-loop residues measured by Chakrapani et al. (2004). Other sources: M2 (Mitra et al., 2005; Purohit et al., 2007), E45 (Purohit and Auerbach, 2007a), and Y127 (Purohit and Auerbach, 2007b).

All structures were displayed by using PYMOL (DeLano Scientific).

Online Supplemental Material

The supplementary animation shows the timing of domains motions in C-–O gating. The frame sequence was generated by simulation (QUB) using the model C↔X1↔X2↔X3↔X4↔O, where C is stable-closed, O is stable-open, and X is a short-lived, nonconducting intermediate state. The rate constants (ms−1) for the individual steps were: C→X1 = 5.3, X1→X2 = X2→X3 = X3→X4 = X4→O = 6000, X1→C = 2370, X2→X1 = 5598, X3→X2 = 4716, X4→X3 = 12000, and O→X4 = 9.09. Each of the bitmaps were made by using PYMOL (the domain motions are arbitrary) and assembled into a movie by using Videomach.

RESULTS

M2–M3 Linker

In all vertebrate α1 subunits the residues between the C terminus of M2 and the N terminus of M3 (positions 270–276) are completely conserved: AVPLIGK. Table I gives the sequence alignment for other mouse AChR subunits, and Fig. 1 shows the structure of this M2–M3 linker region in the Torpedo α subunit (2bg9.pdb; Unwin, 2005). The core of the M2–M3 linker is the sequence PLIG (residues 272–275). In mouse, in 16 AChR subunit sequences the Pro and Leu are completely conserved and the Ile and Gly residues are present in 12 and 13 sequences, respectively.

TABLE I.

M2–M3 Linker Sequence Alignment of Mouse AChR Subunits

Subunit
α1 A V P L I G K
α2 V I P L I G E
α3 V I P L I G E
α4 V I P L I G E
α6 V I P L V G E
α7 S V P L I A Q
α9 – V P L I G K
α10 – V P L I G K
β1 A V P L I I I
β2 D V P L V G K
β3 V I P L I G E
β4 D I P L I G K
δ A I P L V G K
γ A V P L I S K
ɛ S V P L L G R
Open in a new tab

In the α1 subunit, the M2–M3 linker is A270-K276.

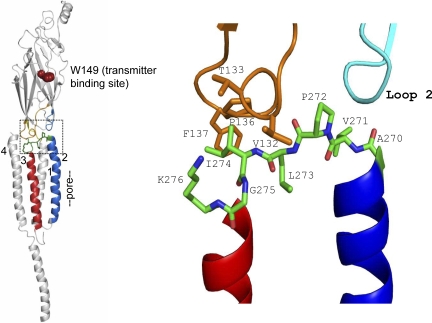
Figure 1.

Figure 1.

Open in a new tab

The αɛ subunit M2–M3 linker (from 2bg9.pdb; Unwin, 2005). Left, in each AChR subunit the extracellular domain (ECD) is mostly β-sheet and the transmembrane domain (TMD) has four α helices. Residue W149 (brown) marks the transmitter binding site, M2 (blue) lines the pore and is linked to M3 (red) at the ECD/TMD interface (boxed). Right, expanded view of the boxed area. M2–M3 linker residues A270-K276 are colored by element: green, carbon; red, oxygen and blue, nitrogen. The colored domains are: orange, cys-loop; cyan, loop 2. M1, M4, loop9, and the preM1 linker have been removed for clarity. The core sequence of the M2–M3 linker is PLIG (272–275).

Previously, S269 (in M2) and Y277 (in M3) were found to have significantly different Φ values, 0.65 ± 0.06 (Mitra et al., 2005) and 0.34 ± 0.11(Cadugan and Auerbach, 2007). We attempted to measure Φ for all seven of the intervening residues (Figs. 2 and 3; Table II). At three positions, 11 different mutants exhibited approximately wild-type gating kinetics (V271→F, I, T, and W; L273→T, V, and Y; K276→A, D, I, and W) and for these residues a Φ-value could not be estimated. At the remaining four positions at least one mutation caused a >10-fold change in Keq and a Φ-value could be estimated. The order of sensitivity, based on the magnitude of the largest excursion in Keq for a point mutation (in both α subunits), was P272 (A→G) > I274 (I→T) > A270 (F→T) > G275 (G→P) (Table III). At A270 and P272 the mutations could either increase or decrease Keq, whereas at the other positions the mutations only decreased Keq or had no effect (Fig. 3). In summary, the P I and G of the core, and the A at the terminus of M2, were sensitive to mutation.

Figure 2.

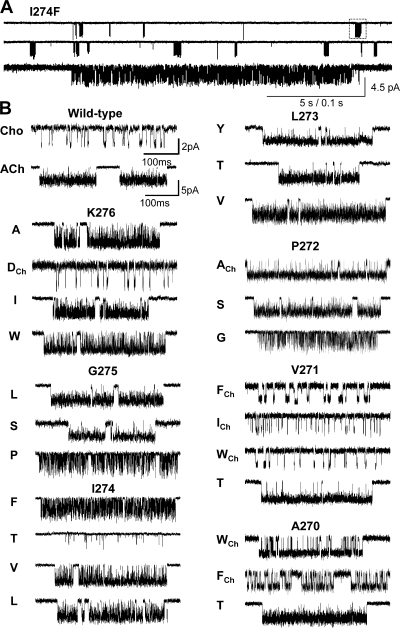
Figure 2.

Open in a new tab

Example single-channel current clusters for different M2-M3 linker constructs. (A) Continuous recording at low time resolution (I274F activated by 500 μM acetylcholine). Openings are down. The long gaps between clusters of opening reflect times when all channels in the patch are desensitized. Each cluster mainly reflects C↔O gating of a single AChR. Below, one cluster shown on an expanded time scale. (B) Example clusters of different constructs. Currents were activated either by 20 mM choline (indicated by a subscript) or by 500 μM ACh.

TABLE II.

Φ Values

Position Φ (±SD) Fold-change in Keq
A270 0.65 (0.07) 150
V271 – 2
P272 0.62 (0.05) 11850
L273 – 4
I274 0.62 (0.04) 2014
G275 0.65 (0.06) 88
K276 – 5
V132 0.75 (0.08) 2820
T133 – 6
H134 0.71 (0.03) 10
F135 0.75 (0.12) 18
F137 – 4
Open in a new tab

The fold-change in Keq is for the most extreme constructs at each position. The REFERs are shown in Figs. 3 and 5. Φ values could not be determined accurately for positions where the fold-change in Keq was <10-fold.

Fig. 3 plots the experimentally determined kinetic parameters in the form of rate-equilibrium free energy relationships (REFERs), the slope of which (around Keq = 1) is called Φ. The Φ values for all four mutation-sensitive residues ranged from 0.62 ± 0.05 (P272) to 0.65 ± 0.07 (L270) (Table II). Overall, the mean value was 0.64, which is the same as those for many residues in the M2 helix (S269, V259, L258, L257, and F256) (Grosman et al., 2000a; Mitra et al., 2005; Purohit et al., 2007). The Φ-value was approximately independent of the agonist used to activate the protein (see the REFERs for A270 and P272, Fig. 3).

Fig. 4 shows currents elicited by different concentrations of ACh for one M2–M3 linker mutation, I274F. The mutation had a large effect on Keq but essentially no effect on Kd, the equilibrium dissociation constant for ACh binding to closed AChRs.

Cys-loop

In the Torpedo AChR structure model, atoms from three cys-loop residues (Fig. 1) contact (<4 Å) residue I274 in the M2–M3 linker: V132, T133, and P136. We examined the effects of mutations of these three residues, plus H134, F135, and F137 (Table III).

Fig. 5 A (right) shows a REFER analysis for four mutations of position V132 (I, H, A, and F). All of the mutations decreased Keq (by up to 2,800-fold, for V→F) and the Φ-value was 0.75 ± 0.08 (Table II). Fig. 5 B (right) shows that six mutations of position T133 were examined (V, A, S, H, I, and F) but the net effect on Keq was only approximately sixfold, so no estimate of Φ was obtained. Fig. 5 C (right) and D (right) show the results for H134 (Q, R, and S) and F135 (Y, L, and T). Here, at least one mutation decreased Keq >10-fold, and corresponding Φ values for these two positions were 0.71 ± 0.03 and 0.75 ± 0.12, respectively. No functional AChRs could be recorded whatsoever for G, A, S, and Y mutations of position P136 (five patches each, ∼10 min per patch). We do not know if these AChRs fail to express or express and fail to gate. Two mutations of F137 (L and Y) exhibited a less than threefold change in Keq (Table III).

Φ Populations and Coupling

Fig. 6 shows the results of using a statistical test (k- means) to ascertain the number of populations of Φ for residues in loop 2, the cys-loop, the M2–M3 linker, and the M2 helix of the α-subunit, and to assign each residue to one of these populations. The most likely number of populations is two. Residues in loop 2 and the cys-loop belong with the group having a mean Φ of 0.77 ± 0.02, and those in the M2–M3 linker and M2 group belong to the group having a mean Φ of 0.63 ± 0.02.

We next measured the coupling energy between I274V in the M2–M3 linker and V132I in the cys-loop. We chose these mutations because each causes a substantial decrease in Keq (3.9- and 17.9-fold, respectively), and because in 2bg9.pdb the distance between these two residues is <4 Å. Combined, these two mutations caused a 161-fold decrease in Keq, whereas independent action predicts that would be only a 69-fold decrease in Keq. This result indicates that there is a modest degree of coupling between the I274 and V132 side chains (+0.51 kcal/mol).

DISCUSSION

In the α-subunit, about half of the residues in the M2–M3 linker and the cys-loop that have been examined so far substantially change Keq. This indicates that these amino acids experience a change in energy between C and O, which implies a change in structure, which implies a gating movement. Clearly, the ECD–TMD interface is a dynamic zone in the diliganded gating TR. The biggest observed energy changes occur in I274 and P272 in the M2–M3 linker and in V132 in the cys- loop. Note that the cys-loop analysis is not yet complete because four residues have not yet been examined in detail (E129, I130, I131, and E139).

The M2–M3 linker and many M2 residues have approximately the same Φ-value, ∼0.64 (Grosman et al., 2000a; Mitra et al., 2005; Purohit et al., 2007). This group constitutes the third Φ-block to move in the α-subunit in the channel-opening process. Φ ∼ 0.93 for the first block (the region surrounding the transmitter binding sites) and Φ ∼ 0.77 for the second block (cys-loop and loop 2). If Φ values provide the relative timing of gating motions, then this pattern suggests that in the TR the motions of the M2–M3 linker and many positions in M2, including residues near equatorial “gate” and the intracellular domain, are approximately synchronous and occur after the motions of the binding sites and loop 2 and the cys-loop. Note that Φ values for M2 residues 260–268 have not yet been reported so we cannot be certain that the M2–M3 linker and the gate motions occur by the movement of a contiguous structural element.

The average Φ-value for V132, H134, and F135 was 0.73, which makes these residues members of the second α-subunit gating block (Φ ∼ 0.77; Fig. 6). Additional members of this Φ-block include other cys-loop residues (D138, Q140), residues in loop 2 (E45, V46, N47, Q48), and Y127 on β-strand 6. In the AChR α-subunit, the 0.77 Φ-block is a slab (∼6 nm3) that is interposed between the transmitter binding site and the top of the TMD (Fig. 7). Because V132 is close to P272 and I274 in the M2–M3 linker, these amino acids may participate in the propagation of the conformational wave between the 0.77 and 0.63 Φ blocks.

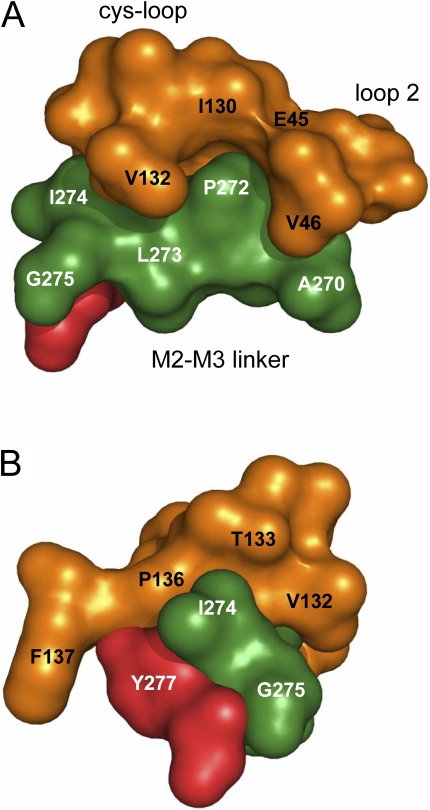
Figure 7.

Figure 7.

Open in a new tab

The ECD–TMD interface. The M2–M3 linker residues that were sensitive to mutation are labeled (P272 > I274 > G275 > A270). (A) Side view, from the middle of the ɛ-subunit. The lumen of the pore is to the right and the membrane bilayer is to the left.Orange, cys-loop (left) and loop 2 (right). Green, M2–M3 linker. Red, residue Y277. The N terminus of the M3 helix is Y277 and the C-terminus of the M2 helix is A270 (see Fig 1). (B) Radial view, from the bilayer.

There is an abrupt, step decrease in Φ (∼0.3 units) between G275 in the M2–M3 linker and Y277 in the M3 helix. The intervening residue, K276, is not sensitive to mutation (to A, D, I, or W) and therefore does not experience a change in energy between C and O. In 2bg9.pdb the atoms of residues G275 and Y277 are separated by <4 Å, yet G275 and its neighbor I274 are part of the Φ = 0.63 block, whereas Y277 is part of the Φ = 0.31 block. Hence, by definition, G275 and Y277 are at a Φ-block boundary. The breakpoint in Φ at K276 suggests that this residue is a point of flexure about which the M2 and M3 helices move, asynchronously, during gating. A similar pattern of a nonmoving residue interposed between amino acid members of two different Φ blocks (also have a different in Φ of ∼0.3 units) was previously observed in the M2 helix of the δ and α subunits (Cymes et al., 2002; Mitra et al., 2005). A nonmoving residue at a Φ-block boundary may be a common, but not absolute, feature of the Φ- map.

Insofar as a change in Keq indicates movement and Φ gives relative temporal information, we can place the cys-loop and M2–M3 linker movements into the overall framework for the α-subunit channel-opening process (see Video 1, available at http://www.jgp.org/cgi/content/full/jgp.200709856/DC1). First, residues near the transmitter binding sites (loops A, B, and C) move (Φ ≈ 0.93; purple; Grosman et al., 2000b; Chakrapani et al., 2003) followed by residues in loop 2 and the cys-loop (Φ ≈ 0.77; orange; Chakrapani et al., 2004). The next group to move is the Φ ≈ 0.63 block (green), which includes the M2–M3 linker and much of M2 (Grosman et al., 2000a; Mitra et al., 2005; Purohit et al., 2007). This map of Φ values is consistent with the notion that during channel opening the presence of an agonist triggers the gating motions of loops A, B, and C, which trigger those in the cys-loop and loop 2, which trigger those in the M2–M3 linker and in many M2 residues. Subsequent α-subunit motions are three residues near the middle of M2 (Purohit et al., 2007) and in M4 (Φ ≈ 0.54; blue; Mitra et al., 2004; Purohit et al., 2007), followed by two M2 equatorial residues plus M3 and preM1 (Φ ≈ 0.31; red; Mitra et al., 2005; Cadugan and Auerbach, 2007; Purohit et al., 2007; Purohit and Auerbach, 2007a). We imagine that the Φ-block gating motions are sequential and stochastic, and that the structural transitions of the TR occur as a random walk, with the conformational dynamics of AChR gating characterized by brownian motion of approximately nanometer-sized domains. We estimate that the time scale of the individual Φ-block motions is in the ∼50-ns range (Auerbach, 2005).

The results shed some light on the mechanisms that have been proposed for the propagation of the AChR channel opening conformational cascade between ECD and the TMD (the cys-loop/loop 2 and M2–M3 linker/M2 Φ blocks). The structure-motivated suggestion of a steric interaction (“pin-into-socket”) between loop 2 and M2 (V46↔S269; Miyazawa et al., 2003) is supported by three functional observations: (1) Φ values decrease abruptly between these two residues (0.78 and 0.65, respectively), (b) the hydrophobicity of the side chains at both positions is correlated with the magnitude of the change in Keq (Chakrapani et al., 2004), and (3) the effects of mutations at these two sites are coupled energetically (Lee and Sine, 2005). In addition, we find that A270 (in M2) is also sensitive to mutation and, because A270 and V46 are close in the Torpedo structure, we propose that this residue is an additional candidate for coupling ECD and TMD gating motions. However, the mutation-induced changes in Keq at P272 or I274 were larger than those at S269 and A270, by more than a factor of 10 (Table III). These sensitive residues are far from the site of the “pin-into-socket” interaction, which suggests that the V46↔S269/A270 coupling energies are only part of the story and that other forces at other sites also contribute to the total ECD↔TMD interaction energy.

With regard to the hypothesis that the isomerization of an M2–M3 linker proline or glycine is an important event in gating, the observation that P, S, and L substitutions at G275, and G, S, and A substitutions at P272 yield functional AChRs indicates that a substantial change in the angle of backbone atoms at either of these two positions is not an absolute requirement for the propagation of the opening conformational change between the ECD and TMD. It is therefore unlikely that a full cis–trans isomerization of the M2–M3 linker backbone is the “trigger” for gating in muscle AChRs, although a partial isomerization of these bonds may occur in the C↔O process.

The M2–M3 linker and cys-loop are key structural elements governing the propagation of the channel-opening and -closing conformational changes between the ECD and TMD. Although we still do not know the precise molecular forces that underpin the ECD↔TMD connection, the results indicate that they are spread along a broad, ∼16-Å boundary that projects radially from the lumen of the pore (residues S269 and A270) to the lipid bilayer. This interface contains atoms from loop 2 and the cys-loop in the ECD, and (at least) M2, M3, and M4 in the TMD, and includes more than a dozen amino acids (Fig. 7). Our result do not support the notion that a single interaction is the “key” event in the C↔O transition. Rather, we think that at the ECD–TMD hydrophobic interactions, charge/dipolar interactions, and, perhaps, small changes in the angles of backbone bonds all contribute to the energy barrier that separates C from O. Finally, it is important to note that residues in the M2–M3 linker and cys-loop in other subunits, and in nearby segments in all subunits (loop 9, the β10–M1 linker, and M1–M4) may also serve to link ECD–TMD gating motions in the AChR.

Supplemental Material

Supplemental Material Index

Acknowledgments

We would like to thank Mary Teeling, Mary Merritt, and Birte Steidl for technical assistance.

This work was supported by the National Institutes of Health (NS-23513).

Olaf S. Andersen served as editor.

Abbreviations used in this paper: AChR, acetylcholine receptor; ECD, extracellular domain; REFER, rate-equilibrium free energy relationship; TMD, transmembrane domain; TR, transition region; wt, wild type.

References

  1. Akk, G., S. Sine, and A. Auerbach. 1996. Binding sites contribute unequally to the gating of mouse nicotinic alpha D200N acetylcholine receptors. J. Physiol. 496:185–196. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Auerbach, A. 2005. Gating of acetylcholine receptor channels: brownian motion across a broad transition state. Proc. Natl. Acad. Sci. USA. 102:1408–1412. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Auerbach, A. 2007. How to turn the reaction coordinate into time. J. Gen. Physiol. 130:543–546. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Auerbach, A., and G. Akk. 1998. Desensitization of mouse nicotinic acetylcholine receptor channels. A two-gate mechanism. J. Gen. Physiol. 112:181–197. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Boehr, D.D., H.J. Dyson, and P.E. Wright. 2006. An NMR perspective on enzyme dynamics. Chem. Rev. 106:3055–3079. [DOI] [PubMed] [Google Scholar]
  6. Bouzat, C., F. Barrantes, and S. Sine. 2000. Nicotinic receptor fourth transmembrane domain: hydrogen bonding by conserved threonine contributes to channel gating kinetics. J. Gen. Physiol. 115:663–672. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Cadugan, D.J., and A. Auerbach. 2007. Conformational dynamics of the αM3 transmembrane helix during acetylcholine receptor channel gating. Biophys. J. 93:859–865. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Campos-Caro, A., S. Sala, J.J. Ballesta, F. Vicente-Agullo, M. Criado, and F. Sala. 1996. A single residue in the M2-M3 loop is a major determinant of coupling between binding and gating in neuronal nicotinic receptors. Proc. Natl. Acad. Sci. USA. 93:6118–6123. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Castillo, M., J. Mulet, J.A. Bernal, M. Criado, F. Sala, and S. Sala. 2006. Improved gating of a chimeric α7-5HT3A receptor upon mutations at the M2-M3 extracellular loop. FEBS Lett. 580:256–260. [DOI] [PubMed] [Google Scholar]
  10. Chakrapani, S., and A. Auerbach. 2005. A speed limit for conformational change of an allosteric membrane protein. Proc. Natl. Acad. Sci. USA. 102:87–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Chakrapani, S., T.D. Bailey, and A. Auerbach. 2003. The role of loop 5 in acetylcholine receptor channel gating. J. Gen. Physiol. 122:521–539. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Chakrapani, S., T.D. Bailey, and A. Auerbach. 2004. Gating dynamics of the acetylcholine receptor extracellular domain. J. Gen. Physiol. 123:341–356. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Cheng, X., I. Ivanov, H. Wang, S.M. Sine, and J.A. McCammon. 2007. Nanosecond time scale conformational dynamics of the human α7 nicotinic acetylcholine receptor. Biophys J. 93:2622–2634. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Colquhoun, D., and A.G. Hawkes. 1981. On the stochastic properties of single ion channels. Proc. R. Soc. Lond. B. Biol. Sci. 211:205–235. [DOI] [PubMed] [Google Scholar]
  15. Corradi, J., G. Spitzmaul, M.J. De Rosa, M. Costabel, and C. Bouzat. 2007. Role of pairwise interactions between M1 and M2 domains of the nicotinic receptor in channel gating. Biophys. J. 92:76–86. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Croxen, R., C. Newland, D. Beeson, H. Oosterhuis, G. Chauplannaz, A. Vincent, and J. Newsom-Davis. 1997. Mutations in different functional domains of the human muscle acetylcholine receptor alpha subunit in patients with the slow-channel congenital myasthenic syndrome. Hum. Mol. Genet. 6:767–774. [DOI] [PubMed] [Google Scholar]
  17. Cymes, G.D., C. Grosman, and A. Auerbach. 2002. Structure of the transition state of gating in the acetylcholine receptor channel pore: a phi-value analysis. Biochemistry. 41:5548–5555. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Edelstein, S.J., and J.P. Changeux. 1998. Allosteric transitions of the acetylcholine receptor. Adv. Protein Chem. 51:121–184. [DOI] [PubMed] [Google Scholar]
  19. Elenes, S., and A. Auerbach. 2002. Desensitization of diliganded mouse muscle nicotinic acetylcholine receptor channels. J. Physiol. 541:367–383. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Elmslie, F.V., S.M. Hutchings, V. Spencer, A. Curtis, T. Covanis, R.M. Gardiner, and M. Rees. 1996. Analysis of GLRA1 in hereditary and sporadic hyperekplexia: a novel mutation in a family cosegregating for hyperekplexia and spastic paraparesis. J. Med. Genet. 33:435–436. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Grosman, C., and A. Auerbach. 2000. Asymmetric and independent contribution of the second transmembrane segment 12′ residues to diliganded gating of acetylcholine receptor channels: a single-channel study with choline as the agonist. J. Gen. Physiol. 115:637–651. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Grosman, C., F.N. Salamone, S.M. Sine, and A. Auerbach. 2000. a. The extracellular linker of muscle acetylcholine receptor channels is a gating control element. J. Gen. Physiol. 116:327–340. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Grosman, C., M. Zhou, and A. Auerbach. 2000. b. Mapping the conformational wave of acetylcholine receptor channel gating. Nature. 403:773–776. [DOI] [PubMed] [Google Scholar]
  24. Grutter, T., L.P. de Carvalho, V. Dufresne, A. Taly, S.J. Edelstein, and J.P. Changeux. 2005. Molecular tuning of fast gating in pentameric ligand-gated ion channels. Proc. Natl. Acad. Sci. USA. 102:18207–18212. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Jardetzky, O. 1996. Protein dynamics and conformational transitions in allosteric proteins. Prog. Biophys. Mol. Biol. 65:171–219. [DOI] [PubMed] [Google Scholar]
  26. Karlin, A. 2002. Emerging structure of the nicotinic acetylcholine receptors. Nat. Rev. Neurosci. 3:102–114. [DOI] [PubMed] [Google Scholar]
  27. Karplus, M., and J. Kuriyan. 2005. Molecular dynamics and protein function. Proc. Natl. Acad. Sci. USA. 102:6679–6685. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Kash, T.L., A. Jenkins, J.C. Kelley, J.R. Trudell, and N.L. Harrison. 2003. Coupling of agonist binding to channel gating in the GABA(A) receptor. Nature. 421:272–275. [DOI] [PubMed] [Google Scholar]
  29. Kusama, T., J.B. Wang, C.E. Spivak, and G.R. Uhl. 1994. Mutagenesis of the GABA rho 1 receptor alters agonist affinity and channel gating. Neuroreport. 5:1209–1212. [DOI] [PubMed] [Google Scholar]
  30. Lee, W.Y., and S.M. Sine. 2005. Principal pathway coupling agonist binding to channel gating in nicotinic receptors. Nature. 438:243–247. [DOI] [PubMed] [Google Scholar]
  31. Lester, H.A., M.I. Dibas, D.S. Dahan, J.F. Leite, and D.A. Dougherty. 2004. Cys-loop receptors: new twists and turns. Trends Neurosci. 27:329–336. [DOI] [PubMed] [Google Scholar]
  32. Lummis, S.C., D.L. Beene, L.W. Lee, H.A. Lester, R.W. Broadhurst, and D.A. Dougherty. 2005. Cis-trans isomerization at a proline opens the pore of a neurotransmitter-gated ion channel. Nature. 438:248–252. [DOI] [PubMed] [Google Scholar]
  33. Lynch, J.W., S. Rajendra, K.D. Pierce, C.A. Handford, P.H. Barry, and P.R. Schofield. 1997. Identification of intracellular and extracellular domains mediating signal transduction in the inhibitory glycine receptor chloride channel. EMBO J. 16:110–120. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Maconochie, D.J., G.H. Fletcher, and J.H. Steinbach. 1995. The conductance of the muscle nicotinic receptor channel changes rapidly upon gating. Biophys. J. 68:483–490. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Mitra, A., T.D. Bailey, and A.L. Auerbach. 2004. Structural dynamics of the M4 transmembrane segment during acetylcholine receptor gating. Structure. 12:1909–1918. [DOI] [PubMed] [Google Scholar]
  36. Mitra, A., G.D. Cymes, and A. Auerbach. 2005. Dynamics of the acetylcholine receptor pore at the gating transition state. Proc. Natl. Acad. Sci. USA. 102:15069–15074. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Miyazawa, A., Y. Fujiyoshi, and N. Unwin. 2003. Structure and gating mechanism of the acetylcholine receptor pore. Nature. 423:949–955. [DOI] [PubMed] [Google Scholar]
  38. Purohit, P., and A. Auerbach. 2007. a. Acetylcholine receptor gating at extracellular-transmembrane domain interface: the ‘pre-M1’ linker. J. Gen. Physiol. 130:559–568. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Purohit, P., and A. Auerbach. 2007. b. Acetylcholine receptor gating: movement in the α-subunit extracellular domain. J. Gen. Physiol. 130:569–579. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Purohit, P., A. Mitra, and A. Auerbach. 2007. A stepwise mechanism for acetylcholine receptor channel gating. Nature. 446:930–933. [DOI] [PubMed] [Google Scholar]
  41. Purohit, Y., and C. Grosman. 2006. Block of muscle nicotinic receptors by choline suggests that the activation and desensitization gates act as distinct molecular entities. J. Gen. Physiol. 127:703–717. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Qin, F. 2004. Restoration of single-channel currents using the segmental k-means method based on hidden Markov modeling. Biophys. J. 86:1488–1501. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Qin, F., A. Auerbach, and F. Sachs. 1997. Maximum likelihood estimation of aggregated Markov processes. Proc. Biol. Sci. 264:375–383. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Rovira, J.C., J.J. Ballesta, F. Vicente-Agullo, A. Campos-Caro, M. Criado, F. Sala, and S. Sala. 1998. A residue in the middle of the M2-M3 loop of the β4 subunit specifically affects gating of neuronal nicotinic receptors. FEBS Lett. 433:89–92. [DOI] [PubMed] [Google Scholar]
  45. Salamone, F.N., M. Zhou, and A. Auerbach. 1999. A re-examination of adult mouse nicotinic acetylcholine receptor channel activation kinetics. J. Physiol. 516:315–330. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Schofield, C.M., A. Jenkins, and N.L. Harrison. 2003. A highly conserved aspartic acid residue in the signature disulfide loop of the α1 subunit is a determinant of gating in the glycine receptor. J. Biol. Chem. 278:34079–34083. [DOI] [PubMed] [Google Scholar]
  47. Shen, X.M., K. Ohno, A. Tsujino, J.M. Brengman, M. Gingold, S.M. Sine, and A.G. Engel. 2003. Mutation causing severe myasthenia reveals functional asymmetry of AChR signature cystine loops in agonist binding and gating. J. Clin. Invest. 111:497–505. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Shiang, R., S.G. Ryan, Y.Z. Zhu, A.F. Hahn, P. O'Connell, and J.J. Wasmuth. 1993. Mutations in the α1 subunit of the inhibitory glycine receptor cause the dominant neurologic disorder, hyperekplexia. Nat. Genet. 5:351–358. [DOI] [PubMed] [Google Scholar]
  49. Shiang, R., S.G. Ryan, Y.Z. Zhu, T.J. Fielder, R.J. Allen, A. Fryer, S. Yamashita, P. O'Connell, and J.J. Wasmuth. 1995. Mutational analysis of familial and sporadic hyperekplexia. Ann. Neurol. 38:85–91. [DOI] [PubMed] [Google Scholar]
  50. Sine, S.M., and A.G. Engel. 2006. Recent advances in Cys-loop receptor structure and function. Nature. 440:448–455. [DOI] [PubMed] [Google Scholar]
  51. Unwin, N. 2000. The Croonian Lecture 2000. Nicotinic acetylcholine receptor and the structural basis of fast synaptic transmission. Philos. Trans. R. Soc. Lond. B Biol. Sci. 355:1813–1829. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Unwin, N. 2005. Refined structure of the nicotinic acetylcholine receptor at 4A resolution. J. Mol. Biol. 346:967–989. [DOI] [PubMed] [Google Scholar]
  53. Unwin, N., A. Miyazawa, J. Li, and Y. Fujiyoshi. 2002. Activation of the nicotinic acetylcholine receptor involves a switch in conformation of the α subunits. J. Mol. Biol. 319:1165–1176. [DOI] [PubMed] [Google Scholar]
  54. Xiu, X., A.P. Hanek, J. Wang, H.A. Lester, and D.A. Dougherty. 2005. A unified view of the role of electrostatic interactions in modulating the gating of Cys loop receptors. J. Biol. Chem. 280:41655–41666. [DOI] [PubMed] [Google Scholar]
  55. Zhou, M., A.G. Engel, and A. Auerbach. 1999. Serum choline activates mutant acetylcholine receptors that cause slow channel congenital myasthenic syndromes. Proc. Natl. Acad. Sci. USA. 96:10466–10471. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Zhou, Y., J.E. Pearson, and A. Auerbach. 2005. Φ-Value analysis of a linear, sequential reaction mechanism: theory and application to ion channel gating. Biophys. J. 89:3680–3685. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental Material Index
jgenphysiol_jgp.200709856_index.html (682B, html)
jgenphysiol_jgp.200709856_1.html (3.7KB, html)
Download video file (6.9MB, mov)

Articles from The Journal of General Physiology are provided here courtesy of The Rockefeller University Press

RESOURCES