Importance of Hydration and Dynamics on the Selectivity of the KcsA and NaK Channels

Abstract

Fundamental concepts governing ion selectivity in narrow pores are reviewed and the microscopic factors responsible for the lack of selectivity of the NaK channel, which is structurally similar to the K⁺-selective KcsA channel, are elucidated on the basis of all-atom molecular dynamics free energy simulations. The results on NaK are contrasted and compared with previous studies of the KcsA channel. Analysis indicates that differences in hydration of the cation in the pore of NaK is at the origin of the lack of selectivity of NaK.

INTRODUCTION

Selectivity is one of the most fascinating properties of ion channels. The x-ray structure of the KcsA channel has revealed the basic architectural organization of a K⁺-selective ion channel (Doyle et al., 1998; Zhou et al., 2001). The recent determination of the structure of the NaK channel by Shi et al. (2006), a nonselective cationic channel apparently able to conduct both K⁺ and Na⁺, provides fresh insights into the possible molecular organization of Na⁺-selective tetrameric channels.

Though there are some notable differences, the overall organization of the nonselective NaK channel is very similar to that of the K⁺-selective KcsA channel. Furthermore, some of the NaK binding sites are almost identical to their KcsA counterparts, as any angstrom-scale differences would be well within the range of atomic thermal fluctuations for flexible protein binding sites at room temperature (even accounting for the moderate resolution afforded by the current diffraction data).

These puzzling observations suggest that some factors, other than the average geometry of the protein atoms, should be responsible for the lack of selectivity of the NaK channel. Previous computational studies of KcsA have shown that it is essential to take the influence of flexibility and dynamical factors into account to explain the microscopic basis of ion selectivity (Noskov et al., 2004). Simple considerations based on static structures appear to be inherently insufficient. The goal of this article is to review the fundamental concepts governing ion selectivity and examine the microscopic factors that could be responsible for the lack of selectivity of the NaK channel using free energy perturbation molecular dynamics (FEP/MD) simulations based on atomic models.

MATERIALS AND METHODS

The atomic simulation system comprises the NaK channel embedded in an explicit dipalmitoylphosphatidylcholine (DPPC) membrane solvated by 150 mM NaCl aqueous solution. The total number of atoms in the system is 56,001. All calculations were performed using the program CHARMM (Brooks et al., 1983) with the PARAM27 force field (MacKerell et al., 1998). The relative free energy of Na⁺ and K⁺ was computed using alchemical FEP/MD simulations (Kollman, 1993). The FEP/MD methodology is identical to that used previously (Noskov et al., 2004). In brief, the system is simulated at constant pressure (1 Atm) and constant temperature (315 K) with periodic boundary conditions (Feller et al., 1995), with no truncation of electrostatic interactions using a particle mesh Ewald algorithm (Essmann et al., 1995) Several of the free energy computations on KcsA (site S1, S2, S3) and NaK (site S2 and S3) were redone using the AMBER force field (Cornell et al., 1995) and the ion parameters from Åqvist (1990). For each site in the NaK channel, the FEP/MD selectivity computations are performed on the basis of representative multi-ion configurations. There are always at least two ions in the pore. It is assumed that ions do not occupy adjacent binding sites in the most probable occupancy states as suggested by previous computations on KcsA (Åqvist and Luzhkov, 2000; Bernèche and Roux, 2001). Furthermore, the site S2 is water filled during the FEP/MD computations for S3 and S4. No ion is detected in this site in the x-ray data, which is indicative of a low affinity site. Accordingly, the occupancy state for the FEP/MD computation on site S2 is [S0=Ca²⁺, S2=K⁺→Na⁺, S3=water, S4=water, Cavity=water]. The state for the S3 computation is [S0=Ca²⁺, S2=water, S3=K⁺→Na⁺, S4=water, Cavity=water]. The state for the S4 computation is [S0=Ca²⁺, S2=water, S3=water, S4=K⁺→Na⁺, Cavity=water]. For the computations on the cavity site, the state is [S0=Ca²⁺, S2=Na⁺, S3=water, S4=water, Cavity= K⁺→Na⁺]. The computed ΔΔG [K⁺ to Na⁺] are −0.9 (−1.1), 1.1 (1.7), −0.9, and −0.6 kcal/mol for S2, S3, S4, and the cavity, respectively (numbers in parenthesis were obtained with the AMBER force field). A trajectory of 2.2 ns following an equilibration of at least 1.5 ns was used for each of the separate free energy calculations. All values are reported in Table I together with previous results on KcsA (Bernèche and Roux, 2001; Noskov et al., 2004). We estimate that the accuracy and overall significance of the calculated free energies is roughly on the order of 1 kcal/mol, based on the difference between the computations with 1K4C (Noskov et al., 2004) and 1BL8 (Bernèche and Roux, 2001) and the comparison between the CHARMM PARAM27 and AMBER force fields. For the simulations with the AMBER force field, the systems were reequilibriated for 1.5 ns before starting the free energy computations. The hydration number of K⁺ and Na⁺ in the various binding sites were computed from the average of 800 ps of MD for each configuration; statistical error was estimated by comparing block averages.

TABLE I.

Calculated ΔΔG (in kcal/mol) for the Binding Sites of KcsA and NaK

Site	KcsA (1K4C)	KcsA (1BL8)	NaK
S0	−1.3	−1.1
S1	2.6 (2.1)	2.8
S2	5.3 (4.8)	6.6	−0.9 (−1.1)
S3	1.8 (2.7)	2.4	1.1 (1.7)
S4	−1.2	−1.5	−0.9
Cavity	−0.8	−0.2	−0.6

The calculations on the KcsA channel were done for the x-ray structures 1K4C (Noskov et al., 2004) and 1BL8 (Bernèche and Roux, 2001) using the CHARMM PARAM27 force field (MacKerell et al., 1998). Results in parentheses were obtained with the AMBER force field (Cornell et al., 1995) and the Åqvist ion parameters (Åqvist, 1990).

The toy models of freely fluctuating ligands include only the ion surrounded by the ligands in the first coordination shell, with nothing else (thus, no periodic boundary conditions and no particle mesh Ewald are applied). For example, in the case of the model with eight carbonyl-like ligands, there are 17 particles (eight carbon C, eight oxygen O, and one ion). The free energy computations for the toy models were performed with the same FEP methodology and the same values of thermodynamic coupling parameter. To ensure thermalization of such a small system, the FEP/MD simulations were generated with Langevin dynamics at a temperature of 315 K with a friction coefficient equal to 25 ps⁻¹ (the value of the friction coefficient has no impact on equilibrium thermodynamics and calculated free energies). The Lennard-Jones parameters and partial charges (see Table S1, available at http://www.jgp.org/cgi/content/full/jgp.200609633/DC1) were all taken from the all-atom PARAM27 CHARMM force field, and the electrostatic interactions between the particles is not altered by any dielectric shielding (the surrounding space is vacuum with dielectric constant equal to 1). The ligands are restrained by a flat-bottom half-harmonic potential. The restraining potential, defined as a function of the distance R between the ion and the oxygen ligands, is equal to K(R − 3.5)² when R > 3.5 Å, and zero otherwise. The force constant, K, is equal to 100 kcal/mol/Ų (the precise value of K has no impact on the results). The ligands around the ion in the toy model are allowed to move freely in any direction and that no restraint prevent the collapse of the ligands to cradle the small Na⁺ ion; absolutely no restraining force is applied to the ligands for R < 3.5 Å. For comparison, the calculations with the toy models were repeated using the AMBER force field. All results are given in Table II.

TABLE II.

The Variation of ΔΔG as a Function of a Toy Model Ligand Composition

Number of carbonyls	Number of water molecules	Number of carboxylates	ΔΔG (kcal/mol)
8	0	0	6.2	(4.1)
7	1	0	4.8	(3.6)
6	2	0	2.3	(3.1)
5	3	0	−0.7	(2.2)
4	4	0	−2.1	(0.5)
6	0	0	3.4	(1.9)
5	1	0	3.2	(1.7)
4	2	0	0.3	(0.9)
7	0	1	−1.1	(−1.0)
6	1	1	−1.3	(−1.2)
5	2	1	−2.0	(−1.9)
4	2	1	−2.8	(−2.2)
3	2	1	−3.4	(−2.5)

The results are based on the FEP computations done on a simple model of one cation surrounded by dynamical ligands allowed to move freely within a sphere of radius 3.5 Å using the CHARMM PARAM27 force field (MacKerell et al., 1998). Results in parenthesis were obtained with the AMBER force field (Cornell et al., 1995) and the Åqvist ion parameters (Åqvist, 1990).

Online Supplemental Material

The supplemental material (available at http://www.jgp.org/cgi/content/full/jgp.200609633/DC1) includes one table (Table S1) with the partial atomic charges and the Lennard-Jones parameters used for the toy models.

RESULTS

Fundamental Concepts

It is worthwhile reviewing the fundamental concepts governing Na⁺/K⁺ selectivity in narrow pores. Although kinetic factors must be taken into consideration for a complete description of ions fluxes, the present discussion will be limited to ion-binding selectivity, which is governed by equilibrium thermodynamics.

Small alkali ions are very strongly hydrated in the bulk phase; the hydration free energy of Na⁺ and K⁺ is about −98 kcal/mol and −80 kcal/mol, respectively (Friedman and Krishnan, 1973). To be “recognized” by a protein, an ion must shed at least part of its first hydration shell in the bound state. For an ion to bind favorably, the free energy cost for dehydration must be compensated by interactions gained in the binding site. Selectivity arises when the difference in free energies of ions in the binding site departs from the corresponding difference in the bulk. It follows that ion selectivity of binding is fundamentally governed by differences in relative free energies, and that the problem of ion selectivity can be stated from the point of view of thermodynamic equilibrium as,

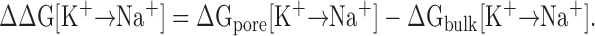(1)

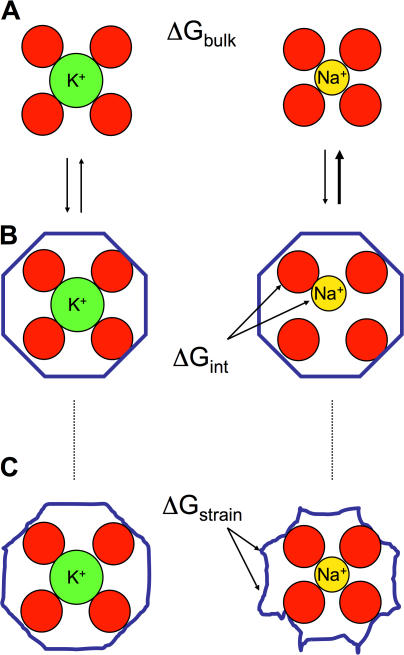
(For simplicity, the bracket [K⁺→Na⁺] will be omitted in the following.) The difference of 18 kcal/mol in the hydration free energies of Na⁺ and K⁺ ions, corresponding to ΔG_bulk, sets the fundamental “baseline” for the Na/K selectivity of all biological ion channels (specific for Na⁺ or for K⁺). At the simplest level, the concepts invoked in host–guest chemistry (Dietrich, 1985), in which a host molecule with a (preorganized) cavity binds an ion of the appropriate radius, provide a basis for a rational discussion of ΔG_pore. For example, selectivity for Na⁺ over K⁺ might be understood by imagining a cavity that would fit Na⁺ well but that would be too small to hold K⁺. In contrast, selectivity for K⁺ over Na⁺ is more puzzling because it is the larger of the two cations that is favored. The most intuitively appealing explanation of K⁺ selectivity is the concept of the “snug-fit” proposed in the early 1970s (Bezanilla and Armstrong, 1972). As illustrated in Fig. 1 (A and B), the snug-fit mechanism posits that the binding site is, for structural reasons, rigidly constrained in an optimal geometry so that a dehydrated K⁺ fits with proper coordination but that Na⁺ is too small and is, thus, poorly coordinated by the host. Selectivity then comes about from the difference in the interaction of the ion with the coordinating ligands compared with the hydration free energy.

Figure 1.

Illustration of fundamental concepts in ion selectivity. In the top, K⁺ and Na⁺ are pictured in bulk solution with their first hydration shell. The difference in hydration free energy ΔG_bulk between these two cations is ∼18 kcal/mol. Binding to a rigid host (B) with a cavity size matching precisely a K⁺ ion (left) does not provide a favorable environment for the smaller Na⁺ (right). In this case, selectivity arises from the poor coordination interaction free energy ΔG_int between the ion and its rigid host. This is the classical snug-fit mechanism (Bezanilla and Armstrong, 1972). However, selectivity may also be achieved by a flexible host (C) able to deform and adapt to both K⁺ and Na⁺ ion, as long as there is a sufficient buildup of strain energy ΔG_strain This situation is characteristic of an induced-fit mechanism.

The concept of snug-fit as pictured in Fig. 1 (A and B) is obviously an idealization. In reality, molecules are flexible and may be able to structurally deform and adapt (to some extent) to a bound ion. This situation, characteristic of an induced-fit mechanism, is pictured in Fig. 1 C. When there is flexibility, the net difference in the direct ion–ligand interaction energy may exactly balance the difference in hydration free energy for both K⁺ and Na⁺ and, yet, selectivity may be preserved as long as there is a sufficient buildup of unfavorable energy to deform and adapt the host for a given ion. This relates to the classical concept of strain energy invoked in host–guest chemistry (Dietrich, 1985). At first sight, the contribution from strain energy may seem somewhat counterintuitive because both ions appear well coordinated in the bound complexes (Fig. 1 C). For example, a visual examination of a crystallographic structure with a bound K⁺ would be unable to reveal if one is dealing with the situation of Fig. 1 B (left) or 1 C (left). Nonetheless, the indirect effect of strain on the relative free energy ΔG_pore is mathematically rigorous and unambiguous. One should note that the concept of strain energy in host–guest chemistry is traditionally associated with structural distortions of the host (e.g., involving bonds, angles, and dihedrals). The implication is that size selectivity would be expected to vanish in the limit of a flexible host without sufficient structural stiffness. Quantitatively, the effective elastic restoring forces associated with the molecular stiffness are inversely proportional to the magnitude of the atomic thermal fluctuations (Allen et al., 2004). It is shown below that local factors—other than architectural deformations—unexpectedly contribute to the strain energy.

The K⁺-selective KcsA Channel

These classical ideas can be tested and illustrated by carrying detailed computations on the basis of the KcsA channel. Results from previous studies of KcsA are summarized in Table I. According to all-atom free energy MD simulations (Noskov et al., 2004), the most selective binding site of the KcsA, S2, favors K⁺ over Na⁺ by ∼5 kcal/mol; the result is 5.3 and 4.8 kcal/mol with the CHARMM PARAM27 (MacKerell et al., 1998) and AMBER (Cornell et al., 1995) force fields, respectively. Nonetheless, the existence of significant thermal fluctuations of the carbonyl groups lining the selectivity filter (∼0.8 Å RMS), much larger than the size difference between Na⁺ and K⁺ (∼0.38 Å), seems somewhat at odds with a very selective binding site. Furthermore, it is difficult to imagine how there could be a sufficient buildup of structural strain energy to explain such a robust selectivity (Allen et al., 2004). The carbonyl ligands in the selectivity filter display “liquid-like” dynamics at the sub-angstrom level. Turning off the carbonyl–carbonyl repulsion annihilates the selectivity of the site S2 (Noskov et al., 2004), which indicates that the carbonyl cage forming the binding site is not significantly restrained by the surrounding atoms. Results with a semisynthetic KcsA-like K⁺ channel recently confirmed the extensive flexibility of the selectivity filter (Valiyaveetil et al., 2006), in accord with the conclusions from previous computational studies (Noskov et al., 2004; Bernèche and Roux, 2005).

This leads to the hypothetical but fundamental question: could selectivity for K⁺ over Na⁺ be maintained, even in the absence of any sub-angstrom structural stiffness? To address this question, we considered an exceedingly simple “toy model” of eight freely fluctuating carbonyl groups (total of 17 particles). This minimalistic model is a caricature of reality intended to illustrate the concept of selectivity by flexible ligands. By construction, the model possesses no sub-angstrom structural stiffness whatsoever; a harmonic force brings back the carbonyls if they get farther than 3.5 Å from the ion, but no structural forces prevent the carbonyls from collapsing to cradle the small Na⁺ ion. Surprisingly, the toy model is found to be robustly selective for K⁺ over Na⁺ by 6.2 kcal/mol using the CHARMM PARAM27 force field (MacKerell et al., 1998) and 4.1 kcal/mol using the AMBER (Cornell et al., 1995) force field. Analysis shows that the contribution from the ion–ligands interaction cancels out exactly the offset in hydration free energy, and that it is the variation in the ligand–ligand electrostatic repulsion that establishes the selectivity for K⁺ over Na⁺.

The role of ligand–ligand repulsion in dynamical systems can be understood very simply by analogy with the concept of strain energy used in host–guest chemistry (Dietrich, 1985). However, while the classical concept of strain energy in host–guest chemistry is traditionally associated with structural deformations of the host, in the present case strain is realized via “through-space” electrostatic interactions between the ligands coordinating the cation without any sub-angstrom information from the architecture of the protein. The strain energy that gives rise to the selectivity for K⁺ over Na⁺ in the toy model corresponds to a buildup of electrostatic repulsion between the ligands forming the coordination shell of the ion. It should be emphasized that the electrostatic repulsion does not prevent the carbonyl oxygens from approaching close enough from one another to form a cage small enough to coordinate the smaller Na⁺ ion; as in the classical view of strain energy (Fig. 1 C), both K⁺ and Na⁺ are well coordinated.

The key role of specific interactions can be highlighted with a thermodynamic decomposition of the results of FEP/MD simulations, ΔG = ΔH − TΔS. This shows that the relative solvation free energy of ions in the binding site, ΔG_pore, is largely dominated by relative enthalpic contributions, ΔH_pore, and that relative entropic effects, −TΔS_pore, are less important (this does not imply that the absolute contribution from entropy is negligible). This is fortunate because variations in ΔH_pore are relatively straightforward to interpret as they involve direct changes in the average potential energy components. The latter can be calculated directly from unbiased all-atom MD simulations of the channel with Na⁺ or K⁺. Here, ΔH_pore is dominated by two opposing terms: the ion–ligand interaction, which favors a small cation, and the ligand–ligand interaction, which favors a large cation. In going from K⁺ to Na⁺, the average change in ion–ligand attraction is about −28.3 kcal/mol, whereas the change in ligand–ligand repulsion is about +14.3 kcal/mol, yielding a ΔΔG of ∼4 kcal/mol favoring K⁺ over Na⁺ (after accounting for the change in ΔG_bulk), close to the result from FEP/MD computations. This analysis explains why turning off the carbonyl–carbonyl repulsion can have a large impact on selectivity in KcsA in all-atom FEP/MD computations, while not affecting the coordination structure (Noskov et al., 2004; Noskov and Roux, 2006). One should note that the ligand–ligand repulsion energy does change when substituting K⁺ by Na⁺ in the binding site, showing that the carbonyls do approach closer from each other to coordinate the smaller Na⁺ ion (i.e., the effect of the repulsion is not to prevent the carbonyl oxygen atoms from approaching closer from each other).

As long as its structural integrity is maintained (within ∼1 Å), a flexible site with eight carbonyl groups has the intrinsic propensity to select K⁺ over Na⁺ by virtue of the electrostatic properties of the ligands. In such a context, selectivity is expected to be very sensitive to the number and the dipole moment of the coordinating ligands. Modifying the number and/or the type of ligands involved in coordination of the ion is thus a potent mechanism for altering the selectivity of a flexible binding site. As illustrated in Table II, small changes in hydration, in particular, can have a big impact. For example, a toy model of eight carbonyls is K⁺ selective (∼6 kcal/mol), but progressively replacing the carbonyls by water molecules leads to a loss of selectivity (Noskov and Roux, 2006). A system of five carbonyls and three waters is nonselective with CHARMM while a system of four carbonyls and four waters is nonselective with AMBER. In both cases, there is a systematic loss of selectivity for each water molecule that replaces a carbonyl group (∼1.8 kcal/mol and 0.8 kcal/mol per water using CHARMM and AMBER, respectively). An interesting question is whether it is possible to achieve selectivity for a smaller ion in the limit of no structural rigidity. One way to select Na⁺ over K⁺ is to introduce a high-field ligand in the first coordination shell of the ion (Eisenman, 1962, Noskov et al., 2004; Noskov and Roux, 2006). Replacement of a single carbonyl by a negatively charged carboxylate group is sufficient to annihilate the K⁺ selectivity in the toy model (−1.1 kcal/mol). For example, a flexible binding site comprising one carboxylate with two water molecules and three carbonyls yields a robust selectivity for Na⁺ (−3.4 kcal/mol with CHARMM and −2.5 kcal/mol with AMBER). Obviously, a number of variations are possible.

The Nonselective NaK Channel

The above considerations provide the essential elements to understand the lack of selectivity of the NaK channel. Previous molecular dynamics (MD) free energy simulations (Bernèche and Roux, 2001; Noskov et al., 2004) with the CHARMM PARAM27 force field (MacKerell et al., 1998) as well as additional computations based on the AMBER force field (Cornell et al., 1995) all indicate that the binding site S2 corresponds to the most K⁺-selective region of the pore of KcsA (see Table I). This is consistent with one of the most striking structural features of the NaK selectivity filter, where the site S2 is widened sufficiently to hold up a “droplet” of approximately three water molecules. To further understand the impact of this structural feature of the NaK pore on selectivity, all-atom free energy MD simulations based on the NaK channel embedded in a solvated lipid membrane were performed (see Fig. 2). The results are summarized in Table I. Those computations confirm that in the NaK channel, the selectivity of the site S2 is annihilated, with a ΔΔG of −0.9 kcal/mol and −1.1 kcal/mol with CHARMM and AMBER, respectively. In NaK, the site S3 is slightly selective for K⁺ (1.1 kcal/mol with CHARMM and 1.7 kcal/mol with AMBER), though somewhat less than in KcsA (1.8 kcal/mol with CHARMM and 2.7 kcal/mol with AMBER). For both KcsA and NaK the site S4 is marginally selective for Na⁺. Therefore, disruption of the site S2 thus appears as the major factor explaining why the NaK channel permits conduction of both K⁺ and Na⁺. This observation is consistent with previous results on KcsA (Bernèche and Roux, 2001; Noskov et al., 2004).

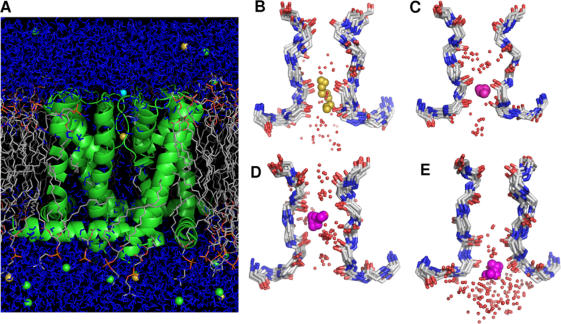
Figure 2.

Molecular dynamics simulations of the NaK channel. (A) Atomic simulation system comprising the NaK channel and the DPPC bilayer solvated by a 150 mM NaCl aqueous solution (total of 56,001 atoms). (B and C) Superposition of 10 instantaneous configurations taken from MD simulations illustrating the coordination and partial hydration of Na⁺ (B) and K⁺ (C) in site S3 (Na⁺, yellow; K⁺, magenta; water oxygens, red dots). (D and E) Superposition of 10 frames from MD simulations illustrating K⁺ coordination and partial hydration in sites S2 (D) and S4 (E). The average number of water is 2.3 around Na⁺ in S3 (B), and is 2.5, 2.1, and 2.4 around K⁺ in S2 (D), S3 (C), and S4 (E).

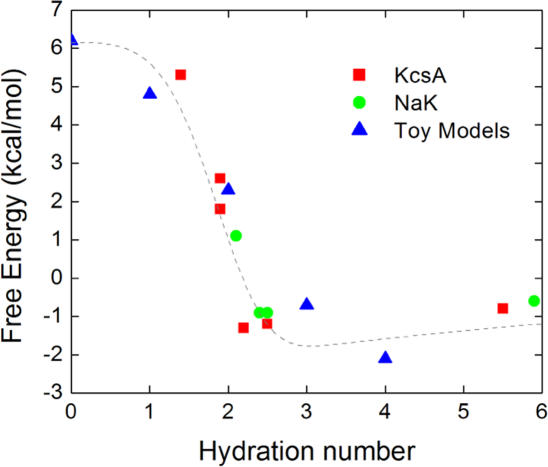
An important factor appears to be the difference in partial ion hydration between the binding sites of KcsA and NaK. Average hydration numbers computed from MD trajectories are reported in Table III. The differences between the various binding sites of KcsA and NaK are small but statistically well defined. A Na⁺ in the binding sites of NaK is slightly more hydrated than in the corresponding KcsA sites. In KcsA, cations (K⁺ or Na⁺) are hydrated typically by less than two water molecules in the selective sites S1–S3. In the NaK channel there are more water molecules in the first shell of K⁺. The differences are more striking in the case of a Na⁺ bound in S3 due to the widening of the pore at S2 (Fig. 2 B); there are 2.3 water molecules for NaK in contrast to 1.9 water molecules for KcsA. Such differences in hydration number between the KcsA and NaK channels are somewhat counterintuitive because in a static view, a bound ion would be expected to make contact with the two adjacent water molecules in the single file along the narrow pore. However, ion, protein atoms, and water molecules are all undergoing thermal fluctuations at room temperature and there are subtle variations. For example, the Na⁺ bound in the S3 site of NaK does not remain at the center of the cage of eight carbonyls, but fluctuates extensively near its upper and lower edge where it can coordinate water molecules (see Fig. 2 B). Transient contacts with additional water molecules are thus possible without significant distortion of the binding sites. Even though the variations in partial hydration are small, they have nonetheless an important impact on relative free energies. This is illustrated in Fig. 3 where the key results from Tables I–III have been combined. The figure shows that an increase in the average hydration number correlates strongly with a loss of selectivity for K⁺ in favor of Na⁺. This qualitative trend appears to hold for the binding sites of the KcsA and NaK channels, as well as for the toy models with carbonyl and water molecules.

TABLE III.

Average Hydration Number of K ⁺ in the Selectivity Filter of KcsA and NaK

Sites	KcsA	NaK
S0	2.2 ± 0.5 (2.4 ± 0.4)
S1	1.9 ± 0.2 (1.9 ± 0.2)
S2	1.4 ± 0.1 (1.4 ± 0.1)	2.5 ± 0.4 (2.7 ± 0.2)
S3	1.9 ± 0.2 (1.9 ± 0.2)	2.1 ± 0.3 (2.3 ± 0.3)
S4	2.5 ± 0.5 (2.2 ± 0.4)	2.4 ± 0.1 (2.3 ± 0.2)
Cavity	5.5 ± 0.2 (6.0 ± 0.2)	5.9 ± 0.1

Number in parentheses is for Na⁺. The averages were determined by counting the water oxygens within a sphere of 3 Å around the ion during MD.

Figure 3.

Relative free energy ΔΔG as a function of the average hydration number. The free energy results were taken from Table I for all the binding sites of KcsA and NaK and from Table II for the toy models with eight ligands (eight carbonyls, seven carbonyls and one water, six carbonyls and two water, etc.). The free energies correspond to the computations with the CHARMM force field. The average hydration numbers were taken from Table III in the case of K⁺ occupying the given binding sites. The dotted line is only a visual guide.

Comparing a Selective and a Nonselective Binding Site

Shi et al. (2006) proposed that structural differences arising from the protein atoms surrounding the ion-binding sites might account (through geometric constraints) for the observed size selectivity of KcsA and NaK. The underlying assumption is that the geometry of the binding sites is more stiffly enforced in the case of the highly selective KcsA (e.g., Fig. 1 B), but not so in the more permissive NaK (e.g., Fig. 1 C). Such a structural mechanism has a clear implication: the geometry of a “stiff” and selective (KcsA) or “flexible” and permissive (NaK) binding site should respond differently to the presence of a bound K⁺ or a Na⁺.

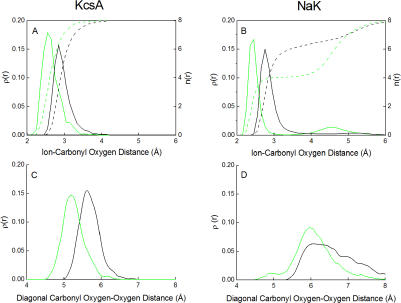
To shed some light on this issue, we compare the site S3 in NaK, which is essentially nonselective, with the site S2 in KcsA, which is highly selective. One would expect that the geometry of S3 in NaK would be significantly different with a bound Na⁺ than with a bound K⁺. In contrast, the geometry of S2 in KcsA should be closely maintained, whether a K⁺ or a Na⁺ is bound. To characterize the average structure of the binding sites in KcsA and NaK, we calculate the ion–carbonyl and carbonyl–carbonyl radial distribution functions from the MD trajectories. The results are shown in Fig. 4. The ion–carbonyl oxygen radial distribution function (top) shows that both ions K⁺ (black) and Na⁺ (green) are in direct contact with their coordinating oxygen ligands in those binding sites; the peaks are around 2.4 and 2.8 Å for Na⁺ (green) and K⁺ (black), respectively. However, there are clear differences in coordination number (dashed line) between the two binding sites. The coordination number rises rapidly up to eight ligands in the case of the S2 site in KcsA, while it rises more slowly in the case of the site S3 in NaK. Notably, there are only four carbonyl oxygens within a distance of 4 Å from a Na⁺ occupying the site S3 of NaK because the Na⁺ ion fluctuates near the edges of the carbonyl cage. The ion is coordinated by ∼4 carbonyls and ∼2.3 water molecules (Table III), for a total of approximately six ligands. Consequently, the cage of eight carbonyls is nearly unperturbed. As shown in Fig. 4 (bottom right), the main peak in the diagonal carbonyl oxygen–oxygen distribution function for the site S3 of NaK shifts by ∼0.1 Å toward shorter distance when a K⁺ (black) is substituted by a Na⁺ (green). In contrast, the corresponding shift in the diagonal carbonyl oxygen–oxygen distribution function is ∼0.4 Å for the site S2 of KcsA (Fig. 4, bottom, left). Such a shift means that the site S2 of KcsA does indeed collapse to cradle the smaller Na⁺ ion. Consistent with these results, the change in the average carbonyl–carbonyl interaction of the selective site S2 of KcsA, with a K⁺ or a Na⁺ bound, is 14.3 kcal/mol according to unbiased all-atom MD simulations (see above). In contrast, the corresponding change is only 0.4 kcal/mol for the nonselective S3 site of NaK, implying that the carbonyl cage does not collapse onto the smaller ion in this case and that no major structural changes are needed to bind Na⁺ or K⁺. Finally, the average root-mean-square deviation of the Na-loaded and K-loaded S3 site relative to the x-ray structure is calculated from the MD trajectory, which is only ∼0.8 Å and ∼0.9 Å, respectively. All those results are consistent with the x-ray data on the NaK channel showing that the structures of the K-loaded and Na-loaded binding sites are very similar.

Figure 4.

Comparison of radial distribution functions for the selective site S2 in KcsA (left) and the permissive site S3 in NaK (right). (Top) Ion–carbonyl oxygen radial distribution function (solid line, axis label on the left) and integrated coordination number (dashed line, axis label on the right) for K⁺ (black) and Na⁺ (green). (Bottom) Oxygen–oxygen radial distribution function for the opposite diagonal sides of the carbonyl cage forming the binding site for K⁺ (black) Na⁺ (green); a similar analysis has been performed by Asthagiri et al. (2006).

To summarize the results from all-atom simulations, the carbonyls of the highly selective S2 site of KcsA collapse onto a bound Na⁺, whereas the permissive S3 site of NaK remains structurally unchanged with Na⁺ or K⁺. Such surprising and counterintuitive results simply cannot be reconciled with traditional arguments that ascribe size selectivity exclusively to structural and geometrical factors. As evidenced by this analysis, the collapse of a carbonyl cage to cradle a bound Na⁺ does not necessarily imply that a site should be nonselective (e.g., S2 in KcsA), and correspondingly, the absence of collapse does not imply that a binding site should be very selective (e.g., S3 in NaK). It should be noted that the present results do not mean that the site S3 of NaK is more rigid than the site S2 in KcsA because the number of water coordinating the ion affect the average geometry of the protein ligands in a flexible binding. The present analysis highlights the importance of taking into consideration the influence of hydration and dynamical factors on the chemistry of ion coordination in discussions of ion selectivity.

DISCUSSION

Ion channels are complex macromolecules and many microscopic factors may have an impact on the selectivity of their binding sites. Because of this complexity, it is necessary to go beyond naive considerations solely based on static structures. In principle, free energy computations based on detailed all-atom MD simulations offer a (the only?) rational approach for assessing the importance of these various factors. Even though present-day simulations could be improved, they are sufficiently accurate to help delineate the physical mechanisms governing ion selectivity in KcsA and NaK.

The structural difference between the central binding site S2 in KcsA and NaK has major consequences. While this site is the most selective in KcsA, it is widened and nonselective in NaK. This loss of selectivity in S2 is the principal reason why the NaK channel is able to conduct Na⁺, unlike KcsA. Furthermore, due to the widened S2 site, the NaK selectivity filter is left with a relatively short-length segment forming the two binding sites S3 and S4. A Na⁺ bound in the S3 site of NaK is slightly more hydrated than would be the case in the S3 site of KcsA. Therefore, in spite of their apparent structural similarity, the chemistry of ion coordination in the S3 site is not truly identical in KcsA and NaK when dynamical hydration effects are taken into account. The calculations show that increased partial hydration is directly implicated in the loss of selectivity at those sites in NaK. In a counterintuitive twist, the calculations also show that the highly selective site S2 in KcsA distorts to coordinate Na⁺ but the nonselective site S3 in NaK does not.

What is the underlying physical mechanism yielding such differences in ion selectivity for binding sites that are seemingly quite similar? The results of the calculations show that selectivity of the binding sites of KcsA and NaK is largely controlled by the dynamical interplay of local ion–ligand and ligand–ligand interactions. Ion–ligand interactions are obviously attractive, while ligand–ligand repulsion acts as a “through-space” electrostatic strain energy. The coordination number alone does not predetermine ion selectivity because both ion–ligand and ligand–ligand interactions depend on the intrinsic physical and electrostatic properties of the ligands, which complicates attempts to achieve mechanistic insight. The key variables that we have identified are the number of coordinating ligands, as well as their particular properties. Most importantly, coordinating oxygen atoms donated by a carbonyl or a water molecule are not equivalent. Different combinations of those ligands can give rise to different K⁺/Na⁺ selectivity, as exemplified by the results of Table II. A dynamical site with eight carbonyl groups is robustly selective for K⁺ over Na⁺, but the selectivity is lost as the carbonyl groups progressively are replaced by water molecules. As illustrated in Fig. 3, relatively minor changes in hydration number have a significant impact on selectivity. According to the present analysis, it appears that tightly controlled dehydration of permeating cations, as enforced by the long and narrow KcsA pore, is an essential aspect that enables the robust selectivity for K⁺ over Na⁺. Because of the widening at the level corresponding to the site S2, the NaK pore allows a minor increase in ion hydration and is permissive to Na⁺.

Consistent with the classical concept of “field strength” introduced by Eisenman, the presence of one high-field ligand such as a carboxylate acidic group shifts selectivity in favor of Na⁺. A robust selectivity for Na⁺ over K⁺ can be achieved, for example, by a dynamical site comprising a few carbonyls, water molecules, and one carboxylate. Other ways may be possible, but these results suggest that partial hydration along the permeation pathway, together with one or two carboxylate groups, might be features of Na⁺-selective channels.

The present study of the KcsA and NaK channels helps to better delineate the role of the different factors affecting ion selectivity in biological systems. Structural forces, by virtue of the three-dimensional organization of the protein, aim at keeping a set of ligands near some configuration in order to allow for favorable coordination of a specific ion. Increasing the structural stiffness to enforce an optimal ligand geometry specifically for K⁺ or Na⁺, evidently, can make a binding site more selective. Such structural forces exist, but there are severe limitations on the stiffness that can be tolerated in the case of ion channels because the ligands must remain sufficiently flexible to allow a high throughput rate. Those limitations may be less stringent in the case of membrane transporters, which operate on much slower timescales; consequently, their ion binding sites could be quite rigid without disrupting function. It is, however, a common misconception that size selectivity can be conferred only by structurally enforcing a precise geometry for the ligands coordinating the ion. As a selective binding site becomes more dynamical and flexible, the dynamical interplay of local ion–ligand and ligand–ligand interactions begins to play an increasingly prominent role. Variations in the type and number of coordinating ligands (including water molecules) offer a wide range of possibilities to engineer robust Na⁺/K⁺ selectivity in flexible binding sites, without a need for significant underlying structural rigidity. The robustness of this fundamental mechanism leads us to conjecture that any existing structural stiffness of the binding sites serve primarily to reinforce the basic trend in selectivity set by the number and type of ligands coordinating the ion.