Randomized algorithms for the low-rank approximation of matrices

Abstract

We describe two recently proposed randomized algorithms for the construction of low-rank approximations to matrices, and demonstrate their application (inter alia) to the evaluation of the singular value decompositions of numerically low-rank matrices. Being probabilistic, the schemes described here have a finite probability of failure; in most cases, this probability is rather negligible (10⁻¹⁷ is a typical value). In many situations, the new procedures are considerably more efficient and reliable than the classical (deterministic) ones; they also parallelize naturally. We present several numerical examples to illustrate the performance of the schemes.

Low-rank approximation of linear operators is ubiquitous in applied mathematics, scientific computing, numerical analysis, and a number of other areas. In this note, we restrict our attention to two classical forms of such approximations, the singular value decomposition (SVD) and the interpolative decomposition (ID). The definition and properties of the SVD are widely known; we refer the reader to ref. 1 for a detailed description. The definition and properties of the ID are summarized in Subsection 1.1 below.

Below, we discuss two randomized algorithms for the construction of the IDs of matrices. Algorithm I is designed to be used in situations where the adjoint A* of the m × n matrix A to be decomposed can be applied to arbitrary vectors in a “fast” manner, and has CPU time requirements typically proportional to k·C_A* + k·m + k²·n, where k is the rank of the approximating matrix, and C_A* is the cost of applying A* to a vector. Algorithm II is designed for arbitrary matrices, and its CPU time requirement is typically proportional to m·n·log(k) + k²·n. We also describe a scheme converting the ID of a matrix into its SVD for a cost proportional to k²·(m + n).

Space constraints preclude us from reviewing the extensive literature on the subject; for a detailed survey, we refer the reader to ref. 2. Throughout this note, we denote the adjoint of a matrix A by A*, and the spectral (l²-operator) norm of A by ‖A‖₂; as is well known, ‖A‖₂ is the greatest singular value of A. Furthermore, we assume that our matrices have complex entries (as opposed to real); real versions of the algorithms under discussion are quite similar to the complex ones.

This note has the following structure: Section 1 summarizes several known facts. Section 2 describes randomized algorithms for the low-rank approximation of matrices. Section 3 illustrates the performance of the algorithms via several numerical examples. Section 4 contains conclusions, generalizations, and possible directions for future research.

Section 1: Preliminaries

In this section, we discuss two constructions from numerical analysis, to be used in the remainder of the note.

Subsection 1.1: Interpolative Decompositions.

In this subsection, we define interpolative decompositions (IDs) and summarize their properties.

The following lemma states that, for any m × n matrix A of rank k, there exist an m × k matrix B whose columns constitute a subset of the columns of A, and a k × n matrix P, such that

1. some subset of the columns of P makes up the k × k identity matrix,

2. P is not too large, and

3. B_m×k·P_k×n = A_m×n.

Moreover, the lemma provides an approximation

when the exact rank of A is greater than k, but the (k + 1)st greatest singular value of A is small. The lemma is a reformulation of theorem 3.2 in ref. 3 and theorem 3 in ref. 4; its proof is based on techniques described in refs. 5–7. We will refer to the approximation in formula 1 as an ID.

Lemma 1.

Suppose that m and n are positive integers, and A is a complex m × n matrix.

Then, for any positive integer k with k ≤ m and k ≤ n, there exist a complex k × n matrix P, and a complex m × k matrix B whose columns constitute a subset of the columns of A, such that

1. some subset of the columns of P makes up the k × k identity matrix,

2. no entry of P has an absolute value greater than 1,

3. ${\Vert P_{k\times n}\Vert }_2\le \sqrt{k\left(n-k\right)}+1$,

4. the least (that is, the kth greatest) singular value of P is at least 1,

5. B_m×k·P_k×n = A_m×n when k = m or k = n, and

6. when k < m and k < n,

where σ_k+1 is the (k + 1)st greatest singular value of A.

Properties 1, 2, 3, and 4 in Lemma 1 ensure that the interpolative decomposition BP of A is numerically stable. Also, property 3 follows directly from properties 1 and 2, and property 4 follows directly from property 1.

Observation 1.

Existing algorithms for the construction of the matrices B and P in Lemma 1 are computationally expensive (see sections 3 and 4 of ref. 5). We use the algorithm of ref. 4 to produce matrices B and P which satisfy somewhat weaker conditions than those in Lemma 1. We construct B and P such that

1. some subset of the columns of P makes up the k × k identity matrix,

2. no entry of P has an absolute value greater than 2,

3. ${\Vert P_{k\times n}\Vert }_2\le \sqrt{4k\left(n-k\right)}+1$,

4. the least (that is, the kth greatest)singular value of P is at least 1,

5. B_m×k·P_k×n = A_m×n when k = m or k = n, and

6. when k < m and k < n,

where σ_{k + 1} is the (k + 1)st greatest singular value of A.

For any positive real number ε, the algorithm can identify the least k such that ‖B P − A‖₂ ≈ ε. Furthermore, the algorithm computes both B and P using at most

floating-point operations, typically requiring only

Subsection 1.2: A Class of Random Matrices.

In this subsection, we describe a class Γ of structured random matrices that will be used in Section 2. A matrix Φ belongs to Γ if it consists of uniformly randomly selected rows of the product of the discrete Fourier transform matrix and a random diagonal matrix. Matrices of this type have been introduced in ref. 8 in a slightly different context.

Suppose that l and m are positive integers, such that l < m. Suppose further that D is a complex diagonal m × m matrix whose diagonal entries d₁, d₂, …, d_m are independent and identically distributed (i.i.d.) complex random variables, each distributed uniformly over the unit circle. Suppose in addition that F is the complex m × m matrix defined by the formula

with $i=\sqrt{-1}$. Suppose moreover that S is a real l × m matrix whose entries are all zeros, aside from a single 1 in row j of column s_j for j = 1, 2, …, l, where s₁, s₂, …, s_l are i.i.d. integer random variables, each distributed uniformly over {1, 2, …, m}. Suppose finally that Φ is the l × m matrix defined by the formula

Then, the cost of applying Φ to an arbitrary complex vector via the algorithm of ref. 9 is

The algorithm of ref. 9 is based on the fast Fourier transform, and is quite efficient in practical applications (in addition to having the attractive asymptotic CPU time estimate in formula 8).

Remark 1.

The integers s₁, s₂, …, s_l used above in the construction of S from formula 7 are drawn uniformly with replacement from {1, 2, …, m}. Our implementations indicate that the algorithms of this note yield similar accuracies whether s₁, s₂, …, s_l are drawn with or without replacement. However, drawing with replacement simplifies the analysis of these algorithms (see ref. 10).

Section 2: Description of the Algorithms

In this section, we describe two numerical schemes for approximating a matrix A with a low-rank matrix in the form of an ID. We also describe a procedure for converting an ID into an SVD.

The first scheme—Algorithm I—is meant to be used when efficient procedures for applying the matrix A and its adjoint A* to arbitrary vectors are available; it is more reliable and parallelizable than the classical power and Lanczos algorithms, and is often more efficient. Algorithm I is described in Subsection 2.1 below.

The second scheme—Algorithm II—deals with the case when A is specified by its entire collection of entries; it is more efficient and parallelizable than the classical “QR” decomposition, power, and Lanczos algorithms used in current numerical practice. Algorithm II is described in Subsection 2.2 below.

Subsection 2.4 describes an efficient procedure for calculating the SVD of A given an ID of A produced by either Algorithm I or Algorithm II.

Subsection 2.1: Algorithm I.

In this subsection, we describe an algorithm for computing an approximation to a matrix A in the form of an ID. The algorithm is efficient when the matrix A* can be applied rapidly to arbitrary vectors. A detailed analysis of the algorithm of this subsection can be found in ref. 11.

Suppose that k, l, m, and n are positive integers with k < l, such that l < m and l < n. Suppose further that A is a complex m × n matrix. Suppose in addition that R is a complex l × m matrix whose entries are i.i.d., each distributed as a complex Gaussian random variable of zero mean and unit variance.

Then, with very high probability whenever l − k is sufficiently large, the following procedure constructs a complex m × k matrix B whose columns consist of a subset of the columns of A, and a complex k × n matrix P, such that some subset of the columns of P makes up the k × k identity matrix, no entry of P has an absolute value greater than 2, and

where σ_k+1 is the (k + 1)st greatest singular value of A. Thus, BP is an ID approximating A.

The algorithm has three steps:

1. Form the product

   
2. Using the algorithm of Observation 1, collect k appropriately chosen columns of Y into a complex l × k matrix Z, and construct a complex k × n matrix P, such that some subset of the columns of P makes up the k × k identity matrix, no entry of P has an absolute value greater than 2, and

   

   where τ_k+1 is the (k + 1)st greatest singular value of Y.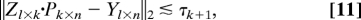

3. Due to Step 2, the columns of Z constitute a subset of the columns of Y. In other words, there exists a finite sequence i₁, i₂, …, i_k of integers such that, for any j = 1, 2, …, k, the jth column of Z is the i_jth column of Y. Collect the corresponding columns of A into a complex m × k matrix B, so that, for any j = 1, 2, …, k, the jth column of B is the i_jth column of A.

If we define C_A* to be the cost of applying A* to a vector, then Step 1 costs l·C_A* floating-point operations. Obviously, Step 2 costs 𝒪(k·l·n·log(n)) operations (see Observation 1). Step 3 consists of moving k·m complex numbers from one location in memory to another, and hence costs 𝒪(k·m) operations.

In all, the algorithm costs at most

floating-point operations, and (as seen from formula 5) typically costs

Remark 2.

The estimate in formula 13 is based on the assumption that the entries of the matrix A are available at no cost. Sometimes, an algorithm for the application of A to arbitrary vectors is available, but one has no access to individual entries of A. In such cases, the k columns of A required by Algorithm I above can be obtained by applying A to an appropriately chosen collection of vectors, for a cost of k·C_A, with C_A denoting the cost of applying A to a vector. Under these conditions, formula 13 becomes

Remark 3.

Obviously, the algorithm of this subsection has a positive probability P_I^fail of failure. The behavior of P_I^fail as a function of l − k is investigated in detail in ref. 11, where the concept of failure for algorithms of this type is defined; ref. 11 gives upper bounds on P_I^fail which are complicated but quite satisfactory. For example, l − k = 20 results in P_I^fail < 10⁻¹⁷, and l − k = 8 results in P_I^fail < 10⁻⁵. Our numerical experience indicates that the bounds given in ref. 11 are reasonably tight.

Subsection 2.2: Algorithm II.

In this subsection, we describe a modification of Algorithm I for computing an ID approximation to an arbitrary m × n matrix A; the modified algorithm does not need a “fast” scheme for the application of A and A* to vectors. A detailed analysis of the algorithm of this subsection can be found in ref. 10.

The modified algorithm, Algorithm II, is identical to Algorithm I of Subsection 2.1, but with the random matrix R used in formula 10 replaced with the matrix Φ defined in formula 7. With this modification, the three-step algorithm of Subsection 2.1 remains a satisfactory numerical tool for the construction of IDs of matrices.

Now, Step 1 requires applying Φ to each column of A, for a total cost of 𝒪(n·m·log(l)) floating-point operations (see formula 8). Steps 2 and 3 cost 𝒪(k·l·n·log(n)) and 𝒪(k·m) operations respectively, being identical to Steps 2 and 3 of Algorithm I.

In all, the modified algorithm costs at most

floating-point operations, and (as seen from formula 5) typically costs

Remark 4.

As with Algorithm I of the preceding subsection, the algorithm of this subsection has a positive probability of failure, to be denoted by P_II^fail. The behavior of P_II^fail as a function of k and l is investigated in ref. 10, where the concept of failure for algorithms of this type is defined; the estimates in ref. 10 are considerably weaker than the behavior observed experimentally. Specifically, ref. 10 shows that P_II^fail is less than C·k²/l, where C is a positive constant independent of the matrix A; in practice, the failure rate of Algorithm II is similar to that of Algorithm I. This discrepancy is a subject of intensive investigation.

Subsection 2.3: Adaptive Versions of Algorithms I and II.

As described in the preceding two subsections, Algorithms I and II require a priori knowledge of the desired rank k of the approximations. This limitation is easily eliminated. Indeed, one can apply Algorithm I or II with k set to some more or less arbitrary number (such as 2, or 20, or 40), and then keep doubling k until the obtained approximation attains the desired precision. The algorithm described in Appendix provides an efficient means for estimating the precision of the obtained approximations. It is easy to see that knowing the desired rank k in advance reduces the cost of constructing the approximation by at most a factor of 2.

The authors have implemented such adaptive versions of both algorithms; in many cases the CPU time penalty is considerably less than a factor of 2. Moreover, much of the data can be reused from one value of k to another, further reducing the penalty. Such modifications are in progress.

Subsection 2.4: From ID to SVD.

In this subsection, we describe a procedure for converting an ID into an SVD. A similar method enables the construction of the Schur decomposition of a matrix from its ID (see, for example, theorem 7.1.3 and the surrounding discussion in ref. 1 for a description of the Schur decomposition).

Suppose that k, m, and n are positive integers with k ≤ m and k ≤ n, B is a complex m × k matrix, and P is a complex k × n matrix. Then, the following four steps compute a complex m × k matrix U whose columns are orthonormal, a complex n × k matrix V whose columns are orthonormal, and a real diagonal k × k matrix Σ whose entries are all nonnegative, such that

The four steps are:

1. Construct a “QR” decomposition of P*, i.e., form a complex n × k matrix Q whose columns are orthonormal, and a complex upper-triangular k × k matrix R, such that

   

   for a cost of 𝒪(n·k²) (see, for example, chapter 5 in ref. 1).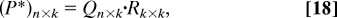
2. Form the complex m × k matrix S via the formula

   

   for a cost of 𝒪(m·k²).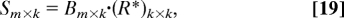
3. Form an SVD of S

   

   where U is a complex m × k matrix whose columns are orthonormal, W is a complex k × k matrix whose columns are orthonormal, and Σ is a real diagonal k × k matrix whose entries are all nonnegative. The cost of this step is 𝒪(m·k²) (see, for example, chapter 8 in ref. 1).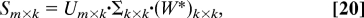
4. Form the complex n × k matrix V via the formula

   

   for a cost of 𝒪(n·k²).

The four steps above compute the SVD in formula 17 of the matrix BP for a cost of

Combining the algorithm of this subsection and the algorithm of Subsection 2.2 yields an algorithm for computing an SVD approximation to an arbitrary matrix for a total cost of

Similarly, combining the algorithm of this subsection and the algorithm of Subsection 2.1 yields an algorithm for computing an SVD approximation to a matrix A when both A and A* can be applied rapidly to arbitrary vectors; however, in this case there exists a more direct algorithm yielding slightly better accuracy (see ref. 11).

Section 3: Numerical Examples

In this section, we describe several numerical tests of the algorithms discussed in this note.

Subsections 3.1 and 3.2 illustrate the performance of Algorithms I and II, respectively. Subsection 3.3 illustrates the performance of the combination of Algorithm II with the four-step algorithm of Subsection 2.4.

The algorithms were implemented in Fortran 77 in double-precision arithmetic, compiled using the Lahey/Fujitsu Express v6.2 compiler with maximum optimization, and run on one core of a 1.86 GHz Intel Centrino Core Duo microprocessor with 2 MB of L2 cache and 1 GB of RAM. To perform the fast Fourier transforms required by Algorithm II, we used a double-precision version of P.N. Swarztrauber's FFTPACK library.

Subsection 3.1: Algorithm I.

This subsection reports results of applying Algorithm I to matrices A given by the formula

where c is the v² × 1 column vector whose entries are all ones, and Δ is the standard five-point discretization of the Laplacian on a v × v uniform grid; in other words, all of the diagonal entries of Δ are equal to −4, Δ_p,q = 1 if the grid points p and q are neighbors, and all other entries of Δ are zeros (see, for example, section 8.6.3 in ref. 12). Thus, A is an n × n matrix, with n = v².

The results of this set of tests are summarized in Table 1 the contents of the columns in Table 1 are as follows:

• n is the dimensionality of the n × n matrix A.

• k is the rank of the matrix approximating A.

• l is the first dimension of the l × m matrix R from formula 10, with m = n.

• σ_k+1 is the (k + 1)st greatest singular value of A, that is, the spectral norm of the difference between A and the best rank-k approximation to A.

• δ is the spectral norm of the difference between the original matrix A and its approximation obtained via the algorithm of Subsection 2.1.

• t is the CPU time (in seconds) taken both to compute the approximation to A via the algorithm of Subsection 2.1, and to check the accuracy of the approximation via the algorithm of Appendix.

The entries for δ in Table 1 display the maximum values encountered during 30 trials; the entries for t display the average values over 30 trials. Each of the trials was run with an independent realization of the matrix R in formula 10.

Table 1.

ID (via Algorithm I) of the n × n matrix A defined in formula 24

n	k	l	σk+1	δ	t
400	96	104	0.504E-16	0.380E-14	0.53E0
1,600	384	392	0.513E-16	0.974E-14	0.91E1
3,600	864	872	0.647E-16	0.181E-13	0.58E2
6,400	1,536	1,544	0.649E-16	0.289E-13	0.24E3
400	48	56	0.277E-08	0.440E-07	0.30E0
1,600	192	200	0.449E-08	0.145E-06	0.43E1
3,600	432	440	0.457E-08	0.210E-06	0.24E2
6,400	768	776	0.553E-08	0.346E-06	0.92E2
10,000	1,200	1,208	0.590E-08	0.523E-06	0.12E3

Subsection 3.2: Algorithm II.

This subsection reports results of applying Algorithm II to the 4,096 × 4,096 matrix A defined via the formula

with the matrices Σ, U, and V defined as follows.

The matrix U was constructed by applying the Gram–Schmidt process to the columns of a 4,096 × (k + 20) matrix whose entries were i.i.d. centered complex Gaussian random variables; the matrix V was obtained via an identical procedure. The matrix Σ is diagonal, with the diagonal entries Σ_j,j = 10^{−15·(j−1)/(k−1)} for j = 1, 2, …, k, and Σ_j,j = 10⁻¹⁵ for j = k + 1, k + 2, …, k + 20. Obviously, the jth greatest singular value σ_j of A is Σ_j,j for j = 1, 2, …, k + 20; the rest of the singular values of A are zeros.

For the direct algorithm, we used a pivoted “QR” decomposition algorithm based upon plane (Householder) reflections, followed by the algorithm of ref. 4.

The results of this set of tests are summarized in Table 2; the contents of the columns in Table 2 are as follows:

• k is the rank of the matrix approximating A.

• l is the first dimension of the l × m matrix Φ from formula 7, with m = 4,096.

• σ_k+1 is the (k + 1)st greatest singular value of A, that is, the spectral norm of the difference between A and the best rank-k approximation to A.

• δ_direct is the spectral norm of the difference between the original matrix A and its approximation obtained via the algorithm of ref. 4, using a pivoted “QR” decomposition algorithm based upon plane (Householder) reflections.

• δ is the spectral norm of the difference between the original matrix A and its approximation obtained via the algorithm of Subsection 2.2.

• t_direct is the CPU time (in seconds) taken to compute the approximation to A via the algorithm of ref. 4, using a pivoted “QR” decomposition algorithm based upon plane (House-holder) reflections.

• t is the CPU time (in seconds) taken both to compute the approximation to A via the algorithm of Subsection 2.2, and to check the accuracy of the approximation via the algorithm of Appendix.

• t_direct/t is the factor by which the algorithm of Subsection 2.2 is faster than the classical algorithm that we used.

The entries for δ in Table 2 display the maximum values encountered during 30 trials; the entries for t display the average values over 30 trials. Each of the trials was run with an independent realization of the matrix Φ in formula 7.

Table 2.

ID (via Algorithm II) of the 4,096 × 4,096 matrix A defined in formula 25

k	l	σk+1	δdirect	δ	tdirect	t	tdirect/t
8	16	0.100E-15	0.359E-14	0.249E-14	0.31E1	0.27E1	1.1
56	64	0.100E-15	0.423E-14	0.369E-14	0.18E2	0.31E1	5.6
248	256	0.100E-15	0.309E-14	0.147E-13	0.77E2	0.70E1	11
1,016	1,024	0.100E-15	0.407E-14	0.571E-13	0.32E3	0.11E3	2.8

Subsection 3.3: SVD of an Arbitrary Matrix.

This subsection reports results of applying the algorithm of Subsection 2.2 and then the algorithm of Subsection 2.4 to the 4,096 × 4,096 matrix A defined in formula 25.

For the direct algorithm, we used a pivoted “QR” decomposition algorithm based upon plane (Householder) reflections, followed by the divide-and-conquer SVD routine dgesdd from LAPACK 3.1.1.

The results of this set of tests are summarized in Table 3; the contents of the columns in Table 3 are as follows:

• k is the rank of the matrix approximating A.

• l is the first dimension of the l × m matrix Φ from formula 7, with m = 4,096.

• σ_k+1 is the (k + 1)st greatest singular value of A, that is, the spectral norm of the difference between A and the best rank-k approximation to A.

• δ_direct is the spectral norm of the difference between the original matrix A and its approximation obtained via a pivoted “QR” decomposition algorithm based upon plane (Householder) reflections, followed up with a call to the divide-and-conquer SVD routine dgesdd from LAPACK 3.1.1.

• δ is the spectral norm of the difference between the original matrix A and its approximation obtained via the algorithm of Subsection 2.2, followed by the algorithm of Subsection 2.4.

• t_direct is the CPU time (in seconds) taken to compute the approximation to A via a pivoted “QR” decomposition algorithm based upon plane (Householder) reflections, followed by a call to the divide-and-conquer SVD routine dgesdd from LAPACK 3.1.1.

• t is the CPU time (in seconds) taken both to compute the approximation to A via the algorithm of Subsection 2.2, followed by the algorithm of Subsection 2.4, and to check the accuracy of the approximation via the algorithm of Appendix.

• t_direct/t is the factor by which the algorithm of Subsection 2.2, followed by the algorithm of Subsection 2.4, is faster than the classical algorithm that we used.

The entries for δ in Table 3 display the maximum values encountered during 30 trials; the entries for t display the average values over 30 trials. Each of the trials was run with an independent realization of the matrix Φ in formula 7.

Table 3.

SVD (via Algorithm II) of the 4,096 × 4,096 matrix A defined in formula 25

k	l	σk+1	δdirect	δ	tdirect	t	tdirect/t
8	16	0.100E-15	0.580E-14	0.128E-13	0.31E1	0.22E1	1.4
56	64	0.100E-15	0.731E-14	0.146E-13	0.19E2	0.34E1	5.6
248	256	0.100E-15	0.615E-14	0.177E-13	0.88E2	0.19E2	4.6

Subsection 3.4: Observations.

The following observations can be made from the numerical experiments described in this section, and are consistent with the results of more extensive experimentation performed by the authors:

• The CPU times in Tables 12–3 are compatible with the estimates in formulae 14, 16, and 23.

• The precision produced by each of Algorithms I and II is similar to that provided by formula 3, even when σ_k+1 is close to the machine precision.

• Algorithms I and II, as well as the classical pivoted “QR” decomposition algorithms, all yield results of comparable accuracies.

• Algorithm II runs noticeably faster than the classical “dense” schemes, unless the rank of the approximation is nearly full, or is less than 6 or so.

• Algorithms I and II are remarkably insensitive to the quality of the pseudorandom number generators used.

Section 4: Conclusions

This note describes two classes of randomized algorithms for the compression of linear operators of limited rank, as well as applications of such techniques to the construction of singular value decompositions of matrices. Obviously, the algorithms of this note can be used for the construction of other matrix decompositions, such as the Schur decomposition. In many situations, the numerical procedures described in this note are faster than the classical ones, while ensuring comparable accuracy.

Whereas the results of numerical experiments are in reasonably close agreement with our estimates of the accuracy of Algorithm I, our numerical experiments indicate that Algorithm II performs better than our estimates guarantee. Comfortingly, the verification scheme of Appendix provides an inexpensive means for determining the precision of the approximation obtained during every run. If (contrary to our experience) Algorithm II were to produce an approximation that were less accurate than desired, then one could run the algorithm again with an independent realization of the random variables involved, in effect boosting the probability of success at a reasonable additional expected cost.

It should be pointed out that although Algorithm II cannot perform worse than our bounds guarantee, it actually performs much better in practice. In fact, Algorithm II yields accuracies similar to those of Algorithm I. This discrepancy is currently a subject of intensive investigation.

Furthermore, there is nothing magical about the random matrix defined in formula 7. We have tested several classes of random matrices that are faster to apply, and that (in our numerical experience) perform at least as well in terms of accuracy. However, our theoretical bounds for the matrix defined in formula 7 are the strongest that we have obtained to date.

To summarize, the randomized algorithms described in this note are a viable alternative to classical tools for the compression and approximation of matrices; in many situations, the algorithms of this note are more efficient, reliable, and parallelizable. Their applications in several areas of scientific computing are under investigation.

Appendix: Estimating the Spectral Norm of a Matrix

In this appendix, we describe a method for the estimation of the spectral norm of a matrix A. The method does not require access to the individual entries of A; it requires only applications of A and A* to vectors. It is a version of the classical power method. Its probabilistic analysis summarized below was introduced fairly recently in refs. 13 and 14. This appendix is included here for completeness.

Suppose that m and n are positive integers, and A is a complex m × n matrix. We define ω to be a complex n × 1 column vector with independent and identically distributed entries, each distributed as a complex Gaussian random variable of zero mean and unit variance. We define ω̃ to be the complex n × 1 column vector ω̃ = ω/‖ω‖₂. For any integer j > 1, we define p_j(A) by the formula

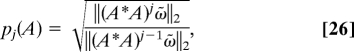which is the estimate of the spectral norm of A produced by j steps of the power method, starting with the vector ω̃ (see, for example, ref. 14).

A somewhat involved analysis shows that the probability that

is greater than $1-4\sqrt{n/\left(j-1\right)}{100}^{-j}$. Needless to say, p_j(A) ≤ ‖A‖₂ for any positive j. Thus, even for fairly small j (we used j = 6 in this note), p_j(A) estimates the value of ‖A‖₂ to within a factor of ten, with very high probability.

This procedure is particularly useful for checking whether an algorithm (such as that described in Subsection 2.2) has produced a good approximation to a matrix, especially when we cannot afford to evaluate all of the entries in the difference between the matrix being approximated and its approximation. For more information, the reader is referred to refs. 13 and 14, or section 3.4 of ref. 10.