Intrinsic single-domain switching in ferroelectric materials on a nearly ideal surface

Abstract

Ferroelectric domain nucleation and growth in multiferroic BiFeO₃ is studied on a single-domain level by using piezoresponse force spectroscopy. Variation of local electromechanical response with dc tip bias is used to determine the size of the domain formed below the conductive scanning probe tip. The domain parameters are calculated self-consistently from the decoupled Green function theory by using tip geometry determined from the domain wall profile. The critical parameters of the nucleating domain and the activation energy for nucleation are determined. The switching mechanism is modeled by using the phase-field method, and comparison with experimental results shows that the nucleation biases are within a factor of ≈2 of the intrinsic thermodynamic limit. The role of atomic-scale defects and long-range elastic fields on nucleation bias lowering is discussed. These measurements open a pathway for quantitative studies of the role of a single defect on kinetics and thermodynamics of first order bias-induced phase transitions and electrochemical reactions.

The electrical control of magnetic ordering in multiferroic materials and self-assembled nanostructures has recently propelled these materials to the forefront of condensed matter physics and materials science (1–4). Studies of these systems provide insight into fundamental mechanisms of coupling between the lattice, spin, and electronic degrees of freedom and resulting order parameters in the bulk and at the interfaces. Furthermore, these systems open a pathway toward device applications including nonvolatile memories (5) and electrically controlled magnetic tunneling junctions, combining nonvolatile electrical writing and magnetic or resistive read-out schemes (6, 7).

Applications of ferroelectric and multiferroic materials in nanoscale devices necessitate the understanding of switching processes in confined and low-dimensional geometries. Because of the restrictions imposed by the size of the active region, only a limited number of domains can nucleate. As the size of the system is reduced, the effects of interfaces and structural defects become statistically more significant. Furthermore, novel types of ferroelectric ordering stabilized by the spatial constraints and depolarization field effects can emerge (8, 9). Dynamic domain behavior and nucleation and growth mechanisms in low-dimensional ferroelectrics, including the switching mechanism in the ideal case, and the role of surfaces, interfaces, and defects in the thermodynamics and kinetics of elementary processes in polarization reversal are the keys to these applications.

The development of piezoresponse force microscopy (PFM) has enabled high-resolution (≈10 nm) imaging of static domain structures (10, 11). Beyond imaging applications, PFM can be used to study domain dynamics and polarization switching on the nanoscale. Application of a dc field to a conductive tip results in local polarization reversal, while subsequent imaging allows visualization of the switched domain. Imaging of the domain size dependence of the voltage pulse duration and magnitude has yielded information on domain wall mobilities and disorder in ferroelectrics (12) and on domain wall pinning on defects (13, 14). However, these studies are time-consuming (several minutes per image), and only relatively large, stable domains can be addressed (lifetimes of >100 s). Therefore, no information on the early phases of the switching process, nucleation mechanisms, or statistical studies of the switching behavior has been reported previously.

Early stages of polarization switching in nanoferroelectrics can be addressed by using piezoresponse force spectroscopy (PFS). PFS measures the local electromechanical hysteresis loops that represent the bias dependence of the local electromechanical response, which is directly related to the size of the domain formed below the tip (15, 16). This approach, in which the atomic force microscope tip acts as a moving top electrode, is similar to measurements using ultra-small capacitors. The electric field is localized below the tip and, hence, polarization switching behavior is probed within a small (10–50 nm) volume (17, 18). Therefore, the number of defects affecting switching in the volume below the tip will necessarily be small, opening the pathway to probing switching behavior in nearly ideal materials and determining the role of single defects in switching. However, the switching mechanism in PFS and the relationship between the measured signal and switched domain size are significantly more complex than in the planar capacitor case, necessitating the development of an appropriate theoretical and experimental framework for data interpretation and analysis.

Here, we develop a self-consistent approach for probing thermodynamics and kinetics of bias-induced phase transitions below the tip. The quantitative interpretation of PFS data enables the parameters of domains formed below the tip to be uniquely determined. We implement this approach to study early-stage polarization switching in multiferroic BiFeO₃. Comparison with the results of phase-field modeling indicates that the switching in PFS is close to the intrinsic thermodynamic limit. This methodology can also be applied to other bias-induced phase transitions that may include material exchange, such as electrochemical reactions, opening a pathway for studying these transformations on a single defect level.

Results

As a model ferroelectric system, we have chosen the epitaxial films of multiferroic BiFeO₃. The high quality of the films ensures a low density of defects such as steps, pinholes, antiphase boundaries, grain boundaries, or interfacial dislocations, with defect spacing significantly larger than the probing volume of PFS. Hence, the properties of the nearly ideal surface in the absence of mesoscopic defects and mediated only by atomic-scale defects, such as oxygen vacancies, can be studied.

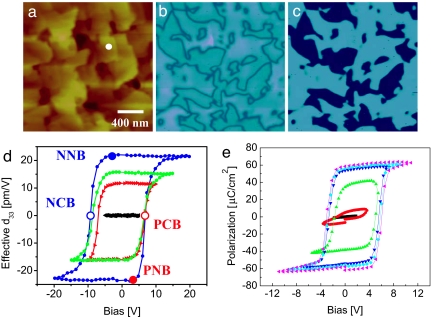
Topographic and PFM images of a BiFeO₃ film are shown in Fig. 1 a–c. PFS hysteresis loops with different dc bias ranges are shown in Fig. 1d. For a small bias window, the response is linear, whereas for larger biases, the hysteresis loop “opens up,” similar to the macroscopic polarization–electric field (P-E) hysteresis loops (Fig. 1e). The observed evolution of the hysteresis loops suggests that the domain growth process is limited by domain nucleation below the tip, as evidenced by a fixed response at low voltages, and a sudden change above a certain critical bias. The coercive biases (corresponding to zero response) determined in the local PFS measurements [6.5 V for positive, and 9.4 V for negative (V_c = 8)] are within a factor of two of the macroscopic measurements [5 V for positive, and 3 V for negative (V_c = 4)]. The asymmetry in the coercive fields arises primarily because of the difference of the electrical boundary conditions at the macroscopic bottom (oxide) and local top (gold-coated tip) electrodes. Recent studies (19) on similar samples with thicknesses from 30 to 2 nm has demonstrated that the asymmetry is almost thickness-independent and thus can be attributed to contact behavior. The similarity between PFS data and macroscopic P-E loops is rather striking given the vastly different mechanisms (multiple domain switching and growth in the macroscopic case vs. single-domain growth in PFS).

Fig. 1.

Macroscopic and local hysteresis measurements in BiFeO₃. (a–c) Surface topography (a), PFM amplitude (b), and phase images (c) of the 200-nm BiFeO₃ surface. (d) Local electromechanical hysteresis loops obtained by PFM (at approximate location marked by white dot in a) in comparison with e. (e) P-E hysteresis loops from macroscopic measurements. Both d and e are plotted as a function of voltage applied to the tip (d) or top electrode (e), illustrating close similarity between switching biases. The z-scale in a is 20 nm.

Discussion

The PFS data represent a convolution between the signal generation volume determined by the probe and the size of the forming domain. Quantitative deconvolution requires the solution of two problems: (i) establishment of the relationship between domain parameters and the PFS signal for a known tip geometry, and (ii) calibration of the tip geometry. Here, we derive the solution for these problems self-consistently in the framework of the linear decoupled theory of Felten et al. (20). The displacement vector u_i(x) at position x, describing tip-bias induced surface displacement directly below the tip, is

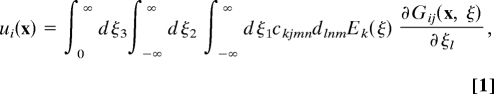where ξ is the coordinate system related to the material, d_lmn are the piezoelectric coefficients, and c_kjmn are the elastic stiffnesses. E_k(ξ) is the electric field produced by the probe, and G_ij(x, ξ) is the elastic Green function (21).

The key parameter in the switching process is the characteristic tip size (e.g., the tip radius of curvature or contact radius), which determines the field structure in the material. Here, we develop an algorithm to determine the tip size self-consistently from the observed domain wall width. The electric field produced by the tip is calculated within a framework of an image charge model either as a single point charge or a set of point charges in a sphere-plane model. For a single point charge, integration of Eq. 1 using the isotropic elastic Green function for a half-plane (21), and Pade analysis of the resulting complex expression, the domain wall profile is derived as

Here, u₀ is the offset accounting for the electrostatic contribution to the signal, and a₀ is the center position of the domain wall. The charge parameters (Q, d) are chosen such that (i) the potential on the surface is equal to the tip bias and (ii) the radius of curvature of the isopotential surface is equal to R₀ at the point of contact. From these conditions, d = ε_eR₀/κ and Q = 2πε₀ε_eR₀U(κ + ε_e)/κ, where κ is the dielectric constant of the material. Eq. 2 is also applicable to the sphere-plane model of the tip, for which

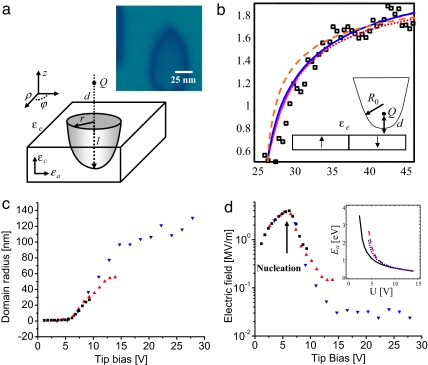
and R₀ is the tip radius of curvature (Fig. 2a).

Fig. 2.

Self-consistent measurements of domain size in a PFS experiment. (a) Schematic of the tip interaction with a semiellipsoidal domain. (Inset) High-resolution PFM amplitude image of a domain wall in BiFeO₃. (b) Domain wall profile and fit by Eq. 2 for different tip models. The dotted curve is the single charge model with d = 14 nm, and solid and dashed curves are the sphere-plane model with R₀ = 15, 50, and 200 nm and ε_e = 81, 10, and 1, respectively. (Inset) Schematic of the model. (c) Domain radius deconvoluted from the hysteresis data in Fig. 1d in the point charge model. (d) Electric field on the domain boundary. (Inset) Activation energy for different models.

The relative contribution of the magnetoelectric coupling to the piezoresponse signal is determined by the dimensionless term κ = μ⁻¹d⁻¹αβ, where d are piezoelectric constants, β are piezomagnetic constants, α are linear magnetoelectric constants, and μ are magnetic permittivities. Estimating d = 50 pm/V, β = 10⁻¹¹ m/A, and α ∼ 10⁻¹⁰ C/(m² Oe) (see ref. 22), the constant κ = 2 × 10⁻⁷. Hence, the magnetoelectric contribution to the PFM signal can be neglected in antiferroelectric multiferroics.

Because the values of the piezoelectric constants d₃₃, d₃₁, and d₁₅, and Poisson's ratio, ν, for BiFeO₃ are not known, we treat d₃₃* = d₃₃ + (1 + 4ν)d₃₁/3 and d₁₅ as fitting parameters. To account for the change in tip-surface contact conditions, the hysteresis data were normalized with respect to the signal on the saturated portion of the curve, and the ratio d₁₅/d₃₃* was kept constant during the fitting. The deconvolution was performed for both sphere-plane and point charge models, and the resulting deviation in the domain radii did not exceed a factor of 2. Similarly, the deconvoluted values of charge-surface separation, d, depends on the ratio d₁₅/d₃₃* only weakly; namely, it varies from 13 nm at d₁₅/d₃₃* = 2 to 18 nm for d₁₅/d₃₃* = 0.5. The fitting of several domain wall profiles using Eq. 2 yields d = 14 nm and d₃₃* = d₁₅ = 43.2 pm/V, as shown in Fig. 2b. In the sphere-plane model, the uncertainty is related to the dielectric constant of the tip-surface medium, and for ε_e = 81 (“free” water), 10 (“bound” water), and 1 (air), the tip radii were estimated as R₀ = 15, 50, and 200 nm. Despite the difference, the effective electric field distribution in these cases is similar, as discussed below.

To determine the domain parameters in PFS, we approximate the domain as a semiellipsoid of diameter r_d and length l_d. The domain shape is usually elongated (19–22), whereas the tip-generated electric field is generally concentrated on the surface, making the domain radius the critical parameter determining the PFS signal. The relationship between the domain radius and the PFM signal can be determined from Eq. 1 for isotropic dielectric material as

where r = r(V_dc) is the voltage-dependent domain radius. The voltage dependence of the domain radius deconvoluted from the data in Fig. 1d is shown in Fig. 2c. Remarkably, we have found that the deconvoluted values of domain diameter differ by no more than ≈5% for the d₁₅/d₃₃* ratio varied from 2 to 0.5. The primary reason for the insensitivity of the deconvolution procedure to the d₁₅/d₃₃* ratio or exact tip model (sphere plane, point charge) is that the corresponding terms in the domain wall profile equation and the hysteresis loop equation have a very similar structure, so the correction largely cancels out. Similarly, the deconvolution is relatively insensitive to the tip radius or the dielectric constant. In other words, the effective tip size is directly related to the measured domain wall width, providing a single relevant length scale of the problem, which only weakly depends on the adopted model for tip geometry.

The evolution of the electric field at the domain boundary is shown in Fig. 2d. The field rapidly decreases with domain size, indicative of a decrease in domain-wall curvature. From Fig. 1d, the critical bias for nucleation, corresponding to a bias at which the PFS signal deviates from the fully saturated signal, is ≈4–5 V at the selected location. The corresponding domain parameters estimated from thermodynamic theory (25) are r_d = 0.8 nm and l_d = 10 nm, and the activation energy for nucleation is estimated to be 1.3 eV. This is in agreement with the recent investigation of thermodynamic nucleation in ultra-thin-film ferroelectric capacitors (27). Note that the electric field at the outer domain boundary is 3 × 10⁸ V/m. In comparison, the intrinsic thermodynamic switching field for BiFeO₃ is estimated to be 1.9 × 10⁸ V/m. Hence, the electric field at the domain wall at nucleation is close to the anticipated field necessary to induce intrinsic switching, suggesting that this may be the dominant mechanism for domain nucleation at ferroelectric surfaces in the absence of defects.

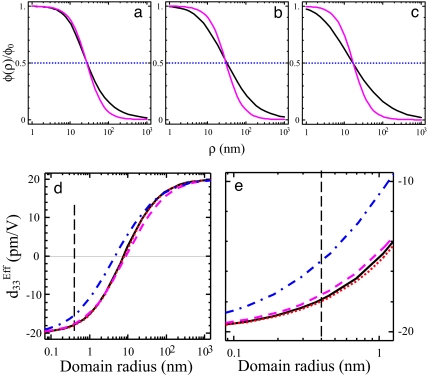
To complement this analysis, we model the domain nucleation process in PFS using the phase-field approach (28). The electrical potential generated on the surface by the PFM tip was approximated by a 2D Lorentzian-like distribution, φ₁(x, y) = φ₀γ²/((x − x₀)² + (y − y₀)² + γ²), where φ₀ is the tip potential and x₀, y₀ are tip coordinates (Fig. 3 a–c). The width of the Lorentzian, γ, is chosen to coincide with the potential distribution width expected for a self-consistently determined tip geometry. The temporal evolution of the polarization vector field is described by the time-dependent Ginzburg–Landau (TDGL) equations,

where L is a kinetic coefficient related to the domain wall mobility.

Fig. 3.

Normalized potential distribution dependence on the radial coordinate from the exact series and the Lorentzian expressions (black and violet curves, respectively). Three sets of parameters are used, namely R₀ = 15 nm, ε_e = 81, γ = 27 nm (a); R₀ = 50 nm, ε_e = 10, γ = 30 nm (b); and R₀ = 200 nm, ε_e = 1, γ = 18 nm (c). Dependence of the PFM response on the nascent domain radius calculated for different tip models. (d) The solid curve is the single charge model with d = 14 nm, dotted, dashed, and dash-dotted curves are for the sphere–plane model with R₀ = 15, 50, and 200 nm and ε_e = 81, 10, and 1, respectively. (e) Details at small values of radius.

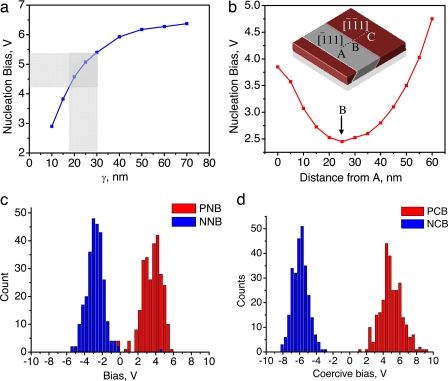
The dependence of nucleation bias on γ for a BiFeO₃ epitaxial thin film consisting of a single rhombohedral domain with polarization direction along [111] is shown in Fig. 4a as a function of characteristic tip size. For the ranges of tip parameters consistent with the measured domain wall width, the intrinsic nucleation bias is ≈4.6 ± 0.5 V depending on the tip model. Note that the absence of thermal fluctuations in phase-field modeling implies that the determined nucleation biases correspond to intrinsic thermodynamic switching in the local field produced by the tip.

Fig. 4.

Phase-field modeling of polarization switching mechanism in BiFeO₃. (a) Variation of nucleation voltage as a function of gamma. (b) Spatial distribution of nucleation potential along the line A–B–C shown by the dotted line in Inset (domain structure under short-circuit boundary conditions). The polarization directions are indicated. (c and d) Histograms of positive and negative nucleation and coercive biases, respectively.

Experimentally measured histograms of nucleation bias for a 3% nucleation threshold (i.e., deviation of response signal from constant) are shown in Fig. 4c, and the corresponding coercive biases are shown in Fig. 4d. The distributions are fairly broad and can be well described by a Gaussian function,

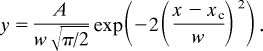For positive and negative nucleation biases (PNB and NNB, respectively) for a 3% threshold, the relevant parameters (x_c ± w) are PNB = 3.7 ± 2.2 V and NNB = −2.8 ± 1.7 V. The effect of the threshold on nucleation bias distributions is summarized in Table 1. For positive and negative coercive biases (PCB and NCB, respectively), the relevant parameters are PCB = 4.9 ± 2.3 V and NCB = −5.6 ± 1.8 V. Remarkably, the average coercive bias is within ≈20% of the macroscopic value.

Table 1.

Positive (PNB) and negative (NNB) nucleation biases for different thresholds

Threshold	PNB	NNB	Average
0.5%	3.2 ± 2.4	−1.2 ± 1.9	2.2 ± 2.1
3%	3.7 ± 2.2	−2.8 ± 1.7	3.3 ± 2.0
10%	4.1 ± 2.3	−3.6 ± 1.1	3.9 ± 1.7
Intrinsic	4.6 ± 0.5	−4.6 ± 0.5	4.6 ± 0.5

The distribution of nucleation biases is fairly broad, indicative of significant disorder. Because of the smallness of the probed volume and the absence of visible topographic defects on the dominant part of the film surface, this can be attributed to variations in contact conditions, the presence of microscopic defects such as vacancies and surface roughness, and long-range strain fields due to domain walls and interfacial dislocations. Because contact quality can only be reduced compared with the ideal, resulting in increased nucleation bias, the defects and long-range field are the likely origin of nucleation bias lowering. The distribution of nucleation biases is then consistent with atomic-scale polar defects affecting switching (e.g., interfacial dipoles or vacancy dipoles, etc.), because fewer larger (>10 nm spacing) defects will not average sufficiently to provide Gaussian statistics. An alternative explanation for the distribution in nucleation biases is the effect of long-range strain fields associated with macroscopic defects. To explore this possibility, the effect of a single-domain wall has been modeled, as shown in Fig. 4b. Notice that the nucleation bias is reduced to 2.5 V at the wall. Furthermore, the effect of the wall is long-range, on the scale of several γ, corresponding to 50–100 nm in this case.

To summarize, the mechanism of single-domain switching in multiferroic BiFeO₃, films were studied self-consistently by using a combination of PFS and phase-field modeling. The average nucleation bias in the PFS experiment (≈3.3 V) is within a factor of 2 of the intrinsic value. The origins of the observed lowering of the nucleation bias can include both atomic-scale defects and long-range elastic fields. In comparison, in macroscopic capacitor experiments, the observed nucleation biases are typically 1–2 orders of magnitude below the thermodynamic limit. Comparison with the results on macroscopic capacitors suggests that local field concentrations due to interface roughness (close to PFM field distributions) can act as nucleation centers.

The approach developed here, based on quantitative piezoresponse spectroscopy, will be indispensable for understanding the fundamental switching mechanisms in low-dimensional ferroelectric materials and polarization-defect interactions, and will allow spatially resolved mapping of nucleation centers in ferroelectrics. This approach can be further extended to other bias-induced local phase transitions, including phase change memories, electrochemical transformations in molecular systems (molecular electromotors) and solid-state materials, and electroactive polymers.

Materials and Methods

Materials.

The BiFeO₃ films (200 nm) were deposited by pulsed laser deposition on a 50-nm conductive SrRuO₃ bottom electrode layer on (001)-oriented SrTiO₃ substrates. During deposition, the substrate temperature was kept at 670°C in 100 mTorr of O₂. After deposition, the sample was annealed at 400°C in oxygen ambient for 1 h. Epitaxial growth and (00l) orientation were confirmed by x-ray diffraction and transmission electron microscopy.

PFM Imaging.

A commercial scanning probe microscopy system (Veeco MultiMode NS-IIIA) equipped with additional function generators and lock-in amplifiers (DS 345 and SRS 830 from Stanford Research Instruments, and 7280 from Signal Recovery) was used for PFM measurements. A custom-built, shielded sample holder was used to bias the tip directly. Measurements were performed by using Pt- and Au-coated tips (NSC-35 C from MikroMasch; l = 130 μm, resonant frequency of ≈150 kHz, spring constant k ∼ 4.5 N/m).

In PFM, a periodic voltage, V_tip = V_dc + V_ac cos ωt, is applied to a conductive atomic force microscope tip in contact with the sample surface. The periodic bias results in a surface deformation due to the converse piezoelectric effect, d = d₀ + d_1ω cos(ωt + ϕ), which is detected as a periodic cantilever displacement at the excitation frequency, ω. The tip is scanned maintaining constant tip-surface force (topographic feedback) to generate images of piezoresponse amplitude, d_1ω, and piezoresponse phase, ϕ. The amplitude is proportional to local electromechanical activity, while the phase is 0° for domains with P·n > 0 and 180° for P·n < 0, where P is the polarization vector and n is the unit normal.

PFM Spectroscopy and SS-PFM.

In PFS, the electromechanical response is measured as a function of tip dc bias, V_dc, applied before measurement (16). Application of sufficiently high constant bias results in the nucleation and subsequent growth of domains of opposite polarity below the tip, with a concurrent change of the PFM signal from PR (initial state) to −PR (switched state). The resulting PR(V_dc) dependence contains information on domain nucleation and growth below the tip. In switching spectroscopy PFM (SS-PFM), the hysteresis loops are acquired at each point in an N × N grid (typically n = 32 − 128) that is further analyzed to yield 2D maps of switching parameters such as the positive and negative nucleation biases and the work of switching (29).

To analyze the statistical distribution of switching biases within the film, we have developed automatic routines for analysis of multiple (10² − 10⁴) hysteresis loops based on a phenomenological fitting function method (30). The nucleation bias is determined as a voltage corresponding to the deviation of the electromechanical response from the remanent value by a predefined value. To establish reliable criterion for domain nucleation onset in the PFS data analysis, the electromechanical response was calculated by using Eq. 3 as a function of domain radius for different tip models. The changes in the electromechanical response as a function of domain radius are shown in Fig. 3 d and e. For a 0.4-nm domain, the deviations are 10.6%, 10.0%, 12.1%, and 23.3% (solid, dotted, dashed, and dash-dotted curves, respectively) for different models. For a 1-nm domain, deviations are 24.5%, 23.2%, 26.2%, and 45.3% (solid, dotted, dashed, and dash-dotted curves, respectively). This strong dependence of signal on domain size even at the early stages of switching is a direct consequence of the 1/r dependence of the corresponding Green function. Realistic nucleation thresholds will be lower because the domain geometry at the early stages is hemispherical, rather than cylindrical, and the mechanical contact area is finite. Hence, we use threshold values of 0.5%, 3%, and 10% to account for these effects, and establish the sensitivity of analysis for a chosen threshold value.

Phase-Field Modeling.

Eq. 4 is solved numerically by using the semiimplicit Fourier spectral method (31). In the simulations, we used a model of 128Δx × 128Δx × 32Δx, with periodic boundary conditions along x₁ and x₂ axes in the film plane, where Δx is the simulation grid spacing. The thickness of the film is taken as h_f = 16Δx. The dielectric stiffness used to calculate the bulk energy along with the elastic and electrostrictive coefficients used in elastic energy calculation are obtained from ref. 31. For elastic energy calculations, we assumed that the substrate exerts a biaxial compressive strain of 1% on the thin film. The gradient energy coefficients were chosen as G₁₁/G₁₁₀ = 0.4. Because of the dearth of experimental values of domain wall width and domain wall energy for the BiFeO₃ system, the width of the 180° domain wall and the corresponding domain wall energy were taken to be similar in magnitude to other perovskite ferroelectric systems (32). For electrostatic energy calculations, we used κ₁₁ = κ₂₂ = κ₃₃ = 100. Effective tip size, γ, is varied from 10 nm to 70 nm in 10-nm steps. The pristine state was chosen as a single rhombohedral domain with polarization along [111]. To find the critical nucleation potential, the potential φ₀ was gradually increased with an increment of 0.05 V, and the domain structure from a previous simulation was used as the input at each increment of the potential. At a critical applied electric potential, a new rhombohedral domain with polarization along [111] was found to nucleate below the tip, and the corresponding electric potential was identified as the nucleation potential.

ACKNOWLEDGMENTS.

We gratefully acknowledge valuable discussions with E. Ward Plummer (University of Tennessee/Oak Ridge National Laboratory). This work was supported by the Division of Materials Sciences and Engineering, Oak Ridge National Laboratory, managed and operated by UT-Battelle for the Office of Basic Energy Sciences, U.S. Department of Energy (S.V.K., B.J.R., and S.J.); the U.S. Department of Energy under Contract DE-FG02-07ER46417 (S.C. and L.Q.C.); and the Director, Office of Science, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering, U.S. Department of Energy under Contract DE-AC02-05CH11231 (Y.H.C., T.Z., and R.R.).