Dodecamer rotor ring defines H⁺/ATP ratio for ATP synthesis of prokaryotic V-ATPase from Thermus thermophilus

Abstract

ATP synthesis by V-ATPase from the thermophilic bacterium Thermus thermophilus driven by the acid-base transition was investigated. The rate of ATP synthesis increased in parallel with the increase in proton motive force (PMF) >110 mV, which is composed of a difference in proton concentration (ΔpH) and the electrical potential differences (ΔΨ) across membranes. The optimum rate of synthesis reached 85 s⁻¹, and the H⁺/ATP ratio of 4.0 ± 0.1 was obtained. ATP was synthesized at a considerable rate solely by ΔpH, indicating ΔΨ was not absolutely required for synthesis. Consistent with the H⁺/ATP ratio, cryoelectron micrograph images of 2D crystals of the membrane-bound rotor ring of the V-ATPase at 7.0-Å resolution showed the presence of 12 V_o-c subunits, each composed of two transmembrane helices. These results indicate that symmetry mismatch between the rotor and catalytic domains is not obligatory for rotary ATPases/synthases.

Members of the F_oF₁ and V-ATPase superfamily (rotary ATPase/synthase) use a rotary catalytic mechanism to perform their specific function (1, 2). The F_oF₁ mainly catalyzes ATP synthesis in mitochondria, chloroplasts, and aerobic bacteria (3, 4). In contrast, V-ATPases exist in the endomembranes of all eukaryotic cells and in the plasma membrane of some specific eukaryotic cells functioning as a proton pump with a variety of cellular functions (2). The homologues of eukaryotic V-ATPases are also found in the plasma membrane of some bacteria (5, 6). Like the F_oF₁, V-ATPase from the thermophilic eubacterium Thermus thermophilus catalyzes ATP synthesis (7, 8). In addition, it has the simplest known subunit structure (Fig. 1a) and is thus an excellent model for studying the mechanism of action of these important molecules. Subunits A and B of V-ATPase are the counterparts of subunits β and α of F_oF₁ ATPase. Three copies of each subunit are arranged around the central rotor, which is made of single copies of subunits D and F. The A₃B₃DF moiety, termed V₁, is responsible for the ATP hydrolysis or ATP synthesis reaction. The remaining subunits, V_o-a (sometimes referred to as subunit I), V_o-c (sometimes referred to as subunit L), and V_o-d, E, and G form the V_o domain of T. thermophilus V-ATPase (9). The V_o-c subunits, which are folded into two transmembrane helices, constitute a membrane-embedded oligomeric ring structure (10). The V_o-c rotor ring and subunit V_o-a form a proton channel, as seen in the c rotor ring of the F_o-a subunit, despite low sequence similarity between the proteins.

Fig. 1.

Measurement of ATP synthesis of the prokaryotic V-ATPase from T. thermophilus. (a) Schematic model for the V-ATPase of T. thermophilus and experimental system. The isolated V-ATPase was reconstituted into liposomes, then energized by an acid-base transition procedure described in Materials and Methods. (b) Raw data of ATP synthesis of the V-ATPase at a ΔpH of 3.3. The proteoliposomes were acidified by soaking in 100 mM maleinate buffer. The reactions were initiated by the addition of acidified proteoliposomes into the base buffer, as indicated by the arrows. The ΔΨ was generated by the addition of different K⁺ concentrations to the outside of the proteoliposomes in the presence of 36 nM valinomycin. The ΔΨ was calculated from the Nernst equation: ΔΨ = 2.303 RT/F log[K_out⁺]/[K_in⁺]. The generated ΔΨ is represented; 118, 87, 59, 28, and 0 mV of ΔΨ correspond to 100, 30, 10, 3, and 1 mM [K_out⁺], respectively. −V-ATPase, liposomes without V-ATPase; +FCCP, in the presence of 50 μM FCCP at 118 mV of ΔΨ. Final concentrations are 0.05 mg/ml of V_oV₁, 1.1 mM ADP, and 200 nM ATP.

The basic mechanism of ATP synthesis for F_oF₁ is well understood, as described below. Briefly, the ring of the F_o-c subunit oligomer and γ-ε subunits of F₁ comprise the central rotor, and together these rotate as a single body (11). The transmembrane electrochemical potential gradient of proton [Δμ̃_H⁺ = PMF × F (PMF, proton motive force; F, Faraday constant)] drives rotation of the rotor ring of F_o relative to the α₃β₃ hexamer of F_1. This causes a conformational change in F₁ through rotation of the γ subunit that results in the synthesis of three ATP molecules for each revolution of the rotor ring (4, 12). Several lines of evidence indicate that the two components of the proton motive force, the transmembrane pH gradient (ΔpH) and the electric potential difference (ΔΨ), are kinetically equivalent, suggesting that both are equally capable of driving ATP synthesis (13, 14). In contrast, Kaim et al. (15, 16) have suggested that ATP synthesis by F_oF₁ depends obligatorily on the transmembrane voltage, and that the ΔpH alone cannot drive ATP synthesis.

In addition, the precise mechanism by which rotation of F_o is driven by the PMF is still unclarified. Junge et al. (17) have proposed a two-channel model; proton translocation through F_o occurs at an access channel to a glutamate on one F_o-c subunit in the rotor ring, and after one revolution of the ring, the proton is released at the other side via an exit channel. In this model, the copy number of the F_o-c subunit in the rotor ring is equal to the number of transported protons per revolution of the ring that directly defines the H⁺/ATP ratio, the number of protons transported through the enzyme per ATP synthesized. Thus, the copy number of subunits in the rotor ring is an important issue in regard to both the energetic and mechanistic considerations of ATP synthesis by rotary ATPase/synthases. Interestingly, the copy number in the rotor ring appears to vary among species (18–22).

In this work, we describe the ATP synthesis reaction of the prokaryotic V-ATPase of T. thermophilus using an acid-base transition procedure and assess the role of ΔpH and ΔΨ in ATP synthesis. In addition, we report a 12 V_o-c oligomer of the V-ATPase and discuss the relationship between the V_o-c subunit stoichiometry and H⁺/ATP ratio estimated by the biochemical assay.

Results

ATP Synthesis of the Prokaryotic V-ATPase from T. thermophilus.

To assess the ATP synthesis reaction of the prokaryotic V-ATPase from T. thermophilus, purified V-ATPase was reconstituted into liposomes by a freeze–thaw-sonication method (23). Features of the proteoliposomes were investigated by electron microscopy. A variety of liposome diameters (50–500 nm) were observed in this preparation [supporting information (SI) Fig. 5a]. The average liposome diameter was estimated to be ≈122 nm (n = 221; see SI Fig. 5b). A protein–liposome stoichiometry is estimated by molar ratio of protein per lipid and diameter of liposomes. With the average of liposome diameter of 122 nm, the protein–liposome stoichiometry is estimated to be 0.29. The variation of proteoliposomes may significantly affect a net amount of ATP-synthesized and kinetic behaviors of ATP synthase in liposomes on a longer time scale. However, as far as the initial rate of ATP synthesis is concerned, ATP synthesis activity is not affected by either diameter of proteoliposomes or protein–liposome ratio. In fact, we found that the initial rate of the ATP synthesis activity was not affected significantly by a difference in protein–liposome ratios ranging from 0.15 to 0.59 (SI Fig. 5c). Thus, we conclude it is reasonable to assume that, under conditions where ΔΨ is fixed, the initial rate of ATP synthesis of a V-ATPase–liposome complex depends solely on ΔpH generated by acid-base transition.

PMF was applied to the proteoliposomes by an acid-base transition procedure, represented schematically in Fig. 1a. The acidification of the proteoliposomes was attained by soaking in an acidification buffer for 5 min. The ATP synthesis rate did not depend on soaking times longer than 2 min, suggesting that equilibration of the internal of proteoliposomes and the external acidification buffer was achieved under this condition. ATP synthesis reactions were initiated by addition of proteoliposome solution acidified with 100 mM maleinate buffer, pH 4.9, into the base buffer containing 100 mM Tricin-Na, pH 8.5; a luciferin/luciferase assay system; 1.1 mM ADP; and 10 mM sodium phosphate. In this condition, the pH of mixtures was 8.3. The generated ATP was monitored as an increase in luminescence intensity. Fig. 1b shows a typical result of the ATP synthesis reaction driven by the V-ATPase. The amount of ATP increased linearly for ≈5 sec (Fig. 1b), then slowed. We refer only to the initial rates, because the PMF decreased because of ion fluxes through the membrane. In these conditions, the ATP synthesis reaction was observed for a few minutes. This indicates that the ΔpH between the inside and outside of the liposome remains for a few minutes during acid-base transition experiments. It is possible that the generated ΔpH or external base buffer might affect the permeability to proton across the membrane of liposomes. The rapid increase of luminescence intensity was abolished by the addition of carbonylcyanide-p-trifluoromethoxyphenylhydrazone (FCCP), a proton ionophore, into the proteoliposome fractions. The ATP synthesis reaction was accelerated by loading of a K⁺ diffusion potential, because of the differences between internal and external K⁺ concentration. The estimated theoretical ΔΨ by the Nernst equation is 118 mV (Fig. 1b). With increasing ΔΨ, the rate of ATP synthesis increased. These results suggest that both ΔpH and ΔΨ are capable of acting as a driving force for ATP synthesis by V-ATPase. The turnover rate of ATP synthesis by V-ATPase was 71 ± 7 s⁻¹ when using 100 mM maleinate with a ΔΨ of 118 mV. We estimated the ATP synthesis rate based on the premise that all V-ATPase molecules were reconstituted into liposome without misorientation. If it is assumed that 50% of the V₁ part in reconstituted V-ATPase oriented outward of the liposomes, the ATP synthesis rate is estimated to have a 2-fold value.

The Effect of Acid Species on ATP Synthesis.

Kaim and Dimroth (15) have shown that dicarboxylic acids such as maleinate or succinate, which are routinely used in acid-base transition procedures, generate not only ΔpH but also ΔΨ. They could detect the membrane permeability of several C¹⁴-labeled dicarboxylic acids and concluded that the concentration gradient of monoanions after dilution of acidified liposomes into a basic buffer drives the efflux of monoanions from liposomes into the outside milieu and as a result creates ΔΨ. Their results prompted an investigation of the effect of acid species on ATP synthesis by V-ATPase in the absence of ΔΨ because of a K⁺ diffusion potential. When 100 mM maleinate was used for the acid-base transition procedure, an ATP synthesis rate of ≈70 s⁻¹ was observed (SI Table 3). Consistent with their report, decreasing the concentration of dicarboxylic acid decreased the rate of ATP synthesis. However, only slightly lower rates of the ATP synthesis reaction were observed when morpholinoethane sulfonic acid (Mes) was used, which contains only one sulfonic residue, as the acid. When 100 mM succinate and malonate were used as the acids, the rates of ATP synthesis were almost identical to that when 100 mM Mes was used. It has been reported that the monovalent acidic species did not generate ΔΨ as a response to the efflux of the acid molecules across the membrane (15). It is not clear why different acid species, e.g., monovalent or divalent, affect the rate of ATP synthesis of the V-ATPase.

The Effects of ΔpH and ΔΨ on ATP Synthesis of the V-ATPase.

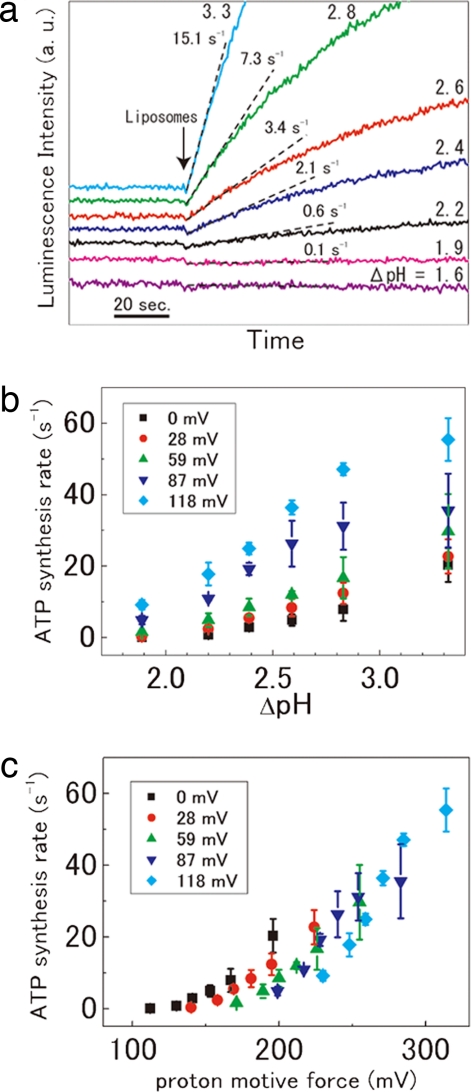
To investigate the effect of ΔpH and ΔΨ on ATP synthesis of the V-ATPase in detail, we measured the rate of ATP synthesis by V-ATPase using 100 mM Mes as the acidification buffer for the acid-base transition procedure. Fig. 2a shows the raw luminescence data at ΔpH values from 1.6 to 3.3 without ΔΨ. Although no ATP synthesis was measurable at a ΔpH of <1.6, a low level of ATP synthesis was detected at a ΔpH of 1.9. The ATP synthesis rates depended on ΔpH and increased with increasing ΔpH. The average ATP synthesis rate was 20 ± 5 s⁻¹ at a ΔpH of 3.3 and a ΔΨ of 0 mV (SI Table 3).

Fig. 2.

Effect of ΔpH and ΔΨ on the ATP synthesis of the V-ATPase. (a) Raw data for ATP synthesis by V-ATPase in the absence of ΔΨ ([K_out⁺] = [K_in⁺] = 1 μM). The proteoliposomes were acidified by soaking in 100 mM Mes buffer, pH 4.7, 5.3, 5.7, 6.1, and 6.4, respectively. (b) The ATP synthesis rate as a function of ΔpH in the presence of constant ΔΨ, 0 mV (black squares), 28 mV (red circles), 59 mV (green triangles), 87 mV (blue triangles), and 118 mV (blue squares). The data are the average of three or four measurements. The error limits are standard deviations. (c) ATP synthesis rate as a function of PMF calculated by the equation; PMF (mV) = 2.303 RT/F ΔpH + ΔΨ.

To estimate the effect of ΔΨ on ATP synthesis, we investigated the ATP synthesis reaction of V-ATPase at various ΔpHs over a range of ΔΨ values. As shown in Fig. 2b, the ATP synthesis rate was increased dramatically with an increase in ΔΨ over the range of ΔpHs. These data suggest that ΔpH and ΔΨ are likely to be thermodynamically equivalent as a driving force for ATP synthesis by V-ATPase. Fig. 2c shows the plot of the ATP synthesis activity as the function of PMF estimated by both ΔpH and ΔΨ. The threshold PMF required for ATP synthesis to occur was ≈110 mV. Thereafter, the rate of ATP synthesis increases exponentially with increasing PMF in the range of 112–314 mV.

H⁺/ATP Ratio of ATP Synthesis by V-ATPase.

To assess the H⁺/ATP ratio, we measured the ATP synthesis rate of the V-ATPase at varying [ATP]/[ADP][Pi] ratio, as represented in Table 1. The theoretical basis for the determination of H⁺/ATP ratio of ATP synthesis reaction was described in a previous report (24). When the ATP synthesis reaction is coupled with the transport of protons, the Gibbs free energy of ATP synthesis reaction (ΔG′) is approximately represented by:

where ΔG^o is the standard Gibbs free energy of ATP synthesis from ADP and Pi, and n is the H⁺/ATP ratio, the number of protons transported for each ATP synthesized. When ATP synthesis and hydrolysis are equilibrated (ΔG′ = 0), we obtain Eq. 2:

Because ΔpH and ΔΨ are thermodynamically equal, as described above, the Δμ̃_H⁺ at thermodynamic equilibrium (Δμ̃_H^+eq) values was obtained from the ΔpH at thermodynamic equilibrium (ΔpH_eq) values by the Eq. 3, taking the constant ΔΨ into consideration:

According to Eqs. 2 and 3, n and ΔG^o can be estimated by measurement of ΔpH_eq at various [ATP]/[ADP][Pi] ratios.

Table 1.

ATP, ADP, and phosphate concentrations in reaction mixtures of ATP synthesis for the different reaction conditions

Condition	ADP, μM	Pi, mM	ATP, nM	RT ln [ATP]/[ADP][Pi], kJ/mol	ΔpHeq
A	75	1.25	436	3.81	1.61 ± 0.04
B	12	1.25	431	8.32	1.81 ± 0.02
C	1.5	1.25	431	13.5	2.04 ± 0.03
D	0.3	0.8	431	18.6	2.26 ± 0.04

The error limits are the standard error. The statistical analysis for calculation of ΔpH_eq is described in SI Table 4.

Fig. 3a shows a typical ATP synthesis reaction by V-ATPase at various [ATP]/[ADP][Pi] ratios (A-D, summarized in Table 1). In all of these experiments, 15 mV of ΔΨ (K_out⁺ = 18 mM, K_in⁺ = 10 mM) was generated by a K⁺ diffusion potential, in addition to the ΔpH. Mes was used at 100 mM as the acidification buffer to avoid a generation of ΔΨ as a response to the efflux of the acid molecules across the membrane. ATP synthesis reactions were initiated by the addition of acidified liposomes, as indicated by the arrow (Fig. 3a). At lower ΔpH conditions, the linearity of the ATP synthesis rate apparently remains for ≈30 sec. In these conditions, we determined ATP synthesis rates by linear fitting with raw data of luminescence for >30 sec to decrease the measurement error due to low signal/noise ratio. Each value was corrected for the change of luminescence intensity before addition of an acidic proteoliposomes (Fig. 3a). We calculated each ΔpH_eq by applying the combined set of experimental rate values (see SI Table 3). Fig. 3b shows the rate of ATP synthesis as function of ΔpH at each [ATP]/[ADP][Pi] ratio condition. An apparent linearity in plots of rate of ATP synthesis vs. ΔpH was observed around ΔpH_eq = 0. Based on the linearity, the ΔpH_eq values were calculated by extrapolation. The obtained ΔpH_eq values at difference [ATP]/[ADP][Pi] ratios are summarized in Table 1. The ΔpH_eq value increased with increasing ADP concentration in the reaction mixture.

Fig. 3.

Rate of ATP synthesis at various [ATP]/[ADP][Pi] ratios. (a) The raw data of ATP synthesis reaction at each [ATP]/[ADP][Pi] ratio (A–D) summarized in Table 1. Each set of raw data was corrected for its baseline. The luminescence was calibrated by the addition of standard ATP. The different ΔpH_eq values are given next to each trace. (b) ATP synthesis and hydrolysis as a function of ΔpH. Each symbol represents data at different [ATP]/[ADP][Pi] ratio conditions (A–D). Arrows indicate ΔpH_eq, where the ATP synthesis rate becomes zero. The data are the average of three to seven measurements. The error limits are the standard deviations. (c) The energy contribution resulting from the [ATP]/[ADP][Pi] ratio as a function of Δμ̃_H^+eq given as the Eq. 3. Error bars in symbols are based on standard error values at each [ATP]/[ADP][Pi] ratio condition (see SI Table 3). The slope gives the H⁺/ATP ratio of n, and the y intercept gives the standard Gibbs free energy of ΔG^o. The estimated n value of 4.0 ± 0.1 from four data points has a 95% confidence interval of 3.7–4.3.

To calculate the H⁺/ATP ratio, the energy contribution resulting from the stoichiometric [ATP]/[ADP][Pi] ratio was plotted against Δμ̃_H^+eq, calculated by Eq. 3. The regression analysis gave a slope of 4.0 ± 0.1, representing the H⁺/ATP ratio, n (Fig. 3c). The y axis intercepts gave the standard Gibbs free energy for the ATP synthesis reaction, ΔG^o, with a value of 39 ± 1 kJ/mol. Statistical information about the calculation of ΔpH_eq, the n value, and ΔG^o is listed in SI Tables 3 and 5.

Determination of the Number of V_o-c Subunits in the Rotor Ring by Cryoelectron Microscopy.

The H⁺/ATP ratio of rotary ATPase/synthase depends on the number of F_o-c/V_o-c subunits in the rotor ring in V_o/F_o. To investigate the stoichiometry, we grew 2D crystals of the V_o ring.

The T. thermophilus V-ATPase subcomplex V_o used for 2D crystallization trials was isolated from T. thermophilus membrane fractions, as described in ref. 9. Fractions containing V_o were pooled, concentrated, and mixed with lipid stock solution. The V_o reconstituted into lipid vesicles through removal of Triton X-100 by dialysis against a detergent-free buffer. When examining the sample by transmission electron microscopy, a large number of vesicles were observed. Almost all of the particles appeared to have a similar shape, and some of them exhibited ordered arrays with a size of up to 600 nm (Fig. 4A). Because of the limited population and the small size of the 2D crystals, it was possible to collect only nontilt images by cryoelectron microscopy.

Fig. 4.

Formation of 2D crystals and projection map. (A) Micrograph of a uranyl acetate-stained 2D crystal. (B) The projection map, calculated from seven merged images, at 7.0-Å resolution, showing an orthogonal arrangement of dodecameric rings. One unit cell is outlined and has the dimensions of a = 83.5 ± 0.6 Å, b = 83.5 ± 0.6 Å, and γ = 90.4 ± 0.4°.

The quality of a typical well diffracting area is demonstrated by the IQ (signal-to-noise-ratio-based index of quality) (SI Fig. 6). Strong diffraction spots were found up to a resolution of 7.0 Å. The best seven images were merged, and a projection map was calculated to a resolution of 7.0 Å (Fig. 4B), resulting in a phase residual of 20.8° (Table 2) demonstrating the reliability of the map. The projection map shows an orthogonal arrangement of ring-like densities, each consisting of an outer, more loosely packed, and an inner, more tightly packed, ring, both containing 12 distinct densities. The 12 distinct densities of the loosely packed outer ring were also clear, even from a projection map from single images. At the obtained resolution of 7.0 Å, it is usually possible to assign α-helices positioned roughly perpendicular to the membrane plane. By taking into account the size and shape of the densities arranged in two concentric rings and comparing our map with the previously published projection map of 2D crystals of c₁₁ rings from Iyobacter tartaricus (25), we conclude these densities correspond to 12 V_o-c rotor subunits, with each subunit contributing one α-helix to the inner and one α-helix to the outer ring.

Table 2.

Electron crystallographic data

Assumed space group	p1
Lattice constant	a = 83.5 ± 0.6 Å, b = 83.5 ± 0.6 Å, γ = 90.4 ± 0.4°
No. of images	7
Range of under focus	8,300 − 11,000 Å
Resolution limit	7.0 Å
No. of independent reflections	209
No. of observed reflections	839
Phase residual (random = 90°)	20.8° (25.7° for 9.8–7.0 Å)

The unit cell parameters were determined as a = 83.5 ± 0.6 Å, b = 83.5 ± 0.6 Å, and γ = 90.4 ± 0.4°, with one unit cell containing two V_o-c rotor rings. When measuring from the edges of the red contour, the outer and inner diameters of the V_o-c rotor ring are 58 and 22 Å, respectively. This size corresponds well to the corresponding measurements of the c₁₁-ring 2D crystals from I. tartaricus of 50 and 17 Å (21). As seen in the projection map of the c₁₁-ring 2D crystals, a handedness of the rings can be distinguished in our projection map. The handedness of each individual ring differs from its four neighboring rings, indicating an upside-down packing in the membrane plane (Fig. 4B).

In our 2D crystallization trials, we used fractions eluted from an anion-exchange column containing all subunits of the V_o complex. However, the projection map shows clear densities of the V_o-c rotor ring only. It is possible that other subunits interacting with the V_o-c rotor ring are dissociated during crystallization.

Discussion

The ATP synthesis reaction of the rotary ATPase/synthase is an important but only partially understood mechanism. The mechanism of ATP synthesis by V- ATPase/synthase is particularly poorly characterized. To investigate the ATP synthesis reaction of V-ATPase, we carried out acid-base transition experiments using proteoliposome containing V-ATPase from T. thermophilus. As shown in SI Table 3, the V-ATPase shows the maximal rate of ATP synthesis reaction of 85 ± 17 s⁻¹ when using 100 mM malonate as the acidification buffer. This ATP synthesis rate is comparable with that reported for of Escherichia coli F_oF₁ (26, 27), indicating that the prokaryotic V-ATPases are an equally effective enzyme for ATP synthesis.

In F_oF₁, whether the ΔpH and ΔΨ are thermodynamically equivalent for ATP synthesis is still a controversial issue. In a study using F_oF₁ from chloroplasts, ATP was synthesized after an acid-base transition in the absence of ΔΨ (28). There were several lines of evidence indicating that both ΔpH and ΔΨ are capable of driving the ATP synthesis reaction (14, 27–29). However, Kaim and Dimroth (15) have reported that the ATP synthesis reaction by E. coli F_oF₁ depends on ΔΨ and could not be energized by ΔpH only (15). In this study, we investigated this controversial issue by examining ATP synthesis by V-ATPase. As shown in Fig. 2, the rate of ATP synthesis increased exponentially with ΔpH. The rate of ATP synthesis also increased with increasing ΔΨ; however, the apparent ATP synthesis reaction of 20 ± 5 s⁻¹ was observed without ΔΨ. The ATP synthesis rate at each ΔpH was apparently accelerated by the additional ΔΨ (Fig. 2b), suggesting that both the ΔpH and ΔΨ act to drive ATP synthesis by V-ATPase. These results are different from those obtained for E. coli F_oF₁ but are consistent with those for chloroplast F_oF₁. It is not clear whether the differences are due to the molecular species of rotary ATPase/synthase or other reasons. Further studies on the ATP synthesis reaction of E. coli F_oF₁ are required to clarify this issue.

H⁺/ATP Ratio of ATP Synthesis of the Prokaryotic V-ATPase.

The H⁺/ATP ratio of the ATP synthesis reaction is an important issue in bioenergetics. However, there is controversy about the precise value with varying ratios of between 2 and 4 being reported (30). Turina et al. (24) reported a model system for determination of the ratio of F_oF₁ from chloroplasts. They measured the ATP synthesis and hydrolysis by acid-base transition at different [ATP]/[ADP][Pi] ratios to determine the Δμ̃_H^+eq where the ATP synthesis and hydrolysis reaction catalyzed by the ATPase/synthase are thermodynamically equivalent. Based on analysis of the [ATP]/[ADP][Pi] ratio as a function of Δμ̃_H^+eq, they reported a H⁺/ATP ratio of ≈4.0. We used this model system to obtain the H⁺/ATP ratio of the prokaryotic V-ATPase. We determined a Δμ̃_H^+eq value at each [ATP]/[ADP][Pi] ratio and calculated the H⁺/ATP ratio n to be 4.0 ± 0.1. The obtained Gibbs free energy ΔG^o with a value of 39 ± 1 kJ/mol at pH_out of 8.3 is in good agreement with the ΔG^o of 37 ± 3 kJ/mol for chloroplast F_oF₁ and the theoretical ΔG^o of 35.6 kJ/mol at pH_out of 8.45 as reported (24).

Our data show that the H⁺/ATP ratio, defined as the number of protons necessary to synthesize one ATP at equilibrium, is ≈4. If rotation of the rotor ring and the DF shaft in the V₁ domain is coupled without slip, the H⁺/ATP ratio of the V-ATPase will be strictly determined by the ratio between copy numbers of catalytic A subunits in V₁ and proton translocating V_o-c subunits in the rotor ring. The catalytic core of the V-ATPase is also composed of three catalytic A subunits as well as F_oF₁. Therefore, our results predict the V_o-c rotor ring to comprise 12 subunits.

Molecular Basis of the H⁺/ATP Ratio of the V-ATPase from T. thermophilus.

By using cryoelectron microscopy, we have revealed a dodecamer ring of the V-ATPase from T. thermophilus. It had been generally accepted that the copy number of F_o-c subunit in F_o-c rotor ring is 12 (31). However, 10, 11, 13, or 14 copies of the rotor ring have been reported (18–22, 32) since the crystal structure of yeast F₁-c₁₀ complex was published (18). None of the earlier reported structural studies detect the originally anticipated number of 12 rotor subunits. Thus, it has been argued that a mismatch in symmetry among the three catalytic β subunits in F₁ and the copy numbers of F_o-c subunits in the rotor ring could be obligatory for ATP synthesis reaction by the rotary ATPase/synthases (18, 19, 32). When the rotor ring is a decamer, the step size of unit rotation does not fit between F₁ and F_o. Because the coiled-coil structure of the γ subunit allows some internal twisting, and the F_o-b dimer of the side stalk has extra flexibility, both can undergo elastic twisting or bending to enable the proper alignment of rotor–stator contacts at both F_o and F₁. This elastic energy due to the symmetry mismatch has been thought to be obligatory for the functioning of the rotary ATPase/synthase.

However, we have found a dodecamer rotor ring in the V-ATPase from T. thermophilus that shows the apparent ATP synthesis activity coupled with downhill proton flow through V_o. The presence of the dodecamer ring in the rotary ATPase/synthase was previously undescribed. Recently, Pogoryelov et al. (33) analyzed the rotor ring of the alkaliphilic cyanobacterium Spirulina platensis by atomic force microscopy and showed a c₁₅ ring that exhibited no symmetry mismatch. Although it was argued that the matching symmetry could be the consequence of the rotor ring's unusual size, it was noted that symmetry mismatch is not obligatory. Thus, we conclude that, independent of the rotor ring's size, symmetry mismatch is not obligatory for ATP synthesis in rotary ATPase/synthases.

Our study has estimated the H⁺/ATP ratio of the V-ATPase of T. thermophilus to be 4, a value consistent with the results from the 2D structural analysis. This suggests a possible tight coupling between the ATP synthesis reaction in V₁ and the down-hill proton movement through V_o.

Materials and Methods

Preparation of the V-ATPase and V_o Domain.

The intact V-ATPase and the V_o were isolated for both ATP synthesis measurements and the formation of 2D crystal, as described in ref. 9. The His-tagged V-ATPase, solubilized from T. thermophilus membrane fraction with a buffer containing 10% Triton X-100, was purified by Ni²⁺ affinity chromatography. The partially purified enzyme was applied to a Resource Q column (6 ml, Amersham Biosciences) equilibrated with 20 mM Tris·HCl (pH 8.0), 0.1 mM EDTA, and 0.05% Triton X-100. The proteins were eluted with a linear NaCl gradient (0–0.5 M). For ATP synthesis experiments, the intact V-ATPase fractions were concentrated, then applied onto a Superdex HR-200 column (GE Healthcare) equilibrated with 20 mM 4-morpholinepropanesulfonic acid, pH 7.0; 100 mM NaCl; 0.05% n-dodecyl β-d-maltoside (DDM). The purified V-ATPase was stored at 4°C until use for the ATP synthesis experiments. Fractions containing V_o were pooled, then concentrated to 2 mg/ml using Amicon ultrafiltration devices (Millipore) and immediately subjected to a 2D crystallization. Protein concentrations were determined by BCA protein assay (Pierce), using V₁ as a standard.

Measurement of ATP Synthesis of the V-ATPase.

The V-ATPase from T. thermophilus was reconstituted into liposomes using a freeze-thaw sonication method. Solid l-α-phosphatydylcholine (Sigma, type II-S) was added into 10 mM Hepes-Na, pH 7.5; 10 mM MgSO₄; 1 mM KCl buffer, then suspended by sonication to a final concentration of 32 mg/ml. The V-ATPase was added to the lipid suspension at a protein concentration of 0.05 mg/ml. The mixture was snap-frozen in liquid nitrogen and immediately thawed by incubation at room temperature. The freeze-thaw process was repeated twice. Acidification of the proteoliposomes and measurement of ATP synthesis were carried out at 25°C. To acidify the interior of proteoliposomes, 40 μl of the proteoliposome solution was mixed with 20 μl of acidification buffer (300 mM Mes, maleinate, succinate, or malonate) and then incubated for 5 min at 25°C. After incubations, the pH of the acidified liposome solutions (ΔpH_in) was measured by a pH glass electrode. ATP Bioluminescence Assay Kit CLS II (Roche) was used for detection of synthesized ATP. The ATP was measured as the increase of intensity of luminescence at 550 nm in an FP 6500 spectro fluorometer (Jasco) without exciting light. For calibration, ATP or ADP was injected into the base buffer as indicated by the arrows (Fig. 1b). The ATP synthesis reaction was initiated by injection of 60 μl of the acidified proteoliposomes into 1 ml of base buffer containing 100 mM Tricin-Na, pH 8.5; 2.5 mM MgSO₄; 10 mM phosphate; 2.2 mg of luciferin/luciferase compound; 1.1 mM ADP; 36 nM valinomycin; and 1–100 mM KCl. After measurement of the ATP synthesis reactions, the pH of the mixtures (ΔpH_out) was directly measured by the pH glass electrode to determine the ΔpH (= ΔpH_out − ΔpH_in).

2D Crystallization, Electron Microscopy, and Image Analysis.

The V_o fraction was mixed with 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) (Avanti Polar Lipids) to a protein-to-lipid ratio (wt/wt) of 0.25. 2D crystallization was performed by dialysis against detergent-free buffer [20 mM Tris·HCl (pH 8.0), 200 mM NaCl, 0.02% NaN₃].

Specimens were prepared for cryoelectron microscopy in 7% trehalose on molybdenum grids by the back-injection method, and images were taken at liquid helium temperature. Electron micrographs were collected with a JEM3100FFC electron microscope equipped with a liquid helium cryostage (34) and an Omega energy filter and operated at an acceleration voltage of 300 kV. Images were recorded on Kodak SO-163 film at a magnification of 40,000 with 2-sec exposure. Images were scanned, and digitized images were processed with a modified version of the MRC image processing programs (35). They were computationally unbent and corrected for the contrast-transfer function (CTF) (36). The CTF parameters of each image were determined by the combination method of square-frequency filtering (37) with Periodogram averaging (38). Seven images were merged to make an averaged projection map at 7.0-Å resolution. Statistics of our electron-crystallographic analysis are summarized in Table 2.