Estimation of multiple transmission rates for epidemics in heterogeneous populations

Abstract

One of the principal challenges in epidemiological modeling is to parameterize models with realistic estimates for transmission rates in order to analyze strategies for control and to predict disease outcomes. Using a combination of replicated experiments, Bayesian statistical inference, and stochastic modeling, we introduce and illustrate a strategy to estimate transmission parameters for the spread of infection through a two-phase mosaic, comprising favorable and unfavorable hosts. We focus on epidemics with local dispersal and formulate a spatially explicit, stochastic set of transition probabilities using a percolation paradigm for a susceptible–infected (S–I) epidemiological model. The S–I percolation model is further generalized to allow for multiple sources of infection including external inoculum and host-to-host infection. We fit the model using Bayesian inference and Markov chain Monte Carlo simulation to successive snapshots of damping-off disease spreading through replicated plant populations that differ in relative proportions of favorable and unfavorable hosts and with time-varying rates of transmission. Epidemiologically plausible parametric forms for these transmission rates are compared by using the deviance information criterion. Our results show that there are four transmission rates for a two-phase system, corresponding to each combination of infected donor and susceptible recipient. Knowing the number and magnitudes of the transmission rates allows the dominant pathways for transmission in a heterogeneous population to be identified. Finally, we show how failure to allow for multiple transmission rates can overestimate or underestimate the rate of spread of epidemics in heterogeneous environments, which could lead to marked failure or inefficiency of control strategies.

One of the principal challenges in epidemiological modeling is to parameterize models with realistic estimates for transmission rates in order to analyze strategies for control and to predict disease outcomes. Although the durations of infectious and latent periods often can be estimated from observation of individuals challenged with inoculum, the probabilities and the associated rates for transmission of infection between infected and susceptible individuals are notoriously difficult to measure or estimate (1, 2). The problem is especially acute in spatially structured, heterogeneous host populations, in which hosts differ in susceptibility and infectivity. The magnitudes of the transmission rates typically change over space, according to the nature of the infected donor and the susceptible recipient, and also may change over time (2). In human diseases, infectivity and susceptibility may be affected by genetic, physiological, or social differences (3–5) as well as by immune and vaccination history. Examples also occur in animal epidemiology, with transmission of infection of a common pathogen within and between species at the landscape scale, such as foot and mouth disease in sheep and cattle (6) or in prophylactic treatment of some herds or animals but not others. Analogous examples occur at two scales in cropping systems, either as mixtures of crop species within fields (7, 8) (where the plant is the unit of epidemiological interest) or as a mosaic of crops, such as wheat and barley with differing susceptibility to a common pathogen, arranged within a landscape (where the field is the unit of epidemiological interest) (9, 10).

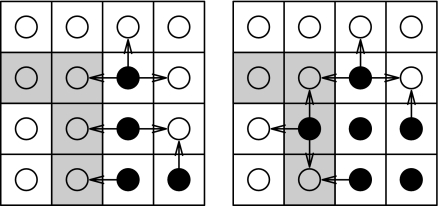
It is now widely acknowledged that host heterogeneity can endow systems with a far more complex range of dynamics, relating to species and population persistence (9, 11, 12) or evolutionary processes (13), than would be exhibited in homogeneous settings. Even for a two-phase system, there may be as many as four distinct rates arising from each combination of transmission between donor (infected) and recipient (susceptible) individual, and as few as one, if hosts respond homogeneously to infection. Together with the spatial distribution or network structure of favorable and unfavorable hosts in the population, multiple transmission rates determine the spatial and temporal evolution of the epidemic in ways that are quite different from homogeneous transmission. Preferential spread on one component, for example, changes the evolution of the contact structure between infected and susceptible sites during the course of the epidemic (Fig. 1). To be able to predict such behavior depends on being able to discriminate differences in transmission rates. Using a combination of replicated experiments, statistical estimation, and stochastic modeling, we show below how failure to account for heterogeneity in transmission rates by assuming a common (average) transmission rate can seriously misinterpret the dynamics of the epidemic.

Fig. 1.

Dynamics of infection in a heterogeneous host population comprising unfavorable (U, gray squares) and favorable (F, white squares) sites. The state of an epidemic is shown for two time points, with solid circles indicating infected hosts and empty circles indicating susceptible hosts. The arrows represent potential transmission routes between infected and neighboring susceptible sites. The figure shows how the localized conditions change with time and how the disease load depends on the relative strength of each of the four possible transmission rates β[., .]. (Left) Total infective challenge on F is 4β[F, F] and 3β[F, U] on U. (Right) As more hosts become infected, this challenge changes to 3β[F, F] + β[U, F] on F and 2β[F, U] + 2β[U, U] on U. Even though the number of transmission pathways has increased from seven to eight, the combined effective challenge may be greater or less than in Left, depending on the relative strength of each of the four transmission rates.

Specifically, we consider spatially heterogeneous epidemic systems in which pathogen spread occurs through a landscape comprising favorable sites (such as a susceptible or untreated host) and less favorable sites (such as partially resistant or treated hosts). We focus on processes and models with a strong network structure with short-range interactions. We develop an innovative statistical methodology for the estimation of transmission parameters for a stochastic model of epidemics in heterogeneous populations and test it on successive spatial maps of epidemics from replicated microcosms of mixed populations of radish and mustard seedlings (henceforth labeled favorable, F, and unfavorable, U, respectively) exposed to the fungal plant pathogen Rhizoctonia solani Kühn. Soil-borne pathogens are important determinants in the dynamics of plant populations in natural environments (14) and in epidemics in agricultural environments (9, 13). The model is formulated as a stochastic, spatially explicit set of transition probabilities using a percolation paradigm for a susceptible–infected (S–I) epidemiological model that previously has been shown to be appropriate for epidemics with short-range, nearest-neighbor contacts on a lattice (15, 16). The S–I percolation model is generalized to allow for multiple sources of infection, including primary (from external inoculum) and secondary (host-to-host) infection. In common with many real-life systems such as measles (17), the infection process is subject to temporal forcing, which is accounted for by differential time-varying rates of infection as the two species become resistant to damping-off disease (see Methods). Parameter estimation is effected by fitting the model to observations of disease spread through time and space in replicated epidemics using a combination of Bayesian inference and Markov chain Monte Carlo simulation, adapted from Gibson et al. (2).

Our specific objectives are:

• to develop methods to fit percolation-based, spatiotemporal models for the spread of epidemics that evolve in heterogeneous environments with local dispersal and time-varying transmission rates within and between species;

• to demonstrate methods for formal comparison of models and to test for significant differences among transmission rates;

• to use parameter estimates to analyze and predict the effects of different degrees of spatial heterogeneity on disease dynamics; and

• to assess whether temporal forcing of transmission rates can be detected with the infrequent sampling typical of large-scale natural systems.

We also address the effect of large-scale (typified by the percentage of area covered by favorable sites) and small-scale (typified by the degree of clustering of favorable sites) heterogeneity on the connectivity within and between favorable and unfavorable sites, and how connectivity and transmission rates determine disease levels by controlling the way an epidemic invades its environment.

Results

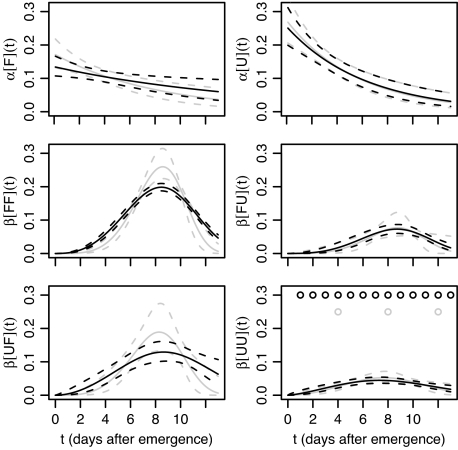
We first identified the parametric forms for time-varying transmission rates (see Methods) from which we conclude that the rate of primary infection declines exponentially with time and the rate of secondary infection rises and falls over time, described by a three-parameter Weibull function. The nuisance parameter used to account for so-called tertiary infection arising from the occasional non-nearest-neighbor transmission was constant throughout the epidemics. Models were compared using the deviance information criterion (DIC) [see Methods and supporting information (SI) Appendix]. Although the particular form of time-dependency for the transmission rates (Fig. 2) reflects the characteristics of the specific system we used to test our method, the methodology introduced below to estimate multiple transmission rates can easily be generalized to any epidemic with or without temporal forcing (see Discussion).

Fig. 2.

Posterior means (solid curves) and 95% credible intervals (dashed curves) for primary [α[F](t) and α[U](t)] and each of the four secondary [β[FF](t), β[FU](t), β[UF](t), and β[UU](t)] transmission rates against time. Results using the full spatiotemporal data are shown in black (with observations at times indicated by black circles in the lower right plot), and the corresponding results, with all but three observations at times 4, 8, and 12 discarded, are shown in gray.

Model Fitting and Comparison of Transmission Rates.

Bayesian methods were used to estimate parameters and to compare transmission rates for the fully parameterized, spatially explicit, stochastic model for time-varying primary and secondary infection rates. We show that not only was there no evidence to support a common rate among and between species but also that the rates of secondary infection differed according to which species was the donor and which the recipient (Table 1, Fig. 2). It follows that there are two transmission rates for primary infection, one per host species, but that the differential transmission of secondary infection needs to be explained by four distinct rates, depending on which species is the donor and which the recipient. The full joint posterior distribution is used to calculate the rates shown in Fig. 2. The corresponding point estimates for parameters together with 95% credible intervals are given in SI Table 3. Both parameters governing primary infection differed between species (Pr(a_U > a_F ∣ data) < 0.0001, Pr(r_U > r_F ∣ data) < 0.01). Because both species were challenged by the same source of inoculum, these differences indicate that although the unfavorable (mustard) sites were initially more susceptible to inoculum, they became resistant more quickly than the favorable (radish) sites (Fig. 2). Interpretation of the various parameters for secondary infection is more complicated, because each set of three parameters contributes jointly to the shape of the secondary transmission rate (Fig. 2). All four within- and between-species transmission rates displayed similar temporal dynamics: the rate of transmission initially increased, followed by a decrease. The absolute values were, however, significantly different for all four transmission rates (Fig. 2, Table 1).

Table 1.

Difference in deviance information criteria (DIC) relative to the best-fitting model, used to confirm absence of common parameters for secondary transmission rates, associated with the donor, the recipient, or both

Model		DIC	p̂
Full		0	21.0
Donors same	β[FF] = β[UF]; β[FU] = β[UU]	25	15.7
Recipients same	β[FF] = β[FU]; β[UF] = β[UU]	482	11.5
Cross same	β[FU] = β[UF]	50	17.3
All rates same	β[FF] = β[FU] = β[UF] = β[UU]	921	7.4

The estimated effective number of parameters is denoted p̂. For brevity, the time dependence of β is omitted.

The largest of the secondary transmission rates unsurprisingly occurred between two favorable sites, followed by the transmission of infection from unfavorable to favorable sites. The rate at which unfavorable sites became infected was lower, in particular for transmission between two unfavorable sites. Overall, however, there were appreciable rates for between-species (UF, FU) transmission of infection with differing magnitudes that could not have been predicted from the within-species (UU, FF) rates (compare Fig. 2).

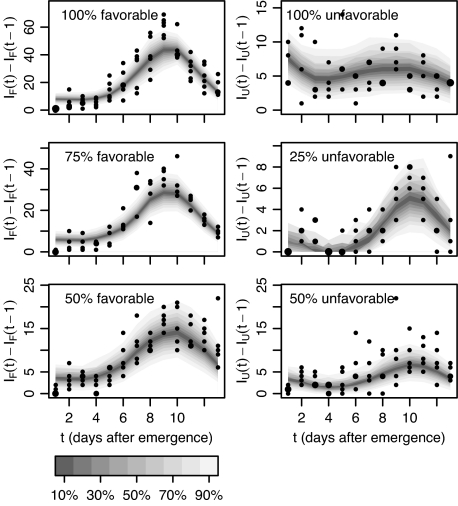
We plot the predicted and measured daily distribution of new infections as a measure of goodness-of-fit (Fig. 3). It is striking that with a single set of parameters, the prediction of the number of new infections for each day agrees well with the measured data for all population structures, representing a wide range of heterogeneity. Although the predicted distributions follow the central trend of the observations, the amount of variability in the number of new infections is underestimated, with more observations falling outside the credible bounds than would be expected. This extra variability may indicate environmental differences between replicates that we have not modeled and which in principle could be remedied by taking a hierarchical Bayesian approach (e.g., refs. 18 and 19).

Fig. 3.

Posterior predictive new infections of daily increments (shaded region corresponds to credible intervals) with observations (points, area of symbols are proportional to the number of observations) for damping-off epidemics in mixed populations comprising 100%, 75%, 50%, or 0% favorable hosts. Predictions take the form of mixture distributions with each component conditional on the previous spatial observation of disease presence in an experimental replicate. Predictions take account of both parametric uncertainty and population stochasticity. I_F(t) and I_U(t) denote the number of infected favorable and unfavorable hosts at time t, respectively.

Sensitivity of Results to Frequency of Observations.

To assess whether or not the temporal change in transmission rates could still have been identified with less intensive sampling, we discard some of the data and repeat the model fitting routine. The inferred posterior mean and 95% credible intervals for the transmission rates, taking observations to be at times 4, 8, and 12 rather than daily until day 13, are plotted in Fig. 2 in gray. The correspondence between the analyses based on the full and reduced data sets is remarkably close. The increase in the variability of the estimates from the reduced data set is small compared with the putative decrease in sampling costs.

Identification of Dominant Pathways for Transmission of Infection.

Estimation of the set of transmission rates for an epidemic in a heterogeneous population of hosts allows us to identify the dominant pathways for infection on which future efforts to control and manage disease should be targeted. We derive the following posterior distributions: the number of hosts in a mixed population that became infected by primary infection and by infection via secondary infection from the same species or class (e.g., favorable–favorable or unfavorable–unfavorable) and between species (e.g., favorable–unfavorable or unfavorable–favorable) (Table 2). In heterogeneous populations, a population with 75% favorable sites (Fig. 4a) provides a well connected network of neighboring favorable sites that is preferentially exploited by the epidemic. Unfavorable sites become infected predominantly from neighboring favorable sites and contribute little to transmission of infection. In contrast, for a population with 50% favorable sites (Fig. 4d), the connectivity of the favorable network is reduced and the contribution of unfavorable sites to the spread of epidemics increased significantly (Table 2). Only by fitting spatial models is it possible to obtain estimates of the most likely pathways for transmission of infection.

Table 2.

Identification of the most likely pathways and sources of transmission of infection in mixed populations, estimated by fitting the model to replicated epidemics of mixed populations with different ratios of favorable (F) and unfavorable (U) plants

Species	100% F	75% F		50% F		100% U
	F	F	U	F	U	U
Primary infection	4.6 (0.2)	4.5 (0.3)	5.8 (0.3)	4.2 (0.3)	5.8 (0.2)	5.7 (0.2)
Secondary transmission from F	58.4 (0.5)	45.4 (0.7)	27.1 (0.9)	25.7 (0.7)	14.5 (0.6)	—
Secondary transmission from U	—	5.0 (0.5)	2.0 (0.5)	13.1 (0.6)	9.3 (0.5)	7.9 (0.3)

The values show the posterior mean (expressed as % of F or U present in the population) of plants that became infected by primary infection, secondary infection from favorable plants, or secondary infection from an unfavorable plant. Tertiary infection accounted for the infection of a further 11–15% of favorable and 4–5% of unfavorable plants. Standard deviations are given in parentheses.

Fig. 4.

Nature and effects of the spatial structure of heterogeneity. When 75% of the population is favorable (a, gray squares), they form a well connected network. At 50%, both favorable and unfavorable (d, white squares) sites form isolated patches. The effect of the fraction of sites in the population that is favorable (b) or unfavorable (e) and the proportion of neighbors of the same type (c and f), a measure of clustering, on levels of disease, with (continuous lines and solid circles) or without (dashed lines and empty circles) inclusion of transmission of disease between favorable and unfavorable sites in the population.

The Effect of Heterogeneity in Population Structure.

Model inferences were used with the estimated parameters to analyze the effect of heterogeneity at two spatial scales: at the large scale, exemplified by the area of the population covered by favorable sites, and at the small scale, exemplified by the clustering of favorable sites within the population. The intuitive expectation here is that an increase in the proportion or clustering of a subpopulation through which disease spreads will lead to an increase in infection as the number of contacts to the same host type increases and a better connected network for transmission of infection is formed (Fig. 4). The proportion of infected hosts in the favorable subpopulation did indeed increase, irrespective of transmission between subpopulations (Fig. 4 b and c). However, the combined effect of the four transmission rates for secondary infection and the evolution of contacts between favorable and unfavorable sites resulted in counterintuitive responses in the unfavorable subpopulation. Here, an increase in the proportion of the unfavorable population resulted in either more or less infection, depending on the relative magnitude of the transmission rates between the two subpopulations (Fig. 4e). A similar dichotomous response resulted from reducing the amount of local clustering (Fig. 4f). We conclude that the effect of a better connected network in the unfavorable subpopulation is offset against a decrease in the number of contacts with the favorable subpopulation within which disease can spread faster. Additional simulations (data not shown) showed that this pattern depends on neither the level of primary infection nor the time-dependency of the transmission rates, but that it does depend on the relative values of the transmission rates.

Discussion

Transmission rates for epidemics are notoriously difficult to quantify (20) and resort is often made to indirect methods of estimation. Our approach introduces and tests a framework for direct estimation of transmission rates from spatiotemporal snapshots of disease spread through heterogeneous populations. By integrating experimentation, modeling, and parameter estimation using Bayesian estimation coupled with Markov chain Monte Carlo simulation, the framework allows identification and analysis of the processes that underlie the spread of disease in heterogeneous populations. We have shown that the following are possible: (i) estimation of multiple transmission rates from spatiotemporal data of disease in heterogeneous (two-phase) environments, (ii) formal comparison of models and tests for significant differences among transmission rates, (iii) identification of the main sources and pathways of infection, and (iv) analysis, using parameter estimates, of how epidemics evolve in response to changes to the heterogeneity of their environment. Although the framework was tested for a full data set of 13 successive spatiotemporal maps for which the observational time scale was well matched to the biological time scale of the system, we have also shown that the method is robust to drastic reduction in the number (three) of snapshots. Small numbers of snapshots are much more typical of epidemics in natural systems (21, 22), and the robustness of the methods to these small samples supports the generality of the statistical framework to nonmodel systems.

Knowing the number and magnitude of transmission rates enabled us to identify the dominant pathways for transmission of infection (Fig. 4). Failure to allow for multiple transmission rates could grossly underestimate or overestimate the rate of spread of disease, especially in inferring the effects of changing the proportion of favorable or unfavorable sites associated with disease-control strategies in a population. For example, at the landscape scale, we may consider vaccinating hosts spatially to control diseases such as foot and mouth (23); the choice of whether to vaccinate all susceptible animals or just cattle, say—without prior knowledge of the resulting transmission rates for the epidemic—could lead to marked failure or inefficiency in prophylactic use.

We developed our methods for a generic model for epidemics (9) where hosts are classified as either susceptible (S) or infected (I) in order to illustrate the approach. Although the model does not include any hidden classes, such as latent infections (1), extra classes can, in principle, be accommodated. The model and approach also readily generalize to multiple phases or host types. If h_j, the heterogeneity covariate of host j, remains categorical, the extension is obvious, although the number of parameters increases quadratically with the number of phases. If h_j represents a continually varying trait, then some functional form (24) must be imposed for the rate β[h_i, h_s](t) of infection from i to s: for example, that β[h_i, h_s](t) is proportional to h_s and constant with time (25).

The plant pathogen experimental microcosm system used here is well suited to testing methodological advances (1, 2). It is repeatable yet introduces stochasticity to replicated epidemics in unpredictable ways that reflect well the uncertainty of biological systems not always captured by computer simulation. Epidemics are short, with completion in 15–20 days, and allow repeated observations, usually at daily intervals, of evolving replicated epidemics. Even in the model system, complexities arise. The rates of primary infection decay exponentially with time; the rise and fall in the rates of secondary infection are consistent with changes in infectivity as plants grow and become stronger donors, offset by increasing resistance as plants age (26). These results are consistent with analyses of epidemics in analogous homogeneous systems, and biological interpretations associated with changing dynamics of host susceptibilities are detailed elsewhere (26). The important feature to note here is that time-dependency of transmission rates is often not known a priori, yet it plays a crucial role in the dynamics of epidemics, especially when it leads to rapid quenching of disease spread (27). Our method enables formal comparison of models to identify appropriate functions for time-dependency of transmission rates.

Time-varying infection rates are not limited to plant diseases. Rates may change as a result of policy [e.g., culling of livestock (28), the imposition of travel restrictions (29)], social reaction to the threat of infections (29), environmental changes (30), or seasonal variation (17). Host age (31) and viral load (32) can also have an effect on transmissibility of infection. The detection of changes depends on sufficient information being present in the available data but does not depend as much on frequent sampling as might be expected: repeating the analysis in this article but omitting 75% of the observation times yields very similar results (Fig. 2).

Although the focus of this article has been on crop mixtures, marked differences in transmissibility of infection within and among classes of hosts are also important determinants of the outcome of disease outbreaks in human and other animal populations. Typical examples include species differences in transmission of the foot and mouth pathogen (28) and polymorphism and recombinational hotspots in susceptibility to malaria (3). Sexual orientation, behavior, and partner choice impose heterogeneities in relation to sexually transmitted diseases (4, 5) as do age (4, 31) and sex (4, 33) for a range of other diseases. Until now, it has been very difficult to parameterize models to take account of such heterogeneities, despite their implicit importance in the dissemination and control of disease, as for example in the recent outbreak of severe acute respiratory syndrome (29).

The main feature of the framework introduced here is that it allows for analysis of epidemics in heterogeneous environments while accounting for two crucial underlying aspects, namely, the contact between sites in the population and real estimates of multiple transmission rates that operate in heterogeneous systems. We have shown that both factors affect the dynamics of epidemics and hence the effectiveness of disease-control strategies. Such strategies could include spatially explicit control by shielding susceptible hosts, fields, or even farms, for example, by the spatial deployment of resistant varieties or a local deployment of a chemical or biological control agent (8, 10, 34). The effectiveness is largely determined by the relative magnitude of the transmission rates. If transmission rates between favorable and unfavorable sites are intermediate or high, we have shown that the levels of disease in sites that are less favorable for spread are dominated by the disease pressure from the favorable sites in the population (Fig. 3). Hence, the heterogeneity of the population determines the underlying landscape within which contacts between infected and susceptible sites, either favorable or unfavorable, are subsequently dynamically generated by the pathogen as it explores specific contacts preferentially. The latter mainly is determined by the relative magnitude of the transmission rates. Knowledge of multiple transmission rates as estimated in this article therefore is essential in addressing epidemiologically important issues such as the minimum spatial coverage of a vaccination treatment required to reduce the risk of invasion (23) or whether or not a susceptible crop or cropping system (e.g., organic farms) can be introduced without enhancing the risk of invasive spread at the regional scale (10). These questions can be addressed only within spatial models. Our method ensures that answers to such questions are statistically sound and fully integrated with experimental trials or field data.

Methods

Model Structure.

The model of Gibson et al. (2) can be readily generalized to represent a mixed-species population. The heterogeneity of the population is described by assigning the covariate h_j to each member j of the population, where h_j takes the values 0, 1 for favorable or unfavorable sites for disease transmission. Let I_j(t) = 1 if j is infected by time t and 0 if still susceptible. In common with most stochastic epidemiological models (1, 35, 36), we assume that Pr(I_s(t + dt) = 1∣I_s(t) = 0) = φ_s(t)dt as dt → 0, where φ_s(t) is the rate of infection of s. In the specific model used here, φ_s(t) is composed of terms representing the rate of primary infection from inoculum at time t if s is inoculated, denoted α[h_s](t), and the rate of secondary infection from each infected neighbor i, denoted β[h_i, h_s](t). We restrict the transmission of primary and secondary infection to nearest-neighboring sites only to accommodate the limited dispersal commonly found for soil-borne pathogens and for which data for model testing were available. A nuisance parameter, termed the rate of tertiary infection, γ[h_s](t), is introduced to allow for a small proportion of non-nearest-neighbor transmission. Using the indicator function 1{A} = 1 if A is true and 0 otherwise, this can be written:

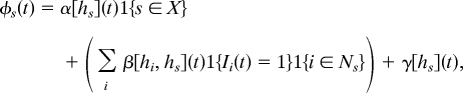where X and N_s are the sets of inoculated hosts and nearest neighbors of s, respectively. The total rate of infection φ_s(t) of a host s therefore depends on the time-varying transmission rates as well as on localized conditions (presence of inoculum, neighboring infectious hosts), which evolve with time and are different for each host (Fig. 1). A range of functional forms were tested for the transmission rates with the following emerging with strong support from the DIC (see below):

in which the rate for primary infection decays exponentially with time, the rate for secondary infection changes nonmonotonically in accordance with a Weibull function, and the rate for background infection is constant. The Weibull function is selected here as a function allowing the expression of rise-and-fall dynamics with analytical integrals.

Bayesian Model Fitting.

We fitted the model using Markov chain Monte Carlo techniques and data augmentation to draw a sample from the joint posterior distribution of model parameters and unobserved infection times and sources of infection for each of the ≈10,000 hosts in the system. The algorithm is quite involved, so details are provided in SI Appendix. The DIC (37, 38) was used to discriminate between competing models.

Experimental Data.

Our methods are applied to epidemics in heterogeneous plant populations in replicated microcosm experiments. Details of the experiments can be found in Otten et al. (39). In summary, dynamics of damping-off epidemics were recorded in populations comprising 414 seedlings of a favorable (radish, Raphanus sativus L., Cherry Belle) or an unfavorable (mustard, Sinapis alba L.) species planted in a square lattice. At the densities used, spread of disease occurs predominantly between nearest neighbors. Populations comprised either 100% favorable, 100% unfavorable, a mixture with 75% favorable and 25% unfavorable, or a 50:50% mixture, with up to six replicates per treatment. The host species at each point on the lattice was randomly selected, and in each tray, 32 randomly selected plants were challenged by inoculum of the soil-borne fungal pathogen R. solani. The position of damped-off plants was recorded daily for 13 days after emergence; to assess the dependency of the method on high-resolution temporal data, we also consider a censoring of the data with observations at 4-day intervals only. The model was fitted to all replicates jointly.