Reconstruction of ancestral protein interaction networks for the bZIP transcription factors

Abstract

As whole-genome protein–protein interaction datasets become available for a wide range of species, evolutionary biologists have the opportunity to address some of the unanswered questions surrounding the evolution of these complex systems. Protein interaction networks from divergent organisms may be compared to investigate how gene duplication, deletion, and rewiring processes have shaped the evolution of their contemporary structures. However, current approaches for comparing observed networks from multiple species lack the phylogenetic context necessary to reconstruct the evolutionary history of a network. Here we show how probabilistic modeling can provide a platform for the quantitative analysis of multiple protein interaction networks. We apply this technique to the reconstruction of ancestral networks for the bZIP family of transcription factors and find that excellent agreement is obtained with an alternative sequence-based method for the prediction of leucine zipper interactions. Further analysis shows our probabilistic method to be significantly more robust to the presence of noise in the observed network data than a simple parsimony-based approach. In addition, the integration of evidence over multiple species means that the same method may be used to improve the quality of noisy interaction data for extant species. The ancestral states of a protein interaction network have been reconstructed here by using an explicit probabilistic model of network evolution. We anticipate that this model will form the basis of more general methods for probing the evolutionary history of biochemical networks.

The complex relationship between an organism's genotype and phenotype is mediated by many interrelated biochemical networks. As our knowledge of these network structures improves, we can start to ask questions about the evolution of cellular systems as a whole, as opposed to studying individual genes and their products in isolation (1, 2). This article extends recent work on the reconstruction of ancestral protein sequences (3, 4) by focusing on interactions between ancestral proteins. Greater understanding of the ancestral configurations of interaction networks would be of immense value in uncovering the processes involved in the evolution of cellular systems.

Analogous to the inference of evolutionary history at the level of the DNA or amino acid sequence, evolutionary biologists would like to be able to infer ancestral protein interactions based only on their observations of networks from extant species. However, current methods of network alignment are generally lacking in any phylogenetic context (5–8). Hence, they have only limited value as quantitative tools for the study of evolution. Here we report the development of a general methodology for the reconstruction of ancestral protein–protein interaction networks by inference over a probabilistic model of interaction network evolution. By applying these methods to the bZIP transcription factor interaction network in chordates, we are able to predict ancestral networks with much greater robustness to measurement error than would be possible by using a naive parsimony-based approach.

The bZIP transcription factors are a family of homo- and heterodimerizing proteins involved in the regulation of development, metabolism, circadian rhythm, and many other cellular processes (9). The characteristic bZIP domain consists of a basic region (contacting the DNA major groove) and a leucine zipper (LZ) that mediates dimerization-specificity. Gene duplication has played a major role in the evolution of the bZIP subfamilies, which are known to have broadly conserved patterns of interactions with each other (10, 11). The relative strengths of pairwise interactions between bZIP proteins have previously been measured experimentally for humans and the yeast Saccharomyces cerevisiae (12). In addition, the relatively simple biophysics of the coiled-coil LZ interaction means that pairs of proteins that form strongly interacting dimers can be predicted reliably from their LZ sequences alone by using computational methods (13): 93% sensitivity at 98% specificity based on a subset of human bZIP pairs with unambiguous experimental results. This combination of accurate genome-scale experimental data (12) and the capacity for highly accurate computer-based interaction prediction directly from amino acid sequences (13) makes the bZIP system useful as a model for investigating methods for ancestral network inference.

Inference of Ancestral Protein Interaction Networks

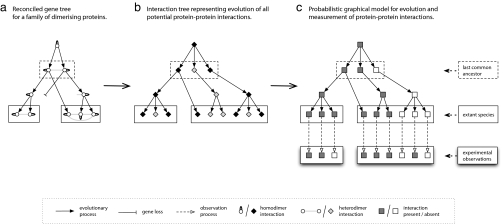
Our method starts with the assumption that it is possible both to construct a reliable phylogeny for the gene family of interest and reconcile this phylogeny with the known species tree, such that all internal nodes are labeled as gene duplication or speciation events (14). Although it would be possible to incorporate phylogenetic uncertainty into a probabilistic model of network evolution, this result would add greatly to the computational burden undertaken. Complete sets of bZIP protein sequences from four chordates [Ciona intestinalis (sea squirt), Takifugu rubripes (pufferfish), Danio rerio (zebrafish), and Homo sapiens (human)] were used to construct such a reconciled gene tree (Fig. 1a). These organisms were selected to give a broad view of chordate evolution while keeping the overall computational problem tractable. By considering all possible homo- and heterodimerizations between pairs of bZIP proteins and how they are related by gene duplication, the gene tree can be transformed into an interaction tree representation (Fig. 1b). Each node in the new tree represents a potential interaction between a pair of proteins. Each directed arc that connects two nodes represents a period between evolutionary events: either speciation or gene-duplication events as derived from the reconciled gene tree. A probabilistic graphical model for the evolution of the protein–protein interaction network is then constructed (Fig. 1c) based directly on the interaction tree. Each potential interaction corresponds to a binary node, which may be on (present) or off (absent). An extra set of terminal nodes is added to the tree to represent binary observations of each potential interaction in each extant species. The arcs connecting to these observation nodes, therefore, represent the process of measurement, which may be expected to be subject to experimental uncertainty. The strengths of the interactions between the LZ regions for each pair of bZIP proteins from these four extant genomes were predicted by using a sequence-based approach (13), and the numerical scores for each pair of proteins were converted to binary data by using an appropriate score threshold. Although these input data were derived from sequence-based analysis, in principle, any discrete or continuous experimental data (e.g., from high-throughput studies) could be used.

Fig. 1.

Derivation of a probabilistic graphical model for the evolution of the bZIP protein interaction network. (a) Starting with a gene phylogeny for a family of dimerizing proteins, this gene phylogeny is first reconciled (14) with a species phylogeny to produce a tree in which every internal node is labeled as a gene duplication or speciation event. (b) The reconciled gene tree can be transformed into an interaction tree, in which each node represents a potential dimerization interaction and each directed edge represents a period of evolutionary time. (c) The interaction tree forms the basis of our probabilistic graphical model, in which potential interactions are represented by binary (on/off) nodes, and a further set of binary leaf nodes is used to represent observations of protein–protein interactions in the extant species. The model can be used to infer the probability of a strong interaction at every internal node and, hence, to reconstruct a protein interaction network for each ancestral species.

The two different types of arcs in Fig. 1c represent the two processes to consider in parametrizing the model: Changes in specificity among the interacting proteins (i.e., rewiring of the interaction network caused by the evolution of protein sequences) and the measurement of the interactions actually present in the extant networks. It is difficult to construct a general mechanistic model for the gain and loss of interactions as a protein interaction network evolves because the relationship between protein sequence and interaction-specificity depends on many factors (1, 15). However, in the case of the bZIP network, the interactions are mediated mainly by the LZ regions. Therefore, we are able to use the experimental data for human proteins (12) to estimate the probabilities of gain and loss of strong interactions as a function of sequence divergence. These probabilities are accurately approximated by logistic functions of the sum of the evolutionary divergence of two proteins [supporting information (SI) Fig. 5]. Beyond a certain evolutionary distance, both of these probabilities plateau off to values representing the overall fraction of possible bZIP pairs that interact. Interaction between two randomly selected bZIP proteins is much more likely than would be expected between two generic proteins. Hence, the maximum probability of interaction gain of 0.08 may appear surprisingly high, but is nonetheless valid for this system. Parameters for the observation nodes were estimated by comparing the experimental human data with the sequence-based predictions (13). Specifically, we calculate two score distributions for pairs of proteins that either interact strongly or do not interact (SI Fig. 6) and, hence, derive conditional probability distributions for the derived binary data.

Using the sequence-based predictions for every possible interaction between a pair of proteins in each of our four extant species as input, we compute the probability of a strong interaction between each pair of proteins in each ancestral species (labeled “Teleost,” “Vertebrate,” and “Chordate”) according to the model. The tree-like structure of our probabilistic graphical model has the consequence that the inference of the ancestral network states is tractable by using belief-propagation techniques (16).

Of course the inference of ancestral states for traits not directly related to gene sequence is not a new problem, and it might reasonably be expected that a parsimony-based approach would yield comparable results without the complications of parameter estimation that are required in the case of the probabilistic method. As a comparison, we therefore reconstructed the ancestral networks by applying an algorithm for finding maximally parsimonious evolutionary histories (17) to our interaction tree (Fig. 1b).

With most protein–protein interaction datasets, it would be impossible to determine which method for ancestral network inference was the more successful because we do not have protein interaction data for the ancestral species. However, the ability to make reliable predictions (13) of interaction strength directly from pairs of LZ sequences permits the construction of a benchmark dataset for the bZIP family by using inferred probability distributions for the amino acid sequences at each ancestral node.

Results and Discussion

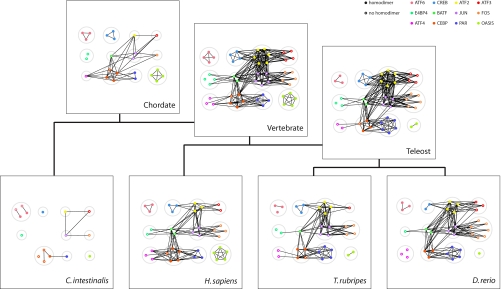
Fig. 2 shows a summary of the results obtained by our probabilistic method of network inference for each of the species in our phylogeny. Many features of the evolution of the bZIP network can clearly be seen in the inferred ancestral networks, including the gain and loss of interactions by sequence divergence, the multiplication of interactions after gene duplication (e.g., in the large number of genes duplicated and retained between Chordate and Vertebrate), and the loss of various genes in the different lineages. As predicted in our earlier work (11), the inferred ancestral Chordate network shares much of its overall topology, in terms of interfamily interactions, with the present-day vertebrate networks. However, the loss of many of its genes during evolution (18) has left the C. intestinalis bZIP network with little resemblance to those of the other chordates in our study.

Fig. 2.

Evolutionary history of the bZIP interaction network in chordates as inferred by our probabilistic method. Each protein is shown as a colored node, and an edge is drawn between two proteins if they have >50% probability of sharing a strong interaction. Filled circles, homodimerizing proteins; open circles, proteins without self-interactions. Proteins are grouped into families by the larger gray circles. Only those bZIP families included in our study are shown. For simplicity, we have combined families where they are closely related (ATF6/XBP and OASIS/OASIS-B). Network visualizations were prepared by using InterView (31).

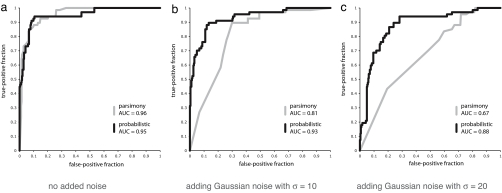
For comparison with these networks, results from the benchmark sequence inference method are shown in SI Fig. 7 and from the alternative, parsimony-based method in SI Fig. 8. To compare the performance of the probabilistic and parsimony-based methods fairly, receiver-operator characteristic (ROC) curves were plotted for the Chordate results (Fig. 3a). Taking the area under curve (AUC) as a measure of predictive power, both methods provide good results (AUC_prob = 0.95; AUC_pars = 0.96). Similarly good results are found for Vertebrate and Teleost (SI Fig. 9a).

Fig. 3.

ROC evaluations of the ancestral Chordate networks inferred by our probabilistic method (black line) and a parsimony-based method (gray line) at varying degrees of input noise. (a) No noise added. (b) Adding Gaussian noise with a SD of 10 to interaction scores. (c) Adding Gaussian noise with a SD of 20 to interaction scores.

Clearly the parsimony-based approach performs well for this system, and this finding is attributable, in part, to the high quality of the input data provided by the LZ interaction prediction software. However, experimental protein–protein interaction datasets usually have many false-positive and false-negative observations (1). We can simulate this situation by adding Gaussian noise with different variances to the interaction scores from which the input data are derived. The results, summarized by the ROC curves for Chordate in Fig. 3 b and c, show that the parsimony-based approach is quite sensitive to measurement error (AUC_pars = 0.81, 0.67), whereas the probabilistic method continues to perform well (AUC_prob = 0.93, 0.88). The levels of noise added correspond to false-positive rates (defined as the proportion of asserted interactions that are false) of 47% and 67%, respectively, relative to the original input data. For comparison, estimated false-positive rates of high-throughput experiments, such as yeast two-hybrid, range from ≈50% to ≈90% in the worst cases (19). Again, similar results are seen for the other two ancestral species (SI Fig. 9 b and c).

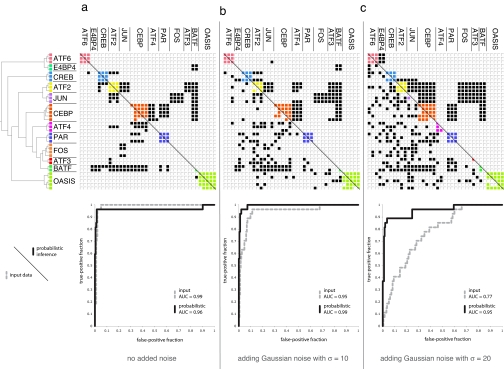
Given these extremely high experimental error rates, there is currently a great deal of interest in methods for increasing the accuracy of protein interaction datasets (19, 20). In addition to predicting interactions for ancestral species, our probabilistic inference method offers a principled way to combine multiple interaction datasets to improve interaction predictions in extant species. Fig. 4 illustrates just such an improvement in the quality of interactions predicted to be present in man, compared with the corresponding input data at varying degrees of noise. Taking a subset of human bZIP pairs with unambiguous experimental results as a gold standard, predictions based on the probabilistic model remain remarkably reliable, compared with the noisy data.

Fig. 4.

Evaluation of the probabilistically inferred human bZIP interactions with various levels of noise applied to the input interaction scores. (a) No noise added. (b) Adding Gaussian noise with a SD of 10. (c) Adding Gaussian noise with a SD of 20. The phylogenetic tree for the human bZIPs is derived from the LZ regions of the bZIP proteins (see Methods). An interaction is represented by a filled cell in the matrix; within-family interactions are colored. (Lower) Input human interaction data. (Upper) Interactions predicted at >50% probability by inference over the full evolutionary model. ROC plots show the quality of each input (dashed gray line) and output (black line) dataset by comparison to a subset of human bZIP pairs with unambiguous experimental interaction data. Interaction matrices were prepared by using TVi (31).

The availability of a comprehensive experimental dataset (12) for the bZIP transcription factor system has enabled us to calculate parameters for modeling the network rewiring process as a function of evolutionary distance, which is an approach that may prove applicable to more general types of protein interaction. Our probabilistic method for the inference of ancestral networks is significantly more robust to experimental noise than a naive maximum parsimony approach. In addition, the same inference process could be used to improve the quality of network datasets for extant organisms by combining evidence across multiple species and/or experiments.

The probabilistic model presented in this study represents an important step forward in the evolutionary analysis of biochemical interaction networks. We currently have a detailed understanding of the important contribution of both small-scale- and whole-genome-mediated gene duplication to evolution both generically (21, 22) and specifically to transcription factor networks (11, 23). However, gene duplication only contributes by providing the raw material for innovation. Functional evolution is a consequence of changes in specificity between proteins, resulting in both the gain and/or loss of interactions. Our approach permits the inference of the evolutionary history of these rewiring events. In conclusion, detailed knowledge of the ancestral states of protein interaction networks will bring insights into the functional evolution of the interactome and the nature of conservation and change in divergent evolutionary lineages.

Methods

The identification of protein sequences for bZIP transcription factors and LZ regions from H. sapiens, D. rerio, T. rubripes, and C. intestinalis was described in our previous study (24). An interaction score was calculated for each potential bZIP interaction within each species by using the software of Fong and Singh (13) with base-optimized weights. Because of atypical features, interactions involving smMaf, lgMaf, and CNC proteins could not be predicted reliably (13), so these families were excluded from the analysis.

LZ regions from all species were aligned by using MUSCLE (25). A consensus maximum likelihood (ML) phylogeny was built by using PROML (26) with the JTT model of amino acid replacement (27). Branch lengths for this consensus tree were calculated by using PAML (28). This tree was reconciled with the species phylogeny by using NOTUNG2 (14) with default settings.

A probabilistic graphical model (Fig. 1c) was built by using Bayes Net Toolbox (BNT) (29). The topology of the model is based on an interaction tree derived from the reconciled gene tree by considering all potential protein–protein interactions that could be descended from a putative ancestral homodimerization interaction by gene-duplication events. Multiple gene duplications occurring between species are assumed to take place in the order given by considering relative branch lengths. Each of the 6,851 internal nodes in the model is binary, representing the presence or absence of a potential interaction. Probabilities for the gain and loss of interactions were modeled as logistic functions (30) of the sum of the branch lengths of the two genes concerned. Parameters were estimated by using experimentally determined true-positive and true-negative human bZIP interactions (12, 13) by considering all potential moves in sequence space, starting from each strongly interacting protein pair (modeling the probability of interaction loss as a function of the sum of JTT evolutionary distances calculated by using PROTDIST) (26) or each noninteracting protein pair (modeling the probability of interaction gain) (SI Fig. 5). Actual values for the probability of interaction gain [i.e., P(interaction present|interaction absent at parent node)] ranged from 0 to 0.08 and for the probability of interaction loss [i.e., P(interaction absent|interaction present at parent node)] from 0 to 0.92. The same experimental data were used to derive score distributions (13) for strongly interacting and noninteracting protein pairs (SI Fig. 6). Normal distributions fitted to these data were used to compute the conditional probability distribution for an additional set of 2,227 binary nodes, representing the Fong/Singh predictions for all bZIP pairs in the four extant species. Numerical scores were converted to binary input data by using a threshold of 30.6, corresponding to the score value for which P(interaction|score) = 0.5. The BELPROP belief-propagation algorithm implemented in BNT (29) was then used to compute the marginal likelihood for the existence of a strong interaction at every internal node given the binary input data for the extant species.

An implementation of the PARS algorithm (17) was applied to the interaction tree to infer the presence of ancestral interactions by maximum parsimony based on the binary interaction evidence for extant species as described earlier. The ratio of penalties (loss of interaction:gain of interaction) used was 1:11.4, corresponding to the relative probabilities in the plateau regions of SI Fig. 5.

A benchmark set of interactions was constructed by using ancestral sequence inference, against which the interactions inferred by the probabilistic and parsimony-based methods could be compared. Probability distributions for the amino acid sequences of every ancestral bZIP protein in the gene tree were inferred by using PAML (28). Taking 1,000 random samples from these distributions, the Fong/Singh software (13) was then used to predict a mean interaction score for every bZIP pair in each ancestral species. Each pairwise score was then converted to a binary prediction of interaction by using a threshold of 30.6. ROC curves were plotted to evaluate performance of the probabilistic and parsimony inference methods against these predictions for the ancestral Chordate (Fig. 3), Vertebrate (SI Fig. 9i), and Teleost (SI Fig. 9ii) networks. In the case of the probabilistic results, a variable cutoff was used on the output interaction probabilities to produce the curve. However, the parsimony-based method gives binary interaction predictions as output. Thus, for these ROC plots, a variable threshold was applied to the scores used as input data. The ROC curves shown in Fig. 4 were derived in a similar manner by using a set of known unambiguous, strongly interacting, or noninteracting human bZIP interactions taken from experimental data (12, 13) as the gold standard.