Neural representations of kinematic laws of motion: Evidence for action-perception coupling

Abstract

Behavioral and modeling studies have established that curved and drawing human hand movements obey the 2/3 power law, which dictates a strong coupling between movement curvature and velocity. Human motion perception seems to reflect this constraint. The functional MRI study reported here demonstrates that the brain's response to this law of motion is much stronger and more widespread than to other types of motion. Compliance with this law is reflected in the activation of a large network of brain areas subserving motor production, visual motion processing, and action observation functions. Hence, these results strongly support the notion of similar neural coding for motion perception and production. These findings suggest that cortical motion representations are optimally tuned to the kinematic and geometrical invariants characterizing biological actions.

Humans can easily perceive and infer emotions and intentions from the movements and actions of other individuals. The perceptual saliency of human movement might be rooted in the close interactions between perception and action (1, 2). Moreover, movements of humans, primates, and possibly also other animals show certain geometric and kinematic regularities, indicating they are governed by a relatively small number of rules, the so-called kinematic laws of motion. These laws of motion were discovered through recording, kinematic analysis, and modeling of the geometrical and temporal features of the hand paths and velocity profiles characterizing these movements. For example, point-to-point reaching movements tend to follow straight hand paths and to have bell-shaped velocity profiles (3). The velocity profiles during curved and handwriting movements are more complicated. As already noted by early investigations, when following a curvilinear trajectory, hand velocity exhibits a strong dependency on the geometrical form of the path. Namely, the hand tends to slow down during more curved segments and to speed up during straighter ones (4). This early observation was later expressed in a more rigorous way by the so-called 2/3 power law (5):

The 2/3 power law links path curvature C and angular velocity A along the movement by a power law with an exponent of 2/3. K is the velocity gain factor, which is piecewise constant during entire movement segments. This law of motion is a ubiquitous feature of human motor behavior, characterizing the kinematic properties of arm movements (5), smooth pursuit eye movements (6), speech movements (7), and movements of the body's center of mass during human gait (8) and of the foot during the swing phase of walking (9).

Neurophysiological studies in monkeys demonstrated that the 2/3 power law reflects the properties of central motion planning processes in motor cortical areas, because the dynamics of population vectors derived from the activity of neurons in the primary motor and premotor cortices comply with this law (10). Those observations have suggested that the 2/3 power law is not just a consequence of low-level biomechanical and peripheral effects, such as the smoothing properties of muscles (11) or the nonlinearities of the mapping between joint and hand coordinates (12).

The 2/3 power law not only is prominent during motor production but also influences visual perception of movement. Viviani and Stucchi (13) examined whether the imprint of this law can also be found during the perception of visual motion. Subjects were asked to observe the rotation of a dot around an ellipse, which was moving according to a power law of the form:

This is an analogous expression to Eq. 1, using tangential velocity, V, rather than angular velocity and radius of curvature, R, rather than the path curvature, C. An exponent of β = 1/3 gives precisely the 2/3 power law. Subjects were instructed to manipulate the value of the exponent β until the dot appeared to move most uniformly. Despite the a priori expectation that motion judged as most uniform should be moving at a constant Euclidean speed (β = 0), subjects chose β values that corresponded closely to the 2/3 power law (β = 1/3). This is quite surprising, given that the dot velocity could vary by 200% in contrast to a constant velocity motion. This finding was recently confirmed by using a larger range of movement speeds and ellipses with different eccentricities and perimeters (14). The observed preference for movements obeying the 2/3 power law, it should be noted, is not a consequence of eye movements (14, 15).

Hence, the 2/3 power law strongly constrains visual perception, but the underlying brain mechanisms responsible for this constraint are still unknown. Furthermore, the evidence for cortical representation of the 2/3 power law in movement production is based on only a few neural recording studies in monkey motor and premotor cortices, but we still lack evidence for the representation of this behaviorally ubiquitous constraint in the human brain.

Here, we used functional MRI (fMRI) to identify the neuronal correlates of the 2/3 power law by presenting visual stimuli that are either consistent or inconsistent with this spatiotemporal invariant. Subjects viewed a cloud of dots moving along elliptical trajectories according to three different types of motion. The experiment included three conditions presented in a block design. Although all possible parameters (i.e., the dimensions and eccentricity of the ellipse and the average velocity of the dots) remained fixed in all conditions, we manipulated the relation between the dots' velocity and the curvature of the ellipse. Three types of motion were created choosing three values (1/3, 0, and −1/3) for the parameter β in Eq. 2. The various conditions were presented in 9-second blocks, interleaved with 6-second periods of fixation. To control for eye movements, subjects were instructed to maintain fixation on a fixation cross at the center of the visual display during the scan. The color of the moving dots changed from white to gray in 50% of the motion blocks (counterbalanced between the three conditions), and subjects were instructed to detect these changes by pressing a button in a response box.

Results

Perception of Different Types of Motion.

To identify brain regions associated with processing of the different types of motion, each condition was contrasted with the other two conditions (Fig. 1 and Table 1).

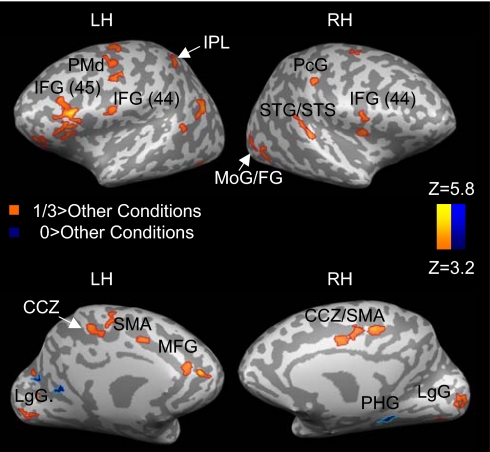
Fig. 1.

Areas of significant activation during perception of different types of motion. Each condition is compared with the two other conditions. CCZ, caudal cingulate zone; IFG, inferior frontal gyrus; LH, left hemisphere; LgG, lingual gyrus; MoG, middle occipital gyrus; PHG, parahippocampal gyrus; PcG, postcentral gyrus; RH, right hemisphere; SMA, supplementary motor area; STG, superior temporal gyrus; STS, superior temporal sulcus. Results are corrected for multiple comparisons at the cluster level (P < 0.05).

Table 1.

Significant clusters of activation obtained when each type of motion was contrasted with the other two types of motion

Region	BA	Side	X Y Z	Z
1/3>[0+(−1/3)]
Ventromedial PFC	11	L	−25,38,5	5.45
Middle frontal gyrus	9	L	−34,27,26	4.07
		R	30,32,24	4.32
Medial frontal gyrus	9	L	−12,39,23	5.63
IFG	9	L	−37,8,22	3.86
			−36,14,37	3.8
IFG	45	L	−47,23,15	5.41
	46	L	−42,34,10	3.72
IFG/precentral gyrus	44	L	−50,1,11	3.72
		R	54,10,10	3.64
PMd	6	L	−49,-8,39	4.19
			−42, 0, 45	4.0
			−39,-7,40	3.61
		R	25,–10,42	3.96
CCZ/ SMA	31,6	L	−3,-5,43	4.55
			−14,−2,37	4.2
		R	1,–8,40	4.56
CCZ	31	L	−4,-26,41	4.35
		R	11,–24,38	4.44
RCZ/pre-SMA	6,24	L	−2,12,43	3.54
Postcentral gyrus	3	L	−27,-24,45	4.3
		R	50,–20,38	4.05
IPL	40	L	−33,-42,43	3.57
STS/STG	22,39	L	−60,-59,21	4.73
		R	58,–33,11	6.69
MTG	22,39	L	−60,-49,7	5.03
			−53,-65,13	3.82
			−48,-60,23	4.1
Lingual gyrus	18	L	−20,-79,−3	4.9
		R	11,–82,-1	4.03
Fusiform gyrus	19,37	L	−39,-76,-13	3.28
		R	39,–63,-5	4.17
Cuneus	17	L	−24,-78,14	5.51
Insula	13	R	37,2,18	4.04
Anterior cerebellum		L	−20,-63,-23	5.76
0>[1/3+(−1/3)]
Lingual gyrus	19	L	−27,-62,5	4.49
Posterior cingulate	29	L	−9,-41,9	4.23
PHG		R	23,–37,-11	3.97

For each cluster, Talairach coordinates at the center of gravity are specified along with the corresponding Brodmann area (BA) and the peak Z score. IPL, inferior parietal lobule; MTG, middle temporal gyrus; PFC, prefrontal cortex; RCZ, rostral cingulate zone. All other abbreviations are as in Fig. 1. Results are corrected for multiple comparisons at the cluster level (P < 0.05). Minimum cluster size, 134 voxels. −1/3>(1/3 + 0). No activations were obtained.

Activation during motion complying with the 2/3 power law was first contrasted with the two other conditions (i.e., 1/3−[0 + [−1/3]]). Activation, mostly lateralized to the left, was found in inferior and medial frontal regions, the bilateral dorsal premotor cortex (PMd), the left supplementary motor area (SMA), the bilateral postcentral gyrus, the left inferior parietal lobule (IPL), the bilateral superior temporal sulcus/gyrus (STS/STG), the left caudal and rostral cingulate zone (CCZ/RCZ), and the left anterior cerebellum. The majority of these brain areas are active during motion planning and execution (16), production of both rhythmic and discrete arm movements (17), movement imitation and mirror system activation (18), motor imagery (19), speech motion perception (20), perception of biological motion (21), and action observation (22) [see supporting information (SI) Table 2 for a more detailed list of studies with similarly activated areas to those shown in Fig. 1 and listed in Table 1]. Thus, our results indicate that motor areas and areas involved in action observation are particularly activated by visual stimuli consistent with a natural law of motion. This potentially indicates specific processing or motor preparatory activity induced by moving visual stimuli.

Next, we checked for activation specific to the “0” and “−1/3” conditions by contrasting each with the two other conditions (Fig. 1; Table 1). Activation specific to the 0 condition was found in left lingual gyrus, left posterior cingulate, and right parahippocampal gyrus. In contrast, no activation was seen when the −1/3 condition was compared with the two other conditions at the same statistical threshold.

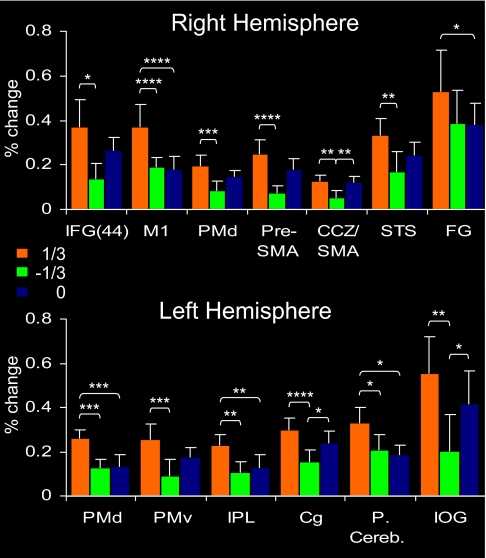
To further compare the three types of motion, we analyzed selected regions of interest (ROIs) functionally defined as clusters of active voxels that were significantly more active in all conditions vs. baseline activity during trials of fixation (i.e., by contrasting (1/3 + 0+[−1/3]) vs. “rest”). Average percent signal change for each of the three conditions was then calculated. This allowed a division of the ROIs into two subgroups: those with a stronger response to the 1/3 condition than to one or both of the other conditions (Fig. 2) and ROIs that were either similarly activated by all three conditions or more strongly activated by the 0 condition (SI Fig. 4). ROIs that were more strongly activated by the 1/3 condition included highly specific motor areas, such as the primary motor cortex (M1), dorsal and ventral premotor cortices (PMd and PMv), and supplementary motor areas (pre-SMA and SMA). Additional regions included the STS that plays a major role in the perception of biological motion (21) and inferior frontal and inferior parietal areas, which are strongly involved in action observation and in the interface between perception and action (22, 23). Additionally, we functionally localized ROIs using a simple motor task (finger tapping). The dominance of visual motion that follows the 2/3 power law in motor and motor-related brain areas was also demonstrated in the ROIs, which were defined by this task (see SI Text). Therefore, the results clearly demonstrate the privileged status of the 1/3 condition over the two other conditions in motor and action-related areas.

Fig. 2.

Analysis of selected ROIs identified by contrasting the combined activation of all three conditions with rest. Shown are ROIs with stronger activation to the 1/3 condition. Error bars represent SEMs. In the right hemisphere, ROIs included IFG/BA 44 (Talairach coordinates: 49,14,8), M1 (38,−17,49), PMd; (30,−12,43), pre-SMA (6,6,46), STS (61,−40,13), CCZ/SMA (7,−5,49), and fusiform gyrus/BA 18 (24,−82,−23). In the left hemisphere, ROIs included PMd (−22,−17,52), ventral premotor (PMv; −47,−2,26), IPL (−33,−51,35), cingulate gyrus (Cg) (−24,−16,46), posterior cerebellum (−41,−58,−32), and inferior occipital gyrus (IOG; −36,−88,−15). * indicates statistically significant difference at P < 0.05; **, P < 0.01; ***, P < 0.001; ****, P < 0.0001

In contrast, ROIs activated similarly by all three types of motion or more strongly by the 0 condition (SI Fig. 4) mainly included posterior visual areas such as the inferior occipital gyrus and the fusiform gyrus. The latter activation may correspond to ventral V3, which is involved in low-level speed discrimination (24).

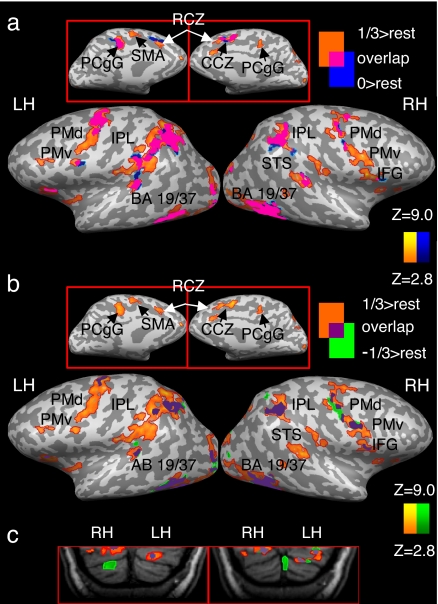
To better assess whether the various types of motion are processed by distinct or overlapping neuronal networks, we contrasted the activity in each condition with rest and superimposed the resulting maps (Fig. 3; SI Table 3). This revealed that the different types of motion were processed by both overlapping and nonoverlapping networks of brain areas. Furthermore, it was again evident that motion following the 2/3 power law is largely processed by a specialized neural network. Activity specific only to the 1/3 condition was found mainly in inferior frontal areas, along the medial wall (including the SMA and RCZ/pre-SMA) and in the basal ganglia (including putamen and caudate). In contrast to the patterns of selective activation observed for the 1/3 condition, the two other conditions appear to be processed almost entirely by neural circuitry shared by all three conditions.

Fig. 3.

Overlapping and nonoverlapping patterns of activation in response to perception of different types of motion. Each condition is compared with rest, and the resulting maps are laid one on top one another. Activation is presented separately for the 1/3 and 0 conditions (a), the 1/3 and −1/3 conditions (b), and in the cerebellum (c). PCgG, posterior cingulate gyrus. All other abbreviations are as in Figs. 1 and 2 and Table 1. Results are corrected for multiple comparisons at the cluster level (P < 0.05).

Overlapping patterns of activation common to all three types of motion were obtained mainly in bilateral posterior visual areas, occipito-temporal cortex (BA 19,37), and in bilateral IPL/intraparietal sulcus. These are some of the major areas for visual motion perception in the human brain (25). A partial overlap among the three conditions or between the 1/3 condition and one of the two other conditions was found in bilateral premotor, primary motor, and supplementary motor areas, bilateral STS/STG, and in bilateral posterior cerebellum. However, the dominance of the 1/3 condition was also evident in these areas (Fig. 3). Some of the activations in motor and motor-related regions in this particular task could reflect the button-pressing task performed by our subjects. However, given that the overlap was only partial and that button pressing was counterbalanced across conditions indicate that this pattern of activity is largely specific to perception of visual motion. For additional support concerning the lack of confounds related to the button-pressing task, a control experiment was carried out. The results of this experiment (detailed in SI Text) confirmed that, even in the absence of a button-pressing task, motor and motor-related regions are responsive to motion that obeys the 2/3 power law.

Motion with a β Exponent >1/3.

Although the results of the different analyses reported above clearly demonstrate that motion that complies with the 2/3 power law is processed by a selective network of cortical and subcortical brain regions, one option that had to be ruled out is that the brain becomes even more responsive when the β exponent (see Eq. 2) becomes larger and more positive. For this purpose, we conducted an additional control experiment in which, in addition to a motion that complied with the 2/3 power law (β = 1/3) and a motion with a constant Euclidean speed (β = 0), we also included another type of motion with a higher value of the exponent β (β = 2/3).

As before, activation during motion complying with the 2/3 power law was contrasted with the two other conditions (i.e., 1/3−[0 + 2/3]). Similarly to the previous results (SI Fig. 5; SI Table 4), this contrast yielded activation in a specific network of brain areas that again included prefrontal cortex, premotor, and supplementary motor and primary motor areas, as well as the postcentral gyrus and the inferior and superior parietal cortices. When the 0 and the 2/3 conditions were each contrasted against the two other conditions, the patterns of activity were very different. Clusters of activation specific to the 2/3 and 0 conditions were generally more posterior and included middle and superior temporal areas, inferior parietal lobule, and lingual gyrus (for a complete list, see SI Table 4). This clearly argues against a monotonic increase of activity with an increase in the value of the β exponent and further supports the special status of motion compatible with the 2/3 power law. Thus, as one moves away in both directions from β = 1/3, the neural response appears weaker and less widespread and includes less, if any, motor- or action-related areas.

Analysis of Eye Movements.

Subjects who participated in the second control experiment were also monitored for eye movements inside the scanner, separately from the scanning sessions, using an MRI compatible pupilometry eye-tracking system. The results of this analysis (see SI Text) indicate that the differential activation obtained for the various types of motion in the main experiment, as well as in the second control experiment, cannot be explained simply by differences between eye movements among the different conditions.

Activation in Area MT/V5.

To rule out the possibility that the differences among the various types of motion merely result from low-level visual processing, we checked for possible differential activations in area MT/V5, which is central to the processing of low-level motion stimuli (25). After functionally localizing this area in each of our subjects using a standard paradigm (26, 27), we compared the activation in MT/V5 across the conditions of the main experiment (1/3, 0, −1/3) and the conditions of the second control experiment (1/3, 0, 2/3). In the data set of the main experiment (SI Fig. 6a), all three conditions activated area MT/V5 bilaterally. A two-way repeated-measure ANOVA failed to reveal significant differences among the conditions [F = 1.64, not significant (ns)] or between the hemispheres (F = 0.67, ns). The interaction between the two factors was also not significant (F = 2.78, ns). Similarly, in the data set of the second control experiment (SI Fig. 6b), there were no significant differences among the conditions (F = 1.609, ns) or between the hemispheres (F = 0.38, ns), and the interaction between these two factors was also not significant (F = 2.65, ns). Altogether, the results of this analysis argue against interpreting the differential activation obtained in different experiments simply by differences in low-level motion processing.

Discussion

Taken together, our findings show that: (i) The activation in response to visual motion obeying the 2/3 power law is considerably stronger and more widespread than to the other types of motion, (ii) motion of a very simple visual stimulus is capable of eliciting activity in a large network composed of areas typically associated with different specialized motor- and action-related functions, and (iii) the different types of visual motion are selectively represented within highly distributed but partially overlapping networks.

The preferential activation of motor-related areas in response to the 2/3 power law may provide a neural underpinning for several behavioral observations. For example, it is nearly impossible to force healthy subjects to generate arm movements that significantly violate this law, even after a lengthy period of practice (28). Additionally, visual and kinesthetic stimuli provide appropriate guidance in motion-tracking tasks only if they comply with this law (28). Moreover, a kinesthetic-based distortion in the perceived geometrical form of the movement's path was obtained when the hand of a blindfolded subject was passively moved in a way violating the 2/3 power law (29). All these observations are consistent with the activations seen in the postcentral gyrus in response to this law. Furthermore, the selective activations in response to the 2/3 power law in the basal ganglia and the cerebellum seem consistent with the role of these areas in motion timing and in the planning and preparation of movement trajectories. Our findings with respect to the 2/3 power law thus provide major evidence for the notion that common codes and/or representations constrain both the interpretation of visual and kinesthetic inputs and the generation of actual movements. Moreover, in relation to the current debate in the literature whether the 2/3 power law has central or peripheral origins (10–12), our findings were based on a visual motion task rather than on actual movement production, thus avoiding the potential artifacts of biomechanical and peripheral factors. Hence, our observations clearly demonstrate that the power law does originate from central mechanisms and is not merely a byproduct of low-level peripheral factors. However, the contribution of such factors to the manifestation of the power law in motor production cannot be ruled out based on our observations.

In recent years, a growing body of evidence has suggested a strong coupling between perception and action (1, 2). Motor theories of action and speech recognition postulate that to recognize actions and speech sounds performed by another individual, a listener or an observer must simulate or run the motor programs for the production of the same sound or action (30). The discovery of mirror neurons in the premotor areas of the monkey brain (23, 31) and analogous mirror systems in the human brain (18, 19, 23) provide further evidence for a strong perception-action coupling (32). For this reason, it is interesting to point out that the network of brain regions we have found to be selective for visual motion that follows the 2/3 power law includes regions in the inferior frontal cortex considered to be part of the human mirror neuron system (see SI Table 2).

The visual response to the 2/3 power law may reflect sensitivity of the visual system to natural motion (33) or the influence of motor production on motion perception (13). Alternatively, the visual, somato-sensory, and motor systems may use a common amodal representation of motion (28). However, our findings demonstrate that the neural circuitry carrying the imprint of the 2/3 power law constraint is not limited to one specific locus or modality but is shared by visual, sensorimotor, and motor cortical and subcortical areas. Thus, the similarities between motor and sensory information processing may reflect the underlying similarities in neural coding and the distributed nature of the global network dealing with movement.

Why is the brain's response to visual motion obeying the 2/3 power law so much stronger and widespread than to other types of motion? The power law may reflect the underlying intrinsic neural dynamics, possibly selected as the default mode, because it optimizes performance, particularly motion smoothness, by minimizing jerk (the rate of change of acceleration) or other higher-order time derivatives of position, as has been shown by numerical simulations and rigorous mathematical analysis (34, 35). In addition, the 2/3 power law also maximizes motion precision (minimizes variance) in the presence of signal-dependent noise (36).

The brain may mature into obeying this law through its exposure to the movements of either objects or of other people and animals. The observed relationship between movement curvature and speed emerges in 3-year-old children (37) and possibly even earlier in very young infants. It is unclear, however, whether the ability to comply with the 2/3 power law is learned through experience or naturally develops either as a consequence of the maturation of the nervous system or through the tuning of the perceptual system to environmental constraints (38).

Here, however, we suggest a previously undescribed interpretation for the observed dominance of the brain's response to the 2/3 power law and the existence of somewhat separate networks for the representation of the different types of motion, which reflect qualitatively different relationships between the geometrical and time-dependent aspects of the movements. We recently showed that the 2/3 power law is equivalent to moving at a constant equi-affine velocity, which is invariant to equi-affine transformations (39–41). Equi-affine metrics differ from Euclidean metrics in that the Euclidean arc-length, serving as a measure of Euclidean distance, is weighted by the path curvature (to the power of 1/3), yielding the equi-affine arc-length. Thus, moving at a constant equi-affine speed amounts to moving at lower speeds during the more curved segments and at higher speeds during the straighter segments of the trajectory. This theoretical notion, combined with our present fMRI results, may suggest that the geometrical and kinematic properties of both visual and motor aspects of motion might be represented not only in terms of Euclidean but possibly also in terms of other non-Euclidean variables.

This possibility is consistent with our finding that activation in response to the constant Euclidean velocity (i.e., β = 0) was stronger than to the other types of motion in specific visual and cingulate areas. Of particular interest is the activation in the right parahippocampal gyrus, which is involved in representing external space and navigational routes (e.g., ref. 42). Hence, for tasks such as visual form perception, spatial memory, and navigation, representations based on Euclidean metrics might be more appropriate. However, brain areas functionally involved in action observation, motor planning and production, and motor imagery and simulation may use representations that depend on geometries that are not Euclidean, thus capturing the invariants of biological movements and actions (41). Thus, our results, which bear on earlier and ongoing theoretical studies, suggest an interesting principle of brain representation: selective activation of brain regions for different laws of motion might reflect tuning to the fundamental geometrical properties of the represented entities. These possibilities and further implications of the current findings and of the suggested geometrical framework remain to be tested in future studies.

Methods

Subjects.

Twenty-five healthy subjects (13 males, 12 females; ages 19–42) participated in the various experiments after signing a written informed consent form, approved by the Ethical Committee of the Tel Aviv Sourasky Medical Center. Fourteen subjects participated in the main experiment, six in the first and five in the second control experiment.

Tasks and Stimuli.

During the fMRI scans, subjects performed an MT/V5 localizer task and the main experimental task involving perception of different types of motion. Stimulus delivery and response acquisition were controlled by using the Presentation software (Neurobehavioral Systems). Stimuli were projected with an LCD projector (NEC, VT660K) onto a tangent screen positioned in front of the subjects' forehead and viewed through a tilted mirror. Responses were gathered with an MRI-compatible response box (HH-1 × 4L, Current Designs).

Perception of Different Types of Motion.

The perception of different types of motion was examined by using a block design paradigm. Stimuli consisted of a cloud of white dots rigidly moving along elliptical paths against a dark background. A cloud rather than a single dot was used to obtain a stronger BOLD response. The eccentricity of the elliptical path, defined as Σ = (1−(B_m/B_M)²)^1/2 where B_M and B_m indicate respectively the ellipses' major and minor semiaxes, was fixed at 0.968 (see ref. 14). The cloud of dots completed one cycle of the elliptical trajectory in 1,500 ms, corresponding to an average velocity of 9.4 cm/sec. Only one parameter was manipulated across the different conditions: the relation between the instantaneous velocity of the cloud of dots and the local curvature of the elliptical path. The instantaneous relation between the dots' velocity and the geometry of the path can be expressed, as shown above, by:

where V is the tangential velocity of the stimulus motion, R is the radius of curvature, and K is the velocity gain factor (a single fixed value of K was used for all conditions). For the purpose of our experiments, we created three velocity profiles by substituting into the equation three values of β: 1/3, 0, and −1/3, with β = 1/3 representing perfect compliance with the 2/3 power law (see SI Fig. 7).

Stimuli were shown in 9-second blocks, interleaved with 6-second periods of fixation. In each block, three dynamic stimuli belonging to only one of the experimental conditions (β = 1/3, β = 0, or β = −1/3) were presented. To avoid adaptation, the cloud's path changed its orientation every second cycle. Thus, in each 9-second block the dots completed six cycles (three orientations × two cycles at each orientation). Three different orientations were used by rotating the major axis by 0, 45, or −45° (see SI Fig. 8). The changes of orientation were counterbalanced across the three conditions. Each of the three conditions was presented for a total of eight blocks resulting in a total of 24 blocks for a total of 420 seconds per session. Subjects were carefully instructed to maintain fixation on a fixation cross at the center of the display throughout the experiment. During presentation, the color of the dots was changed from white to gray for 1 second in 50% of the blocks, which were randomly selected and counterbalanced across conditions. To control for subjects' attention, they were instructed to detect these changes and report them by pressing a button.

Ruling out Confounds Related to Button Pressing.

The design and stimuli of the first control experiment were identical to those of the main experiment. However, the subjects were not required to perform any button-pressing task.

Motion with a β Exponent >1/3.

The design and stimuli of the second control experiment were identical to those of the main experiment. However, instead of the −1/3 condition, it included a condition in which the stimuli moved according to a β exponent of 2/3 which was higher than that of β = 1/3. Similarly to the 1/3 condition, this motion slows down in the more curved parts of the ellipse and accelerates in its straighter parts. However, speed changes are more pronounced for the 2/3 than for the 1/3 condition (see SI Fig. 7).

MT/V5 Localizer.

Area MT/V5 was functionally localized by using a standard paradigm (26, 27). Dynamic vs. stationary dot patterns were presented to the subjects in a block design, in blocks of 9 seconds, interleaved with 6-second fixation blocks. In dynamic blocks, subjects viewed expanding and contracting dots (250 dots; dot diameter of ≈0.2°, within a circular area having a diameter of ≈10°) moving away or toward a fixation cross located at the center of the visual display. In stationary blocks, subjects viewed still dot patterns (three dot patterns, each lasting 2,500 ms, separated from each other by 500 ms to avoid the effects of apparent motion). The task and instructions, including the requirement to fixate throughout the session, were as in the main experiment. Overall, there were 12 stationary and 12 dynamic blocks. The entire session lasted 420 seconds and was performed once by 19 subjects. Left and right MT/V5 were defined as clusters of contiguous voxels in the left and right junctions of the temporal, occipital and parietal lobes, in which the response to dynamic displays was significantly stronger than the response to stationary displays.

Eye Movements.

Eye movements were monitored inside the scanner, separately from the scanning sessions, using an MRI compatible pupilometry eye-tracking system (ASL 5000, Applied Science Laboratories). All subjects who participated in the second control experiment took part in this procedure. However, data from one subject were disqualified because of technical problems during calibration. Vertical and horizontal eye positions during stimulus delivery were recorded while subjects performed one-eye tracking session with the stimuli of the second control experiment (1/3, 0, and 2/3 conditions) and another one with the stimuli presented in the main experiment (1/3, 0, and −1/3 conditions). The results of this procedure are detailed in SI Text.

Imaging Setup.

The experiment was performed on a 3.0-T GE Signa Horizon scanner, equipped with a resonant gradient echo-planar imaging system. All images were acquired with a standard quadrature head coil. Seventeen T1-weighted high-resolution (1 × 1 × 1 mm) anatomical images, as well as 3D spoiled gradient echo sequence (SPGR) images, were acquired for each subject to allow for volume-based statistical analysis. BOLD contrast was obtained with a gradient-echo echo-planar imaging sequence (repetition time = 3,000 ms; echo time = 35 ms; flip angle = 90°; field of view, 24 × 24 cm²; matrix size, 64 × 64). The scanned volume included 38 axial slices of 4-mm thickness.

Data Analysis.

Data analysis was performed with Brain-voyager QX (Brain Innovation). In the first stage of analysis, motion artifacts were corrected, and the data were high-pass-filtered to remove low-frequency artifacts (up to five cycles per experiment). The functional images were then superimposed on 2D anatomical images and incorporated into the 3D data sets through trilinear interpolation. The complete data set was transformed into Talairach space (43). Statistical analysis was based on the general linear model (GLM; see ref. 44), with a regressor for each condition in the experiment. All regressors were modeled as box-car functions convolved with the hemodynamic response function. A hemodynamic lag of 3 or 6 seconds was assumed and verified for each subject.

Multisubject analysis was based on a random-effect GLM (except for the analysis of the control experiments, which was based on a fixed-effect GLM, because of the small sample size). To control for familywise type I error, a cluster threshold adjustment method was used, based on Monte Carlo simulations performed with the Alphasim software (http://afni.nimh.nih.gov). The simulations were based on a whole-brain mask and a connectivity radius of 4.0 mm. The resulting minimum cluster dimensions were transformed to volume space. Thus, a minimum cluster size of 134 voxels was used to correct the statistical maps for multiple comparisons (at P < 0.05). In one contrast, the simulations were based on a slightly higher-voxelwise threshold to decrease the dimensions of the activated clusters. In this analysis (see Fig. 3 and SI Table 2) the simulation-based cluster threshold was 112 voxels.