Bayesian Smoothing with Gaussian Processes Using Fourier Basis Functions in the spectralGP Package

Abstract

The spectral representation of stationary Gaussian processes via the Fourier basis provides a computationally efficient specification of spatial surfaces and nonparametric regression functions for use in various statistical models. I describe the representation in detail and introduce the spectralGP package in R for computations. Because of the large number of basis coefficients, some form of shrinkage is necessary; I focus on a natural Bayesian approach via a particular parameterized prior structure that approximates stationary Gaussian processes on a regular grid. I review several models from the literature for data that do not lie on a grid, suggest a simple model modification, and provide example code demonstrating MCMC sampling using the spectralGP package. I describe reasons that mixing can be slow in certain situations and provide some suggestions for MCMC techniques to improve mixing, also with example code, and some general recommendations grounded in experience.

1. Introduction

Smoothing in the context of spatial modeling and nonparametric regression, often in an additive modelling scenario such as a generalized linear mixed model (GLMM) or generalized additive model (GAM), is a common technique in applied statistical work. A basic general model is

$$\begin{array}{cc}\hfill Y_i& \sim \mathcal{F}(f{(x}_i,{\mathit{s}}_i),k)\hfill \\ \hfill h\left(f({\mathit{x}}_i,{\mathit{s}}_i)\right)& ={\mathit{x}}_i^{\top }\beta +g({\mathit{s}}_i;\theta ),\hfill \end{array}$$ (1)

where Y_i, i = 1, … n, is the ith outcome, F is commonly an exponential family distribution, κ is a dispersion parameter, h(·) is the link function, x_i is a vector of covariates for the ith observation, and g(s_i; θ) is a smooth function, parameterized by θ, evaluated at the location or covariate value of the ith observation, s_i, depending on whether the smooth function is in the spatial domain or covariate space. In this work I focus on settings in which g(·; θ) is a spatial surface, but results hold generally for one dimension and potentially for higher dimensions.

There have been two basic approaches to modelling the smooth function, g(·; θ), each with a variety of parameterizations. One approach considers the function as deterministic within a generalized additive model (GAM) framework (Hastie and Tibshirani 1990; Wood 2006), for example, using a thin plate spline or radial basis function representation with the function estimated via a penalized approach. The other takes a random effects, or equivalent stochastic process, approach in which the smooth function is treated stochastically, potentially via a Bayesian approach. Within this latter approach, one might consider a collection of correlated random effects, in which case (1) is a generalized linear mixed model (GLMM) (McCulloch and Searle 2001; Ruppert, Wand, and Carroll 2003). Alternatively, stochastic process representations such as kriging (Cressie 1993) or Bayesian versions of kriging (Banerjee, Carlin, and Gelfand 2004) usually take g(·; θ) to be a Gaussian process. The random effects approach can also be considered as a stochastic process representation based on the implied covariance function of the process induced by the covariance structure of the random effects. Note that by considering a prior over functions or equivalently over the coefficients of basis functions, the additive model can be expressed in a Bayesian fashion, and there are connections between the thin plate spline and stochastic process approaches (Cressie 1993; Nychka 2000) and also between thin plate splines and mixed model representations (Ruppert et al. 2003). When interest lies in the linear coefficients and the smooth structure/spatial covariance is a nuisance, one approach to fitting such models is via estimating equations (e.g. Heagerty and Lele 1998; Heagerty and Lumley 2000; Oman, Landsman, Carmel, and Kadmon 2007). My primary interest is in situations in which the smooth function is the outcome of interest, for example, in predicting exposure to pollutants or spatial surfaces of climate variables, in which case such methods are not useful.

While models of the form (1) have a simple structure, unless the responses are Gaussian and the sample size is limited, fitting them can be difficult for computational reasons. If the response were Gaussian, there are many methods, both classical and Bayesian, for estimating β, g(·; θ), and θ. Most methods rely on integrating g(·; θ) out of the model to produce a marginal likelihood or posterior, thereby moving the smooth structure out of the mean and into the variance, such that the observations have a simple, mean structure, (in (1) this is linear in a set of covariates), and a variance that is a sum of independent noise and spatially correlated structure. This leaves a small number of parameters to be estimated, often using numerical maximization or MCMC. However, for large n, computations can be burdensome as they involve matrix calculations of O(n³). In the non-Gaussian case and in hierarchical modeling in which the unknown process lies in the hierarchy of the model, this integration cannot be done analytically, which leads to substantial difficulty in fitting the model because of the high dimensional quantities that need to be estimated, as well as burdensome matrix calculations. One set of approaches to the problem focuses on the integral in the GLMM framework, using EM (McCulloch 1994, 1997; Booth and Hobert 1999) and numerical integration (Hedeker and Gibbons 1994; Gibbons and Hedeker 1997) to maximize the likelihood or approximating the integral to produce a penalized quasi-likelihood that can be maximized by iteratively weighted least squares (IWLS) (Ruppert et al. 2003). Likelihood and covariance approximations can reduce the computational complexity of the matrix calculations (Stein, Chi, and Welty 2004; Furrer, Genton, and Nychka 2006), while the gam() function in the mgcv package in R uses the reduced rank thin plate spline approach of Wood (2004) fit by penalized IWLS. Rue and Tjelmeland (2002) exploit computationally efficient methods for fitting Markov random field (MRF) models by approximating stationary GPs using MRFs.

An alternative is to fit a Bayesian version of the model using a computationally efficient basis. The approach introduced by Wikle (2002) approximates a stationary GP structure for g(·; θ) using a spectral representation to decompose the function in an orthogonal basis, in particular using Fourier basis functions and employing the FFT for fast computation (Wikle 2002; Royle and Wikle 2005; Paciorek 2007). While the Fourier basis approach has some adherents and is one of the few efficient alternatives within the Bayesian paradigm, the intricacies and bookkeeping involved in working with the complex-valued basis coefficients make it hard to simply apply the methodology and replicate results. My goal here is to present the representation in detail (Section 2), and provide an R (R Development Core Team 2006) package, spectralGP, (freely available from CRAN, http://CRAN.R-project.org/) for working with the representation that handles the bookkeeping and sampling of coefficients for use within Markov chain Monte Carlo (MCMC) (Section 3). I describe several parameterizations for exponential family data (Section 4), and discuss detailed MCMC implementation and mixing issues that arise in fitting models, as well as general recommendations on parameterizations and sampling techniques (Section 5). I note that my experience shows slower mixing than one would desire; advances in this area are an open area for research.

2. Fourier basis representation

To simplify the notation I use g_s to denote the vector of values calculated by evaluating g(·) for each of the elements of s (e.g., for each observation location), namely g_s = (g(s₁), …, g(s _n))^⊤, suppressing the dependence on hyperparameters. Also, where necessary, I denote a set of unspecified parameters as θ. Proposal values are denoted with a *, e.g., θ*, and vectors of augmented quantities with a tilde, e.g., Ỹ.

2.1. Basic process model

In many Bayesian models, the unknown function, be it a spatial surface or regression function, is a represented as a Gaussian process or by a basis function representation. Diggle, Tawn, and Moyeed (1998) formalized the idea of generalized geostatistical models, with a latent Gaussian spatial process, as the natural extension of kriging models to exponential family responses. They used Bayesian estimation, suggesting a Metropolis-Hastings implementation, with the spatial function sampled sequentially at each observation location at each MCMC iteration. However, as shown in their examples and discussed elsewhere (Christensen, Møller, and Waagepetersen 2000; Christensen and Waagepetersen 2002; Christensen, Roberts, and Sköld 2006), this implementation is slow to converge and mix, as well as being computationally inefficient because of the covariance matrix involved in calculating the prior for g_s.

An alternative approach that avoids large matrix calculations is to express the unknown function in a basis, g_s = Ψu, where Ψ contains the basis function values evaluated at the locations of interest, and estimate the basis coefficients, u. These coefficients are taken to have a prior distribution; constraints on the function, such as degrees of smoothness, are imposed through this prior distribution and the basis choice. When the coefficients are normally distributed, this representation can be viewed as a GP evaluated at a finite set of locations, with Cov(g_s) = ΨCov(u)Ψ^⊤.

Isotropic GPs can be represented in an approximate fashion using their spectral representation as a Fourier basis expansion, which allows one to use the Fast Fourier Transform (FFT) to speed calculations. Here I describe the basic model in two-dimensional space, following Wikle (2002).

The key to the spectral approach is to approximate the function g(·) on a grid, s^#, of size M = M₁ × M₂, where M₁ and M₂ are powers of two. Evaluated at the grid points, the vector of function values is represented as

$${\mathit{g}}_{{\mathit{s}}^{\#}}=\Psi \mathit{u},$$ (2)

where Ψ is a matrix of orthogonal spectral basis functions, and u is a vector of complex-valued basis coefficients, u_m = a_m + b_mi, m = 1, … , M. The spectral basis functions are complex exponential functions, i.e., sinusoidal functions of particular frequencies; constraints on the coefficients ensure that g_s# is real-valued and can be expressed equivalently as a sum of sine and cosine functions. The basis functions represented in the basis matrix, Ψ, capture behavior at different frequencies, with the most important basis functions for function estimation being the low-frequency basis functions. To approximate mean zero stationary, isotropic GPs, the basis coefficients have the prior distribution,

$$\left(\begin{array}{c}\hfill \mathit{a}\hfill \\ \hfill \mathit{b}\hfill \end{array}\right)\sim \mathcal{N}(0,{\Sigma }_{\theta })$$ (3)

where the diagonal (asymptotically; see Shumway and Stoffer (2000, Section T3.12)) covariance matrix of the basis coefficients, Σ_θ, parameterized by θ, can be expressed in closed form (for certain covariance functions) using the spectral density of the covariance function desired to parameterize the approximated GP.

To make this more explicit, consider the Matérn covariance popular in spatial statistics,

$$C(\tau ;\rho ,\nu )={\sigma }^2\frac{1}{\Gamma \left(\nu \right)2^{\nu -1}}{\left(\frac{2\sqrt{\nu }\tau }{\rho }\right)}^{\nu }{\mathcal{K}}_{\nu }\left(\frac{2\sqrt{\nu }\tau }{\rho }\right),$$ (4)

where τ is distance, σ² is the variance of the process, ρ is the range (correlation decay) parameter, and K_ν(·) is the modified Bessel function of the second kind, whose order is the differentiability parameter, ν > 0. This covariance function has the desirable property that sample functions of GPs parameterized with the covariance are ⌊ν − 1⌋ times differentiable. As ν → ∞, the Matérn approaches the squared exponential form, with infinitely many sample path derivatives, while for ν = 0.5, the Matérn takes the exponential form with no sample path derivatives.

The spectral density of this covariance, which is used to calculate the elements of Σ_θ, evaluated at spectral frequency, ω, is

$$\varphi (\omega ;\rho ,\nu )={\sigma }^2\frac{\Gamma (\nu +\frac{D}{2}){\left(4\nu \right)}^{\nu }}{{\pi }^{\frac{D}{2}}\Gamma \left(\nu \right){\left(\pi \rho \right)}^{2\nu }}\cdot {\left(\frac{4\nu }{{\left(\pi \rho \right)}^2}+{\omega }^{\top }\omega \right)}^{-(\nu +\frac{D}{2})},$$ (5)

where D is the dimension of the space (two in this case) and the parameters are as above. For an appropriate set of spectral frequencies, the diagonal elements of Σ_θ are the values of ϕ(·; ρ, ν) at those frequencies, and the off-diagonals are zero.

To construct real-valued processes with the approximate GP distribution based on the complex-valued coefficients given above, some detailed bookkeeping and constraints are required. These details are provided in the Appendix A.1, while details on accounting for the periodicity of the Fourier domain appear in Appendix A.2.

2.2. Computations and statistical modeling of observations

The process at the observation locations is calculated through an incidence matrix, K, which maps each observation location to the nearest grid location in Euclidean space,

$${\mathit{g}}_{\mathit{s}}=\mathit{K}{\mathit{g}}_{{\mathit{s}}^{\#}}=\mathit{K}\Psi \mathit{u}.$$ (6)

For a fine grid, the error induced in associating observations with grid locations should be negligible and the piecewise constant representation of the surface tolerable. This approach amounts to binning the data, with square bins defined by the grid points. An extension would be to do local interpolation between the grid points to define the process values at the data locations, but I do not pursue that here. The computational efficiency comes in the fact that the matrix Ψ, which is M × M, need never be explicitly formed, and the operation Ψu is the inverse FFT, and so can be done very efficiently (O (M log₂(M))). In addition, evaluating the prior for u is fast because the coefficients are independent a priori. This stands in contrast to the standard MCMC setup for GP models, in which the prior on g_s involves an n × n matrix and therefore O(n³) operations. Of course the gridding could be done without the Fourier basis approach, but this would only reduce the computations to O ((M/2^D)³) (the division by 2^D occurs because the padding of Appendix A.2 would not be required). Note that with the gridded approach, the number of observations affects the calculations only through the likelihood, which scales as O(n), because the observations are independent conditional on g_s. The complexity of the underlying surface determines the computational efficiency by defining how large M should be; simple surfaces can be estimated very efficiently even if n is large.

3. R spectralGP package

The spectralGP package for R provides an object-oriented representation of the Fourier basis approach to computation with GPs. The primary purpose of the package is to handle the bookkeeping details, allowing one to easily simulate and plot processes and sample the Fourier basis coefficients within an MCMC. This allows developers to write code to fit models in which a Gaussian process is a component, easily drawing MCMC samples of the coefficients of the process, as described in Section 3.3. Also note that C. Wikle has released Matlab code for the Fourier basis computations on his website (http://www.stat.missouri.edu/~wikle/).

3.1. Description of the package

The key functions in spectralGP are a constructor function, gp(), that creates a gp object, and a number of S3 methods: two MCMC sampling methods for the coefficients, Gibbs.sample.coeff.gp() and propose.coeff.gp(); a method for calculating the proposal density of the current coefficients for use in Metropolis-Hastings sampling, Hastings.coeff.gp(); a method for simulating GPs, simulate.gp(); a method for changing the GP hyperparameter values, change.param.gp(); calculation of the logdensity of the coefficients, logdensity.gp(); and prediction and plotting methods. The function updateprocess.gp() updates the process values based on the current values of the coefficients, while calc.variances.gp() calculates the coefficient variances given the current covariance/spectral density parameters. These latter two functions are generally intended for internal use, but the template code in Appendix B makes use of updateprocess.gp() after changing the coefficient values during a particular type of MCMC step. Auxiliary functions allow for copying, copy.gp(); determining the basic grid used, getgrid.gp(); and extracting the object element names, names.gp(). Several functions deal with conversion between coordinate systems: a simplistic lon/lat to Euclidean x/y projection, lonlat2xy(); mapping a Euclidean domain to (0, 1)^D, xy2unit(); and mapping locations in the domain to the closest grid points, new.mapping(). Several auxiliary functions are borrowed from the fields package, namely rdist.earth() as well as image.plot() and its auxiliary functions, image.plot.info() and image.plot.plt().

I have used native R code for the entire package both for simplicity and because the essential computations within the package are already compiled code, namely the functions, fft(), rnorm(), and dnorm().

spectralGP includes only the spectral density function for the Matérn covariance (and thereby the special case of the exponential covariance) but is easily extendible by writing user-defined spectral density functions that can be used in the constructor function for a creating a new process, gp().

Some additional intricacies included in the package are mentioned parenthetically in Sections 4 and 5 and in Appendix A. Note that in the package, the process is scaled by $1∕\sqrt{M_1{M}_2}$, as described in Section 4.1, relative to the exact process values (21).

3.2. Using environments as objects to allow pass-by-reference

Since a gp object will be used repeatedly during MCMC sampling, I chose to use a pass-by-reference scheme in the coding, using R environments to mimic object-orientation in traditional languages, as suggested by E.A. Houseman. In this way, one can operate on a gp object and change internal elements without having to pass the entire object back from the method function and thereby create a new copy of the gp object or overwrite the old copy by assigning the output to the same name. This is possible because unlike other R objects, environments are not copied when passed to functions. Each instantiation of a gp object is an environment, initialized with a call to new.env() and assigned the class “gp”. The elements of the object, e.g., myFun here, are local variables within the environment, accessed via list-like syntax, e.g., myFun$process. S3 methods are used to operate on the gp objects, with the difference from standard R that global changes can be made to the elements of an object within the method by virtue of those elements residing within an environment. For example, the call, simulate.gp(myFun), samples new coefficients and updates the process based on those coefficients without having to pass myFun back to the calling environment, yet the changes to myFun are effective in the calling environment. Also note that care must be taken when assigning gp objects because environments are not copied when used in assignments; I have created an explicit copy.gp() function to make a new copy of a gp object; assignment merely creates an additional name (i.e., pointer) referencing the existing object, so any changes to the original gp object also occur within the ’new’ object, which just references the original object. I chose not to use S4 methods because my understanding is that their implementation is still somewhat slow and spectralGP works with large objects and substantial computation.

This use of R environments as objects that can be passed by reference is not a standard approach in R, which uses a pass-by-value system. As a result, the package can be nonintuitive to the user, producing changes in the objects as a side effect of the call to a method function, and then returning a null value. However, I believe this is a feature of the approach that is more natural for setting up MCMC sampling, rather than a drawback. There is a single copy of each parameter object that is changed during a sampling step instead of passing back a new copy of the changed object to the calling environment. Unlike most cases in R in which an object is created and then used as an input for additional work but is not modified subsequently (such as use of lm(), following by summary() and plot()), in the MCMC sampling setting, a parameter object needs to be modified repeatedly. It is more natural to pass by reference in this context.

3.3. Using and extending the package

A basic use of the package is to simulate and plot GPs. After setting up the gp object, one can simulate a realization and plot an image of the realization as follows:

myFun=gp(c(256,256),matern.specdens,c(0.3,2))

simulate(myFun)

plot(myFun)

This is computationally efficient because of the use of the FFT. The constructor function isgp(gridsize,specdens,specdens.param,variance.param,const.fixed=FALSE)

The argument gridsize is a scalar for processes on ℜ¹ or vector of length two for processes on ℜ². If gridsize=c(M1,M2), then the effective grid is M₁/2 + 1 by M₂/2 + 1, after accounting for periodicity of the Fourier basis, as discussed in Appendix A.2. Note that if M₁ ≠ M₂, the scaling in the two dimensions is different, which produces an anisotropic process. The argument, specdens, is a spectral density function; currently only a Matérn function, matern.specdens(), with the exponential as a special case, is implemented but users can write their own. The argument, specdens.param, is a scalar or vector of parameters required by specdens; in the Matérn case the first value is the spatial range parameter, ρ, and the second the smoothness or differentiability parameter, ν. The argument, variance.param, is the spatial process variance, σ², while const.fixed=TRUE indicates whether the first basis coefficient, u_0,0, should be fixed to be zero, which eliminates a non-identifiability in the MCMC when a separate mean, μ, is included in the model (Appendix A.3); for simulation of realizations one should use const.fixed=FALSE to preserve the approximate specified covariance for the GP realizations. The plot.gp() method uses arguments similar to those in image while the only argument to simulate.gp() is the gp object itself. While fast simulation of GPs on a discrete grid may be of interest, the primary use of the package is to ease the sampling of the coefficients via MCMC in a Bayesian model context, as follows.

The simplest approach is to sample the coefficients in blocks grouped by basis function frequency, with the code

propose.coeff(object,block,proposal.sd)

where block specifies the block to be sampled (the blocks are created with add.blocks.gp() and using block=0 proposes all of the coefficients at once) and proposal.sd is the user-tunable Metropolis-Hastings proposal standard deviation. The user then needs to write code to accept or reject the proposal by calculating the probability density of any model quantities that depend on the process values (extracted using predict.gp()) and the prior density of the coefficients using logdensity.gp(). predict.gp() by default makes predictions on the effective grid of size M₁/2 + 1 by M₂/2 + 1, but can take the argument newdata as a matrix of prediction locations or the argument mapping as a set of indices indicating the grid cells whose values should be extracted. The set of indices can be created using the method new.mapping(object,locations), where locations is a two-column matrix of location coordinates. More details on this approach are given in Section 4.3, and Appendix B provides template code illustrating this usage.

In certain models, the coefficients can be sampled by a Gibbs sampling step from their exact conditional distribution. The following conditional distribution for the coefficients,

$$\begin{array}{cc}\hfill \mathit{u}\mid \cdot & \sim \mathcal{N}\left(\mathit{V}\frac{s}{{\sigma }_e^2}{\Psi }^{\top }(\mathit{z}-m1),\mathit{V}\right)\hfill \\ \hfill \mathit{V}& ={\left(\frac{s^2}{{\sigma }_e^2}\mathit{I}+{{\Sigma }_{\theta }}^{-1}\right)}^{-1},\hfill \end{array}$$ (7)

arises when the coefficients have prior distribution, u ∼ N(0, Σ_θ) as in (3) and the gridded data or latent process values whose distribution depends on the GP have the distribution, $\mathit{z}\sim \mathcal{N}(m1+s{\Psi }^{\top }(\mathit{z}-m1),{\sigma }_e^2\mathit{I})$. Here m is a mean term, s is a standard deviation term, and ${\sigma }_e^2$ is a residual variance term. Section 4 shows how this conditional distribution arises in several model structures for non-gridded data. Sampling is done with the code

Gibbs.sample.coeff(object,z,sig2e,meanVal,sdVal,returnHastings=FALSE)

where the mapping of the method arguments to the parameters above should be clear. Note that the prior variance structure of the coefficients, Σ_θ, is already part of the gp object. One can also sample coefficients from the distribution (7) even if it is not the exact conditional distribution and base acceptance on the Metropolis-Hastings algorithm. One can calculate the log proposal density, π(u|·), using

Hastings.coeff.gp(object,z,sig2e,meanVal,sdVal)

or as the return value of Gibbs.sample.coeff() with the argument returnHastings=TRUE. To calculate the ratio of proposal densities for the Metropolis-Hastings algorithm, one would first calculate the log proposal density of the current (original) coefficients as the output, oldDensity, from

oldDensity=Hastings.coeff.gp(object,z,sig2e,meanVal,sdVal)

Then, possibly after changing hyperparameter values as part of a joint proposal of hyperparameters and coefficients (Section 5.2) one makes the proposal, u*, using

newDensity=Gibbs.sample.coeff(object,z,sig2e,meanVal,sdVal,returnHastings=TRUE)

which assigns the log proposal density of the proposed coefficients to newDensity. The difference of oldDensity and newDensity is then used as part of the Metropolis-Hastings acceptance decision.

Together these functions allow a developer to easily sample the coefficients within the context of a larger model without worrying about the bookkeeping and technical details of the Fourier basis representation. In Appendix B I provide R template code for various forms (Section 4) of the simple model (1) for data from an exponential family distribution: normal, Poisson, or binomial. The code assumes a constant mean, μ, in place of ${\mathit{x}}_i^{\top }\beta$, and Matérn covariance function with ν fixed. While this is a simple setting, users could take the template code and use it within a more complicated hiearchical model or easily extend to a regression structure in the mean. For example, Paciorek and McLachlan (2007) use a set of gp objects to represent compositional data in a spatial setting with a complicated multinomial-Dirichlet likelihood based on a transformation of the GPs, making use of the block sampling approach. The template code includes code for joint sampling of covariance parameters and process coefficients, which I discuss in Section 5.2 as a way to improve mixing. Developers could build on the template code to include this type of sampling in their own models.

4. Basic MCMC sampling schemes for coefficients

In this section, I describe several parameterizations for simple Bayesian exponential family models with associated MCMC sampling schemes for the Fourier basis coefficients. Bayesian estimation of unknown processes in this framework relies on shrinkage to estimate the large number of coefficients; coefficients of low-frequency basis functions are strongly informed by the data while those of high-frequency basis functions are shrunk strongly toward their prior distributions. These following basic parameterizations can also be used with relatively straightforward modifications in more complicated hierarchical models, although the added complexity may make the simple blocked sampling scheme (Section 4.3) the most feasible approach in that case. Note that for simplicity I consider a scalar mean parameter, μ, but this could be replaced by a regression term, e.g., X_iβ, or other additive components. Also, for more compact notation, I suppress the dependence of Σ_θ on the covariance/spectral density parameters, θ.

4.1. Data augmentation Gibbs sampling for normal data

For Gaussian data with mean function based on the latent process, g(·), a missing data scheme allows for Gibbs sampling of the coefficients. This is a simplification of the Gibbs sampling scheme of Wikle (2002), which is described in Section 4.2.

Take the data model to be

$$\mathit{Y}\sim {\mathcal{N}}_n(\mu 1+\gamma \mathit{K}\Psi \mathit{u},{\eta }^2\mathit{I}),$$ (8)

where μ is the process mean and γ is the process standard deviation with σ² in (4-5) set to one. Since the prior for the coefficients is normal, we have conjugacy, and the conditional distribution for u is

$$\mathit{u}\mid \mathit{y},\cdot \sim {\mathcal{N}}_M\left(\mathit{V}\frac{\gamma }{{\eta }^2}{\left(\mathit{K}\Psi \right)}^{\top }(\mathit{y}-\mu 1),\mathit{V}\right)$$

$$\mathit{V}={\left(\frac{{\gamma }^2}{{\eta }^2}{\Psi }^{\top }{\mathit{K}}^{\top }\mathit{K}\Psi +{\Sigma }^{-1}\right)}^{-1}.$$ (9)

The sample of u represents precision-weighted shrinkage of the data-driven estimates of the coefficients towards their prior mean of zero.

However, this sampling scheme requires calculation of Ψ^⊤K^⊤KΨ, which is not feasible for large number of grid points; note that if K were the identity of dimension M, since Ψ is an orthogonal matrix, this simplifies to

$$\mathit{V}={\left(\frac{{\gamma }^2}{{\eta }^2}\mathit{I}+{\Sigma }^{-1}\right)}^{-1},$$ (10)

which because Σ is diagonal, is easy to calculate. Assuming no more than one observation per grid cell, K = I can be achieved using a missing data scheme by introducing latent pseudo-observations for all grid cells without any associated data, including grid cells in which no data can possibly fall because of padding to account for periodicity (Appendix A.2). Collecting these pseudo-observations into a vector, Ỹ , they can be sampled within the MCMC using a Gibbs step as

$$\stackrel{\sim }{\mathit{Y}}\sim {\mathcal{N}}_{M-n}(\mu 1+\gamma \stackrel{\sim }{\mathit{K}}\Psi \mathit{u},{\eta }^2\mathit{I}),$$ (11)

where the K̃ matrix picks out grid cells with no associated data. With this augmentation, Y in (8-9) is a vector of values on the full grid, Y = (Y _obs, Ỹ), combining actual observations with pseudo-observations, and K = I.

The coefficients can be sampled under this approach (9-10) using

Gibbs.sample.coeff.gp(object,z,sig2e,meanVal,sdVal)

where z is Y , sig2e is η², meanVal is μ, and sdVal is γ. Note that this straightforward expression conceals some details required in working with the complex-valued coefficients. In calculating (γ²/η² + (Σ⁻¹)_ii), one needs to multiple γ²/η² by one-half for all the elements corresponding to complex-valued coefficients to ensure that the scaling is correct as described in Appendix A.1. Also, the operation Ψ^⊤(y-μ1) is the FFT and the correct scaling needs to occur so the result is on the scale of the coefficients. In R, I specify the coefficient variances as M₁M₂ϕ(ω; θ) and update the process as $\Psi \mathit{u}∕\sqrt{M_1{M}_2}$. If I then divide Ψ^⊤(y − μ1) by $\sqrt{M_1{M}_2}$ when sampling the coefficients (9-10), the desired approximate covariance structure for the process is preserved, namely $\Psi \mathit{u}\stackrel{.}{\sim }{\mathcal{N}}_M(0,{\mathit{C}}_{\theta })$, where the matrix, C_θ is defined by C_θ,ij = C(|| s_i − s_j ||; θ) and C(·; θ) is the covariance function whose spectral density defines ϕ(·; θ), e.g., (5). The exact algorithm is given in the Gibbs.sample.coeff.gp() function in the spectralGP package. In Appendix B I provide template code for fitting this parameterization, denoted as Code A.

If there is more than one observation per grid cell, some possible solutions are to use a finer grid or to take $y\left(s_j\right)={\stackrel{-}{y}}_j$, namely the average of the observations in the grid cell. Ideally, one would set ${\eta }_j^2={\eta }^2∕n_j$, but this would require calculation of Ψ^⊤η⁻¹Ψ, where $\eta =\mathrm{diag}\left(({\eta }_1^2,\dots ,{\eta }_M^2)\right)$, which is computationally infeasible. Instead, I suggest using constant η² so long as there are relatively few locations with multiple observations per grid cell. One could also use more extensive data augmentation to supplement the existing observations such that there are n_j pseudo plus true observations per grid cell, with n_j equal to the maximum number of true observations in a cell over all of the grid cells.

Wikle (2002) recommends the uncentered (sensu Gelfand, Sahu, and Carlin 1996) parameterization for the process variance (8), with γ allowed to vary and σ² ≡ 1 in defining the variance of the coefficients (5). He notes that moving the parameter closer to the data improves mixing and helps avoid dependence with ρ. Note that I follow this approach in some cases, while in others, I allow σ² to vary and fix γ ≡ 1. In the spectralGP package, a value of σ² not equal to one is specified with the variance.param argument to gp() and the new.variance.param argument to change.param.gp().

For non-normal data from the exponential family, $Y_i\sim \mathcal{F}\left(h^{-1}\left(f_i\right)\right)$, where f_i = μ + γK_iu, one might use a Metropolis-Hastings version of this Gibbs sampling scheme, again with data augmentation, making use of the linearized observations and working variances used in fitting GLMs in place of y and η² in (9-10). As above, one would need to use a single homoscedastic value for η². I do not pursue this approach for non-normal data further, as I had little success in tuning the proposals to achieve reasonable acceptance, but further research in this area may be worthwhile.

One approach to speeding mixing in the case of normal data is to jointly sample η² and Ỹ by first proposing η²* and then, within the same proposal, sampling from [Ỹ|η²*, ·] via a Gibbs sample, conditional on the proposed value, η²*. Because this joint sample is not from the joint full conditional [Ỹ, η²|·], we need to use Metropolis-Hastings in determining acceptance based on the ratio of the prior for η² and likelihood, π(η²*)L(Y _obs|η²*, ·)/(π(η2)L(Y _obs|η², ·)), where Y _obs is the actual data. Acceptance does not depend on the value of the augmented observations, Ỹ. So one can propose η², decide on acceptance based on the likelihood of the true observations, and then, if accepted, do a Gibbs sample for Ỹ (11). We have effectively integrated Ỹ out of the joint conditional density, π(η², Ỹ|y_obs, ·), thereby sampling η² without dependence on Ỹ (Rue and Held 2005, pp. 141-143). In the iterations, one may also wish to do a separate Gibbs sample for Ỹ alone, apart from the joint sample with η². Template code A in Appendix B also includes modifications for this sampling approach.

4.2. Latent layer Gibbs sampling for exponential family data

Parameterizing with two latent layers (the Wikle parameterization)

For non-normal data, rather than losing the Gibbs sampling structure for the coefficients, Wikle (2002) and Royle and Wikle (2005) embed the spectral basis representation in a hierarchical model with additional latent processes and associated variance components. This approach allows one to do Gibbs sampling in various generalized models in which exponential family outcomes are related to a latent spatial process in the mean structure (1).

To take a concrete example, the model for Poisson data is

$$\begin{array}{cc}\hfill Y_i& \sim \mathcal{P}\left(\exp \left({\lambda }_i\right)\right)\hfill \\ \hfill {\lambda }_i& \sim \mathcal{N}(\mu +\gamma {\mathit{K}}_{\mathit{i}}\mathit{z},{\eta }^2)\hfill \\ \hfill \mathit{z}& \sim {\mathcal{N}}_M(\Psi \mathit{u},{\sigma }_z^2\mathit{I}),\hfill \end{array}$$ (12)

where Ψu is the Fourier basis representation with the prior structure (3). One can easily modify the likelihood and link for other exponential family distributions. The model introduces two variance components, η² and ${\sigma }_z^2$, corresponding to two latent processes, one, λ, defined only at the observation locations, and the second, z, defined for each of the grid cells, including those in which no data can fall, as discussed in Appendix A.2. Note that the variance components account for overdispersion. In Section 5.1, I discuss issues that arise when the data are not overdispersed.

Wikle (2002) suggests a Metropolis-Hastings proposal for λ, with conjugate normal Gibbs sampling for z and u:

$$\begin{array}{cc}\hfill \mathit{z}\mid \lambda ,\cdot & \sim {\mathcal{N}}_M\left({\mathit{V}}_z\left(\frac{\gamma }{{\eta }^2}{\mathit{K}}^{\top }(\lambda -\mu 1)+{\sigma }_z^{-2}\Psi \mathit{u}\right),{\mathit{V}}_{\mathit{z}}\right)\hfill \\ \hfill {\mathit{V}}_{\mathit{z}}& ={\left(\frac{{\gamma }^2}{{\eta }^2}{\mathit{K}}^{\top }\mathit{K}+{\sigma }_z^{-2}\mathit{I}\right)}^{-1}\hfill \\ \hfill \mathit{u}\mid \mathit{z},\cdot & \sim {\mathcal{N}}_M\left({\mathit{V}}_{\mathit{u}}\frac{{\Psi }^{\top }\mathit{z}}{{\sigma }_z^2},{\mathit{V}}_{\mathit{u}}\right)\hfill \\ \hfill {\mathit{V}}_{\mathit{u}}& ={({\sigma }_z^{-2}\mathit{I}+{\Sigma }^{-1})}^{-1}\hfill \end{array}$$ (13)

Similar calculations to those in the previous section are needed in the Gibbs sampling for u to account for the complex-valued coefficients and to scale the proposal correctly. In the spectralGP package, u is sampled using

Gibbs.sample.coeff.gp(object,z,sig2e,meanVal,sdVal)

where z is z, sig2e is ${\sigma }_z^2$ , meanVal is 0, and sdVal is 1. Template code is given in Appendix B as Code B.

Note that sampling can require long chain lengths; Royle and Wikle (2005) used eight chains of length 520,000, retaining every 50th iteration, which suggest slow mixing of the sort I have experienced as well.

A simplified parameterization with a single latent layer (modified Wikle parameterization)

I propose a modification of the model above to eliminate one of the latent layers, thereby moving the coefficients closer to the data in the hierarchy and eliminating z and ${\sigma }_z^2$, which can be difficult to interpret and may not informed by the data (see Section 5.1). The simplified model for Poisson data is

$$\begin{array}{cc}\hfill Y_i& \sim \mathcal{P}\left(\exp \left({\mathit{K}}_{\mathit{i}}\lambda \right)\right)\hfill \\ \hfill \lambda & \sim {\mathcal{N}}_M(\mu 1+\gamma \Psi \mathit{u},{\eta }^2\mathit{I})\hfill \end{array}$$ (14)

where the ith row of K maps the observation to the grid cell in which it falls. One can easily modify the likelihood and link for other exponential family distributions. Here η² accounts for overdispersion. Inference about the unknown smooth function should be based on μ1+γΨu rather than λ, as simulations indicate that inference based on λ has larger posterior variances and is overly conservative for the unknown mean function because λ includes heterogeneity from overdispersion.

One can use Gibbs sampling for the values of λ corresponding to the J grid cells with no observations, denoted λ̃, and for u:

$$\begin{array}{cc}\hfill \stackrel{\sim }{\lambda }\mid \mathit{u},\cdot & \sim {\mathcal{N}}_J\left(\mu 1+\gamma \stackrel{\sim }{\mathit{K}}\Psi \mathit{u},{\eta }^2\mathit{I}\right)\hfill \\ \hfill \mathit{u}\mid \lambda ,\cdot & \sim {\mathcal{N}}_M\left({\mathit{V}}_u\frac{\gamma }{{\eta }^2}{\Psi }^{\top }(\lambda -\mu 1),{\mathit{V}}_{\mathit{u}}\right)\hfill \\ \hfill {\mathit{V}}_{\mathit{u}}& ={\left(\frac{{\gamma }^2}{{\eta }^2}\mathit{I}+{\Sigma }^{-1}\right)}^{-1}.\hfill \end{array}$$ (15)

Again, u can be sampled with

Gibbs.sample.coeff.gp(object,z,sig2e,meanVal,sdVal)

where z is λ, sig2e is η², meanVal is μ, and sdVal is γ. For the elements of λ corresponding to grid cells in which observations fall, λ_obs, I suggest Metropolis proposals, done individually for each individual element, but computed in an efficient vectorized fashion in R. Some intuition for how the information from the data diffuses to the level of the basis coefficients is that the latent layer, λ, allows for some fluidity between the process values and the data: individual sampling of λ_obs for individual grid cells allows the latent layer to accomodate the data based on adjustments to λ_obs at individual locations, while the Gibbs sample of u translates these adjustments to the coefficients. A single joint sample for the elements of λ_obs would likely have slower mixing as it would be trying to sample many grid locations at once, with a single acceptance decision, thereby slowing local adjustments. Template code C is given in Appendix B.

In similar fashion to joint sampling of ( η², Ỹ) in Section 4.1, with the parameterization above, one can improve mixing by jointly sampling η² and λ̃. First propose η²* and then, within the same proposal, sample from $[\stackrel{\sim }{\lambda }\mid {\eta }^{2\ast },\cdot ]$. Because this joint sample is not from the joint conditional of $({\eta }^2,\stackrel{\sim }{\lambda })$, we need a Metropolis-Hastings acceptance decision based on the ratio of the prior for η² and likelihood, π(η²*)L(Y|η²*, λ_obs, ·)/(π(η²)L(Y|η², λ_obs, ·)), with acceptance not depending on the value for the augmented locations, λ̃, thereby effectively integrating λ̃ out of the joint conditional density, $\pi ({\eta }^2,\stackrel{\sim }{\lambda }\mid {\lambda }_{\mathit{obs}},\mathit{y},\cdot )$. So in practice one can propose η²*, decide on acceptance, and then, if accepted, do a Gibbs sample for λ̃ (15). In the iterations, one may also wish to do a separate Gibbs sample for λ̃ alone. Template code C in Appendix B also includes modifications for joint sampling of $({\eta }^2,\stackrel{\sim }{\lambda })$.

4.3. Blocked Metropolis sampling for exponential family data (simple parameterization)

An alternative to Gibbs sampling that avoids the use of the additional hierarchical layers and variance components in Section 4.2 is a simple model with straightforward Metropolis sampling for the coefficients described in Paciorek (2007). This approach has the advantage of tying the coefficients to the data by involving the coefficients directly in the likelihood, without intervening layers. For data that are not overdispersed, the simple model avoids introducing the overdispersion parameter(s), η² (and ${\sigma }_z^2$).

The basic approach is to specify the obvious parameterization in which the data are directly dependent on the latent spatial surface, which for Poisson data is

$$Y_i\sim \mathcal{P}\left(\exp (\mu +\gamma {\mathit{K}}_{\mathit{i}}\Psi \mathit{u})\right).$$ (16)

I suggest sampling the coefficients in a blocked Metropolis scheme, with blocks of coefficients whose corresponding frequencies have similar magnitudes (Paciorek 2007). I use smaller blocks for the low-frequency coefficients, thereby allowing these critical coefficients to move more quickly. The high-frequency coefficients have little effect on the function and are proposed in large blocks. The first block is the scalar, u_0,0, corresponding to the frequency pair, $({\omega }_0^1,{\omega }_0^2)=(0,0)$ (but note that in Appendix A.3 I suggest not sampling this coefficient because of lack of identifiability with respect to μ). The remaining blocks are specified so that the block size increases as the frequencies increase. For example, the next block might include the coefficients whose largest magnitude frequencies are at most one, i.e., $u_{m_1,m_2}\mathrm{s}.\mathrm{t}.\max \{\mid {\omega }_{m_1}^1\mid ,\mid {\omega }_{m_2}^2\mid \}\le 1$, but excluding the previous block, giving the block of coefficients, {u_0,1, u_1,0, u_1,1, u_M1−1,1}. Recall that there are additional coefficients whose largest magnitude frequencies are at most one, e.g., u_M1−1,0 and u_{M1−1,M2−1}, but these are complex conjugates of the sampled coefficients. The next block might be the coefficients whose largest magnitude frequencies are at most two, i.e., $u_{m_1,m_2}\mathrm{s}.\mathrm{t}.\max \{\mid {\omega }_{m_1}^1\mid ,\mid {\omega }_{m_2}^2\mid \}\le 2$, but excluding the previous block elements. The real and imaginary components of the coefficients in each block are proposed jointly, Metropolis-style, from a multivariate normal distribution with independent elements whose means are the current values. Since the coefficients have widely-varying scales, I take the proposal variance for each coefficient to be the product of a tuneable multiplier (one for each block, the proposal.sd argument to propose.coeff.gp()) and the prior variance of the coefficient, which puts the proposal on the proper scale. In the add.blocks.gp() function in spectralGP package, the default blocks are set by grouping coefficients based on the frequency thresholds, 0, 1, 2, 4,…, 2^Q, where Q = log₂(max(M₁, M₂)) − 1. The coefficients can be proposed in spectralGP using propose.coeff.gp(object,block,proposal.sd), with the numbered block to be proposed specified as the argument block. Template code for fitting by this approach is given in Appendix B as Code D.

4.4. Hyperparameter priors

Assuming the Matérn covariance (4-5), the hyperparameters in the various parameterizations are $\theta =(\mu ,\gamma ,\rho ,\nu ,{\eta }^2,{\sigma }_z^2)$, with η² and ${\sigma }_z^2$ not present in some cases. Royle and Wikle (2005) use inverse gamma priors for η² and ${\sigma }_z^2$ with a diffuse normal prior for μ. For ρ they use the reference prior of Berger, De Oliveira, and Sansó (2001) for the Gaussian likelihood case to avoid the use of an improper diffuse prior that could lead to an improper posterior. Paciorek (2007) specifies independent, proper, but non-informative priors for the elements of θ, except for ν, which cannot be estimated for a grid-level process (even for the continuous case, this is difficult to estimate without some observations very close together) and which is fixed in advance ( ν = 4 gives smooth processes with a small number of derivatives).

Gelman (2006) suggests truncated uniform and folded non-central t distributions on the standard deviation scale for variance components and argues against $\mathcal{IG}(∊,∊)$ priors as these have a sharp peak at small values that can strongly affect inference when the data do not constrain the parameters away from zero. Berger et al. (2001) argue for reference priors and against proper but non-informative priors, including truncated distributions, in part because they are concerned about the posterior concentrating at extreme values or on the truncation limit. In the setting here, I believe that the exact form of the priors is not critical, except that it is desirable to keep the parameters in a finite interval to prevent them from wandering in extreme parts of the space in which the likelihood is flat. In cases with sufficient data, the prior should play little role in estimation and prediction. The situations that concern Berger et al. (2001) with regard to truncation and vague proper priors arise when the data provide little information, in which case their concern about the posterior concentrating on the truncation limit seems little different than having it constrained by the reference prior. I discuss identifiability and priors for ${\sigma }_z^2$ and η² in more detail in Section 5.1.

5. MCMC sampling considerations

In Sections 5.1-5.2, I describe some factors that impede mixing and some modifications to the basic sampling schemes discussed above that can help to improve mixing. In Section 5.3 I compare the approaches of Section 4 and make broad recommendations. Appendix A.3 discusses the lack of identifiability of u_0,0 with respect to an overall mean, μ, Appendix A.4 considers reparameterizing the covariance parameters for improved mixing, and starting values are discussed in Appendix A.5. Note that for any particular application, my recommendations may not provide the best mixing, and consideration of alternatives discussed in this paper may improve matters.

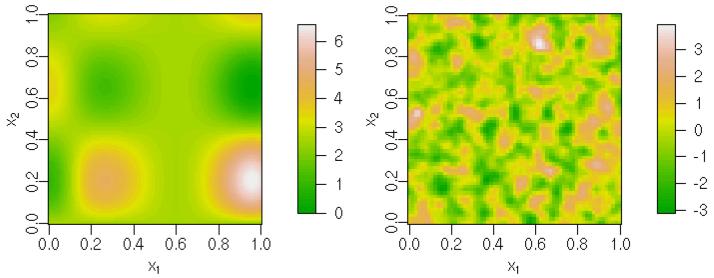
I explored sampling effectiveness using a few simulated datasets, meant to provide a range of function complexity and data intensity. All have Poisson data with the sampling locations sampled uniformly in (0, 1)²: Data1 has 225 observations while Data2 has 1000 observations, both with the mean function, f(x₁, x₂) = 1.9 · (1.35 + exp(x₁) sin(13 ·(x₁ − 0.6)²) · exp(−x₂) sin(7x₂)), used by Hwang, Lay, Maechler, Martin, and Schimert (1994)(Figure 1), a fairly simple function that when fit with a GP has $\widehat{\rho }\approx 0.3$. Data3, Data4, and Data5 use the same mean function; a GP with ρ = 0.05, μ = 0, γ = σ = 1 (Figure 1); and 400, 800, and 2500 observations, respectively (Figure 1).

Figure 1.

Mean functions used in simulated datasets: simple function (left) with $\widehat{\rho }\approx 0.3$ and more complicated GP (right) with ρ = 0.05.

I fit the data with the various parameterizations and sampling schemes using MCMC with a burn-in of 10,000 iterations and runs of 100,000 additional iterations. To assess mixing speed, I considered the trace plots, autocorrelations, and effective sample sizes (ESS) (Neal 1993, p. 105),

$$\mathrm{ESS}=\frac{T}{1+2\sum _{d=1}^{\infty }{\mathrm{Cor}}_d\left(\theta \right)},$$ (17)

where Cor_d(θ) is the autocorrelation at lag d for a given posterior quantity, θ, truncating the summation at the lesser of d = 10000 or the largest d such that Cor_d(θ) > 0.05. I focus on ESS for 1.) the overall log posterior density, π(·|y) (as suggested in Cowles and Carlin (1996) and calculated up to the normalizing constant), 2.) the critical smoothing parameter, ρ, and 3.) a random subset of 200 function estimates.

5.1. Variance component magnitudes and mixing speed

Here I discuss how the magnitude of a key variance component influences mixing.

The influence of the error variance in the normal model

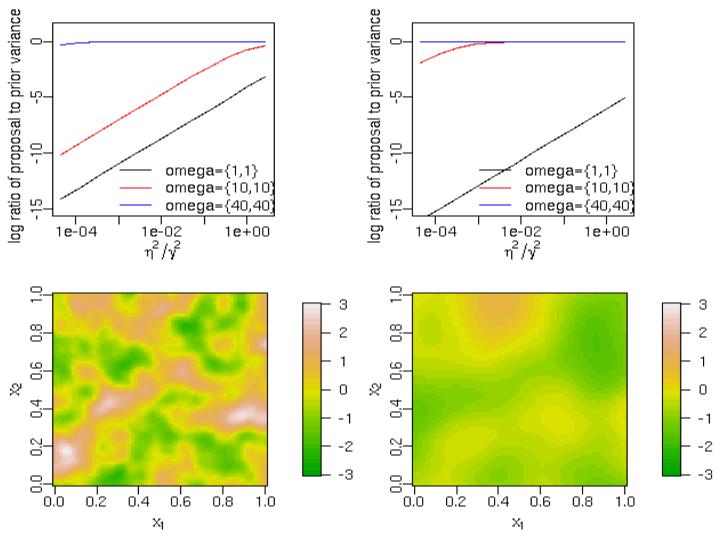
Under the normal model (8), as η² → 0, we have an interpolating surface that passes through the observations. In spatial statistics, such interpolation may arise relatively frequently when measurements are made with little measurement error or there is little fine-scale heterogeneity (Cressie 1993, p. 59). However, a key sampling consideration arising from small values of η² is that the size of MCMC moves for the basis coefficients is quite small. As η² → 0,

$$V(u_i\mid {\eta }^2,\cdot )={\left(\frac{{\gamma }^2}{{\eta }^2}+\sum _{\mathit{ii}}^{-1}\right)}^{-1}\to 0$$ (18)

for the Gibbs sample proposal variance (10). For the coefficients of low-frequency basis functions, which most influence the process estimate, as η² get small, the proposal variance is a small fraction of the magnitude of the coefficient (Figure 2). When η² ≈ 0, the process estimates are specified nearly exactly at the observation locations, and any proposal at those locations is constrained by the observations. This constrains the proposal for the entire spatial process. Mixing can be challenging even if uncertainty away from the observations is substantial and of real interest. While this issue seems likely to arise in other GP representations, except when the process values can be integrated out of the model, the issue is particularly clear with the spectral representation.

Figure 2.

Decay of proposal variances (scaled relative to prior variance) for three representative coefficients as a function of the relative error variance (η²/γ²) for (left column) GPs with ρ = 0.1 and (right column) GPs with ρ = 0.4. Example process realizations are shown in the lower row.

The influence of the dispersion parameter(s) in the exponential family model

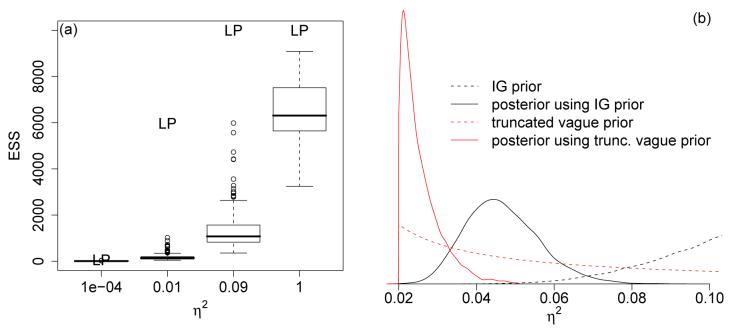
Under the single latent layer model of Section 4.2, the magnitude of the variance component, η², that accounts for overdispersion affects the proposal variances for the coefficients in similar fashion. When there is not overdispersion, the posterior for η² should concentrate near zero. While this might be the correct inference, if the value of η² does approach zero in the MCMC sampling, the chain will mix very slowly, as in the case of normal data, because in (15) V (u_i|η², ·) → 0 as η² → 0 as in (18). Small values of η² result in small proposal variances and slow movement of the coefficients. Figure 3a shows the ESS for the log posterior density and for a sample of function values as a function of fixed η² for Data3, Poisson data generated without overdispersion.

Figure 3.

(a) ESS for a sample of 200 function values (boxplots) and for the log posterior density (‘LP’) as a function of fixed η² for Data2. (b) Posterior densities for η² under an $\mathcal{IG}(0.5,2)$ prior and a lognormal prior truncated at 0.02 for Data3.

In the case of overdispersion, the data can inform η², and inverse gamma prior distributions such as those of Wikle (2002) and Royle and Wikle (2005) may suffice. When there is little overdispersion, these priors are more problematic. Note that the inverse gamma prior has a rapidly-decaying left tail, dropping off as exp(−1/x), so the inverse gamma prior assigns no mass to small values of η², preventing the posterior from having mass in this area. For example, the $\mathcal{IG}(0.5,2)$ prior has very little mass at values less than 0.05 while the $\mathcal{IG}(1,10)$ has very little mass at values less than 0.006. Fitting the model of Section 4.2 to Data2 with the $\mathcal{IG}(0.5,2)$ prior shows that the constraints imposed by the prior cause the posterior to have its mass in the extreme lower range of the prior, while using a truncated lognormal prior results in most of the posterior mass lying at very small values of η² near the truncation point (Figure 3b). This suggests that when the observations exhibit little overdispersion, the prior has substantial impact on the posterior for η².

A prior that weights the model away from small values of η² has the desirable impact of improving mixing at the cost of forcing overdispersion, while use of a prior that allows for small values of η² carries the risk of very slow mixing. This suggests that we might choose a prior or even fix η² in advance to achieve optimal mixing, treating η² as an MCMC tuning parameter. The danger of using large values of η² is that while mixing will improve, the posterior variances of key quantities such as the function estimates will increase, with overly conservative inference and poor predictive ability because of oversmoothing (Table 1). In contrast, for the smallest value of η², coverage is low and predictive ability is poor because of poor mixing. A compromise value of η² (say 0.3² in this case) trades off well between mixing and statistical performance.

Table 1.

For 200 function estimates, average 95% credible interval coverage and length, and test R² of posterior mean (indicating predictive ability), as a function of fixed η² for Data3.

η2	coverage	interval length	test R2
0.012	0.73	1.60	0.33
0.12	0.92	2.45	0.57
0.32	0.93	2.54	0.57
0.52	0.97	2.75	0.53
0.752	0.97	2.89	0.49
12	0.95	2.93	0.50
22	0.94	3.43	0.04

In general, to obtain reliable inference about overdispersion, one would want to initially allow sufficient freedom in one's prior for η² to allow small values of η². However, if the data appear to not be overdispersed and one wants to achieve reasonable mixing, one may want to run a version of the model with a fixed, larger value of η² and report inference for the other aspects of the model based on that MCMC. One can examine interval length as a function of η² in comparison with mixing properties to determine a good value of η². Cross-validation may be helpful for assessing coverage.

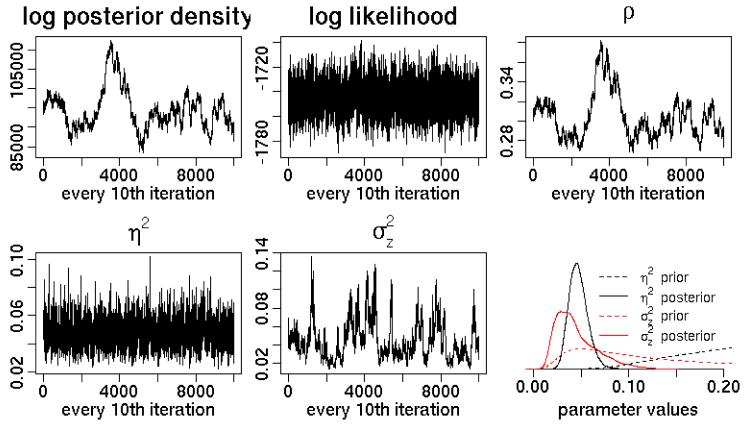
Turning to the model (12), there are two variance components, η² and ${\sigma }_z^2$. Interpretation of these parameters is difficult as the parameterization divides any inherent overdispersion into seemingly non-identifiable components. Royle and Wikle (2005) claim that both η² and ${\sigma }_z^2$ are identifiable with sufficient within-cell replication, with η² accounting for overdispersion within cell, while ${\sigma }_z^2$ represents uncorrelated variability across grid cells, inducing a lack of spatial smoothness beyond that induced by the discretization. Wikle (2002) and Royle and Wikle (2005) sample both components and find reasonable mixing, perhaps because their inverse gamma distributions prevent small values of the components and perhaps because their empirical count data have real overdispersion that provides information about a functional of the variance components $({\eta }^2+{\gamma }^2{\sigma }_z^2)$, while replication provides information about η². In contrast, I have had difficulty achieving reasonable mixing for the two variance components in simulations with no overdispersion $({\sigma }_z^2\equiv {\eta }^2\equiv 0)$ (Figure 4), presumably because of the lack of identifiability and lack of overdispersion. Note how the posteriors for the variance components concentrate on the smallest values allowed by the priors, while at the same time the likelihood mixes well, indicating that the process values, λ, are well-identified by the data and mix well.

Figure 4.

Trace plots for Wikle approach applied to Data2, with lower right subplot showing prior and posterior densities for η² and ${\sigma }_z^2$.

5.2. Joint sampling of hyperparameters and process

The covariance hyperparameters in GP models frequently mix poorly. For illustration, consider ρ. The difficulty in sampling ρ is that a simple Metropolis-Hastings proposal for ρ results in a new set of variances for the coefficients, u. Since these coefficients are not part of the proposal, proposing ρ* can easily produce a low prior density, π(u|ρ*, ·), because the new prior is inconsistent with the current u. For example, with a process generated based on ρ = 0.1, the prior logdensity, log π(u|ρ = 0.1, ·), is 50411 while the prior logdensity, π(u|ρ* = 0.101, ·), is 50387, a change of 24 in the logdensity, despite the fact that surfaces generated based on ρ = 0.1 compared to ρ = 0.101 are indistinguishable even with massive amounts of data, assuming non-negligible error variance. Note that the issue here is not a matter of whether we can sample from the full conditional for ρ; the primary obstacle in sampling ρ is the strong dependence of ρ and u (Rue, Steinsland, and Erland 2004). A better proposal would account for the strong dependence between ρ and u by proposing them jointly, allowing the lower levels of the model hierarchy close to the data to arbitrate between different values of ρ. In the context of Markov random field models, Rue and Held (2005, pp. 142-143) suggest a similar strategy of jointly sampling process values and their hyperparameters.

My strategy is to tie the covariance hyperparameters more closely to the coefficients and hence to the data by having the effects of proposing new hyperparameter values ripple down through the hierarchy of the model. I do this by jointly proposing a hyperparameter, generically denoted θ ∈ {ρ, σ²}, and, then conditional on that hyperparameter and within the same Metropolis-Hastings proposal, proposing the process coefficients from [u|θ*, ·]. This provides a joint proposal for (θ, u) that adjusts u in such a way that it is more consistent with the proposed value, θ*. Parameterizations that permit proposing from the full conditional, [u|θ, ·], are likely to particularly benefit from this approach, with u effectively integrated out of the joint density. Provided the correct Hastings adjustment (ratio of proposal densities) is made, this joint proposal is a standard, valid Metropolis-Hastings sampling scheme, implemented as a marginal proposal for θ and a conditional proposal for [u|θ, ·], with a single acceptance decision, as discussed in Rue and Held (2005, p. 142). I now detail these joint proposals in the three basic sampling schemes described in Section 4.

For the data augmentation sampling approach for normal data, one proposes θ*, and then proposes from the full conditional, [u|θ*, ·] (9). Acceptance is then determined based on the ratio of the proposed and current posterior densities, π(u, θ|y, ·) divided by the Hastings ratio for u (and θ as well if not proposed symmetrically). Note that the proposal for u is conditional on the proposed θ*, so a Metropolis-Hastings acceptance decision is needed because we are not doing a joint Gibbs sample for (u, θ). The Hastings ratio is based on the proposal mean (9) and variance (10), with the variances for complex-valued coefficients scaled by one-half (22) and not including the coefficients that are complex conjugates of sampled coefficients. This is calculated in the spectralGP package using the Hastings.coeff.gp() method or by providing returnHastings=TRUE as an argument to Gibbs.sample.coeff.gp(). Template code is provided in Appendix B as Code E.

In the modified Wikle approach, the presence of the latent λ̃ values (14) distances the coefficients from the data. However, one can mimic the proposal just described by sampling θ and then u from [u|λ, θ*, ·], conditioning on λ rather than y, and being satisfied with a proposal for u that is consistent with the new proposed θ* and the current λ, albeit without any direct influence of the data. Again a Hastings correction is needed, and can be calculated using the Hastings.coeff.gp() function, but with λ taking the place of y. Template code is given as Code F. For the original Wikle approach, z takes the place of λ above.

However, in neither the modified nor original Wikle parameterizations does the sampling directly link θ to the observations, causing there to be no influence of the likelihood on the acceptance. An alternative that carries the changes through to the level of the data is to avoid sampling from the conditionals as described above and instead propose to move u and λ (and z in the Wikle parameterization) in such a way that their prior densities remain constant.

First propose θ*. Then, deterministically propose,

$$u_i^{\ast }=u_i\cdot \frac{\sqrt{{\left({\Sigma }_{{\theta }^{\ast }}\right)}_{i,i}}}{\sqrt{{\left({\Sigma }_{\theta }\right)}_{i,i}}},i=1,\dots ,M.$$ (19)

Modifying u_i based on its prior variance, (Σ_θ)_i,i, allows the hyperparameters to mix more quickly by avoiding proposals for which the original coefficients are no longer probable based on their new prior variances. In the modified Wikle parameterization, one next proposes

$${\lambda }_i^{\ast }={\lambda }_i-\gamma {\left(\Psi \mathit{u}\right)}_i+\gamma {\left(\Psi {\mathit{u}}^{\ast }\right)}_i,$$ (20)

while in the Wikle parameterization, one proposes $z_i^{\ast }=z_i-{\left(\Psi \mathit{u}\right)}_i+{\left(\Psi {\mathit{u}}^{\ast }\right)}_i$ and finally ${\lambda }_i^{\ast }={\lambda }_i-\gamma {\mathit{K}}_i\mathit{z}+\gamma {\mathit{K}}_i{\mathit{z}}^{\ast }$. This approach propagates the changes through the model in a way that ties θ directly to the likelihood. Such deterministic proposals are valid MCMC proposals so long as the Jacobian of the transformation is included in the acceptance ratio, based on a modification of the argument in Green (1995). The Jacobian of the transformation for u cancels with the ratio of the prior distributions for u, π(u*|θ*)/π(u|θ), to give the final Metropolis-Hastings acceptance for the entire joint proposal of (θ*, u*, λ*) or (θ*, u*, z*, λ*) based only on the ratio of the proposed and current prior densities for θ, the proposed and current likelihoods, and any required Hastings ratio to account for non-symmetric proposals for θ. Note that the transformations for z and λ have Jacobian of one. The validity of the deterministic proposal can be seen intuitively by considering Metropolis proposals in place of the transformation (19) with very small proposal variances, ζ² ≈ 0, e.g., $u_i^{\ast }\sim \mathcal{N}(u_i{\left({\left({\Sigma }_{{\theta }^{\ast }}\right)}_{i,i}\right)}^{1∕2}{\left({\left({\Sigma }_{\theta }\right)}_{i,i}\right)}^{-1∕2},{\zeta }^2)$, and calculating the acceptance ratio of such a proposal. Template code for the modified Wikle parameterization is given in Appendix B as Code G. Note that a similar joint proposal could be made for $\theta ={\sigma }_z^2$ to tie this hyperparameter more closely to the data.

For the coefficient block sampling scheme, no Gibbs scheme is available. Instead, one can carry out a joint sample in a similar manner to that just described, by proposing θ* and then proposing u as in (19). Acceptance is determined by the ratio of the proposed and current prior densities for θ and proposed and current likelihoods, and any required Hastings ratio to account for non-symmetric proposals for θ. Template code is given in Appendix B as Code H.

In Table 2, I show a comparison of mixing for the modified Wikle parameterization (14) with 1.) straightforward sampling of γ and ρ, 2.) joint sampling of (σ², u) and of (ρ, u) based on Gibbs samples from [u|σ², ·] and [u|ρ, ·], and 3.) joint sampling via (19-20). Both joint sampling approaches appear to mix much more quickly than the simple Metropolis-Hastings proposals for the hyperparameters. The joint sampling with the full conditional sampling from [u|θ, ·] does not mix as well as using (19-20), perhaps because the conditional Gibbs sample does not modify λ and therefore does not involve the likelihood in the determination of proposal acceptance. Note that for η² ≡ 0.2², the improved mixing of the deterministic shift proposal compared to the conditional Gibbs is even more marked (not shown).

Table 2.

ESS for log posterior density, ρ and median (range) of 200 sample function values by dataset for three sampling approaches: 1.) sampling γ and ρ using simple Metropolis-Hastings, 2.) jointly sampling each of σ² and ρ with u based on conditional Gibbs sample for u, and 3.) jointly sampling each of σ² and ρ with u and λ as in (19-20). η² is fixed at 0.3². ’NM’ indicates that the chain has not burned in or is mixing so slowly as to make calculation of ESS uninformative.

		Sampling Method
Quantity	Dataset	simple: γ,ρ	joint, Gibbs: σ2,ρ	joint, deterministic: σ2,ρ
	Data1	NM	42	193
LP	Data2	NM	87	205
	Data3	NM	17	447
	Data5	NM	143	646
	Data1	NM	37	146
ρ	Data2	NM	70	145
	Data3	NM	15	414
	Data5	NM	125	289
	Data1	549 (28-1898)	510 (34-1338)	597 (90-1808)
f	Data2	1806 (22-3496)	1805 (132-3763)	2137 (229-4231)
	Data3	236 (5-2154)	611 (200-3062)	657 (307-3232)
	Data5	1563 (17-6503)	1964 (519-8958)	2021 (467-8971)

5.3. Empirical comparison of sampling methods and recommendations

Based on the evidence provided in Section 5.2, it appears that joint sampling of θ and u in the modified Wikle parameterization greatly improves mixing, with deterministic sampling of u better than full conditional sampling for u. In Appendix A.4 I also consider reparameterizing (σ², ρ) to reduce potential posterior correlation between these parameters, but find little improvement in mixing.

Here I compare mixing for the three parameterizations in Section 4: the modified Wikle approach with joint sampling of hyperparameters and coefficients, block sampling with joint sampling of hyperparameters and coefficients, and the original approach of Wikle without joint sampling. Since the latter is essentially the same as the modified Wikle approach with one extra layer, I do not devise a joint sampling scheme for it, but rather consider mixing under the sampling approach proposed by Wikle (2002) and Royle and Wikle (2005). In general, the modified Wikle approach outperforms block sampling and the original Wikle approach. Table 3 shows that for the simple function (Data1 and Data2), block sampling is worse than the modified Wikle approach but shows some degree of mixing, while for the more complicated function (Data3 and Data5), the block sampling approach does not appear to have burned in by 100,000 iterations. The original Wikle approach also has not burned in, as judged by the log posterior density and ρ although the sample function values appear to be mixing somewhat. Note that while the increase in sample size (from Data1 to Data2 and from Data3 to Data5) seems to result in somewhat improved mixing, the effect is not substantial.

Table 3.

ESS for log posterior density, ρ and median (range) of 200 sample function values by dataset for the three parameterizations: 1.) modified Wikle with η² fixed at 0.3², 2.) original Wikle parameterization and sampling approach, and 3.) block sampling.

		Sampling Method
Quantity	Dataset	modified Wikle	original Wikle	block sampling
	Data1	193	NM	54
LP	Data2	205	NM	25
	Data3	447	NM	53
	Data5	646	NM	NM
	Data1	146	NM	107
ρ	Data2	145	NM	40
	Data3	414	NM	NM
	Data5	289	22	NM
	Data1	597 (90-1808)	125 (13-321)	551 (247-1166)
f	Data2	2137 (229-4231)	56 (9-166)	473 (198-873)
	Data3	657 (307-3232)	298 (106-737)	33 (7-139)
	Data5	2021 (467-8971)	467 (127-1100)	25 (6-83)

A key question is how fine a resolution to use for the grid. While one does not want to oversmooth by virtue of using too coarse a resolution, finer resolution estimation takes longer to run and can exhibit slower mixing, because of the higher-dimensionality of the coefficients that are fit in the MCMC. My suggestion is to use a grid that is fine enough for reasonable prediction with the expected heterogeneity of the surface, but to make use of sensitivity analyses to choose the grid resolution in light of mixing performance and computational speed. For the simple simulated data with an effective value of ρ ≈ 0.3 (Data1 and Data2), a resolution of k = 128 is probably more than sufficient for good prediction (even coarser resolution might be sufficient), and runs with k = 256 and k = 512 showed slower mixing. For the simulated data with ρ = 0.05 (Data3, Data4, and Data5), k = 128 also seemed to be sufficient. Mixing with k = 256 was not substantially degraded relative to k = 128, but for k = 512, mixing was substantially worse.

These results suggest that mixing using the block sampling approach is substantially slower than the modified Wikle approach, particularly with a more variable underlying process. However, results may depend significantly on the form of the model and the exact data used. In Paciorek (2007), with a coarse grid, simple spatial functions, and binary observations, mixing was reasonable using the block sampling approach. In a multivariate setting within a complicated hierarchical model (Paciorek and McLachlan 2007), with a compound Dirichlet-multinomial likelihood for 10 categories and a coarse 32 by 32 grid, mixing was reasonable, albeit slow, with the block sampling approach, and the modified Wikle approach provided no improvement and was slower to compute.

6. Discussion

This paper introduces an R package for the Fourier basis representation of Gaussian processes, pioneered by Wikle (2002), and provides template code for fitting Bayesian models for exponential family data. The code can be readily adapted for more complicated hierarchical models. I discuss several possible parameterizations, including models allowing for overdispersion, and describe potential nonidentifiability in the hierarchical model of Wikle (2002) that may impact mixing. I document some of the critical issues affecting MCMC mixing in these models, in particular, the difficulty in mixing for ρ in particular and the dependence of mixing speed on the dispersion parameter, η². In models with little noise (interpolating models) or non-Gaussian situations with little overdispersion, a small value of η² can substantially impede mixing. Based on a series of experiments with simulated Poisson data, I recommend use of a modified version of the parameterization of Wikle (2002), with an approach for joint sampling of the hyperparameters and the basis coefficients to more efficiently sample the hyperparameters by tying them more closely to the data. In contrast, while the block sampling approach of Paciorek (2007) works only somewhat less well for a relatively smooth spatial function, it mixes very poorly for a very unsmooth spatial function. However, the block sampling approach has the virtue of avoiding the overdispersion parameter that, if small, can hurt mixing and of simplicity, which may be helpful in more complicated hierarchical models. I could not achieve reasonable mixing of the parameterization and sampling approach suggested in Wikle (2002), presumably because of dataset-dependent differences in mixing, but also possibly because of the difficulty in replicating Bayesian MCMC schemes. Note that these recommendations and conclusions are based on qualitative, rather than exhaustive, testing.

The critical smoothing parameters (ρ and either σ or γ) appear to be the parameters that mix most slowly in the Fourier basis representation, as they are in many spatial models. In particular, ρ changes the amount of smoothing, by changing the prior weights on the basis functions, which vary in their frequency. Changing this parameter changes the form of the model, analogous to adding or subtracting basis functions in a free-knot spline model. Achieving reasonable mixing across model spaces is generally difficult.

Some alternative spatial models, such as thin plate splines and radial basis function models with fixed basis functions (Kammann and Wand 2003; Ruppert et al. 2003) have modeled spatial functions without estimating a spatial correlation parameter, relying solely on variance components (in the radial basis model) to achieve smoothing. O'Connell and Wolfinger (1997) relate the ratio of σ² and η² in a Gaussian setting to the smoothing parameter in a thin plate spline model, and Nychka (2000) speculates that this ratio may be more important than the spatial correlation parameter in smoothing noisy data. Zhang (2004) found that ρ and σ² cannot both be estimated consistently under infill asymptotics. I experimented with fixing ρ and forcing σ² to perform the smoothing role, but found that the model did not estimate the right amount of smoothing and predictive performance was poor. It may be that in this and perhaps other spatial models, models with estimated values of ρ are more efficient. This issue appears not to have been addressed thoroughly in the literature (but see Laslett (1994) and invited comments) and deserves more attention.

One might explore more sophisticated MCMC algorithms to improve mixing. For example, Christensen et al. (2006) develop a data-dependent reparameterization scheme for improved MCMC performance and apply the approach with Langevin updates that use gradient information; while promising, the approach is computationally intensive, again involving n × n matrix computations at each iteration, and software is not available. For the Fourier representation the high-dimensionality and complex values of the basis coefficients pose an impediment to such an approach. Based on the results here, I believe that proposals that jointly consider the key hyperparameters and the basis coefficients are critical in achieving adequate mixing.

One drawback to the GP model presented here is its restriction to stationary GPs. Future work on this model structure to allow for nonstationarity in the spatial process will consider wavelet bases in place of the Fourier basis used here, in particular the two-dimensional wavelet basis used by Matsuo, Paul, and Nychka (2006) to fit irregular Gaussian data in a non-Bayesian fashion. However, mixing may be more challenging in a more complicated model with additional hyperparameters. An alternative relates to the work of Pintore and Holmes (2006), who have extended the Higdon/Paciorek/Stein (Higdon, Swall, and Kern 1999; Stein 2005; Paciorek and Schervish 2006) nonstationary covariance model based on kernel convolutions to the spectral domain. This allows one to build nonstationarity based on a latent process representing spatially-varying ρ or ν. Given the widespread interest in nonstationary and space-time representations, fast computation for such models is of obvious interest, but it is not clear how these covariance structures would be represented in the type of basis function approach developed here.

A. Technical details

A.1. Constructing the gridded process

The details that follow draw on Dudgeon and Mersereau (1984), Borgman, Taheri, and Hagan (1984), and Wikle (2002). The first step in representing the function is to choose the grid size, M_d, in each dimension, d = 1, … , D, to be a power of two. The M_d frequencies in the dth dimension are then ${\omega }^d\in \{0,1,\dots ,\frac{M_d}{2},-\frac{M_d}{2}+1,\dots ,-1\}$, where the superscript represents the dimension. There is a complex exponential basis function for each distinct vector of frequencies, $\omega =({\omega }_{m_1}^1,\dots ,{\omega }_{m_D}^D),m_d\in \{0,\dots ,M_d-1\}$, with corresponding complex-valued basis coefficient, u_m1,…,mD.

First I show how to construct a random, mean zero, Gaussian process in one dimension from the M spectral coefficients, u_m = a_m + b_mi, m = 0, … , M − 1, and complex exponential basis functions, ψ_m(s_j) = exp(iω_ms_j), whose real and imaginary components have frequency ω_m. The circular domain of the process is S¹ = (0, 2π) with the process evaluated only at the discrete grid points, $s_j\in \{0,2\pi \frac{1}{M},\dots ,2\pi \frac{M-1}{M}\}$. To approximate real-valued processes, u₀, … , u_M/2 are jointly independent, u₀ and u_M/2 are real-valued (b₀ = b_M/2 = 0), and the remaining coefficients are determined, u_M/2+1 = ū_M/2−1, … , u_M−1 = ū₁, where the overbar is the complex conjugate operation. This determinism causes the imaginary components of the basis functions to cancel, leaving a real-valued process,

$$\begin{array}{cc}\hfill g\left(s_j\right)& =\sum _{m=0}^{M-1}{\psi }_m\left(s_j\right)u_m=\sum _{m=0}^{\frac{M}{2}}\exp \left(i{\omega }_m{s}_j\right)(a_m+b_{m}i)+\sum _{m=\frac{M}{2}+1}^{M-1}\exp \left(i{\omega }_m{s}_j\right)(a_{M-m}-b_{M-m}i)\hfill \\ \hfill & =a_0+2\sum _{m=1}^{\frac{M}{2}-1}(a_m\cos \left({\omega }_m{s}_j\right)-b_m\sin \left({\omega }_m{s}_j\right))+a_{M∕2}\cos \left({\omega }_{\frac{M}{2}}{s}_j\right).\hfill \end{array}$$ (21)

Hence for a grid of M values, the process is approximated as a linear combination of M spectral basis functions corresponding to M real-valued sinusoidal basis functions, including the constant function (ω₀ = 0). To approximate mean zero Gaussian processes with a particular stationary covariance function, the coefficients have independent, mean zero Gaussian prior distributions with the spectral density for the covariance function, ϕ(·;θ), e.g., (5), determining the prior variances of the coefficients:

$$\begin{array}{cc}\hfill \mathrm{V}\left(u_m\right)=& \varphi ({\omega }_m;\theta )\hfill \\ \hfill \Rightarrow & \{\mathrm{V}\left(a_0\right)=\varphi ({\omega }_0;\theta );\mathrm{V}\left(a_{M∕2}\right)=\varphi ({\omega }_{M∕2};\theta );\hfill \\ \hfill & \mathrm{V}\left(a_m\right)=\mathrm{V}\left(b_m\right)=\frac{1}{2}\varphi ({\omega }_m;\theta ),o.w.\}\hfill \end{array}$$ (22)

.

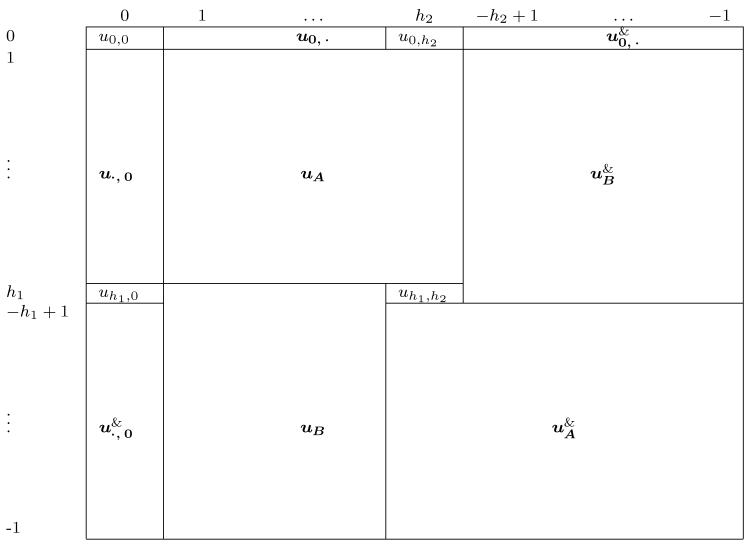
The setup is similar in two dimensions, with a matrix of M = M₁M₂ coefficients, ((u_m1,m2)), m_d ∈ {0, … , M_d − 1}, and corresponding frequency pairs, $({\omega }_{m_1}^1,{\omega }_{m_2}^2)$, and a toroidal domain. As seen in Table 4, many coefficients are again deterministically given by other coefficients to ensure that the process is a linear combination of real-valued sinusoidal basis functions of varying frequencies and orientations in ℜ². The real and imaginary components of each coefficient, u_m1,m2 = a_m1,m2 + b_m1,m2i, are again independent. For $(m_1,m_2)\in \{(0,0),(\frac{M_1}{2},0),(0,\frac{M_2}{2}),(\frac{M_1}{2},\frac{M_2}{2})\},b_{m_1,m_2}=0$ and $\mathrm{V}\left(a_{m_1,m_2}\right)=\varphi ({\omega }_{m_1}^1,{\omega }_{m_2}^2;\theta )$, while for the remaining complex-valued coefficients, $\mathrm{V}\left(a_{m_1,m_2}\right)=\mathrm{V}\left(b_{m_1,m_2}\right)=\frac{1}{2}\varphi ({\omega }_{m_1}^1,{\omega }_{m_2}^2;\theta )$.

Table 4.

Visual display of the spectral coefficients for a two-dimensional process. The frequencies in each dimension are indicated by the row and column labels, with $h_d=\frac{M_d}{2}$ for d = 1, 2. The & operation indicates that one takes the matrix or vector, flips it in both the horizontal and vertical directions (just the horizontal or vertical in the case of a vector) and then takes the complex conjugates of the elements.

A.2. Periodicity and Euclidean domains

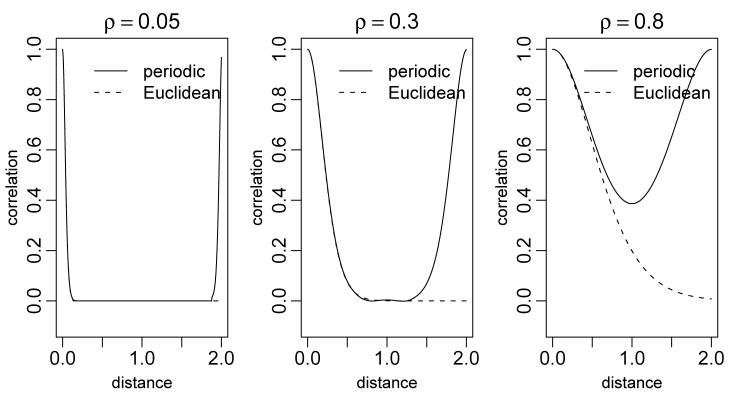
The construction produces periodic functions; in one dimension the process lives on a circular domain, while in two dimensions the process lives on a torus. To work in Euclidean space, we need to map Euclidean space onto the periodic domain. The goal is to use the representation for Euclidean domains without inducing anomalous correlations between locations that are far apart in Euclidean space, but close in the periodic domain. To do this, I suggest mapping the Euclidean domain of interest onto a portion of the periodic domain and ignoring the remainder of the periodic domain as follows.

In one dimension, g(0) = g(2π), so the correlation function, C(τ) = C(g(0), g(τ)) of the process at distances τ ∈ (π, 2π) is the mirror image of the correlation function for τ ∈ (π, 0) with Cor(g(0), g(2π)) = 1 (Figure 5). I avoid artifacts from this periodicity by mapping the interval (0, 2π) to (0, 2) and mapping the original domain of the observations to (0, 1), thereby computing but not using the process values on (1, 2). Note that the use of πρ rather than ρ in (5) allows us to interpret ρ on the (0, 1) rather than (0, π) scale. The modelled process on (0, 1) is a piecewise constant function on an equally-spaced grid of size M/2 + 1. This setup ensures that the correlation structure of the approximating process is close to the correlation structure of a GP with the desired stationary correlation function (Figure 5).

Figure 5.

Comparison of correlation structure of GPs based on the standard Matérn covariance on the Euclidean domain, (0, 2) (dashed lines), and approximate GPs based on the Fourier basis for the periodic domain, (0, 2π), mapped to (0, 2) (solid lines), for three values of ρ. Note that the Euclidean correlation for ρ = 0.05 falls off to zero as rapidly as the periodic case and remains at zero for all remaining distances.

As the higher-dimension analogue of the one-dimensional case, I estimate the process on (0, 1)^D. To do so, I map the periodic domain (0, 2π)^D to (0, 2)^D and then map the observation domain onto the (0, 1)^D portion (maintaining the scale ratio in the different dimensions, unless desired otherwise), thereby calculating but ignoring the process values outside this region. Note that if the original domain is far from square, I unnecessarily estimate the process in large areas of no interest, resulting in some loss of computational efficiency. Wikle (2002) and Royle and Wikle (2005) do not mention the issue of periodicity; it appears that they use a somewhat larger grid than necessary to include all observations (sometimes called padding) and rely on the correlation decaying sufficiently fast that anomalously high correlations between distant observations induced by the periodicity do not occur. For example, notice in Figure 5 that for ρ = 0.05 the correlation does not start to rise again until the distance is almost 2.0, so a small amount of padding would suffice).

A.3. Non-identifiability of u_0,0 and μ

The Fourier basis function corresponding to the coefficient, u_0,0, is a constant function. As such, it is not identifiable with respect to an overall mean parameter, μ, specified outside of the Fourier basis representation of the Gaussian process (12,14,16). One might choose to omit μ from the model, but this would generally be a mistake as the covariance structure (22) imposes a restrictive prior on u_0,0. A large value of γ or σ would allow for a process mean far from zero, but this would also allow the function to have high variability. An example of where the problem arises is a process with large mean, say 100, but whose variability places the function entirely in (99, 101). Such a process would require a large value of u_0,0 but if γ or σ is large enough to allow this, each would be so large as favor process estimates that vary widely around 100. Instead, a separate mean parameter is a better choice that will help to avoid slow mixing because of nonidentifiability. One can fix u_0,0 = 0, without otherwise constraining the model. The spectralGP package can fix the coefficient and ignore it when calculating the prior density of the coefficients; this is done using const.fixed=TRUE as an argument to gp(). However, simulate GP realizations using the Fourier basis approximation, one should not fix this constant, in order to retain the desired approximate covariance structure.

A.4. Reparameterizing the covariance

In a GP model part of the difficulty in estimating the covariance parameters occurs because of limitations on identifiability. The data cannot readily distinguish the overall variability in the function, captured by γ or σ, from the decay in the spatial correlation, captured by ρ. In Bayesian models, these parameters tend to have high posterior correlation, while Zhang (2004) has shown that these two parameters cannot both be estimated consistently under infill asymptotics, but that a functional of the two can be estimated consistently. Note that in thin plate spline models and in the mixed model representation suggested by Kammann and Wand (2003) and Ruppert et al. (2003), there is only one parameter in place of the two covariance parameters here. However, as discussed further in Section 6, comparisons of estimates using the Fourier basis approach here suggest that ρ cannot be fixed in advance without seriously affecting the function estimates because the function heterogeneity is not adequately represented.

Given the results of Zhang (2004), in which the ratio, σ²/ρ^2ν, can be estimated consistently, consider reparameterizing on the log scale as ψ₁ = log σ + log ρ and ψ₂ = log σ − log ρ. This approach uses the centered parameterization, fixing γ ≡ 1. The reparameterization will tend to reduce posterior correlation and allow each parameter to move more freely. Joint sampling as described in Section 5.2 can also be employed with this reparameterization. Template code for sampling based on the reparameterization and joint sampling of the parameters and process values using deterministic conditional proposals for u (19-20) is given in Appendix B as Code I under the modified Wikle parameterization and code J under the block sampling approach.

Since the joint sampling of each of σ² and ρ with u based on deterministic proposals for u and λ appeared to be the best of the options in Section 5.2, in Table 5, I compare mixing for that approach with the (σ², ρ) parameterization and the same joint approach using deterministic proposals with the (ψ₁, ψ₂) parameterization. There is little difference in mixing between the two parameterizations. Table 6 shows posterior correlations of (σ, ρ) and of (ψ₁, ψ₂) based on sampling under the original and the new parameterizations. For Data1, Data2, and Data3, ψ₁ and ψ₂ have little posterior correlation, suggesting that in principle, sampling using the new parameterization would mix more quickly, although this is not the case in Table 5. The minimal difference in mixing was also seen when using the joint sampling with the full conditional samples from [u|θ, ·] and when fixing η² = 0.2² and η² = 0.5², as well as for an alternative reparameterization, ψ₁ = log σ and ψ₂ = log σ − log ρ. In practice, the minimal difference in mixing suggests that the posterior correlation between σ² and ρ is not materially hurting mixing, in sharp contrast to the importance of jointly sampling each covariance hyperparameter with u.

Table 5.

ESS for log posterior density, ρ, and median (range) of 200 sample function values by dataset when sampling is done using the parameterizations: 1.) (ρ,σ²) and 2.) (ψ₁, ψ₂). η² is fixed at 0.3².

		Parameterization
Quantity	Dataset	original: σ2, ρ	Zhang: ψ1, ψ2
	Data1	193	105
LP	Data2	205	244
	Data3	447	443
	Data5	646	777
	Data1	146	56
ρ	Data2	145	157
	Data3	414	431
	Data5	289	426
	Data1	597 (90-1808)	591 (89-1427)
f	Data2	2137 (229-4231)	2154 (235-4274)
	Data3	657 (307-3232)	656 (305-3169)
	Data5	2021 (467-8971)	1972 (469-8879)

Table 6.

Posterior correlations for (log σ, log ρ) and (ψ₁, ψ₂) when sampling is done using the parameterizations: 1.) (σ², ρ) and 2.) (ψ₁, ψ₂). η² is fixed at 0.3².

		Parameterization
Dataset	Posterior correlation	original: σ2, ρ	Zhang: ψ1, ψ2
Data1	Cor(log σ, log ρ)	0.70	0.79
	Cor(ψ1, ψ2)	0.15	0.24
Data2	Cor(log σ, log ρ)	0.81	0.84
	Cor(ψ1, ψ2)	0.08	0.13
Data4	Cor(log σ, log ρ)	0.20	0.21
	Cor(ψ1, ψ2)	0.26	0.26
Data5	Cor(log σ, log ρ)	0.56	0.56
	Cor(ψ1, ψ2)	0.11	0.12

A.5. Starting values

Good starting values for the coefficients can be difficult to determine because of the high dimensionality of the coefficients and lack of a maximum likelihood-based estimate due to the need for shrinkage in estimating the coefficients. In addition, as described in Section A.2, a portion of the domain contains no observations. For the grid points not used to represent the domain of interest (((0, 1)²)^C ∩ (1,2)²), it is helpful to initiate values for these buffering grid points so as to keep the variability and spatial range features of the data similar across the whole domain. This can be achieved by ‘mirroring’ the initial values from the portion of the domain in which the observations lie, as follows, in one dimension,

$$\widehat{g}\left(s_M\right),\dots ,\widehat{g}\left(s_{M∕2+2}\right)\equiv \widehat{g}\left(s_{M∕2}\right),\dots ,\widehat{g}\left(s_2\right).$$ (23)

In two dimensions, the mirroring occurs first across the the line s₁ = 1 (for s₂ < 1) and then across the line s₂ = 1, such that ĝ(s_m1,m2) is defined, for m₁ > M₁/2+1 and m₂ <= M₂/2+1 as ĝ(s_m1,m2) ≡ ĝ(s_M1−m1+2,m2 ). For m₂ > M₂/2 + 1, take ĝ(s_m1,m2) ≡ ĝ(s_m1,M2−m2+2).

In the data augmentation scheme for normal data, I suggest using a gam() fit to estimate the process values, predicting Ỹ values at unobserved locations using the fitted model, mirroring the values, and then doing a Gibbs sample for the coefficients. In the Wikle approach, one can estimate the spatial process at the grid points based on a gam() fit, assign these values to z (λ in the modified Wikle approach) and initialize u via a Gibbs sample. For the block sampling scheme, one might use gam() to estimate the process on the grid, ĝ_s^#, add error and mirror the values, and then set $\mathit{u}={(\frac{{\gamma }^2}{{\eta }^2}\mathit{I}+{\Sigma }^{-1})}^{-1}\frac{\gamma }{{\eta }^2}{\Psi }^{\top }({\widehat{\mathit{g}}}_{{\mathit{s}}^{\#}}-\mu 1)$, mimicing (15).

Some basic experiments with simulated datasets Data1, Data2, Data3, and Data5 suggest little difference between starting the coefficients based on a Gibbs sample and starting at values simulated from the prior conditional on the hyperparameter starting values. Reasonably rapid burn-in occurred when the coefficients were simulated from their prior, although mixing for Data1 was slightly better for the Gibbs sample starting values. For the coefficients corresponding to low frequencies, the long-run estimates are comparable for the different starting values. However, it may be the case that the Gibbs sample starting values are useful in some circumstances.

B. Template code

I provide R template code for MCMC sampling under various parameterizations and sampling schemes described in Sections 4 and 5. The code is designed for the simple model (1) in which the data come from an exponential family distribution: normal, Poisson, or binomial. The code assumes a constant mean, μ, in place of ${\mathit{x}}_i^{\top }\beta$, and Matérn covariance function with ν fixed. While this is a simple setting, users could take the template code and use it within a more complicated hiearchical model or easily extend to a regression structure in the mean. The contribution of this work is to provide code for easy manipulation and MCMC sampling of the Fourier basis representation of the Gaussian process component in the model.

The code makes use of the spectralGP package and uses easily modifiable R functions for the log-likelihood, prior distributions, and Gibbs sampling; the names of these will be obvious in the code. Also note that parameters take the form of R lists, with components that will be obvious from the code. The code does not save iterations, report acceptance rates, or adapt the proposal variances based on acceptance rates, but these features could be readily added. The code assumes the default Matérn spectral density function but the only changes needed to use a different covariance function are to define a new spectral density function, use that function as the argument to the constructor gp(), and define an appropriate prior density for the parameter(s) of the covariance function. If the covariance/spectral density function has a second parameter, the code would need to be modified to allow for MCMC sampling of that parameter; the code currently takes the second parameter, ν, of the Matérn to be fixed.

Next I provide a brief overview of the model structure and sampling approach used in each template code file. The information is summarized in Table 7.

Table 7.

Overview of model structure and covariance parameter sampling algorithms for template code.

Data distribution	Latent structure	Sampling of cov. parameters	Template code
Normal	data augmentation	individually: θ ∊ {σ2,ρ}	A
		joint: {θ,u}, θ ∊ {σ2,ρ}	E
Poisson/binomial	two processes	individually: θ ∊ {σ2,ρ}	B
		individually: θ ∊ {σ2,ρ}	C
Poisson/binomial	one process	joint: {θ,u}, θ ∊ {σ2,ρ}	F
		joint: {θ,u,λ}, θ ∊ {σ2,ρ}	G
		joint: {θ,u,λ}, θ ∊ {ψ1, ψ2}	I
		individually: θ ∊ {σ2,ρ}	D
Poisson/binomial	no process	joint: {θ,u}, θ ∊ {σ2,ρ}	H
		joint: {θ,u}, θ ∊ {ψ1, ψ2}	J

Code A (Section 4.1) In this template, data, Y, are assumed to be normally distributed and are augmented with pseudo-observations, Ỹ,

$$\begin{array}{cc}\hfill \mathit{Y}& \sim {\mathcal{N}}_n(\mu 1+\gamma \mathit{K}\Psi \mathit{u},{\eta }^2\mathit{I})\hfill \\ \hfill \stackrel{\sim }{\mathit{Y}}& \sim {\mathcal{N}}_{M-n}(\mu 1+\gamma \stackrel{\sim }{\mathit{K}}\Psi \mathit{u},{\eta }^2\mathit{I}),\hfill \end{array}$$

which allows Gibbs sampling of the process coefficients, u. The pseudo-observations are also sampled via a Gibbs step. Covariance hyperparameters are sampled individually by Metropolis-Hastings. To speed mixing in some cases, joint sampling of η² and Ỹ is also possible.

Code B (Section 4.2) In this template, data, Y, are taken to be Poisson or binomial, and two latent processes are embedded in the model,

$$\begin{array}{cc}\hfill Y_i& \sim \mathcal{F}\left(h^{-1}\left({\lambda }_i\right)\right)\hfill \\ \hfill {\lambda }_i& \sim \mathcal{N}(\mu +\gamma {\mathit{K}}_{\mathit{i}}\mathit{z},{\eta }^2)\hfill \\ \hfill \mathit{z}& \sim {\mathcal{N}}_M(\Psi \mathit{u},{\sigma }_z^2\mathit{I}).\hfill \end{array}$$

Here λ is sampled via Metropolis-Hastings, and z and u are sampled via Gibbs steps. Covariance hyperparameters are sampled individually by Metropolis-Hastings. There are two overdispersion parameters, η² and ${\sigma }_z^2$, in this model.

Code C (Section 4.2) In this template, data, Y, are taken to be Poisson or binomial, and one latent processes is embedded in the model,

$$\begin{array}{cc}\hfill Y_i& \sim \mathcal{F}\left(h^{-1}\left({\mathit{K}}_{\mathit{i}}\lambda \right)\right)\hfill \\ \hfill \lambda & \sim {\mathcal{N}}_M(\mu 1+\gamma \Psi \mathit{u},{\eta }^2\mathit{I}).\hfill \end{array}$$

I divide the latent process values into a group whose grid cells contain data, λ_obs, which are sampled via Metropolis-Hastings, and the remaining values, λ̃, which are sampled via a Gibbs step. To speed mixing in some cases, joint sampling of η² and λ̃ is also possible. Covariance hyperparameters are sampled individually by Metropolis-Hastings. There is one overdispersion parameter, η², in this model.

Code D (Section 4.3) In this template, data, Y, are taken to be Poisson or binomial, and the likelihood depends directly on the process coefficients,

$$Y_i\sim \mathcal{F}\left(h^{-1}(\mu +\gamma {\mathit{K}}_{\mathit{i}}\Psi \mathit{u})\right).$$

The coefficients, u, are sampled by Metropolis-Hastings in blocks. Covariance hyperparameters are sampled individually by Metropolis-Hastings. The model contains no overdispersion parameter.

Code E (Section 5.2) As in Code A, data, Y, are assumed to be normally distributed and are augmented with pseudo-observations, Ỹ,

$$\begin{array}{cc}\hfill \mathit{Y}& \sim {\mathcal{N}}_n(\mu 1+\mathit{K}\Psi \mathit{u},{\eta }^2\mathit{I})\hfill \\ \hfill \stackrel{\sim }{\mathit{Y}}& \sim {\mathcal{N}}_{M-n}(\mu 1+\stackrel{\sim }{\mathit{K}}\Psi \mathit{u},{\eta }^2\mathit{I}),\hfill \end{array}$$

with the modification that γ ≡ 1 and σ² in (5) is allowed to vary. The process coefficients, u, and pseudo-observations are both sampled via Gibbs steps. In contrast to Code A in which covariance hyperparameters are sampled by Metropolis-Hastings on their own, in this code, each covariance hyperparameter, σ² and ρ, is sampled jointly with u in a Metropolis-Hastings step.

Code F (Section 5.2) As in Code C, data, Y, are taken to be Poisson or binomial, and one latent process is embedded in the model,

$$\begin{array}{cc}\hfill Y_i& \sim \mathcal{F}\left(h^{-1}\left({\mathit{K}}_{\mathit{i}}\lambda \right)\right)\hfill \\ \hfill \lambda & \sim {\mathcal{N}}_M(\mu 1+\gamma \Psi \mathit{u},{\eta }^2\mathit{I}).\hfill \end{array}$$

As in Code C, I divide the latent process values into a group whose grid cells contain data, λ_obs, which are sampled via Metropolis-Hastings, and the remaining values, λ̃, which are sampled via a Gibbs step. In contrast to Code C in which covariance hyperparameters are sampled by Metropolis-Hastings on their own, in this code, each covariance hyperparameter, σ² and ρ, is sampled jointly with u in a Metropolis-Hastings step. There is one overdispersion parameter, η², in this model.

Code G (Section 5.2) As in Code F, data, Y, are taken to be Poisson or binomial, and one latent process is embedded in the model,

$$\begin{array}{cc}\hfill Y_i& \sim \mathcal{F}\left(h^{-1}\left({\mathit{K}}_{\mathit{i}}\lambda \right)\right)\hfill \\ \hfill \lambda & \sim {\mathcal{N}}_M(\mu 1+\gamma \Psi \mathit{u},{\eta }^2\mathit{I}).\hfill \end{array}$$

The one difference from Code F is that here, each covariance hyperparameter, σ² and ρ, is sampled jointly with both u and λ in a Metropolis-Hastings step.

Code H (Section 5.2) As in Code D, data, Y , are taken to be Poisson or binomial, and the likelihood depends directly on the process coefficients,

$$Y_i\sim \mathcal{F}\left(h^{-1}(\mu +\gamma {\mathit{K}}_{\mathit{i}}\Psi \mathit{u})\right).$$

The coefficients, u, are sampled by Metropolis-Hastings in blocks. I divide the latent process values into a group whose grid cells contain data, λ_obs, which are sampled via Metropolis-Hastings, and the remaining values, λ̃, which are sampled via a Gibbs step. In contrast to Code D in which covariance hyperparameters are sampled by Metropolis-Hastings on their own, in this code, each covariance hyperparameter, σ² and ρ, is sampled jointly with u in a Metropolis-Hastings step. The model contains no overdispersion parameter.

Code I (Appendix A.4) As in Code G, data, Y , are taken to be Poisson or binomial, and one latent process is embedded in the model,

$$\begin{array}{cc}\hfill Y_i& \sim \mathcal{F}\left(h^{-1}\left({\mathit{K}}_{\mathit{i}}\lambda \right)\right)\hfill \\ \hfill \lambda & \sim {\mathcal{N}}_M(\mu 1+\gamma \Psi \mathit{u},{\eta }^2\mathit{I}).\hfill \end{array}$$

The one difference from Code G is that here, the covariance parameters are reparameterized as ψ₁ = log σ + log ρ and ψ₂ = log σ − log ρ. Each of ψ₁ and ψ₂ is sampled jointly with u and λ in a Metropolis-Hastings step.

Code J (Appendix A.4) As in Code H, data, Y , are taken to be Poisson or binomial, and the likelihood depends directly on the process coefficients,

$$Y_i\sim \mathcal{F}\left(h^{-1}(\mu +\gamma {\mathit{K}}_{\mathit{i}}\Psi \mathit{u})\right).$$

The one difference from Code H is that here, the covariance parameters are reparameterized as ψ₁ = log σ + log ρ and ψ₂ = log σ − log ρ. Each of ψ₁ and ψ₂ is sampled jointly with u in a Metropolis-Hastings step.