Abstract
Cellular networks are composed of complicated interconnections among components, and some subnetworks of particular functioning are often identified as network motifs. Among such network motifs, feedback loops are thought to play important dynamical roles. Intriguingly, such feedback loops are very often found as a coupled structure in cellular circuits. Therefore, we integrated all the scattered information regarding the coupled feedbacks in various cellular circuits and investigated the dynamical role of each coupled structure. Finally, we discovered that coupled positive feedbacks enhance signal amplification and bistable characteristics; coupled negative feedbacks realize enhanced homeostasis; coupled positive and negative feedbacks enable reliable decision-making by properly modulating signal responses and effectively dealing with noise.
INTRODUCTION
Complex cellular behaviors can be seen as a result of interactions between numerous intracellular or extracellular biomolecules. To figure out cellular behaviors, it is therefore important to investigate the topology of cellular circuits and corresponding dynamical characteristics. As a means of conducting such investigations, network motifs (1) have been proposed and studied in various cellular circuits. For instance, feedback loops (Fig. 1) (2–5) and signaling cascades (6,7) in signaling networks and feedforward loops in gene transcriptional networks (1,8) have been studied. Among those, feedback loops have been identified as playing an important role (9,10) in maintaining cellular homeostasis, producing sustained oscillations (11), and making critical decisions such as cell fate (12,13) and cell development decisions (14).
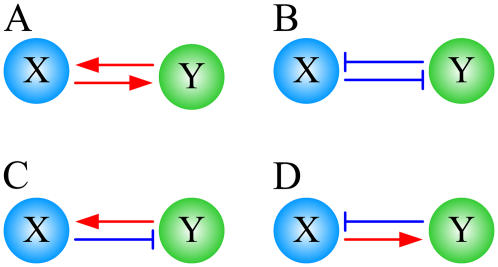
FIGURE 1.
Single feedback loops with two nodes. (A and B) Positive feedback loops. (C and D) Negative feedback loops.
Interestingly, such feedback loops are often found as a coupled structure rather than a single isolated form in various cellular circuits (see Tables 1–3 for summary). There have been some studies on the coupled feedback loops for particular cases (5,15–17), but no unified investigation has been reported. The question is what the advantages are of such coupled feedback loops, since they must have evolved to achieve specific regulatory functions in cellular circuits. To answer this question, we first explore the dynamic characteristics of single feedback loops and then study all possible combinations of such single feedback loops. We can classify the coupled structures of feedback loops into three basic modules: PP (a positive feedback loop + a positive feedback loop) (Fig. 2 A and Table 1), PN (a positive feedback loop + a negative feedback loop) (Fig. 2 B and Table 2), and NN (a negative feedback loop + a negative feedback loop) (Fig. 2 C and Table 3). We can consider any coupled feedback circuit as a combination of these basic modules. For simplicity, we consider the coupled feedback loops that share only one node, but the results can be extended to any topology without loss of generality. Through extensive computer simulations and integrative analysis of all scattered previous experimental results, we discovered that the coupled feedback loops have their own roles, which single feedback loops cannot perform. In particular, we found that PP enhances signal amplification and bistability, NN realizes enhanced homeostasis, and PN guarantees reliable decision-making by properly modulating signal responses and effectively dealing with noise.
TABLE 1.
Sample circuits of PP
| Related network | Coupled feedback loops | Related network | Coupled feedback loops |
|---|---|---|---|
| Ca2+ spikes/oscillations (29) | 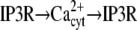 |
Mitotic trigger in Xenopus (21,30) | Weel ⊣ cdc2 ⊣ weel |
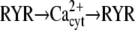 |
Cdc25 → cdc2 → Cdc25 | ||
| Muscle cell fate specification (12) | CDO → MyoD → CDO | Mitotic trigger in Xenopus (21,30) | Myt1 ⊣ cdc2 ⊣ Myt1 |
| Akt2 →MyoD → Akt2 | Cdc25 → cdc2 → Cdc25 | ||
| Muscle cell fate specification (12) | CDO → MyoD → CDO | Start of cell cycle in budding yeast (27,31) | Sic1 ⊣ cdc28 ⊣ Sic1 |
| Myostain → MyoD → Myostain | Cln → cdc28 → Cln | ||
| Galactose-signaling network in yeast (22) | Gal3 → Gal4 →Gal3 | B. subtilis competence event (32) | RoK ⊣ ComK ⊣ RoK |
| Gal2 → Gal4 → Gal2 | ComK → ComK | ||
| Kallikrein-kinin system (28) | PLAT → PLG → PLAT | Th1 and Th2 differentiation (14) | STAT6 → GATA3 → STAT6 |
| F12 → PLG → F12 | STAT4 ⊣ GATA3 ⊣ STAT4 |
TABLE 2.
Sample circuits of PN
| Related network | Coupled feedback loops | Related network | Coupled feedback loops |
|---|---|---|---|
| Mitotic trigger in Xenopus (21,30) | APC ⊣ Cdc2 → APC | Galactose-signaling network in yeast (22) | Gal80 ⊣ Gal4 → Gal80 |
| Cdc25 → Cdc2 → Cdc25 | Gal3 → Gal4 →Gal3 | ||
| Ca2+ spikes/oscillations (29) | 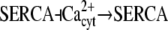 |
Receptor Signals by β-arrestins (33) | c-Src ⊣ GRK → c-Src |
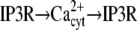 |
G → GRK → G | ||
| Ca2+ spikes/oscillations (29) | 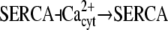 |
B. subtilis competence event (32) | ComS → ComK ⊣ ComS |
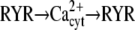 |
ComK → ComK | ||
| Circadian oscillation in Drosophila (11) | Per/Tim ⊣ Clk/Cyc → Per/Tim | Mitotic trigger in Xenopus (21,30) | APC ⊣ Cdc2 → APC |
| PDP1 → Clk/Cyc → PDP1 | Weel ⊣ Cdc2 ⊣ Weel | ||
| Circadian oscillation in Drosophila (11) | Vri ⊣ Clk/Cyc → Vri | Mitotic trigger in Xenopus (21,30) | APC ⊣ Cdc2 → APC |
| PDP1 → Clk/Cyc → PDP1 | Myt1 ⊣ Cdc2 ⊣ Myt1 | ||
| Circadian oscillation in Mammalia (11) | Per/Cry ⊣ Clock/Bmal1 → Per/Cry | Circadian oscillation in Mammalia (11) | Rev-erbα ⊣ Clock/Bmal1 → Rev-erbα |
| Rorα → Clock/Bmal1 → Rorα | Rorα → Clock/Bmal1 → Rorα |
TABLE 3.
Sample circuits of NN
| Related network | Coupled feedback loops |
|---|---|
| Circadian oscillation in Drosophila (11) | Per/Tim ⊣ Clk/Cyc → Per/Tim |
| Vri ⊣ Clk/Cyc → Vri | |
| Circadian oscillation in Mammalia (11) | Per/Tim ⊣ Clk/Cyc → Per/Tim |
| Vri ⊣ Clk/Cyc → Vri | |
| TSH-cAMP signaling pathway in thyrocytes (34) | RGS2 ⊣ AC → RGS2 |
| GRK ⊣AC → GRK | |
| Chemotactic signaling in Ameba (35) | ERK2 → PKA ⊣ ERK2 |
| ACA→ PKA ⊣ ACA | |
| Plant circadian clock (36) | TOC1 → CCA1/LHY ⊣ TOC1 |
| CCA1/LHY ⊣ CCA1/LHY | |
| p53 network (13) | p38MAPK → p53 ⊣ p38MAPK |
| Mdm2 ⊣ p53 → Mdm2 |
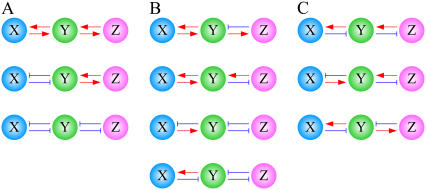
FIGURE 2.
Network motifs of coupled feedback loops. (A) PP structures. (B) PN structures. (C) NN structures.
METHODS
The dynamics of cellular circuits are in general quite complicated due to the nonlinear interactions among the components. Therefore, we focus only on the functional regulatory relationship between two components and develop a mathematical model that can represent such relationships irrespective of particular parameter values. Let us consider two interacting molecules X and Y, and employ Hill functions to describe the biomolecular interactions (see (1,18,19) for Hill-type models). If X activates Y, we can describe the dynamics as follows:
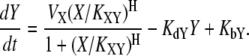 |
(1) |
If X inhibits Y, we can describe the dynamics as follows:
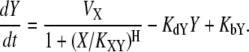 |
(2) |
Here, VX represents the regulatory effect of X, the Hill coefficient H indicates the sensitivity of Y with respect to X, the threshold parameter KXY denotes the threshold of X inducing a significant response of Y, KdY represents the degradation rate constant of Y, and KbY indicates the basal synthesis rate of Y (see Supplementary Material for the meaning of each parameter in the context of dynamics). Let us consider the case where two nodes X and Y commonly regulate Z. In molecular regulatory networks, there might exist several different coregulation mechanisms that can be explained by OR-gate logic or AND-gate logic. Hence, it is difficult to deal with all possible regulation mechanisms in a unified framework. Because we assume that only one of the three nodes (Fig. 2, X) is stimulated in the coupled feedback loop structure, we focus on the competitive OR-gate logic in this article. As in the case of feedforward loops (1), both noncompetitive and competitive binding showed similar results in this case (the AND-gate logic applies to a different situation, where more than one stimulation is given to activate both feedback loops in a coupled structure). With this assumption, we can construct the mathematical models of coupled feedback loops as follows: if both X and Z activate Y, the resulting dynamics are
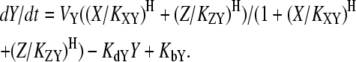 |
(3) |
If X activates Y, but Z represses Y, the resulting dynamics are
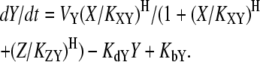 |
(4) |
If both X and Z repress Y, the resulting dynamics are
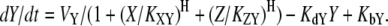 |
(5) |
Based on these basic formulations, we constructed mathematical models for simulations, with an external stimulation given to X (we assume that a stimulation is given to X in an additive manner for all networks). The equations were solved numerically with MATLAB 7.0 (R14) (The MathWorks, Natick, MA). All parameter values were set to 1, except for the Hill coefficient, H, and Kb, unless explicitly stated otherwise. We further set H at 2 and Kb at 0 (see Supplementary Material for detailed explanations on these parameter settings). The bifurcation diagrams (see Fig. 4) were drawn using Matcont 2.8, which is a toolbox of MATLAB.
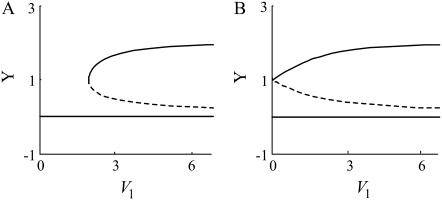
FIGURE 4.
Bifurcation diagrams for a single feedback loop (A) and for PP (B).
In biomolecular regulatory networks, we often cannot distinguish input nodes from output nodes. Hence, we have to consider the product of signs on arrows in the feedback loop. Throughout this article, a positive (negative) feedback loop means a loop whose product of the signs on arrows is positive (negative), as illustrated in Fig. 1, A and B (Fig. 1, C and D). We also note that each node in a network can represent various molecular entities. For instance, the node of a gene regulatory network denotes the gene expression level, whereas the node of a signaling network denotes the level of an activated signaling protein.
RESULTS
Single feedback loops
The main role of positive feedback loops is the amplification of signal. On the other hand, positive feedbacks elongate the time to arrive at a steady state, resulting in a slow response (Fig. 3 D). Such a slow response might be disadvantageous in making an instantaneous decision for critical or lethal stimuli, but it helps to avoid a careless decision. In this regard, the slow response caused by positive feedback loops can be useful in making an important decision, such as those involving cell development and apoptosis. Another property related to positive feedback loops is bistability or, more generally, multistability. A positive feedback induces two stable states depending on the range of feedback strengths (20). In addition, hysteresis can be caused by positive feedback (see (3) for details on bistability and hysteresis). Hysteresis also enables a reliable decision under noisy and fluctuating environments. For instance, the irreversible hysteretic switch realized by positive feedback loops plays an important role in cell cycle or developmental control (14,21–25).
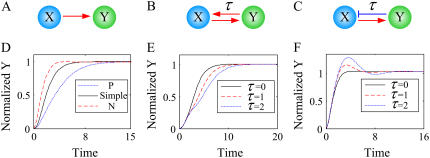
FIGURE 3.
Temporal response curves of Y in the three networks. (A) Simple regulation. (B) A positive feedback loop with a time delay τ. (C) A negative feedback loop with a time delay τ. (D) Temporal response curves of Y in the three networks (A–C) where τ was set to zero. (E) Temporal response curves of Y in the positive feedback loop with time delays τ = 0, 1, and 2. (F) Temporal response curves of Y in the negative feedback loop with time delays τ = 0, 1, and 2.
The main role of negative feedback loops is maintaining the homeostasis of cellular systems. Circadian rhythms (11) and NF-κB oscillations (26) are examples of such regulation by negative feedback loops. Moreover, negative feedback loops play an important role in signal adaptation or desensitization to sustained stimulation, which is often found in various signaling networks. As negative feedback loops usually reduce signal responses, they also function as noise filters and thereby make cells ignore noises in signals. In contrast to positive feedback loops, negative feedback loops accelerate signal responses (Fig. 3 D). Thus, negative feedbacks help to make a prompt decision for strong and critical stimuli. We verified these results for a wide range of parameter values (see Supplementary Material).
As shown in Fig. 3, E and F, the time delays between nodes in a feedback loop affect its dynamics (see Supplementary Material for the detailed method used to obtain Fig. 3, E and F). Fig. 3 E shows that larger time delays between nodes in a positive feedback loop induce slower responses, whereas Fig. 3 F shows that larger time delays between nodes in a negative feedback loop induce oscillations with larger amplitudes (we verified these results for a wide range of parameter values; see Supplementary Material). In this respect, we employ the mathematical models addressing time delay effects in the simulation of oscillatory properties.
Basic modules of coupled feedback loops: PP, PN, and NN
Various cellular circuits have been found to contain feedback loops and, more interestingly, we found that such feedback loops exist as a coupled structure in many cases (Tables 1–3). To investigate the topological property of feedback loops, let us consider a single feedback loop with two nodes (any other structure can be reduced to this topologically equivalent form) and further consider coupled feedback loops that share a common node. These types of coupled feedback structures then provide a basis for all possible coupled feedback structures (see Supplementary Material for more details). There are, in all, 10 possible combinations (Fig. 2), and these can be further classified into three basic modules: PP (a positive feedback loop + a positive feedback loop), PN (a positive feedback loop + a negative feedback loop), and NN (a negative feedback loop + a negative feedback loop). Sample circuits of PP are shown in Table 1, including the muscle cell fate specification network, the galactose signaling network, the mitotic triggering network in Xenopus, and the cell cycle network in budding yeast. Table 2 illustrates sample circuits of PN, including the galactose signaling network in yeast, the mitotic triggering network in Xenopus, the cell-cycle-regulating network in budding yeast, and the circadian networks in Drosophila and Mammalia. Examples of the NN circuit are shown in Table 3, including the ERK signaling network, the chemotactic signaling network in amebae, the p53 network, and circadian networks. Among these examples, some previously known regulation logic on the common nodes is summarized in Supplementary Material, Table S1. We found that most are close to OR-gate logic, and therefore we confine our study to such OR-gate logic, as described in Methods.
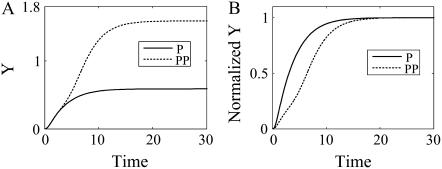
PP induces a slower but amplified signal response and enhances bistability
Since positive feedback loops make signal responses slower and amplify them, both the response time and amplitude increase when two positive feedback loops are coupled (see Fig. 5). We verified these results for a wide range of parameter values (see Supplementary Material). To investigate the effect on bistability of coupling positive feedback loops, we compared the bifurcation diagram of a single positive feedback loop to that of PP (Fig. 4). We found that the parameter range for bistability in the PP model is much broader than that in the single positive feedback model (see Supplementary Material for simulation results for a wide range of parameter values). This implies that coupling positive feedback loops enforces the bistability.
FIGURE 5.
(A) Response curves of a single positive feedback loop (P) and PP. (B) Normalized response curves of P and PP. The values used in the simulations were VX = 0.5, VY = 1, VZ = 0.5, KXY = 1, KYX = 0.5, KYZ = 0.5, KZY = 0.5, KdX = 2, KdY = 0.5, and KdZ = 0.5.
Another study on the noise robustness of PP (15) showed that coupled positive feedback loops with different feedback reaction speeds can effectively reduce the signal noise.
In summary, we found that coupled positive feedback loops can enhance signal amplification and bistability. Actually, such a PP module is found in networks requiring those characteristics. For instance, PP is found in the muscle-cell-fate specification networks (12,13), T-cell differentiation (Th1 cell or Th2 cell) network (14), the cell-cycle start system (27), and Kallikrein-kinin system (28). Since the cell-fate decision, cell differentiation, and cell-cycle start should be irreversible, their switching mechanisms require strong bistability. Therefore, these systems might have evolutionarily acquired PP.
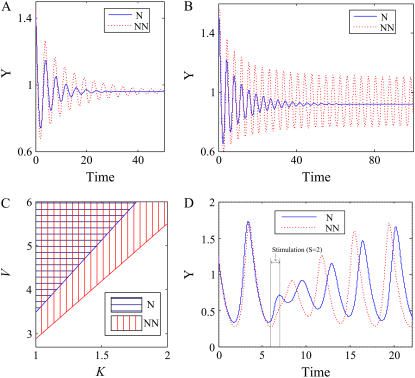
NN enhances sustained oscillations and homeostasis
Negative feedback loops suppress signal amplitudes resulting in noise reduction. If two negative feedback loops are coupled together, such a property gets further enhanced. In addition, coupling negative feedback loops accelerates the response time. On the other hand, we note that many circadian networks and the chemotactic signaling network in ameba, both of which show sustained oscillations, contain NN. Thus, we can speculate that NN enforces the sustained oscillation. Actually, we can verify from Fig. 6 that coupling negative feedback loops enhances oscillations. Fig. 6 A illustrates that coupled negative feedback loops induce damped oscillations with larger amplitudes compared to a single negative feedback loop, and we found that this holds for a wide range of random parameter values. Moreover, coupled negative feedback loops can even induce sustained oscillations with parameters by which a single negative feedback loop shows only damped oscillations (Fig. 6 B). Fig. 6 C shows that coupled negative feedback loops have wider parameter ranges for sustained oscillations compared to a single negative feedback loop. Since coupling negative feedback loops enhances sustained oscillations, we suppose that the sustained oscillation is more robust to noise. Fig. 6 D shows the oscillation profiles of N and NN for a noisy stimulus of short duration at time 6. We found that NN maintains the oscillation period better than N for the given perturbing stimulation. In summary, if negative feedback loops are coupled, then the response time and amplitude are decreased, leading to efficient noise reduction (Fig. 6). In addition, coupling negative feedback loops enhances sustained oscillations and therefore also enhances the restoring mechanism with respect to external perturbations. We verified these results for a wide range of parameter values (see Supplementary Material). Finally, we conclude that coupling negative feedback loops enhances the cellular homeostasis.
FIGURE 6.
Comparing oscillatory behaviors (time delays between nodes are set to 0.3). The simulation settings were KXY = KYX = KZY = KYZ = K and VX = VY = VZ = V. (A) Damped oscillations of N and NN (K = 2, V = 5). (B) A damped oscillation of N and a sustained oscillation of NN (K = 2, V = 6). (C) The K and V parameter ranges of N and NN for sustained oscillations. (D) Oscillation profiles of N and NN when a strong stimulation (S = 2) is given at time 6 (K = 1, V = 8).
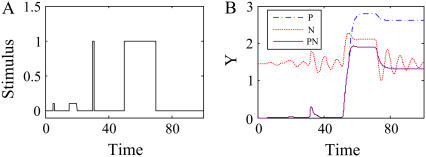
PN effectively modulates signal responses while suppressing noise
PN can have the properties of both positive feedback loops and negative feedback loops. Since negative feedback loops suppress the noise of input signals, PN can reduce noise. In addition, we found that the response time of PN is shorter than that of positive feedback loops but longer than that of negative feedback loops (Fig. 7). On the other hand, bistability is rarely found in PN if its negative feedback is superior. In such a case, PN can induce oscillations (see Supplementary Material for the parameter ranges of oscillation and bistability). However, due to the positive feedback loop, the oscillation is much suppressed compared with the case of negative feedback loops (Fig. 7). We verified this result for a wide range of parameter values (see Supplementary Material). Thus, PN is considered to be a regulatory motif that can efficiently deal with signal noise while achieving proper response time. For instance, Ramsey et al. (5) showed that PN suppresses cellular heterogeneity in the yeast GAL regulon network (5). When positive and negative feedback loops are blocked in the yeast GAL regulon network, a slow and bimodal response to galactose stimulation is observed. This result also implies that most cells respond in a similar way to galactose stimulation because of PN. We also found that PN can reduce the stochastic transcriptional noise while amplifying the signal. This mechanism can be explained as follows: negative feedback loops reduce noise, but they can also suppress signals. This might cause cells to improperly react to a weak stimulation. However, if a positive feedback loop is coupled with the negative feedback loop, signal responses are amplified and cells can make a proper decision even for such weak stimulation. In addition, PN also induces adaptation to a sustained stimulation. Let us consider a cellular circuit that has a fast positive feedback loop (e.g., via protein-protein interactions) coupled with a slow negative feedback loop (e.g., via gene transcription). If a stimulus is applied to this PN, the fast positive feedback loop responds first and the slow negative feedback loop responds afterward. Thus, in the beginning, the signal is amplified by the positive feedback loop and cells respond to the stimulus, but the signal is then reduced or eliminated by the negative feedback loop and cells no longer respond to the stimulus. Kim et al. (17) showed that two positive feedbacks coupled with one negative feedback can efficiently suppress noise, resulting in uniform response profiles (with respect to response duration and amplitude) for similar stimulations. In summary, we conclude that PN has the advantages of both positive feedback loops and negative feedback loops, and that it is the most common regulatory motif, found ubiquitously in various cellular circuits.
FIGURE 7.
(A) Noisy stimulus. (B) Temporal response curves of P, N, and PN to the noisy stimulus in A (V = 2 and K = 0.5). The settings in the simulations were KXY = KYX = KZY = KYZ = K and VX = VY = VZ = V.
DISCUSSION
Feedback loops have been observed in various cellular circuits and we noticed that such feedback loops are coupled with each other in many cases. It is well known that single feedback loops have particular roles. Positive feedback loops amplify signals, cause bistability or hysteresis, and elongate response time, whereas negative feedback loops reduce response signal amplitude and response time, and maintain homeostasis. Such single feedbacks might not be sufficient to cope with various environmental changes or cellular damages, and coupled feedback structures might thus have emerged as a result of evolution. In this spirit, we classified the coupled feedback structures into three modules (PP, PN, and NN) and investigated their respective roles. Finally, we found that coupling feedback loops makes a cellular circuit fault-tolerant with respect to malfunction or mutation of some nodes in the feedback loop. For instance, a single positive feedback with a mutated node cannot properly carry its own role, but PP can still complete the expected role. More importantly, we found that coupling feedback loops strengthens individual feedback loops, thereby enhancing their properties. For instance, PP enhances the amplification of signal responses and bistability, which are the roles of single positive feedback loops; NN enhances sustained oscillation and homeostasis, which are the roles of single negative feedback loops. We also revealed that coupling feedback loops often results in unexpected properties that are not found in either single feedback loop. For instance, PP with different feedback reaction speeds can effectively eliminate signal noise; PN can produce a uniform signal response by properly modulating cellular noise. Another characteristic we found in coupled feedback loops is that they enable cellular systems to produce more various response profiles by controlling an expanded set of parameters such as feedback strength and time delays between nodes.
Although we cannot isolate the role of particular coupled feedback loops if they are embedded in a large complex circuit, this study provides us with a hint as to their hidden role in making up the integrated stimulus-response characteristics. Conversely, we can also infer the global properties of a given cellular circuit by investigating the coupled feedback loops inside. For instance, if a circuit contains many positive feedback loops coupled with each other, we can infer that the system might exhibit strong signal amplification or bistable characteristics. On the other hand, if a circuit contains many negative feedback loops coupled with each other, we can infer that the system might be well regulated for external stimulation and show a relatively fast response. However, we also note that such characteristics of coupled feedback loops are not a simple integrated effect of each individual feedback loop. As an example, all three basic modules PP, PN, and NN appeared to have in common the property of noise robustness.
SUPPLEMENTARY MATERIAL
To view all of the supplemental files associated with this article, visit www.biophysj.org.
Acknowledgments
This work was supported by the Korea Ministry of Science and Technology through the Korean Systems Biology Research Grant (M10503010001-07N030100112), the 21C Frontier Microbial Genomics and Application Center Program (grant MG05-0204-3-0), and a Nuclear Research grant (M20708000001-07B0800-00110), and in part by the Korea Ministry of Commerce, Industry and Energy through the Korea Bio-Hub Program (2005-B0000002).
Editor: Costas D. Maranas.
References
- 1.Mangan, S., and U. Alon. 2003. Structure and function of the feed-forward loop network motif. Proc. Natl. Acad. Sci. USA. 100:11980–11985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Gardner, T. S., C. R. Cantor, and J. J. Collins. 2000. Construction of a genetic toggle switch in Escherichia coli. Nature. 403:339–342. [DOI] [PubMed] [Google Scholar]
- 3.Ferrell, J. E., Jr. 2002. Self-perpetuating states in signal transduction: positive feedback, double-negative feedback and bistability. Curr. Opin. Cell Biol. 14:140–148. [DOI] [PubMed] [Google Scholar]
- 4.Markevich, N. I., J. B. Hoek, and B. N. Kholodenko. 2004. Signaling switches and bistability arising from multisite phosphorylation in protein kinase cascades. J. Cell Biol. 164:353–359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ramsey, S. A., J. J. Smith, D. Orrell, M. Marelli, T. W. Petersen, P. de Atauri, H. Bolouri, and J. D. Aitchison. 2006. Dual feedback loops in the GAL regulon suppress cellular heterogeneity in yeast. Nat. Genet. 38:1082–1087. [DOI] [PubMed] [Google Scholar]
- 6.Mutalik, V. K., A. P. Singh, J. S. Edwards, and K. V. Venkatesh. 2004. Robust global sensitivity in multiple enzyme cascade system explains how the downstream cascade structure may remain unaffected by cross-talk. FEBS Lett. 558:79–84. [DOI] [PubMed] [Google Scholar]
- 7.Kholodenko, B. N. 2006. Cell-signalling dynamics in time and space. Nat. Rev. Mol. Cell Biol. 7:165–176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kalir, S., S. Mangan, and U. Alon. 2005. A coherent feed-forward loop with a SUM input function prolongs flagella expression in Escherichia coli. Mol. Syst. Biol. 1:2005.0006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wolf, D. M., and A. P. Arkin. 2003. Motifs, modules and games in bacteria. Curr. Opin. Microbiol. 6:125–134. [DOI] [PubMed] [Google Scholar]
- 10.Yeger-Lotem, E., S. Sattath, N. Kashtan, S. Itzkovitz, R. Milo, R. Y. Pinter, U. Alon, and H. Margalit. 2004. Network motifs in integrated cellular networks of transcription-regulation and protein-protein interaction. Proc. Natl. Acad. Sci. USA. 101:5934–5939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Paranjpe, D. A., and V. K. Sharma. 2005. Evolution of temporal order in living organisms. J. Circadian Rhythms. 3:7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Spiller, M. P., R. Kambadur, F. Jeanplong, M. Thomas, J. K. Martyn, J. J. Bass, and M. Sharma. 2002. The myostatin gene is a downstream target gene of basic helix-loop-helix transcription factor MyoD. Mol. Cell. Biol. 22:7066–7082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Harris, S. L., and A. J. Levine. 2005. The p53 pathway: positive and negative feedback loops. Oncogene. 24:2899–2908. [DOI] [PubMed] [Google Scholar]
- 14.Yates, A., R. Callard, and J. Stark. 2004. Combining cytokine signalling with T-bet and GATA-3 regulation in Th1 and Th2 differentiation: a model for cellular decision-making. J. Theor. Biol. 231:181–196. [DOI] [PubMed] [Google Scholar]
- 15.Brandman, O., J. E. Ferrell, Jr., R. Li, and T. Meyer. 2005. Interlinked fast and slow positive feedback loops drive reliable cell decisions. Science. 310:496–498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Venkatesh, K. V., S. Bhartiya, and A. Ruhela. 2004. Multiple feedback loops are key to a robust dynamic performance of tryptophan regulation in Escherichia coli. FEBS Lett. 563:234–240. [DOI] [PubMed] [Google Scholar]
- 17.Kim, D., Y.-K. Kwon, and K.-H. Cho. 2007. Coupled positive and negative feedback circuits form an essential building block of cellular signaling pathways. BioEssays. 29:85–90. [DOI] [PubMed] [Google Scholar]
- 18.Locke, J. C., A. J. Millar, and M. S. Turner. 2005. Modelling genetic networks with noisy and varied experimental data: the circadian clock in Arabidopsis thaliana. J. Theor. Biol. 234:383–393. [DOI] [PubMed] [Google Scholar]
- 19.Smolen, P., P. E. Hardin, B. S. Lo, D. A. Baxter, and J. H. Byrne. 2004. Simulation of Drosophila circadian oscillations, mutations, and light responses by a model with VRI, PDP-1, and CLK. Biophys. J. 86:2786–2802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Angeli, D., J. E. Ferrell, Jr., and E. D. Sontag. 2004. Detection of multistability, bifurcations, and hysteresis in a large class of biological positive-feedback systems. Proc. Natl. Acad. Sci. USA. 101:1822–1827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Pomerening, J. R., S. Y. Kim, and J. E. Ferrell, Jr. 2005. Systems-level dissection of the cell-cycle oscillator: bypassing positive feedback produces damped oscillations. Cell. 122:565–578. [DOI] [PubMed] [Google Scholar]
- 22.Acar, M., A. Becskei, and A. van Oudenaarden. 2005. Enhancement of cellular memory by reducing stochastic transitions. Nature. 435:228–232. [DOI] [PubMed] [Google Scholar]
- 23.George, A. J., J. Stark, and C. Chan. 2005. Understanding specificity and sensitivity of T-cell recognition. Trends Immunol. 26:653–659. [DOI] [PubMed] [Google Scholar]
- 24.Callard, R. E., and A. J. Yates. 2005. Immunology and mathematics: crossing the divide. Immunology. 115:21–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Han, Z., L. Yang, W. R. MacLellan, J. N. Weiss, and Z. Qu. 2005. Hysteresis and cell cycle transitions: how crucial is it? Biophys. J. 88:1626–1634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hoffmann, A., A. Levchenko, M. L. Scott, and D. Baltimore. 2002. The IκB-NF-κB signaling module: temporal control and selective gene activation. Science. 298:1241–1245. [DOI] [PubMed] [Google Scholar]
- 27.Levine, K., A. H. Tinkelenberg, and F. Cross. 1995. The CLN gene family: central regulators of cell cycle Start in budding yeast. Prog. Cell Cycle Res. 1:101–114. [DOI] [PubMed] [Google Scholar]
- 28.Kanehisa, M., S. Goto, M. Hattori, K. F. Aoki-Kinoshita, M. Itoh, S. Kawashima, T. Katayama, M. Araki, and M. Hirakawa. 2006. From genomics to chemical genomics: new developments in KEGG. Nucleic Acids Res. 34:D354–D357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Keizer, J., Y. X. Li, S. Stojilkovic, and J. Rinzel. 1995. InsP3-induced Ca2+ excitability of the endoplasmic reticulum. Mol. Biol. Cell. 6:945–951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Solomon, M. J. 2003. Hysteresis meets the cell cycle. Proc. Natl. Acad. Sci. USA. 100:771–772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Ciliberto, A., B. Novak, and J. J. Tyson. 2003. Mathematical model of the morphogenesis checkpoint in budding yeast. J. Cell Biol. 163:1243–1254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Hoa, T. T., P. Tortosa, M. Albano, and D. Dubnau. 2002. Rok (YkuW) regulates genetic competence in Bacillus subtilis by directly repressing comK. Mol. Microbiol. 43:15–26. [DOI] [PubMed] [Google Scholar]
- 33.Shenoy, S. K., and R. J. Lefkowitz. 2005. Seven-transmembrane receptor signaling through β-arrestin. Sci. STKE. 2005:cm10. [DOI] [PubMed] [Google Scholar]
- 34.van Staveren, W. C., D. W. Solis, L. Delys, D. Venet, M. Cappello, G. Andry, J. E. Dumont, F. Libert, V. Detours, and C. Maenhaut. 2006. Gene expression in human thyrocytes and autonomous adenomas reveals suppression of negative feedbacks in tumorigenesis. Proc. Natl. Acad. Sci. USA. 103:413–418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Maeda, M., S. Lu, G. Shaulsky, Y. Miyazaki, H. Kuwayama, Y. Tanaka, A. Kuspa, and W. F. Loomis. 2004. Periodic signaling controlled by an oscillatory circuit that includes protein kinases ERK2 and PKA. Science. 304:875–878. [DOI] [PubMed] [Google Scholar]
- 36.McClung, C. R. 2006. Plant circadian rhythms. Plant Cell. 18:792–803. [DOI] [PMC free article] [PubMed] [Google Scholar]