Protein Shape and Crowding Drive Domain Formation and Curvature in Biological Membranes

Abstract

Folding, curvature, and domain formation are characteristics of many biological membranes. Yet the mechanisms that drive both curvature and the formation of specialized domains enriched in particular protein complexes are unknown. For this reason, studies in membranes whose shape and organization are known under physiological conditions are of great value. We therefore conducted atomic force microscopy and polarized spectroscopy experiments on membranes of the photosynthetic bacterium Rhodobacter sphaeroides. These membranes are densely populated with peripheral light harvesting (LH2) complexes, physically and functionally connected to dimeric reaction center-light harvesting (RC-LH1-PufX) complexes. Here, we show that even when converting the dimeric RC-LH1-PufX complex into RC-LH1 monomers by deleting the gene encoding PufX, both the appearance of protein domains and the associated membrane curvature are retained. This suggests that a general mechanism may govern membrane organization and shape. Monte Carlo simulations of a membrane model accounting for crowding and protein geometry alone confirm that these features are sufficient to induce domain formation and membrane curvature. Our results suggest that coexisting ordered and fluid domains of like proteins can arise solely from asymmetries in protein size and shape, without the need to invoke specific interactions. Functionally, coexisting domains of different fluidity are of enormous importance to allow for diffusive processes to occur in crowded conditions.

INTRODUCTION

Energy converting membranes in mitochondria, chloroplasts, and many bacteria consist of tubes, buds, or sheets that comprise a significant fraction of the internal volume of the organelle or cell. In photosynthetic organisms this proliferation of internal membranes significantly increases the surface area for the absorption and utilization of sunlight by light harvesting (LH) and reaction center (RC) pigment-protein complexes. These protein complexes are functionally connected through excited state energy transfer directed toward the RCs to initiate the primary charge-transfer reactions (1). Among the various photosynthetic purple bacterial species, there is a high similarity between the molecular structures of the individual photosynthetic protein complexes (2–7), an indication of their optimization during at least three billion years of evolution (8). Nevertheless, purple bacteria assemble a variety of photosynthetic unit (PSU) architectures, the simplest being an array of RC-LH1 core complexes, as seen in Blastochloris viridis and Rhodospirillum rubrum (9), whereas other species synthesize peripheral LH complexes, LH2, or configure RC-LH1 into dimeric supercomplexes (10).

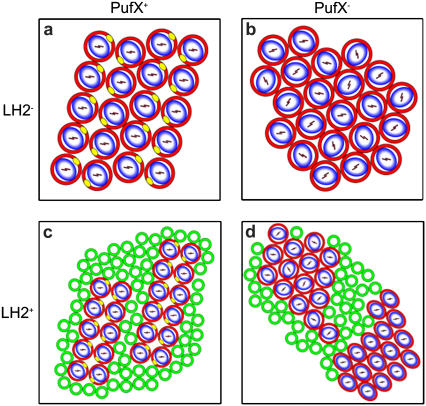
The purple bacterium Rhodobacter sphaeroides is one of the few bacterial photosynthetic species that is open for genetic manipulation and therefore allows a direct comparison of the protein dependency of membrane organization. Aided by the ring-like topography of the cylindrically shaped LH2 and RC-LH1 complexes, the supramolecular organization of the photosystems can be visualized with electron microscopy (9–11) and atomic force microscopy (AFM) (12–14). In addition, the known configuration of the functional chromophores embedded within the LH and RC proteins permits the orientation of these complexes to be probed in intact and oriented membranes with polarized light or linear dichroism (LD) spectroscopy (15,16). Such investigations on Rb. sphaeroides mutant membranes lacking LH2, containing either RC-LH1 monomers or dimers, resulted in the most detailed information on membrane organization (15,16). The results are schematically depicted in Fig. 1, a and b. The panels are arranged to show the effect of the presence or deletion of the determinant gene for dimerization of RC-LH1 complexes, PufX. The most important features are 1) membranes are densely packed with protein; 2) monomeric RC-LH1 complexes configure into a hexagonal packing lattice, whereas dimeric RC-LH1 complexes form rows of dimers; and 3) only dimeric RC-LH1 complexes are rotationally locked into a unique orientation relative to the long axis of the membrane. We also applied these techniques to native, LH2-containing membranes that contain dimeric RC-LH1 complexes. The results are shown in Fig. 1 c. Notably, the presence of LH2 complexes does not influence the configuration of RC-LH1 into rows of dimers, which are now surrounded by some LH2 complexes. Most surprisingly, the orientation of the RC complexes was found to be the same as in LH2-lacking membranes, clearly indicating the long-range ordering of the RC-LH1 supercomplex to be a general principle of design.

FIGURE 1.

Schematic representation of the four different packing lattices of Rb. sphaeroides membranes containing RC-LH1 complexes with and in the absence of PufX and LH2 complexes. a and b use results from Siebert et al. (11) and Frese et al. (15), c from Bahatyrova et al. (12) and Frese et al. (16), and d corresponds to this work. RC-LH1 cores are shown as blue and white ovals enclosed by red circles. PufX is placed according to Roszak et al. (4), Siebert et al. (11), and Frese et al. (15), and it is indicated in yellow. LH2 complexes are shown as green open circles. The orientation of the RC is indicated by the orientation of the special pair of BChls (P), represented by the bars within the blue and white oval. The lattice of the LH2⁺PufX⁻ membranes (lower right panel) is not depicting an observed organization but indicates the occurrence of two types of RC-LH1 packing lattices with uniquely and randomly oriented RCs.

Here we examine the ordering mechanism of the complexes by perturbing the native supramolecular arrangement through the alteration of the shape of one of the two membrane protein complexes. This was achieved by converting the normally dimeric RC-LH1-PufX complex into a monomer via genetically deleting the determinant of dimerization, PufX (11,15,17). We structurally characterized these membranes by means of AFM and polarized light spectroscopy. Results show coexisting crystalline and fluid membrane domains of different curvatures. We also performed Monte Carlo simulations of a membrane model and assessed the effect of the asymmetries in size and shape of the complexes. Simulation results indicate that the combination of crowding and protein geometry drive membrane organization and curvature.

MATERIALS AND METHODS

Bacterial growth

The DD13 double deletion strain, which does not synthesize LH2, LH1, or RC complexes, was complemented with the desired genes encoding RC, LH1, LH1-RC, or LH1-RC-PufX complexes as described in Hunter et al. (18). Transconjugants were grown semiaerobically in the dark on M22+ medium supplemented with neomycin (20 mg ml⁻¹) and tetracycline (1 mg ml⁻¹). Mutant colonies were screened for using a Guided Wave 260 spectrophotometer fitted with a homebuilt petri dish holder. Selected mutants were then grown in liquid culture and intracytoplasmic membranes prepared as described in Dekker and Boekema (19). The intracytoplasmic membrane vesicles for LD and AFM measurement were isolated by rate-zonal sucrose density gradient centrifugation. For LD spectroscopy, membranes were not further treated and prepared as described in the next section. Preparations for AFM were first further pelleted by ultracentrifugation at 100,000 × g for 4 h and resuspended with gentle homogenization in 50 mM HEPES buffer at pH 8 containing 1.0% β-dodecyl maltoside to 16 absorbance units/cm/ml at 875 nm. A total of 250 μl of this sample was loaded onto a 20%/25%/30%/35%/40%/50% w/w sucrose density step gradient in buffer A and centrifuged for 20 h at 200,000 × g using a Beckman SW41 rotor (Fullerton, CA). The fraction containing large membrane fragments was harvested from the 40%/50% interface using a blunted hypodermic syringe and frozen at −20°C until required. The absorbance spectra indicate RC-LH1/LH2 complexes to be present in a ratio of 1:2 (LH2⁺PufX⁺ membranes) and 1:1 (LH2⁺PufX⁻ membranes).

Sample preparation

Membranes were diluted with 10 mM TrisHCI, pH 8.0 before use and for low-temperature measurements glycerol was used at a concentration of 70% (v/v). For the LD measurements the polyacrylamide gels contained 14.5% (w/v) acrylamide and 0.5% N,N′-methylbisacrylamide. After polymerization of the gels with 0.05% (w/v) ammonium persulfate and 0.03% N,N,N′,N′-tetramethylethylenediamine (Sigma, St. Louis, MO) in the dark they were compressed in two perpendicular directions (x and y axes) and the gels expanded along the z axis.

Spectroscopy

Absorption, LD, and light minus dark ΔLD spectra were recorded at 77 K on a homebuilt spectrapolarimeter, with a resolution of 1.5 nm. P⁺ minus P ΔLD spectra were obtained by excitation at 670 nm to avoid photoselection by the polarized light (continuous wave dye-laser, DCM dye, Coherent, St. Louis, MO; CR599, bandwidth of 1 nm, pumped by an Ar⁺ laser, Coherent Innova 310). The power was attenuated to 10 mW/cm². The ΔLD spectra were directly recorded by a lock-in amplifier that was fed by the LD signal, measured with a 3-ms integration time and locked at the 20-Hz laser modulation.

Atomic force microscopy

A small drop of adsorption buffer (10 mM Tris-HCl, pH 7.5, 150 mM KCl, 25 mM MgCl₂) was applied to freshly cleaved mica (Ted Pella, Redding, CA). Consecutively 1 μl of the sample was injected into the thin film. The sample was gently washed with the recording buffer (10 mM Tris-HCl, pH 7.5, 150 mM KCl) after 1 h and placed onto the AFM stage, where 100 μl of recording buffer was added to the liquid cell. A homebuilt AFM was used. Standard Si₃N₄ cantilevers (Veeco Probes, Santa Barbara, CA) had a spring constant of 0.5 N/m. AFM topographs were obtained using tapping mode in liquid. Free tapping amplitude (1–2 nm) and setpoint was adjusted to minimal forces (damping of free tapping amplitude of 5%–10%).

Monte Carlo simulations

Monte Carlo moves sample the configurational space and the connectivity of the triangulated network by attempting to change the position of vertexes and flip the common link between any two neighboring triangles. Only contiguous pairs of triangles sharing a vertex contribute to the average of the local curvature at its position. RC-LH1s constituting a dimer are tied with a permanent rotationally free link. An additional move attempts to modify the projected area of the membrane, and it is associated to an energetic penalty of the same functional form as the first term of Eq. 1: 1/2 k_Ap (A_p − A_p0)²/A_p. We set the compressibility factor k_Ap equal to k_A and a reference projected area A_0p smaller than the tensionless area A₀, such as the whole membrane, can both acquire curvature and remain tensionless at equilibrium. No constraint on the shape of the membrane is imposed. The reference area A₀ sets the desired average area fraction of the complexes at equilibrium.

The topology of the membrane is fixed to a plane, and the saddle-splay modulus is assumed to be uniform. This allows us to make use of the Gauss-Bonet theorem, which ensures that the integrated Gaussian curvature over the whole membrane is a constant and, therefore, it can be dropped from the Helfrich Hamiltonian. We have run simulations with bending rigidities in the range of 20–40 kT, which are typical for biological membranes, as well as area compressibility factors of the order of 10–100 kT/nm². The range for the remaining parameters is defined by the experiments (area fractions within 0.68–0.74) and the geometry of the complexes (size difference and spontaneous curvatures within 0–0.15 σ⁻¹). The results of the simulation model shown in this work remain valid for values of the parameters within the reported ranges. The simulation snapshots and the video were generated using the visual molecular dynamics visualization program (20).

RESULTS AND DISCUSSION

Polarized spectroscopy

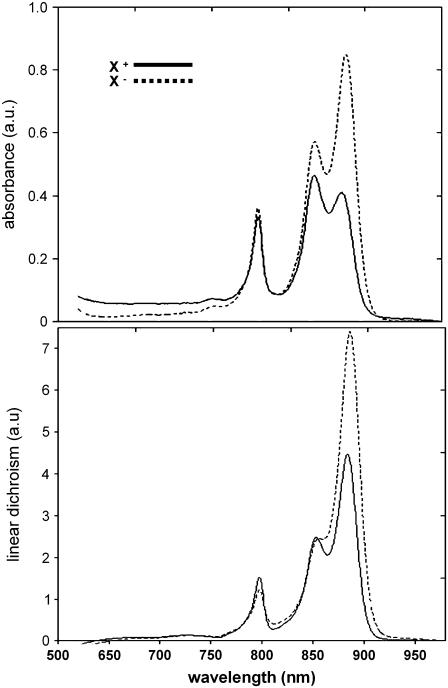
In Fig. 2 we compare the near-infrared absorbance and the difference absorbance between horizontal and vertical polarized light (or LD) spectra for two types of genetically constructed membranes, one containing PufX and RC-LH1 core dimers and the other with no PufX and therefore core monomers. Both types of membrane contain LH2. The spectra are dominated entirely by the chromophores embedded in the LH complexes: LH1 absorbs around 870 nm, whereas LH2 gives rise to two absorbance bands at 800 and 850 nm. The different absorbance ratios of LH1/LH2 for the two membrane types reflect the general variability in LH2 synthesis for photosynthetic membranes. The LH1 chromophores and those giving rise to the 850 nm absorbance of LH2 are held in a very similar orientation and therefore should lead to a similar ratio of LD and absorbance (A) (16). Instead, the LD/A ratio is 1 for LH1 (870 nm) and 0.5 for LH2 (850 nm) for both membrane preparations. We found a similar reduction in LD/A ratio for LH2 relative to LH1 for native membranes before (16). In that study we showed the reduction in LD/A to reflect the abundance of LH2 over RC-LH1 complexes in membrane domains of high curvature. The induction of membrane curvature by LH2 has been shown before in early membrane development studies (21). Our finding of an equal reduction of LD/A in three different membrane preparations strongly corroborates the intrinsic LH2 curvature effect.

FIGURE 2.

Near infrared, low-temperature (77 K) absorbance (top) and LD spectra (bottom) of LH2⁺PufX⁺ (solid) and LH2⁺PufX⁻ (dash) membranes. Spectra are not normalized.

Fig. 3 shows the LD spectra of the chromophores of the RC complexes within intact membranes. RC complexes comprise six chromophores: two strongly coupled bacteriochlorophylls (BChls) absorbing at 870 nm, two accessory BChls absorbing at 800 nm, and two bacteriopheophytins (BPheos) absorbing at 750 nm. Also the LH chromophores absorb at these wavelengths, and we therefore obtain the LD of RCs within membranes from a light-minus-dark difference LD (ΔLD) spectrum. Applying millisecond laser flashes effectively bleaches only the RC chromophores (all processes on the LH complexes are over in picoseconds), and thus only the LD signals of the RC are observed in the difference spectrum. We have shown before that the RCs in membranes from mutants which lack LH2 give rise to two entirely different LD signals, depending on whether or not PufX is present (15). We showed that these two signals reflect the random orientation of the RC in the absence of PufX and the fixed orientation in the presence of PufX (15 and Fig. 1). We stress that these measurements are conducted on an ensemble of membranes and therefore such effects can be obtained only when all of the RC complexes on every membrane have a similar orientation. Moreover, electron microscopy images show all membranes (this work and 16) to be intact and homogeneous without any sign of a tubular membrane fraction (not shown here).

FIGURE 3.

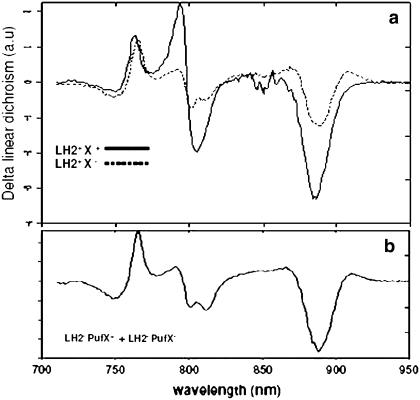
Comparison of the polarization dependence of the absorbance (ΔLD) of the RC chromophores within intact, RC-LH1-LH2^+/− PufX^+/− membranes. (a) 77 K ΔLD spectra of LH2⁺ PufX⁺ (solid) and LH2⁺ PufX⁻ membranes (dashed). Both spectra are normalized on OD_LH1 = 1. (b) Constructed ΔLD spectrum of 1/2 LH2⁻ PufX⁺ plus 1/2 LH2⁻ PufX⁻.

The ΔLD spectrum of PufX⁺LH2⁺ mutant membranes in Fig. 3 shows the exact features of long-range ordered RCs. Despite a small distortion of the signal, arising from a slight heterogeneity in protein organization or membrane morphology, we may conclude that the PufX⁺LH2⁺ membranes and native membranes are highly alike. The ΔLD signals of the LH2⁺PufX⁻ membranes are shown in Fig. 3 a and do not resemble those of the membranes that lack both PufX and LH2. This implies that some order must exist within the LH2⁺PufX⁻ membranes. However, the measured spectrum is not identical to that obtained for PufX⁺LH2⁺ membranes either; hence the order must be partial. We can quantify the amount of order of the membrane complexes by making use of the previously recorded spectra of LH2⁻PufX⁺ and LH2⁻PufX⁻ membranes, which represent the fully ordered and fully disordered situations, respectively (15). A one-to-one linear combination of the two spectra is shown in Fig. 3 b. The similarity between the constructed and the LH2⁺PufX⁻ ΔLD spectra is striking and demonstrates that despite the lack of PufX, which is required to orient RCs in the absence of LH2, about half of the LH2⁺PufX⁻ membranes consist of ordered domains with the orientation of the RC similar to that of the LH2⁻PufX⁺ membranes.

Atomic force microscopy

To investigate the peculiar polarization dependency of LH2⁺PufX⁻ membranes, we used AFM to image adhered membrane fragments at several magnifications. Fig. 4 a shows a large membrane patch with ordered complexes in which the bright protrusions, regularly spaced by 12 nm and with a height of 4 nm relative to the membranous phase, are assigned to the H-subunit of the RC complex (12). This low-magnification image shows that the consequence of converting dimers to monomers was a complete reorganization of the membrane, which now contains extensive, ordered arrays of monomeric RC-LH1 monomers, from which LH2 is largely excluded. Fig. 4 b shows an image of the periplasmic side of the membrane. Because the RC does not protrude from the LH1 ring on this side of the membrane, the semihexagonal arrangement of the exclusively monomeric RC-LH1 complexes is clearly visible. A similar lattice is depicted in Fig. 4 c, but here the RC-LH1 monomers appear in higher packing density. LH2 is underrepresented in AFM images of these membrane patches, because their highly curved domains are rarely stable enough for imaging, as noted in an earlier study (12).

FIGURE 4.

AFM images of membrane patches from Rb. sphaeroides membranes without the PufX polypeptide, which is the determinant of dimerization of RC-LH1 core complexes. Scale bars = 100 nm. (a) AFM image of a membrane fragment from a mutant with no PufX. The image is 3D enhanced to visualize the protruding H-units of the RCs. (b and c) Two AFM images of non-PufX membrane fragments showing the periplasmic side. The insets show zoomed-in images on the areas indicated by the blue boxes and are 3D enhanced for clarity.

The diagrams in Fig. 1 summarize the AFM data in terms of rows of RC-LH1-PufX core dimers interspersed with some LH2 complexes or hexagonal arrays of RC-LH1 core monomers, which largely exclude LH2. The hexagonal configuration of RC-LH1 complexes within the membranes fulfills the main prerequisite for the “order” signal as observed in LD, since this necessitates a uniform packing lattice. The unique orientation of a subset of RCs within the RC-LH1 supercomplex requires an asymmetry within this lattice though. Fig. 4, b and c, may also represent two different packing lattices, a “relaxed” and a “squeezed” one, that may illustrate this packing asymmetry of a subset of RCs. The relaxed hexagonal lattice is highly similar to that of the LH2⁻PufX⁻ membranes, where the RC is rotationally free. The squeezed lattice may represent a strain situation where the RC is locked in a unique orientation. Such strain has been visualized before on 2D crystals of LH1-only complexes that showed the intrinsic deformability of LH1 in the absence of RCs (22).

The effect of the PufX protein on the supramolecular organization

Fig. 1 d presents the configuration of the PSU in the presence of LH2 and lacking PufX. We find that the LH2⁺PufX⁻ membrane partitions into three different domains: a curved LH2, a “disordered” RC-LH1, and an “ordered” RC-LH1 domain. This compartmentalization does not differ to a large extent from the situation in native membranes from Rb. sphaeroides, where the RC-LH1 and LH2 complexes also largely reside in different domains (12,16). Also a third photosynthetic component, the proton-translocating cytochrome bc₁ complex, is expected to reside in a separate domain. In fact, since we find a similar decrease in LD/A ratio for LH2 in all cases (this work and 16), we can conclude that also in native membranes almost all LH2 complexes actually reside in highly curved domains separated from RC-LH1 complexes.

Surprisingly, LD data obtained on LH2-containing membranes demonstrate that it is possible to observe the special orientation of the RC within the LH1 ring when PufX is absent. This orientation is found to be the same for PufX-containing membranes, independent of whether LH2 is present or not. The fact that the orientation of the RC in the crystalline phase is exactly the same for PufX-containing dimers cannot be a coincidence and most likely in both cases reflects specific packing effects. Since in both cases the interaction(s) between the RC and LH1 proteins must be similar, there can be no difference in the arrangement of the LH1 helices around the RC. As a consequence, the packed monomers and PufX-induced dimers must have very similar LH1-helix-helix interactions. We propose the following mechanism of dimerization: in the absence of PufX, the packing of complexes induces a specific configuration of the LH1 helices around the RC, which only in the presence of PufX results in a tight bond leading to dimerization.

In summary, our measurements on native (12,16) and mutated (this work) membranes show that, without changing the fundamental organization of the protein complexes, the deletion of just one polypeptide, PufX, prohibits the LH2 complexes to be interspersed with the semicrystalline lattice of RC-LH1. Both types of membranes contain nearly flat crystalline domains of RC-LH1 and clusters of mostly LH2. More generally, domains of varying crystalline order are observed in almost all photosynthetic membranes from plants (23) and bacterial species (12–14) and also, recently, in mitochondria (24). Although it is often assumed that attractive forces are responsible for the appearance of such domains, our experiments show that a significant change in the interacting protein surfaces does not affect the appearance of ordered and fluid domains. In fact, the commonness of the observed organization suggests that general mechanisms rather than specific protein-protein interactions drive assembly.

Monte Carlo simulations

It is well known in colloid science that entropy alone is sufficient to produce ordered states of noninteracting hard bodies, as well as bulk or microphase separation, through what is known as depletion-induced attraction or macromolecular crowding (25–28). The depletion force is always present in asymmetric mixtures of colloids. However, it is unlikely that depletion interactions are solely responsible for the experimentally observed organization of photosynthetic membranes, because the size asymmetry of the LH2 and RC-LH1 complexes is too small. Indeed, in a quasi-two-dimensional binary system of large and small colloids, the effective entropic attraction between the large colloids is not much larger than 1 kT for size ratios q > 0.3 (29), whereas in Rb. sphaeroides q_LH2/RC-LH1 ∼0.5. An additional factor can be invoked to explain membrane organization, namely protein curvature mismatch. This arises when the faces of two adjacent membrane complexes do not match up when aligned in the membrane plane. Due to the hydrophobic effect, this gives rise to a difference in spontaneous curvature between the complexes (Fig. 5). The relevance of the spontaneous curvature to the packing of membrane proteins is exemplified by the LH2 complex of Rb. sphaeroides, which must have membrane-curving properties, as illustrated by the formation of membrane vesicles in mutant membranes containing only LH2 (30). It has also been shown that membrane curvature increases in line with the LH2 content (31). Also for noncurved proteins this could be relevant in case such proteins preferentially bind curved lipids. This is potentially important, because spontaneous curvature in a phase-separating membrane can generate the formation of budded domains when the line tension of their boundary exceeds the elastic energy cost of budding (32). However, the role of curvature in defining membrane domains without genuine demixing remains largely unexplored. To investigate the combined effects of curvature mismatch and depletion forces on the membranes studied, we performed Monte Carlo simulations using a coarse-grained physical model in which the protein complexes are represented by colloidal bodies that crowd onto a flexible surface.

FIGURE 5.

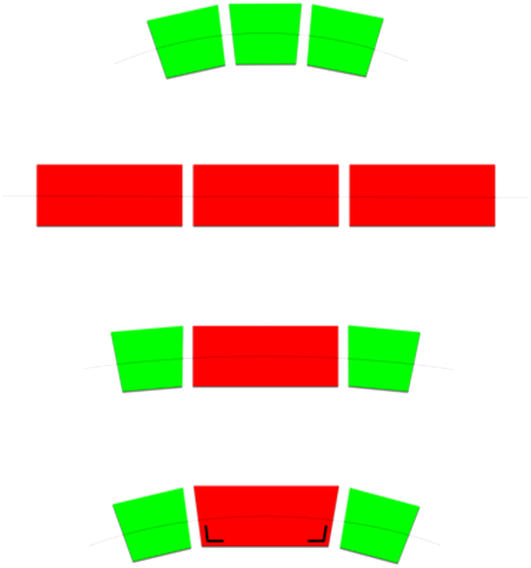
Schematic drawings showing the size and shape differences of the protein complexes and the preferential curvature arising from pairs of contacts. RC-LH1s (red) and LH2s (green) are essentially cylinders of 12 nm and 6 nm of diameter, respectively. Only LH2s have membrane-curving properties, as discussed in the text. A truncated cone indicates this. LH2-LH2 contacts acquire a positive spontaneous curvature c_{0 LH2-LH2} due to the coupling of their truncated-cone shapes (upper row). Cylindrically shaped RC-LH1s preferably flatten the membrane with c_{0 RC-LH1-RC-LH1} = 0 (second row). By geometry, ideally matching RC-LH1s and LH2s generate a curvature c_{0 RC-LH1-LH2}/c_{0 LH2-LH2} = 1/3 (third row). LH2-induced deformation of the more flexible RC-LH1, indicated by an angle mark, increases the former parameter up to 1 (last row).

The model is a dynamically triangulated surface with hard spheres located on the vertexes of the triangles. The change of the position of the vertexes and connectivity of the surface by Monte Carlo sampling mimics the flexibility and fluidity of the membrane. The hard spheres, which represent the protein complexes, travel in three-dimensional (3D) space changing the shape of the surface according to the Helfrich elastic energy H:

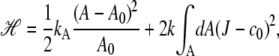which describes the stretching and bending contributions to the free energy of the complexes embedded in the implicit lipid matrix. Here k_A and k are composition-independent constants describing the compressibility and bending rigidity of the membrane, respectively, whereas the departure of the mean curvature J from the spontaneous curvature c₀ is computed locally and integrated over the whole membrane area A using a discretized form of this equation.

In addition to the considerations of size and curvature mismatch between membrane proteins, one further aspect was taken into account in the simulations. Our AFM and LD experiments indicated the deformability of the LH1 complex. The flexibility of the LH1 ring has also been imaged in high detail by EM (32) and AFM (33,34) but has not been observed for LH2. It is therefore highly likely that LH2s induce a deformation of the outer face of neighboring LH1 rings. In our model we introduce this feature in the form of an increased spontaneous curvature factor c_{0 RC-LH1-LH2}/c_{0 LH2-LH2} between RC-LH1 and LH2 neighbors. The local spontaneous curvature c₀ in the model is thus composition dependent, and we investigated the effect of this LH2-induced spontaneous curvature.

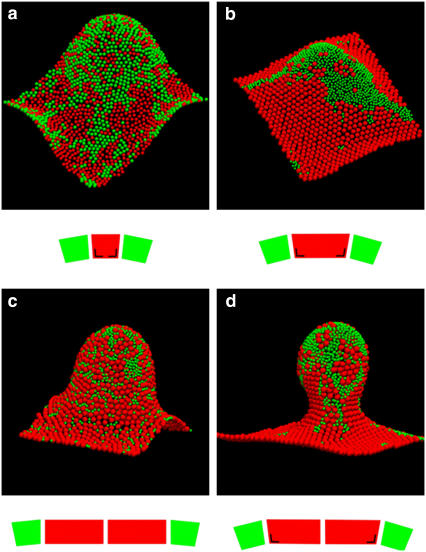
Fig. 6 shows simulation snapshots of equilibrated configurations of the membrane with equally sized monomeric complexes (Fig. 6 a) and with monomers of different size (Fig. 6 b), both including LH2-induced deformation of the RC-LH1 complexes. The difference between the two snapshots demonstrates that size mismatch in the presence of LH2-induced curvature induces demixing and formation of organized large-scale arrays comprising only one type of complex. A comparison of Fig. 6, b and d, highlights the effects of changing monomers to dimers, which exerts a strong influence on the morphology of the simulated membrane by creating budded areas from initially curved regions. In Fig. 6, c and d, we show the effect of the LH2-induced deformation of LH1 complexes, in both cases using dimers of RC-LH1-PufX complexes. In all cases LH2 has a spontaneous curvature, here represented by a conical shape. Note we exaggerated this shape in the figure for clarity; the curvature assigned to LH2 corresponds to a conical angle of only 3°. Although a spontaneous, preferential clustering of LH2 toward the positively curved (∩-shaped) regions of the membrane is seen in Fig. 6 c, this tendency is enhanced when LH2 is allowed to deform RC-LH1-PufX dimers (Fig. 6 d).

FIGURE 6.

Simulation snapshots of equilibrium configurations of the membrane with ∼1500 protein complexes, 50% of them being RC-LH1 (red) and 50% LH2 (green). Periodic boundary conditions ensure that the sides of the membrane in opposite directions match up. The snapshots are accompanied by schematic diagrams illustrating the size ratios and the spontaneous curvature of contacts between RC-LH1 (red) and LH2 (green) complexes. The angle mark drawn on the RC-LH1 truncated cone denotes LH2-induced deformation (see also Fig. 5). Domain formation is enhanced by the size difference of the complexes: (a) equal-size beads, (b) RC-LH1 monomers, and (c) RC-LH1 dimers. Larger crystalline domains of RC-LH1 appear when increasing the spontaneous curvature factor c_{0 RC-LH1-LH2}/c_{0 LH2-LH2} = 1/3 (c) to 1 (a, b, and d). Local compositions couple to the local curvature of the membrane, with flat RC-LH1 regions and positively curved LH2 clusters. The area fraction occupied by the complexes is 0.71 in all simulations but the ones with equal size beads, for which it is 0.68. All simulations were started with a flat random configuration and run at constant c_{0 LH2-LH2} = 0.05 σ⁻¹ (corresponds to a conical angle of ∼3° for the LH2), c_{0 RC-LH1-RC-LH1} = 0, k = 40 kT, and k_A = 10 kTσ⁻², where σ is the diameter of the LH2 complex. RC-LH1s have a diameter of σ in snapshot (a) and 2σ in the rest.

Another consequence is the formation of long-range, long-lived domains of RC-LH1 monomeric or RC-LH1-PufX dimeric complexes. This is in strong contrast to the situation depicted in Fig. 6, a and c, where the much smaller clusters continuously break and merge. Fig. 6 d is a snapshot of the supplementary movie (Supplementary Material). The movie shows a Monte Carlo simulation of the formation of a stable membrane bud, with long-lived crystalline domains of RC-LH1-PufX dimers primarily located on the sides of it and adjoining the fluid LH2 clusters preferentially located at the top. This bears a striking resemblance to the combined results from our AFM and LD studies. The movie highlights the formation of a long axis within the membrane bud and the different curvatures of the RC-LH1 and LH2 domains. We propose here that the curvature of the membrane induces a uniform and directional strain within the packed RCLH1 lattice, leading to the rotational locking of the RCs through the deformable LH1 rings. Two tracer complexes in the movie give a visual notion of the big difference in diffusivity between the ordered RC-LH1 and fluid LH2 domains. The simulations are not intended to mimic the assembly of a biological membrane but to demonstrate the spontaneous formation of domains as a consequence of free energy minimization. Membrane biogenesis in vivo requires assembly factors that can significantly drive local ordering of newly synthesized proteins.

In summary, our results suggest that two cooperative effects drive the formation of domains: crowding and curvature. Crowding favors an entropy-driven attraction between RC-LH1s, arising from the difference in size of the complexes, and their shape mismatch induces local elastic interactions that favor domains and produce membrane curvature. Most generally, our simulations show the interconnection between curvature and size differences operating together to create like protein domains, as a result of which membrane curvature is induced. Monte Carlo simulations indicate as well that the LH2-induced deformation of the RC-LH1 is necessary for the ordering of the RC-LH1 and RC-LH1-PufX complexes and that the formation of domains enhances the formation of buds. Furthermore, our model shows how domain formation and membrane shape can be tuned by changing the size and shape of the protein complexes involved. Photosynthetic membranes provide an excellent example of this, as some species contain LH2 complexes in a variety of sizes: an increasing proportion of larger LH2 complexes results in less demixing, whereas more smaller LH2 leads to protein clustering (13,14). Moreover, in other photosynthetic bacteria demixing can occur to a lesser extent, and less curved lamellae can form instead of buds. This is likely to happen when the shape asymmetry between the complexes vanishes.

CONCLUSIONS

Our findings may be generally applicable to the growth of curved membranes, the formation of specialized protein domains within these membranes, and the effect of protein dimerization on these processes. Functionally, size and shape mismatch can be understood as an effective way to create both fluid and ordered phases in a membrane. Their coexistence ensures that essential diffusion processes remain possible under crowded conditions. At the same time, areas that foster close, regular contacts between complexes guarantee an efficient energy transfer network. The results of this study suggest that size and shape differences between protein complexes in biological membranes may be selected to create a driving force to form functionally important protein domains. Such differences are observed in plants where RC and some LH complexes form large supercomplexes, which can in some conditions configure into structured rows, separated from other LH complexes (23). On the other hand, some photosynthetic bacteria contain RC-LH1 monomers, together with LH2 complexes of variable size resulting in a less well-ordered organization (13). Also the existence of closely packed protein complexes in mitochondria indicates that membrane shape arises from a specific protein geometry (24). Variations in protein geometry can therefore establish diverse strategies to accomplish efficient energy and electron transfers. The interplay between subtle changes in protein size, shape, and content, rather than specific protein-protein interactions, may explain how a preferential organization of protein complexes in crowded biological membranes can be achieved.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.