Transport of Beads by Several Kinesin Motors

Abstract

The movements of beads pulled by several kinesin-1 (conventional kinesin) motors are studied both theoretically and experimentally. While the velocity is approximately independent of the number of motors pulling the beads, the walking distance or run-length is strongly increased when more motors are involved. Run-length distributions are measured for a wide range of motor concentrations and matched to theoretically calculated distributions using only two global fit parameters. In this way, the maximal number of motors pulling the beads is estimated to vary between two and seven motors for total kinesin concentrations between 0.1 and 2.5 μg/ml or between 0.27 and 6.7 nM. In the same concentration regime, the average number of pulling motors is found to lie between 1.1 and 3.2 motors.

INTRODUCTION

Cytoskeletal motors drive the long-range traffic of vesicles, organelles, and other cellular cargoes. They use the free energy released from the hydrolysis of adenosinetriphosphate (ATP) to move actively along the filaments of the cytoskeleton and to perform mechanical work (1,2). One of these motors, conventional kinesin or kinesin-1, which moves along microtubules, has been characterized in much detail. Since a single kinesin-1 motor is sufficient to drive processive movement of a cargo particle (3,4), it has been studied extensively by single-molecule techniques during the last 15 years. On the one hand, these studies have determined the functional relations between motor transport properties such as the motor velocity, randomness parameter, and run-length or walking distance and external control parameters such as ATP concentration and external forces applied, e.g., by optical tweezers (5,6). On the other hand, these experiments have also been used to elucidate the mechanisms underlying the motor movements. It has been shown that kinesin-1 moves in discrete 8-nm steps (7) hydrolyzing one molecule of ATP per step (8–10) and, more recently, that it moves in a hand-over-hand fashion (11–13).

While the behavior of single motors has been studied extensively and characterized in detail, the cooperative transport of a cargo by several motors has received much less attention both for kinesin-1 motors and for cytoskeletal motors in general. The cooperation of several molecular motors is, however, rather common in vivo as revealed by electron microscopy (14,15) and by measurements of velocity and force distributions of cargo particles (16–19). In general, transport of a cargo particle by several motors has several advantages compared to the transport by a single motor. First, several motors can exert larger forces than a single motor. This implies that in a very viscous environment such as the cytoplasm, big cargoes move faster if they are pulled by a larger number of motors (17). The velocity distributions of such cargoes exhibit several maxima as observed in recent experiments (17,19) and as explained by a stochastic model for motor cooperation (20). The larger forces, which become accessible through the cooperation of several motors, may also be necessary to overcome certain force thresholds; an example is provided by kinesin motors which cooperate to pull membrane tubes out of vesicles (21,22). Second, the cooperation of several motors leads to larger walking distances or run-lengths, i.e., the cargo particle remains bound to a microtubule for a longer time and moves over a longer distance before it completely unbinds from it (20). Cargoes pulled by several motors can step from one microtubule to another, so that their run-lengths can exceed the typical length of a microtubule (23,24). The larger run-lengths also enhance active diffusion, i.e., the effectively diffusive motion, which arises from active movements for patterns of microtubules without directional bias (25). Finally, the cooperation of motors may in general facilitate the regulation of the motor-driven motility (26), in particular if different types of motors are attached to the same cargo. The latter situation appears also to be quite common and has been observed for kinesins and dyneins, for kinesins and myosins, as well as for different members of the kinesin family (16,18,27).

In this article, we report measurements of the transport parameters of kinesin-driven beads in vitro where we varied the bead surface coverage by kinesin over a wide range. In particular, we determine the bead velocities, binding frequencies, and run-lengths. Our results are in agreement with the results of previous experiments which addressed kinesin cooperation (10,28). In addition, we determined the average number of kinesins pulling the beads using two independent methods, allowing us to relate the transport parameters of the beads to the number of motors pulling them and overcoming a major limitation of the earlier experiments. We compare the experimental run-length distributions with those obtained from an extension of the stochastic model introduced in our earlier theoretical study (20). The latter comparison provides us with the average number of motors which pull the beads. These numbers are found to be within the range obtained by an independent estimate using data from dynamic light scattering measurements on bead size changes due to kinesin adsorption. In addition to quantifying the relationship between run-lengths and motor numbers, our results also indicate how run-lengths may be engineered for applications of molecular motors in nanotechnology (29,30).

MATERIALS AND METHODS

Protein preparation

Kinesin was purified from porcine brain homogenates by consecutive steps of ion exchange chromatography, microtubule affinity binding, and gel filtration (31). The purified kinesin (heavy chains and light chains) was diluted in our motility buffer, which contained 50 mM imidazole, 0.5 mM EGTA, 0.5 mM MgCl₂, 0.5 mM dithiothreitol, and stabilized by 1 mM glycerol at pH 6.8. In the following, this solution is called buffer A. Tubulin was isolated from porcine brain homogenates by two cycles of temperature-dependent assembly/reassembly (32). Co-purified microtubule-associated proteins were removed by phosphocellulose ion exchange chromatography (33). Motors and microtubules were either assayed immediately or stored in liquid nitrogen. The kinesin and tubulin concentrations were determined by the Lowry method using bovine serum albumin (BSA) as standard (34).

Chamber construction, microtubule alignment, and bead preparation

Bead assays to measure the transport parameters of kinesin-driven beads were performed using a matrix of isopolar aligned microtubules. Aligning microtubules in an isopolar fashion leads to straight tracks, so that the transport is essentially one-dimensional, and prevents hindrance of transport due to crossing microtubules or the simultaneous binding of a bead to two microtubules with opposing orientation. Aligned isopolar microtubules also allow us to study transport distances exceeding the limit of the length of one microtubule. Microtubules were assembled by incubation of tubulin at 37°C with 1 mM GTP and 10 μM taxol. Assembled microtubules (0.5 mg/ml) and kinesin (12.5 μg/ml), together with 5 mM ATP, 100 mM NaCl, and 20 μM taxol in buffer A, were transferred into the experimental chamber, a thin channel with dimensions 50 mm × 4.0 mm × 50 μm, which was built on a glass slide using parafilm tape to form the side walls of the chamber. The coverslip was pretreated with 5 mg/ml BSA. The latter promotes kinesin binding thus forming the binding matrix for the microtubule gliding assay. In the chamber, microtubules performed kinesin-driven gliding along the coverslip. During this gliding assay, a buffer flow through the channel was induced by a filter paper at one end of the channel. The buffer flow (buffer A supplemented with 1 mM GTP, 0.5 mM ATP, and 100 mM NaCl) forces the microtubules to align in a parallel and isopolar fashion (23,35). After the alignment, the microtubules were immobilized by incubation with 0.1% glutaraldehyde in phosphate-buffered saline for 15 min. Both the glutaraldehyde concentration and the incubation time are sufficiently small, so that the properties of kinesin-driven transport are not affected (36). In channels of smaller width (50 mm × 2.2 mm × 0.05 mm), the buffer flow was induced by a motor-driven syringe (23,35). To suppress any buffer flow during the bead assay experiments, both ends of the channel were sealed up with rubber cement after addition of the kinesin-coated beads.

Kinesin-bead solutions were prepared by mixing motor protein, BSA, and buffer A for 10 min, after which carboxylated polystyrene beads with diameter 100 nm (Polyscience, Warrington, PA) were added. The total kinesin concentration was varied between 0.1 and 20 μg/ml, the BSA concentration was 2 mg/ml, and the bead concentration was 14 × 10⁻¹² M. This defined kinesin-bead solution was well stirred and left for another 10 min before 5 mM MgATP were added. Ten or 5.5 μl of the kinesin-bead solutions were introduced into the channel-like chamber and the chamber was closed as described above. All experiments were performed at room temperature (22–25°C).

DLS measurements

Dynamic light scattering (DLS) was used to measure the size distribution of the kinesin-coated beads. The measurements were performed using the noninvasive backscattering ALV-NIBS High Performance Particle Sizer (ALV-Vertriebsgesellschaft, Langen, Germany) supplemented with a 2 mW HeNe laser at a wavelength of 632.8 nm, a detector positioned at the scattering angle of 173°, and a temperature-control jacket for the sample. The analyzed suspensions were prepared as described above. Each suspension was degassed for 15 min to remove air bubbles and placed into a measuring cuvette. The cuvette was sealed to avoid evaporation and left for 5 min to allow temperature equilibration at 25°C. Five to ten measurements, each lasting 180 s, were performed for each kinesin concentration. Dynamic correlation functions were fitted by a second-order cumulant method to obtain the size distributions shown in Fig. 1 a.

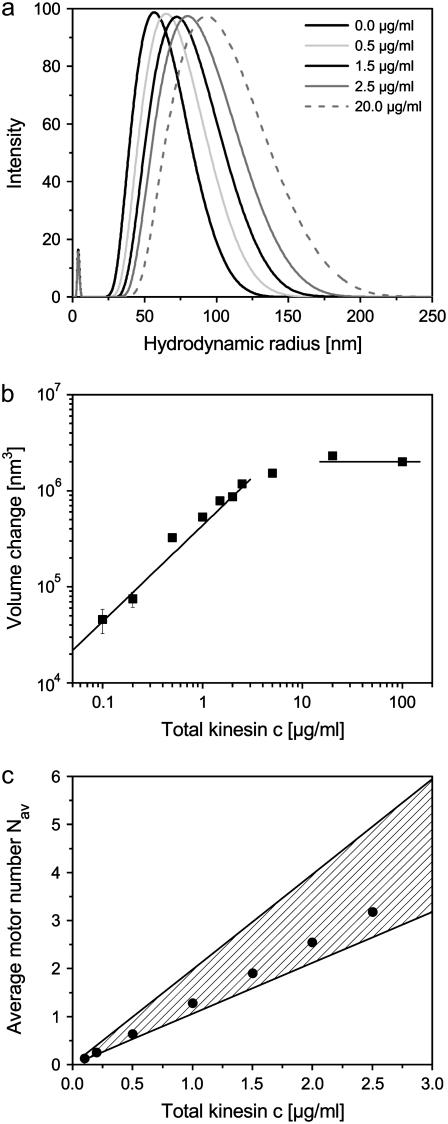
FIGURE 1.

(a) Size distribution of kinesin-coated beads as obtained from dynamic light scattering (DLS) for different kinesin concentrations. (b) Increase of the effective bead volume (as compared to beads without kinesin) as a function of the kinesin concentration. The lines indicate the linear and the saturated regime. (c) Average number of motors involved in the transport of the beads. The shaded region shows the range of motor numbers as estimated from the DLS data (see text), the black dots represent values obtained from fitting the theoretical run-length distributions to the experimental histograms shown in Fig. 3 below.

Microscopy and data analysis

Microtubule gliding and bead movement were observed using video-enhanced phase contrast and video-enhanced differential interference contrast microscopy. For the observations using phase contrast, we used the inverse transmitted light microscope Axiovert 200M (Zeiss, Jena, Germany), equipped with a Plan-Apochromat 100 × oil/1.4 objective, and a digital camera (C5985, Hamamatsu Photonics, Herrsching, Germany). The generated pictures were processed by the digitizer Argus 50 (Hamamatsu Photonics). Differential interference contrast microscopy was performed using the microscope Axiophot (Zeiss) equipped with either a Plan-Neofluar 63 × oil/1.25 or Plan-Neofluar 100 × oil/1.3 objective, a Hamamatsu Chalnicon video camera, type C2400-0,1 and the image processing system Argus 20 (Hamamatsu Photonics). Bead movements were recorded on video tapes. The video sequences were digitized using the imaging analysis system SimplePCI (Compix, Sewickley, PA) resulting in image sequences of two to five frames per second. Each picture sequence was analyzed using a self-written Plug-In for ImageJ (public domain software, http://rsb.info.nih.gov/ij). Bead run-lengths, run times, and velocities were determined from the bead trajectories.

Theoretical run-length distributions

For a given number N of motors attached to a bead in such a way that they can simultaneously bind to a microtubule, the distribution of bead run-lengths is given by

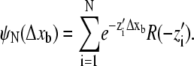(1)

We summarize briefly the derivation of this result (20): The number of motors which are bound to a microtubule and pull the bead changes stochastically between 0 and N. If n motors are bound, the cargo moves with velocity v_n = v, a bound motor unbinds with rate 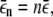and an unbound motor binds with rate 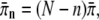where v, 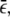and are the velocity, the unbinding rate, and the binding rate for a single motor, respectively. Under our experimental conditions, a run starts when a bead binds to a microtubule by a single motor (n = 1) and ends when all motors are unbound (n = 0). The distribution of distances the cargo has moved in the meantime, ψ_N(Δx_b), is a special case of the distribution of the distance x moved before unbinding if the bead starts with n motors bound, which we denote by ψ_n,N(x), and is given by ψ_N(Δx_b) = ψ_1,N(x = Δx_b). The distributions ψ_n,N fulfill the recursion relation

(2)

with the boundary condition ψ_0,N(x) = δ(x), which is obtained by considering the first step (binding or unbinding of a motor) explicitly and integrating over the possible positions where this event happens. Using Laplace transforms, this integral recursion relation can be converted into an algebraic recursion relation which is solved by a continued fraction (37). In particular, the Laplace transform of ψ_N is then given by

(3)

The latter continued fraction is finite and terminates after N iterations, so that it can be written as a fraction of polynomials. Inverting the Laplace transform (38) then leads to Eq. 1 with lengths scales −z′_i and prefactors R(–z_i) given by the poles and the corresponding residues of the latter fraction of polynomials, respectively.

In the experiments, the maximal number N of pulling motors differs from bead to bead. The theoretical run-length distributions were therefore obtained by averaging over the motor number using a truncated Poisson distribution of the motor number which leads to Eq. 5 as given in Results. The average motor number of the full Poisson distribution, 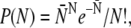is taken to be a linear function of the total kinesin concentration c and given by 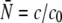with the concentration scale c₀ that will be used as a fit parameter.

The full Poisson distribution P(N) is truncated at a maximal number N_max. The latter is defined by N_beadsP(N_max)/[1 − P(0)] ≥ 1 and N_beadsP(N_max + 1)/[1 − P(0)] < 1, where N_beads is the number of beads with a clear history. This truncation condition is chosen in such a way that the beads with N > N_max can be expected not to be present among the N_beads observed beads. In addition, we normalized the truncated distribution with respect to the moving beads only. In summary, P_tru is defined by

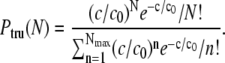(4)

Fitting of run-length distributions

The run-length histograms were fitted with the theoretical run-length distribution as given by Eq. 5 using a short routine written for Mathematica (Wolfram Research, Champaign, IL). The experimental data sets consisted of the walking distance histograms binned into intervals of 1 μm, the total number of analyzed beads, and the corresponding values of the motor concentrations. The number of bins in the histograms does not need to be the same for all sets. Empty bins (no events) were taken into account if events with larger walking distance had been observed.

The fitting procedure varied the two unknown parameters c₀ and to minimize the least-square difference of the experimental data and the theoretical distribution. For all values of c₀ and 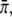we determined numerically 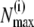for each data set i, and calculated the poles and residues of the finite continued fraction given in Eq. 3 (20) for all N up to the largest 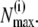We then calculated the theoretical distribution Ψ for all data sets, integrated it over the bin intervals, and renormalized it to the interval of run-lengths for which we had experimentally measured bead runs. The latter step was necessary since the experimental distributions do not cover very large walking distances, because only beads with clear histories were analyzed. The resulting theoretical distributions were compared to the experimental histograms minimizing the sum of the least-square deviations over all included data sets. The average number of motors per moving bead (i.e., averaging only over those beads with at least one motor) was determined by 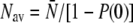for those concentrations for which the run-length distributions had been fitted. For the higher concentrations, we estimated lower bounds for the average motor number by calculating the motor number averaged over all beads (including those without motors) from the effective volume change measured by dynamic light scattering (DLS) (Fig. 1 b) taking the initial linear regime to be given by c/c₀ with the value of c₀ obtained from the run-length distribution fit.

RESULTS

Binding of motors to beads

To study the movement of beads driven by multiple kinesin motors, we performed bead assays using purified porcine brain kinesin which was nonspecifically bound to polystyrene beads 100 nm in diameter (see Materials and Methods). The number of kinesin motors per bead was varied by incubating these beads in kinesin solutions of different concentrations while keeping the bead concentration fixed.

This preparation allows us to vary the number of motors per bead, but does not provide direct information about the actual motor number. We therefore characterized the kinesin-coated beads using DLS to estimate the number of motors attached to the beads. DLS measures the distribution of the effective hydrodynamic radius of the beads. As shown in Fig. 1 a, the DLS data lead to an average radius that increases with increasing motor concentration, while the width of the size distribution remains almost constant. The smaller peak at a hydrodynamic radius of 3.7 nm is due to excess BSA in agreement with earlier measurements (39). To prevent changes in bead size due to increased BSA adsorption, all DLS experiments were done for the same BSA concentration. For the BSA concentration used here, beads are saturated with BSA. We repeated the experiments for some values of the motor concentration using a twofold smaller BSA concentration and obtained the same bead radii as in the experiments using the higher BSA concentration. Excess kinesin could not be detected in these experiments; measurements without beads and with high kinesin concentrations, however, exhibit a weak peak for a hydrodynamic radius of 9.7 nm corresponding to kinesin molecules in their folded state (40).

In Fig. 1 b, we show the corresponding increase of the effective bead volume which should be proportional to the average number of motors bound to the beads. The increase in the effective bead volume is a linear function of the motor concentration for small motor concentrations, but saturates for larger motor concentrations. The saturated volume should correspond to beads that are fully covered by motors. A single motor occupies an area that can be estimated by the size of the kinesin heavy chain cargo domain plus the size of the two light chains which is ∼10 × 30 nm² (41). This implies a maximal number of ∼130 motors which can be bound to a single bead. Assuming that the volume is proportional to the average number of motors at the bead, this allows us to determine the total number of motors at the bead as a function of the motor concentration in solution. In the linear regime for low motor concentrations, this estimate implies that 29 motors are bound to a bead per μg/ml motor concentration in solution.

However, only a fraction of these motors can simultaneously bind to a microtubule. We estimated this fraction by a simple geometric consideration: Motors may bind to the microtubule simultaneously if the difference of their distances from the microtubule (measured from their points of attachment to the bead) is <5–20% of the motor length or <4–16 nm. This estimate implies that a fraction of ∼3–8% of the motors attached to the bead can simultaneously bind to the microtubule. In the linear regime for low motor concentrations c, the average number of potentially pulling motors is then given by N_av ≈ c/c₀ with 0.5 μg/ml ≲ c₀ ≲ 1 μg/ml (see Fig. 1 c).

Transport parameters of kinesin-driven beads

To determine the transport properties of the kinesin-driven beads, we performed bead assays using an array of immobilized isopolar microtubules within a glass channel (23,35) as described in Materials and Methods. In these arrays, the kinesin-driven beads perform one-dimensional unidirectional movements. The microtubule alignment avoids stalling of beads arising from motors pulling in different directions along different tracks. In principle, run-lengths can exceed the lengths of a single microtubule, since beads can switch from one microtubule to another (23,24). With the small beads used for this study (bead diameter 100 nm), however, switching between different microtubules was observed only occasionally and only for high kinesin concentrations.

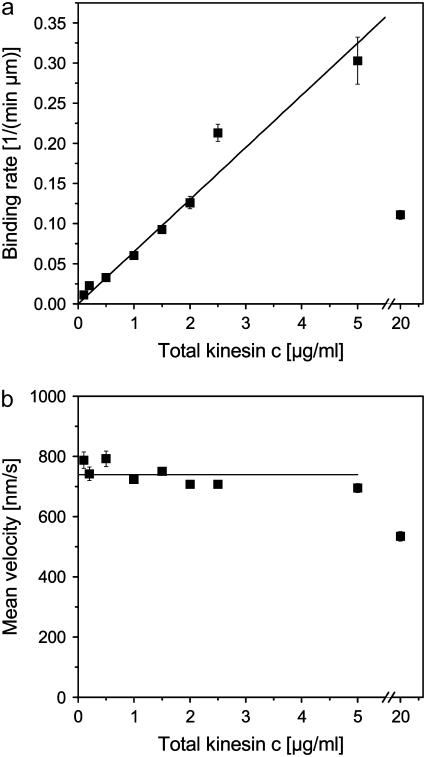
Fig. 2 a shows the bead-microtubule binding rate as defined by the number of beads binding to a microtubule per time and microtubule contour length as a function of the kinesin concentration. For motor concentrations up to 5 μg/ml, the binding rate increases linearly with increasing motor concentration indicating that the motor coverage of the beads is dilute in agreement with the linear increase of the effective bead volume up to a concentration of 2.5 μg/ml as obtained by DLS (Fig. 1 b). For the largest motor concentration we studied (20 μg/ml), however, we observe a much smaller binding rate. Possible explanations for this behavior are discussed below.

FIGURE 2.

(a) Binding rate as defined by the number of beads binding to a microtubule per-μm microtubule length and per-minute and (b) average bead velocity as functions of the kinesin concentration c in the solution from which the motors were bound to the beads. The measured binding rates are fitted by a linear relation and the velocities by a constant for concentrations up to 5 μg/ml (solid lines).

For motor concentrations up to 5 μg/ml, the bead velocities exhibit approximately Gaussian distributions as previously observed for single kinesin motors (see, e.g., (28,42)). For the largest kinesin concentration (20 μg/ml), the velocity distribution is rather broad. The mean velocity as a function of the motor concentration is approximately constant for concentrations up to 5 μg/ml with an average value of 740 nm/s (see Fig. 2 b). The latter observation is in agreement with earlier experiments (3,4). For the beads with the highest motor concentration, however, the average velocity is reduced to 534 nm/s.

For each motor concentration, we measured the run-length of 57–139 beads with a clear history. By clear history, we mean that both the initial binding of the bead to a microtubule and the unbinding from it were observed and that unbinding did not occur due to collisions with optically detectable obstacles such as crossing microtubules or immobilized beads. This implies that long runs where the beads escaped from the microscope window are not included in the following analysis. Together with the fact that beads very rarely switched from one microtubule to another, the requirement of a clear history restricts the lengths of bead runs considered here to below ∼20 μm.

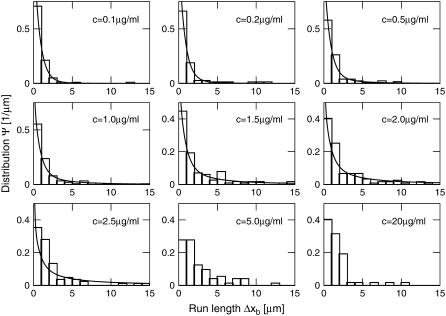
The histograms of the run-lengths as shown in Fig. 3 clearly show an increase in longer runs with increasing motor concentration, again with the exception of the data for the largest motor concentration (20 μg/ml) which exhibits only short runs.

FIGURE 3.

Distributions Ψ of the run-length Δx_b for different motor concentrations c. Histograms show the experimental data, and the solid lines the least-square fit of the theoretical distribution as given by Eq. 5 for concentrations up to 2.5 μg/ml.

For the smallest motor concentration we studied, the run-length distribution is consistent with a single exponential as expected for transport by a single kinesin motor. The average run-length was 0.8 μm, in agreement with previous single molecule experiments (4,8,10,28,43). For larger motor concentrations, large runs are found to be more frequent than one would obtain from a single exponential distribution. Motivated by our recent theoretical analysis of the cargo transport by several motors (20) we analyzed these distribution by sums of exponentials as described in the following section.

Analysis of run-length distributions

To analyze the measured run-length distributions, we extended the model for motor cooperation presented in our earlier theoretical study (20). The latter model describes a cargo to which N motors are firmly attached. These motors bind to and unbind from a microtubule in a stochastic fashion, so that the number of motors pulling the bead varies between 1 and N. Binding or unbinding of one motor is taken to be independent of the binding state of the other motors. The model implies that the run-length distribution for such a bead is given by a sum of N exponentials, where both the scales and the prefactors of the exponentials depend on the binding and unbinding rates and on the velocity of a single motor (see Materials and Methods). Therefore, the number of model parameters which will be used as fitting parameters does not grow with increasing N.

To analyze the experiments, we extended our theoretical description and treated the maximal number N of motors, which pull the beads, as a stochastic variable. Since the binding of motors to the beads is a random process, this distribution is given by a Poisson distribution provided that motor-motor interactions can be neglected. The latter condition is fulfilled for small motor concentrations up to 2.5 μg/ml or 5 μg/ml as can be inferred from the linear increase of the effective bead volume and binding rate as functions of the motor concentrations (see Fig. 1 b and Fig. 2 a, respectively). In our data analysis, this Poisson distribution is truncated at a maximal motor number N_max (see Materials and Methods). The average 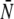of this Poisson distribution depends on the motor concentration in the solution from which the motors are bound to the beads. For small motor concentration c, this dependence is linear with 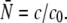The parameter c₀ is used as a fit parameter which allows us to determine how many motors are involved in pulling the beads. It should be in the range estimated from the DLS data, i.e., 0.5 μg/ml ≲ c₀ ≲ 1 μg/ml.

The run-length distribution for our kinesin-driven beads is now given by

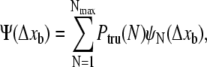(5)

where ψ_N(Δx_b) is the run-length distribution for a bead pulled by N motors as given by Eq. 1 and where P_tru denotes the truncated Poisson distribution of the motor number. The run-length distribution depends on the single motor transport parameters—the velocity v, the unbinding rate 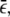and the binding rate 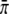—as well as on the concentration c and the parameter c₀. All these parameters are known, with the exception of 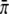and c₀, which we determined by a global least-square fit of the theoretical distribution (Eq. 5) to the experimental run-length histograms. All histograms for different motor concentrations were fitted simultaneously.

The best fit of the seven data sets for motor concentrations up to 2.5 μg/ml (solid lines in Fig. 3) leads to 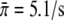and c₀ = 0.79 μg/ml. The value for the single motor binding rate is in good agreement with the corresponding value, which has previously been determined for kinesins at a membrane tube, 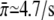(22). The parameter c₀ is found to lie within the range estimated from the DLS data (see solid circles in Fig. 1 c). If we also include the data for the motor concentration of 5 μg/ml, for which the validity of the linear relation between motor concentration and number of motors at the bead is questioned by the DLS data (although it still corresponds to the linear regime of the binding rate), the quality of the fit is slightly reduced and the parameters change to c₀ = 0.98 μg/ml and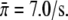

For the best fit to data sets 1–7, we calculated the average number of motors per moving bead N_av (see Materials and Methods), which allowed us to determine in an indirect way how many motors are pulling these beads. The numbers are given in Table 1 together with the values of N_max. For most motor concentrations studied, beads were mainly pulled by one, two, or three motors, while the maximal motor number (which is found on just one or a few beads) ranged between two and seven.

TABLE 1.

Summary of motor numbers for different motor concentrations

Data set	c [μg/ml]	[nM]	Nbeads	Nmax	Nav
1	0.1	0.27	99	2	1.06
2	0.2	0.54	74	2	1.11
3	0.5	1.3	126	3	1.33
4	1.0	2.7	152	5	1.75
5	1.5	4.0	114	6	2.22
6	2.0	5.4	119	7	2.73
7	2.5	6.7	82	7	3.22
8	5.0	13.4	72	—	>3.99
9	20.0	54	59	—	>5.69

Concentration c in μg/ml, corresponding molar concentration in nM, number N_beads of analyzed beads with a clear history, maximal number of motors N_max for the truncation of the Poisson distribution, and average number N_av of motors pulling a bead. For data sets 1–7, which lie within the linear regime (see Fig. 2 a), the average motor numbers are obtained from the fit to the run-length distributions. For data sets 8 and 9, which lie outside this linear regime, lower bounds for the average motor number have been estimated from the DLS data using the value of c₀ obtained from the run-length distribution fit to data sets 1–7.

DISCUSSION

We have determined the transport properties of kinesin-driven beads in vitro as a function of the kinesin concentration or the motor-bead ratio. At the lowest concentration studied, we observed the typical single motor molecule behavior. For larger motor concentrations, beads were pulled by more than a single motor. The bead velocity was approximately independent of the motor concentration and thus the number of motors pulling the beads, which is in agreement with previous studies (3,4,10,28). In contrast to the velocity, both the binding frequencies and the run-lengths of the beads increased strongly with increasing motor number.

We have analyzed the increase in run-length (which had been observed before (10,28)) in a quantitative fashion by comparing the measured run-length distributions with theoretical predictions. In this way, we determined the number of motors involved in the transport. We found that, depending on the motor concentration, the beads are pulled, on average, by 1–3 motors with the maximal motor number ranging up to seven. These numbers are in agreement with the motor numbers estimated from our DLS data. They are also in the same range as the motor numbers that have been reported for transport in vivo (16,17,19).

At the highest motor concentration corresponding to 20 μg/ml, the motility of the beads was reduced and the binding rates, velocities, and run-lengths of the cargo particles were smaller than at lower motor concentrations, similar to earlier observations in microtubule gliding assays with high kinesin surface coverage (44). To fully elucidate what happens at these high motor concentrations, further experiments will be necessary, but the most likely explanation for these observations is that excess kinesins not bound to beads interfere with the bead movements. Two plausible alternative explanations can account for some of the observations, but are not consistent with all of them. First, steric hindrance or exclusion of motors from occupied binding sites could explain the decrease in velocity if the beads are densely packed with motors (20,45,46), since in that case a stepping motor may have to wait if the next binding site of the microtubule is occupied. Our DLS measurements indicate that for high motor concentrations the beads are indeed fully covered by motors. However, steric hindrance would lead to saturation of the binding rate for high motor concentrations rather than to the observed decrease. Second, for high motor concentrations, there could be two layers of motors around the beads and only the motors from the sparse outer layer could make contact with the microtubule. The latter idea would be consistent with the decrease of the binding rate and the run-length, but cannot explain the decrease of the velocity. It is also not consistent with the saturation of the effective bead size as observed by DLS. As mentioned, the most likely explanation is that the decrease in motility is caused by the excess motors in solution which bind to the microtubule and interfere with the bead motility. At this motor concentration, the density of bound excess kinesin on microtubules is estimated to be approximately one motor per six binding sites. Interference via excess motors is consistent with a decrease of all three transport parameters for beads transported by multiple motors, although the decrease in velocity observed here is stronger than in a recent study using kinesins labeled with quantum dots (28). A possible explanation for this stronger decrease of the velocity is that the excess motors (or at least a substantial fraction of them) are in their folded state and thus inactive as suggested by the DLS measurements on solutions without beads.

Our data show in a quantitative fashion that increasing the number of kinesin motors involved in cargo transport increases the run-length of that cargo. Since the run-length of a single kinesin motor is typically only 1 μm, larger run-lengths as achieved by cooperative transport are crucial for long-range transport in vivo where cargoes are typically transported over tens of microns and, in extreme cases such as in axonal transport, over centimeters or even up to a meter (47). While cargoes pulled by multiple motors can essentially move in a directed fashion along microtubules over such large scales (provided they can step from one microtubule to another), single motors or cargoes transported by single motors perform random walks on these large lengths scales which consist of periods of directed movement interrupted by phases of Brownian motion upon unbinding from the microtubule. These random walks lead to strongly reduced effective cargo velocities and, thus, to inefficient transport (45,48). The latter type of random walks has recently been studied for the movements of vesicles in neurites which are presumably pulled by single kinesin motors (49) and for individual quantum-dot labeled kinesins in HeLa cells (50). The large run-lengths due to motor cooperation are also advantageous for bidirectional transport where the effectively diffusive movement is governed by an effective diffusion coefficient which is proportional to the run-length (25). Likewise, the long run-lengths of beads transported by several motors should also be of interest for applications of biomimetic transport systems based on molecular motors in bionanotechnology where typical device sizes also exceed a few microns.

Cargo transport by multiple motors also provides potential mechanisms for the regulation of transport. If a cargo is transported by several motors, the cell can fine-tune the parameters of cargo transport by controlling the number of motors pulling a cargo. For example, it should be advantageous to use several motors with a relatively short run-length rather than one motor with a relatively large one, since this allows the cell to fine-tune the processivity of the cargo simply by activating motors bound to the cargo or by recruiting motors to that cargo. In contrast, for transport by a single motor, the cell only has the options of switching the transport on or off. Likewise, the force generated by a team of motors becomes more tunable if several weaker motors are used rather than one single strong motor. We suggest that, in general, cargo transport by several motors is more accessible to regulatory mechanisms than transport by single motors. This study as well as our previous theoretical one (20) provides a framework for studying such control mechanisms in a quantitative way.

Very recently, a possible regulation mechanism for cooperative cargo transport, based on the interaction of kinesin with tau proteins, has been studied in vitro (51). The motility assay used in this latter study was similar to the one used here but the deposition of the kinesin-coated beads onto the microtubules was performed by optical tweezers. In the concentration regime in which the bead carries several motors, this deposition method is likely to lead to an initial state of the bound bead, in which this bead is connected to the microtubule by several motors. In contrast, for the diffusion-limited binding of beads as studied here, the bead will first bind to the microtubule via a single motor molecule. These two different initial conditions lead to different run-length distributions. If the bead is initially connected by a single motor molecule, its run-length distribution will decrease monotonically as described in our study (see Fig. 3). On the other hand, if the bead is initially connected to the microtubule via several motor molecules, its run-length distribution may exhibit a maximum at several micrometers as reported by Vershinin et al. (51).

In the experiments presented here, we have varied the average number of motors pulling the beads and determined this number by comparison with detailed calculations. An interesting challenge for future work is to develop experimental techniques by which one can directly control the actual motor number on the beads (rather than the average motor number). Using such an experimental system, we would be able to study additional aspects such as the dependence of the cooperative motor transport on the rigidity and strength of motor-bead binding or on the motor arrangement on the beads.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.

APPENDIX ON EXCESS KINESIN

The kinesin-bead solutions used in this study contained excess kinesin, i.e., dissolved kinesin not attached to the beads. In this Appendix, we discuss the amount of excess kinesin as determined via gel electrophoresis, its irrelevance for the transport properties of the beads, and the possible coexistence of several molecular conformations that differ in their binding affinity to the beads.

Amount of excess kinesin

To determine the amount of excess kinesin, four different kinesin-bead solutions with a total kinesin concentration of 0.5, 1.5, 2.5, and 5 μg/ml, respectively, were separated using sodium dodecylsulfate polyacrylamide gel electrophoresis (SDS-PAGE, 5% stacking gel, and 7.5% resolving gels) and silver staining. To quantify the amount of protein, calibration standards of kinesin solutions of different concentrations (without beads) were used. The kinesin bands in the resolving gels were analyzed using the software GelScanV5.1 (BioTec, Frankfurt/Main, Germany). In addition, the kinesin-coated beads were separated by centrifugation and sedimented onto a filter membrane (Nanosep centrifugal device, Pall Life Science, Ann Arbor, MI) with a cutoff of 300 kDa. The probes were centrifuged (5417C, Eppendorf, Hamburg, Germany) at 5100 g for 4 min where g = 9.81 m/s² is the gravitational acceleration. The filtered solution is free of beads but contains the excess kinesin which was also analyzed using the SDS-PAGE method.

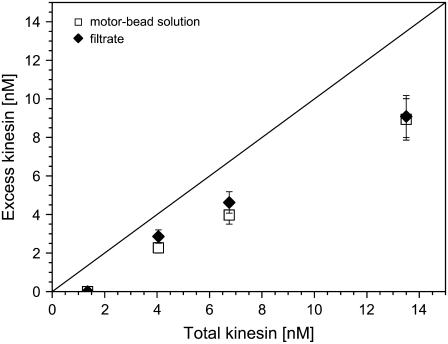
As shown in Fig. 4, the data from both series of experiments are rather consistent and imply that, in the relevant concentration regime, ∼70% of the total amount of kinesin is present as excess kinesin in solution. This is consistent with the following rough theoretical estimate. For a motor concentration of 2.5 μg/ml or 6.7 nM—the upper limit of the linear regime in Fig. 1 b and the largest motor concentration used for the run-length analysis below—our previous estimates about the motor coverage lead to 73 motors per bead. This would imply that the concentration of excess kinesin is ∼5.7 nM or ∼85% of the total concentration of kinesin.

FIGURE 4.

Excess kinesin concentration in the solution as a function of total kinesin concentration in the incubation protocol: One set of data (squares) corresponds to SDS-PAGE of the untreated kinesin-bead solution; the other set of data (diamonds) has been obtained after centrifugation plus filtering of the kinesin-bead solution and subsequent SDS-PAGE of the filtered solution. The straight reference line corresponds to excess kinesin being equal to total kinesin.

Irrelevance of excess kinesin for bead transport

In principle, the presence of excess kinesin could complicate the analysis of the cooperative transport of beads in two different ways. First, it could indicate weak, reversible binding of kinesin to beads and fast exchange of kinesin between solution and bead surfaces. Second, the excess kinesins might bind to the microtubules and then act as obstacles for the bead transport. We have checked via control experiments that both complications do not arise in the concentration regime used for the run-length analysis as explained next.

To investigate this possible interplay of excess kinesin and transport properties, we prepared pairs of identical samples from the same preparation of kinesin-bead solutions. For each pair, one sample was diluted twofold with buffer A (see protein preparation in Materials and Methods), to reduce the concentration of excess kinesin. We then determined the hydrodynamic radii of the beads in the undiluted and diluted solution using DLS. We found that the hydrodynamic radii of the beads in the diluted and undiluted solutions were identical (see Table 2), and that the hydrodynamic radii of the diluted solutions remained constant when DLS measurements were repeated up to 2 h later. Therefore, on the timescale of our experiments, motors are not exchanged between the beads and the excess motor fraction in the solution, and the number N of motors attached to a given bead remains constant.

TABLE 2.

Bead properties in undiluted and diluted solutions

	2.5 μg/ml undiluted	2.5 μg/ml diluted	5 μg/ml undiluted	5 μg/ml diluted
Hydrodynamic bead radius [nm]	83	81	85	87
Average velocity [μm/s]	0.68	0.78	0.70	0.71
Average run-length [μm]	1.70	1.71	1.88	1.93

The quoted motor concentrations are the total kinesin concentrations in the kinesin-bead solutions. The diluted solutions have been obtained by mixing the undiluted ones with buffer A in the ratio 1:1. Even though the diluted solutions contain only half the amount of excess kinesin, they lead to essentially the same hydrodynamic radii and transport properties of the beads.

Second, we measured the velocities and run-lengths after the same pairs of diluted and undiluted solutions had been transferred into the channel-like chamber. The corresponding data are again summarized in Table 2. Inspection of this table shows that the transport properties are not affected by the dilution procedure. We therefore conclude that, at least for the relatively low motor concentrations up to 2.5 μg/ml as used for the run-length analysis, the excess kinesin does not lead to a sufficient number of obstacles on the microtubules to change the bead velocity and/or its run-length. This conclusion is corroborated by the following estimate. From the electrophoresis measurements (see Fig. 4), we conclude that a total kinesin concentration of 2.5 μg/ml leads to an excess kinesin concentration of ∼1.75 μg/ml. Assuming that this excess kinesins can bind to the microtubules and using a dissociation constant of ∼200 nM (28) for binding/unbinding equilibrium, one out of 43 microtubule binding sites would be occupied by excess kinesins. Thus, even at the upper limit of the linear regime in Fig. 1 b, each motor would still be able to make ∼40 steps before it encounters an obstacle. Furthermore, if the bead is pulled by several motors, these motors are likely to be in contact with several protofilaments and, thus, to bypass the obstacle.

Excess kinesin and quasi-irreversibly bound kinesin

In view of the relatively large concentration of excess kinesin, the observed, quasi-irreversible binding of kinesin to beads is somewhat surprising. The combination of these two features seems to indicate that our kinesin-bead solutions, which involve both heavy and light chains of kinesin, contain several species or molecular conformations of this motor. It is now well established that kinesin can attain both an unfolded and a folded conformation even in the absence of light chains (52,53). As mentioned, in the absence of beads, our DLS data exhibit a weak peak in the high kinesin concentration regime that we take as evidence for the folded state. In addition, the presence of light chains has been shown to reduce the binding affinity of kinesin to microtubules (54). Thus, the combination of heavy and light chains may lead to more than two molecular conformations of kinesin in solution as has been recently proposed by Cai et al. (55). It is rather plausible to assume that different molecular conformations will differ in their binding affinity to the beads. Thus, the simplest scenario that explains our observations consists of two populations of kinesins: ∼30% of the kinesin molecules attain a molecular conformation that has a strong binding affinity to the beads, whereas ∼70%, which form the excess kinesin, attain a conformation that can bind only weakly or cannot bind at all to the beads.

The latter scenario is also consistent with the results of another set of control experiments in which we tried to separate kinesin-coated beads and excess kinesin by centrifugation. In these latter experiments, the kinesin-bead solution was centrifuged at low acceleration between 5000 and 10,000 g. Up to ∼15 min were needed to separate the kinesin-bead solution into pellet and supernatant. The pellet should primarily consist of the kinesin-coated beads whereas the supernatant should contain (most of) the excess kinesin. When the pellet was resuspended in buffer A and transferred into the channel-like chamber, we did not detect any movements of the beads. This indicates that the motors in the pellet have been squashed between the beads as one might have expected. However, we also found no motility when we added beads without kinesin to the supernatant and again transferred the resultant solution into the chamber. This observation is again consistent with our interpretation that the excess kinesins bind only weakly or not at all to the beads.

So far, this interpretation is somewhat speculative, and additional experimental studies using, e.g., fluorescence resonance energy transfer would have to be performed to obtain direct information about the molecular conformations of the excess kinesins and their binding properties. In any case, we have directly demonstrated that, in the relevant concentration regime, the presence of excess kinesin has essentially no effect on the hydrodynamic radii and on the transport properties of the beads (see Table 2). Therefore, this excess kinesin is irrelevant for the cooperative transport of beads by several motors as investigated in this study.