Sliding of Alkylating Anticancer Drugs along the Minor Groove of DNA: New Insights on Sequence Selectivity

Abstract

Currently, little is known about the molecular recognition pathways between DNA-alkylating anticancer drugs and their targets despite their pharmacological relevance. In the framework of classical molecular dynamics simulations, here we use umbrella sampling to map the potential of mean force (PMF) associated with sliding along the DNA minor groove of two of these compounds. These are an indole derivative of duocarmycin (DSI) and the putative reactive form of anthramycin (anhydro-anthramycin, IMI). Twenty-three configurations were considered for each drug/DNA complex, corresponding to a movement along ∼3 basepairs. The alkylation site turns out to be the most favorable for DSI, while a barrier of ∼6 kcal/mol separates the reactive configuration of IMI·DNA from the absolute minimum. An analysis of various contributions to the PMF reveals that solvent effects play an important role for the largest and more flexible drug DSI. Instead, the PMF of IMI·DNA overall correlates with changes in the binding enthalpy. Implications of these results on the sequence selectivity of the two drugs are discussed.

INTRODUCTION

Most of the successful anticancer drugs targeting DNA are organic molecules which form noncovalent or covalent interactions in the minor groove with different sequence selectivity (1,2). To rationally design such drugs, both the structure and the microscopic mechanisms underlying drug-target interactions should be known. Furthermore, it is very important to design sequence-selective anticancer molecules (hopefully competitive with regulatory proteins) that bind to regions of DNA involved in replication and transcription processes (3–6).

In this respect, a number of noncovalent binders were well characterized, and sequence-specific readout codes were partly deciphered (1,7). In contrast, the important class of DNA-alkylating agents has received less attention, particularly from a theoretical point of view, partly because of the paucity of experimentally determined structural data (8). Binding of these drugs is believed to occur in two steps (9): the formation of the noncovalent adduct 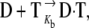followed by the covalent linkage of the drug to the DNA 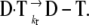The design of new covalent binders requires identification and characterization of the transition state associated with the rate-determining step, since its subtle tuning affects rate and routes of interactions. Both these factors influence the reactivity and consequently the efficacy of the drug (10).

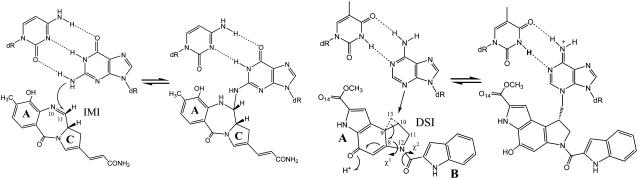
It is commonly accepted that molecular recognition and formation of the noncovalent complex are driven by nonspecific interactions and sequence-specific structural features along the minor groove (8). Recently, molecular dynamics (MD) studies by us (11,12) have provided information at the molecular level on the noncovalent interaction between the DNA and two covalent binders, anthramycin (13–16) and duocarmycin (17,18). Anthramycin alkylates guanines, showing a modest sequence selectivity for PuG*Pu sequences (16), whereas duocarmycin binds to adenines and is very selective toward AT-rich sequences which have to be at least 4 basepairs (bp) long (17,18). Both anthramycin and duocarmycin are powerful cytotoxic agents interfering with transcription and replication processes, and some of their derivatives have entered clinical test phases (19,20). The natural twist of 35° between phenol and pyrrol rings (respectively A and C in Chart 1) gives to anthramycin the ideal shape to fit into the minor groove (14). In contrast, the largest duocarmycin is formed by two moieties connected via an amide link (Chart 1), and to fit into the minor groove it needs a 40° twist around the amide link relative to its conformation in water (18).

For the purposes of this work, we focus on the putative reactive imine form of anthramycin (hereafter IMI, Chart 1) (13–16) and on duocarmycin-SI (hereafter DSI, Chart 1) (17,18). Noncovalent complexes of both IMI and DSI with DNA are mainly stabilized through hydrophobic interactions (11,12). However, although IMI forms a relatively strong H-bond network with DNA (12,14), only one H-bond is formed between DSI and DNA (11,18). In a previous MD simulation performed in our group (12), IMI turned out to slide along the minor groove of a d[GCCAACGTTGGC]₂ duplex, leading to the formation of a nonreactive stable complex. Such a sliding is independent on the initial location of the drug, occurring when IMI sits either at the end or in the middle of a DNA duplex. The same kind of displacement has been observed after docking the molecule to its preferred site, the triplet AGA (16), within a 14-mer duplex (data not shown). Instead, the complex between DSI and the duplex d[GACTAATTGAC]₂ is stable during the whole dynamics (11). It is worthwhile to notice that a similar shuffling mechanism was suggested by footprinting experiments for a photoactive derivative of actinomycin, while noncovalent translocation mechanism has been invoked for the covalent binder CC-1065 (21,22).

As the noncovalent recognition of the preferred DNA sequence may involve a sliding of drugs along the minor groove, knowledge of the energetics of such processes may provide useful information on ligand selectivity and molecular recognition. Here we address this issue by investigating quantitatively the mechanism of sliding of IMI and DSI. Because of the increasing reliability of methods for simulating DNA (23–28), nowadays it has become possible to extract free energies of drug/DNA recognition from MD simulations (29,30). The free energy is then dissected at a qualitative level into its enthalpic and entropic contributions, the rank of which has been shown to depend strongly on the chemical structure of the drug and on the DNA sequence (31,32).

We find that for IMI, binding to the reactive site is less favored than at nearby bp, whereas for DSI the noncovalent binding site coincides with the reactive one, in agreement with previous MD simulations (11,12). Although the potential of mean force (PMF) associated to the sliding of IMI can be roughly rationalized through a simple analysis of drug/DNA enthalpic interactions, solvation effects appear to be much more relevant for DSI as a consequence of more stringent requirements for optimal fit of drug into the minor groove. Our findings suggest the need to consider multiple binding pathways in drug design and provide a rationale for the modest selectivity of anthramycin relative to duocarmycin (18,33).

SYSTEMS AND METHODS

Free energy profiles were calculated as a function of the position of the drug along the minor groove for the noncovalent complexes of IMI with d(GCCAACGTTG*GC)-d(GCCAACGTTGGC) (hereafter IMI·DNA) and DSI with d(GACTAATTGAC)-d(GTCAATTA*GTC) (hereafter DSI·DNA). These are built starting from experimental structures (14,18) by cutting the covalent bond between the carbon of the drug and the nitrogen of the nucleobase and manually pulling out the drugs from the minor groove until the distance d[C-N] was ∼3.3 Å. As DSI moves toward the nearest end of the duplex upon sliding, test calculations were performed to investigate the possible influence of end effects (12). To this end, we constructed an additional 14-mer d(GACGACTAATTGAC)-d(GTCAATTA*GTCGTC) (hereafter DSI·DNAc), and DSI was placed with its reactive carbon C13 in front of the base T24 (corresponding to T21 in DSI·DNA). A 7 ns MD simulation was performed on this system, and analyses were performed on the last 2 ns.

All simulations were carried out using the GROMACS package (34–36). AMBER/gaff force fields (25,26,37,38) were used for the parameterization of oligonucleotides and drugs (see Spiegel et al. (11) and Vargiu et al. (12) and Supplementary Material Tables S1 and S2). Drug structures were optimized by means of DFT calculations at the B3LYP/6-31G(d,p) (39,40) level, using the Gaussian03 package (41). Atomic restrained electrostatic potential (RESP) charges (42) were derived using the resp module of AMBER after wave function relaxation. Potassium ions, modeled with the AMBER-adapted Aqvist potential (43), were added to achieve charge neutrality (22, 20, and 28 in IMI·DNA and DSI·DNA and DSI·DNAc, respectively). Systems were solvated with a cubic box of TIP3P water molecules (44), ensuring that the solvent shell would extend for at least 12 Å around the DNA. Periodic boundary conditions were used, and constant temperature-pressure (T = 300 K, P = 1 atm) dynamics were performed through the Nosé-Hoover (45,46) and Andersen-Parrinello-Rahman (47,48) coupling schemes (τ = 1 ps). Electrostatic interactions were treated using the particle mesh Ewald algorithm (49) with a real space cutoff of 10 Å, the same as for van der Waals interactions. The pair list was updated every 10 steps, and Lincs constraints (50) were applied to all bonds involving hydrogen atoms, allowing us to use a time step of 2 fs. Coordinates were saved each 500 steps, corresponding to 1,000 snapshots per ns. The DNA minor groove width was defined as the distance between sugar C4′ atoms, and it was calculated with the program Curves (51–53).

The PMFs (54) associated to drug sliding along the minor groove of IMI·DNA and DSI·DNA were calculated with the umbrella sampling method (55). The distance between the reactive atoms of drug and DNA base (specifically the C11 atom of IMI to the N2 atom of guanine 10 in the DNA and atom C13 of DSI to atom N3 in adenine 19 of the DNA) was chosen as the reaction coordinate. This simple choice is well suited to describe movements of the drugs that are a few bps long, since both compounds cause no appreciable bending of DNA (11,12). To sample the various conformations corresponding to different positions of the drug along the minor groove, we imposed a harmonic constraint of 15 kcal/(mol·Å²) to the distance d[C-N] from 2.9 Å to 12.1 Å with a step of 0.4 Å. Doing so the total movement of 9.2 Å (slightly less than 3 bps steps) is partitioned into 23 windows (see movies in the Supplementary Material). Initial configurations of each window were generated starting from the reactive one and increasing the distance d[C-N] by steps of 0.2 Å, after 70 ps of equilibration for each d[C-N] value. The weighted histogram analysis method (56) was used to recombine PMF obtained from different windows. As can be seen from insets in Figs. 1 and 2, the error on the calculated PMFs is almost constant, meaning that the reaction coordinate was sampled in a fairly uniform manner.

CHART 1.

Schematic view of alkylation of guanine by IMI (left) and adenine by DSI (right).

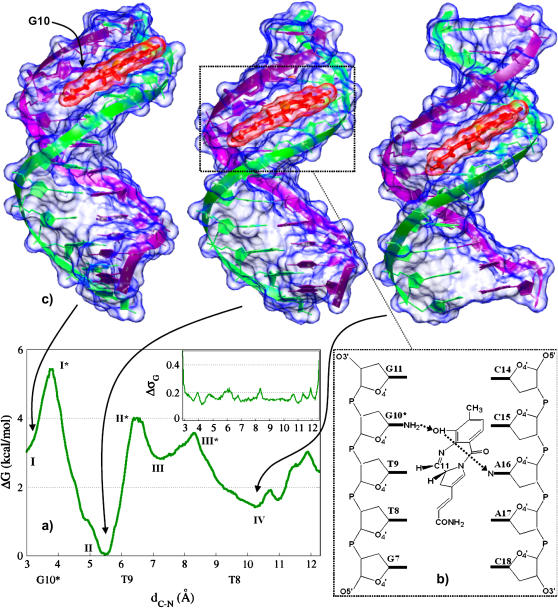
FIGURE 1.

(a) PMF associated to IMI sliding along the DNA minor groove. Standard deviation is reported in the inset. (b) Schematic view of the complex in the configuration corresponding to the free energy minimum. (c) Structures of three relevant conformations of the drug/DNA complex. The second and third structures (from the left) were rotated respectively by ∼30° and ∼100° about the helical axis to center the drug for visualization. Molecular surfaces of drug and DNA are depicted in transparent red and blue, respectively. Figures created with the program VMD (76).

Extended MD simulations of oligonucleotides in water (57) indicate that some of the DNA conformational and helicoidal parameters have relaxation times of ∼0.5 ns. Thus, at least multi-ns trajectories must be collected to obtain well-converged free energy profiles (58,59). Systems investigated here needed almost 4 ns of equilibration phase, although the PMF landscape roughly converged after 2 ns (see Supplementary Material Fig. S1 for the profile of DSI·DNA; similar results are found for IMI·DNA). A further check on the RMSD of drug·DNA complexes indicates that convergence was reached for all of the windows after ∼4 ns (Supplementary Material Fig. 2S, A and B). Thus, we performed 6 ns of MD simulation on each window (for a total of ∼140 ns), and we used the last 2 ns for extracting the PMF and for the structural analysis of the complexes.

The PMF was decomposed as the sum of individual components, each with a physical meaning and evaluated via the force field terms. In particular, we examined variations in the drug-DNA electrostatic and van der Waals interactions, solute adaptation energy, solute configurational entropies, and solvation free energies. Energetic contributions were evaluated as MD averages, using terms in the force field (25,26,38). Van der Waals interactions were roughly estimated by summing the number of hydrophobic contacts for each atom-type pair. For each of these, the equilibrium distance d₀ of the Lennard-Jones potential was estimated (Supplementary Material Table S3, A and B), and we considered a contact if d < (d₀ + 0.2 Å). Solute vibrational entropies were calculated within the harmonic approximation (60), using the nmode module of AMBER 9 (61). As customary (62–64), we selected a subset of structures for this analysis (20 for each relevant configuration, extracted every 0.1 ns from the last 2 ns). These were minimized in the absence of solvent, using instead a dielectric constant ɛ = 4r (r is the interatomic distance in Å) to mimic solvent effects. Then, up to 20,000 steps of minimization with no cutoff for all the interactions were performed, of which the first 100 are steepest descent followed by conjugate gradient, until the RMS of gradient drops below 10⁻⁴ kcal/(mol·Å). The estimate of relative solute conformational entropies is not a trivial task (63,65), in particular for very flexible systems such as oligonucleotides. Moreover, it is not possible to guess a priori how the “spreading” of the dynamics among the various basins of the free energy surface depends on the conformation (i.e., the position of the drug). Note that also using the quasiharmonic model relative entropies are sensitive to the number of independent snapshots considered (63). Therefore, results on conformational entropies should be taken only as suggestive.

Solvent contributions to free energy were calculated using the molecular mechanics-Poisson Boltzmann surface area (MM-PBSA) methodology (62,63); for each relevant configuration we saved 200 snapshots from the last 2 ns of MD runs. Since 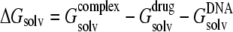and the last two terms in the right-hand side are the same for each configuration of the complex, 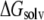is directly proportional to 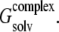Based on this proportionality, only this latter term was evaluated for each relevant configuration of the two complexes. The electrostatic contribution to solvation was evaluated using the Poisson-Boltzmann continuum method (66), as implemented in the module pbsa (67) of AMBER 9. We set the values of internal and external dielectric constants to 1 and 80, respectively, the grid twice as long as the linear dimensions of the solute, and a grid spacing of 0.25 Å. The dielectric boundary is the molecular surface defined by a 1.4 Å probe sphere and by spheres centered on each atom with radii taken from the PARSE (68) parameter set (H = 1.0, C = 1.7, N = 1.5, and O = 1.4 Å, with a value of 2.0 Å for the phosphorus). The boundary dielectric constants were set as the harmonic sum of solvent and solute Debye-Huckel values. Salt effects were not included implicitly in the continuum model. The hydrophobic component of solvation free energy is assumed proportional to the change of the solvent accessible surface area (SASA), 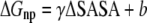where γ = 0.00542 kcal/Ų and b = 0.92 kcal/mol (68). For comparison, we performed MM-PBSA calculations also using a new approach available in the pbsa module of the AMBER 9 package (61,67,69). In this method the nonpolar contribution is cast into two terms, a repulsive one (cavity), correlated to the SASA, and an attractive one (dispersion), calculated through a surface-integration approach (70).

RESULTS AND DISCUSSION

Here we first provide a description of the PMF profiles corresponding to the sliding of IMI and DSI inside the minor groove of oligonucleotides d(GCCAACGTTG*GC)-d(GCCAACGTTGGC) and d(GACTAATTGAC)-d(GTCAATTA*GTC) (IMI·DNA and DSI·DNA) respectively, considering d[C-N] as the reaction coordinate (see Systems and Methods). Note that the standard deviation is very small along the entire sampling interval (≈0.2 kcal/mol, see insets in Figs. 1 and 2), which makes the values of the free energy extracted from our simulations quantitatively reliable. We then analyze, at the qualitative level, the enthalpic and entropic contributions to the PMF from the solute and the effects of the solvent. We close this section by assessing the relevance of end effects (12) on the energetics of the sliding process.

PMF profiles

The PMF of IMI·DNA features four minima (I–IV, Fig. 1). In I, the complex is in its reactive configuration, i.e., carbon C11@IMI faces N2@G10 (d[C-N] ≈ 3 Å). This corresponds to the average structure assumed by the complex during the first 10 ns of a 20 ns long MD simulation (12). From I, a small barrier of 1.5 kcal/mol has to be overcome at transition state I* to reach the absolute minimum II, where d[C-N] ≈ 5.6 Å. In II, C11@IMI sits slightly before the T9 plane (along the direction 3′→5′), and IMI sits at the same location as in the last 10 ns of a 20 ns long MD simulation (12). Interestingly, the barrier from II to I (5.5 kcal/mol) is much larger than that from I to II, consistently with Vargiu et al. (12), which suggests that IMI is stable in II after its departure from I. At larger d[C-N] distances, we find III (7.2 Å) and IV (10.1 Å), in which C11@IMI is located immediately beyond T9 and in front of O2@T8, respectively.

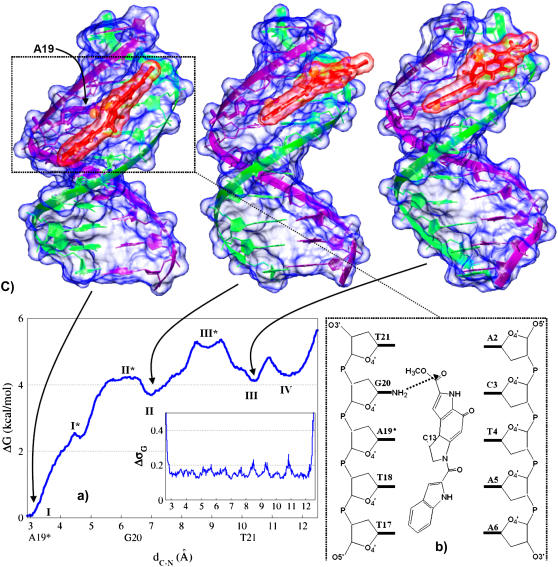
The PMF landscape of DSI·DNA is remarkably different (Fig. 2). Indeed, sliding is hindered by a barrier of ∼4 kcal/mol which traps the drug in the reactive configuration I (corresponding to the absolute minimum in the PMF, along the investigated path). This minimum is followed by three other ones (higher in energy by ∼4 kcal/mol) virtually isoenergetic. In such minima, the reactive group of the drug (in particular C13@DSI) is in front of G20 (II, a very shallow minimum), T21 (III), and between T21 and C22 (IV).

The PMF of IMI·DNA appears to be much rougher than that of DSI·DNA and, in particular, features two configurations corresponding to a larger gain in binding free energy than in the reactive conformation. Results obtained for the two adducts are in line with those extracted from previous MD simulations (11,12) and may partly explain the higher selectivity of duocarmycins as compared to anthramycins (17,33). For instance, in IMI·DNA the reactive configuration should be markedly less populated with respect to II (and competitive with III and IV). In fact, within Arrhenius's theory, and assuming the same prefactor at configurations I and II, the former will be e^(3/0.6) ≈ 150 times less likely. In contrast, in DSI·DNA there is a definite larger gain in the binding free energy at the reactive configuration, with an almost flat PMF landscape elsewhere.

Dissection of the PMFs

The PMF can be interpreted as the change in binding free energy ΔG_b upon drug sliding. To identify the relevant contributions to this process, we can express ΔG_b changes as a sum of individual terms (5,30,71,72). Here we decompose ΔG_b in a term due to solute conformation and interactions between the two moieties (solute terms) and a second one due to the presence of water and counterions (solvent effects):

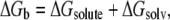(1)

where

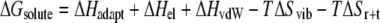(2)

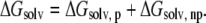(3)

In Eq. 2, ΔH_adapt represents the enthalpic term due to DNA and drug structural deformations upon binding, and ΔH_el and ΔH_vdW are contributions from electrostatic and van der Waals interactions, respectively. We approximately estimated ΔH_adapt and ΔH_el using terms of the AMBER force field (25,26,37,38), whereas ΔH_vdW was assumed to be roughly proportional to the variation in the number of hydrophobic contacts (see Systems and Methods and Supplementary Material Table S3). TΔS_vib and TΔS_r+t are the free energy contributions due to vibrational and translational+rotational entropy changes upon binding. The former was evaluated through normal mode analysis (60), whereas TΔS_r+t was assumed to be sequence independent (32). In Eq. 3, ΔG_solv,p and ΔG_solv,np are respectively the polar (electrostatic) and nonpolar (hydrophobic) contributions to solvation, evaluated here with the MM-PBSA method (see Systems and Methods). We point out that although the PMFs are quantitatively reliable, their dissection into enthalpic, entropic, and solvation terms was carried out using approximated and/or strongly sampling-dependent methods. Thus, these contributions have to be considered qualitatively, and are here used to gain insights into the sources of drug selectivity. In the following, all the values we discuss refer to the reactive configuration in each complex, which is indicated as I.

Solute terms

First, we report the analysis of enthalpic terms for IMI·DNA, summarized in Table 1 and in Fig. 3, a–c, for ΔH_adapt, ΔH_el, and number of contacts, respectively. As shown in Vargiu et al. (12), at I the DNA is distorted in the central C₆G₇ tract with respect to its structure in bulk solvent. The adaptation energy further increases going from I to the maximum I*, whereas drug/DNA interactions weaken. Both this and the previous works indicate that the whole structure relaxes at II (indeed, the conformation assumed by the oligonucleotide is very close to that of canonical B-DNA in aqueous solution), and both electrostatic and van der Waals interactions strengthen. Actually, such interactions are the strongest along the investigated path, whereas the adaptation expense is the lowest. In contrast, the (average) number of direct H-bonds decreases. The subsequent increase in free energy at III* is partially due to the steric clash between the drug acrylamide tail and the amino group of G7. The latter hinders the sliding of the drug, causing a rotation of its principal axis with respect to the oligonucleotide and slightly exposing the molecule to the solvent (see Supplementary Material SM_II). Correspondingly, the number of contacts reaches a minimum in III*, and the minor groove widens in the tract C6…T8 (average width 8 Å with respect to 4 Å at II). Once the guanine amino group is overcome by the drug, a wide free energy minimum is reached in the proximity of T8 (IV). Here, the drug recovers some of the contacts with the DNA backbone.

TABLE 1.

Selected values of solute ΔH_adapt (column II), drug/DNA ΔH_el (column III), number of hydrophobic contacts (column IV), average number of H-bonds (column V), polar (column VI), and nonpolar (column VII) contributions to ΔG_solv

	dC-N (Å)	ΔHadapt	ΔHel	No. contacts	No. H-bonds	ΔGsolv,p	ΔGsolv,np
IMI·DNA	3.2 (I)	0.0(22.7)	0.0(1.6)	15(4)	2.0(0.8)	0.0(34.2)	0.0(2.0)
	3.9 (I*)	+9.6(22.3)	+3.3(1.3)	12(3)	0.9(0.6)	−38.7(50.2)	−2.1(2.4)
	5.6 (II)	−7.0(21.6)	−2.4(1.1)	19(3)	1.2(0.6)	−8.8(47.3)	−4.6(1.8)
	6.5 (II*)	−3.8(21.6)	−1.0(1.8)	13(3)	0.6(0.5)	−17.5(35.4)	+2.0(2.2)
	7.2 (III)	−4.9(22.2)	+1.2(1.1)	11(3)	1.0(0.2)	+11.4(36.7)	+4.2(2.4)
	8.2 (III*)	−1.4(21.8)	+2.2(1.3)	9(2)	0.5(0.3)	−16.4(31.6)	+4.8(1.7)
	10.1 (IV)	−1.5(22.4)	−1.4(1.0)	15(3)	0.5(0.5)	−1.5(53.2)	−2.1(3.0)
DSI·DNA	3.0 (I)	0.0(18.1)	0.0(1.9)	63(10)	0.5(0.3)	0.0(36.0)	0.0(2.0)
	4.3 (I*)	+18.3(18.2)	+6.3(2.0)	47(9)	0.0(0.0)	−60.2(45.6)	+7.4(2.6)
	6.0 (II*)	+18.6(18.1)	+3.6(1.7)	63(11)	0.0(0.0)	−41.3(29.6)	+0.3(2.8)
	7.0 (II)	+17.6(18.2)	+2.2(5.2)	53(12)	0.8(0.4)	−25.6(35.0)	+1.3(2.4)
	8.9 (III*)	+19.9(18.5)	+3.7(2.4)	56(11)	0.0(0.0)	−34.5(40.0)	+1.4(2.5)
	10.3 (III)	+15.7(18.1)	−1.2(2.2)	58(10)	0.9(0.6)	−44.4(41.4)	+3.9(2.0)
	11.9 (IV)	+14.1(18.5)	+5.3(1.5)	54(11)	0.0(0.0)	−49.5(39.1)	+2.9(2.0)

Energies are in kcal/mol and referred to the values at configuration I. Standard deviations are reported in parentheses.

FIGURE 2.

(a) PMF associated to DSI sliding along the DNA minor groove. Standard deviation is reported in the inset. (b) Schematic view of the configuration corresponding to the free energy minimum. (c) Structures of three relevant conformations of the complex. The third structure (from the left) was rotated ∼40° about the helical axis to center the drug for visualization. Molecular surfaces of drug and DNA are depicted in transparent red and blue, respectively.

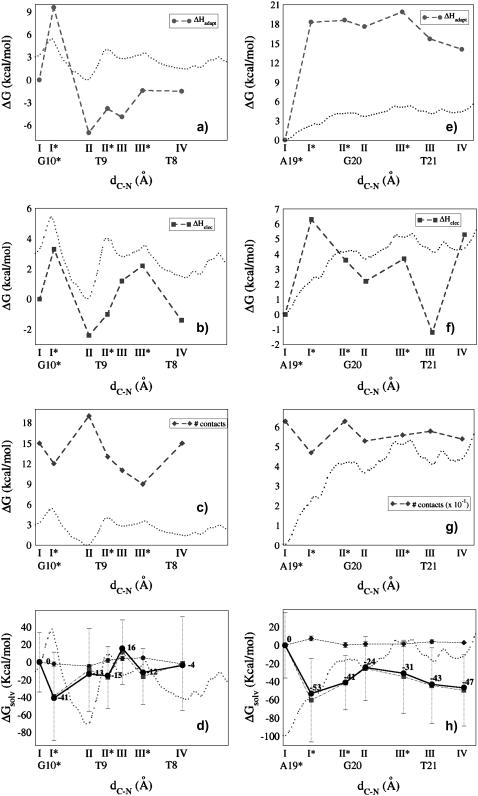
FIGURE 3.

Selected values of (a and e) ΔH_adapt; (b and f) ΔH_elec; (c and g) number of hydrophobic contacts; (d and h) electrostatic (squares, dotted-dashed line), hydrophobic (rhombus, dashed line), and total (circles, solid line) ΔG_solv along the reaction coordinate d[C-N], compared to the PMF (dotted line, and rescaled in (c, d, g, and h) to allow for an easier comparison with ΔG_solv profiles). Data on the left (a–d) refer to IMI·DNA, those on the right (e–h) to DSI·DNA. Solvation free energies were obtained using the method of Luo and co-workers. For a comparison with data obtained using PARSE radii, see Supplementary Fig. S3.

The (solute) enthalpic contributions fairly correlate with the PMF (Fig. 3, a–c), although deviations are present, pointing to the role of solute entropic and/or solvation terms. This is particularly evident at PMF transition states; for example, the sum of the enthalpic terms indicates II* to be lower than III*, whereas in the PMF III* is slightly lower than II* (Table 1). Nevertheless, we can conclude that for IMI·DNA the (solute) ΔH landscape has the same overall trend shown by the PMF.

Concerning solute vibrational entropies, the calculated values at minima of the PMF turn out to scarcely differ (Supplementary Material Table S4), consistent with previous results (12). Given the limitations of the methodology used here (63), we take these values as an indication only that solute entropy does not vary significantly at different configurations.

In DSI·DNA, the free energy absolute minimum I, corresponding to the reactive configuration, shows the lowest ΔH_adapt (Fig. 3 e and Table 1) and the largest number of hydrophobic contacts (Fig. 3 g and Table 1), whereas ΔH_el is very similar to the values in II and III (Fig. 3 f and Table 1). The major source of stabilization in I is the extended pattern of hydrophobic contacts formed between the drug and the DNA, in agreement with experimental suggestions (17,18). The drug is significantly distorted when leaving the reactive configuration: the twist between the two drug moieties increases from ∼20° at I to ∼110° at I*, causing a significant widening of the minor groove (see SM_III). Consequently, the block A (Chart 1), along with the minor groove floor (see also next section and Fig. 3 h), is more solvent exposed, the electrostatic interactions weaken, and the number of drug/DNA hydrophobic contacts decreases drastically. Additionally, the H-bond which forms discontinuously at the reactive configuration is here definitively lost. At II*, both the DNA and the drug are less distorted than in I*, and the number of hydrophobic contacts is the same as in I. Surprisingly, the adaptation cost is essentially the same as in I*. II is characterized by a small gain in electrostatic and adaptation energies as compared to II* and III*, along with the recovery of one H-bond. However, it features fewer hydrophobic contacts than II* and III*. Apart from the reactive configuration, III is the lowest enthalpic minimum; however, its free energy value is almost identical to those at II and IV (Fig. 2 a). In summary, the (solute) enthalpic analysis shows that several points lack correspondence with the PMF, indicating a key role of entropy and/or solvent effects for the sliding process of DSI. Nevertheless, enthalpy contributions unambiguously pinpoint the configuration I as the most stable one, with ΔH_adapt playing a more important role than in IMI·DNA (max ΔΔH_adapt = 18 and 7 kcal/mol for DSI and IMI, respectively).

Finally, we evaluate TΔS_vib at the minima of the PMF. The calculated values show a range of variation comparable to that found for IMI·DNA (Supplementary Material Table S4), and we assume also in the case of DSI to neglect solute entropic contributions to the sliding process.

Solvent effects

The analysis of ΔG_solute carried out above clearly points to the role of solvent for the sliding of the two investigated drugs, in particular for DSI. It is indeed well known that solvent is crucial for nucleic acid structure and stability, and consequently it is important for the binding of drugs to DNA. The development of reliable implicit solvent models and fast finite difference numerical procedures (67–70,73) has made feasible the calculations of solvation free energy via MD simulations. In particular, binding free energies of ligands to DNA calculated with the MM-PBSA method agree fairly well with experimental values (29,30,64).

We evaluate here both electrostatic (ΔG_solv,p) and hydrophobic (ΔG_solv,np) contributions to ΔG_solv, which can be interpreted as the free energy cost for drug desolvation upon binding, using either the “standard” setup (63,68) or the alternative approach available in AMBER (61,67,69,70) (see Systems and Methods). We stress that binding is here always associated to an unfavorable—positive—change in solvation free energy. ΔG_solv profiles evaluated with the two methodologies are very similar, although the second approach (61,67,69,70) highlights the sequence dependence of nonpolar contributions (Figs. 3, d and h, and Supplementary Material Fig. S3). The changes in ΔG_solv turned out to be very large compared to the PMF and characterized by large standard deviations (Fig. 3, d and h), as reported by other authors (30,64). For these reasons, calculated ΔG_solv are only used for qualitative purposes. Nevertheless, some interesting differences between IMI and DSI are observed: i), The cost in desolvation upon formation of the complex ΔG_solv is the highest at the absolute PMF minimum in DSI·DNA (Fig. 3 h), in agreement with the better fit of the drug into the minor groove at I. Already at I*, where drug distortion results in its enhanced solvation, ΔG_solv suddenly decreases and reaches a rough plateau for the other configurations. This behavior mirrors the PMF landscape, where the minimum corresponding to the reactive configuration is the lowest. ii), By contrast, ΔG_solv does not show any clear correlation with the PMF in IMI·DNA. In particular, the deepest minimum in the PMF is not associated with the highest value of ΔG_solv (highest solvation cost). We also notice that density plots for water (SM_II and SM_III) exhibit qualitatively the same trend of the profile of ΔG_solv. In particular, in both IMI·DNA and DSI·DNA I* features, there is more water inside the groove with respect to I, and in IMI·DNA III has the largest desolvation cost, consistent with its very poor hydration (see SM_II). Interestingly, the number of hydrophobic contacts in III is lower than that of II, indicating that this number does not necessarily increase with a lower degree of hydration. This might be due, at least in part, to the “bridging” of the two DNA strands by the drug, which prevents water to access the groove around the binding region (see SM_II).

Within the limitations of our analysis, we conclude that solvent effects may play a key role in DSI·DNA, consistent with the finding that ΔG_solute does not correlate with the PMF. Instead, no clear correlation exists between the PMF and ΔG_solv in IMI·DNA, which is also consistent with the rough correlation found between ΔG_solute and the PMF.

Evaluation of end effects

In our PMF calculations, we selected as starting conformation the alkylation sites of IMI and DSI, as those are the only ones definitely visited by the drugs. These sites correspond to the G10 and A19 in IMI·DNA and DSI·DNA, respectively. (Indicating such nucleobases with the asterisk the sequence are d(GCCAACGTTG*GC)-d(GCCAACGTTGGC) and d(GACTAATTGAC)-d(GTCAATTA*GTC) for IMI·DNA and DSI·DNA, respectively.) When building up the sliding windows as described in Systems and Methods, DSI turned out to slide toward the 3′ end of the strand containing A19, whereas in IMI·DNA the drug moves toward the oligonucleotide center. As a result, the regions explored by the two drugs are slightly different (although it should be noticed that they are comparable, as can be seen from Figs. 1 and 2), and diverse influence of “end effects” (12) might hamper a thorough comparison between the calculated PMFs.

In this respect, we have already shown that end effects play only a minor role on the dynamics of IMI·DNA (12). Here we perform MD calculations to assess the possible influence of such effects on the interaction between DSI and DNA. Specifically, we compare the last 2 ns from MD simulations of two identical tracts DSI·d[GACT]₂ either embedded in the 11-mer DSI·DNA (DSI·d[G₁A₂C₃T₄]₂) or in the 14-mer DSI·DNAc (DSI·d[G₄A₅C₆T₇]₂; see Systems and Methods).

The structure, the conformational flexibility, the hydration of DSI·d[G₁A₂C₃T₄]₂, and DSI·d[G₄A₅C₆T₇]₂ turned out to be rather similar, along with the interactions between DSI and the tracts d[GACT]₂. In fact

1. The structures of DSI·d[G₁A₂C₃T₄]₂ and DSI·d[G₄A₅C₆T₇]₂ are almost superimposable (Supplementary Material Fig. S4), and the calculated RMSD is consistently 0.6 Å. Furthermore, the widths of minor grooves at the binding region are comparable, with or without the presence of three additional nucleobases (Supplementary Material Table S5 and Fig. S4), and, independent from the length of the duplex, DSI does not fit perfectly into the minor groove. In consequence of these structural similarities in both DSI·DNA and DSI·DNAc, the methoxyl-carbonyl ester (Chart 1) of the drug is fully solvated.

2. The number of hydrophobic contacts and H-bonds between DSI and d[GACT]₂ is almost the same (Supplementary Material Table S6).

3. The DSI-O_wat and DSI-H_wat radial distribution functions, which provide information on the solvation of the drug, are rather similar too (Supplementary Material Fig. S5). Consistently, the first and second solvation shells around the drug contain virtually the same number of waters (Supplementary Material Table S5). This is not unexpected due to the excellent superimposition between the two tracts (Supplementary Material Fig. S4) and the comparable hydration of the DSI methoxyl-carbonyl ester. In particular, O14_DSI (Chart 1), which in DSI·DNA is the drug acceptor (pointing to the minor groove) closest to the duplex end, forms in both cases one H-bond with similar lifetimes (Supplementary Material Table S8). Interestingly, the tracts d[G₁A₂]₂ and d[G₄A₅]₂ also do not show relevant differences in their H-bond patterns (Supplementary Material Table S8). Finally, the density plots of waters extracted from MD simulations are rather similar too (Supplementary Material Fig. S6).

4. The values of the root mean-square fluctuations do not differ significantly, apart from the terminal sugar moieties, which are obviously more flexible in DSI·DNA (Supplementary Material Fig. S7).

5. The electrostatic energy between DSI and tracts d[GACT]₂ is exactly the same in both systems (Supplementary Material Table S6).

Summarizing, end effects seem to play a minor role on the interactions between the two drugs and the DNA duplexes, even though they do slightly influence the structure of water within the minor groove. In conclusion, these findings confirm that steric hindrance and optimal interactions with the groove have a prominent role in determining the preferred binding sequence of duocarmycin.

CONCLUSION

The PMFs associated with the sliding of IMI and DSI along the DNA minor groove differ remarkably (Figs. 1 and 2). The reactive configuration is the most favorable for DSI·DNA, whereas in IMI·DNA significant activation energy is required to reach the reactive site moving from the absolute PMF minimum (corresponding to a nonreactive configuration). Results are consistent with previous MD simulations of IMI·DNA (12), showing that the reactive configuration becomes unstable after a few ns and with those of DSI·DNA (11), in which the drug is stable in the reactive configuration for the whole dynamics. Moreover, our findings indicate that the higher specificity of DSI, compared to IMI, correlates with a higher cost for moving the drug from the preferred site, at least for the sequences considered here. End effects turn out not to play a relevant role for the binding.

For both complexes, configurations associated with the absolute minima of the PMF are those with the smallest adaptation cost and the better packing (Table 1). This is consistent with the usual assumption of negligible ΔH_adapt upon drug binding to the preferred sequence in the minor groove (5,30,32). Apart from this common feature, the various contributions to the PMF have different relative weights for the two adducts. In IMI·DNA the changes in enthalpic terms correlate fairly well with the PMF, particularly at the four minima, whereas the ΔG_solv landscape is apparently unrelated to the free energy profile. In DSI·DNA we found instead a rough anticorrelation between ΔG_solv and the PMF profile, whereas enthalpy contributions do not have an overall correspondence with the free energy profile, except for the coincidence of absolute minima.

In summary, our calculations suggest that for alkylating agents, shape complementarity and packing are also significant factors in determining the preferred site of noncovalent binding (30,71,74,75). In addition, they give insights into the way differences in chemical structure, size, and flexibility may influence solvation and molecular recognition along the minor groove. In this respect DSI, due to its larger size relative to IMI, covers more DNA bps and needs to rotate around the linkage between groups A and B (Chart 1) to fit in the preferred sequence. The cost of such a rotation (which was supposed to be a key factor for reactivity) depends on the flexibility and structure of the target DNA sequence. Furthermore, the lack of optimal docking results in a larger drug exposure to the solvent, a feature that we do not find for IMI·DNA, in which drug desolvation cost is uncorrelated to sequence selectivity. This is consistent with the fact that IMI already has the right conformation to fit snugly into the minor groove at different sequences (indeed the reactive configuration does not correspond to a minimum in ΔH_adapt) and features a lower sequence selectivity compared to DSI.

Finally, although speculative, different molecular recognition mechanisms can be proposed for the two drugs investigated here. DSI might first bind to DNA at those sequences characterized by the lowest desolvation cost (the nonpreferred ones) and then easily slide toward the preferred site, corresponding to a funnel in the PMF. In this scenario, solvent effects could be critical for the molecular recognition of DNA by duocarmycins. In contrast, recognition of DNA by anthramycin appears to be more complicated, since, according to our results, no preferred route exists. Moreover, the reactive site can be reached only upon crossing a significant free energy barrier.

Clearly, calculations of free energy barriers to form noncovalent complexes at different sequences, also with drugs other than those considered here, are needed to achieve a general picture of the molecular recognition. However, our results help to rationalize the higher selectivity of duocarmycins compared to anthramycins and point out clearly the possibility of multiple patterns for molecular recognition.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.