Is Arginine Charged in a Membrane?

Abstract

“Charged” amino acids play countless important roles in protein structure and function. Yet when these side chains come into contact with membranes we do not fully understand their behavior. This is highlighted by a recent model of voltage-gated ion channel activity and translocon-based experiments that suggest small penalties to expose these side chains to lipids, opposing the prevailing view in membrane biophysics. Here we employ a side chain analog as well as a transmembrane helix model to determine the free energy as a function of protonation state and position for a lipid-exposed arginine (Arg) residue across a membrane. We observe high free energy barriers for both the charged and neutral states. Due to the stabilizing influence of membrane deformations for the protonated form, the Arg side chain experiences a pK_a shift of ≤4.5 units and remains mostly protonated. The cost for exposing Arg to lipid hydrocarbon is prohibitively high with implications for many membrane translocating processes and the activation mechanisms of voltage-gated ion channels.

Arginine (Arg) is different from other ionizable protein side chains because it really likes to be charged. In fact, its aqueous pK_a of 12–13.7 (1–3) tells us that as little as one side chain in a million may be neutral at pH 7. However, little information is available about the protonation states of ionizable side chains in nonaqueous microenvironments, despite their importance for the structure and function of proteins as well as, for example, the actions of antimicrobial peptides (4), nuclear localization (5), and protein-mediated membrane fusion (6).

An especially interesting situation arises with the voltage-gated ion channels, which utilize Arg side chains to detect transmembrane voltage changes (7). In one particular model, called the “paddle model”, it has been suggested that multiple protonated Arg side chains would move across the membrane, with some being exposed to lipid hydrocarbon (8). This poses two important questions that must be addressed to critically assess such models: what are the underlying thermodynamics governing Arg movement inside the membrane and would Arg remain charged if exposed to the hydrocarbon core?

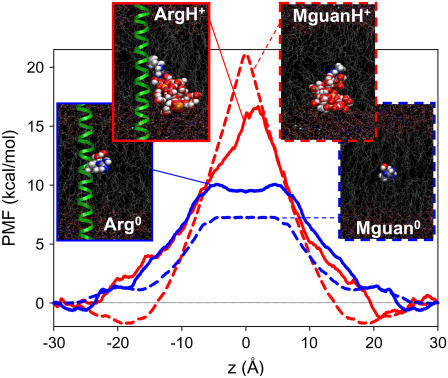
We have previously shown, using fully atomistic molecular dynamics (MD) simulations, that a charged Arg side chain on a model transmembrane segment would experience a large free energy barrier of ∼17 kcal/mol to move across a lipid bilayer (Fig. 1, ArgH⁺) (9). We found that the bilayer will deform around a charged moiety in an attempt to overcome the large dielectric barrier imposed by the membrane. The energetics associated with partitioning from water to the membrane core are therefore not simply associated with dehydration, but also involve strong interactions with water and lipid headgroups drawn into the bilayer core, as well as the free energy costs associated with bilayer deformations.

FIGURE 1.

PMFs for: ArgH⁺ (solid red); MguanH⁺ (dashed red); Arg⁰ (solid blue); and Mguan⁰ (dashed blue). Insets show equilibrated systems for z = 0 Å. Arg (blue/gray balls), helix (green ribbon), DPPC (gray C atoms, orange P atoms), and water (red/white). Atoms in the bilayer core drawn as balls.

This large barrier is in contrast to low (∼2.5 kcal/mol) apparent free energies emerging from cell biology experiments that study the membrane partitioning of a hydrophobic protein segment containing an Arg side chain (10). However, the partitioning environments in this complex translocon system remain unknown and we have shown that those experiments cannot provide spatial definition due to the very design of the host protein (9). Intuitively, however, there may be another explanation for low free energies that involves Arg deprotonation. In fact, experimental studies have shown that nonpolar environments within membrane proteins can lead to large negative pK_a shifts for basic side chains (11,12). But those experiments have not studied the protein periphery and it is not clear that shifts occurring within the protein are related to those of lipid-exposed residues. Thus, currently there exists no experimental results for the thermodynamics or protonation states for ionizable chains in membranes.

We therefore turn to MD simulations to investigate the thermodynamics of both the charged and neutral forms of Arg using well-defined model systems. Although membrane deformations and free energies will depend on the specific sequence and protein fold, we utilize a side-chain analog, methyl-guanidine, as well as a uniformly hydrophobic transmembrane helix, poly-Leu, with central Arg, embedded in a dipalmitoylphosphatidylcholine (DPPC) bilayer. These models allow straightforward interpretation in terms of Arg-membrane interactions, in the absence of other protein interactions, and provide a tractable equilibrium path from aqueous solution to the membrane. Parameters for neutral Arg were developed for this study and shown to reproduce experimental and ab initio energetics (see Supplementary Material).

The insets of Fig. 1 reveal similar deformations to membrane structure whether a charged side chain (ArgH⁺) or analog (MguanH⁺) was forcibly held at its center. Solvation and interaction analysis, reported in the Supplementary Material, reveals similar coordination of ArgH⁺ and MguanH⁺ by approximately five water molecules and approximately one lipid phosphate group, even at the membrane center. The coordination differs, however, at the interface where the analog achieves greater coordination by headgroups and carbonyls (by one to two groups), leading to dramatic variations in interaction energies by up to 100 kcal/mol. The hydration of the analog in the bulk is also increased by two to three waters, which is expected to raise the free energy for the analog to enter the membrane. In contrast, no deformations were seen for the neutral side chain (Arg⁰) or its analog (Mguan⁰); the energetics instead are dominated by dehydration. This absence of deformations is due to water and headgroup interactions being 5–10 times smaller than for charged Arg.

Umbrella sampling (13) was used to compute the potential of mean force (PMF), W(z), as a function of position, z, across the membrane for the helix and analog models (see Supplementary Material). The PMF for ArgH⁺ in Fig. 1 was the result of special biased simulations to overcome difficulties in sampling rotameric states and interfacial connections deep inside the membrane core (9). The problem of sampling interfacial connections is also inherent in the charged analog simulations, likely requiring multimicrosecond simulations for each umbrella sampling window (9), which is currently not feasible. Instead, we have employed a simple procedure (see Supplementary Material) where the correct PMF is

(1)

where k is the Boltzmann constant, T is the temperature, and “near” and “far” indicate PMFs obtained from constrained phase space integrals for two distinct states where the analog is connected to either the near or far interface (with doubly connected states improbable). Differentiating Eq. 1 leads to a Boltzmann-weighted mean force and so this method automatically accounts for force cancellation due to opposite connections near the membrane center and thus the correct PMF shape. Also, because the effect is small (≤kTln2) and is only noticeable within ∼0.5 Å of the membrane center.

Unlike the charged side chain, the resulting MguanH⁺ PMF in Fig. 1 exhibits interfacial binding, owing to greater coordination in the absence of the host helix, and a barrier that is 3–4 kcal/mol higher. The host helix does not just impact side-chain solvation, but also introduces a ∼4 kcal/mol cost for ejecting a nonpolar Leu side chain from the membrane as Arg enters (14). Another difference is the choice of reaction coordinate: either mapping out free energy as a function of helix (where the side chain can snorkel) or side-chain analog position directly. Analysis of a two-dimensional PMF as a function of helix and relative side-chain position (9) reveals that the free energy when the guanidinium is at the membrane center is consistent with the analog barrier.

The neutral side-chain PMF (Fig. 1, Arg⁰) possesses a surprisingly high barrier of ∼10 kcal/mol. We understand this because the translocation involves simple loss of hydration and no membrane deformation to help lower the cost. Moreover, the PMF forms a plateau as dehydration reaches a limit inside the core, rather than climbing to a sharp peak as in the charged case. The neutral analog (Mguan⁰) barrier is ∼7 kcal/mol, lower by ∼3 kcal/mol, and is consistent with experimental partitioning free energies. Apparently the helix has much less effect on the neutral Arg solvation; the dominant contribution being the Leu reference free energy. Importantly, we have revealed large barriers for neutral Arg that suggests deprotonation is not the key to a “free” passage across a lipid membrane.

The typical approach to a pK_a shift calculation is to determine changes in the free energy of deprotonation ΔG_deprot for the process ArgH⁺(z) → Arg⁰(z) + H⁺(aq), at a point z, relative to bulk water z′, directly via a free energy perturbation (15). However, we could not obtain convergence due to the challenge of establishing interfacial connections for partially charged species. We turn instead to a thermodynamic cycle, shown in Fig. 2 A, where ΔΔG_deprot(z′→z) can be seen to equal the difference between the PMFs for charged and neutral Arg,

(2)

FIGURE 2.

(A) Thermodynamic cycle for calculation of deprotonation free energy at position, z, relative to bulk, z′. (B) ΔpK_a profile for the Arg side chain (solid) and analog (dashed).

The pK_a shift for the Arg side chain ( Fig. 2 B) remains close to zero throughout much of the membrane but drops to −4.5 within the central 10 Å. This tells us that an Arg side chain would remain protonated throughout most of the membrane, and that its pK_a would drop to 7.5–9.2 near the bilayer center, where Arg would remain protonated up to 99% of the time at pH 7, and is likely to be always protonated in an acidic medium. Fig. 2 B also shows the ΔpK_a profile for Mguan, revealing a positive shift at the interface due to binding that does not occur for the actual side chain. The ΔpK_a becomes negative within the core, reaching a minimum of −9 and suggesting that the analog would be deprotonated. However, we have shown that energetic variations across the bilayer are exaggerated for the analog molecule and highlights the important role played by the transmembrane segment.

Comparisons with experimental data and ab initio calculations reveal that CHARMM accurately reproduces solvation free energies and Arg-water and headgroup interactions inside the membrane (see Supplementary Material). These studies show that both protonated and neutral PMFs are accurate to within 1–2 kcal/mol and could lead to just ∼1 unit errors in pK_a. Moreover, these errors are almost constant across the membrane, suggesting small effects on pK_a profile shapes.

The lack of deprotonation for the Arg side chain can be attributed both to the large free energy barrier for the neutral species and to the role of membrane deformations that preferentially assist the charged species. Free energy decomposition has shown that the barrier for charged Arg would be doubled without deformations (9), which would lead to complete deprotonation. Interestingly, larger pK_a shifts in nonpolar regions inside membrane proteins (13) may be due to limited hydration and absence of the lipid headgroup interactions that occur for lipid-exposed side chains. Our results suggest that the thermodynamics for Arg on a transmembrane helix would be governed almost exclusively by the protonated state where the barrier for membrane translocation is ∼17 kcal/mol, essentially prohibiting any lipid exposed motion. If a less basic residue such as lysine, with aqueous pK_a ≈ 10.4 (1), were to undergo similar pK_a shifts it would deprotonate inside the membrane. Thus, Arg is a unique side chain that can withstand nonpolar environments, even in the unlikely event that it is isolated in the hydrocarbon core of a membrane.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.