Comparison of the validity of anthropometric and bioelectric impedance equations to assess body composition in adolescent girls

Abstract

Objective:

The purpose of this study was to examine the validity of two anthropometric and four bioelectric impedance (BIA) equations to estimate body composition from dual-energy x-ray absorptiometry (DXA) in adolescent girls of various ethnicities. The rationale for this study was to develop a prediction equation for percent body fat in a multi-ethnic, representative sample of sixth to eighth grade girls.

Design:

One-hundred and sixty-six girls (51 African-American, 45 non-Black Hispanic, 55 non-Hispanic Caucasian, 15 multi-ethnic) participated. Estimates of percent fat and fat-free mass (FFM) from six published BIA and anthropometric equations and the equation developed from this study were compared to body composition determined from DXA. An RJL Systems analyzer was used to measure BIA. Anthropometry included body weight, height, and triceps and calf skinfolds.

Results:

Average (± SD) age, size and body composition was as follows: age, 12.1±1.2 yrs, body mass 52.7±15.9 kg, height, 154.6±8.1 cm; DXA percent fat, 27.9±10.4; fat mass (FM), 15.6±10.2 kg; and fat free mass (FFM) 35.7±6.8 kg. No ethnic differences were found in the relationships between estimated and DXA measured body composition, with the exception of the skinfold equation. The six equations explained on average 82% of the variance in percent fat, 94% of the variance in fat mass, and 88% in fat free mass. Bland–Altman analysis indicated that none of the equations performed satisfactorily in our sample.

Conclusions:

The BIA and anthropometric equations were significantly related to DXA body composition parameters, however none met the criteria for cross-validation.

Introduction

The epidemic of childhood and adolescent obesity [1] has focused attention on the need for accurate field methods to estimate body composition among youth. Characterizing nutritional status during growth, and assessing effects of obesity prevention and treatment interventions among youth require measurement tools suitable for field applications when precise measures such as DXA or hydrodensitometry are not feasible. A number of equations have been developed that estimate body composition from anthropometry (height, weight, skinfolds) or bioelectric impedance (BIA) [2-7]. Both anthropometry and BIA are relatively simple and inexpensive methods compared to laboratory-based procedures such as DXA or hydrodensitometry. A number of skinfold and BIA equations for estimating FM, FFM or body density have been validated against DXA [4] or underwater weighing [5, 8] for specific populations of youth. However, there has been far less effort to cross-validate equations in additional populations. Furthermore, there have been few direct comparisons of equations among a single set of participants in whom appropriate criterion measures are available. Cross validation and direct comparisons would assist in determining which prediction equations are most appropriate for estimating body composition among youth of diverse ethnic backgrounds. There is some indication that prediction equations may not perform equally well in all ethnic groups [9] and therefore comparisons of the performance of equations across ethnic groups would also be useful.

In this study we compared six previously validated equations [2-7] among adolescent girls. Four equations used the BIA method [2, 4, 6, 7] while two employed anthropometric measures [3, 5]. Slaughter et al. [5] and Ellis, et al. [3] included equations exclusively for girls while the other four studies included boys and girls in their equations [2, 4, 6, 7]. The age of the subjects across these studies [2-7] ranged from 3 to 19 years and the sample sizes ranged from 31 [2] to 141 participants [3]. A seventh TAAG equation was developed based on this sample. The data were collected in feasibility phase of the Trial of Activity for Adolescent Girls (TAAG), a multi-site intervention program. We compared measures of percent fat, FM and FFM from DXA scans to estimates of these components from the seven prediction equations. We also compared the performance of these equations in different ethnic groups and described the development of a new equation in this population which was used in the main trial of TAAG. Equations from the six published studies and the TAAG equation can be found in Table 4.

Table 4.

Body composition estimates and coefficients of determination of the various equations.

Method	Percent fat				FM (kg)				FFM (kg)
	M	SD	r2	RMSE	M	SD	r2	RMSE	M	SD	r2	RMSE
DXA	27.9	10.4			15.6	10.2			35.7	6.8
TAAG EQ	27.7	9.8	.88	3.6	15.9	10.2	.96	2.0	36.8	6.6	.92	2.0
BIA
Bray	31.7	8.0*	.84	4.2	17.8	9.8*	.95	2.2	34.9	6.7	.90	2.1
Deurenberg	34.0	6.7*	.84	4.1	18.8	9.3*	.96	2.0	33.9	7.3*	.92	1.9
Goran	30.7	8.9*	.80	4.7	17.2	10.1	.94	2.4	35.4	7.2	.90	2.2
Schaefer	33.7	10.8*	.86	3.9	19.7	12.0*	.96	2.1	33.4	5.2*	.88	2.4
Anthropometry
Slaughter	24.5	8.1*	.74	5.3	13.9	9.0	.89	3.3	38.8	8.2*	.82	2.9
Ellis	30.0	7.9*	.82	4.5	16.9	9.6	.95	2.3	35.8	6.6	.88	1.9

^*P < 0.05 compared to DXA

Equations

TAAG: Percent fat = −23.39 + 2.27 (BMI) + 1.94 (Tri) − 2.95 (Af Am) − 0.52 (age) − 0.06 (BMI × Tri), criterion measure-DXA

DXA adjust FM = 16.0

DXA adjust FFM = 36.7

Bray: Percent fat = (1−(0.4 *R index + 0.148*mass + 3.32) / (0.76* mass)) *100, criterion measure- multiple component

Deurenberg: FFM = 0.448*R index + 0.221*mass + 12.77 *height − 14.7, criterion measure- hydrodensitometry

Goran: FFM = (0.59*R index + 0.065*mass + 0.04) / (0.769 − 0.0025*age), criterion measure-total body water

Schaefer: Percent fat = ((mass − (0.15 + 0.65* R index + 0.68* age)) / mass) * 100, criterion measure-total body potassium

Slaughter: Percent fat = 0.610 * (tri + calf skinfold) + 5.1, criterion measure, multiple component

Ellis: FM (Caucasian or Multi-ethnic) = 0.642*mass − 0.120*height − 0.606*age + 8.98

African-American: FM = 0.0653*mass − 0.163*height − 0.298*age + 10.7

Hispanic: FM = 0.677*mass − 0.217*height + 15.5, criterion measure-DXA

Note

Age (years)

Tri = triceps skinfold (mm)

Af Am = African American

BMI = Body Mass Index (kg·m⁻²)

R = resistance at 50 Hz

Height (cm)

Subjects and methods

Data were collected from a multi-ethnic sample of girls, ages 10–15 years of age residing in three different geographical locations in the United States. Approval for the investigation was obtained from the Institutional Review Boards of the study sites, Tulane University, University of New Orleans, San Diego State University, and the University of Arizona. The University of North Carolina at Chapel Hill was the coordinating center. All parents gave written consent and every girl provided written assent to participate.

Participants

Subjects were recruited by convenience with the goal of including equal numbers of African American, non-Black Hispanic, and non-Hispanic Caucasian girls. Ethnicity was self-reported (http://grants2.nih.gov/grants/guide/notice-files/NOT-OD-01-053.html). Efforts were made to include a wide range in body mass index (BMI) levels. A total of 166 girls participated, with approximately one-third measured at each geographical location. Fifteen of the participants identified themselves as multi-ethnic. Approximately 50% of the subjects had BMI values above the age-specific median (50th percentile) BMI [10].

Procedures

Girls were measured at least three hours after eating during one laboratory visit which lasted approximately one hour. They were asked to wear loose-fitting, lightweight clothing free of metal and to remove all jewelry, hair clips, and shoes. Subjects self-reported information about date of birth, race and ethnicity and underwent the following measurements: height, weight, skinfold thicknesses (triceps and calf), BIA, and percent fat and fat-free mass estimated from whole body DXA scan.

Height and weight

Standing height was measured without shoes using a portable stadiometer (Shorr Productions, Olney, Maryland), and body weight was obtained from a digital scale (Seca 880, Seca Corporation, Hanover, Maryland). Subject weight was recorded to the nearest 0.1 kg and height, to the nearest 0.1 cm. Body height and weight were measured twice and the averages of the two trials were used as the criterion scores. The digital scale was calibrated prior to each measurement session using a 5 kg standard weight [11].

Dual energy x-ray absorptiometry

DXA was used to obtain the criterion measures of FFM and percent body fat. Scans at all three laboratories were made using similar, pencil-beam densitometers from the same manufacturer (Lunar/GE DPX-NT or DPX-IQ, Software version 6.8). The densitometers were calibrated daily against the manufacturer's standard calibration block. Precision (%CV) of fat-free mass values for the three DXA machines ranged from 1–2%. Subjects were scanned in the supine position with their arms by their sides and legs held together with Velcro straps. They were instructed to remain still and not talk during the procedure. The whole body DXA scan took approximately 10 minutes to complete. Tests were conducted and analyzed by a single trained technician at each measurement site. The sum of lean soft tissue, fat and bone mass from DXA was 51.3 kg. Mean scale weight was 1.4 kg higher (52.7 kg). From comparison with cross-validation analysis DXA FM and FFM was adjusted upward by 0.4 kg FM and 1.0 FFM to account for weight discrepancy.

Skinfold measurements

Skinfold thicknesses of the triceps and calf were measured on the right side of the body to the nearest millimeter using a Lange Skinfold caliper (Cambridge Scientific Industries, Inc., Cambridge, MA). Measurements were taken following published guidelines [11] and were repeated in sets of three rotational trials until the difference between the maximum and minimum scores was less than 20%.

Bioelectric impedance

Measures of resistance (R) and reactance (Xc) were obtained using an RJL Systems, Model Quantum II impedance analyzer, a four terminal single frequency impedance plethysmograph with internal calibration. The participants removed their right shoe and sock and reclined in a supine position on a measuring table or a floor mat. The subject's arms were then positioned by their side without touching their body. The subject's legs were positioned so that they did not touch each other. Self-adhesive electrodes were placed on the dorsal surface (top) of the right hand and right foot. Prior to placement of electrodes the skin was wiped with alcohol. Two trials collecting resistance (R) and reactance (Xc) were performed and recorded for each subject. The mean of these two trials was used for analysis.

Development of the TAAG Equation

A prediction equation for percent fat was developed from various demographic and body composition parameters. The independent variables measured in this sample were ethnicity, age, height, weight, calf skinfold, triceps skinfold, and resistance, resistance index (HT²/R), and reactance bioelectric impedance analysis. The validity of the equation was evaluated using the jackknife technique [12]. This technique is appropriate for estimating validity within a sample.

Statistical analysis

Descriptive statistics (means and standard deviations) were computed for the total sample and separately for African-American, Caucasian, Hispanic and Multi-Ethnic girls using anthropometry and BIA indices. Linear regression analysis was used to describe associations of percent fat, FFM and FM values determined from DXA with corresponding estimates from all seven equations examined. Also of interest was whether the prediction equations performed differently in girls of differing ethnicity. We examined this issue by testing for differences in the slopes of the relationships of body composition values estimated from each prediction equation with the criterion measure from DXA. Independent t-tests were employed to compare the mean predicted values from the respective equations with DXA criterion values. Bland-Altman analysis [13] was conducted to assess the agreement of anthropometric or BIA equations and DXA in determining percent body fat. Data were analyzed using the Statistical Analytic Software (SAS Institute, Cary, NC). Statistical significance was set at the 0.05 level.

Results

Physical characteristics of the participants can be found in Table 1. A total of 166 girls completed all testing. The ethnic composition of the sample was 31% (n= 51) African-American, 27% (n=45) Hispanic, 33% (n=55) Caucasian and 9% (n=15) Multi-ethnic. The African-American girls had a greater body mass, body mass index and BIA resistance (Ω) than the Caucasian girls. Age, height, BIA reactance (Ω), and skinfolds were similar across groups.

Table 1.

Physical characteristics of the subjects.

Variable	African-American n=51		Hispanic Caucasian n=45		Multi-Ethnic n=55		Total n= 15		Group n=166
	M	SD	M	SD	M	SD	M	SD	M	SD
Age (y)	12.0	1.1	12.3	1.1	12.1	1.3	12.5	1.0	12.1	1.2
Height (cm)	155.5	7.7	153.8	7.9	154.4	8.9	152.7	7.1	154.6	8.1
Mass (kg)	56.4	18.4*	52.1	14.9	50.0	14.3	51.6	14.7	52.7	15.9
BMI (kg. m2)	23.1	6.4*	21.8	5.3	20.6	4.8	21.9	5.1	21.8	5.5
BIA
Reactance (Ω)	62.2	8.0	62.3	5.1	61.1	7.6	64.8	7.5	62.1	7.5
Resistance (Ω)	608.3	81.3*	652.2	78.5	643.2	86.0	653.9	71.7	635.9	82.2
Skinfolds
Calf (mm)	16.8	7.6	14.9	6.3	16.0	6.7	16.3	6.2	16.0	6.8
Triceps (mm)	16.6	8.2	14.9	5.7	15.4	6.1	17.1	6.7	15.8	6.8

^*P < 0.05 compared to the Caucasian girls

Mass, BMI and resistance significantly differ in African-American versus Caucasian girls. No other significant differences (see text).

In regard to the TAAG equation developed for this study the best fit model for percent fat with the fewest anthropometic predictors yielded an R² of 0.883 with a root mean square errors (RMSE) of 3.61 (Tables 2 and 3). The equation was: DXA percent fat = −23.39 + 2.27 (BMI) + 1.94 (Triceps skinfold, mm) − 2.95(race) − 0.52 (Age, yrs) − 0.06 (BMI x Triceps skinfold, mm) (Table 3). In this equation, if the participant was African-American, race = 1. If the participant was not African-American, race = 0. The jackknife analysis reduced the R-square from 0.883 to 0.874 and increased the RMSE from 3.61 to 3.67.

Table 2.

Regression analysis to predict DXA from anthropometric variables.

Variables	R2	CV %	RMSE
BMI, tricep, race	0.813	16.27	4.53
BMI, tricep, race  BMI*tricep	0.880	13.10	3.65
BMI tricep, race, age,  BMI*tricep	0.883	12.97	3.61

Table 3.

Regression coefficients of TAAG percent fat prediction equation.

Independent variable	Regression coefficient	Standard error	t-value	P-value
Intercept	−23.39	3.691	−6.34	<.0001
BMI (kg/m2)	2.27	0.157	14.43	<.0001
Triceps (mm)	1.94	0.157	12.39	<.0001
Race (African American=1, Other =0)	−2.95	0.627	−4.72	<.0001
Age (years)	−0.52	0.253	−2.07	0.0401
BMI*Triceps	−0.06	0.006	−9.75	<.0001

Note: R² = 0.88, RMSE = 3.61

An important question for the present study is whether the prediction equations are equally accurate for girls of different ethnicity. We tested for interaction between measures derived from each prediction equation of ethnicity using DXA measured variables as the outcome. Using ethnicity as a 4 level categorical variable (Caucasian, African American, Hispanic and Multi-Ethnic) there were statistically significant interactions only for the Slaughter et al. [5] equation for FFM (P < 0.05) and FM (P < 0.001). The relationship between FFM estimated from the Slaughter equation [5] and FFM from DXA in the African-American girls showed a steeper slope compared to other ethnic groups. Conversely, the slope for the relationship between FM estimated by Slaughter, et al. [5] and FM from DXA was flatter in African American girls. Because the associations of estimated FM, FFM, and percent fat were similar across all ethnic groups (with exceptions described above), we combined ethnic groups for the remaining analyses.

Estimates of body composition, coefficients of determination (r²) and RMSE are presented for percent fat, FM and fat-free mass in Table 4. Percent fat and FM were over-estimated by 2.8 to 6.1 percent and 1.3 to 3.2 kg respectively, by the Bray et al. [4] Deurenberg et al. [6] Ellis et al. [3] Goran et al. [2] and Schaefer et al. [7] equations while the Slaughter et al. [5] equation under-estimated percent fat (3.4 percent) and FM (1.7 kg). In regard to FFM, the equations by Deurenberg et al. [6] and Schaefer et al. [7] under-estimated FFM while the Slaughter et al. [5] equation over-estimated FFM. FFM values estimated by the Bray et al. [4] Goran et al. [2] and Ellis et al. [3] equations were similar to DXA values. The Slaughter et al. [5] equation using only skinfolds yielded the lowest r² values for the various components of body composition. Higher r² values were found for all of the equations when examining the relationship between DXA and FM across equations and slightly lower r² values were found with FFM. The r² for BMI and percent fat in this sample was 0.83.

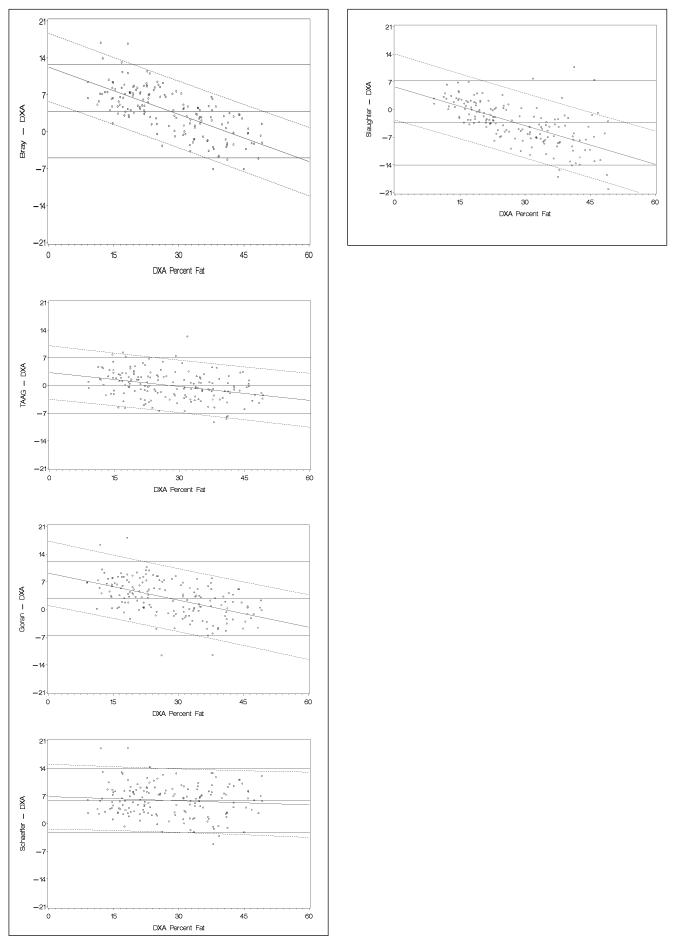
The results of the Bland-Altman analyses are shown in Table 5 and Figure 1. Several equations over-predicted percent fat. The differences between methods (each equation versus DXA) were correlated with the absolute percent fat (DXA) and the slopes of the lines were also examined. We expect a slope for each equation close to zero and a mean difference within ± 3 units for an equation to be cross validated against a new sample. In general, we observed significant correlations between the differences and absolute values which indicated that the magnitude of direction of the error was dependent on the absolute values of percent fat. Correlations for the Bland-Altman analyses ranged from r = −0.09 [7] to −0.85 [6]. Moreover all of the slopes for the various equations were significantly different from zero (−0.23 to −0.41) with the exception of Schaefer, et al. [7] (−0.03). We selected 4 equations to illustrate results using the Bland-Altman approach (see following page).

Table 5.

Comparison of equations for percent fat estimation.

BIA equations	Average			Bland-Altman Limits of agreement
	Diff	r	Slope
BIA equations
Bray – DXA	3.9	−0.69	−0.30*	−5.0, 12.8
Deurenberg – DXA	6.2	−0.85	−0.41*	−3.8, 16.2
Goran – DXA	2.8	−0.51	−0.23*	−6.5, 12.1
Schaefer – DXA	5.9	−0.09	−0.03	−2.2, 14.0
Anthropometry equations
Slaughter – DXA	−3.4	−0.64	−0.33*	−14.0, 7.3
Ellis – DXA	2.1	−0.70	−0.31*	−7.3, 11.5
TAAG EQ – DXA	−0.2	−0.35	−0.12*	−7.3, 7.0

^*P < 0.05

Note: Bland - Altman limits of agreement = ±2 SD

The slope was computed from the association of the criterion score and the respective equation.

r = correlation between the residual and absolute criterion method

Figure 1.

Bland-Altman plots for percent fat.

Discussion

The assessment of weight status or adiposity in developing adolescents is challenging. Weight alone is often not useful because the value does not consider changes in body composition that accompany expected increases in weight due to normal growth [14]. BMI, which adjusts weight for height, is a useful tool when examining large populations of youth [15]. However, because it is based on the growth and development patterns of Caucasian youth, its prediction of adiposity is limited in adolescents of different ethnicities [16, 17]. Moreover, the predictive value of BMI is even less in very lean and very overweight adolescents [14]. In our case we found BMI alone accounted for 55% of the body fat variance. Health professionals must, therefore, rely on measures of body composition to accurately interpret weight status in youth. The determination of body composition is important in nutrition studies that focus on the regulation of growth and development and clinical evaluations of adolescents with chronic disease. Accurate assessment of individual compartments (eg FM, FFM) also ensures appropriate scaling when normalizing other measured variables such as resting metabolism or fitness [18].

The most accurate measures of body composition are obtained from laboratory-based procedures based on multi-component models or the use of DXA which allows for independent estimates of fat, muscle and bone density; however, such relatively expensive measures are not readily available in field and clinical settings [18]. In regard to the six equations examined from the literature, DXA was used as the criterion method in the Ellis et al. [3] equation and as part of a multi-component model in Bray, et al. [4]. In the Slaughter et al. [5] equation, the authors used a multi-component criterion equation which included single-photon absorptiometry.

In contrast to DXA, anthropometry, skinfolds, and BIA are relatively simple and inexpensive methods that have been used extensively in adolescent research [19, 20]. The appropriate choice of prediction equation will vary by setting, population, and purpose. In a situation in which the most accurate values are desired and few of the participants will be at either end of the distribution for body composition, equations with the smallest possible actual differences from DXA will be most desirable, such as the Goran et al. [2] equation for FFM. By contrast, for intervention studies in which the primary interest is in change over time, knowing that the equation estimates equally well across the entire distribution of body composition will be important. This would make the Shaeffer et al. [7] equation a candidate for estimating percent fat, however the large systematic error is a detriment. In general, the broader the distribution of body sizes in a group to be measured, the greater the importance of an equation that estimates equally well across the range of values. With an equation that estimates equally well across the distribution of body size, a correction factor can be applied to all estimates that will work equally well for all participants.

The pattern of over versus underestimation of DXA measured FM, FFM, and percent fat from anthropometric equations that included BIA was not unexpected. BIA is most clearly related to FFM because of the contribution of body hydration to reactance and resistance values. Typically, stature² / bioelectric resistance is highly correlated (r > 0.90) with FFM [20]. In an earlier cross-validation study, Houtkooper et al. [22] reported an adjusted r² of 0.95 with a standard error of 2.1 kg when BIA was used to estimate FFM from hydrodensitometry adjusted for body water (deuterium dilution) in a group of 94 youth aged 10.2 to 14.7 years. In the current paper, the FFM RMSE ranged from 1.9 to 2.4 kg (Table 4). Thus, the equations yielded similar results as Hootkooper [22] for FFM. However, RMSE for percent fat and fat mass were larger for anthropometric equations that included BIA than anthropometric equations that did not include BIA. Further, percent fat and fat weight were consistently overestimated by these equations in comparison to DXA values, at least for the thinner and normal weight girls.

All of the anthropometric equations that included BIA over-estimated percent fat in the underweight but under-estimated percent fat in the overweight, with the exception of the Schaeffer equation [7]. Okasora and colleagues [2] compared body composition estimated by anthropometry and BIA to body composition measured by DXA in 44 girls and 60 boys, aged 6–19 years. BIA percent fat was highly related to DXA percent fat (r² =0.81) for the total sample. However, there was a tendency for BIA to under-estimate percent fat in the overweight subjects and over-estimate percent fat in the underweight subjects as based on percent ideal body weight. Similarly, Fors et al. [24] showed BIA overestimated percent fat in lean children. Thus, our results are similar to those by Okasora et al. [23] and Fors et al. [24]. In contrast, Eisenkolbl et al. [25] after applying a BIA formula [26], found that BIA and DXA were not as highly correlated (r² = .68) and that BIA underestimated percent fat by 12% when compared to DXA [25]. It is clear from the literature that the accuracy of estimating percent fat with BIA is largely due to matching the correct formula to the specific race, gender, age and weight status of the individual. The subjects in the present study were ethnically diverse females. Therefore, equations derived from studies of male and female Caucasian youth may be less accurate than those developed in studies of a given target population.

With regard to the validity of anthropometric equations, the Ellis et al. [3] equation (mass, height, age) over-estimated percent fat while the Slaughter et al. [5] equation under-estimated percent fat. Both equations yielded FM values that were not different from DXA and only the Slaughter et al. [5] equation over-estimated FFM. Even though the Ellis et al. [3] equation over-estimated percent fat, the mean value (30.0%) was similar to the other methods (BIA, skinfolds). Therefore, including only age, weight and height as independent variables, Ellis et al. [3] found comparable body composition estimates as those including BIA or skinfolds as independent variables.

In addition to examining the validity of published equations, we also developed a new equation which included triceps skinfold, body mass index, age and ethnicity (Table 2). Since it was developed (validation, not cross-validation) in this data set, it represents the best ‘fit’ and provides a comparison by which to judge the accuracy of the cross-validated equations. Any cross-validated equation with an RMSE approaching the RMSE for the TAAG equation is likely to be a useful equation. The validity of this equation was examined using the Jackknife technique [12]. As noted in the results, the R² using this method was slightly reduced from 0.883 to 0.874 and the RMSE slightly increased from 3.61 to 3.67. Thus this manipulation had very little impact on the results. Nevertheless, this new equation needs further testing for its applicability to girls of a greater age range and other samples.

In summary, previously published regression equations that included anthropometry and BIA as independent variables generally over-estimated DXA measured percent fat and under-estimated FFM. By comparison, regression equations that included anthropometry and skinfolds, but no BIA information, underestimated DXA measured percent fat and over-estimated FFM. All of the equations examined in the present study did not meet acceptable criteria for cross-validation as field measures of body composition for female youth.