Integration of local pattern elements into a global shape in human vision

Abstract

The spatial extent of the cortical filters selective for different spatial frequencies and orientations is limited. We studied psychophysically how information from the local filters is integrated into global pattern shapes, i.e., whether performance in the identification of a global pattern consisting of small, locally oriented Gabor elements depends on the orientations of those elements. The observer was presented with an E-like stimulus pattern shape comprised of oriented Gabor patches on a blank background, and the performance measure was the threshold contrast for identifying the orientation of the E pattern (four possible rotated orientations). The results showed that contrast thresholds were significantly lower when the local elements all shared the same orientation (e.g., all horizontal) compared with the condition in which the elements had mixed orientations (both horizontal and vertical). The enhancement effect due to uniform local orientations can be explained by two factors: One is local facilitatory interactions between the orientation selective filters, and the other is second-order information integration across the filters.

Neurophysiological studies in the primate visual cortex have convincingly indicated that early visual processing occurs in a spatially discrete manner, i.e., the spatial extent of cortical receptive fields, selective for different spatial frequencies and orientations, is limited (1, 2). Much less is known about the mechanisms by which these discrete samples are integrated into coherent percepts of visual objects. Of interest, recent evidence from single-cell recordings in the monkey cortex suggests that some integration of local information into a global pattern structure may take place quite early, already at the level of V1 and V2 areas of the visual cortex (see, for example, refs 3–5).

Using psychophysical techniques, several studies have investigated the mechanisms that mediate the integration of local elements into a global pattern (6–13). For instance, in one line of investigation, Field et al. (9) studied the ability to detect a contour comprised of oriented Gabor elements among a background also consisting of similar elements. The orientations of the Gabors in a contour to be detected were correlated whereas the elements in the background had random orientations. Their key finding was that, to detect the contour, the orientations of the Gabor elements had to be aligned along a contour path, i.e., performance deteriorated significantly if the orientations of the Gabors were orthogonal to the path.

In most of the recent studies concerned with the integration of local stimulus information into global patterns, the observers’ task was to segregate a target pattern embedded in background noise. In the present study, we attempted to study integration directly by presenting the observer with a single stimulus pattern to be identified in the absence of any background noise. Specifically, the display contained a global pattern shape (an E-like pattern in one of four orientations) consisting of a number of small local elements (oriented Gabor patches) on a blank background, and the performance measure was the threshold contrast for identifying the global pattern (see Fig. 1).

Figure 1.

Suprathreshold illustrations of stimulus patterns used in the experiments. (A) All 17 Gabor elements forming an E pattern share the same orientation. (B) In the stimulus condition of mixed orientations, there are both horizontal and vertical elements in a pattern. (C) An E pattern when the sampling rate is 80%, and all Gabor elements are vertical. (D) Sampling rate is 80%, and the elements are both horizontal and vertical. (E) An E pattern where the center-to-center distance between the Gabor elements is 6 σ (A–D have a center-to-center distance of 3 σ). The elements in this experiment were the same size as in A–D. They were photographically reduced in size.

The purpose of these experiments was to test whether performance in identification of a global pattern consisting of locally oriented Gabor elements depends on the orientations of the local elements, i.e., how information from orientation selective filters is integrated into a global pattern shape. Specifically, we tested whether contrast threshold for identification of a single global pattern is lower when the local elements all share the same orientation (e.g., all horizontal) compared with the condition in which the elements have mixed orientations (i.e., both horizontal and vertical).

METHODS

Stimuli (shown in Fig. 1) were displayed on the face of a Mitsubishi (Nagasaki, Japan) Diamond Scan 20H monitor using a Cambridge Research Systems (Cambridge, U.K.) VSG 2 graphics card with a resolution of 1152 × 960 pixels housed in a Dell 450/M computer. The pixel size was 0.245 × 0.245 mm, and the frame rate was 72 Hz in noninterlaced mode. The average luminance of the display area was 56 cd/m² (2). Gamma correction was applied using one of five palettes of 256 colors from a possible range of 4096 gray levels. The dynamic range and gray level increment was adjusted so that, for the low contrast stimuli used in our study, the smallest contrast step size was on the order of 0.05%. The observer viewed the screen binocularly from a distance of 1 m with normal overhead (fluorescent) illumination.

The pattern to be identified on a blank background was comprised of up to 17 Gabor elements, i.e., the luminance distribution [G(x, y)] of one element is described by a product of circular Gaussian and oriented sinusoid:

1

where σ determines the SD of the Gaussian envelope, θ the orientation, p the period of the modulating sinusoid, and φ the phase of the grating.

In our experiments, σ was fixed at 10 pixels (8.42 arcmin), and the envelope was truncated at + and −1.5 σ [i.e., full width (3σ) of 30 pixels]. The period, p, was set to 10 pixels (i.e., the carrier spatial frequency of each Gabor patch was 7.12 cycles/deg), and the spatial frequency full bandwidth (specified at half the peak amplitude) was 0.55 octaves (the spatial frequency full bandwidth is ≈0.55/N octaves, where n is the number of cycles of the grating within one σ (14) (in our experiments n = 1).

The Gabor elements formed an E-shaped global pattern presented in one of four rotated orientations (up, down, left, or right), and the observer’s task was to identify the pattern orientation (i.e., a four-alternative, forced choice). Unless otherwise specified, the distance between the centers of the Gabor elements was 3 σ, the total size of the global “E” was 2.1° square, and the full extent of the uniform background was 7.7°.

We used two stimulus conditions to study the integration of local elements into a global pattern; in the first (same local orientation), all of the Gabor elements shared the same orientation (θ was either all horizontal or vertical). In the second condition (mixed local orientations), the elements were both horizontal and vertical (with a probability of 0.5 of each element being horizontal or vertical).

Global integration may be more critical to pattern recognition under nonoptimal conditions, e.g., when there is sparse local information, so we varied the number of local elements in the pattern. Thus, a “fully sampled” E pattern was comprised of 17 Gabor elements, and an “undersampled” pattern was comprised of fewer elements (Fig. 1). Undersampling was accomplished by displaying only a specified proportion (60% and 80%) of the Gabor elements (drawn from a uniform distribution) comprising the E pattern. The locations of the elements of an undersampled E pattern were not identical from trial to trial but were randomly selected for each trial. The “missing” elements were replaced by a uniform field.

On each trial, an E pattern was flashed for 500 msec (accompanied by a tone) in the center of the screen, after which the observer gave her/his response by pressing one of four buttons indicating the orientation of the global pattern. Visual feedback was provided after each response.

Contrast thresholds for identifying the orientation of the E pattern were estimated using the method of constant stimuli. Psychometric curves (with five near-threshold contrasts) were obtained for each stimulus condition and sampling rate, and contrast thresholds were estimated based on the Quick algorithm for finding a threshold and slope for a Weibull function. Each estimate, corresponding to the contrast resulting in d′ = 1.0, was based on 125 trials. Final contrast thresholds presented in Results refer to the means of at least four individual threshold estimates. Four practiced observers with normal or corrected-to-normal vision participated in the study. Three of the observers were the authors (B.S., J.S., and D.L.) whereas L.V. was not aware of the purpose of the experiments.

RESULTS AND DISCUSSION

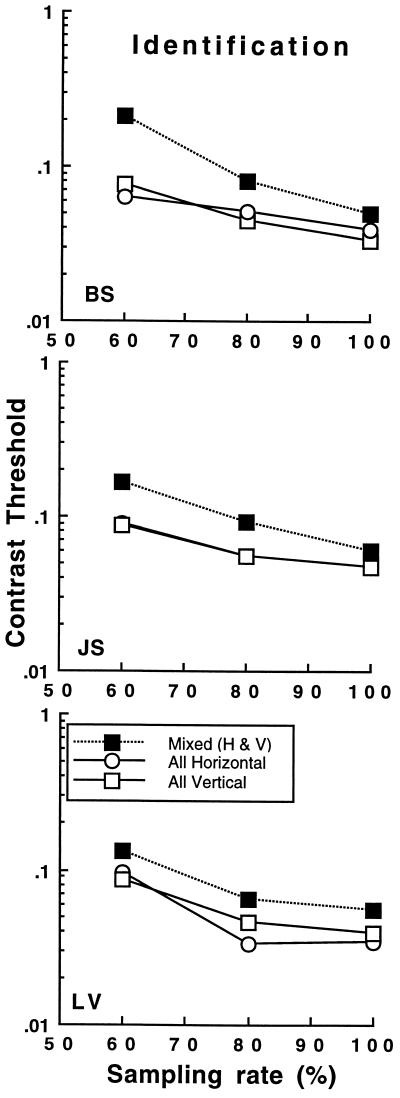
The results shown in Fig. 2 suggest that identification of a global shape is significantly easier when the local elements share the same orientation (horizontal or vertical) compared with the condition when the elements can be both horizontal and vertical. Because contrast thresholds in the stimulus conditions of uniformly horizontal or vertical local orientations were identical, poorer performance in the condition of the mixed orientations could not be due to a possible asymmetry in perceiving horizontal and vertical stimuli. The undersampling of an E pattern resulted in higher thresholds both for the stimulus patterns of uniform and mixed Gabor orientations. For observers B.S. and J.S., performance difference between the conditions of uniform and mixed orientations was somewhat larger with the undersampled stimulus patterns. This trend, however, was not apparent for L.V.

Figure 2.

Contrast threshold for identifying the orientation of an E pattern plotted against the percentage of pattern sampling in two stimulus conditions; all Gabor elements comprising an E pattern shared the same orientation (all horizontal or vertical), or there were both horizontal and vertical elements in a pattern. The SE of contrast thresholds were less than the size of the symbols. Observers were B.S., J.S., and L.V.

To summarize, our results suggest that the mechanisms mediating the perception of a global pattern shape integrate pattern elements more readily when the orientations of those elements are identical, i.e., the pattern perception mechanisms seem to prefer information integration from orientation selective filters tuned to similar orientations (cf. refs. 9 and 12).

In one control experiment, we investigated whether the performance enhancement observed was due to an improvement in the ability to integrate the global shape of local elements per se or whether it resulted from improved visibility of the stimulus patterns. We tested these possibilities in an experiment in which the observer did not have to identify the orientation of an E pattern but simply had to detect it. Detection thresholds were determined using a two-alternative, forced-choice technique; an E pattern at one of four rotated orientations was randomly presented in one of two temporal intervals of 500 msec (signaled by two tones with an interstimulus interval of 500 msec), and the observer’s task was to report which interval contained the E pattern (the nontarget interval was a blank field of the mean luminance). Auditory feedback was provided after each response. The Gabor elements, their center-to-center distance (3 σ), and the procedure for estimating contrast thresholds (also specified at d′ = 1.0) were identical to those in the first experiment.

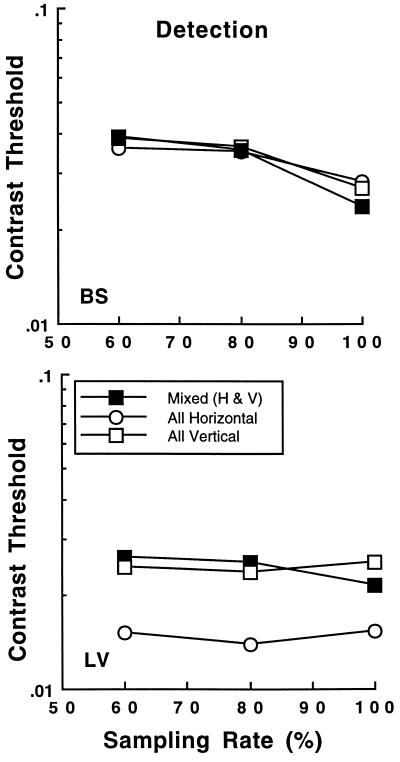
As might be expected, contrast thresholds were lower for detection than identification of an E pattern, and performance differences between the stimulus conditions of uniform and mixed local orientations were much smaller when the task was not to identify pattern orientation but just to detect the presence of the pattern (Fig. 3). For B.S., the stimulus conditions of uniformly horizontal/vertical and mixed orientations produced identical performance. L.V. had an asymmetry between horizontal and vertical orientations so that thresholds for the horizontal Gabors were lower than for the vertical ones. However, her thresholds for the condition of the uniformly vertical orientation were identical to those for the condition of mixed orientations.

Figure 3.

Contrast threshold for detecting the presence of an E pattern plotted against the percentage of pattern sampling in two stimulus conditions. Other details as in Fig. 2.

The results of the detection experiment thus suggest that enhancement in the identification of an E pattern consisting of uniformly oriented local elements did not simply result from improved visibility in the condition of identical orientations. Rather, our results suggest that the integration of pattern elements into a global shape per se may depend on local orientations.

To test how “global” these integration mechanisms are, we varied the distance between Gabor elements. If the enhancement in pattern identification due to uniform local orientations is reduced or eliminated when the inter-element distance is increased, it would suggest that integration across similarly oriented elements can take place only within areas of some limited spatial extent. The size of Gabor elements, the identification task, and the procedure for estimating contrast thresholds were identical to those of the first experiment, except that the distance between the centers of two Gabors was now shorter (1.5 σ, ≈12.6 arcmin) or larger (6 σ, ≈50.5 arcmin) than in the main experiment (3 σ, ≈25.2 arcmin), as shown in Fig. 1E.

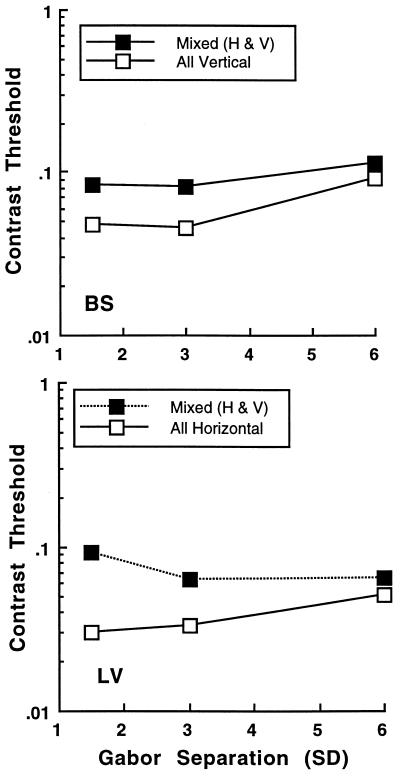
The results of this control experiment (Fig. 4) show that, when the Gabor elements in an E pattern were spaced at a distance of 6 σ (50.5 arcmin) from each other, the enhancement in the identification of the global pattern shape due to the uniform local orientations was greatly diminished. Hence, the mechanisms that integrate information from orientation selective filters tuned to similar orientations seem to operate only over a limited distance. The integration distance of up to 6 σ was equivalent to the maximal range of spatial interactions (five to six periods of the Gabor patch) obtained in a collinear stimulus configuration by Polat and Sagi (15, 16) using a masking paradigm (because in our configuration, one period = σ).

Figure 4.

Contrast threshold for identifying the orientation of an E pattern as a function of inter-element distance. Only one sampling rate (80%) was used in this control experiment. Other details as in Fig. 2.

As noted in the Introduction, there is strong evidence that a contour embedded in a background noise is detected more readily when the orientations of the local elements forming the contour are aligned along it (9). Our psychophysical task (contrast threshold measurements for pattern identification) was quite different from figure-ground segregation tasks that have been used in most of the previous studies concerned with the integration of local stimulus information into a global shape. However, it is possible that the performance enhancement obtained with uniform local orientations in both paradigms might result from a similar phenomenon, i.e., the alignment of Gabor elements along the contours of an E pattern aids integration of local elements and thus the perception of the global shape. We used an E-shaped configuration randomly in four orientations as a stimulus pattern, so the orientations of the Gabor elements forming the four E contours were not exclusively either aligned with or orthogonal to the contours, but an “E” always contained both “aligned” and “orthogonal” local elements.

To study whether the enhancement in the integration of pattern elements due to identical local orientations can be completely explained by the effect of orientation alignment along a global contour, we ran an additional control experiment in which the alignment of local and global orientations was controlled. Instead of using E-shaped patterns of four global contours (“lines” forming an “E”), the stimuli in the control experiment contained three parallel global contours (“bars”), which consisted of Gabor elements identical to those of the first experiment. Specifically, the three parallel global contours were the “legs” of the E-like pattern, without the “backbone.” The three contours were randomly either horizontally or vertically oriented, and the observer’s task was to indicate their global orientation as a two-alternative forced-choice. As in the previous experiments, contrast threshold (specified at d′ = 1.0) for identifying the orientation of the stimulus pattern was estimated. There were three stimulus conditions in this control experiment: In the first condition, all of the local Gabor elements were always aligned with the global contour irrespective of whether it was horizontal or vertical. In the second one, the orientation of the Gabor elements was always orthogonal to the global contour, and in the third condition, individual local elements could randomly be aligned with or orthogonal to the contour (mixed local orientations).

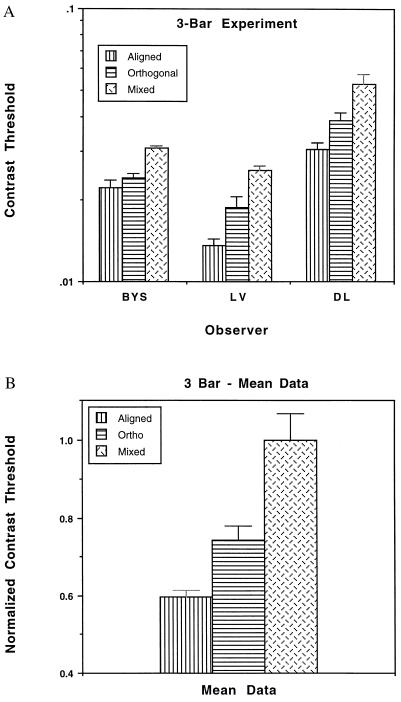
The results of the control experiment (Fig. 5) indicated that the performance enhancement in the stimulus condition of uniform local orientations resulted, at least in part, from the alignment of local orientations along global contour orientations; when the Gabor elements were aligned with the global contour, contrast thresholds were somewhat lower than when they were orthogonal to it. It has to be emphasized, however, that thresholds in both conditions of uniform local orientations (aligned and orthogonal) were significantly lower than in the condition of the mixed local orientations. If we make the assumption that, at the low contrast levels (near threshold) used in our study, cross-orientation inhibition is unlikely, then our results suggest that there are probably two different kinds of enhancement effects. Orientation alignment along the contour axis cannot fully explain the enhancement effects reported here.

Figure 5.

Contrast threshold for identifying the orientation (horizontal vs. vertical) of three parallel global contours consisting of small local Gabor elements. Thresholds were determined in three stimulus conditions. The local elements were either all aligned with or all orthogonal to the global contour or they could be both aligned and orthogonal (i.e., mixed). Only one sampling rate (100%) was used. (A) The three observers’ individual thresholds. (B) Contrast thresholds in the stimulus conditions of aligned and orthogonal Gabor orientations were normalized with respect to the thresholds when the Gabor orientations were mixed. The columns represent the means of the three observers.

To summarize the result of this control experiment, the uniform orientation of local elements may produce two kinds of enhancement effects in the integration of those elements into a global shape. One is due to the alignment of local elements along the orientation of a global contour; the other may result from a second-order information integration from the orientation selective filters tuned to similar orientations. Thus, uniform orientation produces enhanced performance both when local and global contours are aligned and when they are orthogonal (relative to performance with mixed orientations).

The enhancement of integration due to the alignment of Gabor elements is probably based on local interactions that facilitate propagation of neural activity along particular axes (see, for example, refs. 9, 13, 17). Because the interactions are cooperative and local in nature, they are adaptive and able to integrate such complex stimulus features as curvature (9, 18). In our experiments, local facilitatory interactions along individual contours of an E pattern would enhance the perception of the global E shape/orientation. These local interactions could be accomplished in several ways. For example, end-stopped units could play a role in the enhancement effect. A stimulus placed in the end zone of a neighboring filter would reduce inhibition, thus enhancing the response of the filter. This idea has been suggested to explain remote facilitation found in detection experiments (19) and is also consistent with the limited extent of integration.

In addition to the enhancement due to the alignment of local orientations along the orientation of a global contour, the uniformity of local orientations per se facilitated the perception of the global shape. We suggest that there are second-stage neurons whose orientation sensitivity is “hardwired” by virtue of parallel inputs from first-order filters so that these second-order filters would be more sensitive to global orientation. The simplest version of a second-order collector neuron is one in which the outputs of aligned filters are summed. Evidence consistent with such a model was reported recently by Moulden (12).

To summarize, we investigated the mechanisms mediating the perception of a single stimulus pattern presented on a blank background. The results suggest that, in addition to local interactions (alignment of local orientations) that facilitate the perception of global contours, there may be a spatially limited integration mechanism that collects information from orientation selective filters tuned to similar orientations and that enhance the perception of global shape.

Several previous studies have reported that integration of local information can aid “pop-out” or enhance discrimination of figures embedded in distractors (6–13). Our study differs from most of the previous studies in two important respects. First, rather than a figure-ground discrimination, our experiments measured contrast thresholds for pattern (orientation) identification. Second, in many of the previous studies, the target to be detected was a continuously curved, or closed, figure. For example, Kovács and Julesz (10, 11) showed that contrast discrimination of a single-target Gabor probe within a closed contour was enhanced (also by about a factor of slightly greater than two, similar to our results) when a chain of roughly collinear elements is connected across the gaps.

Our results are also in line with those of Caelli and Dodwell (20, 21), who measured the discriminability of small perturbations in the orientations of short line segments when the line segments formed a coherent global shape or when the global structure was weak or random. These global shapes were presented without any background noise, i.e., the perception of a global pattern structure required no figure–ground segregation. Caelli and Dodwell’s (20, 21) results demonstrated that orientation discriminability of the local elements increased significantly in the coherent global shapes.