Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 1998 Sep 15;95(19):11053–11058. doi: 10.1073/pnas.95.19.11053

Complex behavior of self-propagating reaction waves in heterogeneous media

Arvind Varma 1,*, Alexander S Rogachev 1,†, Alexander S Mukasyan 1, Stephen Hwang 1
PMCID: PMC21594  PMID: 9736688

Abstract

Self-propagating high temperature reaction waves, leading to the synthesis of advanced materials, are investigated in a variety of heterogeneous reaction systems by using a digital high-speed microscopic video recording technique. It is shown that, although on the macroscopic length and time scales, the reaction appears to move in a steady mode, on the microscopic level it has a complex character that is related to the reaction mechanism.

Many exothermic chemical reactions can propagate through a mixture of their initial components as self-sustained reaction waves. For gaseous mixtures, this phenomenon, known as “premixed flame”, has been studied for a long time (1, 2). About one-hundred years ago, self-propagating combustion waves were found in so-called “thermite reaction” mixtures consisting of solid oxides (e.g., Fe2O3) and reducing metal (e.g., Al) powders (3). The scope of self-sustained reactions waves was increased significantly some 30 years ago (4), when highly exothermic reactions were shown to propagate through mixtures of fine elemental reactant powders (e.g., Ti + C, Ti + 2B), resulting in the synthesis of refractory compounds (TiC, TiB2, etc.). A characteristic of these systems is that all reactants and products are in their condensed state (i.e., either solid or liquid melt), with negligible amount of vaporized components. When applied to the synthesis of refractory compounds and materials, the process is frequently called “self-propagating high-temperature synthesis” (SHS), also known as “combustion synthesis” or “gasless combustion” or “solid flame” (5–8). Combustion synthesis has generated notable interest because of its potential for producing advanced materials, and many papers concerning this process have been published (9). The process is characterized by extremely high heating rates (up to 106 K/s), high temperatures (up to 3,000–3,500 K), and short times of reaction completion (usually <1 s, sometimes even 10−3-10−2 s). These characteristics, although attractive for the synthesis of unique compounds, also make it difficult to study the mechanism of reaction wave propagation, which is essential to form materials with tailored microstructures and properties (cf. 10–13).

Despite extensive investigations, the mechanism of reaction wave propagation in heterogeneous media, which determines both the wave velocity and temperature–time history in the reaction mixture, still is not understood well. The most prevalent approach is to assume that the reaction propagates in a manner similar to that of homogeneous combustion waves (e.g., gaseous premixed flames), the so-called “quasihomogeneous” approach (14). In this case, the width of the reaction zone is assumed to be much larger than the reactant particle size; hence, the reaction front is not affected by the heterogeneous microstructure of the medium and moves uniformly. However, recent experiments have shown that macroscopically steady reaction fronts in heterogeneous mixtures exhibit random microscopic fluctuations in shape and instantaneous velocity, which are directly related to the microstructure of the reaction mixture (15, 16). These results cannot be described by current combustion theory.

We have developed a technique of digital high-speed microscopic video recording (DHSMVR), which allows in situ observation of rapid processes occurring at the microscopic level. This technique was applied to investigate high-temperature reaction waves in a variety of reaction systems. By using this method, significant information about the microstructure of gasless combustion waves was obtained, and a basis was created for understanding the mechanisms of fast chemical reactions in heterogeneous media.

DHSMVR Technique.

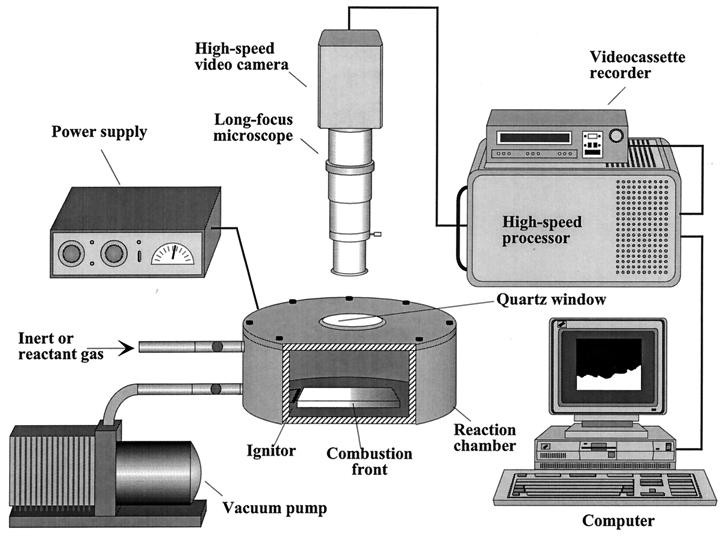
A schematic diagram of the experimental set up is shown in Fig. 1. The propagation of the reaction waves is observed through a quartz window by using a long-focus microscope (K-2, Infinity Photo-Optical, Boulder, CO) attached to a digital high-speed video camera and processor. The spatial resolution of the microscope is 1.7 μm whereas magnification may be varied from 50 to 800×, with the corresponding viewable area varying from 0.15 to 25 mm2. The high-resolution, high-speed black and white video camera (Kodak EktaPro 1000 Imager) attached to the microscope records the events and the images are transferred to the digital processor (Kodak EktaPro Hi-Spec Motion Analyzer). The recording rate varies from 50 to 1,000 frames/s with full screen imaging and can be increased up to 12,000 frames/s by splitting the image. The corresponding total recording time equals 65.5 s for the lowest and 3.2 s for the highest rate. To synchronize the recording with the fast reaction process, a record-stop mode was used. By using the computer access interface, the digital images can be transferred directly to the computer. Once saved on the computer, the images can be processed and analyzed to yield quantitative characteristics of the reaction wave structure, including brightness map, local curvature, and instantaneous velocity. In conjunction with the DHSMVR method, other monitoring also is used. A color video camera (30 frames/s) provides a macroscopic view of the process. Occasionally, a two-color infrared pyrometer (MR-OR10–99C, RCON, Niles, IL) and thermocouples (W-Re 5/26, Omega Engineering, Stamford, CT) are used to measure the sample temperature–time history.

Figure 1.

Figure 1

Open in a new tab

Schematic diagram of the digital high-speed microscopic video recording (DHSMVR) technique.

Clearly, the DHSMVR method described above can be applied to investigate a wide range of rapid processes at the microscopic scale, such as in fluid dynamics (e.g., coalescence and break up of small drops), materials science and mechanics (e.g., formation and propagation of cracks), and chemistry (e.g., reactions on catalyst surfaces), as well as in physics and biology.

Reaction Waves in Heterogeneous Media.

We studied a number of binary reaction systems of the type, A + xB = ABx, where A and B are elemental reactant powders, x is the stoichiometric coefficient, and the product ABx represents ceramic or intermetallic compounds. These gasless reaction systems may be categorized into three types, based on a comparison of the reactant melting points and the highest temperature reached in the combustion wave (Table 1). For the first type, one reactant melts while the other remains solid; for the second type, both reactants melt; and for the third type, both reactants remain solid.

Table 1.

Some characteristic parameters of reaction systems under investigation

Type System: A + xB = ABx Melting point of reagent A (TA) K Melting point of reagent B (TB) K Adiabatic combustion temperature (Tad) K Combustion mode Comments
Ti + 0.8C = TiC0.8 1,933 3,820 3,000 stable TA < Tad < TB
I Ti + 0.4C = TiC0.4 1,933 3,820 2,400 oscillation TA < Tad < TB
Ti + 0.6B = TiB0.6 1,933 2,573 2,000 stable TA < Tad < TB
Ti + Si = TiSi 1,933 1,683 1,942 stable TA,B < Tad
II 5Ti + 3Si = Ti5Si3 1,193 1,683 2,403 stable TA,B < Tad
Ni + Al = NiAl 1,726 933 1,910 stable TA,B < Tad
III Nb + 2B = NbB2 2,741 2,573 2,315 oscillation Tad < TA,B
Ta + C = TaC 3,269 3,820 2,700 oscillation Tad < TA,B
Open in a new tab

The reactant powders were dry-mixed for 7 hr in a ball-mill and were pressed into parallelepiped shaped samples with dimensions 30 × 20 × 5 mm and various porosity in the range from 40 to 60%. The sample was located in the reaction chamber filled with Ar at normal atmospheric pressure, and an electrically heated tungsten wire at one end of the pellet initiated the reaction (see Fig. 1). The reaction then self-propagated through the sample in the form of a bright glowing front. Most studied reactions propagated in a steady mode, i.e., the macroscopic velocity of the reaction front remained constant during the experiment (see Table 1). The self-oscillation mode of propagation also was observed in some systems (Ta + C, Nb + B, Ti + 0.4C) in which the velocity changed periodically. To observe the microscopic mechanism of reaction front propagation, we selected a small area in the middle of the sample and applied the DHSMVR technique to record the reaction wave as it passed through this area.

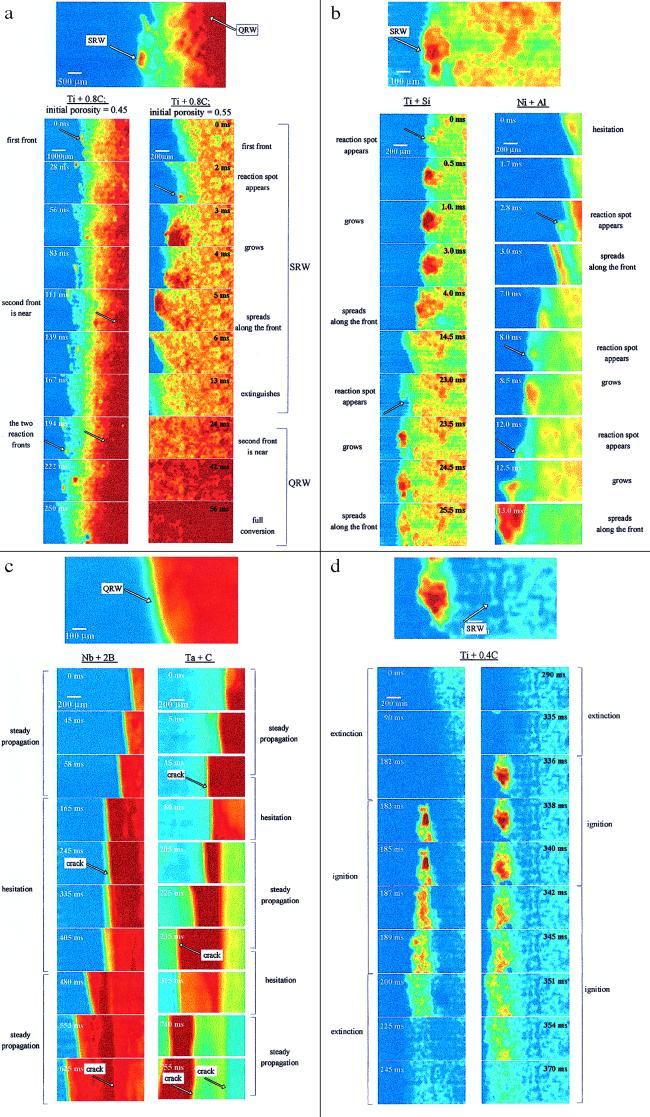
Several characteristic sequences of video pictures for different types of reaction systems are presented in Fig. 2. By using a color map, all gray-scale pictures were digitally transformed into colored versions, to improve the contrast and to show the differences more sharply. Generally, the brighter areas have higher temperature as compared with the darker regions. It appears that the combustion wave has unexpectedly complex dynamics, even for those reactions that traditionally were considered as simple one-step processes. For example, in the Ti + 0.8C mixture (type I), with average particle diameters dTi = 80 μm and dC = 0.1 μm, the reaction wave includes two spatially separated reaction fronts, as shown in Fig. 2a. The first front has a lower average temperature, but relatively bright spots appear randomly, indicating local regions of high temperature along the front. The average size of the hot spot at the moment of its appearance is ≈80 μm, which then spreads out to 400 μm, tarnishes, and dissipates, with the average lifetime of a spot ≈10−2 s. However, in many cases, the hot spot initiates the reaction in the neighboring regions, leading to a virtual propagation of the high temperature spots along the lateral direction of the front. It is important to note that the first front moves forward only as a consequence of appearance of the bright spot, and the overall progress of the front occurs only locally in the vicinity of the spot. Taking into account all of these features, we can designate this mode of propagation as a “scintillating reaction wave” (SRW). This first spot-type reaction front is followed by a second continuous front (see Fig. 2a) in which a relatively smooth temperature rise takes place. In contrast to the first front, the second reaction wave moves uniformly, and there is practically no variation of brightness along the surface of this front; hence, it qualifies as a quasihomogeneous reaction wave (QRW).

Figure 2.

Figure 2

Figure 2

Open in a new tab

Microstructures of combustion wave. (a) Type I system: melting of one reactant. (b) Type II system: both reactants melt. (c) Type III system: no melting of reactants (crack-induced oscillations). (d) Type I system: thermo-kinetic oscillations.

We also have found that dimensions of the hot spots correlate with the average particle size of titanium in this system and that the distance between the two fronts increases with increasing porosity of the reaction mixture. Thus, the SRW mode of propagation becomes more visible in high porous mixtures composed from coarse powders. It is worth stressing that, because of the short lifetime of the scintillation (<10−2 s) and the relatively short distance between the fronts (0.5 to 2.5 mm), the SRW can be observed only with magnification and recording rates >103 frames/s.

In other systems (type II), the reaction wave propagates solely by the SRW mode (Fig. 2b). For example, in the Ti + Si mixture, the reaction front has a scintillating nature, and we observe no notable increase of temperature beyond the front. The product is melted totally, and convection movements of the viscous liquid product are observed easily immediately after the front passes the image area. Patterns of the reaction propagation in the Ti + Si and Ni + Al mixtures (see Fig. 2b) indicate that, in both cases, the reaction front moves by the SRW mode. Because the temperature does not increase behind the SRW front (in contrast to Fig. 2a), and no unreacted components are detected in final products of these mixtures, we may conclude that the reaction is essentially complete during the lifetime of the high temperature spots.

In the third class of systems (type III), such as Nb + 2B or Ta + C, in which no reactant melts at the combustion temperature, the microstructure of the reaction wave corresponds to the QRW mode, as shown in Fig. 2c. The temperature increases uniformly along the front, and propagation, when it occurs, is steady. However, at the macroscopic level, these systems exhibit oscillations (17, 18). The DHSMVR technique allows us to understand why the macroscopic oscillations occur. It is seen from the microscopic Fig. 2c that cracks form periodically just ahead of the combustion front, resulting in hesitation of its movement. For example, in the Nb + 2B system (dNb = 5 μm, dB = 0.1 μm; porosity = 50%), the space frequency of cracks appearance is ≈2 per millimeter. The reaction front propagates uniformly between cracks, with velocity 100 mm/s, and then it stops at the crack for ≈0.3s. After this hesitation, when the other side of the crack becomes heated to a critical temperature, the reaction wave initiates again and the cycle repeats.

The crack-induced oscillations described above are qualitatively different from those observed in other systems, such as Ti + xC mixtures, with x < 0.6. For example, in Ti + 0.4C mixture, we have observed periodic extinction of the combustion wave followed by ignition of the unreacted layer ahead of the front, as shown in Fig. 2d. The delay between extinction of the previously burned layer and initiation of the next is ≈0.1 s. It is interesting that no cracks appear in the sample and that the reaction follows the SRW mode. Therefore, we may conclude that the oscillations in this case occur because the heat of reaction is not high enough to maintain a steady state propagation of the reaction wave (so-called “thermo-kinetic oscillations”), as has been recognized in the prior literature (19, 20).

DISCUSSION

The general idea about uniform movement of combustion waves, suggested by Mallard and Le Chatelier (1) more than 100 years ago, is that layer-by-layer propagation occurs because of initiation of the reaction between premixed components by heat conducting from a neighbor layer in which the exothermic reaction is proceeding. Thus, the propagation is determined by two main factors: kinetics of the reaction heat evolution and mechanism of heat transfer from the reaction zone to the unreacted mixture. Generally speaking, various combustion theories differ by different assumptions made a priori about these two factors. The earlier theories of flame propagation (1, 21, 22) assumed that chemical reaction starts at some fixed ignition temperature, Tig, that is generally much lower that the maximum temperature of combustion, Tc. Because it is difficult to assign a physical meaning to Tig for premixed gaseous mixtures, modern combustion theories commonly use high activated Arrhenius-type kinetics for the rate of reaction. This approach yields a principal conclusion that heat evolution is negligible in the wide range of temperature up to values close to Tc, and, hence, propagation of the reaction wave is governed by the rate of heat evolution at Tc itself (23).

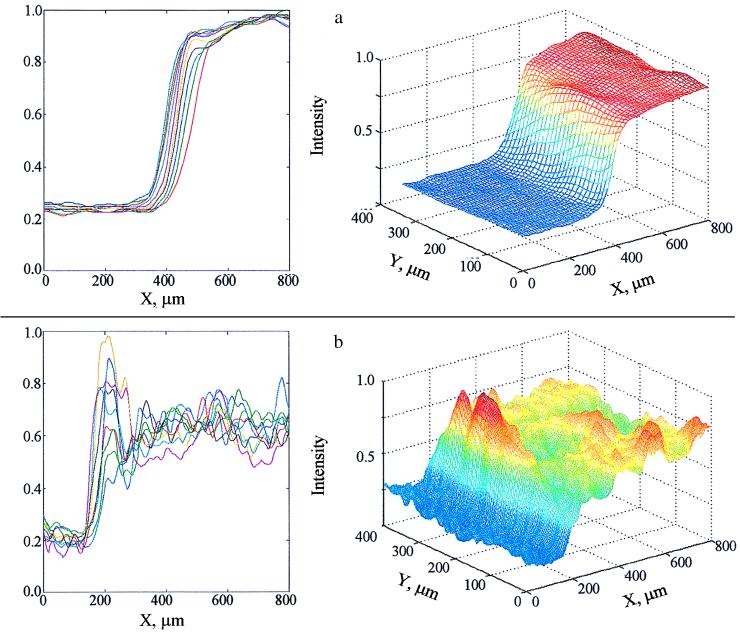
An important common feature of all combustion theories is that temperature increases monotonically and the temperature profile maintains a constant shape when the reaction wave propagates with constant velocity. This behavior qualitatively corresponds to the QRW mode of propagation, and an example of this type of temperature profile is shown in Fig. 3a. However, the results of DHSMVR experiments have shown unequivocally that microstructural mechanism of high-temperature reaction waves in heterogeneous media has unique complex features which have not been considered to date. The thermal structure of SRW presented in Fig. 3b shows a definite nonmonotonic behavior of temperature. The local overheating (scintillation) on the frontier of the reaction wave indicates areas of extremely high rates of reaction, where time of reaction is much less than characteristic time required for heat dissipation into surrounding areas. At first sight, it is also surprising that this extraordinarily fast reaction starts not at the highest temperature but in the dark periphery of the reaction wave, where temperature is low as compared with the maximum temperature of the process (see Fig. 3 a and b). It is worth reiterating that on macroscopic length (≈1 mm) and time (≈10−1 s) scales, the front appears to move in a steady mode.

Figure 3.

Figure 3

Open in a new tab

Typical two-dimensional and three-dimensional thermal structures of combustion wave. (a) QRW mode. (b) SRW mode.

Let us now consider possible mechanisms for this phenomenon. Detailed analysis of the microscopic images shows that fast rearrangement of the microstructure occurs at the moment when bright spots appear. Because the SRW mode has been observed only in those systems where at least one reactant melts (see Table 1), we may suggest, therefore, that it is the melting process that leads to transformation of the microstructure and local acceleration of the reaction.

It is interesting to note that, as a rule, for type I systems, particle size of the nonmelting reactant B is much smaller than particle size of the melting reactant A. For example, in the Ti-C system, the most commonly used Ti powder has particles of ≈50 μm whereas carbon particles rarely exceed 0.1 μm (carbon black). When the temperature in the combustion front reaches the melting point of reactant A, it melts and spreads over the surface of reactant B, which remains solid [so-called “infiltration spreading” (24)]. It is clear that, before spreading, because of porosity, the contact area between reactants does not exceed the specific surface of reactant A, and after spreading, it becomes equal to the specific surface of reactant B. Elementary calculation shows that, for the Ti-C system, the ratio of specific reactant surfaces is SC/STi ≈ (mBρAdA)/(mAρBdB) ≈ 270, where m, ρ, and d are mass fraction, density, and particle size, respectively. Further, diffusion coefficients in liquid phase are higher as compared with the solid phase. Hence, in a very short time (<10−2 s), both the contact area between reactants and the reaction rate increase enormously at the melting point of reactant A. The isolated hot-spots (scintillations), ahead of the QRW, are a consequence of chemical reaction acceleration occurring locally because of preferential heat transfer pathways existing in the heterogeneous reaction medium (25).

We can expect an even more dramatic increase of the reaction rate for type II systems, in which combustion temperature exceeds melting points of both reactants. It was shown (26) that, when both reactants melt, one after another, coalescence of liquid drops in the combustion front results in fast (10−2 s) diffusional homogenization of the components. Further, unlike infiltration spreading, acceleration of the reaction because of coalescence of drops can occur at any ratio of the reactant particle sizes.

Thus, we may conclude that the reaction intensifies sharply when the temperature reaches the melting point of one (or both) reactants. Hence, the melting point plays the role of ignition temperature (Tig), which may be much smaller than the maximum combustion temperature, Tc (see Table 1). On the other hand, again because of heterogeneity of the reaction medium (porosity and interparticle contact), the process of heat transfer from the reacted to the unreacted (solid) parts of the mixture is relatively slow. The measured average time between appearance of two consecutive spots is ≈5× larger than the reaction time (i.e., lifetime of the scintillation). For these reasons, we observe fast local increase of temperature when one metal particle melts, followed by energy dissipation from this region (local decreasing of temperature), and followed once again by ignition of the next spot after some delay period. These phenomena are observed as the SRW mode of the heterogeneous reaction propagation.

In addition, when both reactants melt (type II system), the reaction starts at the melting point of the low-melting reactant and proceeds fast until complete conversion, that is why the reaction occurs solely by the SRW mode (see Fig. 3b). If only one reactant melts (type I systems), the possibility exists that the reaction may hesitate at some intermediate degree of conversion: for example, in the Ti-C system, when all carbon particles are covered with the primary product layer (TiCx) (10) and further interaction of reactants is governed by relatively slow diffusion through this solid layer. In this case, we may expect only partial conversion in the hot spots followed by a relatively wide reaction zone, as in the titanium–carbon system (Fig. 2a).

In summary, it appears that the characteristics of self-propagating high-temperature reaction waves in heterogeneous mixtures are much more complex than believed heretofore. It is shown that, although on the macroscopic length and time scales, the reaction appears to move in a steady mode, on the microscopic level it has a complex character that is related to the reaction mechanism. However, we may classify these waves into two types, according to their microstructures: quasihomogeneous reaction wave (QRW) and scintillating reaction wave (SRW). In different systems, the reaction wave may propagate by either a single mode or by a combination of the two modes, where the SRW mode precedes the QRW. Because the SRW mode occurs in systems in which at least one reactants melts, it is expected to be the prevalent mode for gasless reaction wave propagation in heterogeneous media.

It is worth noting that the reaction wave propagation behavior identified here could be observed only because of the high spatial and temporal resolution of the used experimental technique. The phenomena discussed in this work contribute toward a fundamental understanding of combustion processes in heterogeneous media and, it is hoped, will catalyze further research in this important field.

Acknowledgments

We are grateful to the National Science Foundation (Grant CTS-9528941) for financial support. A portion of this work was conducted while one of the authors (A.S.R.) visited the University of Notre Dame under a U.S.–Russia joint cooperative research program (supplement to Grant CTS-9528941).

ABBREVIATIONS

DHSMVR

digital high-speed microscopic video recording

SRW

scintillating reaction wave

QRW

quasihomogeneous reaction wave

Footnotes

This paper was submitted directly (Track II) to the Proceedings Office.

References

  • 1.Mallard E, Le Chatelier A. Ann Mines. 1883;4:274–381. [Google Scholar]
  • 2.Lewis B, Von Elbe G. Combustion Flame and Explosion of Gases. New York: Academic; 1961. [Google Scholar]
  • 3.Goldschmidt H. Z Elektrochem. 1898;4:494–498. [Google Scholar]
  • 4.Merzhanov A G, Borovinskaya I P. Dokl Chem (Transl of Dokl Akad Nauk) 1972;204:429–431. [Google Scholar]
  • 5.Munir Z A, Anselmi-Tamburini U. Mater Sci Rep. 1989;3:277–365. [Google Scholar]
  • 6.Wiley J B, Kaner R B. Science. 1992;255:1093–1097. doi: 10.1126/science.255.5048.1093. [DOI] [PubMed] [Google Scholar]
  • 7.Merzhanov A G. Combust Sci Technol. 1994;98:307–336. [Google Scholar]
  • 8.Varma A, Rogachev A S, Mukasyan A S, Hwang S. Adv Chem Eng. 1998;24:79–226. [Google Scholar]
  • 9.SHS Bibliography. Int J SHS. 1996;5:309–508. [Google Scholar]
  • 10.Rogachev A S, Mukasyan A S, Merzhanov A G. Dokl Phys Chem (Transl of Dokl Akad Nauk) 1987;297:1240–1243. [Google Scholar]
  • 11.Aleksandrov V V, Korchagin M A, Boldyrev V V. Dokl Phys Chem (Transl of Dokl Akad Nauk) 1987;292:114–116. [Google Scholar]
  • 12.Wong J, Larson E M, Holt J B. Science. 1990;249:1406–1409. doi: 10.1126/science.249.4975.1406. [DOI] [PubMed] [Google Scholar]
  • 13.Rogachev A S, Shugaev V A, Kachelmyer C R, Varma A. Chem Eng Sci. 1994;49:4949–4958. [Google Scholar]
  • 14.Aldushin A P, Khaikin B I. Combust Explos Shock Waves (Engl Transl) 1974;10:273–283. [Google Scholar]
  • 15.Mukasyan A S, Hwang S, Rogachev A S, Sytchev A, E, Merzhanov A G, Varma A. Combust Sci Technol. 1996;115:335–353. [Google Scholar]
  • 16.Hwang S, Mukasyan A S, Rogachev A S, Varma A. Combust Sci Technol. 1997;123:165–183. [Google Scholar]
  • 17.Merzhanov A G, Filonenko A K, Borovinskaya I P. Dokl Chem (Transl of Dokl Akad Nauk) 1973;208:122–125. [Google Scholar]
  • 18.Shkiro V M, Nersisyan G A. Combust Explos Shock Waves (Engl Transl) 1978;14:121–122. [Google Scholar]
  • 19.Shkiro V M, Doronin V M, Borovinskaya I P. Combust Explos Shock Waves (Engl Transl) 1980;16:13–18. [Google Scholar]
  • 20.Holt J B, Munir Z A. J Mater Sci. 1986;21:251–259. [Google Scholar]
  • 21.Mason W, Wheeler R V. J Chem Soc. 1917;CXI:1044–1057. [Google Scholar]
  • 22.Daniell P J. Proc R Soc London Ser A. 1930;126:393–405. [Google Scholar]
  • 23.Zeldovich Y B, Barenblatt G I, Librovich V B, Makhviladze G M. Mathematical Theory of Combustion and Explosions. New York: Plenum; 1985. [Google Scholar]
  • 24.Dullien F A L. Porous Media: Fluid Transport and Pore Structure. San Diego: Academic; 1992. [Google Scholar]
  • 25.Adler P M. Porous Media: Geometry and Transport. Boston: Butterworth–Heinemann; 1992. [Google Scholar]
  • 26.Varma A, Kachelmyer C R, Rogachev A S. Int J SHS. 1996;5:1–26. [Google Scholar]

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES