Structural analysis of cloned plasma membrane proteins by freeze-fracture electron microscopy

Abstract

We have used freeze-fracture electron microscopy to examine the oligomeric structure and molecular asymmetry of integral plasma membrane proteins. Recombinant plasma membrane proteins were functionally expressed in Xenopus laevis oocytes, and the dimensions of their freeze-fracture particles were analyzed. To characterize the freeze-fracture particles, we compared the particle cross-sectional area of proteins with α-helical transmembrane domains (opsin, aquaporin 1, and a connexin) with their area obtained from existing maps calculated from two-dimensional crystals. We show that the cross-sectional area of the freeze-fracture particles corresponds to the area of the transmembrane domain of the protein, and that the protein cross-sectional area varies linearly with the number membrane-spanning helices. On average, each helix occupies 1.40 ± 0.03 nm². By using this information, we examined members from three classes of plasma membrane proteins: two ion channels, the cystic fibrosis transmembrane conductance regulator and connexin 50 hemi-channel; a water channel, the major intrinsic protein (the aquaporin 0); and a cotransporter, the Na⁺/glucose cotransporter. Our results suggest that the cystic fibrosis transmembrane conductance regulator is a dimer containing 25 ± 2 transmembrane helices, connexin 50 is a hexamer containing 24 ± 3 helices, the major intrinsic protein is a tetramer containing 24 ± 3 helices, and the Na⁺/glucose cotransporter is an asymmetrical monomer containing 15 ± 2 helices.

The structural elucidation of membrane proteins has been slow because of technical difficulties in obtaining large quantities of purified integral membrane proteins and because of the formidable task of preparing crystals of purified membrane proteins that diffract at high resolution. Of the hundreds of membrane proteins identified, the structure of only a handful has been solved at atomic resolution, and secondary structure has been obtained only for a few others (1). Although three-dimensional maps at atomic resolution remain the ultimate goal of structural studies, low-resolution structural information such as subunit or oligomeric composition of channels, receptors, and transporters can be extremely useful in advancing our understanding of the relationship between structure and function.

One approach to low-resolution structural studies is to use freeze-fracture electron microscopy, which provides images of integral membrane proteins that appear as intramembrane particles in the protoplasmic (P) or the exoplasmic (E) face of the fractured membrane (2, 3). This approach involves an analysis of the dimensions of the protein particles in freeze-fracture images and, in the past, has been used to identify protein species of natural membranes (e.g., thylakoid membranes) (4) or proteins reconstituted in proteoliposomes (e.g., refs. 5 and 6). But these approaches cannot be universally applied to all membrane proteins because not all are present in high quantities in native tissues and, in addition, the majority of membrane proteins still pose significant resistance to purification and reconstitution techniques.

With the introduction of highly efficient heterologous expression systems, it has become possible to express heterologous integral membrane proteins at high levels and to study the freeze-fracture particles of these proteins with little or no contamination from the endogenous particles of the expression system (7). Xenopus laevis oocytes are ideal for this purpose, because they are capable of efficiently translating and processing cRNAs coding for a large number of integral membrane proteins; these proteins are inserted into the plasma membrane and appear as particles in the P fracture face (7, 8). Oocytes contain a very low number of endogenous proteins in the plasma membrane, and these proteins are homogenous in size (8). These characteristics of the oocyte expression system, together with the availability of structural information for several integral membrane proteins, allowed us to express membrane proteins of known structure and function in the oocyte plasma membrane to study the relationship between protein structure and the dimensions of the freeze-fracture particle. This information was then used to examine the oligomeric structure of other membrane proteins.

EXPERIMENTAL PROCEDURES

Oocytes and Clones.

X. laevis oocytes were injected with cRNA for bovine opsin (9), mouse connexin 50 (Cx50) (10), human aquaporin (AQP1) (11), bovine lens major intrinsic protein (MIP or AQP0) (12), rabbit Na⁺/glucose cotransporter (SGLT1) (13), or human cystic fibrosis transmembrane conductance regulator (CFTR) (14). Functional and immunoblot assays showed that all of the above proteins are fully functional and appear as protein species of the expected molecular weight when expressed in oocytes (7, 15–20; G.A.Z., unpublished results for Cx50).

Freeze-Fracture and Electron Microscopy.

After functional measurements (electrophysiological or water permeability assays), control oocytes and oocytes expressing recombinant membrane proteins were fixed and prepared for freeze-fracture microscopy (7). In some cases, functional assays were not performed on the very oocytes used for structural studies but were performed on oocytes from the same batch injected with the same cRNA. Our freeze-fracture methodology differs from that in most other studies in that, in producing the replicas, we shadow at 80° instead of 45°. This simple experimental manipulation produces shorter shadows and greatly simplifies measurements of the freeze-fracture particles. For particle density determinations, images of the P fracture face were enlarged to a final magnification of ×75,000 and digitized. Particle densities were determined by counting P face particles from known areas of the membrane (image software, National Institutes of Health, Bethesda, MD).

Measurement of Freeze-Fracture Particles.

For each recombinant protein, particles were sampled from at least four P fracture face replicas from at least two oocytes. Particle diameter was measured directly from the negative by using a comparator (Model 6c, Nikon) at a final magnification of ×250,000. The diameter was obtained by measuring the width of the particle edge-to-edge in a direction perpendicular to the direction of the shadow. Triplicate measurements of individual particles revealed a ±0.5-nm error of measurement. Therefore, a bin size of 0.5 nm was chosen, and the frequency histograms were plotted at the center of the bin (see Figs. 2–4). The accuracy of the diameter measurements was tested by measuring the diameter of 10-nm gold particles (Chemicon) placed directly on Formvar-coated copper-mesh grids (10.0 ± 0.4 nm; n = 114). The precision of our platinum–carbon-coating procedure is indicated by the fact that histograms obtained from replicas of SGLT1-expressing oocytes revealed an identical particle size for SGLT1 over a 3-year period.

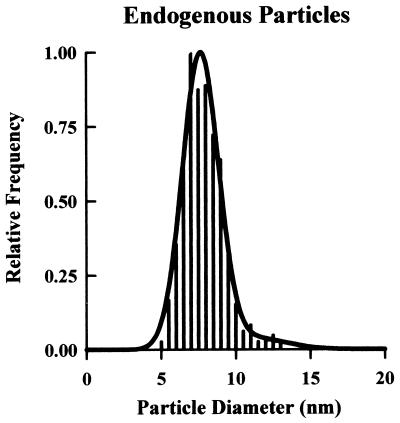
Figure 2.

Size distribution of P face endogenous particles. With respect to size, control oocytes exhibit a fairly uniform particle population; ≈93% have a mean diameter of 7.6 ± 0.5 nm, and ≈7% measure 11.1 ± 1.0 nm (N = 875).

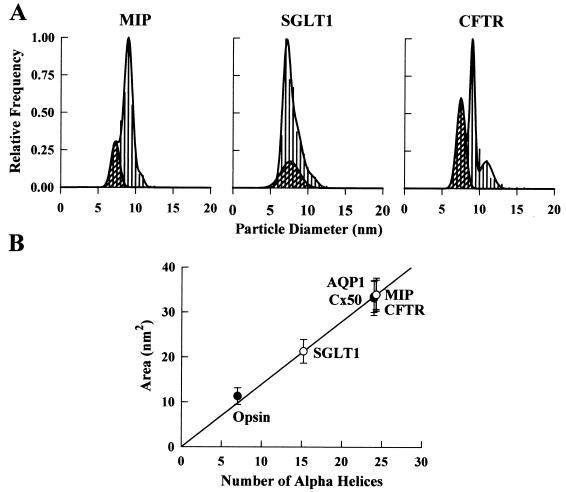
Figure 4.

Size distribution of P face particles in oocytes expressing MIP, SGLT1, and CFTR. (A) MIP particles demonstrated a single population at 9.0 ± 0.3 nm (N = 430). The particle density in this oocyte was 3,288 ± 136/μm² (n = 2,878). SGLT1 particles appeared at 7.1 ± 0.2 (48%) and 8.2 ± 0.4 nm (52%) (N = 640). In this oocyte, the particle density was 2,070 ± 130/μm² (n = 2,163). CFTR particles were 9.0 ± 0.2 nm in diameter (N = 500). A larger particle (11.0 ± 0.8 nm) appeared in the CFTR frequency histogram that coincides with the larger endogenous particles but was present at a higher relative frequency (≈10% of exogenous particles). Particle density was 678 ± 27/μm² (n = 944). Cross-hatched regions correspond only to the 7.6-nm P face endogenous particles as confirmed by particle density determinations. (B) Relationship between the transmembrane domain cross-sectional area and the number of transmembrane α-helices. The straight line corresponds to the linear regression through the AQP1, opsin, and Cx50 data (•) (slope, 1.40 ± 0.03 nm²/helix). ○, Calculated cross-sectional areas of MIP, SGLT1, and CFTR.

To determine the size of integral proteins from the dimensions of their freeze-fracture particles, it was necessary to estimate the thickness of the platinum–carbon film deposited to produce the replicas. The platinum–carbon coat thickness was obtained by comparing the dimensions of AQP1 and opsin freeze-fracture particles with the dimensions obtained from corresponding projection maps of two-dimensional crystals (21, 22). The difference was 2.4 ± 0.4 nm, which corresponds to a film thickness of 1.2 ± 0.2 nm. The film thickness predicted by the manufacturer (Balzers 400K) under our experimental conditions (1 × 10^–7 mbar, 1,440–1,800 V accelerating voltage, and 70 mA emission current) is 1.7 ± 0.2 nm, and the two estimates differ from each other by approximately the thickness of a single platinum atom.

Data Analysis.

Particle diameter measurements were plotted as frequency histograms (23) that were fitted to a multiple Gaussian function:

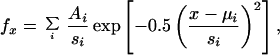where f_x is the frequency of occurrence of a particle of size x, x is the measured diameter of a given particle (nm), A is an approximation of the area underneath the curve of a given particle population, μ is the mean diameter of a given population (nm), s is the standard deviation of the population diameter, and i is an integer from 1 to the total number of particle populations. For sample sizes, N refers to the number of diameter measurements, and n refers to the number of particles counted for particle density determinations. Results from individual oocytes are presented, but each experiment was repeated in two to four oocytes. All values are reported as mean ± SEM.

RESULTS

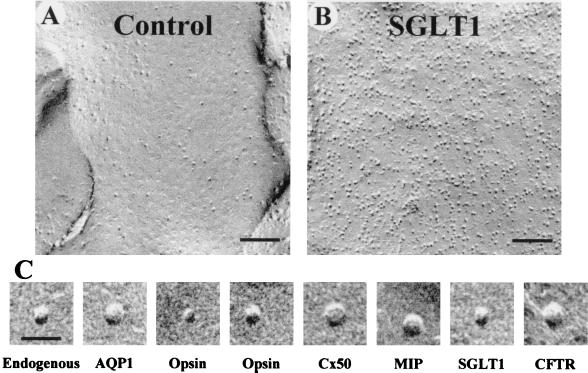
Native X. laevis oocytes contained a low number of endogenous proteins in the P face of the plasma membrane (355 ± 21/μm²; Fig. 1A).When recombinant membrane proteins were expressed in oocytes, the density of the particles in the P face of the plasma membrane increased; this increase in particle density was proportional to the level of functional activity (7). For example, in an oocyte expressing SGLT1, the particle density increased to 3,287 ± 112/μm² (Fig. 1B) and was associated with an increase in glucose uptake from 3 × 10^–4 pmol/s (control oocytes) to 4.3 pmol/s. In oocytes expressing various membrane proteins, the density ranged from 800 to 3,300/μm² (Table 1). The observation that the expression of different proteins leads to the appearance of P face particles of different size (Fig. 1C) prompted us to carry out a detailed characterization of the size of endogenous and heterologous freeze-fracture particles. To study the size of the proteins in the plasma membrane, we constructed size (diameter) frequency histograms of the particles in the P face of the plasma membrane.

Figure 1.

P face freeze-fracture micrographs of the plasma membrane of X. laevis oocytes. (A) The P face of control oocytes shows a low density of particles at 355 ± 21/μm² (n = 2,130). (B) In an oocyte expressing SGLT1, the density of the particles increased to 3,287 ± 112/μm² (n = 2,565). (C) High-magnification representative images of endogenous P face particles, AQP1, the short axis of opsin, the long axis of opsin, Cx50, MIP, SGLT1, and CFTR. [Bars = 100 nm (A and B) and 20 nm (C).]

Table 1.

Freeze-fracture particles of heterologous proteins

	Density*, μm−2	Diameter†, nm	a/b Ratio	Area‡, nm2	Number of helices§
Opsin	1444  ± 43	(a) 4.4  ± 0.4	1.3	11  ± 2	8  ± 1
		(b) 3.3  ± 0.5
Cx50	1415  ± 81	6.5  ± 0.5	1	34  ± 4	24  ± 3
APQ1	825  ± 63	6.5  ± 0.5	1	33  ± 4	24  ± 3
MIP	3288  ± 136	6.6  ± 0.5	1	34  ± 4	24  ± 3
SGLT1	2070  ± 130	(a) 5.8  ± 0.6	1.2	21  ± 3	15  ± 2
		(b) 4.7  ± 0.5
CFTR	678  ± 27	6.6  ± 0.4	1	34  ± 3	25  ± 2

^*Total density of P face particles. Density of the endogenous P face particles was 355 ± 21/μm². 

^†Diameters were corrected for the thickness of the platinum-carbon film by subtracting 2.4 ± 0.4 nm from the mean diameters obtained from the frequency histograms (see Experimental Procedures). 

^‡Cross-sectional area was obtained by assuming a circular geometry for Cx50, AQP1 and MIP , and CFTR and an elliptical geometry for opsin and SGLT1. 

^§Predicted number of helices was calculated by using 1.40 ± 0.03 nm²/helix (see Fig. 3B). Values are means ± SEM. 

First, we analyzed the frequency histogram of control oocytes. The endogenous particles fell into two size populations; 93% had a mean diameter of 7.6 ± 0.5 nm, and 7% had a mean diameter of 11.1 ± 1.0 nm (Fig. 2). The low density and uniform size of the endogenous proteins in the oocyte plasma membrane facilitated our interpretation of the frequency histograms in oocytes expressing recombinant proteins (Figs. 3 and 4). Depending on the protein expressed, the frequency histograms exhibited one or more particle populations. Two approaches were used to differentiate the size of the expressed membrane proteins from the endogenous ones. First, if the size of the protein of interest was sufficiently different from the endogenous particles, a distinct new population was observed in the frequency histogram; e.g., AQP1, Cx50, MIP, and CFTR (Figs. 3A and 4A). Second, advantage was taken of the relative frequency of various populations in the histogram. For example, in an oocyte expressing AQP1, there were two major particle populations of 7.3 ± 0.6 and 8.9 ± 0.2 nm. By determining the area underneath the curve of each population in the frequency histogram and assuming that the 7.3 ± 0.6 nm particle corresponds to the endogenous particles (45% of total), it was estimated that the increase in particle density was ≈2.2-fold (Fig. 3A). Particle density determination in the same oocyte demonstrated a ≈2.3-fold increase over control oocytes (825 ± 63 vs. 355 ± 21/μm²). Therefore, the combined analysis of particle density and frequency histogram allowed us to conclude that the 8.9-nm particle was AQP1.

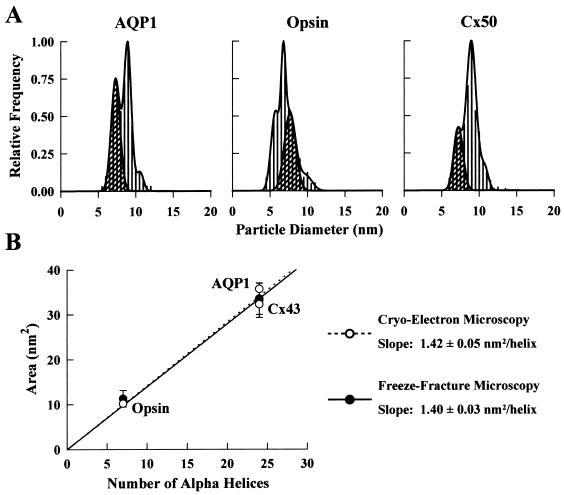
Figure 3.

Size distribution of P face particles in oocytes expressing AQP1, opsin, and Cx50. (A) In an oocyte expressing AQP1, there was a population of particles with a mean diameter of 8.9 ± 0.2 nm (N = 449) in addition to the endogenous particles. The particle density in this oocyte was 825 ± 63/μm² (n = 982). In oocytes expressing opsin, two particle populations occurred with similar frequency: 5.7 ± 0.3 nm (43%) and 6.8 ± 0.1 nm (57%) (N = 912). Particle density was 1,444 ± 43/μm² in this oocyte (n = 1,903). Cx50 particles had a mean diameter of 9.0 ± 0.3 nm (N = 411). The particle density in this oocyte was 1,415 ± 81/μm² (n = 1,763). The small population of apparently larger size (≈11 nm) in all of the above histograms corresponds to the population of larger endogenous particles (see Fig. 2). Cross-hatched regions correspond only to the 7.6-nm P face endogenous particles as confirmed by particle density determinations. (B) Relationship between the transmembrane domain cross-sectional area and the number of transmembrane α-helices. Freeze-fracture data for AQP1, opsin, and Cx50 (•) agree well with those from two-dimensional crystals of AQP1, opsin, and Cx43 (○) (1.40 ± 0.03 vs. 1.42 ± 0.05 nm²/helix).

If there was an increase in particle density and functional assays indicated the presence of the expressed protein but no new population was apparent in the frequency histogram, we deduced that the heterologous particles were approximately the same size as the endogenous ones. For example, in an oocyte expressing SGLT1 (Fig. 4A), the particle density increased to 2,070 ± 130/μm², but the particles were apparently similar in size to the endogenous ones. An analysis of the frequency histogram revealed two populations of 7.1 ± 0.2 (48%) and 8.2 ± 0.4 (52%) nm, respectively. These two populations were independent of the level of SGLT1 expression (data not shown). Thus, frequency histograms and particle density measurements complement one another to rule out or to establish the existence of a particle population with a size similar to that of the endogenous particles.

A single heterologous particle population was interpreted as a symmetrical protein whose cross-sectional geometry can be approximated by a circle (e.g., AQP1, Cx50, MIP, and CFTR). In the case of AQP1, this interpretation is consistent with the map calculated from cryoelectron images of two-dimensional crystals (21). Two closely sized populations, which occur with similar frequency (e.g., opsin and SGLT1; see Figs. 3A and 4A), suggest the presence of one asymmetric particle; i.e., a/b > 1, where a and b are the long and short axes. Theoretically, asymmetric particles might be expected to yield a broadening of the peak in the frequency histogram with the mean value in between the two extreme measurements. But computer simulations confirm that imposing a 0.5-nm bin size in the frequency histograms can artificially separate the possible range of measurements for an asymmetric protein into two populations (confirmed for opsin and SGLT1). Our observation of opsin asymmetry (a/b ≈ 1.3) is consistent with the map calculated from two-dimensional crystals (22). For protein area measurements, circular cross-sectional geometry (πr²) was assumed for symmetric particles, and elliptical (πab/4) for asymmetric ones (Figs. 3B and 4B). The results of the frequency histogram analyses are summarized in Table 1.

DISCUSSION

We have taken advantage of the low density and homogenous size of the plasma membrane proteins of oocytes, as well as the ability of these cells to insert a large number of copies of functional recombinant proteins into the plasma membrane, to study the relationship between protein structure and the size of the corresponding freeze-fracture particles. We expressed six integral plasma membrane proteins in oocytes; two water channels, AQP1 and MIP; two ion channels, CFTR and Cx50; one receptor, opsin; and one cotransporter, SGLT1. By constructing size (diameter) frequency histograms of the freeze-fracture particles, we were able to assign specific particle populations to specific recombinant proteins in the plasma membrane. The diameters were then used to calculate the cross-sectional area of the heterologous proteins.

To interpret the size of the recombinant freeze-fracture particles from the frequency histograms, it was first necessary to clarify how variations in protein molecular mass, glycosylation, helical packing, and asymmetry alter the dimensions of the particles. Particle diameter was not correlated with protein molecular mass because Cx50 and AQP1, which have different masses (298 vs. 112 kDa), exhibited similar diameters (Fig. 3A; Table 1). In addition, glycosylated AQP1 (16) and nonglycosylated MIP (17) particles, which have similar polypeptide molecular weights, also had similar diameters (cf. Figs. 3A and 4A). Therefore, variations in protein mass and glycosylation do not appear to affect the particle diameter (cross-sectional area); however, such variations may alter the particle height (volume).

To examine the influence of helical packing on plasma membrane protein structure, we took advantage of existing projection maps calculated from cryoelectron microscopy images of two-dimensional crystals of opsin (22), Cx43 (24), and AQP1 (21). A plot of protein cross-sectional area as a function of the number of α-helices [opsin, 7; Cx43, 24; and AQP1, 24 (25, 26)] produced a linear relationship with a slope of 1.42 ± 0.05 nm²/helix, which corresponds to the average area occupied by a single helix (Fig. 3B). That the plot included the area of the opsin monomer (elliptical), AQP1 tetramer, and Cx50 hexamer suggested that variations in helix packing, subunit assembly, or the presence or absence of a “pore” did not significantly alter the area estimates, because the contribution of each of these factors is within the error of our measurements.

Having established a relationship between the cross-sectional area and the number of transmembrane α-helices, we examined this relationship by using freeze-fracture data. The Cx50 and AQP1 freeze-fracture particles each exhibited a single Gaussian distribution, which indicates a symmetrical shape (Fig. 3A); the calculated areas of the transmembrane domain (circular geometry) were in close agreement with those obtained from the projection maps (Fig. 3B). The high degree of homology between the two gap junction proteins, Cx50 and Cx43 (27), and the close match of the particle dimensions suggest that Cx50 is a hexamer composed of 24 ± 3 helices (Table 1). The histogram for opsin particles revealed two populations with equal frequency (Fig. 3A; Table 1); these populations were interpreted to represent the short and long axes of opsin because of their consistence with the dimensions obtained from projection structures (22). The area calculated by assuming an elliptical cross-sectional geometry was indistinguishable from that of the projection structure of opsin two-dimensional crystals (22) (Fig. 3B). Therefore, opsin appears as a monomer with ≈30% asymmetry in the oocyte plasma membrane. The agreement between the freeze-fracture and crystal data allowed us to establish a relationship between the freeze-fracture particle cross-sectional area and the number of transmembrane α-helices. The slope of this plot was statistically equivalent to that obtained from the crystal data (1.40 ± 0.03 nm²/helix) (Fig. 3B).

That a small fraction of the total mass of AQP1, opsin, and connexins is predicted to be extramembrane (25, 26, 28, 29) suggests that the diameter of the freeze-fracture particle is directly correlated with the cross-sectional area of the protein embedded in the membrane. To examine this further, we analyzed freeze-fracture particles from the postsynaptic membrane of the Torpedo electric organ (data not shown), in which the nicotinic acetylcholine receptor is found at very high densities. By comparing our estimate from freeze-fracture measurements (5.2 ± 0.5 nm) with various sections in the three-dimensional projection map of the acetylcholine receptor (30), we found that the freeze-fracture measurement corresponds to the membrane-spanning region (≈5.1 nm) and not to the large extracellular domain. This observation indicates that the cross-sectional area of the freeze-fracture particle corresponds to the area of the transmembrane domain of integral membrane proteins.

Our analysis was extended to three additional membrane proteins for which little or no structural information is available; MIP (AQP0), a water channel; SGLT1, a cotransporter; and CFTR, an ion channel (Fig. 4; Table 1). As MIP belongs to the same family of water channels as AQP1, it is not surprising that the particles of AQP1 and MIP exhibited a similar size and shape. The cross-sectional area calculated for MIP predicts 24 ± 3 helices, which is consistent with a tetrameric assembly of six transmembrane-helix subunits (31, 32).

The frequency histogram for SGLT1 indicated the presence of two apparent particle sizes with the same frequency of occurrence (Fig. 4A). We interpreted this finding as indicative of a single protein with ≈25% asymmetry. Assuming an elliptical geometry, the cross-sectional area predicts 15 ± 2 transmembrane helices. Because experimental evidence indicates 14 transmembrane helices (33, 34), our data suggest that SGLT1 is a monomer in the oocyte plasma membrane. By using radiation inactivation, the size of the SGLT1 functional transporting unit was estimated to be 290 kDa (35), which was interpreted as evidence for a homotetramer of 73 kDa subunits. The reason for this discrepancy is presently unclear. In view of the recent suggestion that the radiation-inactivation size of the renal SGLT1 varies with the experimental condition (36), additional studies are needed to clarify this discrepancy.

The histogram for CFTR suggested the presence of a single symmetrical molecule consisting of 25 ± 2 helices. The CFTR monomer contains 12 putative transmembrane helices (19); consequently, the particles may correspond to CFTR dimers. Functional evidence for dimers comes from patch-clamp experiments in which strong positive cooperative gating leads to a simultaneous opening of pairs of CFTR channels (37, 38). Prior treatment of CFTR-expressing oocytes with forskolin/3-isobutylmethylxanthine did not alter the CFTR particle size (data not shown), suggesting that cAMP-dependent protein kinase A phosphorylation of CFTR does not alter the dimeric assembly.

Our analysis may be extended to freeze-fracture data already available for other proteins, provided that the thickness of the platinum–carbon film is known. For example, when the freeze-fracture measurement of the lactose permease reconstituted in proteoliposomes (5) is subjected to our analysis, a monomeric protein of 12 transmembrane helices is predicted that is consistent with a wealth of information available for this membrane protein (39). Our analysis of the acetylcholine receptor particles from the postsynaptic membrane of the Torpedo electric organ predicts that this receptor should contain 15 ± 2 helices, and not the 20 helices suggested by hydrophobicity analysis of the α₂βγδ subunits (40). This discrepancy may be accounted for if the acetylcholine receptor transmembrane domain contains a mixture of α-helices and β-pleated sheets (30, 41), leading to a smaller than expected cross-sectional area. Therefore, in the absence of additional data, the applicability of our method is limited to plasma membrane proteins with entirely α-helical transmembrane domains. Because bacterial membrane proteins are not targeted to the plasma membrane when expressed in oocytes, we have not been able to analyze membrane proteins with transmembrane domains made up entirely of β sheets (e.g., bacterial porins).

In summary, the cross-sectional area and asymmetry of the transmembrane domain of recombinant α-helical integral plasma membrane proteins can be determined by using the Xenopus oocyte expression system and freeze-fracture electron microscopy. The area is proportional to the number of transmembrane helices and, along with secondary structure models, can provide information on the oligomeric assembly of the functional protein in the oocyte plasma membrane.

ABBREVIATIONS

P

protoplasmic

Cx50

connexin 50

AQP

aquaporin

MIP

major intrinsic protein

CFTR

cystic fibrosis transmembrane conductance regulator

SGLT1

Na⁺/glucose cotransporter