Visualization of Tensor Fields Using Superquadric Glyphs

Abstract

The spatially varying tensor fields that arise in magnetic resonance imaging are difficult to visualize due to the multivariate nature of the data. To improve the understanding of myocardial structure and function a family of objects called glyphs, derived from superquadric parametric functions, are used to create informative and intuitive visualizations of the tensor fields. The superquadric glyphs are used to visualize both diffusion and strain tensors obtained in canine myocardium. The eigensystem of each tensor defines the glyph shape and orientation. Superquadric functions provide a continuum of shapes across four distinct eigensystems (λ_i, sorted eigenvalues), λ₁ = λ₂ = λ₃ (spherical), λ₁ < λ₂ = λ₃ (oblate), λ₁ > λ₂ = λ₃ (prolate), and λ₁ > λ₂ > λ₃ (cuboid). The superquadric glyphs are especially useful for identifying regions of anisotropic structure and function. Diffusion tensor renderings exhibit fiber angle trends and orthotropy (three distinct eigenvalues). Visualization of strain tensors with superquadric glyphs compactly exhibits radial thickening gradients, circumferential and longitudinal shortening, and torsion combined. The orthotropic nature of many biologic tissues and their DTMRI and strain data require visualization strategies that clearly exhibit the anisotropy of the data if it is to be interpreted properly. Superquadric glyphs improve the ability to distinguish fiber orientation and tissue orthotropy compared to ellipsoids.

Biologic tissue structure and tissue function can be characterized by tensor descriptions of their measured diffusion and strain patterns. Basser et al. (1) produced the first diffusion tensor (DT) magnetic resonance imaging (MRI) data and visualizations in samples of pork loin and ex vivo cat brain. Tensor data are frequently measured with MRI and they most commonly arise in DT imaging of the brain (2), heart (3), and other tissues (4), as well as in the strain fields of deforming myocardium (5,6).

Tensors can be described as isotropic or anisotropic. Isotropic tensors have the same components in all rotated coordinate systems and as such are all of the form pI, where p is a scalar and I is the identity tensor. Isotropic structure and isotropic function have no preferred directions of structural or functional organization. Anisotropic tensor components are dependent upon the chosen coordinate system and therefore have a preferred coordinate system wherein the tensor is diagonalized, giving rise to preferred directions. Two common subsets of anisotropic tensors are transversely isotropic tensors and orthotropic tensors. Transversely isotropic tensors have components that are independent of rotation about a specific axis and hence have a single preferred direction of structural or functional organization (e.g., skeletal muscle or large white matter tracts in brain). Orthotropic tensors have three mutually orthogonal preferred directions of structural or functional organization (e.g., myocardium). The orthotropic properties of myocardium have been under study since their first description by LeGrice et al. (7). Most importantly the orthotropic nature of myocardial structure has been shown to play an important role in systolic wall thickening (8).

Creating informative and intuitive visualizations of anatomic structure and physiologic function is challenging due to the multivariate nature of spatially varying tensor data. Three-dimensional diffusion and strain tensors can be represented by real-valued symmetric 3 × 3 matrices and can be decomposed into a local eigensystem consisting of three real-valued mutually orthogonal eigenvectors and three real-valued eigenvalues. Such decomposition provides a natural coordinate system for representing diffusion and strain tensors that is independent of the laboratory frame of reference. The family of objects used to visualize the tensor components is called “glyphs.” Glyph-based visualization uses surfaces to describe tensor shape. The eigenvectors are used to define the local glyph orientation and the eigenvalues are used to scale the glyph lengths. Many basic glyph shapes are possible; among them are ellipsoids, cylinders, and cuboids. Classically, the diffusion measures made in a DTMRI experiment are visualized using ellipsoids whose major and minor axes are scaled by the eigenvalues and whose orientation is determined by the eigenvectors (9).

In order to facilitate the interpretation of diffusion tensor data Pajevic and Pierpaoli described color schemes useful for representing the orientation of anisotropic tissues (10). Others have reduced the multivariate tensor data to scalars through the use of scalar tensor invariants and other scalar tensor contractions (11,12). This effectively reduces the multivariate tensors to a single component of interest. Although this approach is useful, it doesn't facilitate the understanding of how various tensor components relate to one another within a voxel or between neighbors. On the other hand, when using ellipsoid glyphs to gain a more complete understanding of tensor structure, shading ambiguity and lack of features on the glyph surface can confound appreciation of glyph shape and orientation. Specifically, it is generally difficult to understand how secondary and tertiary eigenvectors are oriented or to appreciate differences in eigenvalues.

Ideally spatially varying tensors fields would be visualized in such a way that the orientation and the length scales could be simultaneously visualized and spatial trends could be viewed. Toward that end we present results obtained from using a novel technique for visualizing canine myocardial DTMRI data and high-resolution myocardial DENSE strain data obtained in canines using superquadric parametric functions to render the tensors as glyphs (13).

METHODS

All animal procedures followed the guidelines issued by the National Institutes of Health's Animal Care and Use Committee. The data used for this study were acquired as a part of other studies.

Diffusion Tensor MRI

Following a separate set of experiments the canine was given an injection of 5000 (1000 units/mL) units of heparin, followed by an injection of 20 meq KCl (2 meq/mL). A lateral thoracotomy, followed by pericadectomy and cutting of the great vessels, allowed removal of the heart. The left and right main coronary arteries were canulated and flushed with phosphate-buffered isotonic saline to flush the vasculature of blood. Following this, the aorta was canulated and the heart was retrograde perfused with phosphate-buffered isotonic saline with a pressure of 60 mm Hg to flush blood and induce tissue turgor. The heart was then placed in a phosphate-buffered isotonic saline bath, which served to reduce body forces acting on the heart and as a reservoir for collecting perfusate for recirculation. Once the perfusate leaving the coronary sinus was free of blood the solution was recirculated. In order to rigidly fix the heart for DTMRI two tines of a custom-built rigid nylon fork were introduced into the right and left ventricular cavities via the tricuspid and mitral valves, respectively. The ventricles were then filled via a trans-mitral and trans-tricuspid injection of vinyl polysiloxane impression material (3M Company, St. Paul, MN), which rigidly fixed the ventricles to the fork and in relation to each other. The retrograde perfusion, bath submersion, and ventricular filling with vinyl polysiloxane all serve to fix the heart in an end diastolic configuration. Once the polysiloxane had cured the perfusate was switched to a 5% formaldehyde solution to fix the tissue for imaging and long-term storage.

DTMRI data were collected using a 1.5-T GE CV/i scanner (GE, Waukeesha, WI) and a four-element phased-array knee coil. A similar imaging protocol has been reported previously (3) and is concisely reviewed herein. A three-dimensional fast spin echo sequence was modified to include diffusion weighting gradients. The diffusion encoding directions were optimized according to Jones et al. (14) and the b-values were optimized according to Papadakis et al (15). The 10 noncollinear diffusion gradients with maximum b-values of 1470 sec/mm² were collected along with a single null image. The field of view was 100 × 100 × 86.4 mm and the acquisition matrix was 128 × 128 × 96, resulting in 780 × 780 × 900 μm voxels. The repetition time was 600 msec and a multiecho readout was used with echo times of 62 and 72 msec. Ten acquisitions of each direction were acquired and averaged. The tensor data were reconstructed from the magnitude images using linear regression of the logarithm of the corrected echo intensities and the components of the b-value matrix.

3D DENSE Imaging

Images were acquired using an imaging sequence based on a previously reported technique (6). In brief, the canine subjects were anesthetized and instrumented with a magnetic resonance compatible right atrial pacing lead. The canine was paced 10% above intrinsic rhythm at a rate of 120 beats/min. A trigger pulse from the respirator was used to initiate an integer number of cardiac pacing pulses so that the cardiac pacing rate was four times the respiratory rate and remained phase locked. This provided a way to image for extended durations without the need for breath holds.

Imaging was performed on a 1.5-T Siemens Magnetom scanner using a single surface coil. Displacement encoded data were acquired with a 3D DENSE sequence that utilized a FISP-like readout and acquired 16 echoes per respiratory cycle. The field of view was 192 × 120 mm with a slice thickness of 3 mm and the acquisition matrix was 128 × 64 × 16. The image data were reconstructed with zero filling resulting in isotropic voxels with dimensions of 1.5 × 1.5 × 1.5 mm. For the displacement encoded experiment the magnetization preparation pulses were applied at end diastole and readout at end systole. To obtain a complete set of 3D displacements three imaging experiments were used, each of which required 192 respiratory cycles and took approximately 6 min.

Superquadric Glyphs

We briefly review the method described by Kindlmann (13). Superquadric shape functions represent a broad spectrum of shapes ranging from discs and spheres to cubes and stellates, all of which can be derived from the parametric equation

$$p(\theta ,\varphi )=\left(\begin{array}{c}\hfill {\cos }^{\beta }\varphi \hfill \\ \hfill -{\sin }^{\alpha }\theta {\sin }^{\beta }\varphi \hfill \\ \hfill {\cos }^{\alpha }\theta {\sin }^{\beta }\varphi \hfill \end{array}\right),$$ [1]

where p, the parameterized glyph surface, is a function of both the azimuthal (θ ∈ [0,2π)) and the polar (ϕ ∈ [0,π]) coordinates and α and β control the overall superquadric shape. The exponentiation is signed: x^a = sign(x) |x|^a. A judicious choice of α and β is needed to produce a subset of superquadric shapes that smoothly vary between the four basic eigenvalue configurations: λ₁ = λ₂ = λ₃ (spherical), λ₁ = λ₂ > λ₃ (oblate), λ₁ > λ₂ = λ₃ (prolate), and λ₁> λ₂> λ₃ (cuboid), where λ_i are the sorted eigenvalues. Hence, α and β are chosen such that β ≤ α ≤ 1 so that the shape set is limited to convex geometries. Given a set of sorted eigenvalues such that λ₁ ≦ λ₂ ≦ λ₃, the shape of a real symmetric tensor, as determined by its eigenvalues, can be parameterized by the geometric shape metrics c_L, c_P, and c_S (16). The equations describing this parameterization follow:

$$c_{\mathrm{L}}=\frac{{\lambda }_1-{\lambda }_2}{{\lambda }_1+{\lambda }_2+{\lambda }_3},c_{\mathrm{P}}=\frac{2({\lambda }_2-{\lambda }_3)}{{\lambda }_1+{\lambda }_2+{\lambda }_3},c_{\mathrm{S}}=\frac{3{\lambda }_3}{{\lambda }_1+{\lambda }_2+{\lambda }_3}.$$ [2-4]

The variables c_L, c_P, and c_S are measures of the linear, planar, and spherical anisotropy, respectively, and by definition c_L + c_P + c_S = 1. These geometric shape metrics determine the superquadric shape by constraining the α and β exponents in Eq. [1]. By definition, the superquadric function has a single axis about which it is symmetric, but in order to accommodate two axis symmetric configurations (high c_L and high c_P) two axes of symmetry must be used. In order to maintain a smooth shape variation across the basic eigenvalue configurations the superquadric shape functions are parameterized as follows:

$$c_{\mathrm{L}}\ge c_{\mathrm{P}}\Rightarrow \{\begin{array}{c}\alpha ={(1-c_{\mathrm{P}})}^{\gamma },\beta ={(1-c_{\mathrm{L}})}^{\gamma }\hfill \\ p(\theta ,\varphi )=\left(\begin{array}{c}\hfill {\cos }^{\beta }\varphi \hfill \\ \hfill -{\sin }^{\alpha }\theta {\sin }^{\beta }\varphi \hfill \\ \hfill {\cos }^{\alpha }\theta {\sin }^{\beta }\varphi \hfill \end{array}\right)\hfill \end{array}\phantom{\}}$$ [5]

$$c_{\mathrm{L}}<c_{\mathrm{P}}\Rightarrow \{\begin{array}{c}\alpha ={(1-c_{\mathrm{L}})}^{\gamma },\beta ={(1-c_{\mathrm{P}})}^{\gamma }\hfill \\ p(\theta ,\varphi )=\left(\begin{array}{c}\hfill {\cos }^{\alpha }\theta {\sin }^{\beta }\varphi \hfill \\ \hfill {\sin }^{\alpha }\theta {\sin }^{\beta }\varphi \hfill \\ \hfill {\cos }^{\beta }\varphi \hfill \end{array}\right)\hfill \end{array}\phantom{\}}.$$ [6]

It can be shown that at the transition between the two parameterizations (e.g., when c_L = c_P = 0.5) the glyph shape is identical even though the parameterizations are different.

The role of the free parameter γ is to highlight differences in eigenvalues by varying the sharpness of the edges on the glyphs. When γ = 0 the superquadric function analytically reduces to that of a sphere; hence, the depiction of eigenvalue differences is minimized. As γ is increased the glyph edge sharpness is increased and the depiction of eigenvalue differences is enhanced. The parameter γ is somewhat arbitrarily chosen to have a value of 3 to 6 for the shapes used herein. Further considerations for this parameter are found in the Discussion.

The continuum of possible glyphs shapes and their relationship to c_L, c_P, and c_S are shown in Fig. 1. The edges of the glyphs signify anisotropy and distinct edges reflect confidence in the ability to discern distinct eigenvalues. In general, when two eigenvalues are similar the glyphs are cylindrical, reflecting transverse isotropy. If λ₁ = λ₂ > λ₃ then the glyphs are oblate, c_P = 1, and c_L = 0. If λ₁ > λ₂ = λ₃ then the glyphs are prolate, c_P = 0, and c_L = 1. As the anisotropy decreases (c_P → 0 c_L → 0, while c_S → 1) the eigensystem becomes isotropic and there is little confidence in the eigenvectors. When c_L ≈ 0.5, c_P ≈ 0.5, and c_S ≈ 0 then there are three distinct eigenvalues and the orthotropic nature of the tensor is reflected in the cuboid shape with distinct edges.

FIG. 1.

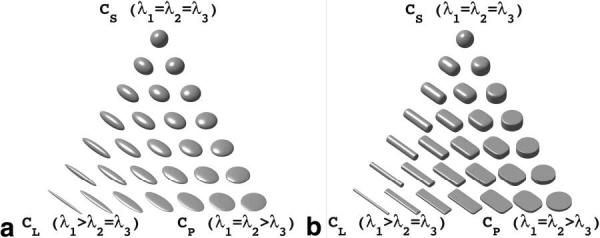
Continuum of superquadric and ellipsoid glyph shapes demonstrates how they reflect various geometric shape metrics (Eqs. [2-4]). (a) The spherical glyphs at the top are characterized by a large spherical geometric shape metric (large c_S) and as such are largely isotropic. The bottom left glyphs are prolate with a high linear geometric shape metric (high c_L) and are transversely isotropic. The bottom right glyphs are also transversely isotropic, but are oblate with a high planar geometric shape metric (high c_P). (b) The glyphs at the vertices of the superquadric glyph triangle have increased edge definition when compared to the ellipsoidal glyph triangle. The superquadric glyphs in the middle of the glyph triangle, representing orthotropic anisotropy, convey the orthotropy better compared to ellipsoidal glyphs.

In comparison to existing ellipsoid or box glyphs, these glyphs have the advantage of clarifying shape differences without inappropriately emphasizing the tensor orientation determined by its eigenvectors. When representing λ₁ = λ₂ = λ₃ as a cube the resulting shape has distinct, but nonmeaningful face normals; hence, a spherical shape is more meaningful. When λ₁ = λ₂ = λ₃, the superquadric glyph is spherical, reflecting the numerical indeterminacy of the eigenvectors. For the case of three distinct eigenvalues, the cuboid glyph reflects the eigenvalues with its edge lengths and the eigenvectors with its face normals.

Data Visualization

For each DTMRI pixel the local eigensystem was used to define a superquadric glyph. For a given tensor the c_L, c_P, and c_S metrics define the superquadric geometry as per Eqs. [5] and [6]. A length scale then multiplies the tessellated surface points so that the shape reflects the proper proportions of λ₁:λ₂:λ₃. In the case of diffusion tensors the length scales are simply its eigenvalues. The calculation of strain tensors from DENSE displacement data requires taking spatial derivatives. In order to display the strain tensors the resultant strain field was interpolated to each image pixel location for visualization. Furthermore, for strain tensors the stretch ratios, rather than the eigenvalue strains, are used as the length scales. The stretch ratios (ξ_i) can be obtained from the diagonalized Lagrangian strain tensor (E) knowing that ${\xi }_{\mathrm{i}}=\sqrt{2E_{\mathrm{i}}+1}$. This is necessary so that for E_i < 0 (i.e., shortening strains) the length scales are greater than zero and as such 0 < ξ_i < 1. For E_i ≥ 0 (i.e., lengthening strains) we find 1 ≤ ξ_i ≤ ∞.

In each figure the glyphs are shown at each pixel location using Phong lighted surfaces to enable three-dimensional visualization. Color coding the glyphs adds additional insight to tensor field trends. Myocardial tissue microstructure is observed to be orthotropic (7) and as such color schemes that highlight orthotropy in structure and function are of interest. To that end an orthotropy index was defined as

$$\mathrm{LP}\text{ratio}=c_{\mathrm{L}}∕(c_{\mathrm{L}}+c_{\mathrm{P}}).$$ [7]

Glyphs that exhibit an LP ratio of 0.5 have three distinct eigenvalues and are highly orthotropic, while LP ratios of 0 or 1 reflect purely linear anisotropy or purely planar anisotropy, respectively. All renderings were generated using Matlab (The Mathworks, Natick, MA) and an 800-MHz PowerPC G4 (Apple Computers, Cupertino, CA).

RESULTS

Superquadric glyph rendering of DTMRI and DENSE strain data were used to characterize previously unreported features of myocardial structure and to compactly display many features of myocardial function. All images were generated with custom Matlab code and required less than 30 sec to render. The signal to noise (SNR) of the null images used for the diffusion tensor reconstruction was 202. The SNR of the DENSE images was 13, which results in a noise-based displacement error of 100, 60, and 30 μm in the x-, y-, and z-directions, respectively.

DTMRI

Left Ventricle Anterolateral Wall

The myofiber arrangement in the heart is complex, but highly organized. A well-known feature of the myofiber architecture is the transmural variation in fiber angle (16). This feature is clearly emphasized in the anterolateral wall of the canine heart in Fig. 2 through the use of superquadric glyphs and their inherent edge definition. The fiber angle, herein, is defined as angular deviation of the primary eigenvector from the circumferential-radial plane when looking from the epicardial wall toward the endocardial wall. The myofibers in Fig. 2 are seen to rotate in a left-handed helix from approximately 60° degrees on the epicardium, through approximately 0° in the midwall, to approximately 75° on the endocardium. The most endocardial glyphs represent trabecular tissue. The cuboid shape of the glyphs adds edge definition that facilitates observation of the fiber angle. The transmural fiber helix is less obvious when rendered with ellipsoids due to the loss of edge distinction and any orthotropic information is lost because the secondary and tertiary eigenvalues are not easily visualized (data not shown). Figure 2 highlights the orthotropy of the tissue by colorizing based on the LP ratio and demonstrates that the myocardium from midwall to endocardium is highly orthotropic. In Fig. 2, the glyph shapes, especially in the midwall, appear relatively cuboid, indicating three distinct eigenvalues, which is consistent with LP ratios of 0.4 to 0.6. Qualitatively the glyph shapes and orientations in the midwall and endocardium resemble the expected myocardial sheet structure. Such distinct directions of diffusion may indicate distinct higher-order structural features such as myocardial laminae or sheets (7). Epicardial fibers appear to have high c_L components and hence less distinct orthotropy. When the same tensors are rendered as ellipsoids the orthotropic nature of the diffusion tensors is not as evident.

FIG. 2.

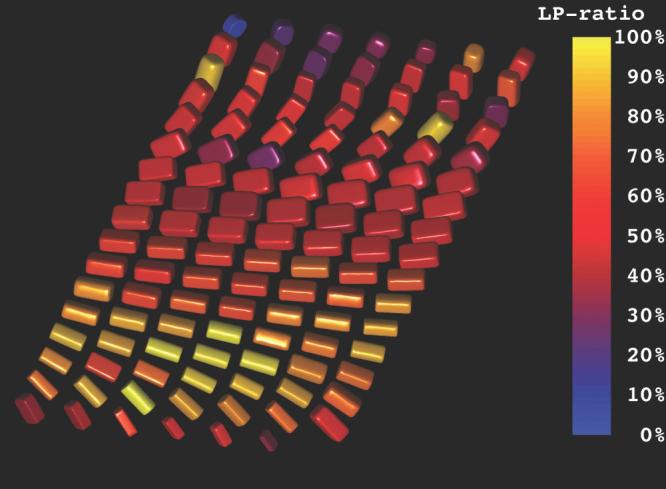
Demonstration of both the transmural arrangement of myofibers and the distinct orthotropy of the tissue structure in the anterolateral wall of the left ventricular using superquadric glyphs. The myofiber orientations are indicated by the orientations of the long glyph edges. The overall superquadric glyph shape and the coloration represent the tissue orthotropy. The epicardium is in the foreground and the endocardium is in the background. Distinct tensor orthotropy is visible in the midwall and endocardial glyphs as exhibited by LP ratios (Eq. [7]) near 0.5.

Right Ventricular Insertion

Figure 3 shows a rendering of the diffusion tensors at the insertion of the right ventricle into the left ventricle at the mid-ventricular level. At the right ventricular endocardial juncture of the two ventricular walls the superquadric glyphs are disk-like and the LP ratio is near zero, indicating highly planar anisotropy. This suggests a branching fiber architecture and represents a region whose diffusion might be better represented as the superposition of two overlapping anisotropic structures. Such a solution was suggested by Tuch et al. for crossing fiber tracks in the brain (18). The superquadric glyph renderings help motivate histologic examination that could verify the existence of a branching fiber structure. In the same figure, left ventricular septal myocardium and endocardial regions of the right ventricular wall exhibit distinct orthotropy (LP ratio ∼ 0.5). The epicardium tends to remain linearly anisotropic, except in the interventricular sulcus where myocardium, vessels, and fat are found and greater heterogeneity of diffusion tensors is observed.

FIG. 3.

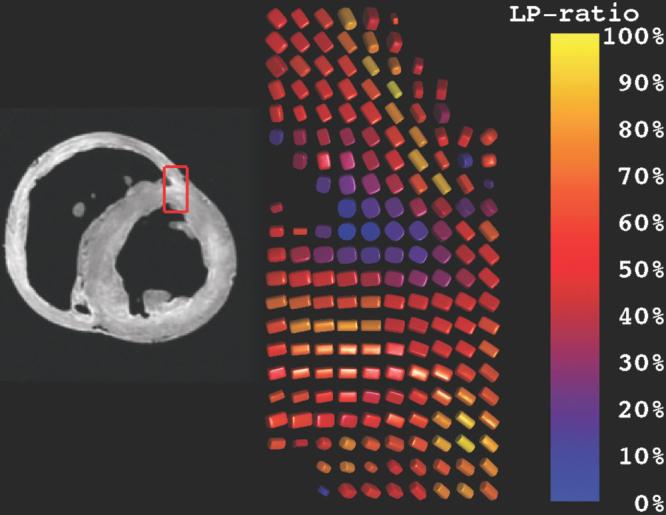
Rendering of diffusion tensors near the junction of the right and left ventricles. The coloration reflects the degree of orthotropy characterized by the LP ratio (Eq. [7]). Diffusion tensors near the endocardial margin of the RV–LV juncture have high c_P (planar anisotropy) and hence low LP ratios, possibly indicating a branching fiber architecture. Elsewhere, glyphs in the midwall have LP ratios of ∼0.5, possibly indicating laminar orthotropic architecture structure, while epicardial glyphs tend to be linearly anisotropic and hence have high LP ratios.

Anterior Papillary Muscle

The myofiber arrangement within a papillary muscle is known to course along the long axis of the papillary muscle body. Figure 4 shows a long-axis cross section of the anterior papillary muscle. The glyphs within the papillary muscle body point along its long axis, exhibit linear anisotropy, and appear largely cylindrical. Higher-order structure, such as laminar sheet organization, has not been reported in papillary muscles and these data do not support their existence. Glyphs near the papillary-endocardial border smoothly vary from cuboid (∼50% LP ratio) in the midwall, through disk-like (low LP ratio), and back to cuboid as the papillary muscle body is approached. High c_P regions are largely disk-like, indicating that these regions likely contain multiple fiber directions and are not well characterized by a single diffusion tensor. Instead these local diffusion tensors glyphs may indicate a branching structure where it is likely that fibers within a voxel course along both the predominant papillary muscle axis and the expected endocardial fiber direction.

FIG. 4.

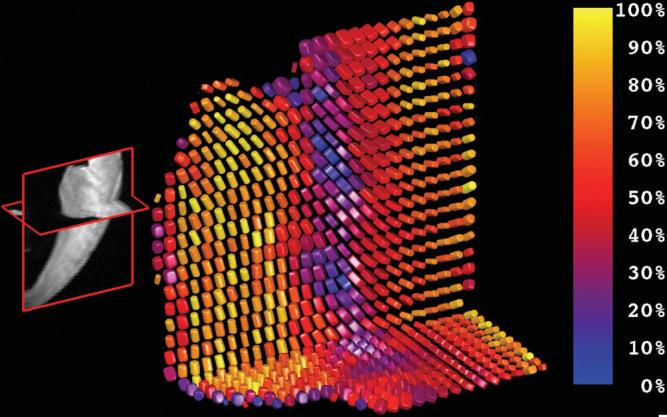
Diffusion tensor structure of the anterior papillary muscle and its insertion to the left ventricular wall. The grayscale image on the left exhibits long-axis and short-axis cross sections of the anterior papillary muscle where it inserts on the left ventricular free wall. The group of cylindrical superquadric glyphs on the left have high linear anisotropy (high c_L) and high LP ratio (yellow) and comprise the anterior papillary muscle. These glyphs reflect the expected histologic tissue structure. The glyphs with greatest orthotropy (∼50% LP ratio, red) appear in the midwall and resemble the expected sheet organization. Most epicardial glyphs (right-hand edge) exhibit high linear anisotropy and therefore high LP ratio and appear as yellow cylinders.

Figure 4 also exhibits the local diffusion tensor anisotropy in a short-axis transmural section of left ventricular anterior free wall that includes the anterior papillary muscle. Here the papillary muscle fibers are shown to exhibit largely linear (high c_L) anisotropy and a high CP ratio (∼100%). The anterior papillary glyphs, as well as the subepicardial glyphs, appear mostly cylindrical. The mid-wall glyphs that show distinct orthotropy (∼50% CP ratio) exhibit a continuity of structure that resembles the expected sheet organization.

Strain

The renderings of high-resolution DENSE strain tensors compactly exhibit many characteristics of myocardial function. The expected modes of deformation include transmural thickening, circumferential shortening, longitudinal shortening, and ventricular torsion. All of these features are evident in the superquadric glyph renderings of a section of transmural strain tensors at the mid-ventricular level of the inferolateral wall (Fig. 5). The ability to resolve the spatial dependence of these strain components is due to the high-resolution DENSE strain imaging technique used to obtain these data. The data exhibit a primary direction of thickening along the radial direction (i.e., long axis of glyphs are oriented from epicardium to endocardium). The superquadric length scales reflect the stretch ratios and the colorization codes for radial Lagrangian strain. A transmural gradient in wall thickening that increases from the epicardium to the endocardium is evident. The trabecular and papillary regions of myocardium are shown to exhibit little radial thickening. Furthermore, the other stretch ratios exhibit shortening that is not parallel to the local circumferential and longitudinal directions, but rather at a significant angular deviation from those coordinate directions. This deviation reflects the underlying left-handed torsion of the ventricle as well as the general circumferential and longitudinal shortening. These features are not as readily visualized when rendered with ellipsoids.

FIG. 5.

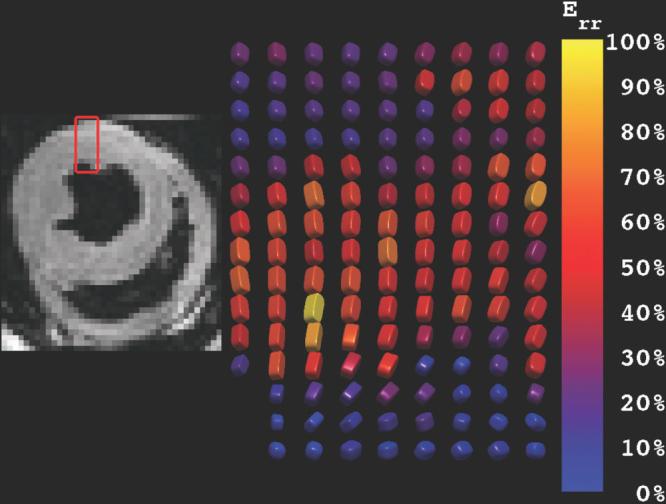
Superquadric glyph rendering of transmural radial Lagragian strains in the inferolateral freewall of the canine ventricle. The glyphs are generally radially oriented and exhibit a transmural gradient in wall thickening. Furthermore, the other stretch ratios exhibit shortening that is not parallel to the local circumferential and longitudinal directions, but rather at a significant angular deviation from those coordinate directions. This deviation reflects the underlying left-handed torsion of the ventricle as well as the general circumferential and longitudinal shortening.

In Fig. 5 it is evident that the primary directions of shortening are not coaxial with the local fiber direction at all transmural locations. Whereas the fiber angle is seen to rotate through ∼120° (Fig. 2), the primary directions of shortening rotate very little. This is consistent with the findings of Waldman et al. (19).

DISCUSSION

Superquadric parametric functions provide an intuitive basis for visualization of spatially varying tensor fields. Without the visual queues provided by the superquadric glyphs the spatial trends in tensor anisotropy are difficult to assess qualitatively. The ability to effectively scrutinize the data is an important first step in being able to quantify regional variations and trends in large tensor field data sets. Quantitative analysis is thereby aided, as relevant and important trends are made more obvious during data exploration. This visualization strategy directly resulted in the ability to characterize features of myocardial structure that have not previously been reported, such as the apparent branching structure of myocardial fibers near the interventricular sulcus and near endocardial–papillary muscle junctures. The qualitative agreement of the diffusion orthotropy observed in Figs. 2-4 with the expected tissue orthotropy should be validated with tissue histology.

For tensor fields that exhibit high linear anisotropy the data can be displayed as a vector field of the primary eigenvectors. If, however, the data are not known to be highly linearly anisotropic, then the use of superquadric glyphs is advantageous. The proposed superquadric glyph technique provides visual cues (sharp edges) only when there is a distinct fiber direction and conveys otherwise meaningful information when a distinct fiber is not present through the use of cuboid, oblate, and spheroid shapes.

Two key features arise through the use of superquadric glyphs. First, the superquadric glyphs clearly reflect the eigenvector orientation when the eigenvectors are unique. This is a result of the distinct edge rendering that arises with increasing amounts of anisotropy. Second, the superquadric glyphs distinctly represent the orthotropic tensors as a cuboid, which is especially important for visualizing the orthotropic nature of biologic structure and function. These features are not readily evident in renderings that use ellipsoids and can be misleading if renderings are made with cuboids alone. When the eigenvalues are similar, as may occur in low SNR imaging, the superquadric shape masks the mathematical ambiguity of the eigenvector orientation with more rounded shapes. If the SNR is high and the eigenvalues are distinct then the shapes have more distinct edge features.

In the set of superquadric parametric functions (Eqs. [5] and [6]) there is a free parameter, γ, that is generally chosen to have a value of 3 to 6. This parameter modulates the curvature of the superquadric glyph edges, which has the effect of determining how distinctly the eigenvector orientation is indicated. For γ = 0 the superquadric equations analytically reduce to the equations for a sphere, whereas for γ = ∞ the superquadric equations generally represent cubes. Future work will use an estimate of image SNR to quantify the confidence in eigenvector determination at low anisotropies, which in turn can lead to a more principled choice of γ.

The LP ratio has the advantage that it clearly distinguishes among three unique types of anisotropy: linear anisotropy, planar anisotropy, and orthotropy. Other anisotropy metrics such as fractional or relative anisotropy distinguish between isotropy and general anisotropy, but do not distinguish well among different forms of anisotropy. The definition of the orthotropy index (LP ratio) could be improved. The equation is ill-defined for spherical tensors where c_L and c_P are zero. The c_L, c_P, and c_S metrics depend upon eigenvalue sorting and hence the statistical properties of these metrics are possibly poorly behaved. This is more important for quantitative tensor characterization than for qualitative analysis. A visualization scheme that utilized parameterization based on invariant tensor properties would avoid eigenvalue sorting bias and likely improve quantitative assessment.

Rendering speeds were suitable for interactive viewing (free rotation) with dozens of glyphs, but slowed significantly with hundreds of glyphs. Rendering efficiency could be improved by reducing the number of faces for glyphs with high curvatures (e.g., boxes can be efficiently rendered with six faces, while spheres require many more) with little loss in shape information.

Finally, although this technique was demonstrated for use with three-dimensional tensors, it is equally applicable to two-dimensional tensors such as those acquired with conventional breath-held DENSE strain imaging.

CONCLUSION

Visualization of diffusion tensors with ellipsoids, while physically meaningful, is limited. Superquadric glyphs display eigenvector information by enhancing glyph edges when appropriate and thereby enhance visualization of fiber orientation. Furthermore, the inability to distinguish distinct orthotropic regions with ellipsoids is greatly improved with superquadric glyphs without a loss in the ability to interpret linear, planar, and spherical anisotropy. Furthermore, the superquadric parametric functions used herein facilitate the visualization of spatially varying tensor data. The orthotropic nature of DTMRI and strain tensor data requires visualization strategies that clearly exhibit the anisotropy of the data if they are to be interpreted properly. The superquadric glyphs are easily generated and they greatly facilitate data exploration and lead directly to observation of regions of unique tensor anisotropy. This visualization technique was used to explore myocardial DTMRI and DENSE tensor data, but is clearly applicable to visualization of tensors acquired in brain, skeletal muscle, intervertebral discs, or other tissues.