Plantar shear stress distributions: Comparing actual and predicted frictional forces at the foot-ground interface

Abstract

Plantar shear stresses are believed to play a major role in diabetic ulceration. Due to the lack of commercial devices that can measure plantar shear distribution, a number of mathematical models have been developed to predict plantar frictional forces. This study assessed the accuracy of these models using a custom built platform capable of measuring plantar stresses simultaneously. A total of 48 (38 healthy and 10 diabetic) human subjects (75 ± 20kg, 41 ± 20 yrs, 32 male, 16 female) were recruited in the study. Plantar force data were collected for 2 seconds at 50Hz. Two models (M1 and M2) reported in the literature by different groups were used to predict local shear stresses. Root mean squared errors (RMSE) were calculated to compare model data with the actual data, focusing on three parameters: location, magnitude and timing of peak shear components. RMSE values of estimated peak AP and ML shear locations were 3.1 cm and 2.2 cm for M1 and 3.1 cm and 2.1 cm for M2, respectively. Magnitude RMS error values for M1 were found to be 86.6 kPa in AP shear and 38.5 kPa in ML shear, whereas these values were determined to be 97.8 kPa and 63.5 kPa respectively by M2. Time to peak shear RMSE values averaged 17.2% in terms of the gait duration. In conclusion, shear models that were evaluated in this study performed variously depending on the shear parameter.

INTRODUCTION

Early identification of patients that are at risk of developing diabetic foot ulcers is vital in preventing serious consequences such as amputation. Foot pressure distribution measurement is a well-established technique in the assessment of diabetic foot conditions (Cavanagh et al., 2000). However, efforts to establish a relationship between plantar pressure values and foot lesions have only yielded moderate correlations (Armstrong et al, 1998). Furthermore, while relatively high shear forces may act on the sole of the foot, the role that shear plays in the foot pathologies is not clearly understood. Efforts to study this aspect of foot-ground interactions have been hampered by a lack of instrumentation for quantifying shear force distributions.

Frictional shear forces have been observed to reduce both the amount of pressure and the time required to develop a decubitus ulcer in test animals (Dinsdale, 1974). Among researchers who have investigated plantar shear distribution under the foot, Pollard and Le Quesne (1983) observed neuropathic ulceration at the sites of maximal shear. Unfortunately the instrumentation developed to measure plantar shear were limited in terms of (i) being capable of recording only uniaxial shear (i.e. antero-posterior), (ii) suffering low spatial resolution (Davis et al., 1998) or (iii) not being practical (Tappin et al, 1980; Akhlaghi and Pepper, 1996; Lord and Hosein, 2000) due to calibration difficulties and cross-talk between shear and pressure channels.

A number of investigators have established 2D models to predict shear under the foot. A decade ago Abuzzahab et al. (1997) attempted to estimate shear distribution, based on local pressure data and global ground reaction forces. Their aim was to create a kinetic model of the foot and the ankle where they distributed shear loads to each segment of the foot based on the arithmetic contribution of the local vertical forces to the global normal force (Model 1). Giacomozzi and Macellari (1997) took a similar approach but also incorporated the free moment (Model 2) into their calculations (Giacomozzi and Macellari, 1997).

None of these models, however, have been validated. Our aim in this study was to compare plantar shear stress data collected with a custom-built device (Davis et al., 1998), with the predicted results of Models 1 and 2.

METHODS

A total of 48 volunteers were recruited for the study among which 10 were diagnosed with diabetic neuropathy. Exclusion criteria included, (i) gross foot deformities (minor clawing of the toes was permissible), (ii) prior foot surgeries and (iii) foot pain. Table 1 displays the characteristics of the subjects. The study was explained to the volunteers before their participation and they signed an informed consent form.

Table 1.

Characteristics of the subjects

No of subjects	48 (16 female, 32 male, 10 diabetic neuropathic, 38 healthy)
Age (years)	41 ± 20 (13–83)
Weight (kg)	75 ± 20 (41–140)

Values are presented as the mean ± standard deviation, with the range in parentheses.

The custom built system consists of 80 transducers arranged in an 8×10 array, each with a surface area measuring 1.27×1.27 cm. The device was set flush with the ground to create a platform measuring 11.4×14.2 cm with 1.5 mm space in between each sensor. Although the overall size of the device was not large enough to permit force measurements under the entire plantar surface, it was large enough to examine the forefoot area. This region is of primary interest since diabetic ulcers mostly occur in the forefoot area (Oyibo et al., 2000; Caselli et al., 2002). The platform enabled data collection at 50Hz, for periods up to 3 seconds. The measuring device utilized strain gauge technology (Davis et al., 1998). The data recorded by the platform had an average error percentage of 1.0%, 4.6% and 5.0% respectively for pressure, antero-posterior and medio-lateral shear channels.

The 2-step method was preferred in data acquisition (McPoil et al., 1999). The tests were carried out for only one foot (left or right), 3 trials for each subject.

A normal force value of 5 N was used as a threshold to determine the “active” sensors. Global normal (F_N), antero-posterior (F_AP) and medio-lateral (F_ML) shear forces were calculated by summing up the normal (N), antero-posterior (AP) and medio-lateral (ML) forces measured by each active transducer. A proportionality ratio (k) was found for active sensors by dividing the measured local N force to F_N. To calculate local shear forces according to the Model 1 (Abuzzahab et al., 1997) the following equations were used;

• Model 1:

  $$f_{\mathit{\text{AP}}\hspace{0.17em}i}=k_i{F}_{\mathit{\text{AP}}}\mathrm{i}=1,2‥‥80$$ (1)

  $$f_{\mathit{\text{ML}}\hspace{0.17em}i}=k_i{F}_{\mathit{\text{ML}}}\mathrm{i}=1,2‥‥80$$ (2)

• Model 2 including the free moment (Giacomozzi and Macellari, 1997):

  $$f_{\mathit{\text{AP}}i}=k_i{F}_{\mathit{\text{AP}}}-\mid f_{\mathit{\text{Mi}}}\mid \text{sin}{\alpha }_{i}x\mathrm{i}=1,2‥‥80$$ (3)

  $$f_{\mathit{\text{ML}}i}=k_i{F}_{\mathit{\text{ML}}}+\mid f_{\mathit{\text{Mi}}}\mid \text{cos}{\alpha }_{i}y\mathrm{i}=1,2‥‥80$$ (4)

f_Mi is the local shear force on a unit area generated by the free moment that acts about the center of pressure (COP) of the forefoot, x and y are unit vectors of the x and y axes, respectively. α denotes the angle between the vector that connects the COP and the particular sensor and x axis.

Three characteristic parameters were extracted from the experimental, Model 1 (M1) and Model 2 (M2) datasets: peak shear magnitudes, location and time to peak shear forces. Peak force magnitudes, regardless of direction, were picked throughout the whole gait data. Force to stress conversion was performed by dividing the measured force by sensor surface area. Positive (+) values of antero-posterior shear stresses refer to stresses on the skin pointing towards anterior direction whereas negative (−) values posterior direction. Similarly stresses towards lateral and medial directions were denoted by (+) and (−) signs respectively.

The x and y coordinates for the locations of the peak shear stresses were determined for each dataset. For each trial actual gait duration was identified. The time when the peak shear stress occurred according to the three datasets were recorded as a percentage of the actual gait time. Statistical analysis included root mean squared error (RMSE) values. Location errors were presented by calculating the Euclidian distances between the actual peak shear sites and the estimated ones.

Results

RMSE values of the estimated shear stress parameters are given in Table 2. Both models were able to predict the locations of peak ML shear component to within 2.2 cm. However the error values increased up to 3.1 cm in AP shear case. Actual and estimated peak AP and ML stress profiles of a representative subject are given in Figure 1 and Figure 2. In the given specific case peak actual AP shear occurred under the second toe; however estimated sites by both models were distant from the actual location (Figure 1). On the other hand both models determined the location of peak ML stress correctly (Figure 2). In general, actual peak AP and ML shear stresses took place 2.7 cm apart whereas the distance between peak AP and ML shear sites was 0.5 cm and 0.9 cm, respectively for M1 and M2.

Table 2.

Comparison of peak actual and predicted shear stress parameters

	M1 AP	M2 AP	M1 ML	M2 ML
Magnitude RMSE (kPa)	86.6	97.8	38.5	63.5
Peak stress location RMSE (cm)	3.1	3.1	2.1	2.2
Time to peak shear RMSE (% gait)	18.0	17.4	18.6	14.9

Figure 1.

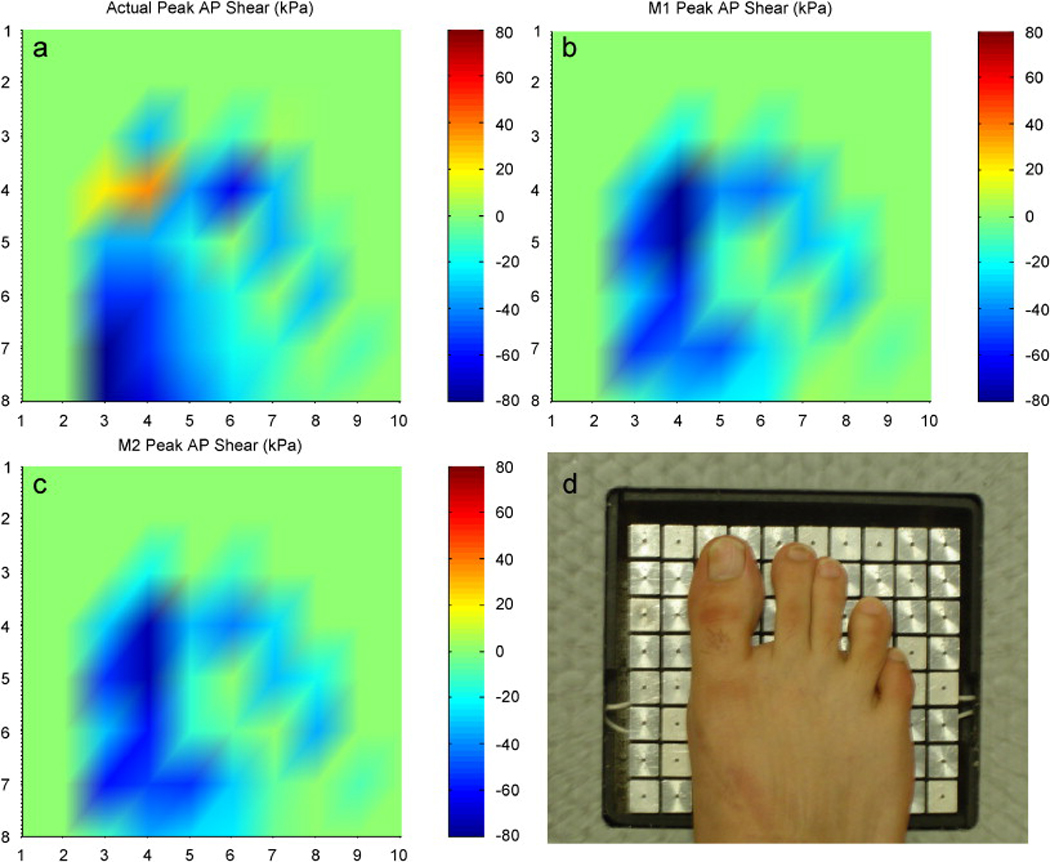
Peak plantar AP stress profiles of a representative subject: a) Actual shear, b) Model 1 prediction, c) Model 2 prediction (units are in kPa) d) foot placement

Figure 2.

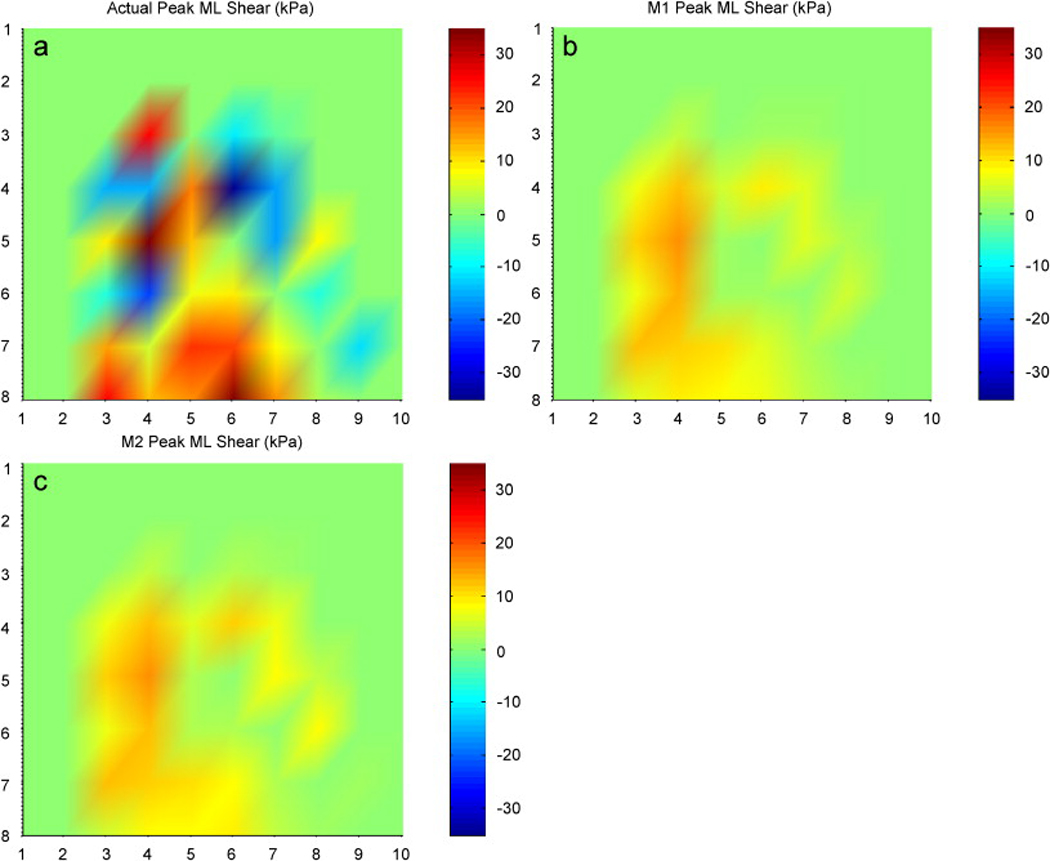
Peak plantar ML stress profiles of a representative subject: a) Actual shear, b) Model 1 prediction, c) Model 2 prediction (units are in kPa). Peak stress was seen under the same region (first metatarsal head) in each case.

Actual peak AP and ML shear stresses yielded mean absolute magnitudes of 76.1 kPa and 50.9 kPa, respectively. Predicted peak AP shear stress magnitudes had RMSE values as high as 97.8 kPa. RMSE values decreased quantitively in the ML shear case however error to actual ratio was still high in M2 prediction. The most accurate magnitude estimation was in the M1 ML shear case with a 76% RMSE to actual ratio.

RMSE results by both models ranged between 14.9% and 18.6% for the time to peak shear parameter.

Discussion

The models developed to predict plantar shear distribution have not been validated before. This study has revealed that the performance of both models varied according to the shear parameter. Time to peak shear was predicted by an average of 17%, considering all four situations. Location errors might not be considered significant if one assumes the average length of the human foot is 25 cm (≈10 inches). However in clinical applications that require sensitive peak shear coordinates both M1 and M2 might be questioned. With about 100% error levels peak shear magnitude determination was the field where the models were the least successful.

M1 was observed to perform better than M2 in magnitude estimation. Their results were almost identical in finding peak shear locations. Time to peak shear was the only category where M2 won against M1.

The authors believe the reason that the models could not achieve their mission with shear magnitudes is mainly due to the lack of the linear relationship between pressure and shear stresses that was assumed. Plantar shear magnitudes probably are influenced by local differences in frictional properties and/or intrinsic muscle activities.

The kinetic coefficient of friction (COF) is given by the ratio of shear to normal force at a given time. The product of the kinetic COF and local normal forces in fact reveals the sliding friction force. Having the local shear forces calculated by this approach, M1 practically assumes that the whole plantar surface is sliding against the supporting media during the gait cycle. However our experience and results did not confirm this sliding foot assumption.

This study had limitations related to the spatial resolution and overall size of the device. The threshold value used to determine active sensors eliminated some of the partial sensor contact cases. Data processing proceeded assuming full contact in the remaining situations. Only walking was assessed, and this was restricted to barefoot locomotion. Considering the relatively small size of the device and the elderly subjects, visually aiming for the platform was allowed. The decision was based on the report by Grabiner et al. (1995), which has shown that targeting of a force plate did not produce different ground reaction force data.

In summary, to our knowledge this is the first study that has attempted to validate previously developed plantar shear distribution models. Our results indicate that distribution of plantar shear should be measured, particularly if one is interested in the magnitudes of shear components.