Conformational gating of the electron transfer reaction Q_A^−⋅Q_B → Q_AQ_B^−⋅ in bacterial reaction centers of Rhodobacter sphaeroides determined by a driving force assay

Abstract

The mechanism of the electron transfer reaction, Q_A^−⋅Q_B → Q_AQ_B^−⋅_, was studied in isolated reaction centers from the photosynthetic bacterium Rhodobacter sphaeroides by replacing the native Q₁₀ in the Q_A binding site with quinones having different redox potentials. These substitutions are expected to change the intrinsic electron transfer rate by changing the redox free energy (i.e., driving force) for electron transfer without affecting other events that may be associated with the electron transfer (e.g., protein dynamics or protonation). The electron transfer from Q_A^−⋅ to Q_B was measured by three independent methods: a functional assay involving cytochrome c₂ to measure the rate of Q_A^−⋅ oxidation, optical kinetic spectroscopy to measure changes in semiquinone absorption, and kinetic near-IR spectroscopy to measure electrochromic shifts that occur in response to electron transfer. The results show that the rate of the observed electron transfer from Q_A^−⋅ to Q_B does not change as the redox free energy for electron transfer is varied over a range of 150 meV. The strong temperature dependence of the observed rate rules out the possibility that the reaction is activationless. We conclude, therefore, that the independence of the observed rate on the driving force for electron transfer is due to conformational gating, that is, the rate limiting step is a conformational change required before electron transfer. This change is proposed to be the movement, controlled kinetically either by protein dynamics or intermolecular interactions, of Q_B by ≈5 Å as observed in the x-ray studies of Stowell et al. [Stowell, M. H. B., McPhillips, T. M., Rees, D. C., Soltis, S. M., Abresch, E. & Feher, G. (1997) Science 276, 812–816].

Protein dynamics play an important role in many biological processes (1), including electron transfer reactions (2). When protein changes precede and are slower than the intrinsic rate of electron transfer, protein dynamics will control the rate of reaction. This situation has been called conformational gating (2). In this work, we study the role of protein dynamics in an electron transfer reaction of the bacterial reaction center (RC). The RC is a membrane protein that mediates the light-induced electron and proton transfer reactions in bacterial photosynthesis. (3) After photoexcitation of the primary donor, a bacteriochlorophyll dimer (D), an electron is transferred from the donor via a bacteriopheophytin (BPhe) to the tightly bound primary quinone, Q_A (k ≃ 10¹⁰ s⁻¹). Subsequent electron transfer occurs from Q_A^−⋅ to the secondary quinone, Q_B, with observed rate, k_AB⁽¹⁾ ≃ 10⁴ s⁻¹ (4, 5), that is,

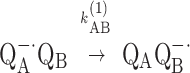1

The observed rate (10⁴ s⁻¹) and activation energy (≈200 to 500 meV) measured for the electron transfer between the two quinones are within ranges that are common for reactions governed by protein dynamics. Previous studies have suggested that this reaction is accompanied by conformational changes (6–10). In this work, we examine the role of conformational gating in the observed reaction (Eq. 1).

A simplified gating model for Q_B reduction involves two consecutive steps:

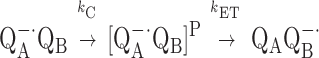2

where Q_A^−⋅Q_B represents the initial state, [Q_A^−⋅Q_B]^P is the state activated for electron transfer and, Q_AQ_B^−⋅ is the final product state. In this model, the overall (observed) rate of the reaction depends on the values of k_ET and k_C (2). If k_C < k_ET, the reaction is conformationally gated. If k_C > k_ET, the reaction is rate-limited by electron transfer. To determine which of these two cases prevails, a driving force assay was used (11). In this assay, quinones with different redox potentials (i.e., driving force) are substituted for Q_A, thereby changing the driving force for electron transfer and, thus, the intrinsic rate constant, k_ET. This will change the overall rate k_AB⁽¹⁾ if electron transfer is rate limiting but will not change k_AB⁽¹⁾ if the reaction is gated.

Naphthoquinones (NQ) with redox potentials different from that of native Q₁₀ were substituted into the Q_A site whereas Q₁₀ was retained in the Q_B site. (11–13). The substitution of Q_A changes the intrinsic rate of electron transfer, k_ET, without affecting k_C since the Q_B site is unchanged and the structures of the substituted Q_A molecules are nearly identical. By using this procedure, the observed rate k_AB⁽¹⁾ was measured as a function of the driving force for electron transfer, from which the mechanism of the k_AB⁽¹⁾ reaction was determined. A preliminary account of this work has been published (14).

MATERIALS AND METHODS

Sample Preparation.

RCs from Rhodobacter sphaeroides strains R26.1 and 2.4.1 were isolated and purified in lauryldimethylamine-N-oxide (LDAO) as described (15). The ratios of absorbance (A^280nm/A^800nm) of the purified RCs were <1.25. Q_A and Q_B were removed from RCs as described (16). Reduced R. sphaeroides cytochrome (cyt) c₂ was purified as described (17). Q₁₀, MQ₀, MQ_P, and MQ₄ were obtained from Sigma. 2,3,5-trimethyl-1,4-naphthoquinone (Me₃NQ) and 2,3,6,7-tetramethyl-1,4-naphthoquinone (Me₄NQ) kindly were provided by J. M. Bruce (Univ. of Manchester, U.K.). They all were solubilized in ethanol before use. Q₁₀ also was solubilized in 1% LDAO and 1% Triton X-100. Unless otherwise indicated, experiments were performed in BMK buffer, which consisted of 0.04% β–d-dodecyl-maltoside, 10 mM KCl, 0.1 mM EDTA, and 5 mM of each of the following buffers: citrate, mes, pipes, tris, ches, and caps. Reagents were of analytical grade; their sources are given in ref. 11.

A detailed procedure for reconstitution of the Q_A binding site with naphthoquinone and Q_B binding site with ubiquinone has been presented (11). The occupancy of the Q_A and Q_B sites after reconstitution were determined from the amplitudes of transients associated with charge recombination, k_AD (D⁺Q_A^−⋅ → DQ_A), and k_BD (D⁺Q_AQ_B^−⋅ → DQ_AQ_B) (18). One-hundred percent Q_A site occupancies and 75–90% Q_B site occupancies were achieved at pH 7.2.

Electron Transfer Measurements.

Absorbance changes were measured at 23°C by using a single beam spectrophotometer of local design (19). Voltage output was recorded on a digital oscilloscope (LeCroy 9310M, Chestnut Ridge, NY) and was digitally filtered (LabView, National Instruments, Austin, TX) and fitted (Peakfit, Tablecurve, or Sigmaplot, Jandel, San Rafael, CA). Actinic illumination was provided by a pulsed dye laser (PhaseR DL2100c, 590 nm, ≈0.2 J/pulse, 0.4-μs full width at half maximum) or by a ruby laser (Optic Technologies Model 130, 695 nm, ≈0.5 J/pulse, ≈10-ns full width at half maximum). Laser light intensity was determined to be saturating (>98%) before and after each set of experiments.

The Electron Transfer from Q_A^−⋅ to Q_B Was Measured by Three Independent Methods.

(i) Optical absorbance changes at 412 and 470 nm. The difference in extinction between ubisemiquinone and naphthosemiquinones provides a spectral signature of the electron transfer, (NQ)_A^−⋅Q_B → (NQ)_AQ_B^−⋅, in hybrid RCs. Peaks in the differential extinction occur at wavelengths of 412 and 470 nm (20, 21). In native RCs, Q_A and Q_B are the same (Q₁₀); there is, however an absorption change at 412 nm caused by an electrochromic shift of the BPhe absorption. No electrochromic shift is observed at 470 nm.

(ii) Optical absorbance changes at 757 nm.

At this wavelength, the absorption changes associated with electron transfer, Q_A^−⋅Q_B → Q_AQ_B^−⋅, are caused by an electrochromic shift of the BPhe absorption (9). The observed kinetics were corrected for fluorescent artifacts by subtracting the absorbance changes when electron transfer was blocked by terbutryne.

(iii) Two-flash cyt c₂ assay (22).

Optical absorbance changes at 865 nm or at 550 nm were measured after two laser flashes separated by a variable time interval, Δt, from 1 to 10,000 μs. The fraction of photoactive RCs, f(Δt) = 1 − exp[−(k_AB⁽¹⁾Δt)], was calculated from the absorbance change at 865 nm due to oxidation of the primary donor, D, from the relation

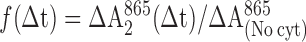3

where ΔA₂⁸⁶⁵(Δt) is the absorbance change induced by the second flash, and ΔA_{(No cyt)}⁸⁶⁵ is the absorption change after a single flash in the absence of cyt c₂. Normalization of the data required correction for several small effects, whose magnitudes were determined independently, i.e., (i) the fraction of RCs without a functional Q_B, (ii) the fraction of RCs without cyt c₂²⁺ bound before the first flash, (iii) the thermodynamic equilibrium between the Q_A^−⋅Q_B and Q_AQ_B^−⋅ states, and (iv) the exchange of cyt c₂³⁺ for cyt c₂²⁺ between flashes.

From absorption changes at 550 nm, which result from cyt c₂²⁺ oxidation, the fraction of photoactive RCs was obtained from

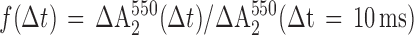4

where ΔA₂⁵⁵⁰(Δt) is the absorbance change induced by the second flash given Δt seconds after the first and ΔA₂⁵⁵⁰(Δt = 10 ms) is the absorbance change induced by the second flash given 10 ms after the first. Because at 10 ms the reaction is complete, ΔA₂⁵⁵⁰(Δt = 10 ms) is the maximum possible change. Normalization to ΔA₂⁵⁵⁰(Δt = 10 ms), instead of the amplitude change induced by the first flash, avoids the need to apply corrections i, ii, and iii.

RESULTS

Hybrid RCs [(NQ)_(A), Q_10(B)].

Hybrid RCs containing different naphthoquinones in the Q_A site and Q₁₀ in the Q_B site [(NQ)_(A), Q_10(B)] were prepared and assayed as described in Materials and Methods. The fraction of hybrid RCs, [(NQ)_(A), Q_10(B)]/{[(NQ)_(A), Q_10(B)] + [Q_10(A), Q_10(B)]}, ranged from 0.45 to 0.80 for samples containing MQ_P, MQ₄, Me₃NQ, and Me₄NQ. A lower value of 0.35 was determined for samples with MQ₀. From measurements of the recombination rates k_AD and k_BD, the in situ free-energy changes relative to Q₁₀, δΔG⁰ of the substituted quinones were obtained (see Table 1) (11–13, 23, 24).

Table 1.

Parameters describing the characteristic time of electron transfer, Q_A⁻⋅Q_B → Q_AQ_B⁻, in hybrid and native RCs

QA	δΔG0, meV	Two-flash assay	Optical absorption change assays
		865 and 550 nm	412 nm	470 nm	757 nm	1/kAB(1), μs (avg)
Q10	0	47 μs (37%)	120 μs (−27%)	NA	27 μs (26%)	110  ±  3
		200 μs (57%)			250 μs (74%)
MQ0	15  ±  5	ND	42 μs (36%)	48 μs (25%)	76 μs (47%)	150  ±  20
			340 μs (27%)	310 μs (58%)	320 μs (53%)
MQP	−35  ±  9	ND	51 μs (27%)	32 μs (44%)	64 μs (29%)	140  ±  30
			220 μs (43%)	230 μs (45%)	260 μs (71%)
MQ4	−46  ±  9	ND	47 μs (18%)	50 μs (13%)	51 μs (28%)	150  ±  20
			240 μs (42%)	210 μs (77%)	170 μs (72%)
Me3 NQ	−95	ND	52 μs (15%)	44 μs (23%)	33 μs (35%)	190  ±  30
			270 μs (48%)	340 μs (63%)	230 μs (65%)
Me4 NQ	−120  ±  10	46 μs (48%)	50 μs (24%)	NA	50 μs (42%)	140  ±  20
		200 μs (49%)	320 μs (34%)		320 μs (58%)

Data were fitted with two exponentials. The characteristic times are given in microseconds together with their relative contributions in parenthesis (757 nm). The percent amplitude relative to the steady-state change (NQ_A^−⋅ minus Q₁₀⁻₍₁₃₎ is given in parentheses for 412 and 470 nm. δΔG⁰ is given relative to Q₁₀, which is defined as 0. The tabulated values in the seventh column represent the average 1/e time of the three methods. Errors were calculated as the SD of the mean. NA, not applicable; ND, not determined. 

Determination of Electron Transfer Rates, Q_A^−⋅Q_B → Q_AQ_B^−⋅, in Hybrid [(NQ)_(A), Q_10(B)] and Native (Q_10(A), Q_10(B)) RCs.

The electron transfer rates k_AB⁽¹⁾ were determined by three independent methods described in Materials and Methods. The use of several methods helped to guard against possible artifacts caused by transient signals not associated with electron transfer. Of particular importance is the two-flash functional assay that directly measures electron transfer. The decay kinetics were fitted by one or two exponential rate constants (see Table 1). The fitted values should be viewed as empirical parameters and are not intended to imply a mechanism. Biexponential decays were observed even with Q₁₀ in both binding sites and, therefore, are not related to the mixture of hybrid and native RCs. The results of the kinetic measurements are described below.

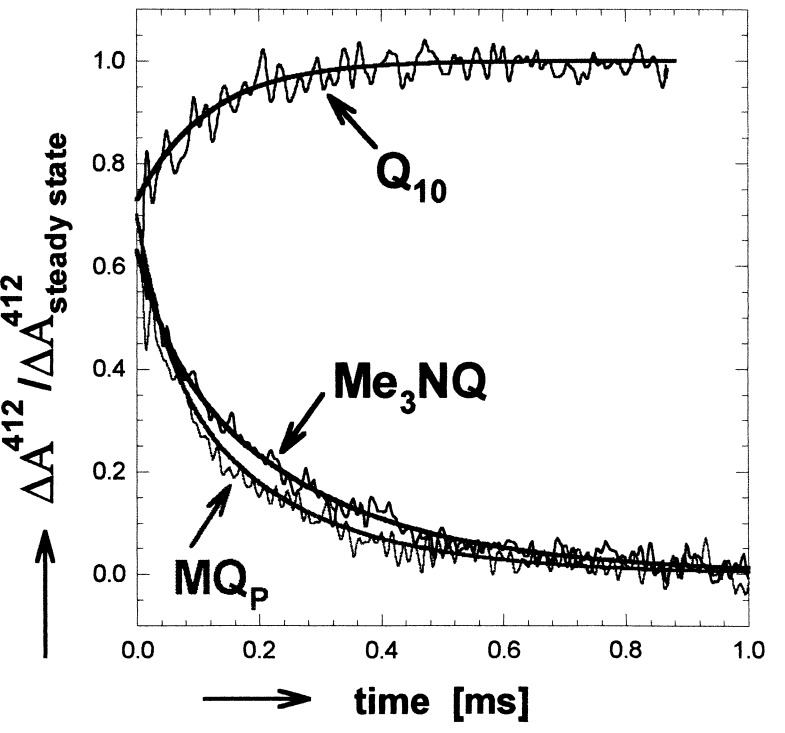
Transient absorbance changes at 412 nm after a laser flash are shown for hybrid and native RCs in Fig. 1. The solid lines represent fits to a biexponential function. Despite the change in electron driving force, the decay rates of the two hybrid samples were essentially the same. The amplitudes were normalized by using the steady-state semiquinone absorption spectra (with Δɛ^{412 nm}_{(NQ⁻−Q10⁻⁾} = 4.3 mM⁻¹ cm⁻¹) (11, 20, 21). In native RCs, the absorbance change is caused by an electrochromic shift of the BPhe absorption. The same shift is assumed to be present also in hybrid RCs. To estimate the fraction of hybrid RCs displaying the measured electron transfer, the electrochromic shift observed for native RCs must be added to the absorbance changes of hybrid RCs. This results in an amplitude for the (NQ)_A^−⋅ transient decay that is 90 ± 5% of the steady-state (i.e., expected) semiquinone decay.

Figure 1.

Optical absorbance changes at 412 nm associated with electron transfer from Q_A^−⋅ to Q_B in hybrid (Me₃NQ^−⋅ or MQ_P^−⋅ in the Q_A site and Q₁₀ in the Q_B site) and native (Q₁₀ in both Q_A and Q_B sites) RCs. In native RCs, the absorbance change is due to an electrochromic shift of the BPhe absorption. In hybrid RCs, the main effect is caused by the difference in extinction coefficient between the naphthosemiquinones (NQ^−⋅ in the Q_A site and Q₁₀^−⋅ in the Q_B site). The observed transients in hybrid RCs are reduced by the electrochromic shift, which was assumed to be the same as that observed in native RCs. The data for the hybrid RCs were normalized to the expected absorption determined from the known difference in extinction coefficients between (NQ)_A^−⋅ and Q₁₀^−⋅ (11, 20, 21). A shallow slope determined by monitoring the recombination reactions (D⁺Q_A^−⋅ → DQ_A and D⁺Q_AQ_B^−⋅ → DQ_AQ_B) was subtracted for clarity. Addition of terbutryne, which inhibits electron transfer to Q_B, eliminated the transient kinetic phases. [Conditions: 5 μM 2.4.1RCs, BMK buffer (pH = 7.2), 0.03% LDAO. Spectral bandwidth, 10 nm].

At 470 nm, no electrochromic shifts are observed, and, therefore, no transient signals are obtained in native RCs. The amplitudes of the observed transients in hybrid RCs caused by (NQ)A−⋅ absorption decay amounted to 89 ± 5% of the expected steady-state signal (with Δɛ(NQ−470 nm−Q10−) = 2.5 mM−1 cm−1 for MQ0, MQP, and MQ4 (20, 21) and 5.0 mM−1 cm−1 for Me3NQ) (11). The characteristic times associated with the observed transients at 470 nm were, within experimental error, the same as those obtained at 412 nm (see Table 1).

The transient absorption changes at 757 nm that arise from an electrochromic shift associated with k_AB⁽¹⁾ (9, 21, 25, 26) were measured in native as well as in all hybrid RCs. The data were fitted with a biexponential function and were in general agreement with the results obtained by the other methods. Replacement of Q₁₀ with Q₂ and Q₀ in the Q_B site had no effect on the observed decays rates.

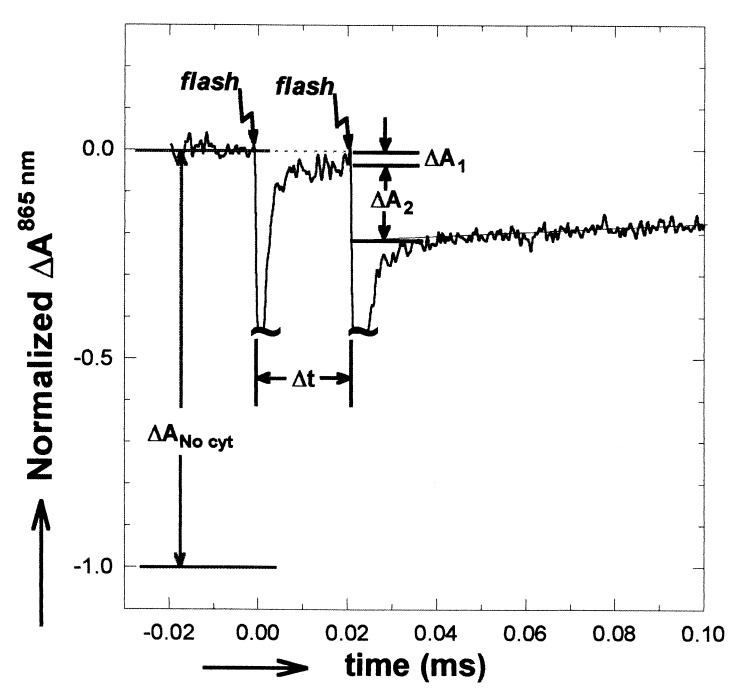
The functional two-flash assay was performed at two wavelengths (865 and 550 nm) for hybrid and for native RCs. The result of an 865 nm assay is shown in Fig. 2. After one laser flash, the charged species, D⁺Q_A^−⋅Q_B, was formed. Cyt c₂²⁺ reduced the primary donor to form DQ_A^−⋅Q_B (τ = 0.8 μs in RCs with a bound cyt c₂²⁺). A small residual absorbance (ΔA₁) remained due to RCs without cyt c₂²⁺ bound before the first flash. For RCs in which a second flash was given before the electron left Q_A^−⋅, no charge separation on the timescale of our experiments and consequently no optical transients were observed. In RCs in which electron transfer had occurred before the second flash, the photoactive state, DQ_AQ_B^−⋅, could undergo charge separation (to form D⁺Q_A^−⋅ Q_B^−⋅) with a concomitant optical absorbance change observable at 865 nmΔA₂. The absorbance change after the second flash is directly related to the rate of electron transfer (see Eq. 3). Similar measurements of optical absorbance changes at 550 nm (not shown) caused by oxidation of cyt c₂²⁺ by D⁺ after a second flash also were made (see Eq. 4).

Figure 2.

Optical absorbance changes at 865 nm for native RCs in the presence of cyt c₂²⁺ after two laser flashes spaced Δt apart. Laser flash artifacts are truncated. The ratio of ΔA₂ to ΔA_{No cyt} gives the fraction of photoactive RCs at the time of the second flash (see Eq. 3). ΔA₁ is due to the fraction of RCs that do not have a bound cyt c₂²⁺. Addition of terbutryne to inhibit electron transfer to Q_B eliminated the absorbance change in response to the second laser flash. (Conditions: 3 μM 2.4.1 RCs with Q₁₀ reconstituted into the Q_A and Q_B sites by addition of Q₁₀ in LDAO. After reconstitution, LDAO was 0.03%. 100 μM cyt c₂²⁺, 5 μM ascorbate, 1 mM Tris, and 0.04% maltoside; spectral bandwidth, 10 nm.)

The applicability of the measurements at 865 nm is limited to the time interval 1 μs < Δt < 100 μs. The lower limit is given by the electron transfer time from cyt c₂²⁺ to D⁺ (≈0.8 μs). The upper limit is given by the cyt c₂³⁺/cyt c₂²⁺ exchange time (0.5–0.7 ms): If cyt c₂³⁺/cyt c₂²⁺ exchange takes place between flashes, D⁺ will be reduced by cyt c₂²⁺. Accurate measurements at 550 nm were obtained only for time intervals Δt > 40 μs because of the relatively poor signal-to-noise ratio associated with the small difference in extinction between oxidized and reduced cyt c₂ (≈21 mM⁻¹ cm⁻¹). For time 40 μs < Δt < 100 μs, measurements were performed at both wavelengths; the two sets of measurements agreed within experimental error.

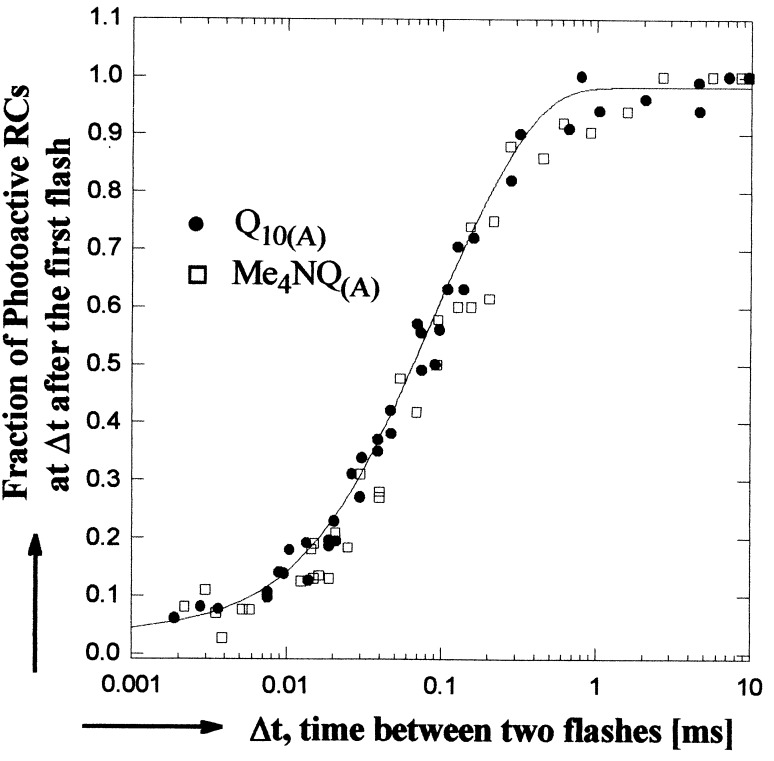
The normalized fraction of photoactive RCs (calculated by using Eqs. 3 and 4) is plotted in Fig. 3 as a function of the time interval between flashes for RCs having either Q₁₀ or Me₄NQ in the Q_A site. The solid line represents a biexponential fit to the data (see Table 1). The results in Fig. 3 show that the rate of electron transfer is the same for both quinones. RCs from the strain 2.4.1 containing carotenoid were used for the studies shown in Fig. 3 to eliminate a small absorption change at very short times in carotenoid-free RCs (R26.1). Control experiments (not shown) confirmed that 2.4.1 and R26.1 RCs display the same electron transfer rates.

Figure 3.

The fraction of photoactive RCs as a function of the time interval between two laser flashes for native (•), and hybrid (□) RCs. The solid line represents a least squares biexponential fit to the data. A minimum of 20 min dark recovery was allowed between sets of flashes. (865 nm assay conditions given in Fig. 2; at 550 nm, cyt c₂²⁺ concentration was reduced to ≈30 μM; spectral bandwidth, 4 nm.)

The results determined from the three independent methods are consistent with one another (Table 1). A model independent way to compare the data from samples with different Q_A molecules is to compare the time required to decay to 1/e of the initial state. The 1/e times, averaged over the three methods, for RCs with various quinones in the Q_A sites are similar and show no correlation with the redox potential of Q_A (see Table 1). The rates of each of the two components of the biexponetial fit derived from the two-exponential analysis also do not vary systematically with driving force.

pH Dependence of Electron Transfer in Hybrid (Me₃NQ_(A), Q_10(B)) and Native (Q_10(A), Q_10(B)) RCs.

The rate k_AB⁽¹⁾ was measured at 470 and 757 nm over the pH range of 4.7 to 10.3 for hybrid RCs with Me₃NQ in the Q_A site and for native RCs. The rate was independent of the driving force throughout the entire range. The hybrid RCs retained the pH dependence of native RCs; that is, the rate was pH-independent below pH 8 and decreased by a factor of ≈10 per pH unit above pH 8 (19, 25, 27).

Effect of Exogenous Quinone Concentration [Q₁₀] on Electron Transfer.

We measured the effect of quinone concentration [Q₁₀] on k_AB⁽¹⁾ in native RCs. One phase of the biexponential rate was unaffected by [Q₁₀] and remained ≈7,000 s⁻¹ whereas the second rate depended strongly on [Q₁₀] (e.g., at 5 μM [Q₁₀], k₂ = 1,300 s⁻¹ and, at 85 μM [Q₁₀], k₂ = 25,000 s⁻¹). These experiments are still in progress.

DISCUSSION

In this work, we tested whether conformational changes or intrinsic electron transfer determines the kinetics of the observed reaction, Q_A^−⋅Q_B → Q_AQ_B^−⋅, in RCs from R. sphaeroides. This was accomplished by substituting naphthoquinone molecules with redox potentials different from that of native Q₁₀ into the Q_A binding site while retaining Q₁₀ in the Q_B site. The experimental results showed that the observed reaction rates were independent of the electron transfer driving force.

Analysis of the Driving Force Assay.

For a typical electron transfer reaction, the observed rate depends on the free energy for electron transfer as given by the Marcus theory (28):

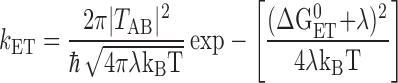5

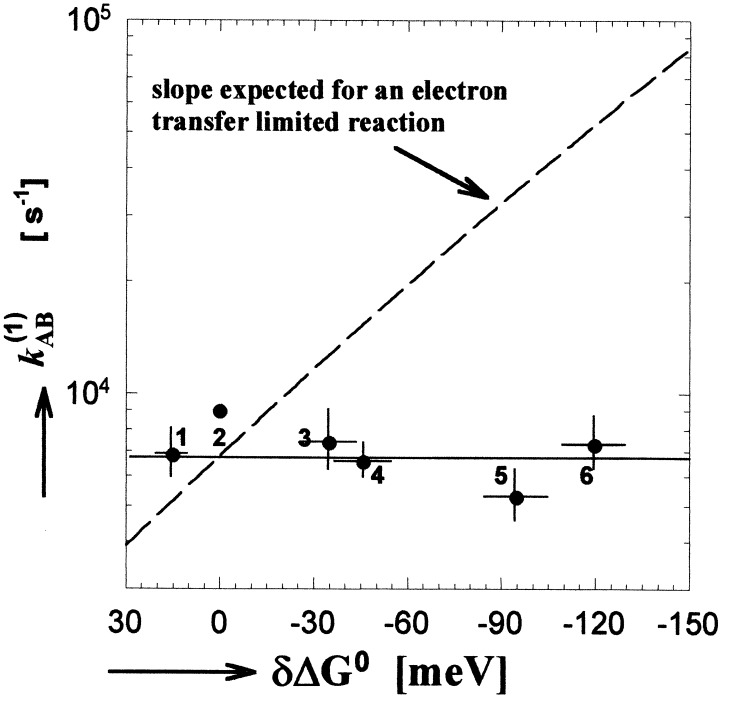
where k_ET is the intrinsic electron transfer rate constant, ΔG_ET⁰ is the free energy for electron transfer (defined as the energy of the final minus the initial state), λ is the reorganization energy, T_AB is the tunneling matrix element, and k_BT is the thermal energy. In principle, the independence of k_AB⁽¹⁾ on ΔG_ET⁰ could be caused by the reaction being activationless (−ΔG_ET⁰ = λ). However, this is not the case for k_AB⁽¹⁾, for which a large activation energy is observed (9, 19, 29, 30). Values for λ and ΔG_ET⁰ have been determined to be ≈1.1 eV and ≈−0.1 eV, respectively (13, 19, 31, 32). For these values, k_ET is expected to vary by a factor of 10 over the range of free energy spanned in this study* (see dashed line in Fig. 4). This is in contrast to the observed invariance of the rate with electron transfer driving force shown in Fig. 4. A fit of the data to a biexponential function (see Table 1) shows that neither component of the decay depends on electron transfer driving force. These results show that k_AB⁽¹⁾ is not limited by electron transfer.

Figure 4.

The electron transfer rate k_AB⁽¹⁾ as a function of redox free energy (driving force) for electron transfer (data from the second and seventh columns of Table 1). The solid line gives a best fit to the data. The dashed line represents the dependence predicted by the Marcus theory for an electron transfer limited reaction using the measured free energy difference between the initial, Q_A^−⋅Q_B, and final, Q_AQ_B^−⋅, states of 60 meV (19) and 1.1 eV for the reorganization energy (13, 31). Error bars represent one SD of the mean. Quinones incorporated into the Q_A site listed in order of decreasing redox potential were: 1, MQ₀; 2, Q₁₀; 3, MQ_P; 4, MQ₄; 5, Me₃NQ; and 6, Me₄NQ. Redox energies are quoted with respect to Q₁₀ (see • without error bars).

Conformational Gating.

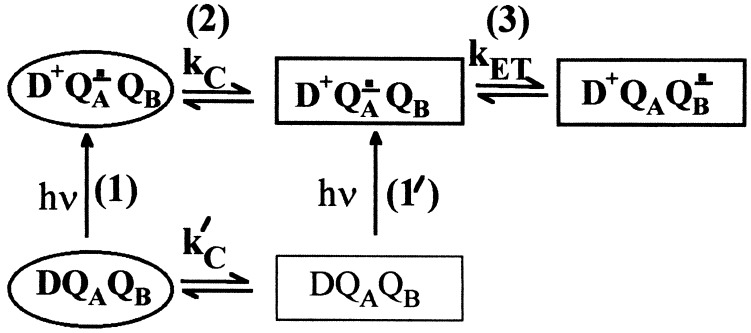
The independence of k_AB⁽¹⁾ on driving force can be explained by a conformational gating mechanism (2). Fig. 5 depicts a kinetic scheme for an electron transfer reaction coupled with a conformational change. The protein can exist in two different states indicated by different shapes in Fig. 5: the D (oval) and P (rectangle) states, for Distal and Proximal, as will be discussed below. In the D state, Q_B is in an inactive conformation, and electron transfer is impaired; in the P state, Q_B is in the active configuration, and electron transfer can proceed. The rate of equilibration between the D and P states in the dark is k_c^′. The gating model requires that, in the dark, the RC is predominantly in the D state. Light excitation results in formation of D⁺Q_A^−⋅Q_B, with Q_B inactive. Conversion to the Q_B active configuration occurs with the conformational gating rate k_C. Once the RC is in the Q_B active configuration, electron transfer can occur with a rate k_ET (given by Eq. 5). Thus, for the conformational gating model the observed k_AB⁽¹⁾ ≃ 10⁴ s⁻¹ = k_C. The intrinsic electron transfer rate must be much greater than the observed rate (i.e., k_AB⁽¹⁾ ≪ k_ET). This is consistent with recent calculations suggesting that the intrinsic electron transfer rate for this reaction is >>10⁴ s⁻¹ (33). The model is also consistent with the work of Li et al. (30). These authors reported an additional fast phase (in the 10⁵−10⁶ s⁻¹ range) in the k_AB⁽¹⁾ kinetics measured at 398 nm and attributed this phase to electron transfer in a population of RCs active for electron transfer in the dark (i.e., our P state in the dark; see Fig. 5).

Figure 5.

Proposed model for conformational gating of electron transfer from Q_A^−⋅ to Q_B. Two conformational states are shown, distal (D; oval), which is inactive, and proximal (P; rectangle), which is active in electron transfer. The main sequence of steps in the reaction are (1) excitation of RCs in the distal state, (2) conversion to the proximal state, and (3) electron transfer. A fraction of RCs in the proximal state before light excitation may give rise to a faster observed rate through reactions 1′ and 3.

The gating model accounts for the observation by Kleinfeld et al. (6) that electron transfer from Q_A^−⋅ to Q_B proceeds in RCs cooled to cryogenic temperature under illumination but does not proceed in RCs cooled in the dark. RCs frozen in the dark are in the inactive conformation (D state). At low temperature, there is insufficient thermal energy for conformational interconversion. RCs cooled under illumination are frozen in the active P state, which explains the observed electron transfer in these RCs.

Molecular Basis of the Gating Mechanism.

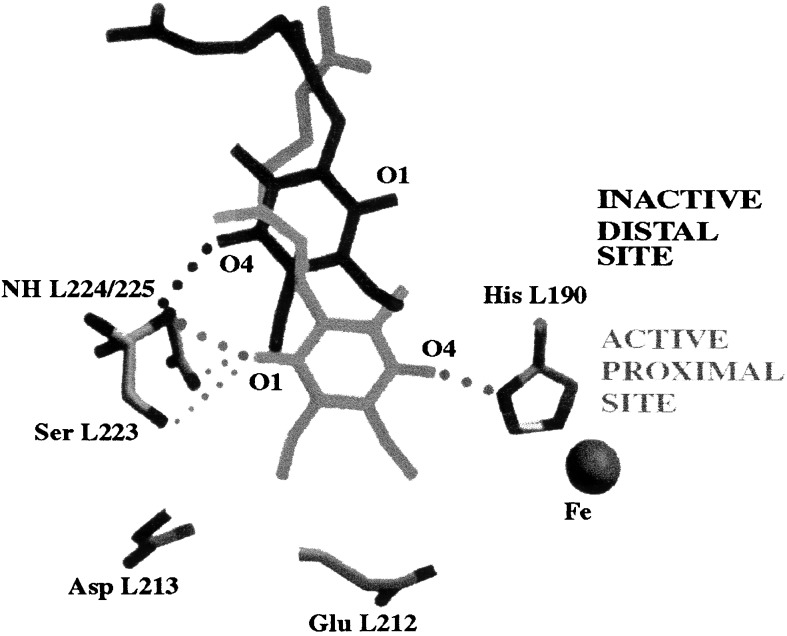
Structural changes responsible for the gating. Structural changes involved in the gating process were elucidated recently by comparing the x-ray crystal structure of the RC cooled to cryogenic (90 K) temperatures under illumination (light structure, D⁺Q_AQ_B^−⋅) with the structure of the RC cooled in the dark (dark structure, DQ_AQ_B) (10). In the light structure, Q_B had moved closer to Q_A and had undergone a 180° propeller twist about the isoprenoid chain (see Fig. 6). The movement of Q_B is expected to affect both the rate and thermodynamic equilibrium of the electron transfer reaction. The more direct pathway (and shorter distance) between Q_A^−⋅ and Q_B in the light structure increases the rate of electron transfer. The greater number of hydrogen bonds to Q_B, compared with the dark structure, stabilizes Q_AQ_B^−⋅ with respect to Q_A^−⋅Q_B, thereby increasing the driving force for electron transfer. The position of Q_B in the light structure, hydrogen bonded to Ser-L223 and to His-L190, corresponds to the active P (proximal) conformation in Figs. 5 and 6. The position of Q_B in the dark structure, hydrogen-bonded only to the amide hydrogen of Ile-L224, corresponds to the inactive D (distal) conformation in Figs. 5 and 6. Thus, the conformational gating step involves the movement of Q_B by ≈5 Å from the distal to the proximal site.

Figure 6.

Comparison of the binding positions for Q_B determined from the light (D⁺Q_A Q_B^−⋅) and dark (DQ_AQ_B) x-ray crystal structures of the RC (10). Movement from an inactive–distal (black) to an active–proximal (gray) binding site is proposed as the major structural change involved with conformational gating of electron transfer from Q_A^−⋅ to Q_B. Hydrogen bonding partners are connected by dotted lines. Modified from ref. 10.

What controls the kinetics of the gating process?

The unhindered movement and rotation of the quinone in solution would proceed on the nanosecond timescale (34, 35), that is, 4–5 orders of magnitude faster than the observed value of 1/k_AB⁽¹⁾. Consequently, the rate of Q_B movement from the distal to the proximal site must be controlled by a process other than diffusion. What is the rate limiting step for the Q_B movement? Several possibilities can be envisioned; three of these are discussed below.

The most likely gating process is associated with protein dynamics that allow the quinone to move into the proximal position. Support for gating by protein dynamics comes from experiments that showed (i) light-induced proton binding changes on the timescale of k_AB⁽¹⁾ that occur in the absence of electron transfer from Q_A^−⋅ to Q_B (36), (ii) light-induced electrogenic transients in the absence of electron transfer from Q_A^−⋅ to Q_B with the same rate and pH dependence as k_AB⁽¹⁾ in native and EQ(L212) mutant RCs (8), and (iii) the importance of protein fluctuations in electron transfer reactions of the RC (37, 38). Structural changes associated with protein dynamics should, in principle, be observable in the x-ray crystal structures. However, no large changes between protein structures of light and dark adapted RCs were reported (10). The largest change was the loss of electron density for Glu-H173 (close to Q_B) in the light structure, which was attributed to greater disorder. The absence of large changes can be explained if the gating is due to protein “breathing” modes not detected at the cryogenic temperatures at which the structures were determined or if the gating motion involves only small movements of many parts of the protein or changes in water structure around the quinone region, not sufficiently well resolved in the x-ray crystal structures.

Another possibility is that conformational changes at the Q_B site are triggered by Q_A reduction. In the gating scheme shown in Fig. 5, a triggering mechanism implies that coupling between the Q_A and Q_B sites exists and that k_C > k_C^′. Evidence for coupling comes from experiments which show (i) an altered recombination rate (D⁺Q_A^−⋅ → DQ_A) and EPR spectrum of Q_A^−⋅ when inhibitors are present in the Q_B site (19, 39) and (ii) proton binding by amino acids near Q_B in response to Q_A reduction (32, 40, 41). Electrostatic calculations also suggest coupling between the Q_A and Q_B binding sites (42, 43).

A third possibility is that the rate-limiting step involves the breaking of the intermolecular interactions between Q_B in the distal state and the protein. The result reported in this work and by McComb et al. (44), that the rates of k_AB⁽¹⁾ for RCs with Q₁₀, Q₂, or Q₀ in the Q_B site are the same, excludes interactions associated with the isoprenoid tail as rate limiting. However, interactions of the quinone head group, for example, π-stacking with Phe-L216 or hydrogen-bonding between the O-4 carbonyl of Q_B and the amide hydrogen of Ile-L224, may limit the rate of movement between the D and P states.

Non-Exponential Rates.

The kinetics of k_AB⁽¹⁾ observed in this study were nonexponential and could be fitted with a biexponential function. Biphasic rates have been reported by several groups (9, 30, 45). In this work one component of the rate was observed to depend on the exogenous quinone concentration. We postulate that the origin of this component of the kinetics is associated with the fraction of RCs that do not have a bound quinone in the Q_B site. In these RCs, the rate limiting (gating) step is associated with quinone binding. This may explain both the variability and the discrepancy between rates reported by different groups. The discussion of the molecular basis of the gating mechanism presented in the previous section refers to the invariant part of the kinetics associated with those RCs that have a bound quinone.

Conformational Gating in Other Systems.

Electron transfer reactions gated by ligand binding or redox-state dependent protein changes occur in other biological systems (46, 47). It is likely that some of the electron transfer reactions of energy transducing proteins, including cytochrome oxidase, cyt b₆f/cyt bc₁, complex I, and others are conformationally gated. For example, crystallographic data of the bc₁ complex show an ≈10 Å movement of the Fe-S subunit between two sites, one for reduction of the Fe-S center by ubiquinol and another for oxidation of the Fe-S center by cytochrome c (48, 49). To understand protein-catalyzed electron transfer reactions in general, it is necessary to establish whether the intrinsic reaction step or the associated conformational changes are rate limiting. The technique described in this work, whereby the free energy for electron transfer is varied by cofactor substitution, illustrates a general approach to investigate reaction mechanisms and energetics.

ABBREVIATIONS

RC

bacterial reaction center

NQ

naphthoquinone

Me₃NQ

2,3,5-trimethyl-1,4-naphthoquinone

Me₄NQ

2,3,6,7-tetramethyl-1,4-naphthoquinone

LDAO

lauryldimethylamine-N-oxide

cyt c₂

R. sphaeroides cytochrome c₂

BPhe

bacteriopheophytin

MQ₀

menadione

MQ_P

vitamin k₃

MQ4

menatetronone