1. Introduction
A fundamental problem in the analysis of biosurveillance data is the need to aggregate data collected from care-seeking behavior into well-defined categories suitable for routine monitoring. For example, it is common to aggregate data about individual emergency department (ED) or outpatient physician visits into daily counts of visits for respiratory complaints for particular geographical regions such as zip codes [1-6]. Outbreak detection algorithms then analyze, for example, the time series of daily counts of ED visits for respiratory syndrome.
Biosurveillance systems also monitor aggregates or categories of over-the-counter healthcare (OTC) products for signs of outbreaks of various diseases. There is evidence that monitoring certain categories of products can provide early warning of certain disease outbreaks. Examples include cold remedies—but not antipyretics—for Influenza B outbreaks [7], pediatric electrolytes for seasonal outbreaks of respiratory and gastrointestinal illness in children [8], and OTC diarrhea remedies for waterborne Cryptosporidium outbreaks [9-11].
However, there has been little research into which aggregates of biosurveillance data are best for the monitoring of outbreaks of various diseases. There has been minimal discussion of even the criteria for choosing the best aggregates. Ultimately, the choice of aggregate is only one factor that determines the overall utility of a biosurveillance system in terms of lives saved, morbidity prevented, and the cost of the system. Given the near-impossibility of isolating all other factors (statistical outbreak detection algorithms, biosurveillance personnel, outbreak characteristics, etc.), measuring the utility of aggregates in this way is impractical (for certain, we cannot conduct randomized, controlled trials). One obvious criterion for choosing aggregates is outbreak detection performance: aggregates that provide earlier, more sensitive detection of outbreaks with fewer false alarms are better than aggregates that provide later, less sensitive detection with more false alarms. However, there is no guarantee that aggregates better for the detection of past influenza outbreaks, for example, will necessarily be better for detecting future influenza outbreaks. Additionally, users of biosurveillance systems also need to interpret and typically investigate further any alarms that analysis of biosurveillance data may trigger, and thus it is likely to be important also that aggregates have a logical meaning according to users' knowledge of infectious diseases.
The typical approach to forming aggregates, including categories of OTC products, is to have human experts create aggregates using their knowledge of infectious disease [3, 12, 13]. For example, Wagner et al. divided cold relief products into four categories based on age group (adult vs. pediatric) and dose form (liquid vs. tablets, capsules, and other ‘solid’ forms) [3].
This approach has limitations. There are no studies confirming that these distinctions are important for the detection of certain outbreaks, or that these are the only distinctions that are relevant. Furthermore, experts can disagree on the best way to form aggregates. For example, Mikosz et al. found that two research groups used different definitions of the aggregate called gastrointestinal syndrome for grouping ED visits [14]. In particular, one research group included abdominal pain in their definition and the other group did not.
Another approach to forming aggregates is to apply machine learning techniques to historical data sets. These techniques fall into two general categories: supervised clustering and unsupervised clustering. The main advantage of supervised clustering is that it can form clusters specific to particular disease outbreaks, such as influenza outbreaks. The main limitations are that it requires multiple outbreaks to avoid overfitting, and obtaining gold standard data from multiple outbreaks is difficult. The advantage of unsupervised clustering is that gold standard data from multiple outbreaks are not required. Although its main limitation is that the clusters it forms may be irrelevant, it does have the ability to find relevant clusters in many domains other than biosurveillance. In the remainder of this paper, our focus is unsupervised clustering.
The only study to apply unsupervised clustering to the problem of forming categories of OTC products (of which we are aware) is one by Magruder et al [15]. They first grouped products together into 61 low-level categories qualitatively based on age group (adult, pediatric, infant), dose form (e.g., tablet, liquid, inhaler), and indication (e.g, fever, cough, allergy). They then formed time series for each of the 61 low-level categories and used standard hierarchical clustering techniques to group them into 16 product categories. They used a distance metric to guide the clustering, which they computed as follows:
where c1 and c2 are two categories of OTC products and M1 and M2 are statistical models of the aggregated sales of the categories (M1) and individual sales of the categories (M2). Thus, the lower the distance metric, the more similar the aggregated sales were to the sales of each individual category. They chose an arbitrary threshold for the distance metric, leading to a final set of 16 product categories.
The procedure of Magruder et al. has several limitations. First, it requires a qualitative step that employs domain expertise to construct groupings of OTC products into low-level categories based on age group, dose form, and indication. In addition to the effort required in this step, it also means that their procedure cannot find subsets of the low-level categories that might be interesting or more naturally cluster together but are unanticipated by experts. For example, it may be that smokers with a chronic cough typically buy different cough syrup products than people with influenza. But since adult cough syrup is already a low-level category, the method would not be able to discover the distinction, if it exists, or rule it out if it does not exist. A second limitation of the procedure is its use of a stepwise hierarchical clustering procedure. Because of its stepwise nature, hierarchical clustering fails to evaluate many possible clusters, and thus it may miss better clusters.
We addressed these limitations by developing an unsupervised time-series clustering procedure that uses individual product time series as input and uses a stochastic clustering procedure to explore more fully the space of possible groupings. One difficulty with using time series for individual products as input is that manufacturers bring new products to market and phase out older products regularly. As we shall discuss, our method addresses this difficulty. Another difficulty is that promotions may dramatically affect individual product sales and our method handles promotional effects as well. In this paper, we describe the unsupervised clustering method and an experiment we conducted to assess its validity.
2. The unsupervised clustering procedure
The unsupervised clustering procedure uses Markov chain Monte Carlo simulation to estimate parameters of a Bayesian clustering model. Although our underlying model is Bayesian, we are primarily interested in obtaining a single clustering of time series rather than exploring the full posterior distribution over the parameters of the model.
2.1 Bayesian clustering model
Suppose that there are n time series, X1(•),…,Xn (•), each of which is defined on a grid t = 1,…,m and has non-negative integer values. Each time series belongs in exactly one of C clusters. The map from time series to cluster is given by δ, that is, δ(j) = i when time series j is in cluster i. Each cluster has a parameter that represents the average shape for time series that belong to the cluster. For cluster i, this shape parameter is denoted by λi (•), and is defined on the grid t = 1,…,m. As λi only represents the shape of time series in cluster i, λi is constrained to sum to unity, . Further, because the time series X1 (•),…,Xn (•) have non-negative values, λi (t) ≥ 0.
One of the challenges of modeling over-the-counter healthcare products is handling drastic changes in sales volume. It is not uncommon for a product to have virtually no sales for several months before a sharp increase in sales. Similarly, product sales sometimes drop off substantially if the product is taken off the market by the producer, or taken off the shelf by a retailer. Hence, two products could have very similar sales histories for 10 months, but in the remaining two months, sales of one of the products may decrease dramatically. As our clusters are trying to find products with similar sales histories, we would not want those two products to end up in two different clusters simply due to the loss in sales over the last two months. We therefore use a change-point model to accommodate such time series that have a dominant interval that may be surrounded on one or both sides by an inferior sales interval.
We model Xj (t), for j = 1,…,n and t = 1,…,m as independent Poisson random variables. Let μj (t) denote the mean of Xj (t). For t in the dominant interval [sj,ej], μj (t) is equal to a factor αj times the cluster shape at time t,λδ(j) (t). For t outside of the dominant interval [sj,ej ], μj (t) is equal to θj. More formally, let λ = (λ1,…,λC), α = (α1,…,αn), δ = (δ1,…,δn), θ = (θ1,…,θn), s = (s1,…,sn), and e = (e1,…,en). Then
The observed data in the above model are the time series X = (X1,…,Xn). We assume that the number of clusters C is known. The remaining parameters, λ, α, δ, θ, s, and e are all unknown. To complete the model, we must specify our prior distributions on λ, α, δ, θ, s, and e.
Prior distribution of λ
The cluster shapes, λ1,…,λC are independent a priori with Dirichlet(1,…,1) prior distributions. The Dirichlet(1,…,1) distribution is a uniform distribution over the space of nonnegative functions that sum to one.
Prior distribution of α
The scale factors α1,…,αn are independent a priori, and we use the non-informative and improper prior distribution π (αj) ∝1 for each j. Observe that αj will approximately equal the sum of the time series Xj when sj = 1 and ej = m because . As is often not known (at least in our applications) and varies dramatically across time series, we use an improper prior to avoid placing too little prior weight around .
Prior distribution of δ
The cluster identifiers δ(1),…,δ(n) are independent, and identically distributed uniformly on {1,…,C}.
Prior distribution of θ
We set θ1,…,θn to be independent and identically distributed gamma variates with shape parameter 4 and rate 8. Under this distribution, the prior expected value of θj is 0.5 and the standard deviation is 0.25. These values were chosen based on the role of θj, the mean of time series j during its inferior intervals.
Prior distribution of s and e
The prior for the start and end time points for the dominant interval of time series j is slightly more complicated because the start and end points are necessarily correlated due to their constraint that sj < ej. We use the prior
Under this prior, the marginal priors for sj and ej are
The above prior implies that sj is more likely to be near 1 than near m∕2, the middle. Similarly, ej is more likely to be near m than near m∕2. This prior is consistent with our intention that sj should only move away from 1 when there is strong evidence to do so, and ej should only move away from m when there is strong evidence to support such a move.
Finally, we note that the above model is quite large. In fact, there are C (m − 1) + 5n free parameters in the model. If there are 100 time series of 100 time-points each, and 4 clusters, then there are 4×99 + 5×100 = 896 free parameters in the model.
2.2 Markov chain Monte Carlo
Markov chain Monte Carlo is a popular method for estimating parameters in Bayesian models [16, 17]. In this approach, we generate a large sample of values from the posterior distribution. The sample can then be used to obtain point estimates for parameters (for example, the sample average is an estimate for the posterior mean), or to create credible regions, which are the Bayesian analogs of confidence regions.
It is often the case, however, that the full posterior distribution over all parameters in the model is unwieldy. The Gibbs sampler is one approach for sampling from a multidimensional distribution. In this approach, each parameter is sampled successively from the conditional posterior distribution given the remaining parameters.
The Gibbs sampling routine that we used to fit the model described above has four main components: sampling α, sampling δ, sampling θ, and sampling s and e.
Sampling α
The conditional posterior distribution of αj given the remaining parameters is gamma, specifically, , where α−j denotes the vector of α parameters, excluding αj.
Sampling δ
The conditional posterior probability that δ(j) = i given the remaining parameters is proportional to . We can compute this quantity for each i, and then divide these values by their sum to obtain the conditional posterior probabilities.
Sampling θ
The conditional posterior distribution of θj given the remaining parameters is gamma, specifically, , where θ−j denotes θ excluding θj.
Sampling s and e
The conditional posterior distribution of (sj, ej) is proportional to
To sample from this distribution, we use Metropolis-Hastings sampling [16]. Metropolis-Hastings algorithm is often used when only the functional form of the conditional posterior distribution is known. The idea is that instead of sampling from the actual conditional posterior distribution, we sample from a proposal distribution that we can sample from easily, and then compute an acceptance probability that we use to determine whether the sampled value should be kept or rejected. Here we use the prior distribution for (sj, ej) as the proposal distribution.
In order to significantly reduce the computation time required to fit the model, we do not sample from the conditional posterior distribution of λ. Instead, we set λ to be equal to the mode of its conditional posterior distribution. This computational shortcut does cause the model to be overfit. We adopted this approach, however, because we are primarily interested in finding a single good clustering, rather than the full posterior over the model parameters, and the time savings is substantial.
3. Evaluation of procedure
We evaluated our procedure by applying it to a historical data set of OTC product sales. Our hypothesis was that the procedure could find categories that had clinically relevant distinctions.
3.1 Methods
We applied the procedure to a 3-year historical data set of OTC product sales that we obtained from AC Nielsen, Inc. This data set covered the years 2002-2004. It consists of weekly counts of sales of individual products aggregated over a 30-county area in western Pennsylvania. AC Nielsen groups OTC products into its own category scheme and we applied our procedure to the set of “cold relief” products in that data set. This AC Nielsen created category includes medications for the treatment of cold, influenza, and allergy symptoms in liquid, tablet, and lozenge form. Overall, there were 768 unique products that had nonzero sales during the time period 2002-2004.
Because of the constraint to fix the number of clusters, we ran the procedure on the 768 time series a total of four times for cluster sizes of 2, 3, 4, and 8. For each run of the procedure, we plotted the time series of each product cluster and manually analyzed the products contained in each. Because the National Retail Data Monitor currently monitors four manually created subcategories of cold-relief products—cold-relief adult liquid, cold-relief adult tablet, cold relief pediatric liquid, and cold relief pediatric tablet—we tabulated the number of products from each of these four categories that appeared in each cluster. If we found important distinctions among clusters in the types of products they contained (other than age group and dose form), we included these distinctions in the tabulation as well.
3.2 Results
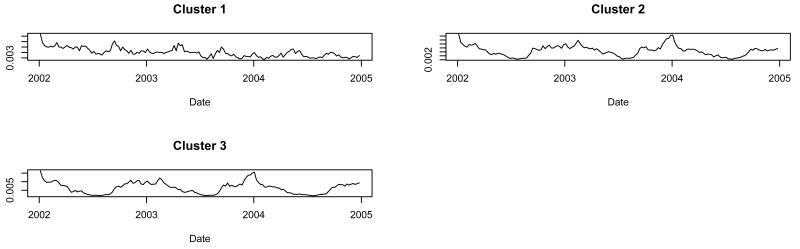
When we ran the procedure constrained to two clusters, the two clusters the procedure created had very different time series (Figure 1). When we observed the products in each cluster, we found a predominance of products for the treatment of allergy symptoms in cluster 2 and a predominance of products for the treatment of cold, cough, and influenza (or non-allergy) symptoms in cluster 1 (Table 1). The allergy cluster (cluster 2) had significant peaks in the spring and fall of each year (Figure 1), whereas the non-allergy cluster (cluster 1) had significant peaks coincident with the influenza outbreaks of 2002-2003 and 2003-2004. Of the 28 allergy products in cluster 1, 13 had product descriptions that indicated the product treated both cold and allergy symptoms. Of the 68 non-allergy products in cluster 2, 31 contained pseudoephedrine as an active ingredient.
Fig. 1.
Cluster shapes found when we ran the procedure on three years of OTC product salesdata and constrained the procedure to find twoclusters.
Table 1.
Numbers of Products of Each Type in Each Cluster. Numbers in parentheses are percentages of the number of products in the cluster.
| Cluster | Adult | Child | Liquid | Tablet | Allergy | Non-allergy | Total |
|---|---|---|---|---|---|---|---|
| 1 | 420 (83.7) | 82 (16.3) | 176 (35.1) | 326 (64.9) | 28 (5.6) | 474 (94.4) | 502 |
| 2 | 242 (91.0) | 24 (9.0) | 30 (11.3) | 236 (88.7) | 198 (74.4) | 68 (25.6) | 266 |
| 1 | 209 (90.1) | 23 (9.9) | 30 (12.9) | 202 (87.1) | 166 (71.6) | 66 (28.4) | 232 |
| 2 | 240 (83.6) | 47 (16.4) | 81 (28.2) | 206 (71.8) | 48 (16.7) | 239 (83.3) | 287 |
| 3 | 213 (85.5) | 36 (14.5) | 95 (38.2) | 154 (61.8) | 12 (4.8) | 237 (95.2) | 249 |
| 1 | 186 (83.4) | 37 (16.6) | 69 (30.9) | 154 (69.1) | 34 (15.2) | 189 (84.8) | 223 |
| 2 | 176 (89.8) | 20 (10.2) | 30 (15.3) | 166 (84.7) | 124 (63.3) | 72 (36.7) | 196 |
| 3 | 133 (86.9) | 20 (13.1) | 53 (34.6) | 100 (65.4) | 7 (4.6) | 146 (95.4) | 153 |
| 4 | 167 (85.2) | 29 (14.8) | 54 (27.6) | 142 (72.4) | 61 (31.1) | 135 (68.9) | 196 |
| 1 | 69 (90.8) | 7 (9.2) | 20 (26.3) | 56 (73.7) | 17 (22.4) | 59 (77.6) | 76 |
| 2 | 100 (87.7) | 14 (12.3) | 16 (14.0) | 98 (86) | 98 (86.0) | 16 (14.0) | 114 |
| 3 | 129 (84.9) | 23 (15.1) | 66 (43.4) | 86 (56.6) | 2 (1.3) | 150 (98.7) | 152 |
| 4 | 103 (78.0) | 29 (22.0) | 51 (38.6) | 81 (61.4) | 4 (3.0) | 128 (97.0) | 132 |
| 5 | 93 (87.7) | 13 (12.3) | 24 (22.6) | 82 (77.4) | 25 (23.6) | 81 (76.4) | 106 |
| 6 | 27 (93.1) | 2 (6.9) | 2 (6.9) | 27 (93.1) | 27 (93.1) | 2 (6.9) | 29 |
| 7 | 98 (90.7) | 10 (9.3) | 12 (11.1) | 96 (88.9) | 49 (45.4) | 59 (54.6) | 108 |
| 8 | 43 (84.3) | 8 (15.7) | 15 (29.4) | 36 (70.6) | 4 (7.8) | 47 (92.2) | 51 |
|
| |||||||
| Total* | 662 | 106 | 206 | 562 | 226 | 542 | 768 |
This row is the total number of products out of the 768 that have the attribute. It does not represent the sum of the column. Note that adult + child = 768, liquid + tablet = 768, and allergy + non-allergy = 768.
When we ran the procedure constrained to three clusters, clusters 2 and 3 had similar time series, unlike that of cluster 1 (Figure 2). When tabulated according to the four NRDM categories with an allergy vs. non-allergy distinction, clusters 2 and 3 were both non-allergy predominant clusters whereas cluster 1 was an allergy predominant cluster (Table 1).
Fig. 2.
Cluster shapes found when we constrained the procedure to find three clusters.
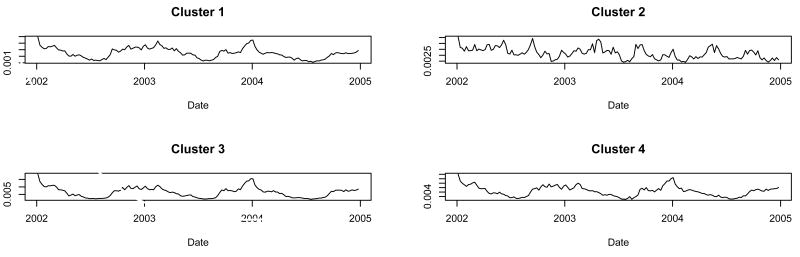
When we ran the procedure constrained to four clusters, clusters 1, 3, and 4 had similar time series and cluster 2 had a different time series (Figure 3). When tabulated according to the four NRDM categories with an allergy vs. non-allergy distinction, cluster 2 was the only allergy-predominant cluster (Table 1). Cluster 3 was the non-allergy predominant cluster that included the fewest allergy products. There was no predominance of products by age group or dose-form in cluster 1 or cluster 4.
Fig. 3.
Cluster shapes found when we constrained the procedure to find four clusters.
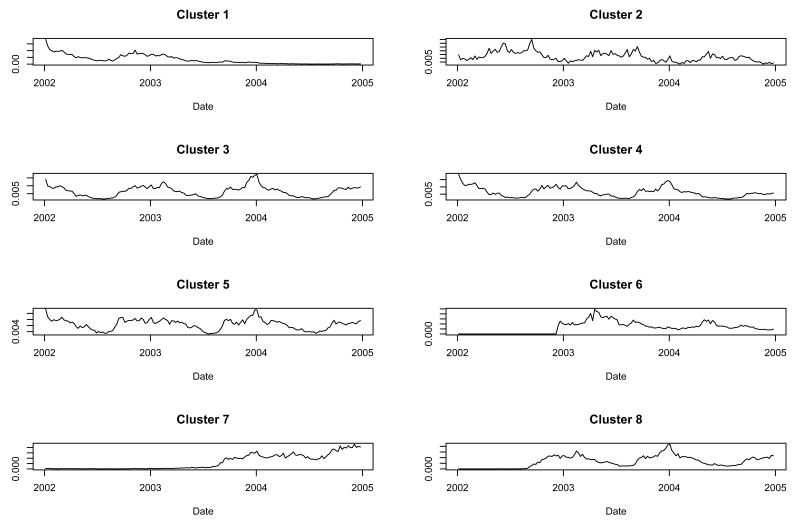
When we ran the procedure constrained to eight clusters, the time series for clusters 1, 3, 4, 5, and 8 were similar aside from differences due to non-trivial inferior sales intervals for products falling into clusters 1 and 8 (Figure 4). The remaining three clusters were fairly unique. Clusters 1, 3, 4, 5, and 8 had a predominance of non-allergy products (Table 1). Clusters 2 and 6 had a predominance of allergy products and cluster 7 was contained nearly equal numbers of allergy and non-allergy products. There was no consistent age group or dose form predominance in the clusters.
Fig. 4.
Cluster shapes found when we constrained the procedure to find eight clusters.
4. Discussion
We created an unsupervised clustering procedure that clusters individual time series into groups of time series with similar temporal trends. The evaluation showed that the procedure is capable of handling large datasets and discovering clinically relevant distinctions. The execution time of the procedure was always under one hour in our applications, and therefore the procedure is practical for use in monitoring and updating categories of OTC products on a monthly or even weekly basis (at present, the NRDM receives product updates four times per year).
The primary limitation of the procedure is that it overfits the time series data to find the required number of clusters. Hence, if the number of clusters is set too high, the procedure will find subtle differences in the time series that may not be of practical importance. When we evaluated the procedure using four clusters we found that three of the clusters (clusters 1, 3 and 4) were very similar. Similarly, when we ran the procedure using eight clusters, clusters 1, 3, 4, 5, and 8 are very similar aside from inferior sales intervals at the end of cluster 1 and the beginning of cluster 8, which are explicitly modeled at the product-level through the sj,ej, and μj parameters.
We found using the procedure that the time series for clusters that contained predominantly allergy products had biannual peaks in the spring and fall, whereas time series for clusters that contained predominantly non-allergy products had peaks coincident with influenza outbreaks. If age-group and dose-form distinctions among cold-relief products are clinically important for seasonal respiratory diseases such as influenza, bronchiolitis due to Respiratory Syncytial Virus, and upper respiratory infections due to various viruses, then they appear to be dominated by the allergy vs. non-allergy distinction and our procedure did not detect them. Further research is necessary to determine whether, when using OTC cold-relief products for influenza surveillance, it is necessary or even desirable to make dose form and age group distinctions.
Although the evaluation study showed that clinically relevant clusters can be found by our clustering procedure, additional research is necessary to validate that such clusters are useful for outbreak detection. Specifically, future work should measure the outbreak detection performance of a detection system that uses the found clusters, and compare the performance to the same system using either aggregates constructed from domain knowledge or gold standard clinical data[18].
Overall, it appears as though seasonal respiratory diseases cause similar symptoms (cough, fever, congestion) that lead to purchase of the same products for treating these symptoms. There was no category impacted by influenza that was not also impacted by other respiratory diseases as evidenced by the seasonal increases in sales before and after influenza outbreaks in all non-allergy predominant clusters. In other words, we did not find any cluster that whose sales appeared to reflect influenza outbreaks alone.
Acknowledgments
This work was supported by grant 1 R21 LM008278-01 from the National Library of Medicine and Pennsylvania Department of Health Award number ME-01-737. The authors thank ACNielsen Corporation for supplying data for this study, and two anonymous reviewers for their helpful suggestions.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Lewis MD, Pavlin JA, Mansfield JL, O'Brien S, Boomsma LG, Elbert Y, et al. Disease outbreak detection system using syndromic data in the greater Washington DC area. Am J Prev Med. 2002;23(3):180–6. doi: 10.1016/s0749-3797(02)00490-7. [DOI] [PubMed] [Google Scholar]
- 2.Tsui FC, Espino JU, Dato VM, Gesteland PH, Hutman J, Wagner MM. Technical description of RODS: A real-time public health surveillance system. J Am Med Inform Assoc. 2003;10(5):399–408. doi: 10.1197/jamia.M1345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Wagner MM, Robinson JM, Tsui FC, Espino JU, Hogan WR. Design of a national retail data monitor for public health surveillance. J Am Med Inform Assoc. 2003;10(5):409–18. doi: 10.1197/jamia.M1357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Heffernan R, Mostashari F, Das D, Karpati A, Kuldorff M, Weiss D. Syndromic surveillance in public health practice, New York City. Emerg Infect Dis. 2004;10(5):858–64. doi: 10.3201/eid1005.030646. [DOI] [PubMed] [Google Scholar]
- 5.Reis BY, Mandl KD. Syndromic surveillance: the effects of syndrome grouping on model accuracy and outbreak detection. Ann Emerg Med. 2004;44(3):235–41. doi: 10.1016/j.annemergmed.2004.03.030. [DOI] [PubMed] [Google Scholar]
- 6.Sniegoski C. Automated Syndromic Classification of Chief Complaint Records. Johns Hopkins University APL Technical Digest. 2004;25(1):68–75. [Google Scholar]
- 7.Welliver RC, Cherry JD, Boyer KM, Deseda-Tous JE, Krause PJ, Dudley JP, et al. Sales of nonprescription cold remedies: a unique method of influenza surveillance. Pediatr Res. 1979;13(9):1015–7. doi: 10.1203/00006450-197909000-00014. [DOI] [PubMed] [Google Scholar]
- 8.Hogan WR, Tsui FC, Ivanov O, Gesteland PH, Grannis S, Overhage JM, et al. Detection of pediatric respiratory and diarrheal outbreaks from sales of over-the-counter electrolyte products. J Am Med Inform Assoc. 2003;10(6):555–62. doi: 10.1197/jamia.M1377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Rodman J, Frost F, Davis-Burchat L, Fraser D, Langer J, Jakubowski W. Pharmaceutical sales: A method of disease surveillance? J Environ Health. 1997:8–14. [Google Scholar]
- 10.Proctor ME, Blair KA, Davis JP. Surveillance data for waterborne illness detection: an assessment following a massive waterborne outbreak of Cryptosporidium infection. Epidemiol Infect. 1998;120(1):43–54. doi: 10.1017/s0950268897008327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Stirling R, Aramini J, Ellis A, Lim G, Meyers R, Fleury M, et al. Waterborne cryptosporidiosis outbreak, North Battleford, Saskatchewan, Spring 2001. Can Commun Dis Rep. 2001;27(22):185–92. [PubMed] [Google Scholar]
- 12.Centers for Disease Control and Prevention. Syndrome Definitions for Diseases Associated with Critical Bioterrorism-associated Agents. [Accessed on 2005, May 11];2003 Available at: http://www.bt.cdc.gov/surveillance/syndromedef/index.asp.
- 13.Tsui F, Wagner M, Dato V, Chang C. Value of ICD-9-coded chief complaints for detection of epidemics. Proceedings of the Fall Symposium of the American Medical Informatics Association. 2001:711–715. [PMC free article] [PubMed] [Google Scholar]
- 14.Mikosz CA, Silva J, Black S, Gibbs G, Cardenas I. Comparison of two major emergency department-based free-text chief-complaint coding systems. MMWR Morb Mortal Wkly Rep. 2004;53(Suppl):101–5. [PubMed] [Google Scholar]
- 15.Magruder SF, Lewis SH, Najmi A, Florio E. Progress in understanding and using over-the-counter pharmaceuticals for syndromic surveillance. MMWR Morb Mortal Wkly Rep. 2004;53(Suppl):117–22. [PubMed] [Google Scholar]
- 16.Gilks WR, Richardson S, Spiegelhalter DJ. Markov Chain Monte Carlo in Practice. London: Chapman and Hall/CRC; 1996. [Google Scholar]
- 17.Robert CP, Casella G. Monte Carlo Statistical Methods. 2nd. Springer; 2004. [Google Scholar]
- 18.Wagner M. Methods for Evaluating Surveillance Data. In: Wagner M, Moore A, Aryel R, editors. Handbook of Biosurveillance. New York: Elsevier; 2006. [Google Scholar]