Abstract
Current methods of forcing end-tidal PCO2 (PETCO2) and PO2 (PETO2) rely on breath-by-breath adjustment of inspired gas concentrations using feedback loop algorithms. Such servo-control mechanisms are complex because they have to anticipate and compensate for the respiratory response to a given inspiratory gas concentration on a breath-by-breath basis. In this paper, we introduce a low gas flow method to prospectively target and control PETCO2 and PETO2 independent of each other and of minute ventilation in spontaneously breathing humans. We used the method to change PETCO2 from control (40 mmHg for PETCO2 and 100 mmHg for PETO2) to two target PETCO2 values (45 and 50 mmHg) at iso-oxia (100 mmHg), PETO2 to two target values (200 and 300 mmHg) at normocapnia (40 mmHg), and PETCO2 with PETO2 simultaneously to the same targets (45 with 200 mmHg and 50 with 300 mmHg). After each targeted value, PETCO2 and PETO2 were returned to control values. Each state was maintained for 30 s. The average difference between target and measured values for PETCO2 was ± 1 mmHg, and for PETO2 was ± 4 mmHg. PETCO2 varied by ± 1 mmHg and PETO2 by ± 5.6 mmHg (s.d.) over the 30 s stages. This degree of control was obtained despite considerable variability in minute ventilation between subjects (± 7.6 l min−1). We conclude that targeted end-tidal gas concentrations can be attained in spontaneously breathing subjects using this prospective, feed-forward, low gas flow system.
Manipulation of arterial oxygen (O2) and carbon dioxide (CO2) levels has long been used in physiological and clinical studies of, for example, cerebral blood flow and control of breathing (Bradley & Leith, 1978; Ellingsen et al. 1987; Laffey & Kavanagh, 1999; Kaanders et al. 2002; Ide et al. 2003; Floyd et al. 2003; Xie et al. 2005). In the past, precise independent control of arterial gases in humans has usually been achieved by adjusting inspired gas concentrations on a breath-by-breath basis to attain target end-tidal values (Richardson et al. 1966; Weil et al. 1970; Moore et al. 1984; Ellingsen et al. 1987). However, breath-by-breath variations in respiratory frequency and tidal volume (VT) in spontaneously breathing subjects result in an increased variability in end-tidal gas concentrations in a manner that tends to confound closed loop control. For example, a short, small volume breath results in both a lower end-tidal fractional concentration of CO2 (FETCO2), which would suggest the need for a higher inspired fractional concentration of CO2 (FICO2) for the next breath, as well as a relatively smaller alveolar ventilation ( ), which would indicate the need for a lower inspired FICO2 for the next breath. As a result, closed-loop end-tidal forcing requires a very sophisticated prediction–correction scheme. It also requires means to avoid problems inherent in any feedback system, such as signal drift, phase lags and instability, leading to signal oscillations (Smith et al. 1978). The introduction of increasingly sophisticated algorithms over the past decade (Robbins et al. 1982a,Robbins 1982b; Howard et al. 1995; Howson et al. 1987), and the use of rapid gas analysers have enabled such end-tidal forcing methods to improve their performance and thus enable a number of sophisticated physiological studies that were not previously feasible (Pandit et al. 2003; Poulin et al. 1996, Poulin 1998, Poulin 2002). However, these closed-loop methods still have some drawbacks. They require very high gas flows to meet peak inspiratory flows, and their implementation technology remains bulky, complex and expensive. End-tidal forcing is therefore unsuitable for clinical use and remains restricted to laboratory settings.
), which would indicate the need for a lower inspired FICO2 for the next breath. As a result, closed-loop end-tidal forcing requires a very sophisticated prediction–correction scheme. It also requires means to avoid problems inherent in any feedback system, such as signal drift, phase lags and instability, leading to signal oscillations (Smith et al. 1978). The introduction of increasingly sophisticated algorithms over the past decade (Robbins et al. 1982a,Robbins 1982b; Howard et al. 1995; Howson et al. 1987), and the use of rapid gas analysers have enabled such end-tidal forcing methods to improve their performance and thus enable a number of sophisticated physiological studies that were not previously feasible (Pandit et al. 2003; Poulin et al. 1996, Poulin 1998, Poulin 2002). However, these closed-loop methods still have some drawbacks. They require very high gas flows to meet peak inspiratory flows, and their implementation technology remains bulky, complex and expensive. End-tidal forcing is therefore unsuitable for clinical use and remains restricted to laboratory settings.
As a result, many clinical (Vesely et al. 2001; Mikulis et al. 2005; Venkataraman et al. 2005; Xie et al. 2005) and field (Sato et al. 1992) studies have relied on simple breathing circuits that enable maintenance of isocapnia and iso-oxia independent of changes in ventilation and ventilatory pattern. The main advantage of such circuits over the end-tidal forcing technique is that they are self-regulating and do not require sophisticated feedback protocols. The major limitations of such circuits, however, are their inability to precisely target desired end-tidal CO2 and O2 concentrations and to control them independently.
Our aim was to extend the capability of these self-regulating systems to allow prospective targetting and control of end-tidal PCO2 and PO2 (PETCO2 and PETO2) independently of each other in spontaneously breathing subjects. Our goal was to simplify the method sufficiently to make it suitable for application in such clinical settings as MRI suites, ophthalmology clinics and vascular ultrasound labs. We illustrate the suitability of our method for clinical testing laboratories by using it to produce rapid cyclic step-changes in both PETCO2 and PETO2 with short duration steady states – a feature critical in MRI imaging where inherent drift in the baseline MRI signal requires multiple comparative measurements to be made between two steady-states in order to improve statistical matching of the MR signal to end-tidal gas concentrations (Vesely et al. 2001). It is important to point out that the purpose of this study was not to provide a rigorous validation of the ‘clamping’ properties of the sequential gas delivery (SGD) circuit, which has already been done (Banzett et al. 2000; Somogyi et al. 2005), but rather to illustrate two new concepts, namely the ability to precisely target PETCO2 and PETO2 and control them independently.
Methods
Rationale
See Table 1 for a list of the abbreviations used in the following description. In a steady state, FETCO2 reflects the alveolar fractional concentration of CO2 (FACO2), which is determined by the metabolic CO2 production ( ) and
) and  , according to the equation:
, according to the equation:
| (1) |
Gas exchange occurs as gases diffuse down their partial pressure gradients, and the partial pressure of a gas in the alveoli is a function of its concentration and the ambient barometric pressure according to the equation:
| (2) |
where Pgas is the partial pressure of a gas in mmHg, Fgas is its fractional concentration, Pbar is ambient barometric pressure in mmHg, and 47 is the partial pressure of water vapour at body temperature in mmHg.
Table 1.
List of abbreviations
| Abbreviation | Definition |
|---|---|
| Alveolar ventilation | |
| Metabolic CO2 production | |
| Metabolic O2 consumption | |
| Flow of Gas 1 | |
| Minute ventilation | |
| Alveolar fractional concentration of CO2 | |
| Alveolar fractional concentration of O2 | |
| End-tidal fractional concentration of CO2 | |
| End-tidal fractional concentration of O2 | |
Fractional concentration of CO2 in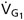
|
|
Fractional concentration of CO2 in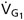
|
|
| Inspired fractional concentration of CO2 | |
| G1 | Gas 1, entering SGD circuit on inspiratory side |
| G2 | Gas 2, entering SGD circuit after depletion of Gas 1, previously exhaled gas |
| End-tidal PCO2 | |
| End-tidal PO2 | |
| SGD | Sequential gas delivery |
| VDAN | Anatomical dead space |
| Volume of Gas 1 | |
| VT | Tidal volume |
In this paper we will refer to both partial pressures and fractional concentrations, as the former is often more familiar to the reader and the latter is required for mass balance calculations.
Sequential gas delivery
In a steady state,  for any subject is constant. To control FACO2 and
for any subject is constant. To control FACO2 and  we adjust the composition and flow of gas entering an SGD circuit (Somogyi et al. 2005) (Fig. 1). We refer to the gas entering the SGD on the inspiratory side as Gas 1, symbolized as G1 (and its volume and flow into the SGD circuit as VG1 and
we adjust the composition and flow of gas entering an SGD circuit (Somogyi et al. 2005) (Fig. 1). We refer to the gas entering the SGD on the inspiratory side as Gas 1, symbolized as G1 (and its volume and flow into the SGD circuit as VG1 and  , respectively). Gas 2 (G2) refers to the gas entering the lung during inspiration following the exhaustion of G1 in the inspiratory reservoir. In the case of the SGD circuit in Fig. 1, G2 is previously exhaled gas that is rebreathed from the expiratory reservoir via the bypass conduit.
, respectively). Gas 2 (G2) refers to the gas entering the lung during inspiration following the exhaustion of G1 in the inspiratory reservoir. In the case of the SGD circuit in Fig. 1, G2 is previously exhaled gas that is rebreathed from the expiratory reservoir via the bypass conduit.
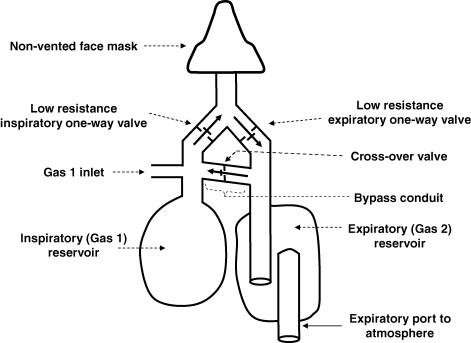
Figure 1.
Schematic of the modified sequential gas delivery circuit The manifold attached to the non-vented mask is separated into inspiratory and expiratory limbs using one-way low resistance valves. The two limbs are connected via a bypass limb with a one-way cross-over valve that has an opening pressure greater than that of the other two valves. During exhalation, all of the exhaled gas is directed through the expiratory limb into the atmosphere, with the last portion of the exhaled breath trapped in the expiratory reservoir. At the same time, Gas 1 (G1) collects in the inspiratory reservoir. At the beginning of inhalation, G1 is drawn from the Gas 1 inlet and the inspiratory reservoir. If minute ventilation exceeds the flow of G1 during inhalation, G1 in the reservoir is depleted and the reservoir collapses. The negative pressure in the inspiratory limb causes the cross-over valve to open and the balance of the breath is then made up of Gas 2 from the expiratory reservoir.
In the following arguments we will derive a series of five rules, using classical physiological principles, that apply to SGD circuits, and which permit prospective determination of end-tidal partial pressures of O2 (PETO2) and CO2 (PETCO2) in spontaneously breathing subjects. Although derivation of these rules and the accompanying examples may seem a little pedantic to experienced respiratory physiologists, we feel that this approach will allow the reader to better understand the underlying theory.
Relationship of  to alveolar ventilation (
to alveolar ventilation ( )
)
Suppose that a subject is breathing spontaneously on a SGD circuit and  into the circuit is gradually reduced until the inspiratory reservoir collapses on average at the end of each inspiration.
into the circuit is gradually reduced until the inspiratory reservoir collapses on average at the end of each inspiration.  at this point will be equal to subject's minute ventilation (
at this point will be equal to subject's minute ventilation ( ) (Fig. 2, stage A). If
) (Fig. 2, stage A). If  is then reduced further, the cross-over valve will open and the balance of inspiration will be composed of G2. However, with small reductions in
is then reduced further, the cross-over valve will open and the balance of inspiration will be composed of G2. However, with small reductions in  below the subject's
below the subject's  , FETCO2 does not rise despite rebreathing of the exhaled gas (Somogyi et al. 2005) (see stylized capnograph tracing in Fig. 2, stage B). This apparent contradiction can be explained by referring to a simple lung model consisting of anatomical dead space (VDAN) in series with alveolar space. Since G2 is only inspired after all of G1 has entered the lung, G2 is initially distributed exclusively to VDAN and therefore has a negligible effect on alveolar gas exchange. In fact, FETCO2 remains constant until
, FETCO2 does not rise despite rebreathing of the exhaled gas (Somogyi et al. 2005) (see stylized capnograph tracing in Fig. 2, stage B). This apparent contradiction can be explained by referring to a simple lung model consisting of anatomical dead space (VDAN) in series with alveolar space. Since G2 is only inspired after all of G1 has entered the lung, G2 is initially distributed exclusively to VDAN and therefore has a negligible effect on alveolar gas exchange. In fact, FETCO2 remains constant until  is reduced sufficiently below
is reduced sufficiently below  to diminish the fresh gas delivered to the alveoli, i.e. until
to diminish the fresh gas delivered to the alveoli, i.e. until  is decreased. In this circumstance, the reduction of G1 is compensated by an increase in G2 (Fig. 2, stage D). Thus, the
is decreased. In this circumstance, the reduction of G1 is compensated by an increase in G2 (Fig. 2, stage D). Thus, the  at which FETCO2 starts to increase corresponds to the subject's
at which FETCO2 starts to increase corresponds to the subject's  (
( – VDAN) as illustrated in Fig. 2, stage C. At such a
– VDAN) as illustrated in Fig. 2, stage C. At such a  , all of VDAN is filled with G2 (Fig. 2, stage C) and any further reduction in
, all of VDAN is filled with G2 (Fig. 2, stage C) and any further reduction in  effectively reduces
effectively reduces  , causing a corresponding increase in FETCO2 (Fig. 2, stage D). We conclude that the following rule applies to the SGD circuit:
, causing a corresponding increase in FETCO2 (Fig. 2, stage D). We conclude that the following rule applies to the SGD circuit:
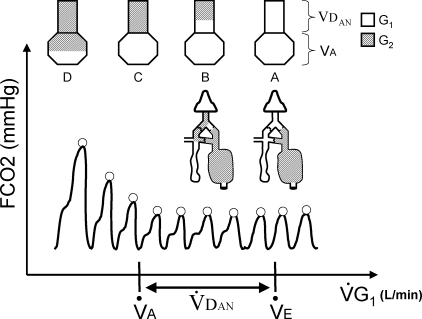
Figure 2.
Changes in end-tidal partial pressure of CO2 ( , ○) in response to progressive decrease in the flow of Gas 1 (
, ○) in response to progressive decrease in the flow of Gas 1 ( ) Also shown in the figure is the stylized raw capnograph tracing (continuous line). At the top of the figure, the observed results are explained with a lung model consisting of anatomical dead space (VDAN) in series with alveolar volume (VA). If
) Also shown in the figure is the stylized raw capnograph tracing (continuous line). At the top of the figure, the observed results are explained with a lung model consisting of anatomical dead space (VDAN) in series with alveolar volume (VA). If  exceeds minute ventilation (
exceeds minute ventilation ( ), then the lung is only filled with Gas 1 (G1). When, on average, the inspiratory reservoir of the SGD circuit collapses at the end of each inspiration,
), then the lung is only filled with Gas 1 (G1). When, on average, the inspiratory reservoir of the SGD circuit collapses at the end of each inspiration,  equals
equals  (stage A). If
(stage A). If  is less than
is less than  , Gas 2 (G2) starts to enter the lungs via a bypass conduit of the SGD circuit. This is confirmed by a characteristic rebreathing ‘shoulder’ at the end of the inspiratory portion of the raw CO2 tracing. G2 remains trapped in VDAN (stage B), however, and therefore has no effect on
, Gas 2 (G2) starts to enter the lungs via a bypass conduit of the SGD circuit. This is confirmed by a characteristic rebreathing ‘shoulder’ at the end of the inspiratory portion of the raw CO2 tracing. G2 remains trapped in VDAN (stage B), however, and therefore has no effect on  .
.  only starts to increase when G2 starts to enter alveoli (stage D). The
only starts to increase when G2 starts to enter alveoli (stage D). The  when
when  values start to increase corresponds to the alveolar ventilation (
values start to increase corresponds to the alveolar ventilation ( ). At this point, all of VDAN is occupied by G2 (stage C).
). At this point, all of VDAN is occupied by G2 (stage C).
Rule 1: Whenever  is less than or equal to
is less than or equal to  (or
(or  is greater than or equal to
is greater than or equal to  ), then
), then  determines
determines  .
.
Concept of ‘neutral gas’
When  is less than or equal to
is less than or equal to  , VDAN is filled with previously expired gas, so that the gas in the expired gas reservoir will have a composition that differs from that of a subject breathing room air with a
, VDAN is filled with previously expired gas, so that the gas in the expired gas reservoir will have a composition that differs from that of a subject breathing room air with a  greater than
greater than  . Instead of being filled with a ‘mixed expired gas’ consisting of a combination of alveolar gas and G1 from VDAN it is filled only with mixed alveolar gas, because the gas in VDAN is previously expired gas. Mixed alveolar gas is, by definition, fairly well equilibrated with pulmonary capillary blood (West, 1990) and reflects average arterial blood gas partial pressures as long as there are negligible effects from alveolar dead space ventilation and shunt. Therefore mixed alveolar gas re-entering the alveolar space from VDAN during inspiration, increases lung volume but does not affect the FACO2 and alveolar fractional concentration of O2 (FAO2) (Comroe, 1956; Somogyi et al. 2005). We therefore designate mixed alveolar gas as ‘neutral’ with respect to any effect it will have on the concentrations of alveolar gases, and formulate the following rule that applies to the SGD circuit.
. Instead of being filled with a ‘mixed expired gas’ consisting of a combination of alveolar gas and G1 from VDAN it is filled only with mixed alveolar gas, because the gas in VDAN is previously expired gas. Mixed alveolar gas is, by definition, fairly well equilibrated with pulmonary capillary blood (West, 1990) and reflects average arterial blood gas partial pressures as long as there are negligible effects from alveolar dead space ventilation and shunt. Therefore mixed alveolar gas re-entering the alveolar space from VDAN during inspiration, increases lung volume but does not affect the FACO2 and alveolar fractional concentration of O2 (FAO2) (Comroe, 1956; Somogyi et al. 2005). We therefore designate mixed alveolar gas as ‘neutral’ with respect to any effect it will have on the concentrations of alveolar gases, and formulate the following rule that applies to the SGD circuit.
Rule 2: A gas can be considered ‘neutral’ with respect to  if its concentration is equal to that in the mixed alveolar gas. Similarly, any component of a gas mixture can be considered ‘neutral’ with respect to
if its concentration is equal to that in the mixed alveolar gas. Similarly, any component of a gas mixture can be considered ‘neutral’ with respect to  if the concentration of that component gas is equal to that in the mixed alveolar gas.
if the concentration of that component gas is equal to that in the mixed alveolar gas.
The formulation of Rule 2 extends the argument presented in the preceding paragraph by introducing the concept of a ‘component gas’. From the previous discussion, it should be clear that expired (alveolar) gas is ‘neutral’ with respect to the alveolar exchange of both O2 and CO2. Moreover, these two component gases may be treated independently in terms of their neutrality. For example, if G2 has the same CO2 concentration as that of mixed alveolar gas but an O2 concentration equal to that of air, then G2 is neutral only with respect to CO2. In this case, increasing  does not affect FETCO2, but does increase FETO2 as if breathing air. The converse argument can be made for making G2 neutral with respect to O2 and not CO2.
does not affect FETCO2, but does increase FETO2 as if breathing air. The converse argument can be made for making G2 neutral with respect to O2 and not CO2.
Independence of end-tidal gas concentrations from changes in 
FETO2 and FETCO2 change from one breath to the next in spontaneously breathing subjects due to variations in VT. For example, increasing VT increases FETO2 and decreases FETCO2. For a subject breathing via an SGD circuit, when  exceeds
exceeds  , an increase in VT draws G1 from the VDAN into the alveoli, thereby increasing
, an increase in VT draws G1 from the VDAN into the alveoli, thereby increasing  . This situation is equivalent to the subject breathing normally without the SGD circuit (Fig. 3A). By contrast, with
. This situation is equivalent to the subject breathing normally without the SGD circuit (Fig. 3A). By contrast, with  set at or below
set at or below  , VDAN is filled with previously exhaled gas (Fig. 2, stages C and D) that is ‘neutral’ with respect to
, VDAN is filled with previously exhaled gas (Fig. 2, stages C and D) that is ‘neutral’ with respect to  (Rule 2). Therefore in this situation, while a larger VT draws gas from VDAN into the alveoli (Fig. 3B), the composition of gas in VDAN is neutral and so does not change FETO2 and FETCO2. Thus, FETO2 and FETCO2 are determined only by
(Rule 2). Therefore in this situation, while a larger VT draws gas from VDAN into the alveoli (Fig. 3B), the composition of gas in VDAN is neutral and so does not change FETO2 and FETCO2. Thus, FETO2 and FETCO2 are determined only by  (Rule 1) which remains constant, unaffected by the increase in Vt. A similar argument can be made for changes in respiratory frequency; as respiratory frequency increases, each breath will get a reduced fraction of the
(Rule 1) which remains constant, unaffected by the increase in Vt. A similar argument can be made for changes in respiratory frequency; as respiratory frequency increases, each breath will get a reduced fraction of the  and a complementary increase in
and a complementary increase in 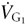 . No matter how much
. No matter how much  increases, the net
increases, the net  cannot exceed
cannot exceed  . From this argument we can formulate the following rule that applies to the SGD circuit.
. From this argument we can formulate the following rule that applies to the SGD circuit.
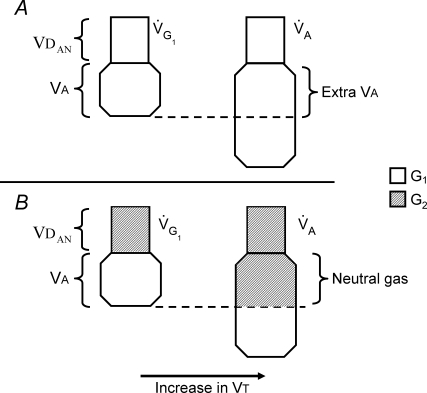
Figure 3.
The effect of changes in tidal volume (VT) on alveolar ventilation when breathing on a sequential gas delivery (SGD) circuit When the flow of Gas 1 exceeds alveolar ventilation (panel A), the increase in VT causes G1 trapped in the anatomical dead space (VDAN) to enter alveoli (VA), providing extra alveolar ventilation. If the flow of G1 is equal to or less than alveolar ventilation (panel B), all of VDAN is filled with the previously exhaled gas (G2) that is ‘neutral’ with respect to alveolar ventilation (see Rule 2 in text). An increase in VT causes G2 to enter VA, but because the volume of G1 available for gas exchange is not altered, alveolar ventilation does not change.
Rule 3: If  is less than or equal to
is less than or equal to  , FETO2and FETCO2 are independent of
, FETO2and FETCO2 are independent of  .
.
This rule is true with respect to both steady-state conditions and to breath-by-breath analysis. For example, if the peak inspiratory flow on any one breath exceeds  , then the balance of the breath will be made up by the ‘neutral’ gas from the expiratory reservoir and the
, then the balance of the breath will be made up by the ‘neutral’ gas from the expiratory reservoir and the  will remain constant.
will remain constant.
The principles expounded above can be illustrated by formulating some example questions, and answering them serves to introduce Rule 4.
Example 1: a subject's normal  is 5 l min−1 and PETCO2 is 40 mmHg. An SGD circuit is placed on the subject's face, and the unfamiliarity of the situation causes the subject to breathe at 8 l min−1. If G1 is air, what
is 5 l min−1 and PETCO2 is 40 mmHg. An SGD circuit is placed on the subject's face, and the unfamiliarity of the situation causes the subject to breathe at 8 l min−1. If G1 is air, what  will maintain isocapnia: is it 5 or 8 l min−1?
will maintain isocapnia: is it 5 or 8 l min−1?
The correct answer is 5 l min−1. In order to maintain isocapnia, we have to control the subject's  at the normal value. According to Rule 1, this can be done by setting
at the normal value. According to Rule 1, this can be done by setting  equal to
equal to  .
.
Example 2: if the subject in example 1 doubles his  from 8 to 16 l min−1 (while
from 8 to 16 l min−1 (while  remains constant at 5 l min−1), will the PETCO2 increase, decrease or remain constant?
remains constant at 5 l min−1), will the PETCO2 increase, decrease or remain constant?
As long as  is set at the subject's
is set at the subject's  , doubling
, doubling  (from 8 to 16 l min−1) will only result in a proportional increase in
(from 8 to 16 l min−1) will only result in a proportional increase in 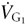 (from 3 to 11 l min−1). Since G2 gas is previously expired gas and therefore ‘neutral’ with respect to
(from 3 to 11 l min−1). Since G2 gas is previously expired gas and therefore ‘neutral’ with respect to  (Rule 2) and
(Rule 2) and  is unchanged (5 l min−1 during both protocols), PETCO2 remains constant (Rule 3).
is unchanged (5 l min−1 during both protocols), PETCO2 remains constant (Rule 3).
Example 3: suppose that in Example 2, both  (5 l min−1 of air) and
(5 l min−1 of air) and 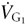 (11 l min−1 of previously exhaled gas) were premixed and delivered together to the G1 port. What happens to PETCO2 (note, CO2 is now present in the inspired gas)?
(11 l min−1 of previously exhaled gas) were premixed and delivered together to the G1 port. What happens to PETCO2 (note, CO2 is now present in the inspired gas)?
It is perhaps not intuitively obvious, but PETCO2 does not change. PETCO2 is determined by  , and in an SGD circuit, because G2 has no effect on the PETCO2 (Rule 2),
, and in an SGD circuit, because G2 has no effect on the PETCO2 (Rule 2),  is determined entirely by
is determined entirely by  (Rule 1). Mixing
(Rule 1). Mixing  and
and 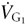 does not change
does not change  , so that administering the two flows together results in the same PETCO2 as delivering them sequentially. The counterintuitive concept in this example is that PETCO2 does not change despite the presence of CO2 in the inspired gas!
, so that administering the two flows together results in the same PETCO2 as delivering them sequentially. The counterintuitive concept in this example is that PETCO2 does not change despite the presence of CO2 in the inspired gas!
This does not contradict our contention that the order of presentation of gases to the lungs is important for maintaining control of end-tidal gas concentrations. Although G1 in this example contains CO2, we are still assuming that it is inhaled first, reaches the alveoli and establishes the alveolar ventilation for its component gases. Any additional gases that are inhaled as G2 are ‘neutral’ with respect to gas exchange, and allow the alveolar ventilation to be fixed independent of minute ventilation.
The argument illustrated by Example 3 can be expressed by the following rule that applies to the SGD circuit, and is further illustrated in Example 4 that follows.
Rule 4: If CO2 is present in  , then
, then  can be separated into two virtual compartments: a ‘fresh gas flow’ (with no CO2) that determines
can be separated into two virtual compartments: a ‘fresh gas flow’ (with no CO2) that determines  for CO2 elimination, and a ‘neutral gas flow’ (with a CO2 concentration equal to that of the neutral gas). Similarly, the O2 in
for CO2 elimination, and a ‘neutral gas flow’ (with a CO2 concentration equal to that of the neutral gas). Similarly, the O2 in  can be divided into ‘fresh gas’ and ‘neutral gas’ components.
can be divided into ‘fresh gas’ and ‘neutral gas’ components.
Example 4: a subject whose  is 5 l min−1 is breathing on an SGD circuit at a
is 5 l min−1 is breathing on an SGD circuit at a  equal to 10 l min−1. Initially, G1 is air and
equal to 10 l min−1. Initially, G1 is air and  is 5 l min−1. The subject's resting FETCO2 is 0.056 (PCO2 = 40 mmHg). Using these data, the following questions can be answered utilizing the rules and equations previously derived.
is 5 l min−1. The subject's resting FETCO2 is 0.056 (PCO2 = 40 mmHg). Using these data, the following questions can be answered utilizing the rules and equations previously derived.
First, what is the subjects  ? The answer may be derived using the equation:
? The answer may be derived using the equation:
| (3) |
and where FETCO2≈FACO2, and  =
=  . In this case,
. In this case,  = 5 × (0.056–0) = 0.280 l min−1.
= 5 × (0.056–0) = 0.280 l min−1.
Second, if  is constant, what happens to FETCO2 if the fractional concentration of CO2 in G1 is changed from 0 to 0.021? Rearranging the equation (3) as:
is constant, what happens to FETCO2 if the fractional concentration of CO2 in G1 is changed from 0 to 0.021? Rearranging the equation (3) as:
| (4) |
then FETCO2 = (0.280/5) + 0.021 = 0.077 (i.e. PCO2 = 55 mmHg).
Finally, what happens to FETCO2 if the  is increased to 8 l min−1? Increasing
is increased to 8 l min−1? Increasing  from 5 to 8 l min−1 increases
from 5 to 8 l min−1 increases  from 5 to 8 l min−1 (Rule 1) (assuming
from 5 to 8 l min−1 (Rule 1) (assuming  is not limiting). Using equation (4), FETCO2 = (0.280/8) + 0.021 = 0.056 (i.e. PCO2 = 40 mmHg).
is not limiting). Using equation (4), FETCO2 = (0.280/8) + 0.021 = 0.056 (i.e. PCO2 = 40 mmHg).
From this example we note that FETCO2 when  = 8 l min−1 and FCO2 in G1 = 0.021, is the same as that when
= 8 l min−1 and FCO2 in G1 = 0.021, is the same as that when  = 5 l min−1 and FCO2 in G1 = 0. This conclusion may be stated as a general principle for CO2: the net
= 5 l min−1 and FCO2 in G1 = 0. This conclusion may be stated as a general principle for CO2: the net  resulting from a
resulting from a  with any FCO2 can be determined by dividing
with any FCO2 can be determined by dividing  into a virtual component with no CO2 and a virtual component with CO2 at a concentration identical to that of ‘neutral’ gas. The virtual component volume with no CO2 provides the effective
into a virtual component with no CO2 and a virtual component with CO2 at a concentration identical to that of ‘neutral’ gas. The virtual component volume with no CO2 provides the effective  for CO2 (i.e. CO2 exchange). The remaining virtual component with the neutral CO2 makes no contribution to CO2 exchange.
for CO2 (i.e. CO2 exchange). The remaining virtual component with the neutral CO2 makes no contribution to CO2 exchange.
This principle is the basis for using a SGD circuit to adjust FETCO2 to a targeted value and maintain it in the face of changes in breathing pattern. For  less than
less than  ,
,  and the concentration of CO2 in G1 can be used to manipulate
and the concentration of CO2 in G1 can be used to manipulate  for CO2 independent of
for CO2 independent of  . By the same argument,
. By the same argument,  and its O2 concentration can be manipulated to change
and its O2 concentration can be manipulated to change  for O2. In this way the obligatory link between FETCO2 and FETO2 can be dissociated so as to also allow independent targeting of FETO2. A final example demonstrates this latter aspect.
for O2. In this way the obligatory link between FETCO2 and FETO2 can be dissociated so as to also allow independent targeting of FETO2. A final example demonstrates this latter aspect.
Example 5: a subject ( = 5 l min−1) is breathing on a SGD circuit at 15 l min−1. Initially, G1 is air,
= 5 l min−1) is breathing on a SGD circuit at 15 l min−1. Initially, G1 is air,  = 5 l min−1, and resting FETO2 is 0.16.
= 5 l min−1, and resting FETO2 is 0.16.
First, what is the subject's  ? The answer may be derived as before but using the equation:
? The answer may be derived as before but using the equation:
| (5) |
and assuming that FETO2≈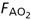 ·FIO2 is fractional concentrations of O2 inspired gas. Assuming that FIO2 is 0.21 (concentration of O2 in air), FETO2≈FAO2, and that
·FIO2 is fractional concentrations of O2 inspired gas. Assuming that FIO2 is 0.21 (concentration of O2 in air), FETO2≈FAO2, and that  =
=  , then
, then  = 5 × (0.21 – 0.16) = 0.250 l min−1.
= 5 × (0.21 – 0.16) = 0.250 l min−1.
Second, if  is constant, what happens to FETO2 if the fractional concentration of O2 in G1 is changed from 0.21 to 0.18? Rearranging the equation (5) as:
is constant, what happens to FETO2 if the fractional concentration of O2 in G1 is changed from 0.21 to 0.18? Rearranging the equation (5) as:
| (6) |
and assuming FETO2≈FAO2, then FETO2 = 0.18− (0.250/5) = 0.13.
Finally, what happens to FETO2 if  is increased by 8 l min−1? According to Rule 1, in a SGD circuit
is increased by 8 l min−1? According to Rule 1, in a SGD circuit  determines
determines  . So when
. So when  is increased from 5 to 13 l min−1, then
is increased from 5 to 13 l min−1, then  increases from 5 to 13 l min−1. Using equation (6); FETO2 = 0.18 – (0.250/13) = 0.16.
increases from 5 to 13 l min−1. Using equation (6); FETO2 = 0.18 – (0.250/13) = 0.16.
This example is the converse of the previous example for CO2 and illustrates the same principle, but this time for O2. FETO2 when  = 13 l min−1 and FO2 in G1 = 0.18 is the same as that when
= 13 l min−1 and FO2 in G1 = 0.18 is the same as that when  = 5 l min−1 and the FO2 in G1 = 0.21. Thus, a
= 5 l min−1 and the FO2 in G1 = 0.21. Thus, a  with any FO2 can be separated into two virtual components: (1) a virtual flow of gas with an FO2 concentration equal to that of the neutral gas, and (2) a virtual flow of gas with an FO2 different from that of the neutral gas that will constitute
with any FO2 can be separated into two virtual components: (1) a virtual flow of gas with an FO2 concentration equal to that of the neutral gas, and (2) a virtual flow of gas with an FO2 different from that of the neutral gas that will constitute  for O2 (i.e. O2 exchange). This principle for O2 is analogous to Rule 4 for CO2, and can be stated as Rule 5 for any gas in SGD circuits as follows:
for O2 (i.e. O2 exchange). This principle for O2 is analogous to Rule 4 for CO2, and can be stated as Rule 5 for any gas in SGD circuits as follows:
Rule 5:  can be arithmetically separated into two components: one with the same composition as the neutral gas – neutral
can be arithmetically separated into two components: one with the same composition as the neutral gas – neutral  (
( 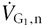 ); the other with a composition different from the neutral gas – fresh
); the other with a composition different from the neutral gas – fresh  (
( 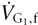 ), which constitutes
), which constitutes  .
.
It follows from the above arguments that in a SGD circuit the following three parameters can be manipulated to control PETCO2 and PETO2 independent of  :
:
 – changes in
– changes in  affect both
affect both  and PETO2, as long as
and PETO2, as long as  ⇋
⇋ ;
;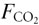 in
in  – this will allow independent control of
– this will allow independent control of  for CO2, and hence PETCO2, if
for CO2, and hence PETCO2, if  remains constant;
remains constant;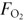 in
in  – this will allow independent control of
– this will allow independent control of  for O2, and hence PETO2, if
for O2, and hence PETO2, if  remains constant.
remains constant.
In the preceding discussion we assigned gas flows and concentrations in a SGD breathing circuit as  ,
,  and
and  . We can now use the known relationships between
. We can now use the known relationships between  ,
,  and
and  to FETCO2 and FETO2 to determine
to FETCO2 and FETO2 to determine  and its composition to attain target end-tidal gas concentrations (see Appendix A for a full derivation of the equations).
and its composition to attain target end-tidal gas concentrations (see Appendix A for a full derivation of the equations).
For FETCO2:
(Appendix A, eqn (A3)) where FACO2 is the target fractional alveolar concentration of CO2, 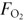 is the fractional concentration of CO2 in
is the fractional concentration of CO2 in  and
and  is the minute flux of CO2 at the lungs (which is equal to minute metabolic CO2 production at steady state).
is the minute flux of CO2 at the lungs (which is equal to minute metabolic CO2 production at steady state).
For FETO2:
(Appendix A, eqn (A5)) where FAO2 is the target alveolar fractional concentration of O2, 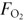 is the fractional concentration of O2 in
is the fractional concentration of O2 in  and
and  is the minute flux of O2 at the lungs (equal to minute metabolic O2 consumption at steady state).
is the minute flux of O2 at the lungs (equal to minute metabolic O2 consumption at steady state).
Although resting  and
and  can be easily estimated from the subject's age, height and weight using standard tables (Nunn, 1993), they can also be conveniently measured using an SGD circuit (see Appendix B).
can be easily estimated from the subject's age, height and weight using standard tables (Nunn, 1993), they can also be conveniently measured using an SGD circuit (see Appendix B).
Apparatus
We built a custom three-gas blender to allow us to control the composition and flow of G1. The blender incorporates precise flow meters to measure flow (TSI 4100, TSI, Shoreview, MN, USA), voltage controlled orifices to control the flow (VSO NC-6511-VE-Q8, Pneutronics, Hollis, NH, USA), and gas sensors for CO2 (IR1507, Servomex, Fairfax, CA, USA) and O2 (UFO130-2, Teledyne-AI, City of Industry, CA, USA). An electronic pressure transducer (Model 163PC01D36, Honeywell, NJ, USA) sensing pressure in the face mask was used to detect inspiration and expiration. Expiratory VT was measured using a turbine (Universal Ventilation Meter, VacuMed, Ventura, CA, USA).
A 12-bit digital-to-analog converter (DAQCard-6024E, National Instruments, Austin, TX, USA) interfaced the measurements with a laptop computer, where input/output signal processing, data analysis and all calculations were carried out by a specially written computer program (LabView, National Instruments, Austin, TX, USA). CO2 and O2 concentrations and mouth pressure data were digitized and recorded continuously at 40 Hz. The pressure transducer signal was used to calculate respiratory rate (f) and to help identify end-tidal values from raw CO2 and O2 data. VT and f were used to calculate  . Breath-by-breath PETCO2, PETO2, f, VT and
. Breath-by-breath PETCO2, PETO2, f, VT and  were recorded continuously.
were recorded continuously.  and
and  were calculated as the product of
were calculated as the product of  and the absolute difference between the concentrations of CO2 and O2 in G1 and those in the mixed expired gas (see Appendix 2). Given the target PETCO2 and PETO2, and the measured
and the absolute difference between the concentrations of CO2 and O2 in G1 and those in the mixed expired gas (see Appendix 2). Given the target PETCO2 and PETO2, and the measured  and
and  , the program calculated
, the program calculated  ,
, 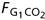 and
and 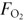 from Appendix Aequations (A3) and (A5). Fractional concentrations were converted to partial pressures using the dry barometric pressure on the day of the experiment. Appropriate corrections were made to convert from atmospheric temperature, pressure, saturation (ATPS) to body temperature, pressure, saturation (BTPS).
from Appendix Aequations (A3) and (A5). Fractional concentrations were converted to partial pressures using the dry barometric pressure on the day of the experiment. Appropriate corrections were made to convert from atmospheric temperature, pressure, saturation (ATPS) to body temperature, pressure, saturation (BTPS).
A commercial SGD circuit (Hi-Ox80, VIASYS HealthCare, Yorba Linda, CA, USA) was modified by attaching the turbine and an expiratory gas reservoir in series to its expiratory limb. Gas was sampled from the mask or the expiratory gas reservoir. The G1 outlet of the gas flow controller was attached to the fresh gas inlet of the SGD circuit.
Protocol
After receiving institutional Research Ethics Board approval, we obtained a signed informed consent from six healthy subjects (5 males, 1 female; age 24.7 ± 4.4 years, height 178.3 ± 8.7 cm, weight 70.7 ± 8.5 kg; means ± s.d.) to participate in the study. All procedures conformed with the Declaration of Helsinki. Subjects were seated comfortably in a chair and the face mask applied. The elastic straps on the mask were tightened to assure a good seal to the face. If required, adhesive tape (Tegaderm, 3M Health Care, St Paul, MN, USA) was used to seal any leaks.  was initially set to 8 l min−1 of air. Subjects were allowed to acclimatize to breathing on the circuit for at least 10 min. Once PETO2 and PETCO2 stabilized (less than 2 mmHg variability over 2 min), the three-way stopcock attached to the gas sampling port of the device was turned so that gas was sampled from the expiratory reservoir. Values for FCO2 and FO2 from the expiratory reservoir averaged over at least 30 s were used to calculate
was initially set to 8 l min−1 of air. Subjects were allowed to acclimatize to breathing on the circuit for at least 10 min. Once PETO2 and PETCO2 stabilized (less than 2 mmHg variability over 2 min), the three-way stopcock attached to the gas sampling port of the device was turned so that gas was sampled from the expiratory reservoir. Values for FCO2 and FO2 from the expiratory reservoir averaged over at least 30 s were used to calculate  and
and  (see Appendix 2 for details). Once
(see Appendix 2 for details). Once  and
and  were measured, the sampling port was redirected to sample expired gas at the face mask.
were measured, the sampling port was redirected to sample expired gas at the face mask.  ,
, 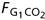 and
and 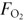 were then altered according to the principles described above, to achieve target values of PETCO2 and PETO2.
were then altered according to the principles described above, to achieve target values of PETCO2 and PETO2.
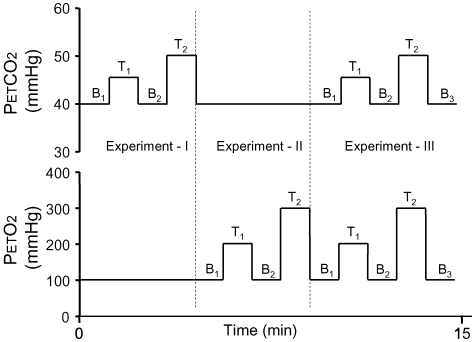
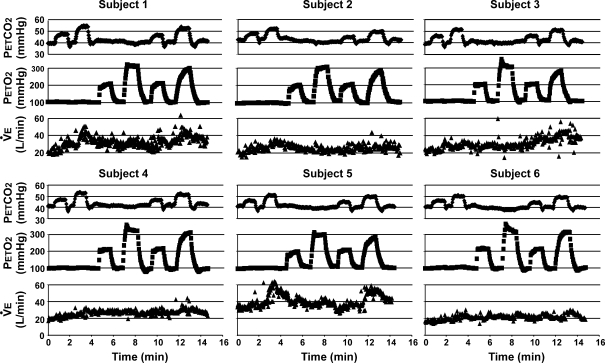
A total of three experiments were performed (Fig. 4). In experiment I, we maintained normoxia (PETO2 = 100 mmHg) while targeting two levels of PETCO2, returning to baseline PETCO2 between each target level. The first target PETCO2 level (I-T1) was 5 mmHg above initial baseline followed by a targeted return to baseline (I-B2). The second target PETCO2 (I-T2) was 10 mmHg above baseline (I-B2) followed by a return to baseline (II-B1). In experiment II, PETO2 was controlled during normocapnia (PETCO2 = 40 mmHg). The first target PETO2 (II-T1) was 100 mmHg above baseline (II-B1) followed by a return to baseline (II-B2). The second target PETO2 (II-T2) was 200 mmHg above baseline (II-B2) followed by a return to baseline (III-B1). In experiment III, both PETCO2 and PETO2 were targeted simultaneously. The first target levels (III-T1) were a change of PETCO2 and PETO2 from baseline (III-B1) to +5 and +100 mmHg, respectively, followed by a return to baseline (III-B2). The second target levels (III-T2) were a change of PETCO2 and PETO2 from baseline (III-B2) to +10 and +200 mmHg, respectively, followed by a return to baseline (III-B3). To demonstrate the versatility and robustness of the method targeting various levels of PETCO2 and PETO2 we performed experiments I–III sequentially, maintaining baseline and target PETCO2 and PETO2 values for a duration of 30 s.
Figure 4.
Experimental protocol A total of three experiments were performed. During experiment I  was varied to + 5 (I-T1) and + 10 mmHg (I-T2) from baselines (I-B1 and I-B2) before being returned to baseline II-B1. During experiment II
was varied to + 5 (I-T1) and + 10 mmHg (I-T2) from baselines (I-B1 and I-B2) before being returned to baseline II-B1. During experiment II  was varied to +100 (II-T1) and +200 mmHg (II-T2) from baselines (II-B1 and II-B2) before being returned to baseline III-B1. During experiment III, both
was varied to +100 (II-T1) and +200 mmHg (II-T2) from baselines (II-B1 and II-B2) before being returned to baseline III-B1. During experiment III, both  and
and  were varied simultaneously to the same targets as those attained during experiments II and III.
were varied simultaneously to the same targets as those attained during experiments II and III.
We entered the same target PETCO2 and PETO2 levels and sequence duration for each subject. Given the subject's  and
and  the computer automatically chose the
the computer automatically chose the  ,
, 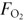 and
and 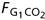 sequence required to carry out all three experiments using Appendix A eqns (A3) and (A5). All calculations were done prospectively prior to the start of experiment and feedback control was not used during the experiment. In order to produce rapid changes in end-tidal gases, we used an ‘overshooting’ technique (Banzett et al. 2000) by targeting higher-than-required end-tidal values for the first 2–3 breaths for rising gas concentrations and lower-than-required values for the first 2–3 breaths on descending gas concentrations.
sequence required to carry out all three experiments using Appendix A eqns (A3) and (A5). All calculations were done prospectively prior to the start of experiment and feedback control was not used during the experiment. In order to produce rapid changes in end-tidal gases, we used an ‘overshooting’ technique (Banzett et al. 2000) by targeting higher-than-required end-tidal values for the first 2–3 breaths for rising gas concentrations and lower-than-required values for the first 2–3 breaths on descending gas concentrations.  was arbitrarily raised to 15 l min−1, a value above the resting
was arbitrarily raised to 15 l min−1, a value above the resting  of all subjects, in order to speed up transitions between steady-states. The inspiratory reservoir was placed loosely on the palm of the subject's hand and the subject was instructed to breathe such that the inspiratory reservoir was empty at the end of most breaths. As a result, the baseline
of all subjects, in order to speed up transitions between steady-states. The inspiratory reservoir was placed loosely on the palm of the subject's hand and the subject was instructed to breathe such that the inspiratory reservoir was empty at the end of most breaths. As a result, the baseline  during the experiment was at least 15 l min−1 or more in all subjects (Fig. 5).
during the experiment was at least 15 l min−1 or more in all subjects (Fig. 5).
Figure 5.
End-tidal partial pressure of CO2 ( ) and O2 (
) and O2 ( ) and minute ventilation (
) and minute ventilation ( ) data from all subjects Note that subjects were asked to empty the inspiratory reservoir at the end of most breaths. Since
) data from all subjects Note that subjects were asked to empty the inspiratory reservoir at the end of most breaths. Since  was set to 15 l min−1 in order to speed up transitions between steady-states, the baseline
was set to 15 l min−1 in order to speed up transitions between steady-states, the baseline  was at least 15 l min−1 or greater in all subjects. As a result, the normal increases in ventilation that would be seen during a significant hypercapnic challenge and natural breathing are not observed in this experiment.
was at least 15 l min−1 or greater in all subjects. As a result, the normal increases in ventilation that would be seen during a significant hypercapnic challenge and natural breathing are not observed in this experiment.
Subject safety
The composition of G1 can be controlled by mixing pure O2, CO2 and N2. Because accidental inspiration of either pure CO2 or pure N2 can cause lethal hypoxaemia, we only used gas mixtures containing at least 10% O2. We further limited the CO2 source gas to 40% CO2 (10% O2, balance N2) to prevent an accidental inspiration of high concentrations of CO2. These restrictions placed significant limits on the PETO2 and PETCO2 values that could be targeted and complicated the calculations of the combinations of flow of the source gases required to attain the target 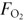 and
and 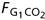 . To make sure that our algorithms for these complex functions resulted in safe inspired gas concentrations at all combinations of target values, we added a series of alarm features designed to indicate when the calculated
. To make sure that our algorithms for these complex functions resulted in safe inspired gas concentrations at all combinations of target values, we added a series of alarm features designed to indicate when the calculated 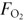 and
and 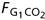 were not attainable with our series of gas mixtures, or the actual inspired concentrations were outside the designated safe range.
were not attainable with our series of gas mixtures, or the actual inspired concentrations were outside the designated safe range.
Statistical analysis
One-way repeated measures analysis of variance (1-way RMANOVA) was used to compare initial baseline PETCO2 and PETO2 (stage I-B1) to the rest of the corresponding baseline PETCO2 (stages I-B2, II-B1, II-T1, II-B2, II-T2, III-B1, III-B2 and III-B3) and PETO2 (stages I-T1, I-B2, I-T2, II-B1, II-B2, III-B1, III-B2 and III-B3). Dunnett's test was used for post hoc comparison when necessary. A t test was used to compare the PETCO2 values reached at stages I-T1 and I-T2 to those at stages III-T1 and III-T2, respectively. Similarly, the PETO2 values attained at stages II-T1 and II-T2 were compared to those at stages III-T1 and III-T2, respectively. Statistical significance was assumed when P < 0.05.
Results
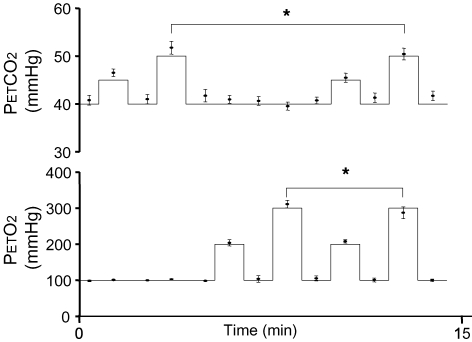
Individual results for all subjects are shown in Fig. 5. Intra-subject steady-state variabilities in PETCO2, PETO2 and  are summarized in Table 2. Target and measured PETCO2 values from all stages in all experiments for all subjects were pooled and are presented in Fig. 6. Experimental data for both PETCO2 and PETO2 (filled circles in Fig. 6) closely followed the target values (continuous line). The average absolute difference between target and measured values for PETCO2 was 1 mmHg, and for PETO2 was 4 mmHg. PETCO2 varied by ± 1 mmHg and PETO2 by ± 5.6 mmHg (s.d.) over the 30 s stages.
are summarized in Table 2. Target and measured PETCO2 values from all stages in all experiments for all subjects were pooled and are presented in Fig. 6. Experimental data for both PETCO2 and PETO2 (filled circles in Fig. 6) closely followed the target values (continuous line). The average absolute difference between target and measured values for PETCO2 was 1 mmHg, and for PETO2 was 4 mmHg. PETCO2 varied by ± 1 mmHg and PETO2 by ± 5.6 mmHg (s.d.) over the 30 s stages.
Table 2.
Intra-subject steady-state variability in  ,
,  and
and 
| Subject | PETCO2 (mmHg) | PETCO2 (mmHg) | V˙E (l min−1) |
|---|---|---|---|
| 1 | 0.2 (0.1–0.8) | 0.6 (0–6.3) | 3.4 (1.9–7.6) |
| 2 | 0.3 (0.1–0.5) | 0.7 (0–8.4) | 2.8 (1.6–4.3) |
| 3 | 0.2 (0.1–1.3) | 0.9 (0.3–5.7) | 2.7 (1.6–8.9) |
| 4 | 0.2 (0.1–1.5) | 1.2 (0.3–3) | 1.7 (1–5.3) |
| 5 | 0.2 (0.1–0.7) | 1 (0.3–6.2) | 2.8 (1.6–7.7) |
| 6 | 0.2 (0.1–0.6) | 1.9 (0.3–7) | 1.8 (1.1–3.7) |
Data are median (range) of standard deviations.
Figure 6.
Pooled end-tidal 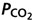 and
and 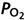 data from all subjects Continuous lines represent ideal target responses at each stage of the protocol. Circles represent experimental data (mean ± s.d.). *Statistically significant differences (P < 0.05).
data from all subjects Continuous lines represent ideal target responses at each stage of the protocol. Circles represent experimental data (mean ± s.d.). *Statistically significant differences (P < 0.05).
This degree of control of end-tidal gases was obtained despite large inter- and intrasubject variability in  (Fig. 5). PETO2 (1-way RMANOVA, P = 0.136) and PETCO2 (1-way RMANOVA, P = 0.01, Dunnett's test P > 0.05) returned to baseline after each targeted value. There were also no differences between PETCO2 in stages I-T1 and III-T1 (paired t test, P = 0.061) and PETO2 in stages II-T1 and III-T1 (paired 2 tail t test, P = 0.249). The only statistically significant differences were observed between stages I-T2 and III-T2 for PETCO2 (paired 2 tail t test, P < 0.001) and stages II-T2 and III-T2 for PETO2 (paired 2 tail t test, P = 0.019).
(Fig. 5). PETO2 (1-way RMANOVA, P = 0.136) and PETCO2 (1-way RMANOVA, P = 0.01, Dunnett's test P > 0.05) returned to baseline after each targeted value. There were also no differences between PETCO2 in stages I-T1 and III-T1 (paired t test, P = 0.061) and PETO2 in stages II-T1 and III-T1 (paired 2 tail t test, P = 0.249). The only statistically significant differences were observed between stages I-T2 and III-T2 for PETCO2 (paired 2 tail t test, P < 0.001) and stages II-T2 and III-T2 for PETO2 (paired 2 tail t test, P = 0.019).
Discussion
Main findings
In this study we demonstrate that PETCO2 and PETO2 can be repeatedly targeted independently and maintained for at least 30 s in spontaneously breathing subjects using a SGD breathing circuit. Previous methods for end-tidal forcing have used closed loop feedback methods to control end-tidal gas concentrations. This is the first demonstration of an effective method of prospectively targeting end-tidal gas values and attaining them in an open loop fashion. The measured experimental data followed the targeted values closely, i.e. ± 1 mmHg for PCO2 and ± 4 mmHg for PO2 so that the variability in the partial pressures of end-tidal gases at each stage was minimal, despite substantial variability in  .
.
Improvement over previous methods
In their study, Banzett et al. (2000) successfully demonstrated the ‘clamping’ characteristics of the SGD circuit, i.e. they successfully maintained PETCO2 and PETO2 constant despite significant changes in ventilation. In our study we extended the functionality of the SGD circuit by demonstrating ‘targeting’, i.e. how a series of target PETCO2 and PETO2 values can be attained independent of each other and independent of  . Our findings are notable in that the ‘targeting’ and ‘clamping’ were achieved without use of any feedback algorithms. This is in contrast to dynamic end-tidal forcing that uses advanced prediction–correction schemes to target and control end-tidal gases. Since our method does not rely on feedback control, it is also ‘protected’ from the usual problems associated with feedback control, such as signal drift, phase lags and instability, leading to signal oscillations (Smith et al. 1978). This may prove useful in applications such as MRI, where the presence of high magnetic fields dictates that all measurement apparatus have to be situated in the control room for safety and interference-prevention purposes. As a result, several gas sampling lines have to be extended from the control room to the MRI suite delaying expired gas analysis and thereby complicating feedback control.
. Our findings are notable in that the ‘targeting’ and ‘clamping’ were achieved without use of any feedback algorithms. This is in contrast to dynamic end-tidal forcing that uses advanced prediction–correction schemes to target and control end-tidal gases. Since our method does not rely on feedback control, it is also ‘protected’ from the usual problems associated with feedback control, such as signal drift, phase lags and instability, leading to signal oscillations (Smith et al. 1978). This may prove useful in applications such as MRI, where the presence of high magnetic fields dictates that all measurement apparatus have to be situated in the control room for safety and interference-prevention purposes. As a result, several gas sampling lines have to be extended from the control room to the MRI suite delaying expired gas analysis and thereby complicating feedback control.
In the present study we used an automated gas sequencer that included CO2 and O2 gas analysers and a stand-alone pneumotachometer. In contrast to dynamic end-tidal forcing that requires these apparatus for feedback control, our method only uses them to record the end-tidal and ventilation data. Furthermore, gas flows in our method only have to match the subject's minute ventilation (5–15 l min−1, depending on the protocol). In contrast, the end-tidal forcing technique requires gas flows that are high enough to meet individual peak inspiratory flows that can be as high as 50–300 l min−1. This makes our method less bulky and more suitable for use in clinical settings.
Modification of the method for studies of ventilation
In the present study the subjects increased their  above their resting values by hyperventilation. This was done in order to shorten the lung washout time and thereby speed up transitions between steady-states. As a result, the subjects'
above their resting values by hyperventilation. This was done in order to shorten the lung washout time and thereby speed up transitions between steady-states. As a result, the subjects'  were not allowed to vary naturally. If it is desirable to study the natural ventilatory responses to changes in end-tidal gases, however, the subject can be asked to breathe normally and
were not allowed to vary naturally. If it is desirable to study the natural ventilatory responses to changes in end-tidal gases, however, the subject can be asked to breathe normally and  can be set equal to subject's
can be set equal to subject's  (which can be estimated from standard tables or from subject's
(which can be estimated from standard tables or from subject's  and PETCO2). With an SGD circuit, PETCO2 and PETO2 will become independent of
and PETCO2). With an SGD circuit, PETCO2 and PETO2 will become independent of  as soon as the
as soon as the  is set equal to subject's
is set equal to subject's  (Rule 3). The experimenter (or computer) can then adjust the concentrations of CO2 and O2 in
(Rule 3). The experimenter (or computer) can then adjust the concentrations of CO2 and O2 in  using eqns (A3) and (A5) (from Appendix A) to produce desired changes in the PETCO2 and PETO2, while recording the natural ventilatory response of the subject. In theory, a specific pattern of changes can be preprogrammed into the computer to attain desired input functions (e.g. linear, step-like, sinusoidal, etc.).
using eqns (A3) and (A5) (from Appendix A) to produce desired changes in the PETCO2 and PETO2, while recording the natural ventilatory response of the subject. In theory, a specific pattern of changes can be preprogrammed into the computer to attain desired input functions (e.g. linear, step-like, sinusoidal, etc.).
Independent control of end-tidal gases
SGD circuits have been used previously to control PETCO2 independently of ventilation (Sato et al. 1992; Sommer et al. 1998; Banzett et al. 2000; Vesely et al. 2001). However, changes in PETCO2 resulted in tandem changes in PETO2 and both were dependent on the flow of ‘fresh gas’ (i.e.  ) into the circuit. We used the unique property of the SGD circuit to dissociate this obligatory link between PETCO2 and PETO2. With the SGD circuit, the volume of fresh gas available to the alveoli for gas exchange is fixed by
) into the circuit. We used the unique property of the SGD circuit to dissociate this obligatory link between PETCO2 and PETO2. With the SGD circuit, the volume of fresh gas available to the alveoli for gas exchange is fixed by  . We introduce here the concept of ‘neutral gas’ to rationalize the relationship between FCO2 and FO2 in
. We introduce here the concept of ‘neutral gas’ to rationalize the relationship between FCO2 and FO2 in  and the target PETCO2 and PETO2. The property of the SGD circuit that permits fixing
and the target PETCO2 and PETO2. The property of the SGD circuit that permits fixing  independent of ventilation allows changes in end-tidal gas concentrations to be sustained in the face of the inevitable ventilatory responses to the induced changes in PETO2 and PETCO2.
independent of ventilation allows changes in end-tidal gas concentrations to be sustained in the face of the inevitable ventilatory responses to the induced changes in PETO2 and PETCO2.
Composition of G2
In the present study, the composition of G2 was passively adjusted during each breath by providing the subject's own expiratory gases for rebreathing. It is possible to use an external source for G2, for example from a pressurized tank via a demand regulator (see Sommer et al. 1998), if one needs to control only one of the end-tidal gases. However, the composition of G2 can be such that any of its component gases are ‘neutral’ with respect to the alveolar gas.
The circuit used in the present study could be modified by placing a CO2 scrubber in the bypass conduit, and in this configuration, any G2 that is inhaled from the expiratory reservoir will have all its CO2 removed, thereby providing ‘extra’ for CO2 exchange. Because the O2 concentration of G2 will still approximate that of the alveolar gas, G2 remains ‘neutral’ with respect to O2. In such a SGD circuit a subject can hyperventilate and reduce PETCO2 to an extent determined by minute ventilation yet maintain PETO2 constant throughout. To make a circuit that does the reverse – allows PETO2 to vary with ventilation but maintain isocapnia – one simply uses a Sommer circuit (Sommer et al. 1998) and provides G2 with FO2 equal to that in G1 and ‘neutral’FCO2.
for CO2 exchange. Because the O2 concentration of G2 will still approximate that of the alveolar gas, G2 remains ‘neutral’ with respect to O2. In such a SGD circuit a subject can hyperventilate and reduce PETCO2 to an extent determined by minute ventilation yet maintain PETO2 constant throughout. To make a circuit that does the reverse – allows PETO2 to vary with ventilation but maintain isocapnia – one simply uses a Sommer circuit (Sommer et al. 1998) and provides G2 with FO2 equal to that in G1 and ‘neutral’FCO2.
Limitations and further suggestions
In the course of developing the theoretical basis of our method we made the simplifying assumption that the inhaled gas is distributed exclusively to anatomical dead space and alveoli. In reality, however, some of the inhaled gas will be distributed to the physiological dead space, which would confound the targeting of PETCO2 and PETO2. However, other methods of controlling end-tidal gases including the end-tidal forcing will be equally affected by physiological dead space.
In the present study, we only tested the newly described ‘targeting’ characteristics of an SGD circuit that permit independent control of PETCO2 and PETO2.‘Clamping’ characteristics of an SGD circuit were previously validated by Banzett et al. (2000) and Somogyi et al. (2005).
It is important to point out that errors in the measurement of  and
and  will likely affect the targeting, but not the ‘clamping’, characteristics of the circuit. In our experience, however, small changes in
will likely affect the targeting, but not the ‘clamping’, characteristics of the circuit. In our experience, however, small changes in  and
and  have minimal effect on the outcome of the study. However, this requires further formal investigation, perhaps during steady-state exercise studies.
have minimal effect on the outcome of the study. However, this requires further formal investigation, perhaps during steady-state exercise studies.
The SGD circuit used in the current study does not behave ideally. During the rebreathing phase of inspiration, any G2 flowing through the bypass conduit into the inspiratory side of the circuit is ‘contaminated’ by G1 flowing constantly into the inspiratory reservoir. This limitation may be overcome by temporarily shutting off  during the rebreathing phase of inspiration and then delivering a compensatory higher flow during the first second of expiration to maintain an average
during the rebreathing phase of inspiration and then delivering a compensatory higher flow during the first second of expiration to maintain an average  . We suggest that this limitation may have only a small effect and its compensation may not be necessary in all circumstances, but we did not verify this notion in the present study.
. We suggest that this limitation may have only a small effect and its compensation may not be necessary in all circumstances, but we did not verify this notion in the present study.
The method we used targets the equilibrium steady state PETCO2 and PETO2. Depending on the size of the transition and how long it is to be maintained, further accommodation must be made for filling or emptying body stores of CO2 and O2. Rapid changes in O2 can be induced and maintained relatively easily because only the fast compartment, consisting of the lung and possibly the blood, need be accounted for. On the other hand, the body has large CO2 stores (∼120 l) (Cherniack & Longobardo, 1970). For a rapid up or down transition, only the fast compartment (i.e. the lung) needs to be taken into account. However, if a change to a higher PCO2 level is to be sustained indefinitely, the transition to that equilibrium state should take into account the slower compartments (i.e. blood, tissue). Since metabolic CO2 production is small (∼0.240 l min−1) relative to CO2 stores (∼ blood 2.7 l, tissues ∼120 l), filling of slower compartments can take a long time. This time can be shortened by supplying CO2 to inspired gas from an external source. The same reasoning applies when a sustained transition to a new lower equilibrium PCO2 is required. In this case, as before, the initial rate of change in the transition is determined by the emptying of the fast compartment. For more sustained reductions in PCO2 the kinetics of emptying the slower body stores (i.e. blood and tissue) need be taken into account. The  required to sustain a targeted lower PCO2 will consist of the
required to sustain a targeted lower PCO2 will consist of the  required to remove the CO2 produced by metabolism plus the ‘extra’
required to remove the CO2 produced by metabolism plus the ‘extra’ needed to remove the CO2 delivered to the lungs from the slower compartments of the CO2 stores (blood and tissue).
needed to remove the CO2 delivered to the lungs from the slower compartments of the CO2 stores (blood and tissue).
Conclusions
We have used a feed-forward control method to implement rapid transitions to targets for PETCO2 and PETO2 in spontaneously breathing subjects. The method is based on well accepted physiologic principles, and requires relatively simple, inexpensive apparatus.
Appendix A
Derivation of the equations
It follows from Principle 5 that  can be separated into fresh gas component (
can be separated into fresh gas component (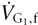 ), which is also equal to
), which is also equal to  , and neutral gas component (
, and neutral gas component (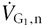 ), which we call ‘neutral’ gas ventilation, or
), which we call ‘neutral’ gas ventilation, or 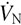 . Mathematically, this can be expressed as follows.
. Mathematically, this can be expressed as follows.
For CO2 according to mass balance:
| (A1) |
where  , FICO2 and FNCO2 are the fractional concentrations of CO2 in
, FICO2 and FNCO2 are the fractional concentrations of CO2 in  ,
,  and
and 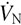 , respectively.
, respectively.
Assuming that inspiratory and expiratory volumes are equal, the flux of CO2 at the lungs is summarized by the following equation:
Solving for FICO2:
| (A2) |
Substituting eqn (A2) into eqn (A1):
Recall that FNCO2≈FACO2 (Principle 1) and that 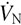 =
=  –
– ,
,
Solving for  , this simplifies to:
, this simplifies to:
| (A3) |
The above equation should hold true for any gas that is excreted by the body.
Similarly, the mass balance equation for O2:
| (A4) |
Since the flux of O2 at the lungs can be described by the equation:
and FNO2×FAO2 (Principle 1),
| (A5) |
Note that the change in sign (from negative to positive) compared to analogous eqn (A3) reflects O2 consumption in place of CO2 production.
Equations (A3) and (A5) can be used to calculate the composition and flow of G1 that will result in desired target FACO2 and FAO2 at steady-state (fractional target concentrations can be easily converted to partial pressures by multiplying them by dry barometric pressure), if the  and
and  are known. (Note that the desired target FACO2 and FAO2 will only be reached if metabolic
are known. (Note that the desired target FACO2 and FAO2 will only be reached if metabolic  and
and  are equal to respiratory
are equal to respiratory  and
and  , i.e. the system is in dynamic equilibrium.)
, i.e. the system is in dynamic equilibrium.)
Although  and target fractional concentrations used in eqns (A3) and (A5) are known, the other two parameters (
and target fractional concentrations used in eqns (A3) and (A5) are known, the other two parameters ( and
and  ) are a property of each individual subject. They are related to subject's age, body mass and height and can be easily estimated from standard tables. (Note, the values given in standard tables are at standard temperature, pressure and dry gas. They have to be converted to body temperature, pressure and saturated gas prior to use in these equations.) Alternatively,
) are a property of each individual subject. They are related to subject's age, body mass and height and can be easily estimated from standard tables. (Note, the values given in standard tables are at standard temperature, pressure and dry gas. They have to be converted to body temperature, pressure and saturated gas prior to use in these equations.) Alternatively,  and
and  can be easily measured in each subject using a SGD circuit.
can be easily measured in each subject using a SGD circuit.
Appendix B
Measurement of  and
and  using a SGD circuit
using a SGD circuit
At steady-state, metabolic  and
and  are equal to respiratory
are equal to respiratory  and
and  . Standard methods of estimating
. Standard methods of estimating  and
and  at steady-state employ collection of the expired gas in a reservoir (e.g. Douglas bag) from a subject breathing air at rest. Since there is no CO2 in the inspired gas (air), all of the CO2 in the reservoir at the end of the collection period must have come from metabolic CO2 production by the subject. Thus:
at steady-state employ collection of the expired gas in a reservoir (e.g. Douglas bag) from a subject breathing air at rest. Since there is no CO2 in the inspired gas (air), all of the CO2 in the reservoir at the end of the collection period must have come from metabolic CO2 production by the subject. Thus:
| (A6) |
where Vbag is the volume of gas in the bag at the end of the collection, t is the collection time in minutes, and FbagCO2 is the fractional concentration of CO2 in the bag. Similarly, the difference in O2 concentration between air and the gas in the reservoir must be due to O2 consumption by the subject.  can therefore be calculated as follows:
can therefore be calculated as follows:
| (A7) |
where FbagO2 is the fractional concentration of O2 in the bag. FbagO2 has to be subtracted from the fractional concentration of O2 in air, which is approximately 0.21.
In the SGD circuit, all of the delivered gas,  , eventually ends up in the expiratory reservoir. The concentrations of O2 and CO2 in the reservoir at any given
, eventually ends up in the expiratory reservoir. The concentrations of O2 and CO2 in the reservoir at any given  will therefore be proportional to the subject's metabolic O2 consumption and CO2 production. Equations (A6) and (A7) can be rewritten to apply to SGD circuit as follows:
will therefore be proportional to the subject's metabolic O2 consumption and CO2 production. Equations (A6) and (A7) can be rewritten to apply to SGD circuit as follows:
However, the concentrations of O2 and CO2 in the expiratory reservoir fluctuate throughout expiration. In order to obtain a representative estimate of metabolic parameters, the concentrations of O2 and CO2 in the expiratory reservoir should be averaged over time (30–60 s is usually adequate). For additional confidence, repeated measurements of  and
and  can be made to yield average values.
can be made to yield average values.
References
- Banzett RB, Garcia RT, Moosavi SH. Simple contrivance ‘clamps’ end-tidal PCO2 and PO2 despite rapid changes in ventilation. J Appl Physiol. 2000;88:1597–1600. doi: 10.1152/jappl.2000.88.5.1597. [DOI] [PubMed] [Google Scholar]
- Bradley ME, Leith DE. Ventilatory muscle training and the oxygen cost of sustained hyperpnea. J Appl Physiol. 1978;45:885–892. doi: 10.1152/jappl.1978.45.6.885. [DOI] [PubMed] [Google Scholar]
- Cherniack NS, Longobardo GS. Oxygen and carbon dioxide gas stores of the body. Physiol Rev. 1970;50:196–243. doi: 10.1152/physrev.1970.50.2.196. [DOI] [PubMed] [Google Scholar]
- Comroe JH. The Lung, Clinical Physiology and Pulmonary Function Tests. Chicago: Year Book Publishers; 1956. [Google Scholar]
- Ellingsen I, Hauge A, Nicolaysen G, Thoresen M, Walloe L. Changes in human cerebral blood flow due to step changes in PAO2 and PACO2. Acta Physiol Scand. 1987;129:157–163. doi: 10.1111/j.1748-1716.1987.tb08054.x. [DOI] [PubMed] [Google Scholar]
- Floyd TF, Clark JM, Gelfand R, Detre JA, Ratcliffe S, Guvakov D, Lambertsen CJ, Eckenhoff RG. Independent cerebral vasoconstrictive effects of hyperoxia and accompanying arterial hypocapnia at 1 ATA. J Appl Physiol. 2003;95:2453–2461. doi: 10.1152/japplphysiol.00303.2003. [DOI] [PubMed] [Google Scholar]
- Howard LS, Barson RA, Howse BP, McGill TR, McIntyre ME, O'Connor DF, Robbins PA. Chamber for controlling end-tidal gas tensions over sustained periods in humans. J Appl Physiol. 1995;78:1088–1091. doi: 10.1152/jappl.1995.78.3.1088. [DOI] [PubMed] [Google Scholar]
- Howson MG, Khamnei S, McIntyre ME, O'Connor DF, Robbins PA. A rapid computer controlled binary gas mixing system for studies in respiratory control (Abstract) J Physiol. 1987;403:103P. [Google Scholar]
- Ide K, Eliasziw M, Poulin MJ. The relationship between middle cerebral artery blood velocity and end-tidal PCO2 in the hypocapnic-hypercapnic range in humans. J Appl Physiol. 2003;95:129–137. doi: 10.1152/japplphysiol.01186.2002. [DOI] [PubMed] [Google Scholar]
- Kaanders JH, Bussink J, van der Kogel AJ. ARCON: a novel biology-based approach in radiotherapy. Lancet Oncol. 2002;3:728–737. doi: 10.1016/s1470-2045(02)00929-4. [DOI] [PubMed] [Google Scholar]
- Laffey JG, Kavanagh BP. Carbon dioxide and the critically ill – too little of a good thing? Lancet. 1999;354:1283–1286. doi: 10.1016/S0140-6736(99)02388-0. [DOI] [PubMed] [Google Scholar]
- Mikulis DJ, Krolczyk G, Desal H, Logan W, Deveber G, Dirks P, Tymianski M, Crawley A, Vesely A, Kassner A, Preiss D, Somogyi R, Fisher JA. Preoperative and postoperative mapping of cerebrovascular reactivity in moyamoya disease by using blood oxygen level-dependent magnetic resonance imaging. J Neurosurg. 2005;103:347–355. doi: 10.3171/jns.2005.103.2.0347. [DOI] [PubMed] [Google Scholar]
- Moore LG, Huang SY, McCullough RE, Sampson JB, Maher JT, Weil JV, Grover RF, Alexander JK, Reeves JT. Variable inhibition by falling CO2 of hypoxic ventilatory response in humans. J Appl Physiol. 1984;56:207–210. doi: 10.1152/jappl.1984.56.1.207. [DOI] [PubMed] [Google Scholar]
- Nunn JF. Applied Respiratory Physiology with Special Reference to Anaesthesia. 4. London: Butterworth-Heinemann; 1993. [Google Scholar]
- Pandit JJ, Mohan RM, Paterson ND, Poulin MJ. Cerebral blood flow sensitivity to CO2 measured with steady-state and Read's rebreathing methods. Respir Physiol Neurobiol. 2003;137:1–10. doi: 10.1016/s1569-9048(03)00089-2. [DOI] [PubMed] [Google Scholar]
- Poulin MJ, Fatemian M, Tansley JG, O'Connor DF, Robbins PA. Changes in cerebral blood flow during and after 48 h of both isocapnic and poikilocapnic hypoxia in humans. Exp Physiol. 2002;87:633–642. doi: 10.1113/eph8702437. [DOI] [PubMed] [Google Scholar]
- Poulin MJ, Liang PJ, Robbins PA. Dynamics of the cerebral blood flow response to step changes in end-tidal PCO2 and PO2 in humans. J Appl Physiol. 1996;81:1084–1095. doi: 10.1152/jappl.1996.81.3.1084. [DOI] [PubMed] [Google Scholar]
- Poulin MJ, Liang PJ, Robbins PA. Fast and slow components of cerebral blood flow response to step decreases in end-tidal PCO2 in humans. J Appl Physiol. 1998;85:388–397. doi: 10.1152/jappl.1998.85.2.388. [DOI] [PubMed] [Google Scholar]
- Richardson DW, Kontos HA, Shapiro W, Patterson JL., Jr Role of hypocapnia in the circulatory responses to acute hypoxia in man. J Appl Physiol. 1966;21:22–26. doi: 10.1152/jappl.1966.21.1.22. [DOI] [PubMed] [Google Scholar]
- Robbins PA, Swanson GD, Howson MG. A prediction-correction scheme for forcing alveolar gases along certain time courses. J Appl Physiol. 1982a;52:1353–1357. doi: 10.1152/jappl.1982.52.5.1353. [DOI] [PubMed] [Google Scholar]
- Robbins PA, Swanson GD, Micco AJ, Schubert WP. A fast gas-mixing system for breath-to-breath respiratory control studies. J Appl Physiol. 1982b;52:1358–1362. doi: 10.1152/jappl.1982.52.5.1358. [DOI] [PubMed] [Google Scholar]
- Sato M, Severinghaus JW, Powell FL, Xu FD, Spellman MJ., Jr Augmented hypoxic ventilatory response in men at altitude. J Appl Physiol. 1992;73:101–107. doi: 10.1152/jappl.1992.73.1.101. [DOI] [PubMed] [Google Scholar]
- Smith DM, Mercer RR, Eldridge FL. Servo control of end-tidal CO2 in paralyzed animals. J Appl Physiol. 1978;45:133–136. doi: 10.1152/jappl.1978.45.1.133. [DOI] [PubMed] [Google Scholar]
- Sommer LZ, Iscoe S, Robicsek A, Kruger J, Silverman J, Rucker J, Dickstein J, Volgyesi GA, Fisher JA. A simple breathing circuit minimizing changes in alveolar ventilation during hyperpnoea. Eur Respir J. 1998;12:698–701. doi: 10.1183/09031936.98.12030698. [DOI] [PubMed] [Google Scholar]
- Somogyi RB, Vesely AE, Preiss D, Prisman E, Volgyesi G, Azami T, Iscoe S, Fisher JA, Sasano H. Precise control of end-tidal carbon dioxide levels using sequential rebreathing circuits. Anaesth Intensive Care. 2005;33:726–732. doi: 10.1177/0310057X0503300604. [DOI] [PubMed] [Google Scholar]
- Venkataraman ST, Hudson C, Fisher JA, Flanagan JG. The impact of hypercapnia on retinal capillary blood flow assessed by scanning laser Doppler flowmetry. Microvasc Res. 2005;69:149–155. doi: 10.1016/j.mvr.2005.02.003. [DOI] [PubMed] [Google Scholar]
- Vesely A, Sasano H, Volgyesi G, Somogyi R, Tesler J, Fedorko L, Grynspan J, Crawley A, Fisher JA, Mikulis D. MRI mapping of cerebrovascular reactivity using square wave changes in end-tidal PCO2. Magn Reson Med. 2001;45:1011–1013. doi: 10.1002/mrm.1134. [DOI] [PubMed] [Google Scholar]
- Weil JV, Byrne-Quinn E, Sodal IE, Friesen WO, Underhill B, Filley GF, Grover RF. Hypoxic ventilatory drive in normal man. J Clin Invest. 1970;49:1061–1072. doi: 10.1172/JCI106322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- West JB. Respiratory Physiology: The Essentials. 4. Baltimore: Williams & Wilkins; 1990. [Google Scholar]
- Xie A, Skatrud JB, Khayat R, Dempsey JA, Morgan B, Russell D. Cerebrovascular response to carbon dioxide in patients with congestive heart failure. Am J Respir Crit Care Med. 2005;172:371–378. doi: 10.1164/rccm.200406-807OC. [DOI] [PubMed] [Google Scholar]
Disclosure
A patent has been filed for the method described in the present paper, with some of the authors named as co-inventors (Marat Slessarev, Eitan Prisman, Cliff Ansel, George Volgyesi and Joseph Fisher).