Abstract
Numerous experimental studies have demonstrated that mild hypothermia is a rather promising therapy for acute brain injury in neonates. Because measurement of the resultant cooling of human brain in vivo is beyond current technology, an understanding of physical factors limiting the possible brain cooling would be a substantial achievement. Herein brain cooling by external head cooling devices is studied within the framework of an analytical model of temperature distribution in the brain. Theoretical limits on brain hypothermia induced by such devices are established. Analytical expressions are obtained that allow evaluation of changes in brain temperature under the influence of measurable input parameters. We show that a mild hypothermia can be successfully induced in neonates only if two necessary conditions are fulfilled: sufficiently low cerebral blood flow and sufficiently high value of the heat transfer coefficient describing the heat exchange between the head surface and a cooling device.
Keywords: Brain temperature distribution, Brain cooling, Cerebral blood flow, Brain hypothermia
Introduction
Numerous experimental studies have demonstrated that a mild hypothermia (defined here as reflecting a brain temperature between 33 and 36°C) is a rather promising therapy for acute brain injury in neonates (see e.g., Bona et al. 1998; Colbourne and Corbett 1995; Edwards et al.1995; Eicher et al. 2005; Gluckman et al. 2005; Gunn 2000; Gunn et al. 1998, 1997; Iwata et al. 2005; Laptook et al. 1994; Nedelcu et al. 2000; Shankaran et al. 2005; Sirimanne et al. 1996; Speer and Perlman 2006; Thoresen et al. 1995; Tooley et al. 2003; Vannucci and Perlman 1997; Wyatt and Robertson 2005 and references therein), leading to substantial improvement in neuropathological, electrophysiological and functional outcomes. Recently published results of a pilot trial (Eicher et al. 2005) and multicentre randomized trials (Gluckman et al. 2005; Shankaran et al. 2005) also confirmed that brain cooling can improve neurodevelopmental outcome in infants with neonatal encephalopathy.
There are two main strategies for implementing hypothermia non-invasively: brain cooling by means of external head cooling devices and whole-body cooling. In the randomized trial (Gluckman et al. 2005), brain cooling has been implemented by fitting a cooling cap around the head and maintaining the rectal temperature at 34-35°C. The results of this trial suggest that “although induced head cooling is not protective in a mixed population of infants with neonatal encephalopathy, it could improve survival without severe neurodevelopmental disability in infants with less severe amplitude integrated EEG (aEEG) changes” (Gluckman et al. 2005). In Shankaran et al. (2005), a systematic hypothermia was accomplished by placing infants on a water blanket precooled to 5°C and regulating the temperature of the blanket to maintain an esophageal temperature of 33.5°C for 72 h. The authors inferred that “whole-body hypothermia reduces the risk of death or disability in infants with moderate or severe hypoxicischemic encephalopathy” (Shankaran et al. 2005). Different eligibility criteria of these trials do not allow a direct comparison of the strategies and a question “which of the two cooling strategies is an optimal one?” remains unclear so far (Papile 2005). Animal models (e.g., Laptook et al. 2001) demonstrated that selective head cooling leads to more pronounced effects, whereas the results of the aforementioned trials on humans (Gluckman et al. 2005; Shankaran et al. 2005) are ambiguous.
One of the crucial questions in selecting a proper cooling approach relates to understanding how different cooling strategies actually cool the brain. Because measuring the resultant cooling of human brain in vivo is beyond current technology, developing a biophysical framework describing the determinants of temperature changes in human brain and establishing limits for possible brain cooling would be a substantial achievement. In the present study, we theoretically analyze brain cooling by an external head cooling device and provide analytical expressions that allow evaluation of changes in brain temperature under the influence of such a device.
While under normal physiological conditions tissue temperature in the deep brain regions is expected to be slightly higher than the temperature of arterial blood (Yablonskiy et al. 2000), the situation can be different in the superficial brain regions due to the heat exchange with the environment. Computer simulations in adult (Nelson and Nunneley 1998; Zhu and Diao 2001) and neonatal (van Leeuwen et al. 2000) human brain suggest temperature can be substantially different from deep brain values only in the regions near the brain surface. A recently proposed theoretical model (Sukstanskii and Yablonskiy 2004, 2006) experimentally verified in (Zhu et al. 2006) attributed this phenomenon to the temperature shielding effect of blood flow. Here, cerebral blood flow (CBF) efficiently protects deep brain tissues from temperature changes by replenishing tissue heat losses to the surroundings. The temperature shielding effect of blood flow quantifies the means by which cerebral blood flow prevents “extracranial cold” from penetrating deep brain structures. Significant temperature gradients take place only near the brain surface and exponentially decrease with distance from the brain surface with the characteristic shielding length (hereafter denoted Δ), which is inversely proportional to the square root of CBF (Sukstanskii and Yablonskiy 2004; Zhu et al. 2006).
Typically, CBF in adult humans is about 50 ml/100 g/min resulting in Δ about 3-4 mm. This number is much smaller than the human brain diameter of about 14 cm. It means that the temperature in the adult human brain should be practically homogeneous except for a narrow (∼Δ) shell near the brain surface. However, in newborn infants (especially, preterm), the CBF may be very low [less than 10 ml/(100 g min), e.g., (Altman et al. 1993, 1988; Powers 1993; Volpe 2001)], and the characteristic shielding length Δ may be substantially higher (up to 1-1.5 cm), allowing extracranial cold from a cooling device to penetrate rather deep into the brain. Given that a typical diameter of a neonatal brain is about 10 cm, a rather substantial part of the brain can be cooled down in this case.
Another important issue is the heat exchange between the head surface (scalp) and the surroundings (e.g. cooling device), described by the heat transfer coefficient (denoted hereafter h). As we show below, to achieve the goal of deep brain cooling, one needs to use a device providing a high value of h. Ideally, such a device should maintain a temperature of the scalp equal to its own temperature (formally, this ideal situation corresponds to an infinitely high heat transfer coefficient). We call this an “ideal cooling device (ICD)”. Of course, the ICD cannot be realized in practice; however, the results for this limiting case provide some boundaries of what can be achieved under a given cooling device temperature and CBF.
Previous theoretical studies of temperature distribution in the brain were based on numerical solutions of the bioheat equation (Pennes 1948) and provided important insights into the problem of brain cooling (Nelson and Nunneley 1998; van Leeuwen et al. 2000; Zhu and Diao 2001). In contrast to these numerical methods, we demonstrate here that temperature distribution may be analyzed by virtue of a relatively simple analytical approach. We derive simple analytical expressions for the temperature distribution in the brain making it possible to analyze the brain temperature response to external head cooling for a broad range of input parameters. In particular, we will show that there are two necessary conditions for successful achievement of mild brain hypothermia: a low value of cerebral blood flow and a sufficiently high value of the heat transfer coefficient describing heat exchange between the brain and the cooling device.
Theoretical approach
Our approach is based on a bio-heat equation originally proposed by (Pennes 1948) for description of the temperature distribution in organs. We consider the head as a system consisting of cerebral tissue with overlaying layers of cerebrospinal fluid (CSF), skull and scalp. The temperature distributions in these four regions, Tj(r) (j = 0,1,2,3 corresponds to brain tissue, CSF, skull and scalp, respectively), can be found as a solution of a set of static bio-heat equations (we are interested here only in a steady-state temperature distribution):
| (1) |
where kj, ρj, Fj, Taj, qj are thermal conductivity, density, blood flow, arterial blood temperature and metabolic heat production rate in the corresponding region, respectively; ρb and cb are the density and specific heat of blood. The first term in this equation describes heat conductance. The second term represents heat removed by blood flow; it is derived under the assumption that the blood temperature equilibrates with the tissue temperature in the capillary bed (Pennes 1948). The third term in Eq. (1) describes the heat generated by metabolic processes.
As can be seen from the solution of these equations (see below), temperature distribution in deep brain regions is homogeneous and is mainly determined from the dynamic equilibrium of heat generated by oxygen metabolism in the brain tissue and heat removed by cerebral blood flow. This equilibrium results in the deep brain (core) temperature, Tb (Yablonskiy et al. 2000):
| (2) |
Thus, the core temperature is higher than that of arterial blood by the “metabolic temperature shift” (MTS) Tm0. For typical values of the parameters for the adult brain, the MTS is Tm0 = 0.36°C (Yablonskiy et al. 2000). This quantity is in a good agreement with experimental data (Hayward and Baker 1968; Nybo et al. 2002).
In CSF, blood flow and metabolic heat production are absent. In the skull, these quantities are very small (Olsen et al. 1985) and can be ignored. Therefore, the temperature distribution in CSF and skull can be described by a simplified equations ▽2Tj(r) = 0, j = 1, 2, instead of Eqs. (1).
Heat exchange with a cooling device (or with air, if device is absent) can modify the uniformity of the brain temperature distribution near the brain surface. To address this issue, the set of Eqs. (1) should be solved along with the boundary conditions at the interfaces brain/CSF, CSF/skull, skull/scalp and scalp/cooling device (or scalp/air) (see Appendix, Eqs. 11). These boundary conditions reflect the fact that no heat dissipation takes place on the interfaces between the regions; hence temperature and the normal component of heat flow should be continuous on each of these interfaces. The heat exchange between the scalp and the cooling device (or between the scalp and air) with a given temperature Te is described by the heat transfer coefficient, h, which effectively takes into account all physical mechanism contributing to this exchange: heat conduction, radiation, air convection, water evaporation, etc.
This type of problem can be solved analytically only in some simple geometries (e.g., plane, cylinder, sphere), whereas the actual geometry of the head is rather complicated. However, the problem under consideration can be substantially simplified. Indeed, due to the temperature shielding effect of blood flow (Sukstanskii and Yablonskiy 2004, 2006; Zhu et al. 2006), the temperature distribution in the brain is homogeneous except of a thin superficial layer of characteristic length Δ:
| (3) |
Typically, Δ in adult humans is about 3-4 mm. For large animals that have head diameter of several centimeters and higher (this includes adult humans, diameter of ∼15 cm, neonates, diameter of ∼6 cm, most primates, etc), the temperature distribution near the brain surface can be treated as a one-dimensional problem, with temperature depending only on the distance from the brain surface. Thus, the brain can be considered as a region (say, x < 0), covered by three layers of thickness d1, d2, d3 corresponding to CSF, skull and scalp, respectively. Although such a “one-dimensional” model ignores the fine structure of the brain, it reflects the main features of temperature distribution and physical mechanisms affecting it.
A solution of the bio-heat Eqs. (1) in the four regions, j = 0,1,2,3, is given in the Appendix, Eqs. (12). Specifically, in the brain (x < 0), the temperature distribution is exponential:
| (4) |
Here parameter Δ is the characteristic shielding length in the brain, defined by Eq. (3); Tbs is temperature at the brain surface (e.g., at the brain/CSF interface, x = 0):
| (5) |
where Ts = Ta3 + Tm3 is the temperature that would exist in the scalp in the absence of heat exchange, Tm3 = q3/ρ3ρbcbF3 is the metabolic temperature shift in the scalp; R = r0 + r1 + r2 + r3; rj = dj/kj, (j = 1,2,3) are the thermal resistances (per unit area) of the CSF, skull and scalp, respectively; r0 = Δ/k0 is the effective thermal resistance of the superficial layer of the brain (of thickness Δ); η = d3/Δs; Δs = (k3 / ρ3ρbcbF3)1/2 is the characteristic shielding length in the scalp. As blood flow in the scalp is typically about 10 ml/100 g/min (van Leeuwen et al. 2000), the corresponding shielding length Δs is about 7 mm. This value is much bigger than the scalp thickness d3 (about 1-2 mm). Under this condition, the parameter η is small and the general cumbersome expression for Tbs can be written in the following rather simple form:
| (6) |
Equations (2), (4) and (6) provide a simple means to evaluate temperature distribution in the head.
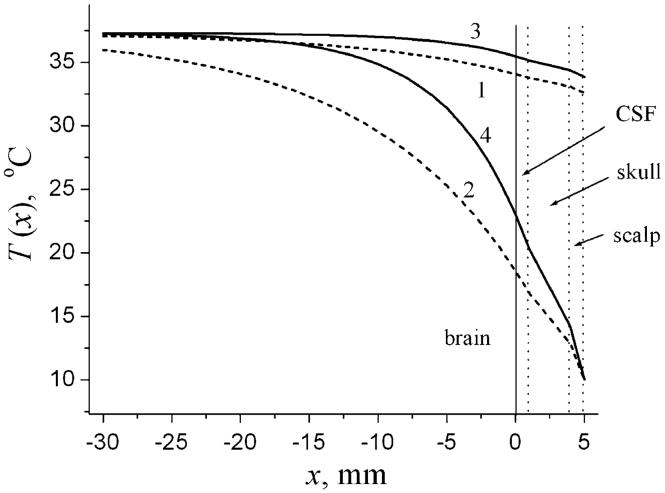
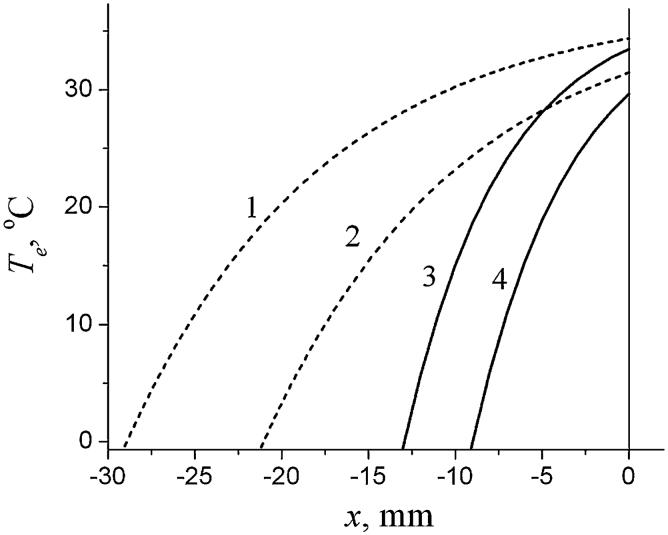
Equations (5) and (12) (plus expressions for other coefficients appearing in Eqs. (12)) provide an analytical solution to the problem and allow analyzing the influence of different parameters on the temperature distribution in the head. An example of temperature distribution is shown in Fig. 1 for two values of CBF F0 and two values of heat transfer coefficient h: the “normal” value, h = h(norm) = 8 W/(m2 °C), corresponding the situation without cooling device, and h → ∞ corresponding to the limiting case of the ICD. Generally speaking, the “normal” value of the heat transfer coefficient, h(norm), certainly depends on many parameters (humidity, skin wetness, insulation, exposure to fan, etc.) and can therefore vary in a rather broad range (see, for instance, Sari et al. 2004). A value h(norm) = 8 W/(m2 °C) was selected and used hereafter just for illustration purposes (the same value was used in another theoretical paper devoted to numerical analysis of temperature distribution in the neonatal brain (van Leeuwen 2000)).
Fig. 1.
Temperature distribution, T(x), in the head for low CBF (dashed lines 1, 2) and normal CBF (solid lines 3,4). Lines 1, 3 correspond to h = h(norm) = 8 W/(m2 °C). Lines 2, 4 correspond to the ICD (formally, h → ∞). A solid vertical line at x = 0 denotes the brain surface (interface brain/CSF), dashed vertical lines correspond to the interfaces CSF/skull, skull/scalp and head surface. The arterial blood temperature and the metabolic temperature shift in the brain and the scalp are Ta0 = Ta3 = 37°C, Tm0 = Tm3 = 0.3°C; Te = 10°C Other parameters of the model for all graphs hereafter are chosen similar to those as in the numerical model used in (van Leeuwen et al. 2000): ρ0 = ρ3 = 1.03g/cm3, ρb = 1.05 g/cm3, cb = 3.8 J/(g °C), k0,1,2,3 = (5.03, 5.82, 6.5, 3.4)·10- 1 W/(m °C), F3 = 10 ml/(100 g min). The thicknesses of the layers (CSF, scalp. skull)): d1 = 0.1 cm, d2 = 0.3 cm, d3 = 0.1 cm
In the case of the ICD, the temperature at the head surface coincides with the temperature of the cooling device Te and does not depend on the deep brain temperature, whereas for h = h(norm), it deviates from the deep brain temperature Tb only by 2-3°C. It is also important to note that deep in the brain (at distance about 2 cm from the surface), the temperature practically coincides with Tb for normal CBF even in the case of ICD. This is also the case for low CBF and “normal” h = h(norm). Only in the case of ICD and low CBF, the temperature at the distance of about 2 cm from the brain surface can substantially deviate from Tb.
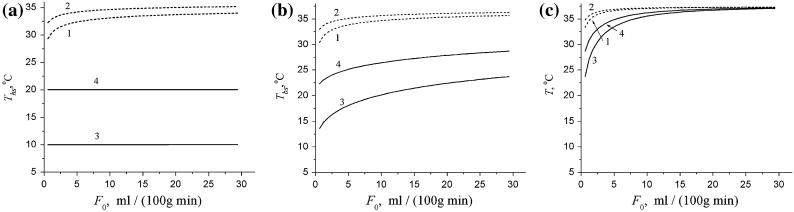
The dependence of temperature on CBF, F0, at three characteristic locations (head surface, Ths = T(x = d), brain surface, Tbs = T(x = 0), and 2 cm deep in the brain, T(x = - 2)) is presented in Fig. 2 for a “normal” value of the heat transfer coefficient, h = h(norm) and for the case of ICD (h → ∞) and two values of Te, 20° and 10° C. Figure 2 demonstrates that for the normal value of the heat transfer coefficient, the temperature at the brain and head surfaces may be lower than the core temperature in the brain, Tb (37.3°C in our case), by several degrees (depending on F0 and Te); however, at the distance 2 cm from the brain surface it only slightly deviates from Tb even for extremely low CBF. The situation is different for the case of ICD. In this case, the temperature at the head surface coincides with Te (as it should be according to the definition of ICD); the temperature at the brain surface is substantially lower than the core temperature; the temperature at the distance 2 cm from the brain surface can also be lower than Tb by several degrees, provided that the CBF is also rather low (less than 10 ml/(100 g min)).
Fig. 2.
The temperatures at the head surface Ths (a), at the brain surface Tbs (b), and at the distance x = 2 cm from the brain surface (c) as functions of the CBF for two values of CBF, for the normal value of the heat transfer coefficient, h = h(norm) = 8 W/(m2 °C) (dashed lines 1, 2) and for the case of ICD (h → ∞, solid lines 3, 4) and 2 values of Te, 10°C (lines 1, 3) and 20°C (lines 2, 4)
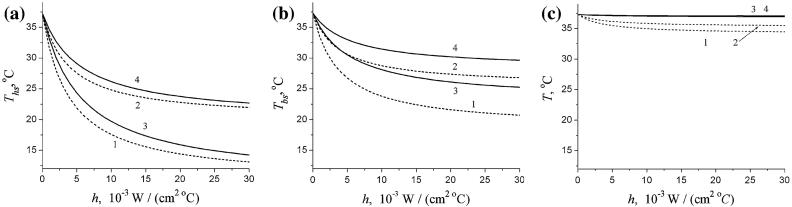
Figure 3 presents the temperature at the head surface Ths, at the brain surface Tbs, and at the distance x = 2 cm from the brain surface as functions of the heat transfer coefficient h for two values of CBF, and and two values of Te, 10°C and 20°C. For both the normal and low CBF, the temperature at the head surface and at the brain surface decreases rather substantially as the heat transfer coefficient increases. However, the temperature at the distance 2 cm from the brain surface in the case of normal CBF does not depend on Te (lines 3 and 4 practically coincide) and remains practically flat with increasing h. However, for the case of low CBF, this temperature drops about 2-3°C (depending on Te) when the heat transfer coefficient becomes 10-15 times higher than its normal value h(norm) = 8 W/(m2°C) and then remains practically unchanged.
Fig. 3.
The temperatures at the head surface Ths (a), at the brain surface Tbs (b), and at the distance x = 2 cm from the brain surface (c) as functions of the heat transfer coefficient h for two values of CBF, (dashed lines 1, 2) and (solid lines 3, 4) and two values of Te, 10°C (lines 1, 3) and 20°C (lines 2, 4)
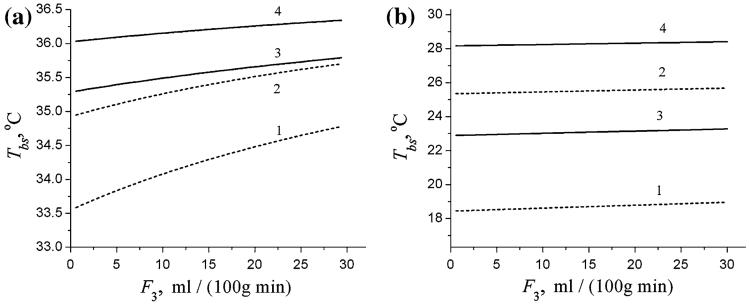
The dependence of the brain surface temperature Tbs, on the blood flow in the scalp F3 is demonstrated in Fig. 4 for the same set of CBF values ( and ) and Te (10 and 20°C) as in Fig. 3. Figure 4a and b correspond to the “normal” value of the heat transfer coefficient, h = h(norm), and to the case of the ICD, h → ∞, respectively. As we can see, even an increase in blood flow in the scalp up to high non-physiological value of 30 ml/100 g/min does not affect substantially the temperature of the brain surface.
Fig. 4.
The temperatures at the brain surface, Tbs, as functions of blood flow in the scalp F3 for two values of CBF, (dashed lines 1, 2) and (solid lines 3, 4) and two values of Te, 10°C (lines 1, 3) and 20°C (lines 2, 4). a h = h(norm) = 8 W/(m2 °C); b ideal cooling device, h → ∞
The analytical expressions for temperature distribution in the brain (Eqs. (4) and (5) or their simplified form in Eqs. (4) and (6)) allow answering a practically important question: what temperature Te of a cooling device should be used to decrease the temperature at a targeted distance x from the brain surface by a desired amount δT = Tb - T (other parameters fixed). The previous figures demonstrate that temperature deep in the brain can be substantially decreased only by maintaining high heat transfer coefficient (ideally, by using the ICD). To establish theoretical limits for deep brain cooling, we plot in Fig. 5 the temperature of the ICD required for decreasing brain temperature by a desired δT at a given distance x from the brain surface for two values of CBF ( and ). Obviously, cooling temperature (coinciding with the scalp temperature in the case of the ICD) below 0°C is unacceptable. Therefore, restricting to Te > 0°C, for the normal value of CBF, , a temperature decrease by 2°C can not be achieved deeper than 1.5 cm from the brain surface; for a 4°C-decrease, this depth is less than 1 cm. However, for low CBF, , the 2°C-decrease can be achieved at 3 cm from the brain surface; this might be sufficient for effective deep brain hypothermia.
Fig. 5.
The temperature of the ideal cooling device, Te, required for decreasing brain temperature at a distance x from the brain surface by δT = 2°C (lines 1 and 3) and by δT = 4°C (lines 2 and 4) for two values of CBF, (dashed lines 1, 2) and (solid lines 3, 4)
The difference between the core temperature Tb and the temperature at the brain surface Tbs is proportional to the heat flux Q through the head surface (see Eq. (18) in the Appendix), which is equal to the amount of heat being removed by the external cooling device per unit time per unit area of the head surface. In the small-η approximation, the flux Q is equal to
| (7) |
Combining Eq. (7) with Eq. (4), the temperature distribution in the brain can be expressed in terms of Q:
| (8) |
It is important to note that Q remains finite even in the case of ICD, when the heat transfer coefficient tends to infinity. Using Eq. (8), we can find the distance from the brain surface at which the temperature decrease δT can be achieved for a given flux Q:
| (9) |
Discussion
In this study, we derived analytical equations that allow straightforward theoretical estimates on the limits of possible temperature reduction in the brain by external head cooling devices. The main factors affecting the temperature distribution in the brain are the CBF F0, the temperature of incoming arterial blood Ta, the temperature of cooling device Te, and the heat transfer coefficient h between this device and the head surface.
In the deep brain, the core temperature Tb is practically homogeneous and slightly higher than the temperature of incoming arterial blood Ta due to metabolic heat generation. From the thermodynamic point of view, cerebral blood flow serves in this region as a “cooler” for the brain tissue, removing heat produced by brain metabolism. A different situation takes place in the superficial brain, where the temperature is usually lower than Ta due to the heat exchange with the cooling device (or with air, if the device is absent). In this region, blood flow serves as a “heater”, shielding the internal brain region from external cold assault—this is the model of temperature shielding effect of blood flow (Sukstanskii and Yablonskiy 2004,2006; Zhu et al. 2006). This effect plays the leading role in protecting the brain from external cooling, whereas the thermal resistance of the intermediate layers between the brain and the device (CBF, skull, scalp) plays a secondary role. Simple Eqs. (4, 6) and (8) provide a useful platform for analyzing the influence of different factors on brain temperature distribution.
First, Eqs. (4) and (6) show that significant temperature gradients exist only in the superficial brain layer with a thickness defined by the characteristic temperature shielding length Δ. This parameter is inversely proportional to the square root of CBF and in normal adults with a typical CBF about 0-60 ml/100 g/min, the characteristic length Δ is about 3-4 mm. In normal newborn infants with a typical CBF about 20-30 ml/100 g/min, characteristic length Δ is about 6-7 mm. Our analysis shows that a targeted mild hypothermia (2-3°C temperature decrease) in deep brain (2-3 cm from the brain surface) can be achieved only if CBF is less than 10 ml/100 g/min. Such a low value of CBF has been observed in preterm as well in full-term infants (Altman et al. 1988). Thus, a prognosis for successful achievement of mild hypothermia in deep brain regions should be associated with sufficiently low CBF. This result makes it possible to introduce a necessary eligibility criterion for using brain cooling by means of external head cooling device for achieving mild hypothermia therapy: CBF should be lower than 10 ml/100 g/min. This leads to a long characteristic shielding length Δ and allows “cold assault” to penetrate deeper in the brain. Note also that CBF in neonates can substantially fluctuate depending on their activity, especially sleep/awake cycles. These fluctuations will affect the characteristic temperature screening length, hence efficiency of brain cooling. Also, thermal receptors in the skin may react to head cooling by increasing metabolism of brown adipose tissue and consequently increasing temperature of arterial blood perfusing brain. This mechanism may affect successful achievement of mild hypothermia in deep brain regions.
Second, Eqs. (4) and (6) demonstrate that the low value of CBF is a necessary but not sufficient condition for inducing mild hypothermia deep in the brain by the external head cooling devices. Another condition is an existence of a sufficiently large temperature difference between the deep brain region and the brain surface, Tb - Tbs. As follows from Eq. (6), this can be achieved only for sufficiently high values of the heat transfer coefficient when h ≫ R-1. It means that the mild hypothermia in the deep brain can be achieved only by using external head cooling devices that provide sufficiently high values of the heat transfer coefficient. A high value of h requires a very tight contact between the head surface and the cooling device (cooling hat, for instance). In the hypothetical limit of the ICD, the heat transfer coefficient tends to infinity, h-1 → 0, and the temperature at the brain surface becomes close to the temperature of the cooling device, Te. Of course, the ICD cannot be realized in practice; however, the results for this limiting case provide some boundaries of what can be achieved under a given CBF and cooling device temperature, Te. In this limiting case, h ≫ R-1, the temperature difference Tb - Tbs and the heat flux through the head surface Q become independent of h and reach their maximum values (see Eqs. 6, 7):
| (10) |
The thermal resistances r1,2,3 of the intermediate layers (CSF, scalp, skull) entering the parameter R in Eq. (10) vary for the neonatal head in the interval 0.2 × 10- 2-0.5 × 10- 2 °C m2/W, whereas the effective thermal resistance of the superficial layer of the brain, r0, is significantly higher: r0 = 1.07 × 10- 2 °C m2/W for normal CBF, and r0 = 2.14 × 10- 2 °Cm2/W for low CBF, . Hence, the parameter r0 is a major component in R, especially, in the case of low CBF. According to these estimates and Eq. (10), the maximum values of Tb - Tbs and Q that can be achieved with ICD are about 1/2·(Tb - Te), Qmax ∼ 5·(Tb - Te) mW/cm2 in case of normal CBF and about 2/3·(Tb - Te), Q∼ 3·(Tb - Te) mW/cm2 for low CBF. On the other hand, for a typical value of the heat transfer coefficient, h = h(norm) = 8 W/(m2 °C, the quantity h- 1 ≫ R, r0 making temperatures Tbs and Ths only slightly different from the core temperature Tb. In this case, even at the brain surface, temperature cannot be lower than Tb by more than 2-3°C, whereas at the distance of 2-3 cm from the brain surface, the temperature practically coincides with Tb even at very low CBF.
It should also be noted that results of brain cooling by means of external head cooling devices in small animal models cannot be directly applied to humans. Indeed, in small animals, the characteristic temperature shielding length Δ can be comparable to the small animal head size leading to the presence of temperature gradients across the whole brain. Hence, a mild hypothermia can be induced across the whole small-animal brain.
Conclusion
Within the framework of the analytical model of temperature distribution in the brain, it was demonstrated that a mild hypothermia can be successfully induced in neonates by means of external head cooling devices if two necessary conditions are fulfilled: sufficiently low cerebral blood flow and sufficiently high value of the heat transfer coefficient describing the heat exchange between the head surface and the cooling device. The first condition establishes an eligibility criterion for using head cooling devices for achieving mild hypothermia therapy. The second condition imposes technical requirements on the cooling device.
Acknowledgments
The authors are grateful to Professor Mark S. Conradi for discussion and helpful comments. This study was supported by NIH Grant RO1-NS41519.
Appendix
The boundary conditions for the bio-heat Eq. (1) at the internal interfaces brain/CSF (x = 0), CSF/skull (x = d1), skull/scalp (x = d1 + d2) and at the external head surface (scalp/air, x = d = d1 + d2 + d3), are
| (11) |
where prime denotes a derivative with respect to the coordinate x; Te is the temperature of the cooling device; h is a heat transfer coefficient; d1, d2, d3 are the thicknesses of CSF, skull and scalp, respectively.
A solution to the bio-heat Eq. (1) is sought in the form:
| (12) |
where Tb = Ta0 + Tm0, Ts = Ta3 + Tm3 is the temperature that would exist in the scalp in the absence of heat exchange, Tm3 = q3/ρ3ρbcbF3 is the metabolic temperature shift in the scalp; Tbs is the temperature at the brain surface, Δ = (k0/ρ0ρbcbF3)1/2, Δs = (k3/ρ3ρbcbF3)1/2. The parameter Tbs and the coefficients Aj, Bj can be found by substituting Eqs. (12) into the boundary conditions (11). In particular, the parameter Tbs entering the temperature distribution in the brain (first line in Eqs 12) is equal to
| (13) |
where R = r0 + r1 + r2 + r3; rj = dj/kj, (j = 1,2,3) are the thermal resistances (per unit area) of the CSF, skull and scalp, respectively; r0 = Δ/k0 is the effective thermal resistance of the superficial layer of the brain (of thickness Δ); η = d3/Δ s. Other coefficients Aj, Bj in Eqs. (12) do not appear in the function T0(x) (which is of main interest for us) and have much more cumbersome structure than Eq. (13), therefore we do not present them here. However, explicit expressions for these coefficients are used for numerical calculations of the temperature distribution in the head.
If the parameter η is small, η ≪ 1, the general expression for Tbs and the coefficients Aj, Bj can be substantially simplified:
| (14) |
Another important characteristic temperature—the temperature on the head surface, Ths, in this approximation takes the form:
| (15) |
The flux of heat Q through the head surface is equal to (per unit area)
| (16) |
If η ≪ 1, this flux can be written as:
| (17) |
Combining Eqs. (17) and the first line in Eq. (14), the temperature at the brain surface can be expressed I terms of Q:
| (18) |
References
- Altman DI, Perlman JM, Volpe JJ, Powers WJ. Cerebral oxygen metabolism in newborns. Pediatrics. 1993;92:99–104. [PubMed] [Google Scholar]
- Altman DI, Powers WJ, Perlman JM, Herscovitch P, Volpe SL, Volpe JJ. Cerebral blood flow requirement for brain viability in newborn infants is lower than in adults. Ann Neurol. 1988;24:218–226. doi: 10.1002/ana.410240208. [DOI] [PubMed] [Google Scholar]
- Bona E, Hagberg H, Loberg EM, Bagenholm R, Thoresen M. Protective effects of moderate hypothermia after neonatal hypoxia-ischemia: short- and long-term outcome. Pediatr Res. 1998;43:738–745. doi: 10.1203/00006450-199806000-00005. [DOI] [PubMed] [Google Scholar]
- Colbourne F, Corbett D. Delayed postischemic hypothermia: a six month survival study using behavioral and histological assessments of neuroprotection. J Neurosci. 1995;15:7250–7260. doi: 10.1523/JNEUROSCI.15-11-07250.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edwards AD, Yue X, Squier MV, Thoresen M, Cady EB, Penrice J, Cooper CE, Wyatt JS, Reynolds EO, Mehmet H. Specific inhibition of apoptosis after cerebral hypoxia-ischaemia by moderate post-insult hypothermia. Biochem Biophys Res Commun. 1995;217:1193–1199. doi: 10.1006/bbrc.1995.2895. [DOI] [PubMed] [Google Scholar]
- Eicher DJ, Wagner CL, Katikaneni LP, Hulsey TC, Bass WT, Kaufman DA, Horgan MJ, Languani S, Bhatia JJ, Givelichian LM, Sankaran K, Yager JY. Moderate hypothermia in neonatal encephalopathy: efficacy outcomes. Pediatr Neurol. 2005;32:11–17. doi: 10.1016/j.pediatrneurol.2004.06.014. [DOI] [PubMed] [Google Scholar]
- Gluckman PD, Wyatt JS, Azzopardi D, Ballard R, Edwards AD, Ferriero DM, Polin RA, Robertson CM, Thoresen M, Whitelaw A, Gunn AJ. Selective head cooling with mild systemic hypothermia after neonatal encephalopathy: multicentre randomised trial. Lancet. 2005;365:663–670. doi: 10.1016/S0140-6736(05)17946-X. [DOI] [PubMed] [Google Scholar]
- Gunn AJ. Cerebral hypothermia for prevention of brain injury following perinatal asphyxia. Curr Opin Pediatr. 2000;12:111–115. doi: 10.1097/00008480-200004000-00004. [DOI] [PubMed] [Google Scholar]
- Gunn AJ, Gluckman PD, Gunn TR. Selective head cooling in newborn infants after perinatal asphyxia: a safety study. Pediatrics. 1998;102:885–892. doi: 10.1542/peds.102.4.885. [DOI] [PubMed] [Google Scholar]
- Gunn AJ, Gunn TR, de Haan HH, Williams CE, Gluckman PD. Dramatic neuronal rescue with prolonged selective head cooling after ischemia in fetal lambs. J Clin Invest. 1997;99:248–256. doi: 10.1172/JCI119153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayward JN, Baker MA. Role of cerebral arterial blood in the regulation of brain temperature in the monkey. Am J Physiol. 1968;215:389–402. doi: 10.1152/ajplegacy.1968.215.2.389. [DOI] [PubMed] [Google Scholar]
- Iwata O, Thornton JS, Sellwood MW, Iwata S, Sakata Y, Noone MA, O’Brien FE, Bainbridge A, De Vita E, Raivich G, Peebles D, Scaravilli F, Cady EB, Ordidge R, Wyatt JS, Robertson NJ. Depth of delayed cooling alters neuroprotection pattern after hypoxia-ischemia. Ann Neurol. 2005;58:75–87. doi: 10.1002/ana.20528. [DOI] [PubMed] [Google Scholar]
- Laptook AR, Corbett RJ, Sterett R, Burns DK, Tollefsbol G, Garcia D. Modest hypothermia provides partial neuroprotection for ischemic neonatal brain. Pediatr Res. 1994;35:436–442. [PubMed] [Google Scholar]
- Laptook AR, Shalak L, Corbett RJ. Differences in brain temperature and cerebral blood flow during selective head versus whole-body cooling. Pediatrics. 2001;108:1103–1110. doi: 10.1542/peds.108.5.1103. [DOI] [PubMed] [Google Scholar]
- Nedelcu J, Klein MA, Aguzzi A, Martin E. Resuscitative hypothermia protects the neonatal rat brain from hypoxicischemic injury. Brain Pathol. 2000;10:61–71. doi: 10.1111/j.1750-3639.2000.tb00243.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson DA, Nunneley SA. Brain temperature and limits on transcranial cooling in humans: quantitative modeling results. Eur J Appl Physiol. 1998;78:353–359. doi: 10.1007/s004210050431. [DOI] [PubMed] [Google Scholar]
- Nybo L, Secher NH, Nielsen B. Inadequate heat release from the human brain during prolonged exercise with hyperthermia. J Physiol. 2002;545(Pt2):697–704. doi: 10.1113/jphysiol.2002.030023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olsen RW, Hayes LJ, Wissler EH, Nikaidoh H, Eberhart RC. Influence of hypothermia and circulatory arrest on cerebral temperature distribution. J Biomech Eng. 1985;107:354–360. doi: 10.1115/1.3138569. [DOI] [PubMed] [Google Scholar]
- Papile LA. Systemic hypothermia—a “cool” therapy for neonatal hypoxic-ischemic encephalopathy. N Engl J Med. 2005;353:1619–1620. doi: 10.1056/NEJMe058199. [DOI] [PubMed] [Google Scholar]
- Pennes HH. Analysis of tissue and arterial blood temperature in the resting human forearm. J Appl Physiol. 1948;1:93–122. doi: 10.1152/jappl.1948.1.2.93. [DOI] [PubMed] [Google Scholar]
- Powers WJ.Cerebral blood flow and metabolism in newborn infants. What can they teach us about stroke? Stroke 199324I33–I34.discussion I35-37 [PubMed] [Google Scholar]
- Sari H, Gartner M, Hoeft A, Candas V. Glove thermal insulation: local heat transfer measures and relevance. Eur J Appl Physiol. 2004;92:702–705. doi: 10.1007/s00421-004-1136-z. [DOI] [PubMed] [Google Scholar]
- Shankaran S, Laptook AR, Ehrenkranz RA, Tyson JE, McDonald SA, Donovan EF, Fanaroff AA, Poole WK, Wright LL, Higgins RD, Finer NN, Carlo WA, Duara S, Oh W, Cotten CM, Stevenson DK, Stoll BJ, Lemons JA, Guillet R, Jobe AH. Whole-body hypothermia for neonates with hypoxic-ischemic encephalopathy. N Engl J Med. 2005;353:1574–1584. doi: 10.1056/NEJMcps050929. [DOI] [PubMed] [Google Scholar]
- Sirimanne ES, Blumberg RM, Bossano D, Gunning M, Edwards AD, Gluckman PD, Williams CE. The effect of prolonged modification of cerebral temperature on outcome after hypoxic-ischemic brain injury in the infant rat. Pediatr Res. 1996;39:591–597. doi: 10.1203/00006450-199604000-00005. [DOI] [PubMed] [Google Scholar]
- Speer M, Perlman JM. Modest hypothermia as a neuroprotective strategy in high-risk term infants. Clin Perinatol. 2006;33 doi: 10.1016/j.clp.2005.11.012. [DOI] [PubMed] [Google Scholar]
- Sukstanskii AL, Yablonskiy DA. An analytical model of temperature regulation in human head. J Therm Biol. 2004;29:583–587. [Google Scholar]
- Sukstanskii AL, Yablonskiy DA. Theoretical model of temperature regulation in the brain during changes in functional activity. Proc Natl Acad Sci USA. 2006;103:12144–12149. doi: 10.1073/pnas.0604376103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thoresen M, Penrice J, Lorek A, Cady EB, Wylezinska M, Kirkbride V, Cooper CE, Brown GC, Edwards AD, Wyatt JS, et al. Mild hypothermia after severe transient hypoxia-ischemia ameliorates delayed cerebral energy failure in the newborn piglet. Pediatr Res. 1995;37:667–670. doi: 10.1203/00006450-199505000-00019. [DOI] [PubMed] [Google Scholar]
- Tooley JR, Satas S, Porter H, Silver IA, Thoresen M. Head cooling with mild systemic hypothermia in anesthetized piglets is neuroprotective. Ann Neurol. 2003;53:65–72. doi: 10.1002/ana.10402. [DOI] [PubMed] [Google Scholar]
- van Leeuwen GMJ, Hand JW, Lagenduk JJW, Azzopardi DV, Edwards AD. Numerical modeling of temperature distribution within the natal head. Pediatr Res. 2000;48:351–356. doi: 10.1203/00006450-200009000-00015. [DOI] [PubMed] [Google Scholar]
- Vannucci RC, Perlman JM. Interventions for perinatal hypoxic-ischemic encephalopathy. Pediatrics. 1997;100:1004–1014. doi: 10.1542/peds.100.6.1004. [DOI] [PubMed] [Google Scholar]
- Volpe JJ. Neurology of the newborn. W.B.Saunders Co; Philadelphia: 2001. [Google Scholar]
- Wyatt JS, Robertson NJ. Time for a cool head-neuroprotection becomes a reality. Early Hum Dev. 2005;81:5–11. doi: 10.1016/j.earlhumdev.2004.10.014. [DOI] [PubMed] [Google Scholar]
- Yablonskiy DA, Ackerman JJH, Raichle ME. Coupling between changes in human brain temperature and oxidative metabolism during prolonged visual stimulation. PNAS. 2000;97:7603–7608. doi: 10.1073/pnas.97.13.7603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu L, Diao C. Theoretical simulation of temperature distribution in the brain during mild hypothermia treatment for brain injury. Med Biol Eng Comput. 2001;39:681–687. doi: 10.1007/BF02345442. [DOI] [PubMed] [Google Scholar]
- Zhu M, Ackerman JJ, Sukstanskii A, Yablonskiy DA. How the body controls brain temperature: the temperature shielding effect of cerebral blood flow. J Appl Physiol. 2006;101:1481–1488. doi: 10.1152/japplphysiol.00319.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]