Abstract
Migration of eukaryotic cells toward a chemoattractant often relies on their ability to distinguish receptor-mediated signaling at different subcellular locations, a phenomenon known as spatial sensing. A prominent example that is seen during wound healing is fibroblast migration in platelet-derived growth factor (PDGF) gradients. As in the well-characterized chemotactic cells Dictyostelium discoideum and neutrophils, signaling to the cytoskeleton via the phosphoinositide 3-kinase pathway in fibroblasts is spatially polarized by a PDGF gradient; however, the sensitivity of this process and how it is regulated are unknown. Through a quantitative analysis of mathematical models and live cell total internal reflection fluorescence microscopy experiments, we demonstrate that PDGF detection is governed by mechanisms that are fundamentally different from those in D. discoideum and neutrophils. Robust PDGF sensing requires steeper gradients and a much narrower range of absolute chemoattractant concentration, which is consistent with a simpler system lacking the feedback loops that yield signal amplification and adaptation in amoeboid cells.
Introduction
Directed cell migration is a critical process in many diverse physiological and pathological settings, such as the immune response, embryogenesis, and tumor metastasis. Chemotaxis, or migration biased toward a gradient of soluble chemoattractant, has been studied extensively in the context of two model cell types: neutrophils and the slime mold Dictyostelium discoideum (Devreotes and Zigmond, 1988). Although these professional migrating cells respond to distinct stimuli, their chemotactic mechanisms exhibit several common features. Their respective chemoattractants bind and activate G protein–coupled receptors (GPCRs), leading to signal transduction through phosphoinositide (PI) 3-kinase and the production of 3′ PI lipids in the plasma membrane, which is a pathway that modulates Rac and Cdc42 GTPases and, thus, actin-based cell motility (Ridley, 2001; Wang et al., 2002; Merlot and Firtel, 2003; Srinivasan et al., 2003). In response to spatially uniform stimulation, both cell types exhibit accumulation of 3′ PIs and desensitization of this response within seconds (Stephens et al., 1991; Meili et al., 1999), which is often followed by spontaneous polarization of 3′ PI signaling and cell motility in a random direction (Zigmond and Sullivan, 1979; Servant et al., 2000; Postma et al., 2004). Such adaptation allows these cells to respond definitively to relative changes in chemoattractant concentration. Thus, in response to shallow chemoattractant gradients (∼1% or greater across the cell), there is a dramatic and persistent spatial polarization of 3′ PI signaling and membrane extension in the direction of the gradient (Zigmond, 1977; Parent et al., 1998; Servant et al., 2000), which is sensitive to the relative steepness of the chemoattractant gradient and far less so to its midpoint concentration (Janetopoulos et al., 2004). These phenomena have, in recent years, prompted the analysis of these sensitive spatial sensing mechanisms using conceptual (Parent and Devreotes, 1999; Weiner, 2002; Devreotes and Janetopoulos, 2003) as well as mathematical (Meinhardt, 1999; Narang et al., 2001; Postma and Van Haastert, 2001; Levchenko and Iglesias, 2002; Ma et al., 2004; Subramanian and Narang, 2004; Skupsky et al., 2005) models, which typically invoke locally activated positive feedback loops and long-range inhibition to simultaneously explain the responses to uniform and gradient stimulation. In the neutrophil system, a Rac-to–PI 3-kinase feedback loop has been identified as a core mechanism in the robust activation of PI 3-kinase and gradient sensing (Servant et al., 2000; Weiner et al., 2002; Srinivasan et al., 2003).
Another example of chemotactic sensing is that of dermal fibroblasts in wound healing (Singer and Clark, 1999). PDGF, produced by platelets and macrophages, forms a gradient in the tissue and serves as a potent chemoattractant and mitogen, thus accelerating the rate of fibroblast invasion into the fibrin clot (Deuel et al., 1991; Heldin and Westermark, 1999). As with the aforementioned cell types, fibroblast motility and PDGF-stimulated chemotaxis rely on the activation of PI 3-kinase (Kundra et al., 1994; Wennström et al., 1994a,b; Wymann and Arcaro, 1994), and PDGF gradients elicit intracellular 3′ PI gradients in the plasma membrane (Haugh et al., 2000). However, it is currently unknown whether or not there is a common signal transduction mechanism shared by all of these cell types in the regulation of 3′ PI–mediated spatial gradient sensing. Indeed, there are indications that the PDGF-sensing mechanism differs. Migration of fibroblasts is far slower than that of amoeboid cells and is driven as much by differential adhesion as by membrane protrusion (Lauffenburger and Horwitz, 1996), suggesting distinct requirements for gradient sensing. PDGF signals through members of the receptor tyrosine kinase family, which activate different PI 3-kinase isoforms from those activated by GPCRs (Vanhaesebroeck et al., 2001). Most significantly, it is well established that PI 3-kinase signaling in response to uniform PDGF stimulation is not marked by rapid adaptation; although subject to receptor down-regulation on the time scale of hours, 3′ PI levels achieve a quasi–steady state after ∼5–10 min (Hawkins et al., 1992; Jackson et al., 1992; Haugh et al., 2000; Park et al., 2003).
In this paper, we present a quantitative analysis of PDGF gradient sensing in fibroblasts using a combination of mathematical modeling and live cell total internal reflection fluorescence (TIRF) imaging. Compared with the chemotactic responses of D. discoideum and neutrophils, we report that the PDGF gradient–sensing mechanism in fibroblasts is less sensitive and strongly depends on both the relative PDGF gradient and its midpoint concentration. Optimal gradient sensing is observed in a narrow range of intermediate midpoint PDGF concentrations that yield near maximal PDGF receptor–mediated PI 3-kinase recruitment without saturating receptor occupancy. The model quantitatively matches the spatial pattern and kinetics of 3′ PI signaling without including positive or negative feedback loops, and, accordingly, we show that Rho family GTPases are not required for PDGF-stimulated PI 3-kinase activation. These results indicate that although similar pathways are used across diverse cell/receptor systems, the regulatory mechanisms governing the sensitivity of PDGF gradient detection are fundamentally different from those characterized for classic GPCR-mediated chemotaxis.
Results
Model analysis predicts three concentration regimes of PDGF gradient sensitivity
Faced with the apparent molecular and phenomenological differences between PDGF gradient sensing in fibroblasts and 3′ PI–mediated spatial sensing in D. discoideum and neutrophils, mathematical models were formulated based on the simplest possible mechanism (see Materials and methods and supplemental Modeling details, available at http://www.jcb.org/cgi/content/full/jcb.200509028/DC1). Conceptually, our models allow for local activation of PI 3-kinase but not global regulation of PI 3-kinase or 3′ PI–consuming enzymes. PI 3-kinase signaling at different locations only affect one another through depletion of a common cytosolic PI 3-kinase pool and through lateral diffusion of 3′ PI lipids, effects which our previous studies suggest are important; the recruitment of PI 3-kinase by PDGF receptors can be saturated at submaximal receptor occupancy (Kazlauskas and Cooper, 1990; Park et al., 2003), and the spatial range of 3′ PI lipids in PDGF-stimulated fibroblasts (∼10 μm) can be significant compared with cellular dimensions (Haugh et al., 2000; Schneider and Haugh, 2004; Schneider et al., 2005).
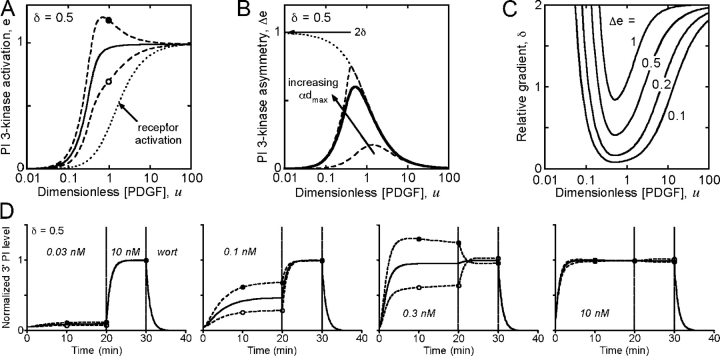
From an analysis of the model equations, which relate the difference in PI 3-kinase enzyme recruitment between the front and back of the cell (Δe) to the corresponding difference in receptor dimerization/activation (Δd) at quasi–steady state, one predicts three distinct regimes of gradient sensitivity (Fig. 1, A–C). At low midpoint concentrations of PDGF, most of the PI 3-kinase remains in the cytosol, and PI 3-kinase recruitment is simply proportional to the local density of activated receptors. In other words, gradient sensing is absolute:
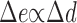 |
(1) |
Figure 1.
Sensitivity of the PDGF gradient–sensing mechanism: mathematical modeling predictions. (A–C) Predictions based on the quasi–steady-state model of receptor activation (equation 7) and pseudo-equilibrium binding of PI 3-kinase (equation 8). (A) Dimensionless PI 3-kinase recruitment, e, as a function of midpoint PDGF concentration, with a 50% gradient across the cell, at the front (closed circle) and back (open circle) relative to the gradient and averaged over the cell membrane (solid line); the receptor activation level, 〈d〉, is also shown (dotted line). The adjustable parameters are the maximum activated receptor/PI 3-kinase ratio (αd max = 10) and dimensionless dissociation constant of the receptor/PI 3-kinase interaction (κE = 0.1). These values yield saturable PI 3-kinase activation, matching the population dose responses reported in Park et al. (2003). (B) Difference in e between the front and back, Δe, for the parameter values in A (solid curve). Also shown are results assuming stoichiometric binding (κE = 0) with αd max values of 1 and 10 (dashed line) and in the limit of infinite αd max (dotted line); the latter is equivalent to the relative receptor activation gradient, Δd/〈d〉. (C) Values of the relative gradient δ and midpoint PDGF concentration that yield a given Δe; αd max = 10 and κE = 0.1. (D) Front (closed circle), back (open circle), and average (solid line) 3′ PI levels were calculated as a function of time using a kinetic receptor activation model (see supplemental Modeling details, available at http://www.jcb.org/cgi/content/full/jcb.200509028/DC1) under conditions that mimic our experimental protocol. A 50% gradient of varying midpoint PDGF concentration, as indicated, was administered for 20 min followed by a uniformly saturating dose (10 nM) for another 10 min. Thereafter, PI 3-kinase activity was turned off as if inhibited by wortmannin (wort).
PDGF receptor dimerization is cooperative (Park et al., 2003), yielding a modest amplification with respect to the PDGF gradient in this regime (at most twofold).
As the midpoint PDGF concentration is increased, overall PI 3-kinase recruitment approaches saturation (〈e〉 ≈ 1). In this regime, a specific location on the membrane binds its share of the limiting PI 3-kinase pool according to its local activated receptor density compared with the average. Here, gradient sensing is relative:
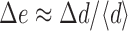 |
(2) |
At extremely high PDGF concentrations, however, all receptors are saturated with ligand, and the cell is unable to sense the gradient:
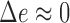 |
(3) |
A number of testable predictions emerge from this simple model (Fig. 1, A–C), which we will show to be valid in fibroblasts responding to PDGF gradients: (1) The gradient in PI 3-kinase signaling, Δe, is sensitive to both the relative PDGF gradient (defined as δ; equation 6) and its midpoint concentration, with the greatest sensitivity at intermediate midpoint concentrations. (2) Both the peak value of Δe and the range of midpoint PDGF concentrations that yield robust intracellular 3′ PI gradients (Δe > 0.1, for example) are determined by the degree of PI 3-kinase saturation. With the parameter values constrained to approximately match the dose responses of receptor and PI 3-kinase activation measured in our cells (Park et al., 2003), the peak Δe ∼ δ, and the effective range of midpoint PDGF concentrations spans roughly two logs. (3) At intermediate concentrations of PDGF, where the gradient sensitivity is greatest, PI 3-kinase activation at the front of the cell exceeds the level observed under receptor-saturating conditions. Hence, if gradient stimulation is followed by a high uniform dose of PDGF, PI 3-kinase signaling at the front will be forced to decrease.
A more detailed kinetic model, accounting for PDGF receptor binding, dimerization, and internalization, was used to calculate 3′ PI levels as a function of time in a typical cell stimulated with various gradients (assumed here to be established immediately at t = 0; Fig. 1 D). For now, tempering of the 3′ PI gradient by lateral diffusion is neglected. After 20 min of gradient stimulation, the PDGF concentration is switched to a uniformly saturating value for a period of 10 min followed by rapid inhibition of PI 3-kinase and decay of the 3′ PI level. These conditions reflect the protocol used in our experiments, and the calculated kinetics support the predictions of the quasi–steady-state model.
Gradient sensing in fibroblasts is optimized in a relatively narrow range of PDGF concentrations, which is consistent with saturation of PI 3-kinase recruitment
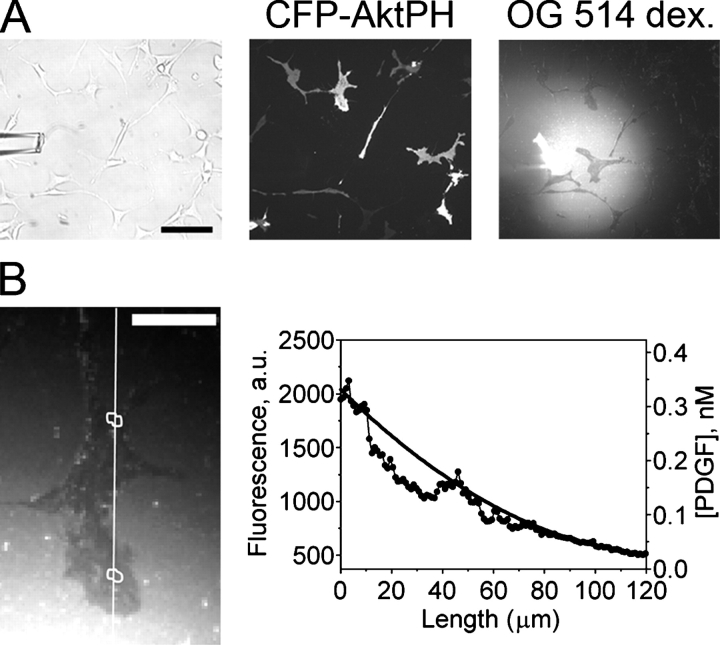
The CFP-tagged pleckstrin homology domain of Akt (CFP-AktPH) was used as a specific biosensor for 3′ PI production at the plasma membrane. Using a micropipette coloaded with PDGF and a fluorescent volume marker (Oregon green [OG] 514–dextran), CFP-AktPH–transfected fibroblasts were presented with gradients of PDGF, and the local marker concentration and intracellular CFP-AktPH translocation were monitored using TIRF microscopy (Fig. 2). By varying the concentration of PDGF in the pipette across different experiments and observing cells at different distances from the source, we systematically analyzed responses to PDGF fields with varying midpoint concentration and gradient steepness. After 20 min of gradient stimulation, a high concentration of PDGF was added uniformly to normalize the response at each location. Subsequently, a high concentration of wortmannin was added to rapidly block PI 3-kinase and, thus, to assess the degradation of 3′ PI lipids and the contribution of cytosolic CFP-AktPH to the overall TIRF fluorescence.
Figure 2.
TIRF imaging of extracellular and intracellular gradients. (A) A micropipette was coloaded with Oregon green (OG) 514–dextran and a prescribed concentration of PDGF, and PDGF gradients were presented to NIH 3T3 fibroblasts transfected with CFP-AktPH. Bar, 100 μm. (B) Although the TIRF excitation of the volume marker is partially occluded by the cells (Lanni et al., 1985), the surrounding regions allow the estimation of the PDGF concentration profile across the cell, as described in Materials and methods. The solid curve in the plot is the best polynomial fit to the fluorescence profiles on either side of the cell, along the line scan depicted in the TIRF image. Bar, 30 μm.
For each cell, regions that define its front and back with respect to the gradient were chosen, and their respective kinetics were assessed. It is important to distinguish between the cell orientation relative to the gradient and the morphological polarity of the cell established before stimulation. Protruding membrane structures at leading edges tend to be localized hot spots of PI 3-kinase signaling in our cells, with elevated 3′ PI levels relative to neighboring regions, whereas cold spots with depressed 3′ PI levels are sometimes observed at the cell's trailing end. These regions, which are apparent after uniform saturation with PDGF, have been characterized in detail previously (Schneider et al., 2005) and were intentionally avoided in this analysis.
PI 3-kinase signaling responses to PDGF gradients of varying midpoint concentration and steepness were consistent with model predictions (Fig. 3). Proper gradient sensing was apparent within a relatively narrow range of PDGF concentration, as PDGF gradients with low midpoint concentrations elicited little change in the TIRF profile, whereas cells exposed to gradients with very high midpoint concentrations showed little change after the uniform stimulus; optimal gradient sensing was often accompanied by a decrease in fluorescence at the front and a corresponding increase at the back after the uniformly saturating dose (Fig. 3 A). In all cases, the observed kinetics were consistent with those calculated in Fig. 1 D. It should be noted that these experiments were performed at room temperature to inhibit cell motility (Haugh et al., 2000) so that the regions would remain stationary during the experiment. The qualitative predictions of the model were also validated in experiments conducted at 37°C, in which spatially biased membrane-spreading events were also observed (Fig. S1, available at http://www.jcb.org/cgi/content/full/jcb.200509028/DC1).
Figure 3.
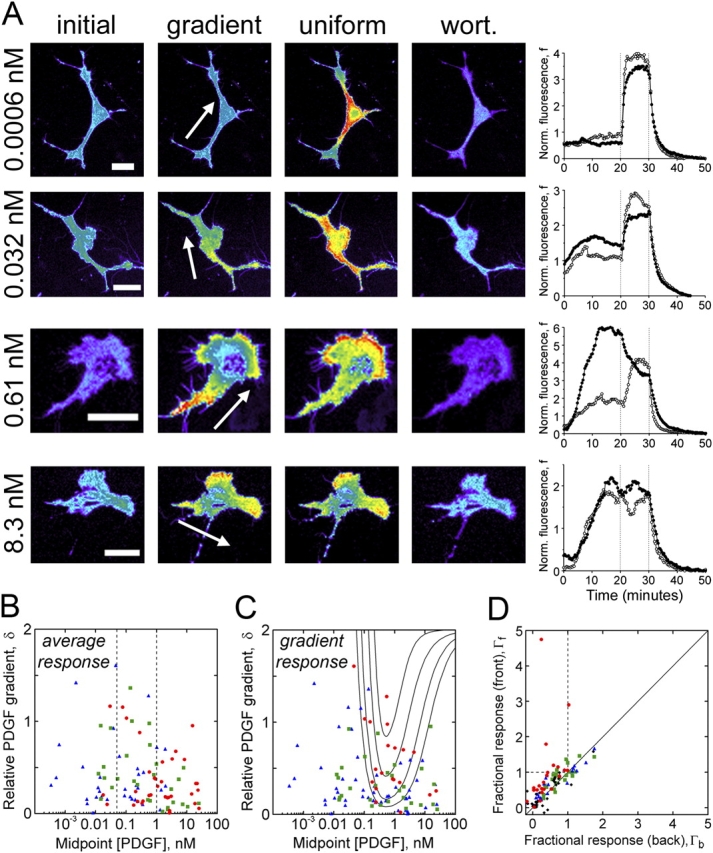
Sensitivity of the PDGF gradient–sensing mechanism: experimental validation. (A) Representative cell responses to steep PDGF gradients with different midpoint concentrations. The montages shows TIRF images acquired prestimulus (initial), at the peak of the gradient response, after bolus addition of 10 nM PDGF (uniform), and after PI 3-kinase inhibition with wortmannin (wort). The arrows indicate PDGF gradient orientation from high to low, and the relative gradients δ across these four cells were 0.75, 0.63, 0.75, and 0.59 (from top to bottom). Bars, 30 μm. The normalized TIRF intensities at the front (closed circles) and back (open circles) of each cell with respect to the gradient are shown as a function of time, with dotted lines indicating the additions of uniform PDGF and wortmannin. (B–D) The local normalized response to the gradient stimulation is defined as Γ (equation 5). (B) Whole cell average responses, 〈Γ〉, of individual cells to various gradients tend to increase with midpoint PDGF concentration and are not affected by gradient steepness. Values of 〈Γ〉 were classified as low (<0.3; blue triangles), intermediate (0.3–0.7; green squares), or high (>0.7; red circles). PDGF concentration cut-offs of 0.05 and 1 nM (vertical dotted lines) demarcate cell populations that tend to exhibit low or high average responses. (C) The difference in response between the front and back is optimized at intermediate PDGF concentrations and depends on the gradient steepness. Values of ΔΓ were classified as low (<0.1; blue triangles), intermediate (0.1–0.3; green squares), or high (>0.3; red circles). The quasi–steady-state model results from Fig. 1 C, with L* = 1 nM, are overlaid for comparison. (D) Fractional responses at the front and back are plotted for the cells depicted in B and C and are grouped according to the midpoint concentration and steepness of the PDGF gradient: black diamonds, <0.1 nM PDGF; blue triangles, 0.1–2 nM PDGF and δ < 0.3; red circles, 0.1–2 nM PDGF and δ > 0.3; green squares, >2 nM PDGF.
To analyze these responses more quantitatively, for a total of 99 cells, we defined the fractional gradient response, Γ, which compares the local TIRF intensity at the height of the gradient response with those recorded before stimulation and after uniform saturation (equation 5). Based on our proposed mechanism, it is expected that the whole cell–averaged response, 〈Γ〉, is sensitive to the midpoint PDGF concentration of the gradient (as one would observe in response to uniform PDGF stimulation) but not its steepness. This was confirmed in our analysis (Fig. 3 B). Higher PDGF concentrations tend to elicit higher average responses, although it is also noted that there is significant cell-to-cell variability in the dose response. The switch from predominantly low (〈Γ〉 < 0.3) to predominantly high (〈Γ〉 > 0.7) average responses occurs within a range of midpoint PDGF concentrations that is consistent with previous uniform stimulation experiments (Haugh et al., 2000; Park et al., 2003). At PDGF concentrations below 0.05 nM, the percentages of cells classified as having low/intermediate/high 〈Γ〉 are 62/27/12, whereas at concentrations above 1 nM, these percentages are 15/29/56; cells seeing midpoint PDGF concentrations between these cut-offs exhibit a balanced spectrum of responses (percentages of low/intermediate/high 〈Γ〉 are 36/33/31). All three pair-wise comparisons of mean 〈Γ〉 values among these cell populations are significant at the 0.05 level by one-sided t tests. Using the more stringent Tukey-Kramer test, all but the comparison between >1 nM and 0.05–1 nM populations are significant at the 0.05 level.
The quality of the gradient-sensing response was assessed in terms of the difference in Γ between the front and back (ΔΓ). In contrast with the whole cell–averaged response, robust front-to-back asymmetry (ΔΓ > 0.3) was only predominant in cells exposed to fairly steep PDGF gradients, with intermediate midpoint concentrations spanning a range of roughly two logs (Fig. 3 C). In accord with the models, this intermediate range is shifted slightly toward higher PDGF concentrations compared with the dynamic range for the average response; an overlay of the curves from Fig. 1 C underscores the good correspondence with model predictions. At midpoint PDGF concentrations <0.1 nM, only 1/31 cells (3%) exhibited a robust gradient-sensing response, and PDGF gradients with midpoint concentrations >2 nM also yielded a low percentage (3/24 cells or 13%). Gradients with intermediate midpoint concentrations (0.1–2 nM) are further subdivided into low and high steepness (cut-off of δ = 0.3), eliciting robust gradient-sensing responses 14% (3/21) and 57% (13/23) of the time, respectively. The superiority of the latter population, which included 8 of the top 10 ΔΓ values, is further supported by pair-wise comparisons of its ΔΓ mean with those of the three other populations, which were all significant at the 0.05 level by the Tukey-Kramer test.
Another way to assess the gradient responses is by plotting the Γ value of the front versus that of the back for each cell; cells were grouped according to the four subpopulations outlined in the previous paragraph (Fig. 3 D). Cells exposed to gradients with intermediate concentrations and high steepness were much more likely to lie above the y = x line (ΔΓ > 0) on this plot, which is indicative of proper gradient sensing. Consistent with another model prediction, several of these cells populated the upper left quadrant (Γf > 1 and Γb < 1), meaning that the TIRF intensity at the front decreased and the intensity at the back increased after the uniform stimulation.
Spatial modeling of gradient responses and comparison with intracellular TIRF profiles
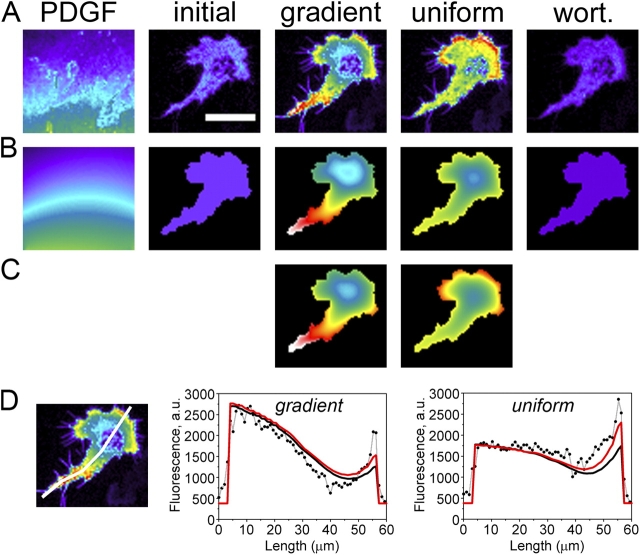
To refine our quasi–steady-state model of PDGF gradient sensing, finite element calculations were performed that allowed us to directly compare the predicted fluorescence profile, f (equation 4), with the acquired TIRF images at each point in the contact area (Fig. 4). The actual PDGF concentration field and irregular cell geometry are inputs to the model, which accounts for pseudo-steady receptor and PI 3-kinase activation as well as lateral diffusion of 3′ PI lipids and recruitment of the CFP-AktPH probe from the cytosol. Order of magnitude estimates of the model parameter values were assigned based on our previous experimental and modeling studies of fibroblast responses to uniform PDGF stimulation (Haugh et al., 2000; Park et al., 2003; Haugh and Schneider, 2004; Schneider and Haugh, 2004; Schneider et al., 2005) and to approximately match the overall fluorescence intensities observed before stimulation and after uniform saturation. No parameters were fitted to the gradient response.
Figure 4.
Spatial modeling of intracellular TIRF profiles. (A) TIRF images showing the extracellular OG 514–dextran profile (PDGF) and intracellular CFP-AktPH profiles as in Fig. 3 A (the cell is the same as in Fig. 3 A, with midpoint [PDGF] = 0.61 nM and δ = 0.75). All CFP-AktPH images use the same absolute pseudocolor scale, and the OG 514–dextran image is scaled such that black is the background and white is the TIRF intensity at the pipette tip. Bar, 30 μm. (B) Virtual images obtained from finite element calculations (see supplemental Modeling details for specifics and parameter definitions, available at http://www.jcb.org/cgi/content/full/jcb.200509028/DC1). Dimensionless parameter values describing 3′ PI diffusion and the AktPH interaction are the same as those used previously (Haugh and Schneider, 2004; Schneider and Haugh, 2004; Schneider et al., 2005: Da = 3; μ = 5; κP = 2; υt = e + x 0(1 − 〈e〉); and υb = x 0(1 − 〈e〉). Parameters describing the PDGF dose response have the same values used in Figs. 1 and 3: αd max = 10; κE = 0.1; and L* = 1 nM. The two remaining parameter values (σ = 15.0 and x 0 = 0.016) were specified to match the overall fluorescence intensities observed before stimulation and after uniform PDGF stimulation. (C) Finite element calculations accounting for enhanced 3′ PI levels in leading edge hot spots. Hot spots were modeled as regions with locally enhanced PI 3-kinase activity (υb = υt = e + x 0[1 − 〈e〉]) and slower 3′ PI diffusion coefficient (reduced by half). Other parameters are as in B except σ = 16.3 and x 0 = 0.015. (D) Comparison of observed (dots) and calculated (solid lines; the model with hot spots is in red) TIRF profiles along the line scan indicated.
The resulting TIRF profiles were compared with experimental images for one of the cells from Fig. 3 A that was exposed to steep PDGF gradients (Fig. 4, A–C). Two versions of the model were used; the second, depicted in Fig. 4 C, partially accounts for the aforementioned hot spots observed at the cell's preexisting leading edge, which, incidentally, is at the “back” of the cell relative to the gradient. Hot spots are modeled simply as regions of the membrane with locally increased PI 3-kinase activity and slower 3′ PI diffusion (Schneider et al., 2005). The hot spots may also be more responsive to lower PDGF concentrations than the rest of the membrane; the average Γ value of the hot spot regions is 0.68 compared with 0.38 for the adjacent region defining the back of the cell. This effect was not included in this model, and, consequently, the hot spot fluorescence intensities observed in the gradient response are somewhat higher than those predicted by the model. Even with rough parameter estimates and a relatively crude model of the hot spot regions, the agreement between observed and simulated CFP-AktPH translocation patterns is quite close, and the model can readily produce the observed steepness of the intracellular TIRF gradient (Fig. 4 D; analysis of another cell is shown in Fig. S2, available at http://www.jcb.org/cgi/content/full/jcb.200509028/DC1).
Kinetic analysis of responses to transient PDGF pulses
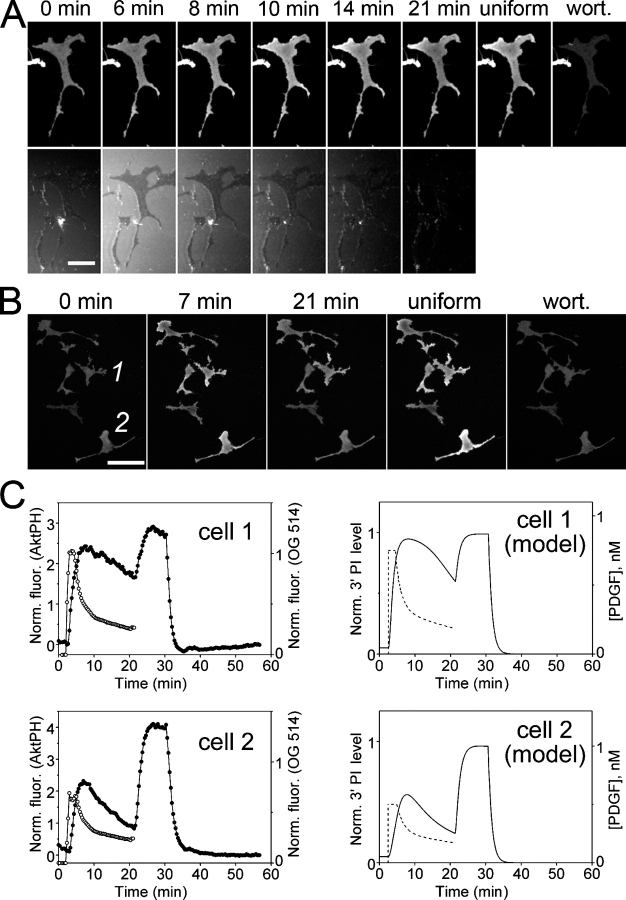
Another test of a mathematical model is its ability to reproduce the cellular response to a transient or pulsed stimulus, an approach that can indicate the presence of feedback interactions (Bhalla et al., 2002). To determine whether our model could explain the 3′ PI responses to transient PDGF stimulation, PDGF was pulsed from the micropipette for a certain period, and CFP-AktPH translocation during and after the pulse was recorded using TIRF microscopy (Fig. 5). By adjusting the flow rate, the PDGF gradient during the pulse could be tuned to be steep (Fig. 5 A and Video 1, available at http://www.jcb.org/cgi/content/full/jcb.200509028/DC1) or essentially uniform across cellular dimensions (Fig. 5, B and C). In both situations, PI 3-kinase signaling tends to persist for several minutes after decay of the stimulus; in fact, the peak response was typically observed minutes after the PDGF concentration began to drop. Our kinetic model captures this behavior. It predicts that the 3′ PI decay will lag whenever the duration of the pulse is insufficient for establishing a quasi–steady state (∼5–10 min), with the time interval of the lag and rate of decay after the peak depending on the degree of PI 3-kinase saturation. Persistence of 3′ PI levels after PDGF withdrawal is not attributed to positive feedback but rather to the fairly slow kinetics of PI 3-kinase redistribution to the cytosol and 3′ PI turnover, and the model and experiment are in quantitative agreement when one allows for modest cell-to-cell variation in receptor and PI 3-kinase expression levels (Fig. 5 C).
Figure 5.
PI 3-kinase signaling kinetics in response to transient PDGF stimulation. (A) A CFP-AktPH–transfected fibroblast was stimulated with a moving PDGF gradient for 21 min, after which 10 nM PDGF (uniform) and wortmannin (wort.) were added as in Fig. 3. The time course montage shows TIRF images of the CFP-AktPH translocation (top) and OG 514–dextran gradient (bottom). Bar, 30 μm. Video 1 shows this time course (available at http://www.jcb.org/cgi/content/full/jcb.200509028/DC1). (B) TIRF images of CFP-AktPH–transfected fibroblasts treated with a brief pulse of PDGF at 2 min, 10 nM PDGF (uniform) at 20 min, and wortmannin (wort.) at 30 min. Bar, 60 μm. (C) The left panels plot average normalized TIRF intensity in the CFP-AktPH (closed circles) and OG 514–dextran (open circles) channels as a function of time for the two cells indicated in B. The right panels are the corresponding kinetic model calculations (see supplemental Modeling details). The dashed curves show the PDGF concentration time courses assumed for each cell before the addition of the 10-nM PDGF bolus.
Rho family GTPases are not required for PDGF-stimulated PI 3-kinase activation
Our mathematical description of PDGF gradient sensing does not invoke feedback loops, so we sought to rule out the need for Rho family GTPases in amplifying PI 3-kinase activation in our system (Fig. 6). Such feedback is plausible given that PI 3-kinase regulatory subunits can interact directly with Rac-GTP (Tolias et al., 1995; Bokoch et al., 1996). In differentiated HL-60 cells, inactivation of Rho family GTPases by Clostridium difficile toxin B treatment ablated 3′ PI accumulation in response to chemoattractants but not to insulin (Servant et al., 2000; Weiner et al., 2002). The latter signals through insulin and insulin-like growth factor receptors, which, like PDGF receptors, are receptor tyrosine kinases.
Figure 6.
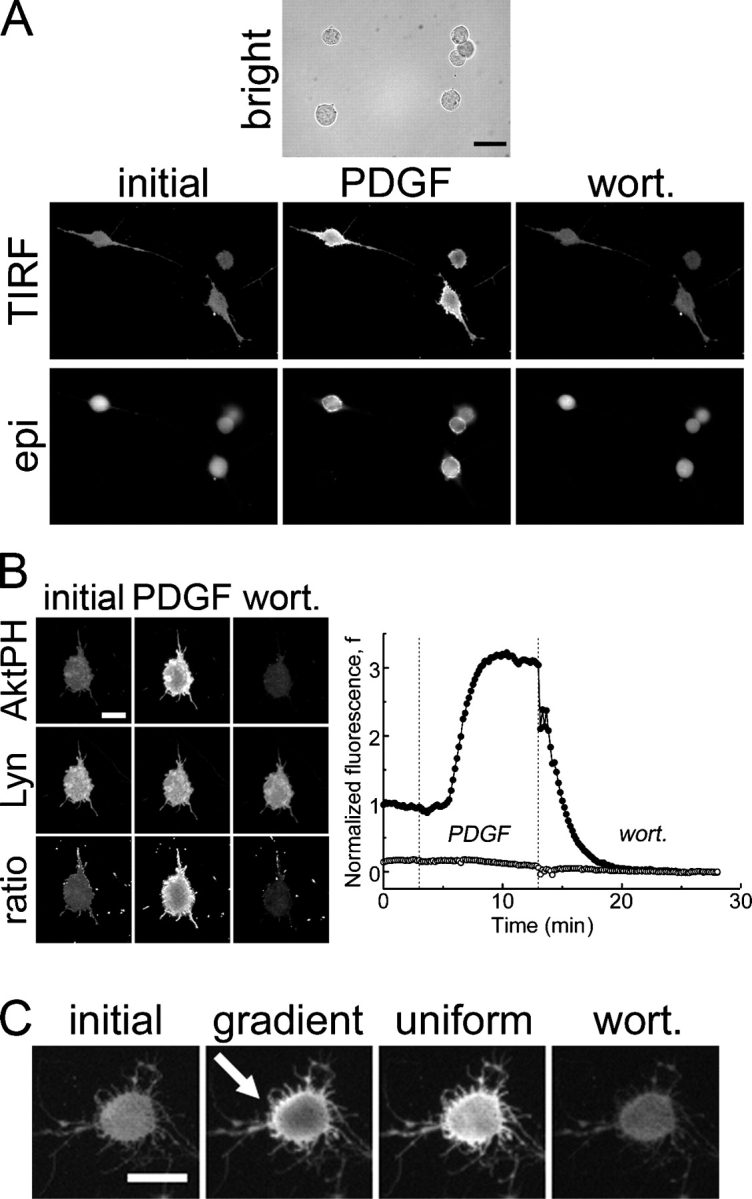
PDGF-stimulated PI 3-kinase activation is not dependent on Rho family GTPases. (A) Bright field, TIRF, and epifluorescence images of GFP-AktPH–transfected fibroblasts that were pretreated with C. difficile toxin B responding to successive additions of 10 nM PDGF and wortmannin (wort). Inactivation of Rho family GTPases dramatically alters cell morphology but not PDGF-stimulated PI 3-kinase activation. Bar, 30 μm. (B) TIRF images of a fibroblast cotransfected with YFP-AktPH and the membrane marker Lyn-CFP treated as in A. Ratio images are YFP/CFP. The average normalized TIRF intensity is plotted as a function of time for the YFP-AktPH (closed circles) and Lyn-CFP (open circles) channels; the dotted lines indicate the additions of uniform PDGF and wortmannin. (C) PDGF gradient sensing after inactivation of Rho family GTPases. Toxin-treated cells typically showed AktPH translocation in TIRF but not a definite gradient-sensing response, which was expected given the relatively small cell dimensions. The cell shown is one of those in which a noticeable gradient response was seen. The arrow indicates the PDGF gradient orientation from high to low. (B and C) Bars, 15 μm.
In fibroblasts, C. difficile toxin B treatment yielded the characteristic depolarized, rounded cell morphology and significantly smaller contact areas (Fig. 6 A) but did not compromise cell viability as judged by trypan blue exclusion (not depicted). In response to PDGF stimulation, these cells responded with the normal several-fold increase in TIRF excitation of fluorescent AktPH. To ensure that the fluorescence profile was not caused by differential adhesion across the contact area or other membrane artifacts in toxin-treated cells, experiments were performed using cells coexpressing YFP-AktPH and the membrane marker Lyn-CFP (Fig. 6 B). Although there were some regions with higher YFP-AktPH and Lyn-CFP TIRF intensities, ratio images confirmed specific PDGF-induced 3′ PI production with similar radial profile and kinetics as compared with cells not treated with the toxin.
When toxin-treated fibroblasts were exposed to PDGF gradients, CFP-AktPH translocation was readily observed, and asymmetric TIRF profiles consistent with proper gradient sensing were seen in some cells (Fig. 6 C). This outcome was not as robust as in our other gradient experiments, however, which was to be expected given the much smaller distance across the cells (∼15 μm). This yields both smaller relative PDGF gradients and significant tempering of the intracellular 3′ PI gradient through lateral diffusion of the lipid.
Discussion
Using a combination of quantitative modeling and analysis, we have demonstrated that 3′ PI–mediated PDGF gradient sensing in fibroblasts is sensitive to both the relative steepness and midpoint concentration of the gradient. Strong responses require relatively steep gradients (δ > 0.3) and intermediate midpoint PDGF concentrations spanning a relatively narrow range (0.1–2 nM). In the context of our models, these midpoint concentrations yield near maximal PI 3-kinase activation without saturating PDGF receptor binding. These characteristics and the lack of rapid adaptation in response to uniform PDGF stimulation suggest a different and simpler gradient-sensing mechanism from those in fast migrating amoeboid cells such as D. discoideum and neutrophils. Accordingly, our model contains no feedback amplification or inhibition, with receptor signaling in different locations coupled only through exchange of PI 3-kinase molecules from a common cytosolic pool, yet the model is quantitatively consistent with experimental observations.
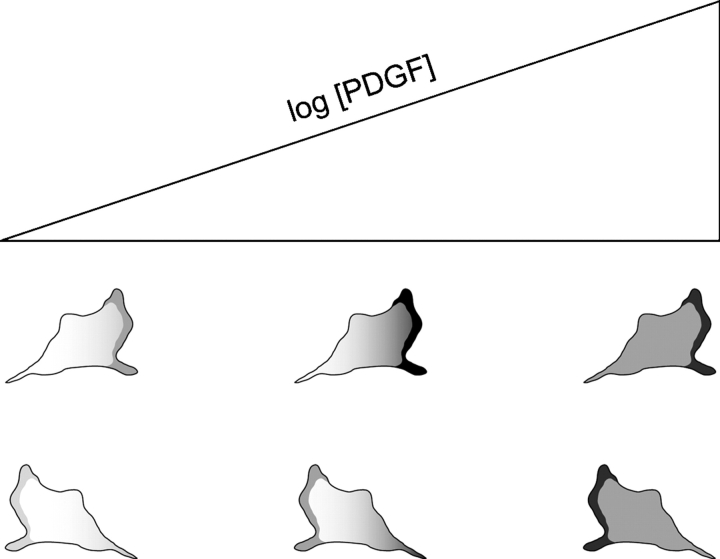
Another wrinkle in the PDGF-sensing mechanism is the influence of 3′ PI hot spots, which we recently characterized in the context of uniform PDGF stimulation (Schneider et al., 2005). Regions of locally enhanced 3′ PI levels have also been observed in chemoattractant-stimulated D. discoideum (Postma et al., 2004) and primary dendritic cells (Arrieumerlou and Meyer, 2005), although there are differences in the kinetics across cell types. In PDGF-stimulated fibroblasts, hot spots exhibit characteristics that are consistent with locally enhanced PI 3-kinase activation and reduced 3′ PI turnover, and it is conceivable that feedback loops upstream of PI 3-kinase are spatially focused in these regions. Their localization in apparent membrane protrusion structures at the leading edges suggests involvement of the cytoskeleton and/or Rho family GTPases and an importance in cell motility. Thus, as illustrated in Fig. 4, the overall asymmetry in PI 3-kinase signaling depends on the morphological polarity of the cell relative to the gradient. A conceptual model emerges in which cells integrate both intrinsic and external spatial biases in order to migrate persistently toward PDGF gradients (Fig. 7).
Figure 7.
Integration of external and intrinsic biases in PDGF gradient sensing. Cells are depicted at three positions in a PDGF gradient corresponding to low, intermediate, and high midpoint concentrations. Optimal sensing of the external gradient is seen in a narrow range of intermediate concentrations that is sufficient for maximal PI 3-kinase activation at the plasma membrane. Higher concentrations that saturate receptor occupancy have a leveling effect on PI 3-kinase recruitment across the cell. Hot spots of PI 3-kinase signaling are located at the leading edge and other regions of membrane protrusion, imposing an intrinsic, localized bias that depends on the cell's direction of movement. Thus, when a cell is oriented toward the PDGF source (top), signaling in hot spots tends to synergize with the external gradient, whereas the two spatial biases are in conflict when the cell is oriented away from the source (bottom). This suggests a mechanism by which a fibroblast would migrate with even greater speed and/or persistence when its trajectory is properly aligned with the gradient.
The mechanism of PDGF gradient sensing is logical in light of the physiology of fibroblast invasion during wound healing, a process that evolves over several days. With PDGF and other factors produced specifically in the fibrin clot and dermal fibroblasts found in the adjacent tissue, a PDGF concentration profile will naturally arise within hours. One would expect the steepest PDGF gradient at the clot–dermis interface initially, and this gradient could be quite sharp if the relative PDGF diffusion and proteolysis rates in the tissue are favorable. The overall fibroblast response is slow, and the directness of their migration does not need to change with time. Furthermore, PDGF receptor signaling is pleiotropic, influencing fibroblast proliferation and survival in addition to chemotaxis. Desensitization of PI 3-kinase signaling would compromise these other functions, which generally depend on the absolute concentration of the stimulus.
This is not to say that PDGF receptor–mediated signaling through PI 3-kinase and other pathways is unregulated. Activated PDGF receptors are rapidly internalized, mediating receptor down-regulation and establishment of a true steady state after ∼1 h of constant stimulation. This mode of regulation may provide the answer to the next, most important question with regard to fibroblast invasion of wounds: if chemotaxis is sensitive to the gradient steepness and absolute concentration of PDGF, how can this sensitivity be maintained as the fibroblast front (granulation tissue) progresses deeper into the clot? In solid tissue, it is likely that endocytosis of active PDGF–PDGF receptor complexes contributes significantly to the clearance of PDGF from the extracellular milieu, which is an effect that would be fibroblast density dependent. The invading granulation tissue could thus shape and maintain a relatively constant and sharp PDGF gradient, spanning the optimal midpoint concentration at its leading front.
Given the complexity of cell polarity, cytoskeletal dynamics, and overall migration processes as well as the issues raised above concerning the integrated physiological system, it is reasonable to expect that mathematical modeling and other quantitative approaches will be increasingly valuable in their analysis. Especially when designed in tandem with experiments, as applied here to PDGF gradient sensing, such approaches can reveal and aid in characterizing the key underlying mechanisms.
Materials and methods
Reagents, cDNA constructs, and cell culture
Enhanced GFP-AktPH and its cyan- and yellow-emitting variants CFP- and YFP-AktPH were used as described previously (Schneider and Haugh, 2004; Schneider et al., 2005). Membrane-targeted Lyn-CFP contained the palmitoylation sequence from Lyn (Teruel et al., 1999) cloned into pECFP-N1. NIH 3T3 fibroblasts (American Type Culture Collection) were subcultured, transfected, and serum starved as described previously (Schneider and Haugh, 2004). In some cases, cells were treated with 10 ng/ml C. difficile toxin (List Biological Laboratories) during serum starvation. The imaging buffer was composed of 20 mM Hepes, pH 7.4, 125 mM NaCl, 5 mM KCl, 1.5 mM MgCl2, 1.5 mM CaCl2, 10 mM glucose, and 2 mg/ml fatty acid–free BSA. Other reagents included PDGF-BB (PeproTech), OG 514–dextran (40 kD; Invitrogen), and wortmannin (Calbiochem).
TIRF microscopy
TIRF microscopy is a mode of live cell imaging whereby fluorophores within ∼100 nm of the membrane contact area are selectively excited (Axelrod, 2001; Steyer and Almers, 2001; Toomre and Manstein, 2001). Our prism-based TIRF microscope was described previously (Schneider and Haugh, 2004). In brief, this system was built around a microscope (Axioskop 2 FS; Carl Zeiss MicroImaging, Inc.) with 20× NA 0.5 or 40× NA 0.8 water immersion objectives (Achroplan; Carl Zeiss MicroImaging, Inc.) and a 0.63× camera mount. TIRF excitation was from two laser heads (Melles Griot): a tunable wavelength Ar ion laser head emitting lines of 488 (GFP at 60 mW) or 514 nm (YFP/OG 514 at 60 mW) and a HeCd laser head emitting a 442-nm line (CFP at 120 mW). Band-pass emission filters (Chroma Technology Corp.) were 480/30 nm (CFP), 515/30 nm (GFP), and 535/30 nm (YFP and OG 514). Digital images were acquired using a cooled CCD camera (ORCA ER; Hamamatsu) and Metamorph software (Universal Imaging Corp.), with 2 × 2 binning and a fixed exposure time × gain setting of ∼400 ms for GFP, YFP, and OG 514–dextran and ∼2,400 ms for CFP.
PDGF gradients were produced and imaged as follows: a micropipette, pulled to a diameter of ∼50 μm and backfilled with a solution of 0–30 nM PDGF and 5 μM OG 514–dextran in imaging buffer, was controlled using a syringe pump (World Precision Instruments) and micromanipulator (Applied Scientific Instrumentation). Once a suitable field of cells had been chosen, the pump was set to a flow rate of 30–80 nl/min, and sequential TIRF images of CFP-AktPH and the OG 514–dextran gradient were acquired every 20 s. Except where noted otherwise, all experiments were performed at room temperature (26–29°C). Controls with no PDGF in the tip verified that cells were not stimulated by either the small flow or volume marker.
Gradient association/dissociation experiments and analysis of fluorescence profiles
In the gradient association/dissociation protocol, cells are stimulated with a PDGF gradient for 20 min, followed by a uniformly saturating PDGF dose (10 nM) for 10 min, after which a high dose of wortmannin (5 μM) is added to rapidly block PI 3-kinase activity. Extensive controls have been described previously (Schneider and Haugh, 2004; Schneider et al., 2005). The intracellular TIRF above background, F, was normalized by its value at the end of the fluorescence decay, F cyt, to yield the normalized fluorescence, f, as a function of position and time (Schneider and Haugh, 2004):
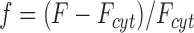 |
(4) |
The fractional gradient response, Γ, relates the fluorescence observed after gradient stimulation to the initial prestimulus value and the peak value observed after uniform stimulation (all averaged over 1-min intervals):
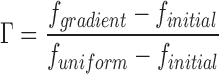 |
(5) |
Thus, a Γ value of zero indicates that gradient stimulation elicited no change from the initial fluorescence, whereas a value of one indicates that the fluorescence did not change after the addition of 10 nM PDGF. The average response, 〈Γ〉, is defined using whole cell–averaged f values, whereas the ability to sense the gradient is quantified as the difference in Γ values between front and back regions (∼25 pixels) relative to the gradient (ΔΓ = Γf − Γb).
The PDGF (ligand) concentration, [L], as a function of position was estimated by assuming that the highest OG 514–dextran TIRF intensity above background, at the point nearest the pipette, corresponds to the concentration of PDGF loaded in the pipette; accordingly, this fluorescence value does not change when the flow rate is increased. At steady state, the relative gradient is insensitive to any (small) difference in diffusion coefficient between PDGF and OG 514–dextran, and so the proportionality of the two concentrations was assumed at all locations. TIRF excitation of the volume marker is partially occluded by cells; hence, PDGF concentrations at the front and back regions of the cell, [L]f and [L]b, were estimated as follows: a line scan was drawn through the two regions and extending outside of the cell contact area boundaries. The fluorescence values across this line scan were averaged over the same time interval used to calculate f gradient, and PDGF concentrations were estimated by fitting the portions of the line scan outside the contact area to a polynomial (Fig. 2 B). The relative PDGF gradient, δ, is defined as
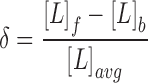 |
(6) |
Cells were chosen for analysis based on the following criteria. At all times, the whole cell value of F must be at least 250 fluorescence units above background, and the average OG 514–dextran fluorescence around the cell during gradient stimulation must be at least 100 fluorescence units above background. Finally, the cell must show a significant whole cell response to the uniform stimulation (f uniform − f initial > 0.3).
Mathematical model formulation
Here, we outline the basic modeling assumptions and methods, which build upon previous studies (Haugh et al., 2000; Park et al., 2003; Haugh and Schneider, 2004; Schneider and Haugh, 2004; Schneider et al., 2005); a more complete description of the model equations and their derivation is provided in the supplemental Modeling details.
We used two different models to describe the activation of PDGF receptors. An experimentally validated kinetic model of PDGF receptor binding, dimerization, and endocytosis as a function of time was described previously (Park et al., 2003), to which we have added receptor synthesis and basal turnover. The output of the model is the dimer fraction, d, calculated as a function of time using standard numerical integration. After ∼5–10 min of PDGF stimulation, PI 3-kinase activation reaches a plateau, for which a simplified, quasi–steady-state model is adequate, with
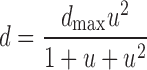 |
(7) |
The dimensionless PDGF concentration u is related to the actual PDGF concentration through the scaling constant L*, which is the concentration of PDGF that yields one-third maximum receptor phosphorylation. Together, these models accurately and quantitatively describe the kinetics and cooperative dose–response behavior of PDGF receptor phosphorylation in our cells (Park et al., 2003).
Receptor-mediated recruitment of PI 3-kinase activity to the plasma membrane depends on both the local and average density of activated receptors because receptors draw upon a common cytosolic PI 3-kinase pool. Our model is simplified by assuming fast diffusion of PI 3-kinase in the cytosol and pseudo-equilibrium binding with activated receptors. The dimensionless PI 3-kinase (enzyme) recruitment as a function of position, e(ξ), is thus given by
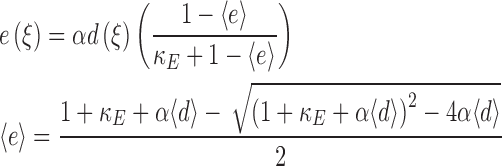 |
(8) |
The relationship between e and d is defined by the relative receptor/PI 3-kinase expression ratio α and the dimensionless receptor/PI 3-kinase dissociation constant κE; variables in elbow brackets signify spatial averages.
Membrane 3′ PI is produced locally by the receptor-bound enzyme, and there is also a contribution from cytosolic PI 3-kinase, which defines the basal 3′ PI level. 3′ PI lipids are degraded by a constitutive first-order mechanism as described previously (Schneider and Haugh, 2004).
Spatial modeling, in which the contact area geometry and lateral diffusion of 3′ PIs are explicitly considered, was implemented using FEMLAB finite element modeling software (Comsol). The pseudo–steady-state receptor activation model (equation 7) was used in these calculations. The geometry of the cell was constructed as described previously (Schneider et al., 2005), with PI 3-kinase activation in the nonadherent membrane only (Haugh et al., 2000; Schneider and Haugh, 2004). Normalized fluorescence is calculated by assuming pseudo-equilibrium binding of the GFP-AktPH probe (Haugh and Schneider, 2004).
Online supplemental material
The Modeling details supplement provides a more complete description of the model equations and their derivation. Fig. S1 shows representative responses to the gradient association/dissociation protocol at 37°C. Fig. S2 presents a spatial modeling analysis of another cell as performed in Fig. 4. Video 1 shows side-by-side time courses of the moving PDGF gradient and PI 3-kinase signaling response for the experiment depicted in Fig. 5 A (7.5 frames/s and 150× speed up). Online supplemental material is available at http://www.jcb.org/cgi/content/full/jcb.200509028/DC1.
Acknowledgments
We thank Professor Nina S. Allen and the Cellular and Molecular Imaging Facility at North Carolina State University for technical guidance.
This work was supported by grants from the Office of Naval Research (N00014-03-1-0594), the Whitaker Foundation (RG-01-0150), and the Cell Migration Consortium Modeling Initiative. Microscopy equipment was purchased using funds from a New Faculty Award to J.M. Haugh from the Henry and Camille Dreyfus Foundation.
Abbreviations used in this paper: AktPH, pleckstrin homology domain of Akt; GPCR, G protein–coupled receptor; OG, Oregon green; PI, phosphoinositide; TIRF, total internal reflection fluorescence.
References
- Arrieumerlou, C., and M. Meyer. 2005. A local coupling model and compass parameter for eukaryotic chemotaxis. Dev. Cell. 8:215–227. [DOI] [PubMed] [Google Scholar]
- Axelrod, D. 2001. Total internal reflection fluorescence microscopy in cell biology. Traffic. 2:764–774. [DOI] [PubMed] [Google Scholar]
- Bhalla, U.S., P.T. Ram, and R. Iyengar. 2002. MAP kinase phosphatase as a locus of flexibility in a mitogen-activated protein kinase signaling network. Science. 297:1018–1023. [DOI] [PubMed] [Google Scholar]
- Bokoch, G.M., C.J. Vlahos, Y. Wang, U.G. Knaus, and A.E. Traynor-Kaplan. 1996. Rac GTPase interacts specifically with phosphatidylinositol 3-kinase. Biochem. J. 315:775–779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deuel, T.F., R.S. Kawahara, T.A. Mustoe, and G.F. Pierce. 1991. Growth factors and wound healing: platelet-derived growth factor as a model cytokine. Annu. Rev. Med. 42:567–584. [DOI] [PubMed] [Google Scholar]
- Devreotes, P., and C. Janetopoulos. 2003. Eukaryotic chemotaxis: distinctions between directional sensing and polarization. J. Biol. Chem. 278:20445–20448. [DOI] [PubMed] [Google Scholar]
- Devreotes, P.N., and S.H. Zigmond. 1988. Chemotaxis in eukaryotic cells: a focus on leukocytes and Dictyostelium. Annu. Rev. Cell Biol. 4:649–686. [DOI] [PubMed] [Google Scholar]
- Haugh, J.M., and I.C. Schneider. 2004. Spatial analysis of 3′ phosphoinositide signaling in living fibroblasts: I. Uniform stimulation model and bounds on dimensionless groups. Biophys. J. 86:589–598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haugh, J.M., F. Codazzi, M. Teruel, and T. Meyer. 2000. Spatial sensing in fibroblasts mediated by 3′ phosphoinositides. J. Cell Biol. 151:1269–1279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hawkins, P.T., T.R. Jackson, and L.R. Stephens. 1992. Platelet-derived growth factor stimulates synthesis of PtdIns(3,4,5)P3 by activating a PtdIns(4,5)P2 3-OH kinase. Nature. 358:157–159. [DOI] [PubMed] [Google Scholar]
- Heldin, C.-H., and B. Westermark. 1999. Mechanism of action and in vivo role of platelet-derived growth factor. Physiol. Rev. 79:1283–1316. [DOI] [PubMed] [Google Scholar]
- Jackson, T.R., L.R. Stephens, and P.T. Hawkins. 1992. Receptor specificity of growth factor-stimulated synthesis of 3-phosphorylated inositol lipids in Swiss 3T3 cells. J. Biol. Chem. 267:16627–16636. [PubMed] [Google Scholar]
- Janetopoulos, C., L. Ma, P.N. Devreotes, and P.A. Iglesias. 2004. Chemoattractant-induced phosphatidylinositol 3,4,5-trisphosphate accumulation is spatially amplified and adapts, independent of the actin cytoskeleton. Proc. Natl. Acad. Sci. USA. 101:8951–8956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kazlauskas, A., and J.A. Cooper. 1990. Phosphorylation of the PDGF receptor β-subunit creates a tight binding site for phosphatidylinositol-3 kinase. EMBO J. 9:3279–3286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kundra, V., J.A. Escobedo, A. Kazlauskas, H.K. Kim, S.G. Rhee, L.T. Williams, and B.R. Zetter. 1994. Regulation of chemotaxis by the platelet-derived growth factor receptor-β. Nature. 367:474–476. [DOI] [PubMed] [Google Scholar]
- Lanni, F., A.S. Waggoner, and D.L. Taylor. 1985. Structural organization of interphase 3T3 fibroblasts studied by total internal reflection fluorescence microscopy. J. Cell Biol. 100:1091–1102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lauffenburger, D.A., and A.F. Horwitz. 1996. Cell migration: a physically integrated molecular process. Cell. 84:359–369. [DOI] [PubMed] [Google Scholar]
- Levchenko, A., and P.A. Iglesias. 2002. Models of eukaryotic gradient sensing: application to chemotaxis of amoebae and neutrophils. Biophys. J. 82:50–63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma, L., C. Janetopoulos, L. Yang, P.N. Devreotes, and P.A. Iglesias. 2004. Two complementary, local excitation, global inhibition mechanisms acting in parallel can explain the chemoattractant-induced regulation of PI(3,4,5)P3 response in Dictyostelium cells. Biophys. J. 87:3764–3774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meili, R., C. Ellsworth, S. Lee, T.B.K. Reddy, H. Ma, and R.A. Firtel. 1999. Chemoattractant-mediated transient activation and membrane localization of Akt/PKB is required for efficient chemotaxis to cAMP in Dictyostelium. EMBO J. 18:2092–2105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meinhardt, H. 1999. Orientation of chemotactic cells and growth cones: models and mechanisms. J. Cell Sci. 112:2867–2874. [DOI] [PubMed] [Google Scholar]
- Merlot, S., and R.A. Firtel. 2003. Leading the way: directional sensing through phosphatidylinositol 3-kinase and other signaling pathways. J. Cell Sci. 116:3471–3478. [DOI] [PubMed] [Google Scholar]
- Narang, A., K.K. Subramanian, and D.A. Lauffenburger. 2001. A mathematical model for chemoattractant gradient sensing based on receptor-regulated membrane phospholipid signaling dynamics. Ann. Biomed. Eng. 29:677–691. [DOI] [PubMed] [Google Scholar]
- Parent, C.A., and P.N. Devreotes. 1999. A cell's sense of direction. Science. 284:765–770. [DOI] [PubMed] [Google Scholar]
- Parent, C.A., B.J. Blacklock, W.M. Froehlich, D.B. Murphy, and P.N. Devreotes. 1998. G protein signaling events are activated at the leading edge of chemotactic cells. Cell. 95:81–91. [DOI] [PubMed] [Google Scholar]
- Park, C.S., I.C. Schneider, and J.M. Haugh. 2003. Kinetic analysis of platelet-derived growth factor receptor/phosphoinositide 3-kinase/Akt signaling in fibroblasts. J. Biol. Chem. 278:37064–37072. [DOI] [PubMed] [Google Scholar]
- Postma, M., and P.J.M. Van Haastert. 2001. A diffusion-translocation model for gradient sensing by chemotactic cells. Biophys. J. 81:1314–1323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Postma, M., J. Roelofs, J. Goedhart, H.M. Loovers, A.J. Visser, and P.J.M. Van Haastert. 2004. Sensitization of Dictyostelium chemotaxis by phosphoinositide-3-kinase-mediated self-organizing signalling patches. J. Cell Sci. 117:2925–2935. [DOI] [PubMed] [Google Scholar]
- Ridley, A.J. 2001. Rho GTPases and cell migration. J. Cell Sci. 114:2713–2722. [DOI] [PubMed] [Google Scholar]
- Schneider, I.C., and J.M. Haugh. 2004. Spatial analysis of 3′ phosphoinositide signaling in living fibroblasts: II. Parameter estimates for individual cells from experiments. Biophys. J. 86:599–608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneider, I.C., E.M. Parrish, and J.M. Haugh. 2005. Spatial analysis of 3′ phosphoinositide signaling in living fibroblasts, III: Influence of cell morphology and morphological polarity. Biophys. J. 89:1420–1430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Servant, G., O.D. Weiner, P. Herzmark, T. Balla, J.W. Sedat, and H.R. Bourne. 2000. Polarization of chemoattractant receptor signaling during neutrophil chemotaxis. Science. 287:1037–1040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singer, A.J., and R.A.F. Clark. 1999. Mechanisms of disease: cutaneous wound healing. N. Engl. J. Med. 341:738–746. [DOI] [PubMed] [Google Scholar]
- Skupsky, R., W. Losert, and R.J. Nossal. 2005. Distinguishing modes of eukaryotic gradient sensing. Biophys. J. 89:2806–2823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Srinivasan, S., F. Wang, S. Glavas, A. Ott, F. Hofmann, K. Aktories, D. Kalman, and H.R. Bourne. 2003. Rac and Cdc42 play distinct roles in regulating PI(3,4,5)P3 and polarity during neutrophil chemotaxis. J. Cell Biol. 160:375–385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stephens, L.R., K.T. Hughes, and R.F. Irvine. 1991. Pathway of phosphatidylinositol(3,4,5)-trisphosphate synthesis in activated neutrophils. Nature. 351:33–39. [DOI] [PubMed] [Google Scholar]
- Steyer, J.A., and W. Almers. 2001. A real-time view of life within 100 nm of the plasma membrane. Nat. Rev. Mol. Cell Biol. 2:268–275. [DOI] [PubMed] [Google Scholar]
- Subramanian, K.K., and A. Narang. 2004. A mechanistic model for eukaryotic gradient sensing: spontaneous and induced phosphoinositide polarization. J. Theor. Biol. 231:49–67. [DOI] [PubMed] [Google Scholar]
- Teruel, M.N., T.A. Blanpied, K. Shen, G.J. Augustine, and T. Meyer. 1999. A versatile microporation technique for the transfection of cultured CNS neurons. J. Neurosci. Methods. 93:37–48. [DOI] [PubMed] [Google Scholar]
- Tolias, K.F., L.C. Cantley, and C.L. Carpenter. 1995. Rho family GTPases bind to phosphoinositide kinases. J. Biol. Chem. 270:17656–17659. [DOI] [PubMed] [Google Scholar]
- Toomre, D., and D.J. Manstein. 2001. Lighting up the cell surface with evanescent wave microscopy. Trends Cell Biol. 11:298–303. [DOI] [PubMed] [Google Scholar]
- Vanhaesebroeck, B., S.J. Leevers, K. Ahmadi, J. Timms, R. Katso, P.C. Driscoll, R. Woscholski, P.J. Parker, and M.D. Waterfield. 2001. Synthesis and function of 3-phosphorylated inositol lipids. Annu. Rev. Biochem. 70:535–602. [DOI] [PubMed] [Google Scholar]
- Wang, F., P. Herzmark, O.D. Weiner, S. Srinivasan, G. Servant, and H.R. Bourne. 2002. Lipid products of PI(3)Ks maintain persistent cell polarity and directed motility in neutrophils. Nat. Cell Biol. 4:513–518. [DOI] [PubMed] [Google Scholar]
- Weiner, O.D. 2002. Regulation of cell polarity during eukaryotic chemotaxis: the chemotactic compass. Curr. Opin. Cell Biol. 14:196–202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiner, O.D., P.O. Neilsen, G.D. Prestwich, M.W. Kirschner, L.C. Cantley, and H.R. Bourne. 2002. A PtdInsP3- and Rho GTPase-mediated positive feedback loop regulates neutrophil polarity. Nat. Cell Biol. 4:509–512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wennström, S., P. Hawkins, F. Cooke, K. Hara, K. Yonezawa, M. Kasuga, T. Jackson, L. Claesson-Welsh, and L. Stephens. 1994. a. Activation of phosphoinositide 3-kinase is required for PDGF-stimulated membrane ruffling. Curr. Biol. 4:385–393. [DOI] [PubMed] [Google Scholar]
- Wennström, S., A. Siegbahn, K. Yokote, A. Arvidsson, C.-H. Heldin, S. Mori, and L. Claesson-Welsh. 1994. b. Membrane ruffling and chemotaxis transduced by the PDGF β-receptor require the binding site for phosphatidylinositol 3′ kinase. Oncogene. 9:651–660. [PubMed] [Google Scholar]
- Wymann, M., and A. Arcaro. 1994. Platelet-derived growth factor-induced phosphatidylinositol 3-kinase activation mediates actin rearrangements in fibroblasts. Biochem. J. 298:517–520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zigmond, S.H. 1977. Ability of polymorphonuclear leukocytes to orient in gradients of chemotactic factors. J. Cell Biol. 75:606–616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zigmond, S.H., and S.J. Sullivan. 1979. Sensory adaptation of leukocytes to chemotactic peptides. J. Cell Biol. 82:517–527. [DOI] [PMC free article] [PubMed] [Google Scholar]