Computational imaging in cell biology

Abstract

Microscopy of cells has changed dramatically since its early days in the mid-seventeenth century. Image analysis has concurrently evolved from measurements of hand drawings and still photographs to computational methods that (semi-) automatically quantify objects, distances, concentrations, and velocities of cells and subcellular structures. Today's imaging technologies generate a wealth of data that requires visualization and multi-dimensional and quantitative image analysis as prerequisites to turning qualitative data into quantitative values. Such quantitative data provide the basis for mathematical modeling of protein kinetics and biochemical signaling networks that, in turn, open the way toward a quantitative view of cell biology. Here, we will review technologies for analyzing and reconstructing dynamic structures and processes in the living cell. We will present live-cell studies that would have been impossible without computational imaging. These applications illustrate the potential of computational imaging to enhance our knowledge of the dynamics of cellular structures and processes.

Dynamic processes are at the very basis of cellular function. In an attempt to understand these processes, cellular structures have been studied in fixed and living specimens by various microscopic techniques including phase contrast, differential interference contrast, and confocal microscopy. Fluorescent dyes such as fluorescein and rhodamine, together with recombinant fluorescent protein technology (Chalfie et al., 1994) and voltage- (Loew, 1992) and pH-sensitive dyes (Adie et al., 2002) allow virtually any cellular structure to be tagged. In combination with techniques in live cells like FRAP (Axelrod et al., 1976) and fluorescence resonance energy transfer (Sekar and Periasamy, 2003), it is now possible to obtain spatio-temporal, biochemical, and biophysical information about the cell in a manner not imaginable before.

Evolution of quantitative live-cell microscopy

Live-cell image analysis started with the earliest microscopists. Although most of these measurements were based on manual inspection and intervention, with the advent of fluorescence microscopy, many studies also involved quantitative imaging of living cells either using video or CCD cameras (Inoue, 1981; Allen and Allen, 1983). In the early years of live-cell microscopy, methods for segmentation and tracking of cells (Berg and Brown, 1972; Berns and Berns, 1982) were rapidly developed and adapted from other areas. Nowadays, techniques for fully automated analysis and time–space visualization of time series from living cells involve either segmentation and tracking of individual structures, or continuous motion estimation (for an overview, see Fig. 1) . For tracking a large number of small particles that move individually and independently from each other, single particle tracking approaches are most appropriate (Qian et al., 1991).

Figure 1.

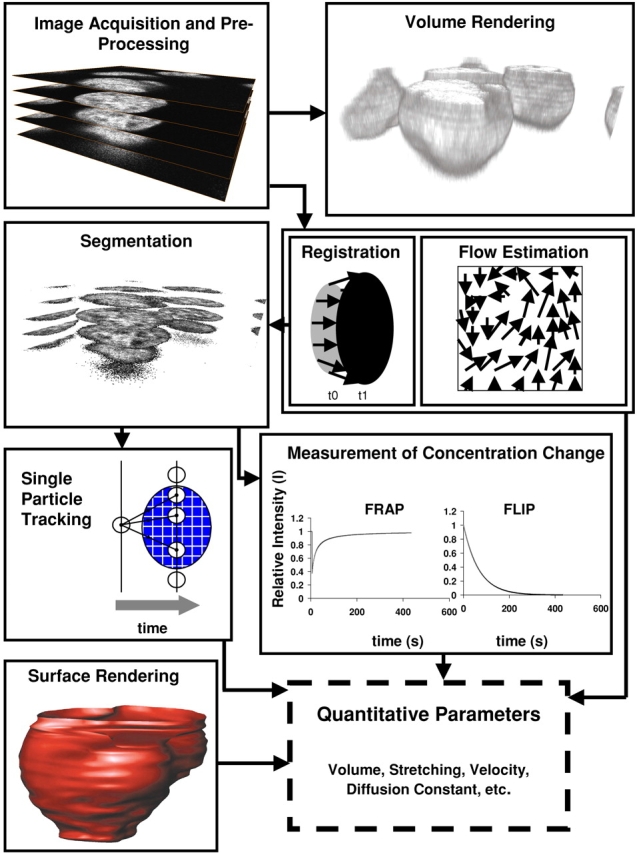
The typical workflow in computational imaging is presented. Once the images have been acquired by microscopy and preprocessed to improve the signal-to-noise ratio, they can be directly visualized by methods like volume rendering. For multiple objects in motion, single particle tracking, in which a particle is tracked over different time-steps, is the most direct method used. It provides access to parameters such as velocity, acceleration, and diffusion coefficients. Segmentation is the basis for both surface rendering and kinetic measurements. Surface rendering is obtained after segmentation of contours in each individual section and gives rise to volumetric measurements such as volume and surface area. Measurements of concentration changes for segmented areas in FRAP or fluorescence loss in photobleaching experiments give rise to estimates of kinetic parameters such as diffusion and binding coefficients. Image registration is used to measure elastic or rigid changes of form. It is also often used to correct for global movement before further quantitative analysis. The estimation of flow of gray values is an approach to quantify mobility in continuous space. All these processes lead to accurate estimates of quantitative parameters.

For the determination of more complex movement, two independent approaches were initially developed, but recently have been merged. Optical flow (Mitiche and Bouthemy, 1996) methods estimate the local motion directly from local gray value changes in image sequences. Image registration (Terzopoulos et al., 1991; Lavallee and Szeliski, 1995) aims at identifying and allocating certain objects in the real world as they appear in an internal computer model. The main application of image registration in cell biology is the automated correction of rotational and translational movements over time (rigid transformation). This allows the identification of local dynamics, in particular when the movement is a result of the superposition of two or more independent dynamics. Registration also helps to identify global movements when local changes are artifacts and should be neglected.

Single particle tracking

The basic principle of single particle tracking is to find for each object in a given time frame its corresponding object in the next frame. The correspondence is based on object features, nearest neighbor information, or other inter-object relationships. Object features can be dynamic criteria such as displacement and acceleration of an object as well as area/volume or mean gray value of the object. Optical flow has been defined as the motion flow (i.e., the motion vector field) that is derived from two consecutive images in a time series (Jähne, 2002). If optical flow is continuous, corresponding objects in subsequent images should be similar. However, due to high levels of noise, this assumption is usually distorted, and standard region-based matching techniques give unsatisfactory results (Anandan, 1989). A more reliable tracking approach involves fuzzy logic-based analysis of the tracking parameters (Tvarusko et al., 1999).

Image registration

Image registration enables a computer to “register” (apprehend and allocate) certain objects in the real world as they appear in an internal computer model. Initially, only rigid transformations were used to superimpose the images, whereas nowadays, research is focused on the integration of local deformations.

A parametric image registration algorithm specifies the parameters of a transformation in a way that physically corresponding points at two consecutive time steps are brought together as close as possible. Such algorithms have been broadly studied in medical imaging and cell biology (Maintz and Viergever, 1998; Bornfleth et al., 1999). Although one class of algorithms operates on previously extracted surface points (Lavallee and Szeliski, 1995), other algorithms register the images directly based on the gray-value changes. Nonrigid deformations, i.e., transformations others than rotation and translation, present an active body of research in computer vision. Nonrigid approaches differ with respect to the underlying motion model (Terzopoulos et al., 1991; Szeliski, 1996). Most commonly, a cost or error function is defined and an optimization method is chosen that iteratively adjusts the parameters until an optimum has been achieved. Other approaches extract specific features (e.g., correspondence between points) that serve as a basis for directly calculating the model parameters (Arun et al., 1987; Rohr, 1997).

Computer vision

Computer vision is a discipline that focuses on information extraction from the output of optical sensors, and on the representation of this information in an internal computer model (Faugeras, 1993). A computer vision framework for detecting and tracking diffraction images of linear structures in differential interference contrast microscopy was developed for measuring deflections of clamped microtubules with a freely moving second end (Danuser et al., 2000). Based on measurements of thermal fluctuations, it was possible to derive the elasticity of the microtubule. Further, prior knowledge based on geometric and dynamic models of the scene can lead to restoration of information beyond the resolution limit of an imaging system (Danuser, 2001). This super-resolution concept was illustrated by the stereo reconstruction of a micropipette moving in close proximity to a stationary target object.

Visualization

Complex dynamic processes in cells should ideally be studied in three spatial dimensions over time. Thereby, large and complex data sets typically consisting of 5,000–10,000 single images are generated. Such data are virtually impossible to interpret without computational tools for visual inspection in space and time.

Typically, 3-D images have been represented as stereoscopic pairs or as anaglyphs by pixel shift method (White, 1995). Displaying time series as movies is still a widely used method for visual interpretation. For fast-moving objects such as trafficking vesicles imaged with high time resolution, time-lapse movies are very informative. However, for much slower nuclear processes or for processes with mixed kinetics that need to be observed over a longer period of time, the total number of time points for imaging are limited due to the photo toxicity of the light exposure during in vivo observation (Konig et al., 1996). Therefore, an interpolation between consecutive time steps is required to reconstruct intermediate time steps. As a “side effect,” additional information about the continuous development of the observed processes between the imaged time steps (subpixel resolution in time) is achieved, and quantitative information can be derived (see next section).

Although early studies explored 4-D data sets by simply browsing through an image gallery and highlighting interactively selected structures (Thomas et al., 1996), better 4-D imaging data are achieved by computer graphics. Two commonly used rendering algorithms for displaying 3-D structures are volume rendering and surface rendering (Chen et al., 1995; Fig. 1). Volume rendering is a technique for visualizing complex 3-D data sets without explicit definition of surface geometry. Volume visualization is achieved in three steps: classification, shading, and projection. The classification step assigns a level of opacity, contrast, and color to each voxel in the 3-D volume (e.g., Wright et al., 1993). Then, shading techniques are used to simulate both the object surface characteristics and the position and orientation of surfaces with respect to light sources and the observer. The colored, semitransparent volume is then projected onto a plane perpendicular to the observer's direction. A ray is cast into the volume through each grid point on the projection plane. As the ray progresses through the volume, it computes the color and opacity at evenly spaced sample locations, and finally yields a single pixel color. Although volume rendering techniques provide a satisfactory display of biological structures, this method is limited to pure visualization and does not deliver quantitative information. In addition, the high anisotropy typical for live-cell imaging with low z-resolution limits the quality of this visualization technique.

These limitations are overcome by surface-rendering techniques, where the object surface is represented by polygons. The polygonal surface is displayed by projecting all the polygons onto a plane that is perpendicular to a selected viewing direction. The user can examine the displayed structure by changing the viewing direction interactively. The most commonly used method to triangulate the 3-D surface is the Marching Cube algorithm (Cline et al., 1988). The 3-D structure is defined by a threshold value throughout the data set, constructing an isosurface. The drawback of this method is that the surface of many biological structures cannot be defined using a single intensity value, resulting in loss of relevant information.

Quantitative image analysis

A great advantage of the combination of segmentation and surface reconstruction is the immediate access to quantitative information that corresponds to visual data (Eils et al., 1996; Gerlich et al., 2001; Gebhard et al., 2002). These approaches were designed to deal particularly with the high degree of anisotropy typical for 4-D live-cell recordings and to directly estimate quantitative parameters, e.g., the gray values in the segmented area of corresponding images can be measured to determine the amount and concentration of fluorescently labeled proteins in the segmented cellular compartments.

Measuring concentration changes by FRAP and fluorescence loss in photobleaching have become standard methods to evaluate diffusion, binding, and trafficking in live cells (for review see Phair and Misteli, 2001). These methods give direct access to kinetic parameters such as the diffusion coefficient of molecules (Axelrod et al., 1976; Edidin et al., 1976; Siggia et al., 2000) or exchange rates of molecules between different compartments (Hirschberg et al., 1998; Phair and Misteli, 2001). In combination with motion estimation techniques, parameters such as the velocity of the mass center for individual objects or for each point on the object surface can be readily accessed. Further, local parameters such as acceleration, tension, or bending (Bookstein, 1989) can be estimated. During motion estimation, global quantities are estimated such as the parameters of rotation and translation (Germain et al., 1999). The evolution of these eigenvalues can be used to characterize and analyze the observed motion.

Statistical analysis of velocity histograms can be applied to compute peak velocities corresponding to the most frequently occurring velocity values (Uttenweiler et al., 2000). Additionally, the dynamics of different objects can be compared by their velocity histograms. An alternative technique for statistical analysis is the confinement tree analysis of the intensity image (Mattes et al., 2001). For different threshold levels, objects (confiners) are segmented in the image. Calculated for different levels, the confiners define a confinement tree. Besides the estimation of global quantitative values (e.g., the global homogeneity of the motion), this approach allows the analysis and comparison of movements.

A challenge for future work is to better understand the biomechanical behavior of cellular structures, e.g., cellular membranes, by fitting a biophysical model to the data—an approach already successfully implemented in various fields of medical image analysis (Ferrant et al., 2001).

Applications

In vivo images of GFP-tagged proteins combined with computational imaging has revealed the dynamic organization of various nuclear subcompartments in the interphase nucleus. One example is the dynamics of nuclear speckles. Live-cell microscopy images of labeled pre-mRNA splicing factors were examined for evidence of regulated dynamics by computational segmentation and tracking (Eils et al., 2000). It was shown that the velocity and morphology of speckles, as well as budding events, were related to transcriptional activity.

Studies on nuclear architecture have revealed that chromatin (Marshall et al., 1997) undergoes slow diffusional motion, and that this movement is confined to relatively small regions in the nucleus. Importantly, the constraint on diffusional motion is regulated throughout the cell cycle (Heun et al., 2001; Vazquez et al., 2001). A long-standing question has been whether nuclear compartments can also undergo directed, energy-dependent movements, thereby providing a potential mechanism of regulated gene expression. Computational imaging revealed that several nuclear subcompartments do undergo directional transport dependent on metabolic energy (Calapez et al., 2002; Muratani et al., 2002; Platani et al., 2002).

The role of dynamic tension in actin polymerization in motile cells was investigated by analyzing polarized light images of the flow of the actin network and the motion of actin bundles and filopodia in crawling neurons (Oldenbourg et al., 2000). In a study on nuclear envelope breakdown, quantification and visualization of four-channel images with labeled chromatin, lamin-B receptor, nucleoporin, and tubulin (Beaudouin et al., 2002) revealed that piercing of the nuclear envelope by spindle microtubules was the mechanism responsible for forming the initial hole during nuclear envelope breakdown. To further investigate stresses on the nuclear envelope during breakdown, a crosswise grid pattern was bleached onto the nuclear envelope before breakdown. Stresses detected during hole formation were compared for the different grid vertices with respect to the positions of the hole, thus providing information about localized stresses during the tearing process (Mattes et al., 2001). Conversely, the effect of stress on the morphology of cells has been measured using an experimental approach of imposing known stresses on cells in solid-state culture. Changes in height, width, volume, and surface area of the cell are measured from 3-D confocal microscopy images, helping to understand the mechano-transduction response (Guilak, 1995).

The positioning of chromosomes during the cell cycle was investigated in live mammalian cells with a combined experimental and computational approach. In contrast to the random behavior predicted by a computer model of chromosome dynamics, a striking order of chromosomes was observed throughout mitosis (Gerlich et al., 2003). Further, strong similarities between daughter and mother cells were found for mitotic single chromosome positioning. These results support the existence of an active mechanism that transmits chromosomal positions from one cell generation to the next.

Summary

Computational imaging has been proven to be a powerful and integral part of cell biology. Computational imaging provides an important building block for the description of biological phenomena on a quantitative level, which is a prerequisite for mathematical models of dynamic structures and processes in the cell. In combination with models of biochemical processes and regulatory networks, computational imaging as part of the emerging field of systems biology (Kitano, 2002) will lead to the identification of novel principles of cellular regulation derived from the huge amount of experimental data that are currently generated.