Chromosomes are predominantly located randomly with respect to each other in interphase human cells

Abstract

To test quantitatively whether there are systematic chromosome–chromosome associations within human interphase nuclei, interchanges between all possible heterologous pairs of chromosomes were measured with 24-color whole-chromosome painting (multiplex FISH), after damage to interphase lymphocytes by sparsely ionizing radiation in vitro. An excess of interchanges for a specific chromosome pair would indicate spatial proximity between the chromosomes comprising that pair. The experimental design was such that quite small deviations from randomness (extra pairwise interchanges within a group of chromosomes) would be detectable. The only statistically significant chromosome cluster was a group of five chromosomes previously observed to be preferentially located near the center of the nucleus. However, quantitatively, the overall deviation from randomness within the whole genome was small. Thus, whereas some chromosome–chromosome associations are clearly present, at the whole-chromosomal level, the predominant overall pattern appears to be spatially random.

Introduction

Elucidation of the large-scale spatial organization of chromosomes in the interphase cell nucleus has been a theme for more than a century (Rabl, 1885). Potential applications include insights into developmental changes, gene regulation, gene interactions, replication timing, and DNA damage processing. The large-scale spatial geometry is determined in part by systematic biological factors and in part by randomizing factors, such as Brownian motion. Although it is reasonably clear that systematic biology dominates at the molecular (nanometer and smaller) level, it is less clear whether randomness or systematic biology dominates spatial relations among entire chromosomes.

At the chromosomal level, some systematic patterns have been clearly established, primarily through specific fluorescent labeling. First, there is convincing evidence that each chromosome predominantly occupies its own micrometer-scale territory during interphase (for review see Cremer and Cremer, 2001). Second, gene-dense chromatin domains and gene-poor domains exhibit different higher-order nuclear patterns (Croft et al., 1999; Boyle et al., 2001; Cremer and Cremer, 2001; Tanabe et al., 2002), although these patterns may well vary from cell type to cell type (Cremer et al., 2001). However, what is not clear is the overall importance of these large-scale correlations compared with the large-scale randomizing processes that also occur (Lesko et al., 1995; Cafourková et al., 2001; Edelmann et al., 2001; Misteli, 2001; Chubb et al., 2002). We address this question by looking for quantitative evidence of chromosome–chromosome spatial associations during cell-cycle interphase for all heterologous pairs of normal human chromosomes.

Ionizing radiation as a probe of large-scale chromosomal organization

The question of large-scale chromosomal organization can be approached by using ionizing radiation as a probe (Savage, 1993, 2000; Tanaka et al., 1996; Kreth et al., 1998; Lukáscaronová et al., 1999; Cafourková et al., 2001; Nakamura et al., 2001). Ionizing radiation efficiently produces chromosome breaks, and a pair of breaks in two different chromosomes can misrepair to produce an interchange, an exchange-type chromosome aberration involving the two chromosomes. The formation probability of an exchange is strongly dependent on the spatial distance between the damage sites in the genome (Brenner, 1987; Sachs et al., 1997; Savage, 2000; Hlatky et al., 2002); consequently, an enhanced yield of interchanges between two particular chromosomes indicates that these two chromosomes are, on average, closer to each other than expected had they been randomly located relative to one another. Thus, quantifying interchange probabilities for all heterologous chromosome pairs allows conclusions to be drawn about all possible spatial correlations between heterologous chromosomes in the genome.

Results

Experimental design

The measured chromosome–chromosome interchanges resulted from misrejoining of randomly located DNA double-strand breaks induced by sparsely ionizing radiation delivered in vitro during the G₀/G₁ phase of the cell cycle. Interchanges were detected using the multiplex FISH (mFISH)* technique (Greulich et al., 2000; Loucas and Cornforth, 2001). Each chromosome is “painted” a different color (Fig. 1), allowing measurement of the number of metaphase cells that have one or more junctions between particular colors, indicative of misrepair between the corresponding pair of chromosomes. In male human cells, 24 different colors are involved, so correlations between 1/2 × 24 × 23 = 276 heterologous chromosome pairs can be investigated; similarly, there are 1/2 × 23 × 22 = 253 heterologous pairs in female human cells, and 1/2 × 22 × 21 = 231 heterologous autosome pairs.

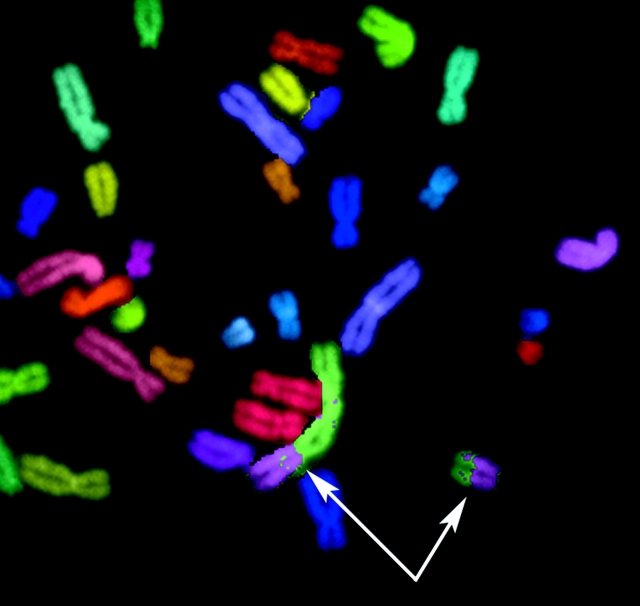
Figure 1.

Example of a chromosome–chromosome interchange, visualized with mFISH. Detail from a metaphase spread, containing a simple dicentric interchange between chromosomes 2 and 8, resulting in two color junctions. This metaphase contributes one to the row 2 column 8 entry in Table I.

The interchange results were measured in peripheral blood lymphocytes, irradiated in vitro, derived from two male donors at the University of Texas Medical Branch (Galveston, TX), and from five donors (two female, three male) at the Technical University of Munich (Munich, Germany). A total of nine data sets were taken, one for each of the five Munich donors, and two each for the two Texas donors (where two different radiation doses were used).

To assess chromosome–chromosome associations common to all individuals (including both genders), the nine data sets referred to above were combined, where appropriate. It follows that our main results are for the autosomes, with the sex chromosomes analyzed separately. As detailed in Materials and methods, statistical tests on the autosome interchange data showed that the nine data sets could legitimately be combined together, in as much as there was no statistically significant evidence that they followed different underlying distributions.

The experimental design had good statistical power, i.e., had a high probability of detecting quite small deviations from randomness. A measure of the overall deviation from randomness produced by a particular chromosome cluster is given by the effect size (Eq. 5; Cohen, 1988). The current experiment had at least an 80% probability of detecting small-to-medium (and larger) clustering effect sizes.

Participation of individual chromosomes in interchanges

As a precursor to analyzing the chromosome–chromosome interchange data for nonrandom effects, it is first necessary to estimate the individual sensitivity to radiation of each of the chromosomes. These measured one-chromosome yields are (a) needed (see Materials and methods) when analyzing the pairwise interchange data in Table I for randomness or correlations; (b) directly obtained from the interchange data (Table I) by summing over all interchange yields involving each given chromosome (no models are used); (c) an indicator of the sensitivity of each chromosome to radiation; (d) expected and observed to depend systematically on individual chromosome DNA content (Fig. 2).

Table I. Interchange yields for each heterologous autosome pair.

	Chromosome number
Chromosome number	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	SUM
1	20	17	24	16	13	16	11	14	16	10	6	2	7	11	9	13	5	8	9	8	15	250
2		24	16	20	18	7	13	11	9	17	17	10	5	18	7	10	3	5	6	7	11	254
3			11	16	19	13	12	15	9	11	12	13	10	4	10	8	6	9	7	8	6	240
4				11	10	13	9	15	13	6	11	12	13	8	12	11	5	4	8	6	3	221
5					10	14	10	10	12	16	14	14	8	13	5	10	4	4	6	5	2	220
6						6	12	16	13	6	16	9	11	9	7	2	6	7	4	3	5	202
7							8	8	7	13	13	4	10	4	8	9	7	4	9	4	1	178
8								7	6	11	4	12	9	8	5	7	7	2	6	1	3	163
9									9	16	4	13	15	10	10	9	11	3	3	3	3	205
10										7	10	7	6	7	7	7	7	3	7	4	2	168
11											13	2	7	10	8	10	5	7	7	3	6	191
12												6	8	4	5	6	2	7	6	2	4	170
13													11	5	4	4	8	3	4	3	6	152
14														10	5	4	9	1	3	8	6	166
15															11	8	2	4	5	5	2	158
16																10	8	10	11	6	6	164
17																	4	2	5	4	7	150
18																		1	7	3	0	110
19																			3	0	3	90
20																				3	2	121
21																					1	87
22																						94

Each entry shows the number of cells observed with at least one color junction (i.e., interchange) between two heterologous autosomes, j and k, denoted f(j,k). For example, the number of metaphases that contained one or more interchanges between chromosome 3 and chromosome 4 is f(3,4) = 11, shown in row 3, column 4. Data are pooled for all individuals and all doses; the total of all entries, T, is 1,877. The final column, headed "SUM", gives the one-chromosome yields, f(j), for each of the 22 autosomes, obtained by summing the numbers for pairwise interchange yields involving chromosome j.

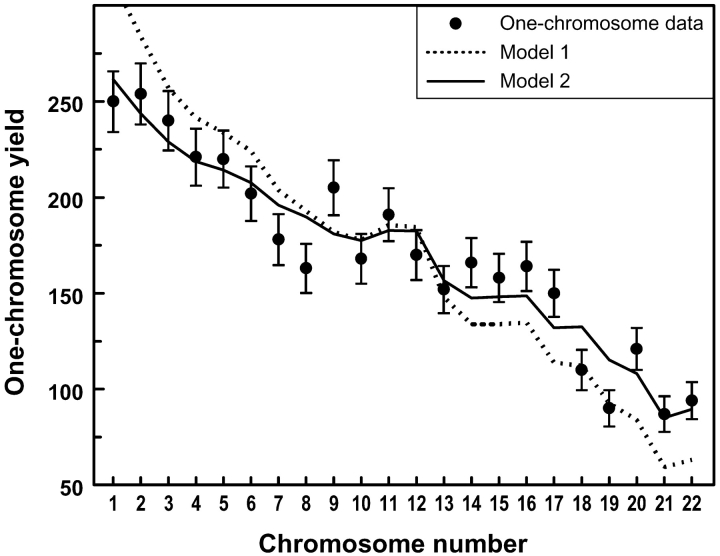
Figure 2.

Individual autosome yields. Data points are measured one-chromosome yields, f(j), indicators of the sensitivity of each chromosome to radiation. Error bars are ± 1 SEM. The dashed line gives the prediction of a model in which the individual chromosome sensitivities are linearly proportional to DNA content (Model 1), and the solid line is the prediction of a model (Model 2) based on proportionality to {DNA content}^2/3. Model predictions were made as described previously (Vázquez et al., 2002). Our analyses of pairwise interchange yields and chromosome–chromosome spatial correlations were based on Table II, which used the data points shown here but did not require any theoretical model for how one-chromosome yields depend on DNA content.

Fig. 2 shows the measured one-chromosome yields for the 22 autosomes. Although a mechanistic interpretation of these one-chromosome yields is not necessary for the chromosome clustering analysis which is the main subject of this work, it is of interest to compare the results with different theoretical models based on DNA content. The data are inconsistent (P < 0.001) with a model that assumes that individual chromosome sensitivity (here reflecting the probability that a given chromosome will participate in any interchange, given spatially random breaks in the genome) is proportional to the DNA content of that chromosome; as shown in Fig. 2, large chromosomes participate less frequently than predicted by such a model, and small chromosomes participate more frequently. A possible explanation of this pattern is that interchanges may mainly involve chromatin at or near chromosome territory surfaces (Cremer et al., 1996), rather than occurring uniformly throughout entire chromosomes. Based on such surface interactions, individual whole-chromosome sensitivity might be expected to be approximately proportional to {DNA content}^2/3 (Cigarrán et al., 1998), and the predictions of such a model (Fig. 2) were indeed consistent with the data.

It should be emphasized that, although these one-chromosome yields are used when interpreting the chromosome–chromosome interchange data of Table I in terms of pairwise spatial correlations (see below), individual variations in chromosome sensitivity do not necessarily imply deviations from pairwise randomness. For example, suppose one particular chromosome participated in interchanges much more frequently than expected, resulting in an unexpectedly large one-chromosome yield; if the other chromosomes were randomly located relative to it, the chromosome “partners” for these extra interchanges should still be randomly apportioned, based on their own one-chromosome yields.

Chromosome–chromosome spatial associations

Given the observed one-chromosome yields, we used an essentially model-independent approach, described in detail in Materials and methods, to quantify possible chromosome–chromosome associations. The data that are analyzed (Table I) give, for each of the 231 heterologous autosome pairs, the number of cells observed with at least one color junction, i.e., that contain one or more interchanges between a given heterologous autosome pair.

It is seen in Table I that, as expected, smaller chromosomes generally undergo fewer interchanges. Visual inspection of the data suggests that there are no very major deviations from randomness, in the sense of an entry being very much larger than the average of nearby entries; there are also only two zero entries. Thus, it is not immediately clear if statistical fluctuations can account for some of the entries being somewhat larger or smaller than one might predict by looking at neighboring entries. Therefore, formal statistical tests (Materials and methods) were applied to see if the data did contain significant evidence for chromosome clusters.

The values shown in Table II quantify the deviations, Δ (Eq. 3), from randomness for each of the 231 heterologous autosome pairs. A positive (negative) Δ value for a particular pair of chromosomes implies that breaks in that pair of chromosomes misrepair to form interchanges more (less) often than expected based on a random model; this implies a positive (negative) spatial correlation between the two chromosomes in that pair, because the closer together two chromosome breaks are located, the higher the probability that they will mutually misrepair to create an interchange (Brenner, 1987; Sachs et al., 1997; Savage, 2000).

Table II. Deviations from randomness for each heterologous autosome pair.

	Chromosome number
Chromosome number	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22
1	0.3	−0.1	2.0	0.0	−0.4	0.9	−0.2	−0.2	1.2	−1.0	−1.8	−2.7	−1.4	−0.1	−0.8	0.7	−1.0	0.7	0.2	0.8	3.3
2		1.5	−0.1	1.0	0.8	−1.6	0.4	−1.0	−0.9	0.8	1.3	−0.3	−2.0	2.0	−1.4	−0.2	−1.7	−0.5	−0.9	0.3	1.7
3			−1.1	0.2	1.4	0.2	0.3	0.2	−0.7	−0.6	0.1	0.8	−0.4	−2.1	−0.3	−0.7	−0.5	1.2	−0.4	0.9	−0.1
4				−0.8	−0.8	−0.6	−0.4	0.6	0.8	−1.7	0.1	0.8	0.8	−0.6	0.6	0.6	−0.7	−0.6	0.2	0.3	−1.1
5					−0.7	0.9	0.0	−0.8	0.5	1.2	1.1	1.5	−0.7	1.0	−1.6	0.2	−1.0	−0.6	−0.5	−0.1	−1.6
6						−1.3	0.9	1.2	1.1	−1.5	2.1	0.1	0.5	0.0	−0.7	−2.2	0.0	0.9	−1.1	−0.8	−0.1
7							0.0	−0.7	−0.5	1.1	1.6	−1.3	0.6	−1.4	0.0	0.6	0.7	−0.2	1.3	−0.1	−1.7
8								−0.8	−0.6	0.8	−1.3	2.0	0.6	0.3	−0.9	0.1	1.0	−0.1	0.3	−1.4	−0.6
9									−0.2	1.5	−1.8	1.5	1.8	0.3	0.2	0.1	1.9	−0.9	−1.5	−0.9	−1.0
10										−0.7	0.7	0.0	−0.6	−0.1	−0.2	0.0	0.9	−0.5	0.6	0.0	−1.1
11											1.3	−2.1	−0.6	0.6	−0.2	0.7	−0.3	1.1	0.3	−0.7	0.5
12												−0.4	0.1	−1.3	−1.0	−0.4	−1.4	1.4	0.2	−1.0	−0.2
13													1.5	−0.6	−1.1	−0.9	1.6	−0.4	−0.5	−0.3	1.1
14														1.0	−0.9	−1.1	1.8	−1.5	−1.1	2.1	0.9
15															1.4	0.6	−1.3	0.1	−0.1	0.7	−1.0
16																1.2	1.4	3.0	2.4	1.1	0.9
17																	−0.2	−0.9	0.0	0.3	1.6
18																		−1.0	1.8	0.3	−1.7
19																			0.0	−1.4	0.5
20																				0.1	−0.6
21																					−0.8

For each heterologous autosome pair, the corresponding entry shows a model-free measure (Eq. 3) of the deviation of the observed interchange yield (Table I) from that expected if all the autosomes were randomly located relative to each other. A positive value indicates an excess of observed images, implying that two autosomes are, on average, closer to each other than expected. A negative value indicates a pair further apart from each other than expected. Entries in boldface indicate a statistically significant correlation or anticorrelation, if used to confirm an independently derived association (see Materials and methods). For example, the value 3.3 for interchanges between chromosome 1 and chromosome 22, suggests a possible spatial association.

By combining (Eq. 4) the measures of deviation from randomness of each autosome pair given in Table II, overall randomness was globally tested. The assumption of overall pairwise randomness among all autosomes was rejected (P = 0.02 compared with a rejection criterion of P < 0.05) indicating that, overall, the autosomes are not randomly located with respect to one another. In the next section, we investigate which clusters of chromosomes may be responsible for this non randomness, and assess how large a deviation from overall spatial randomness they produce.

Specific chromosome clusters and their significance

To identify which groups of autosomes were responsible for the deviations from spatial randomness, various spatial groupings of chromosomes that have been suggested in the literature were investigated. In parallel, standard data-mining techniques were used to make ab-initio searches for chromosome clusters in our data set.

Several groups have suggested that gene-rich chromosomes tend to cluster together in the nuclear interior (Boyle et al., 2001; Cremer and Cremer, 2001), and we analyzed our data to assess the various chromosome clusters suggested in the literature in this context. For the group of five chromosomes {Nos. 1, 16, 17, 19, 22} suggested by Boyle et al. (2001) to be preferentially located near the nuclear centroid, our null hypothesis was that the 10 pairs involving these chromosomes do not interact more often, compared with other pairs, than in a spatially random situation. This null hypothesis was rejected using the test described in Materials and methods (P < 0.001), confirming a statistically significant spatial association among these five chromosomes.

However, it is important to note that this five-chromosome cluster {Nos. 1, 16, 17, 19, 22} still produces only a small deviation from overall randomness amongst all the autosome pairs. A measure of the overall deviation from randomness which a particular cluster contributes is the effect-size index (Eq. 5; Cohen, 1988); for the {Nos. 1, 16, 17, 19, 22}-cluster, the effect-size index is small (w = 0.12, see Materials and methods), and when pairs formed from these five chromosomes were excluded from the analysis, randomness could no longer be rejected for the remaining pairs.

We also investigated other specific clusters of chromosomes suggested by various authors, who used a variety of different techniques. Examples are the five nucleolus chromosomes {Nos. 13, 14, 15, 21, 22} (for review see Krystosek, 1998); three centrally located chromosomes {Nos. 17, 19, 20} (Cremer et al., 2001); the pair {Nos. 8, 11} (Nagele et al., 1999); the pair {Nos. 14, 18} (Lukáscaronová et al., 1999); and the pairs {Nos. 13, 21} and {Nos. 14, 22} (Alcobia et al., 2000). Our data were not inconsistent with the existence of these clusters, but in none of these cases were the results statistically significant; in each of these cases the effect-size index was small, suggesting that, even if the clusters were real, they would make only small contributions to nonrandomness over the whole genome.

As well as assessing chromosome clusters that have previously been suggested, we used data-mining techniques to search, ab initio, for possible clusters reflected in our data set. Data mining was carried out with standard hierarchical cluster analysis methodologies, for example through average-linkage dendrograms (Jain and Dubes, 1988); this analysis suggested four possible clusters of chromosomes, {Nos. 1, 7, 16, 17, 19, 20, 22}, {Nos. 4, 8, 9, 13, 14, 21}, {Nos. 2, 5, 11, 15}, and {Nos. 3, 6, 10, 12}. However, these clusters were not easily reproducible using other clustering algorithms, suggesting that, even if these clusters were real, their contribution to overall nonrandomness would be small. However, it is of interest to note that the group of five chromosomes {Nos. 1, 16, 17, 19, 22} suggested by Boyle et al. (2001)(and see above) to be preferentially located towards the nuclear center, is a subset of the first of these data-mined clusters {Nos. 1, 7, 16, 17, 19, 20, 22}.

As well as correlations, the data show some evidence of anticorrelations between pairs of chromosomes. Many of the most highly anticorrelated pairs involve a large and a small chromosome (Table II), recalling the suggestions by Cremer et al. (2001) and Sun et al. (2000) that, in some cells, there is a correlation between chromosome size and radial location. Our data are consistent with a spatial anti-correlation between chromosomes 18 and 19 (Table II), pointed out by both Croft et al. (1999) and Tanabe et al. (2002), though the anticorrelation was not statistically significant (P = 0.26).

Sex chromosomes

Because of gender specificity, possible clustering involving at least one of the sex chromosomes was assessed separately for males and for females. Both for males, and also for females, statistical tests (Materials and methods) allowed pooling of the corresponding chromosome–chromosome interchange yield data shown in Table III.

Table III. Sex chromosomes: interchange and one-chromosome yields.

	Chromosome number
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	X	SUM	M1	M2
F:X	8	1	6	3	6	6	3	2	2	3	6	4	2	2	0	1	5	0	0	2	1	0		63	54.4	52.6
M:X	4	2	2	4	6	8	4	3	3	2	6	4	0	2	0	3	0	2	3	1	0	1	0	61	74.9	73.1
M:Y	2	0	4	3	0	1	0	2	6	0	1	1	1	0	2	2	1	1	1	1	2	2	1	34	25.4	36.1

Corresponding to Table I for autosomes, each entry shows the number of cells observed with at least one color junction (i.e., interchange) between a sex chromosome and another chromosome. The notations F:X and M:X refer to interchanges involving the X chromosome in females and in males respectively; M:Y refers to interchanges involving the Y chromosome in males. The last three columns show the measured summed one-chromosome yields f(j) (SUM, compare Table I), and corresponding predictions (compare Fig. 2) if the individual chromosome sensitivities were linearly proportional to chromosome DNA content (column M1), or if they were proportional to {DNA content}^2/3 (column M2).

Table III also gives results on one-chromosome yields for the X and Y chromosomes, corresponding to the autosome results shown in Fig. 2. As with the autosomes, a model in which individual chromosome sensitivity is proportional to chromosomal DNA content provides a worse fit to the data than proportionality to {DNAcontent}^2/3, again suggesting that the interchanges occur between sites at or near the periphery of chromosome territories (Cremer et al., 1996).

Table IV, corresponding to Table II for the autosomes, quantifies deviations from randomness of interchange yields for pairs involving at least one sex chromosome; overall, the results in Table IV did not indicate statistically significant deviations from randomness (P = 0.23 for males, P = 0.21 for females).

Table IV. Sex chromosome pairs: deviations from randomness.

	Chromosome number
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	X
F:X	2.0	−1.4	1.0	−0.3	1.5	1.0	−0.3	−0.6	−0.5	0.0	2.1	0.8	−0.5	−0.8	−1.4	−1.0	1.1	−1.5	−1.0	0.1	−0.5	−1.1
M:X	−0.1	−1.1	−1.0	0.2	1.1	2.7	0.8	0.3	−0.3	−0.4	1.4	0.7	−1.5	−0.2	−1.6	0.2	−1.5	0.4	1.1	−0.7	−1.1	−0.4
M:Y	−0.2	−1.5	1.2	0.7	−1.4	−0.6	−1.2	0.5	2.9	−1.2	−0.6	−0.4	−0.2	−1.1	0.5	0.5	−0.2	0.2	0.1	−0.1	1.6	1.3	0.4

Corresponding to Table II for autosomes, each entry quantifies the deviation of the observed interchange yield (Table III) from that expected if all the chromosomes were randomly located relative to each other. As before, the notations F:X and M:X refer to interchanges involving the X chromosome in females and in males respectively; M:Y refers to interchanges involving the Y chromosome in males. Entries in boldface indicate a statistically significant correlation or anti-correlation, if used to confirm an independently derived association. Overall, pairs involving the sex chromosomes do not show statistically significant deviations from randomness.

Discussion

The large number of observed interchanges resulted in good statistical power to identify quite small deviations from randomness throughout the genome, interpreted as either spatial clustering effects, or unusually large separations between chromosome pairs. The overall pattern was one of dominant spatial randomness, modulated by a relatively small amount of clustering of chromosomes. The most significant chromosomal cluster was {Nos. 1, 16, 17, 19, 22}, a grouping previously suggested by Boyle et al. (2001). This five-chromosome cluster is responsible for most of the observed deviation from randomness amongst all 22 autosomes.

We found some evidence supporting a number of other spatial associations among specific chromosomes that had been suggested in the literature, but in these cases the degree of clustering was not large enough to reach statistical significance. In some cases, the explanation may be that spatial correlations between parts of chromosomes, such as the short arms of the nucleolar chromosomes (e.g., Krystosek, 1998), do not necessarily imply a strong spatial correlation among entire chromosomes; our whole-chromosome results do not preclude systematic associations between specific small sites (e.g., Neves et al., 1999). In other cases, clustering may be weak, transient or variable from cell type to cell type.

In summary, for the first time, chromosome exchanges between all possible heterologous pairs of normal human chromosomes were examined in vitro, to look for quantitative evidence of chromosome–chromosome spatial associations in the entire interphase genome. Data pooling analyses suggest that the conclusions are not specific to individual donors and apply to both sexes. Although clear evidence for chromosome clustering was found, spatial associations caused by systematic biological mechanisms appear to be modulations of a more dominant pattern of spatial randomness.

Materials and methods

mFISH cytogenetics

All data are for peripheral blood lymphocytes from healthy human donors, acutely irradiated in vitro with high-energy, sparsely ionizing, photons. Data were derived from cells from two male donors at the University of Texas Medical Branch at Galveston, and from five donors (two female, three male) at the Technical University of Munich. For the Texas data, other aspects of which were presented previously in a different context (Loucas and Cornforth, 2001), samples were exposed during the G₀/G₁ part of the cell cycle to radiation doses of 2 or 4 Gy, after which the mFISH technique was used to score aberrations at the first subsequent metaphase, as described earlier (Cornforth, 2001). There is good evidence that there is no significant loss of photon-induced aberrations from G₀/G₁ through G₂ (Terzoudi and Pantelias, 1997). The Munich data set consists of samples exposed to a 3-Gy radiation dose during G₀/G₁ as described in the paper by Greulich et al. (2000), with previous results from that paper now supplemented by additional mFISH data. Further technical details of the techniques used can be found in Cornforth (2001) and Greulich et al. (2000).

Data such as those shown in Table I and Table III give the number of metaphase cells containing at least one interchange for each particular chromosome pair, i.e. involving a junction between the two corresponding mFISH colors (compare Fig. 1). This specific endpoint, of metaphase number for each color junction, was the most robust available, being relatively insensitive to potential problems involving apparently incomplete aberrations. Exchanges not involving a color junction (intrachromosomal exchanges or interchanges between homologues) were not included in the data analysis, because their detection efficiency is different. Our data analysis did not require distinguishing complex interchanges (Savage, 1998) from simple ones.

Pooling data

We investigated whether the interchange data could be pooled within any of the following subgroups: (a) all female donors; (b) all male donors; and (c) data on the 22 autosomes in 1,587 cells from all donors, irrespective of origin, sex or radiation dose. In assessing the validity of pooling data from different individuals and somewhat different doses, our analysis requires only homogeneity of relative interchange yields for different chromosome pairs.

The Kruskal-Wallis test (Siegel and Castellan, 1988) was used to assess whether the data within the various subgroups could be pooled. For example, for subgroup 3 (all autosomes, all donors, all doses) the data were analyzed as nine singly ordered 231-element vectors, where nine rows refer to different donors and/or different doses, 231 (=1/2 × 22 × 21) specifies the numbers of different autosome pairs, and the vector ordering was determined by the product of the DNA contents of the two autosomes. The null hypothesis, that the nine data sets are samples from the same underlying ordered distribution, could not be rejected (P = 0.11, compared with a rejection criterion of P < 0.05). Likewise, for all chromosomes for all females, and for all chromosomes for all males, pooling was not rejected, with respective p-values of 0.6 and 0.18. We report mainly on the fully pooled autosome results, subgroup three, for which both the statistical power and the generality is largest.

Testing for spatial association between chromosomes

The null hypothesis of random chromosome–chromosome spatial associations was assessed by a method designed to circumvent theoretical assumptions about aberration formation mechanisms or the radiosensitivity of individual chromosomes. Specifically, we tested for randomness among all autosomes by testing each interchange yield, f(j,k) in Table I, for “independence”, defined by f(j,k) having, for j not equal to k, the product form

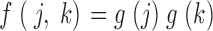(1)

Here the single-chromosome factors g(k) were estimated as follows: if independence held, summing Eq. 1 over j ≠ k would give

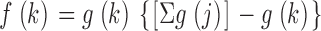(2)

where f(k) is the one-chromosome yield (Table I; Fig. 2), and Σ denotes a sum including j=k. Eq. 2 can be iteratively solved to estimate the one-chromosome factors g(k) in terms of our measured one-chromosome yields f(k).

Given these estimates for g(k), deviations from randomness for each possible chromosome pair, as defined by Eq. 1, were assessed by computing the quantity

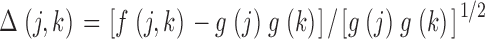(3)

for each heterologous autosome pair (Table II). The overall test statistic

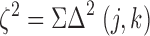(4)

can then be computed, where Σ here denotes a sum over all the heterologous autosome pairs (Table II). The probability (p-value) of finding a ξ² value at least as large as the observed value was determined by Monte Carlo simulations, assuming that each f(j,k) value is binomially distributed, with mean g(j)g(k). Pooled data for all chromosomes for females only and for males only were similarly analyzed, with results involving at least one the sex chromosomes shown in Tables III and IV.

This approach to analyzing clustering does not require any theoretical assumptions about how the one-chromosome yields f(k) depend on DNA content; instead, the experimental one-chromosome yields are utilized. Nor does it presuppose specific assumptions about the enzymatic and biophysical mechanisms of interchange formation. For example, suppose chromosome A and chromosome B are, on average, much closer in space than randomness would indicate. Then on a “two-hit” biophysical model (Savage, 1998), where interchanges are due to the pairwise misrejoining of two radiation-produced chromosome breaks, the chance for such a misrejoining between chromosomes A and B is enhanced, because on average the two relevant breaks are closer, and proximity enhances misrejoining probabilities, as discussed above. But, equally, using a “one-hit” biophysical model (Goodhead et al., 1993) where a single radiation-produced break can lead to recombination with a portion of the genome showing microhomology, there would again be extra misrejoinings between chromosomes A and B: for a radiation-produced break on chromosome A, the chance of utilizing the microhomology on chromosome B rather than elsewhere in the genome would be enhanced by the spatial proximity, and vice-versa for a break produced on chromosome B. So with either the two-hit or the one-hit biophysical model, the extra interchange yield would lead to a positive entry in Table II or IV, from which we would infer spatial proximity between chromosomes A and B; thus, our approach to assessing chromosome proximity through interchange aberration yields does not depend on the correctness of any particular postulated mechanism of interchange formation.

The tests described above allow us to test for randomness of chromosome–chromosome pairwise associations throughout the genome. In order to test for specific chromosome geometric associations, for example chromosome clusters previously suggested in the literature, we used the directional test statistic Σ Δ(j,k), where Σ denotes a sum over all pairs that can be formed from the chromosomes in the proposed association. One-sided p-values for this directional test statistic were determined by Monte Carlo simulations, treating yields for the proposed association pairs as binomial random variables and fixing all the remaining yields. The same technique was used to determine which entries in Tables II and IV to display in bold-face, with P = 0.05 as the criterion of significance.

How small a deviation from randomness is detectable? Effect-size index and statistical power

In searching for clustering effects against a null hypothesis of large-scale randomness, it is important to quantify just how small a degree of chromosome clustering the experiments could, in principle, detect. As a measure of the overall deviation from nonrandomness which a particular cluster contributes, we use the effect-size index (w), defined in Cohen (1988)

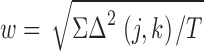(5)

where Δ(j,k) is given by Eq. 3, T is the number of data entries (here, 1,877; Table I), and Σ denotes a sum over all the heterologous autosome pairs. Cohen (1988) argues that w = 0.5 indicates a large deviation from randomness, w = 0.3 indicates a medium-sized deviation, and w = 0.1 indicates a small deviation, whereas w = 0 indicates no deviation from randomness. For illustration, Table V shows representative examples of specific (hypothetical) chromosome–chromosome clustering situations that would be categorized in different effect-size regimes. For example if chromosomes 1 and 2 underwent interchanges 3.1 times as often as they would under random conditions (enhancement factor = 3.1), and if all the other 230 interchange yields were completely random, the effect-size index would be 0.3, i.e., a medium effect size.

Table V. Illustration of effect-size categories of various (hypothetical) chromosome clusters.

	Small effect size	– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – –>			Medium effect size
	w ≤ 0.1		w = 0.175	w = 2	w = 3
Clustered chromosomes	Enhancement factors
1,2	≤1.9		2.4	2.6	3.1
1,22	≤2.5		3.4	3.7	4.6
21,22	≤3.7		5.4	6.0	7.8
13,14,15,21,22	≤1.5		1.8	1.9	2.2

The (hypothetical) autosome clusters are quantitatively defined here in terms of the enhancement factor by which the yield of interchanges between the autosomes in the cluster is increased, due to their mutual proximity. Corresponding effect sizes were calculated using Eq. 5 and Cohen (1988). Results are based on 1,877 data entries, as in Table I.

Table VI shows the corresponding estimated power of our particular experiments to detect clusters with different effect sizes. In the present context, power is the fraction of experiments that would detect a given (real) effect with statistical significance (P < 0.05). The results in Table VI indicate that the experiment had good power (≥80%) to detect small-to-medium (and larger) clustering effects.

Table VI. Experimental power to detect chromosome clusters of differing effect sizes.

	Small effect size	– – – – – – – –>		Medium effect size
Effect size index	w ≤ 0.1	w = 0.175	w = 0.2	w = 0.3
Power	≤22%	80%	92%	∼100%

The power is the probability that an experiment of the size of this one would detect a chromosomal cluster which has a given effect size. The results indicate that the experiment had good power (≤80%) to detect small-to-medium (and larger) clustering effects. Clusters with still larger effect sizes would also be detectable with essentially 100% probability. Results, for autosomes from all individuals combined, are based on a significance level α = 0.05, on 1,877 data entries in Table I, and on 208 degrees of freedom. Calculations used the algorithm of Milligan (1979).